Примеры решения задач с векторами
Векторы используются во многих науках, таких как: математика, физика, геометрия и многие другие прикладные науки. На практике они позволяют не выполнять ненужных операций и сокращают время на выполнение задач. Поэтому для будущих специалистов очень важно понять теорию векторов и научиться решать с ними проблемы.
Прежде чем изучать примеры решения проблем, советуем вам изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Векторные координаты
пример
Запись \(\ \overline{a}=(5 ;-2) \) означает, что вектор \(\ \overline{a} \) имеет следующие координаты: абсцисса равна 5, ордината равна -2.
пример
Векторы и дан \(\ \overline{a}=(-3 ; 5) \) и \(\ \overline{b}=(0 ;-1) \) . Найти векторные координаты \(\ \overline{c}=\overline{a}+\overline{b} \)
\(\ \overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4) \)
Пример
 {\circ}
\)
{\circ}
\)Разложение вектора по ортам координатных осей
пример
Зная разложение вектора \(\ \overline{a} \) на базисной системе векторов: \(\ \overline{a}=3 \overline{i}-\overline{k} \)запишите координаты этого вектора в пространстве.
Коэффициенты ортов являются координатами вектора, поэтому из того, что \(\ \overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k} \) мы получаем \(\ \overline{a}=(3 ; 0 ;-1) \)
Пример
Вектор \(\ \overline{a} \) определяется его координатами: \(\ \overline{a}=(2 ;-1 ; 5) \) запишите разложение этого вектора по осям осей.
Координаты вектора представляют собой коэффициенты по осям координатных осей при разложении вектора в основную систему векторов, поэтому требуется разложение:
\(\ \overline{a}=2 \overline{i}-\overline{j}+5 \overline{k} \)
Скалярное произведение векторов
Пример
Рассчитайте скалярное произведение векторов \(\
\overline{a}
\) и \(\
\overline{b}
\) , если их длины равны 2 и 3 соответственно, а угол между ними равен 60 °. {\circ}=6 \cdot \frac{1}{2}=3
\)
{\circ}=6 \cdot \frac{1}{2}=3
\)
Пример
Найти скалярное произведение векторов \(\ \overline{a}=(3 ;-1) \) и \(\ \overline{b}=(-2 ; 7) \)
Скалярное произведение
\(\ \overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13 \) Векторное произведение векторов пример
Найти векторное произведение векторов \(\ \overline{a}=(6 ; 7 ; 10) \) и \(\ \overline{b}=(8 ; 5 ; 9) \)
Составляем определитель и вычисляем его:
\(\ \overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|= \)
\(\ =\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)= \)
\(\ =13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26) \)
Смешанное произведение векторов
Пример

Рассчитать объем пирамиды, построенной на векторах \(\ \overline{a}=(2 ; 3 ; 5), \overline{b}=(1 ; 4 ; 4), c=(3 ; 5 ; 7) \)
Мы находим смешанное произведение указанных векторов, для этого составляем определитель, в строки которого записываем координаты векторов \(\ \overline{a}, \overline{b} \) и \(\ \overline{c} \):
\(\ (\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{ccc}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3- \)
\(\ -3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4 \)
\(\ V_{\mathrm{пир}}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}(\mathrm{куб} . \mathrm{ед.}) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Действия над векторами и свойства векторов Смешанное произведение векторов Векторное произведение векторов Скалярное произведение векторов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Векторы |
| Понятие вектора |
| Координаты вектора |
| Длина вектора |
| Равенство векторов |
| Умножение вектора на число |
| Сложение и вычитание векторов |
| Скалярное произведение векторов |
| Примеры решения задач |
Понятие вектора
Рассмотрим две произвольные точки. Если соединить эти точки стрелкой (рис.1),
Если соединить эти точки стрелкой (рис.1),
Рис.1
то мы получим вектор.
Точку, из которой стрелка выходит, называют началом вектора. Точку, в которую стрелка входит, называют концом вектора.
Чтобы отличить вектор от отрезка с концами в тех же точках, используют обозначение (рис.2) или (рис.3).
| Рис.2 | Рис.3 |
| Рис.2 |
| Рис.3 |
Иногда для вектора используют обозначения (рис.4) или (рис.5).
| Рис.4 | Рис.5 |
| Рис.4 |
Рис. 5 5 |
Если две точки (начало и конец вектора) совпадают, то говорят, что эти точки задают нулевой вектор.
Координаты вектора
Рассмотрим произвольный вектор и предположим, что в пространстве задана декартова прямоугольная система координат Oxyz (рис.6).
Рис.6
Если в системе координат Oxyz точки A и B имеют координаты
| A = (a1; a2; a3) и B = (b1; b2; b3) , | (1) |
то координатами вектора называют набор чисел
| (2) |
Этот определение часто формулируют так: «Для того, чтобы найти координаты вектора, нужно из координат конца вектора вычесть координаты начала вектора».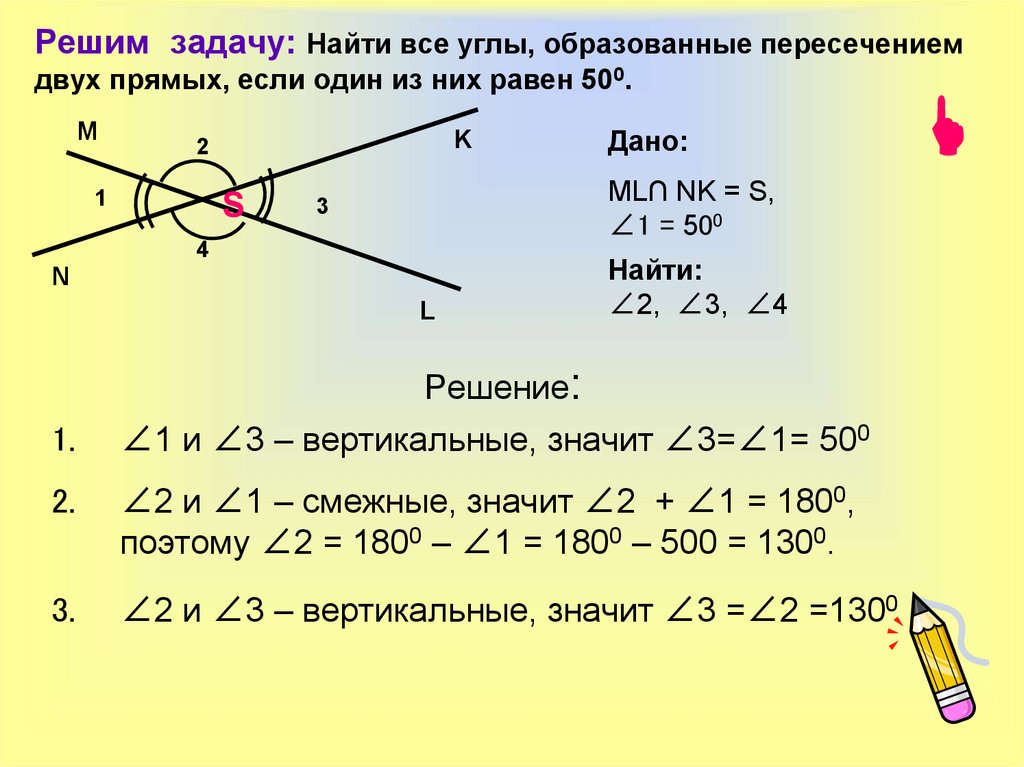
Замечание. В случае, когда рассматриваются векторы, лежащие на некоторой координатной плоскости, в формулах (1) и (2) не будет третьих координат. Если же рассматриваются векторы, лежащие на некоторой координатной прямой, то в формулах (1) и (2) останутся только первые координаты.
Длина вектора
Длиной (модулем) произвольного вектора называют длину отрезка AB
Длина вектора , координаты которого имеют вид
вычисляется по формуле
| (3) |
Этот факт часто формулируют так: «Длина вектора равна корню квадратному из суммы квадратов его координат».
Замечание. В случае, когда рассматриваются векторы, лежащие на координатной плоскости, формула (3) принимает вид
| (4) |
и совпадает с формулой, позволяющей найти расстояние между двумя точками координатной плоскости.
В случае, когда рассматриваются векторы, лежащие на координатной прямой, формулы (3) и (4) принимают вид
.
Равенство векторов
Векторы называют коллинеарными векторами, если они лежат на одной прямой или на параллельных прямых.
Два вектора
и
являются коллинеарными векторами тогда и только тогда, когда их координаты пропорциональны.
Другими словами, векторы являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства
a1 = tb1, a2 = tb2, a3 = tb3.
Два вектора называют сонаправленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 7.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в одну сторону (концы векторов будут лежать на одном луче).
Рис.7
Два вектора называют противоположно направленными, если, во-первых, они коллинеарные, а, во-вторых, направлены так, как показано на рисунке 8.
Другими словами, если совместить начала этих векторов, то они окажутся лежащими на одной прямой, при этом будут направлены в разные стороны (концы векторов будут лежать по разные стороны от их общего начала).
Рис.8
Определение. Два вектора равны, если, во-первых, они сонаправленные, а, во-вторых, имеют одинаковую длину.
Другими словами, если совместить начала этих векторов, то их концы совпадут.
Замечание. Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.
Два вектора равны тогда и только тогда, когда у них совпадают наборы координат.
Умножение вектора на число
В результате умножения любого вектора на любое действительное число k получается такой вектор , который удовлетворяет следующим условиям:
- При k > 0 вектор сонаправлен с вектором ;
- При k < 0 вектор противоположно направлен с вектором ;
- Длина вектора равна длине вектора , умноженной на число |k|.
Если вектор имеет координаты
то вектор имеет координаты
Другими словами, если вектор умножается на число, то и все его координаты умножаются на это число.
Сложение и вычитание векторов
Для того, чтобы найти сумму двух произвольных векторов и нужно совместить начало вектора с концом вектора . Тогда началом вектора будет начало вектора , а концом вектора будет конец вектора (рис.9).
Тогда началом вектора будет начало вектора , а концом вектора будет конец вектора (рис.9).
Рис.9
При этом, если
и
то
Этот факт часто формулируют так: «При сложении векторов их координаты складываются».
Для того, чтобы найти разность двух произвольных векторов и нужно воспользоваться формулой
Операция вычитания двух векторов наглядно изображена на рисунке 10.
Рис.10
При этом, если
и
то
Этот факт часто формулируют так: «Для того, чтобы найти координаты вектора , нужно из координат вектора вычесть координаты вектора ».
Скалярное произведение векторов
Определение. Скалярным произведением векторов и , которое обозначается называют число, равное произведению длин векторов и , умноженному на косинус угла между этими векторами (рис.11).
Скалярным произведением векторов и , которое обозначается называют число, равное произведению длин векторов и , умноженному на косинус угла между этими векторами (рис.11).
Рис.11
Таким образом,
| (5) |
Из формулы (5) вытекает соотношение
которое можно сформулировать так: «Модуль вектора равен корню квадратному из скалярного произведения вектора на себя».
Следствие 1. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Утверждение. Если в декартовой прямоугольной системе координат векторы имеют координаты
| и | (6) |
то их скалярное произведение выражается формулой:
| (7) |
Другими словами, в декартовой прямоугольной системе координат скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Замечание. Зная координаты векторов (6), из формул (3), (5) и (7) можно найти косинус угла между векторами и
Примеры решения задач
Пример 1. При каких значениях параметра p векторы и перпендикулярны?
Решение. Воспользовавшись формулой (7), получим
Ответ: 4.
Пример 2. При каких значениях параметров α и β векторы (α; – 2; 5) и (1; β; – 4) коллинеарны?
Решение. Векторы, в силу изложенного выше, являются коллинеарными тогда и только тогда, когда существует такое действительное число t, что выполняются равенства:
Ответ: .
Пример 3. Длины векторов и равны 2 и 1 , соответственно, а угол между ними равен 60° . Найти длину вектора .
Решение. Рассмотрим рисунок 12.
Рассмотрим рисунок 12.
Рис.12
Воспользовавшись теоремой косинусов, получим
Ответ: .
Пример 4. Длины векторов и равны 3 и 1, соответственно, а угол между ними равен 60°. Найти длину вектора .
Решение. Рассмотрим рисунок 13.
Рис.13
Воспользовавшись теоремой косинусов, получим
Ответ: .
Пример 5. Найти угол между векторами (3; 6; 2) и (4; 7; 4) .
Решение. Воспользовавшись формулой (8), получим
Ответ: .
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Задачи на вектора в пространстве с решением
Примеры решения задач с векторами
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Теоретический материал по теме – координаты вектора.
Запись означает, что вектор имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Задание. Заданы векторы и . Найти координаты вектора
Решение.
Задание. Вектор . Найти координаты вектора
Решение.
Задание. Найти координаты вектора , если
Решение.
Длина (модуль) вектора
Теоретический материал по теме – длина вектора.
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Задание. Найти длину вектора
Решение. Используя формулу, получаем:
Используя формулу, получаем:
Угол между векторами
Теоретический материал по теме – угол между векторами.
Задание. Известно, что скалярное произведение двух векторов , а их длины . Найти угол между векторами и .
Решение. Косинус искомого угла:
Задание. Найти угол между векторами и
Решение. Косинус искомого угла
Задание. Найти угол между векторами и
Решение. Косинус искомого угла:
Разложение вектора по ортам координатных осей
Теоретический материал по теме – разложение вектора по ортам.
Задание. Зная разложения вектора по базисной системе векторов: , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , получаем, что
Задание. Вектор задан своими координатами: . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора – это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
Скалярное произведение векторов
Теоретический материал по теме – скалярное произведение векторов.
Задание. Вычислить скалярное произведение векторов и , если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия , , а , то
Задание. Найти скалярное произведение векторов и
Решение. Скалярное произведение
Векторное произведение векторов
Теоретический материал по теме – векторное произведение векторов.
Задание. Найти векторное произведение векторов и
Решение. Составляем определитель и вычисляем его:
Смешанное произведение векторов
Теоретический материал по теме – смешанное произведение векторов.
Задание. Вычислить объем пирамиды, построенной на векторах , ,
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов , и :
Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов , и :
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Векторная алгебра для чайников
В этом разделе вы найдете бесплатные решения задач по векторной алгебре: вектора, углы, взаимное расположение на плоскости и пространстве, базис из векторов, действия с векторами и т.п.
Решения задач с векторами
Задача 1. На оси $Ох$ найти точку, равноудаленную от точек $А(2;-4;5)$ и $В(-3;2;7)$.
Задача 2. Написать разложение вектора $X$ по векторам $(a, b, c)$.
Задача 3. Найти косинус угла между векторами $AB$ и $AC$.
Задача 4. Вычислить площадь треугольника с вершинами $$A=(-4;4;4), B=(3;1;0), C=(-1;0;6).$$
Задача 5. Компланарны ли вектора $a, b, c$? $$a=(-3;2;1), b=(3;1;2), c=(3;-1;4)$$
Задача 6. Заданы два вектора в пространстве. Найти:
а) их сумму;
б) их разность; косинус угла между ними;
в) их векторное произведение.
$a=(0;1;1), b=(-2;0;1).$
Задача 7. Сила $F$ приложена к точке $А$. Вычислить:
а) работу силы $F$ в случае, когда точка её приложения, двигаясь прямолинейно, перемещается в точку $В$;
b) модуль момента силы $F$ относительно точки $В$.
Задача 8. Найти ранг и базис системы векторов, перейти к новому базису. Записать разложения векторов по найденным базисам.
Задача 11. Написать разложение вектора $ar$ по векторам $ar, ar, ar$.
Задача 13. Вычислить площадь параллелограмма, построенного на векторах $ar
$, $ar$.
Применение векторов к решению задач
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Сущность векторного метода для решения геометрических задач
Сущность векторного метода для решения геометрических задач
2. Общая схема для решения геометрических задач векторным методом
3. Примеры типов задач, которые решаются векторным методом
4. Примеры задач на применение векторного метода
Сущность векторного метода для решения геометрических задач
Векторный метод решения задач основан на решении задач с использованием аппарата векторной алгебры.
Применение векторной алгебры к решению геометрических задач основано на следующих основных утверждениях.
Утверждение 1 (Необходимое и достаточное условие коллинеарности векторов): Два ненулевых вектора $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны тогда и только тогда, когда существует действительное число $k\ne 0$, такое, что удовлетворяется следующее равенство
Утверждение 2: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ не коллинеарны, то любой вектор $\overrightarrow{c}$, компланарный с данными векторами можно представить в виде линейной комбинации и притом единственным образом:
Утверждение 3: Любой вектор $\overrightarrow{d}$ в трехмерном пространстве можно разложить по трем некомпланарным векторам $\overrightarrow{a}$, $\overrightarrow{b}$ и $\overrightarrow{c}$:
При решении задач векторным методом также применяются такие понятия, как сложение, вычитание векторов, умножение вектора на число, а также понятие скалярного произведения векторов.
Общая схема для решения геометрических задач векторным методом
При решении геометрических задач векторным методом рекомендуется пользоваться следующей схемой:
Провести анализ условия задачи:
а) Выяснить в какой системе координат (двумерной или трехмерной) рассматривается данная задача;
б) Записать, что нам дано, что нужно найти или доказать, а также построить чертеж по условию задачи.
Перевести условие задачи и требования к векторному виду.
Составить векторные соотношения, соответствующие тому, что дано в задаче и привести их к векторным соотношениям, соответствующим требованиям задачи.
Перевести полученный результат на геометрический язык.
Примеры типов задач, которые решаются векторным методом
Приведем теперь примеры классических задач, решаемых с помощью векторного метода (Не приводя их решений).
Задачи на доказательство параллельности.
Задачи на нахождение отношений, в котором точка делит отрезок.

Задачи на доказательство принадлежности трех точек одной прямой.
Задачи на доказательство принадлежности четырех точек одной плоскости.
Задачи на доказательство перпендикулярности.
Задачи на вычисление длины отрезка.
Задачи на нахождение величины угла.
Задачи на вычисление площадей и объемов геометрических фигур.
Примеры задач на применение векторного метода
Далее рассмотрим ряд задач, которые решаются с помощью векторного метода.
Пример 1
Доказать, что линия, соединяющая середины диагоналей произвольной трапеции параллельна основаниям этой трапеции и равна их полуразности.
Доказательство.
Пусть нам дана трапеция $ABCD.$ $MN$ — отрезок, соединяющий середины диагоналей данной трапеции (рис. 1).
Рисунок 1.
Докажем, что $MN=\frac{AD-BC}{2}$ и $MN||AD$
Рассмотрим вектор $\overrightarrow{MN}$. Используя правило многоугольника для сложения векторов, с одной стороны, получим
Используя правило многоугольника для сложения векторов, с одной стороны, получим
\[\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\]
С другой стороны
\[\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CB}+\overrightarrow{BN}\]
Сложим два последних равенства:
\[2\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}+\overrightarrow{MC}+\overrightarrow{CB}+\overrightarrow{BN}\]
Так как $MN$ — отрезок, соединяющий середины диагоналей, то
\[\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{0},\ \overrightarrow{DN}+\overrightarrow{BN}=\overrightarrow{0}\]
Тогда получим
\[2\overrightarrow{MN}=\overrightarrow{AD}+\overrightarrow{CB}=\overrightarrow{AD}-\overrightarrow{BC}\]
То есть
\[\overrightarrow{MN}=\frac{\overrightarrow{AD}-\overrightarrow{BC}}{2}\]
Так как $\overrightarrow{AD}\ и\ \overrightarrow{BC}$ сонаправлены, то $\overrightarrow{MN}||\overrightarrow{AD}$.
Из этого получаем, что $MN=\frac{AD-BC}{2}$ и $MN||AD$
ч. т. д.
Пример 2
На сторонах треугольника $ABC$ взяты точки $L,\ M,\ K$, так что $\left|BL\right|=3\left|AL\right|,\ \left|BM\right|=2\left|CM\right|,\ \left|AK\right|=2|CK|$. Найти, в каком отношении прямая $KL$ делит отрезок $AM$.
Решение.
Обозначим через точку $E$ — точку пересечения отрезка $AM$ с прямой $KL$(рис. 2).
Рисунок 2.
Найдем $\left|AE\right|:|EM|$
Введем, для удобства, следующие обозначения: $\overrightarrow{AB}=\overrightarrow{b},\ \overrightarrow{AC}=\overrightarrow{c}$, $\overrightarrow{AE}=x\overrightarrow{AM},$ $\overrightarrow{LE}=y\overrightarrow{LK}$
Воспользуемся далее правилом треугольника для сложения векторов. С одной стороны получим
\[\overrightarrow{AE}=x\overrightarrow{AM}=x\left(\overrightarrow{AB}+\overrightarrow{BM}\right)=x\left(\overrightarrow{b}+\frac{2}{3}\left(\overrightarrow{c}-\overrightarrow{b}\right)\right)=\frac{2}{3}x\overrightarrow{c}-\frac{1}{3}x\overrightarrow{b}\]
С другой стороны
\[\overrightarrow{AE}=\overrightarrow{AL}+\overrightarrow{LE}=\overrightarrow{AL}+y\overrightarrow{LK}=\frac{1}{4}\overrightarrow{b}+y\left(\frac{2}{3}\overrightarrow{c}-\frac{1}{4}\overrightarrow{b}\right)=\frac{2}{3}y\overrightarrow{c}+\frac{1}{4}\overrightarrow{b}-\frac{1}{4}y\overrightarrow{b}\]
Тогда
\[\frac{2}{3}x\overrightarrow{c}-\frac{1}{3}x\overrightarrow{b}=\frac{2}{3}y\overrightarrow{c}+\frac{1}{4}\overrightarrow{b}-\frac{1}{4}y\overrightarrow{b}\]
Получаем систему:
Рисунок 3.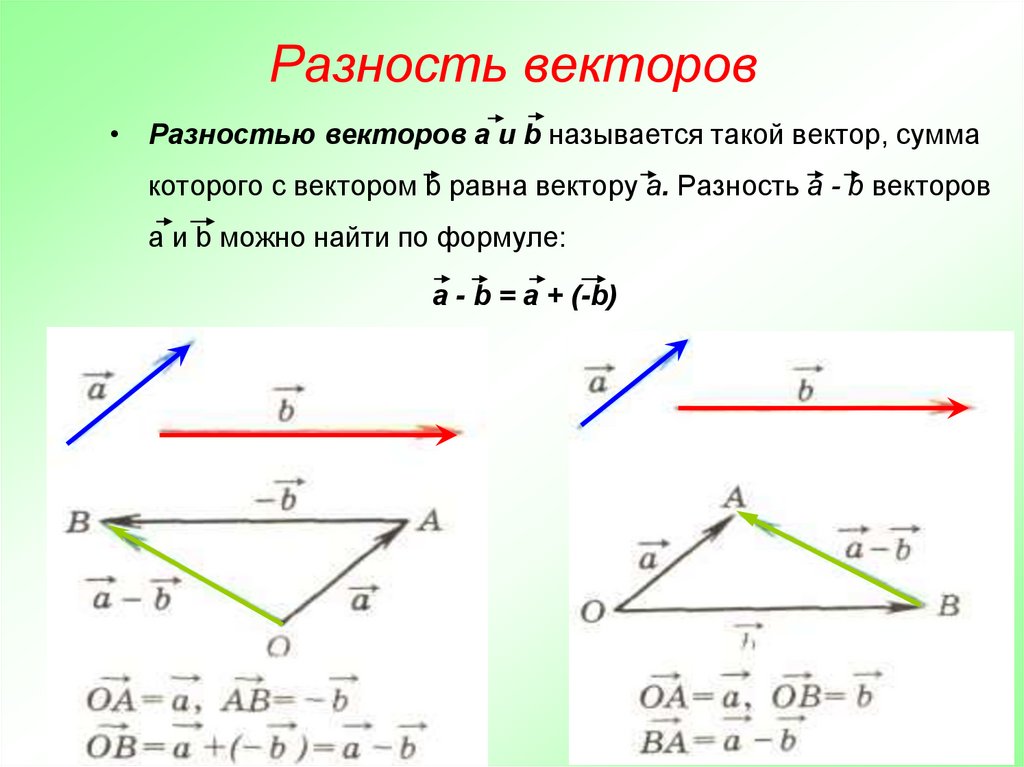
$\overrightarrow{AE}=\frac{3}{7}\overrightarrow{AM}$, следовательно
Ответ: $3:4.$
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 01.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Применение векторов к решению задач 8 класс онлайн-подготовка на Ростелеком Лицей
Выражение вектора через два неколлинеарных
Напомним, что мы уже изучили некоторые факты о векторах, и теперь умеем определять равные векторы, коллинеарные векторы, сонаправленные и противоположно направленные. Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Пример 1 – задача 769: отрезок ВВ1 – медиана треугольника . Выразите через векторы и векторы , , и .
Отметим, что векторы и неколлинеарны, то есть прямые АВ и АС не параллельны.
В дальнейшем мы узнаем, что любой вектор может быть выражен через два неколлинеарных вектора.
Выразим первый вектор (см. Рис. 1): , т. к. по условию ВВ1 – медиана треугольника, значит, векторы и имеют равные модули, кроме того, очевидно, что они коллинеарны и при этом сонаправлены, значит, данные вектора равны.
Рис. 1
Для выражения следующего вектора воспользуемся правилом параллелограмма для вычитания. Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Вектор является противоположным к заданному вектору , отсюда .
Вектор аналогично вектору можно представить в виде разности векторов . При выражении следует учесть тот факт, что точка В1 является серединой отрезка АС, значит, векторы и равны, значит, вектор можно представить как удвоенное произведение вектора .
Перед решением задачи мы сказали, что через заданные два неколлинеарных вектора можно выразить любой вектор. Выразим, например, медиану АА1 (см. Рис. 2).
Получили систему уравнений, выполним их сложение:
Векторы в сумме составляют нулевой вектор, так как они коллинеарны и противонаправлены, а модули их равны, таким образом получаем:
Рис. 2
Поделим обе части уравнения на два, получим:
Из данной задачи можно сделать вывод, что если заданы два неколлинеарных вектора, то любой третий вектор на плоскости можно однозначно выразить через эти два вектора. Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Свойство средней линии треугольника
Пример 2: доказать с помощью векторов свойство средней линии треугольника (см. Рис. 3).
Задан произвольный треугольник , точки M и N – середины сторон АВ и АС соответственно, MN – средняя линия треугольника. Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Доказательство данного свойства аналогично для треугольника и трапеции.
Рис. 3
Выразим вектор двумя способами:
Получили систему уравнений:
Выполним сложение уравнений системы:
Сумма векторов – это нулевой вектор, длины этих векторов равны по условию, кроме того, они очевидно коллинеарны и противонаправлены. Аналогично суммой векторов будет нулевой вектор. Получаем:
Поделим обе части уравнения на два:
Таким образом, мы получили, что средняя линия треугольника равна половине его основания. Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Таким образом, мы доказали свойство средней линии трапеции при помощи векторов.
Свойство точки пересечения медиан треугольника
Пример 3: задан произвольный треугольник (см. Рис. 4). В нем проведены медианы АА1, ВВ1, СС1. Точка пересечения медиан – М. Вектор соответствует силе , – силе , – силе . Доказать, что .
Напомним, что медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины.
Иногда точку пересечения медиан называют центром тяжести треугольника.
Выполним сложение векторов , воспользуемся для этого правилом параллелограмма (см. Рис. 5).
Рис. 4
Получаем:
С другой стороны, , так как BMCD – параллелограмм, диагонали параллелограмма точкой пересечения делятся пополам, А1 – точка пересечения диагоналей параллелограмма, значит, отрезки МА1 и А1D равны, отсюда, по свойству точки пересечения медиан, длины векторов и равны, но данные векторы противонаправлены, а значит, их сумма
Рис. 5
5
равна нулевому вектору. Мы помним, что вектор , а вектор , таким образом, , что и требовалось доказать.
Неравенство треугольника
Пример 4 – задача 773: докажите, что для любых векторов и справедливо следующее неравенство:
Решение: представим разность векторов в виде суммы: . Также обратим внимание на тот факт, что длины противонаправленных векторов и равны: . Таким образом, можно переписать исходное выражение:
Для удобства введем новую переменную: и перепишем выражение:
. А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке. Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.
 : Просвещение, 2006.
: Просвещение, 2006. - Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Cleverstudents.ru (Источник).
Домашнее задание
- Задание 1: заданы два неколлинеарных вектора и . Постройте векторы: ; ; .
- Задание 2: заданы два коллинеарных вектора и . Постройте векторы: ; ; .
- Задание 3: докажите, что для любого вектора справедливы равенства: ; .
8 класс. Геометрия. Векторы. Применение векторов к решению задач. — Векторы. Повторение теории. Решение задач с применением векторов.
Комментарии преподавателяПовторение теории. Задачи
Напомним, что существуют такие физические величины, для которых важна не только величина, но и направление. Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.
Такие величины называются векторными, или векторами, и обозначаются они направленным отрезком, то есть таким отрезком, у которого отмечены начало и конец. Введено было понятие коллинеарных векторов, то есть таких, которые лежат либо на одной прямой, либо на параллельных прямых.
Мы рассматриваем вектор, который можно отложить от любой точки, заданный вектор от произвольно выбранной точки можно отложить единственным образом.
Было введено понятие равных векторов – это такие сонаправленные векторы, длины которых равны. Сонаправленными называются коллинеарные векторы, направленные в одну сторону.
Были введены правила треугольника и параллелограмма – правила сложения векторов.
Заданы два вектора – векторы и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . – направленный отрезок, точка А – его начало, а точка В – конец. Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: – правило треугольника (см. Рис. 1).
Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: – правило треугольника (см. Рис. 1).
Рис. 1
Задано два вектора – векторы и . Найдем сумму этих двух векторов по правилу параллелограмма.
Откладываем из точки А вектор и вектор (см. Рис. 2). На отложенных векторах можно построить параллелограмм. Из точки В откладываем вектор , векторы и равны, стороны ВС и
Рис. 2
АВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма.
Для сложения нескольких векторов применяют правило многоугольника (см. Рис. 3). Нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее, когда все векторы отложены – соединить начальную точку с концом последнего вектора, в итоге получится сумма нескольких векторов.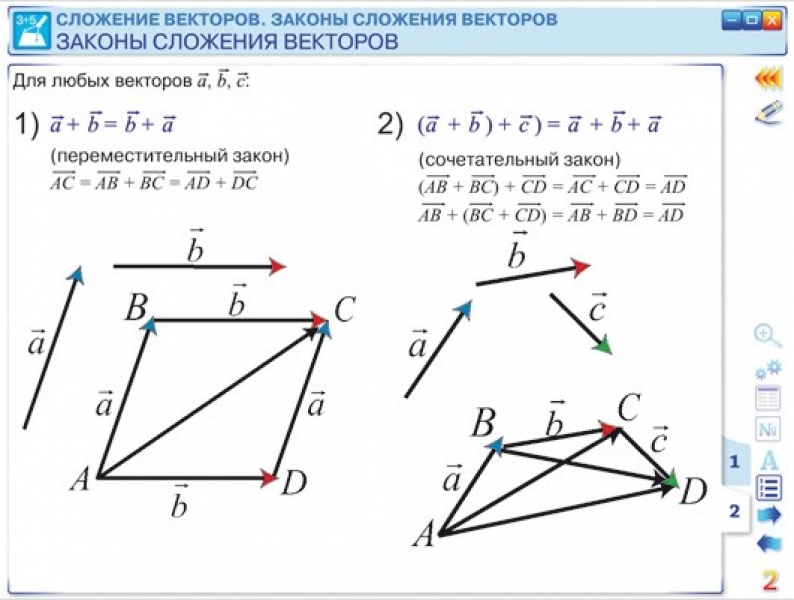
Рис. 3
Кроме того, мы рассмотрели понятие обратного вектора – вектора, имеющего такую же длину, как заданный, но ему противонаправленного.
Пример 1 – задача 747: выпишите пары коллинеарных сонаправленных векторов, которые определяются сторонами параллелограмма; укажите противоположно направленные векторы;
Задан параллелограмм MNPQ (см. Рис. 4). Выпишем пары коллинеарных векторов. В первую очередь это векторы и . Они не только коллинеарные, но и равные, т.к. они сонаправлены, и длины их равны по свойству параллелограмма (в параллелограмме противоположные стороны равны). Следующая пара . Аналогично
Рис. 4
выпишем коллинеарные векторы второй пары сторон: ; .
Противоположно направленные векторы: , , , .
Пример 2 – задача 756: начертите попарно неколлинеарные векторы , и . Постройте векторы ;; ;.
Для выполнения данного задания можем пользоваться правилом треугольника или параллелограмма.
Способ 1 – с помощью правила треугольника (см. Рис. 5):
Рис. 5
Способ 2 – с помощью правила параллелограмма (см. Рис. 6):
Рис. 6
Комментарий: мы применяли в первом способе правило треугольника – откладывали из произвольно выбранной точки А первый вектор, из его конца – вектор, противоположный второму, соединяли начало первого с концом второго, и таким образом получали результат вычитания векторов. Во втором способе мы применили правило параллелограмма – построили на нужных векторах параллелограмм и его диагональ – искомую разность, помня тот факт, что одна из диагоналей – это сумма векторов, а вторая – разность.
Пример 3 – задача 750: докажите, что если векторы и равны, то середины отрезков AD и BC совпадают. Докажите обратное утверждение: если середины отрезков AD и BC совпадают, то векторы и равны (см. Рис. 7).
Докажите обратное утверждение: если середины отрезков AD и BC совпадают, то векторы и равны (см. Рис. 7).
Из равенства векторов и следует, что прямые АВ и CD параллельны, и что отрезки АВ и CD равны. Вспомним признак параллелограмма: если у четырехугольника пара противоположных сторон лежит на параллельных прямых, и их длины равны, то данный четырехугольник – параллелограмм.
Рис. 7
Таким образом, четырехугольник ABCD, построенный на заданных векторах, – параллелограмм. Отрезки AD и BC являются диагоналями параллелограмма, одно из свойств которого: диагонали параллелограмма пересекаются и в точке пересечения делятся пополам. Таким образом, доказано, что середины отрезков AD и BC совпадают.
Докажем обратное утверждение. Для этого воспользуемся другим признаком параллелограмма: если в некотором четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. Отсюда четырехугольник ABCD – параллелограмм, и его противоположные стороны параллельны и равны, таким образом, векторы и коллинеарны, очевидно, что они сонаправлены, и модули их равны, отсюда векторы и равны, что и требовалось доказать.
Отсюда четырехугольник ABCD – параллелограмм, и его противоположные стороны параллельны и равны, таким образом, векторы и коллинеарны, очевидно, что они сонаправлены, и модули их равны, отсюда векторы и равны, что и требовалось доказать.
Пример 4 – задача 760: докажите, что для любых неколлинеарных векторов и справедливо неравенство (см. Рис. 8)
Отложим из произвольной точки А вектор , получим точку В, из нее отложим неколлинеарный ему вектор . По правилу параллелограмма или треугольника получим сумму векторов – вектор . Имеем треугольник .
Длина суммы векторов соответствует длине стороны АС треугольника. По неравенству треугольника длина стороны АС меньше, чем сумма длин двух других сторон АВ и ВС, что и требовалось доказать.
Рис. 8
Применение векторов к решению задач
Напомним, что мы уже изучили некоторые факты о векторах, и теперь умеем определять равные векторы, коллинеарные векторы, сонаправленные и противоположно направленные. Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Пример 1 – задача 769: отрезок ВВ1 – медиана треугольника . Выразите через векторы и векторы , , и .
Отметим, что векторы и неколлинеарны, то есть прямые АВ и АС не параллельны.
В дальнейшем мы узнаем, что любой вектор может быть выражен через два неколлинеарных вектора.
Выразим первый вектор (см. Рис. 1): , т. к. по условию ВВ1 – медиана треугольника, значит, векторы и имеют равные модули, кроме того, очевидно, что они коллинеарны и при этом сонаправлены, значит, данные вектора равны.
Рис. 1
Для выражения следующего вектора воспользуемся правилом параллелограмма для вычитания. Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Вектор является противоположным к заданному вектору , отсюда .
Вектор аналогично вектору можно представить в виде разности векторов . При выражении следует учесть тот факт, что точка В1 является серединой отрезка АС, значит, векторы и равны, значит, вектор можно представить как удвоенное произведение вектора .
Перед решением задачи мы сказали, что через заданные два неколлинеарных вектора можно выразить любой вектор. Выразим, например, медиану АА1 (см. Рис. 2).
Получили систему уравнений, выполним их сложение:
Векторы в сумме составляют нулевой вектор, так как они коллинеарны и противонаправлены, а модули их равны, таким образом получаем:
Рис. 2
2
Поделим обе части уравнения на два, получим:
Из данной задачи можно сделать вывод, что если заданы два неколлинеарных вектора, то любой третий вектор на плоскости можно однозначно выразить через эти два вектора. Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Пример 2: доказать с помощью векторов свойство средней линии треугольника (см. Рис. 3).
Задан произвольный треугольник , точки M и N – середины сторон АВ и АС соответственно, MN – средняя линия треугольника. Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Доказательство данного свойства аналогично для треугольника и трапеции.
Рис. 3
Выразим вектор двумя способами:
Получили систему уравнений:
Выполним сложение уравнений системы:
Сумма векторов – это нулевой вектор, длины этих векторов равны по условию, кроме того, они очевидно коллинеарны и противонаправлены. Аналогично суммой векторов будет нулевой вектор. Получаем:
Аналогично суммой векторов будет нулевой вектор. Получаем:
Поделим обе части уравнения на два:
Таким образом, мы получили, что средняя линия треугольника равна половине его основания. Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Таким образом, мы доказали свойство средней линии трапеции при помощи векторов.
Пример 3: задан произвольный треугольник (см. Рис. 4). В нем проведены медианы АА1, ВВ1, СС1. Точка пересечения медиан – М. Вектор соответствует силе , – силе , – силе . Доказать, что .
Напомним, что медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины.
Иногда точку пересечения медиан называют центром тяжести треугольника.
Выполним сложение векторов , воспользуемся для этого правилом параллелограмма (см. Рис. 5).
Рис. 5).
Рис. 4
Получаем:
С другой стороны, , так как BMCD – параллелограмм, диагонали параллелограмма точкой пересечения делятся пополам, А1 – точка пересечения диагоналей параллелограмма, значит, отрезки МА1 и А1D равны, отсюда, по свойству точки пересечения медиан, длины векторов и равны, но данные векторы противонаправлены, а значит, их сумма
Рис. 5
равна нулевому вектору. Мы помним, что вектор , а вектор , таким образом, , что и требовалось доказать.
Пример 4 – задача 773: докажите, что для любых векторов и справедливо следующее неравенство:
Решение: представим разность векторов в виде суммы: . Также обратим внимание на тот факт, что длины противонаправленных векторов и равны: . Таким образом, можно переписать исходное выражение:
Для удобства введем новую переменную: и перепишем выражение:
. А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке. Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке. Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Итак, мы вспомнили все основные определения и свойства векторов, вспомнили основные операции над векторами, рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/vektory/vektory-povtorenie-teorii-zadachi
http://interneturok.ru/ru/school/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/8-itogovyj-test-po-teme-vektory-variant-1.html
http://metodbook.ru/index.php/matematika/9-testy-po-geometrii-9-klass/9-itogovyj-test-po-teme-vektory-variant-2. html
html
http://uslide.ru/images/22/28455/960/img5.jpg
http://www.studfiles.ru/html/2706/538/html_OqWQ3sDQeV.5bGa/htmlconvd-WBhq8w_html_73af1ab4.png
http://uchkollektor39.ru/uploads/images/items/29cc1d8d90989d9f0e3df70c3d95a9ee.jpg
http://rushkolnik.ru/tw_files2/urls_3/891/d-890061/890061_html_m5ff065f.jpg
http://cs1-48v4.vk-cdn.net/p24/3551abddfac0c8.mp3?extra=amJxaBk9gfTT0lPmsOEwb8Rn_T2twbNJh2OUazYT-T9cSSu4_1787ibMzOu6ytv1rZKrpdEq7XnWZN1f-bjAuKyWIFf7mzw
http://matssir.ucoz.ru/_ld/0/33_G8p84-85.pptx
http://nsportal.ru/sites/default/files/2014/05/11/vektory._dokazatelstvo.pptx
http://v.5klass.net/zip/b66d124d0243f848a0bf454b75404034.zip
Решение задач с векторами
Горячая математикаМы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.
Скорость:
Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.
Пример :
Мяч брошен с начальной скоростью 70 футов в секунду, под углом 35 ° с горизонталью. Найдите вертикальную и горизонтальную составляющие скорости.
Позволять в представить скорость и использовать данную информацию, чтобы написать в в форме единичного вектора:
в знак равно 70 ( потому что ( 35 ° ) ) я + 70 ( грех ( 35 ° ) ) Дж
Упрощая скаляры, мы получаем:
в ≈ 57,34 я + 40.15 Дж
Поскольку скаляры являются горизонтальной и вертикальной компонентами в ,
Следовательно, горизонтальная составляющая
57,34
футов в секунду, а вертикальная составляющая
40. 15
футов в секунду.
15
футов в секунду.
Сила:
Сила также представлена вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, представляет собой векторную сумму этих сил.
Пример :
Две силы Ф 1 а также Ф 2 с величинами 20 а также 30 фунт соответственно действуют на объект в точке п как показано. Найдите результирующие силы, действующие на п .
Сначала мы пишем Ф 1 а также Ф 2 в виде компонентов:
в ≈ 57,34 я + 40.15 Дж
Упрощая скаляры, мы получаем:
Ф 1 знак равно ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) Дж знак равно 20 ( 2 2 ) я + 20 ( 2 2 ) Дж знак равно 10 2 я + 10 2 Дж Ф 2 знак равно ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) Дж знак равно 30 ( − 3 2 ) я + 30 ( 1 2 ) Дж знак равно − 15 3 я + 15 Дж
Итак, результирующая сила Ф является
Ф знак равно Ф 1 + Ф 2 знак равно ( 10 2 я + 10 2 Дж ) + ( − 15 3 я + 15 Дж ) знак равно ( 10 2 − 15 3 ) я + ( 10 2 + 15 ) Дж ≈ − 12 я + 29Дж
Работа:
Работа
Вт
сделано силой
Ф
при движении по вектору
Д
является
Вт
знак равно
Ф
⋅
Д
.
Пример :
Сила задается вектором Ф знак равно 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9) . Найдите проделанную работу.
Сначала мы находим Displacement.
Вектор смещения
Д знак равно 〈 5 − 1 , 9 − 3 〉 знак равно 〈 4 , 6 〉 .
По формуле совершенная работа равна
Вт знак равно Ф ⋅ Д знак равно 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 знак равно 26
Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа равна 26 фут-фунт
Как решать задачи кинематики: руководство по векторам
Эта статья является третьей главой в серии о том, как понимать задачи кинематики и подходить к ним. В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.
В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.
Есть много способов думать о векторах, но основное определение — это величина (число) и направление. Так что «четыре метра на восток» — это просто вектор в словесной форме. Вы также можете думать о векторе как о стрелке; он указывает определенное расстояние в определенном направлении.
Все это векторы, причем красивые векторы.
Добавление векторовДобавление векторов работает не так, как добавление чисел. Мы не можем просто суммировать величины (это распространенная ошибка), потому что это не учитывает направление. В конце концов, если вы пройдете 8 метров на восток, а затем 5 метров на запад, вы не окажетесь в 13 метрах от того места, откуда начали; вам будет всего 3 года (мы видели вариант этой идеи в главе 1, посвященной перемещению)
При сложении векторов вместо суммирования величин мы наклеиваем один на конец другого и смотрим, где они окажутся.
Итак, если я хочу добавить этот вектор к этому вектору
, я могу соединить их вместе, чтобы получить:
Мы называем красный вектор «результирующим», потому что он является результирующим. от сложения двух векторов вместе
Компоненты вектораЧтобы прояснить векторы, мы часто записываем их как сумму их «компонентов». Каждый компонент сообщает, как далеко заходят векторы в определенном направлении. Обычно согласованный набор направлений составляет x̂, ŷ , ẑ . В книгах по физике эти направления иногда называют х , х , k̂ , потому что они глупы (на самом деле это делается для упрощения векторных полей, когда дело доходит до продвинутого уровня).
Почему это работает? Добавление вектора! Поскольку векторы складываются, мы можем думать о каждом векторе как о сумме 2 (в 2D) или 3 (в 3D) векторов, которые движутся только в направлениях x, y или z.
Допустим, вы получили вектор с определенной величиной и углом от горизонтали (также известный как ось x) и хотите найти компоненты векторов. Это очень распространено в кинематике и за ее пределами, но как вы это делаете? Ответ тот же, что и у любой успешной фолк-рок группы: правильное использование треугольников.
Помните, мы разделили наш вектор на компоненты? Вы могли заметить, что компоненты и исходный вектор образуют прямоугольный треугольник. Это связано с тем, что оси x и y по определению всегда расположены под углом 90° друг к другу. Вы также можете помнить из геометрии, что если у нас есть угол и гипотенуза прямоугольного треугольника, то мы можем найти другие стороны (называемые катетами) с помощью SOH-CAH-TOA.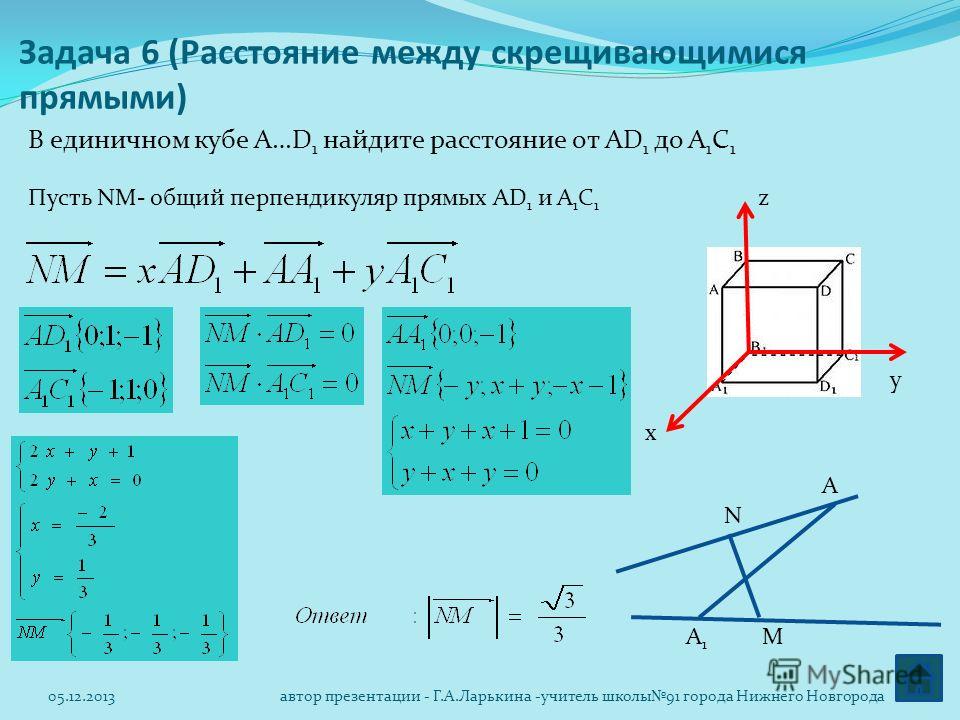
Вы можете найти более подробные обзоры в Интернете, но основная идея SOH-CAH-TOA заключается в том, что синус угла равен стороне, противоположной углу деленная на гипотенузу (таким образом, S=O/H или SOH). Точно так же косинус равен прилежащей стороне относительно гипотенузы (C=A/H), а тангенс равен противолежащей стороне прилежащей стороны (T=O/A). Используя это, легко доказать, что вертикальный катет, направление y, нашего составного треугольника будет гипотенузой*sin(угол). Или, поскольку гипотенуза — это исходный вектор, векторная величина*sin(угол). Точно так же направление x будет просто векторной величиной * cos (угол).
Пример: Нахождение компонентов вектораУ меня есть вектор величиной 5 метров, который направлен вверх и вправо под углом 37 градусов к оси x. Я хочу знать форму компонента. Давайте проработаем это.
Шаги:
- Нарисуйте вектор.

- Добавьте треугольные ножки.
- Математика
Y-направление = величина * sin(угол) = 5 метров * sin (37) = 3 метра
x-направление = величина * cos(угол) = 5 метров * cos (37) = 4 метра
- Подставьте решения в определение вектора
Вектор = 3x̂ + 4 х
Тада, просто как π!
Иногда вам могут быть заданы компоненты вектора, и вы хотите найти общую величину и угловое направление этого вектора. И снова на помощь приходят треугольники.
Величину вектора легко вычислить по теореме Пифагора. Из теоремы Пифагора a 2 +b 2 =c 2 , поэтому, когда мы применим это к векторам: компонент) 2 .
Чтобы найти угловое направление вектора, мы можем использовать арктангенс. Поскольку тангенс равен стороне, противоположной прилежащей стороне (T=O/A):
tan(угол вектора)=(y-компонента)/(x-компонента)
Затем используйте функцию invtan на вашем калькуляторе, чтобы найти обратную сторону этого тангенса, которая дает вам угол.
Лучшее в векторных компонентах то, что они упрощают добавление векторов. Пока мы сохраняем компоненты x, y и z разными, мы можем просто добавлять компоненты. Таким образом, если V 1 = (x 1 , y 1 , z 1 ) и V 2 = (x 2 , y 2 , z 2 , z0253 2 ), то вектор их суммы равен V 1 +V 2 =(x 1 +x 2 , y 1 +y 2 2 905 1 2 , 3 z 90 2 ). Когда у вас есть этот новый вектор, вы можете использовать предыдущий раздел, чтобы найти величину и угловое направление.
Заключение Теперь мы знаем, что такое вектор, как разделить его на компоненты, как сложить эти компоненты и как рекомбинировать его по величине и углу. В нашем следующем блоге мы обсудим, как использовать эти векторы для кинематики в двух измерениях.
Решения и примеры для физики
Векторы могут использоваться для решения множества задач, которые включают в себя такие величины, как ускорение, импульс, сила, скорость и перемещение.
В чем разница между скалярами и векторами?
Скаляр — это величина, которая имеет нет направление . Это просто шкала таких величин, как килограммы или сантиметры. Например, ваш вес и рост выражаются через количество и единицу измерения, но не имеют направления. Примерами скалярных величин являются скорость, масса, температура, энергия, длина и расстояние.
Скаляр — это величина, которая имеет нет направление . Это просто шкала таких величин, как килограммы или сантиметры. Например, ваш вес и рост выражаются через количество и единицу измерения, но не имеют направления. Примерами скалярных величин являются скорость, масса, температура, энергия, длина и расстояние.
Рис. 1. Вес – это скалярная величина. Источник: oatsy40, Flickr (CC BY 2.0).
Вектор , , с другой стороны, имеет величина и направление . Импульс объекта, например, равен его массе на ускорение и имеет направление, которое делает его векторной единицей. Примерами векторных величин являются скорость, ускорение, импульс, смещение и сила, включая вес.
Рис. 2. Ускорение является векторной величиной. Источник: Никос Кутулас, Flickr (CC BY 2.0).
Разложение векторов на компоненты
Разложение векторов на компоненты помогает нам, когда мы имеем дело с сложные векторные задачи . Чтобы разложить вектор на его компоненты, нам нужно измерить горизонтальную и вертикальную длину вектора и указать эти длины как две отдельные величины. Давайте посмотрим на пример ниже, чтобы лучше понять концепцию.
Найдите компоненты вектора, показанного ниже.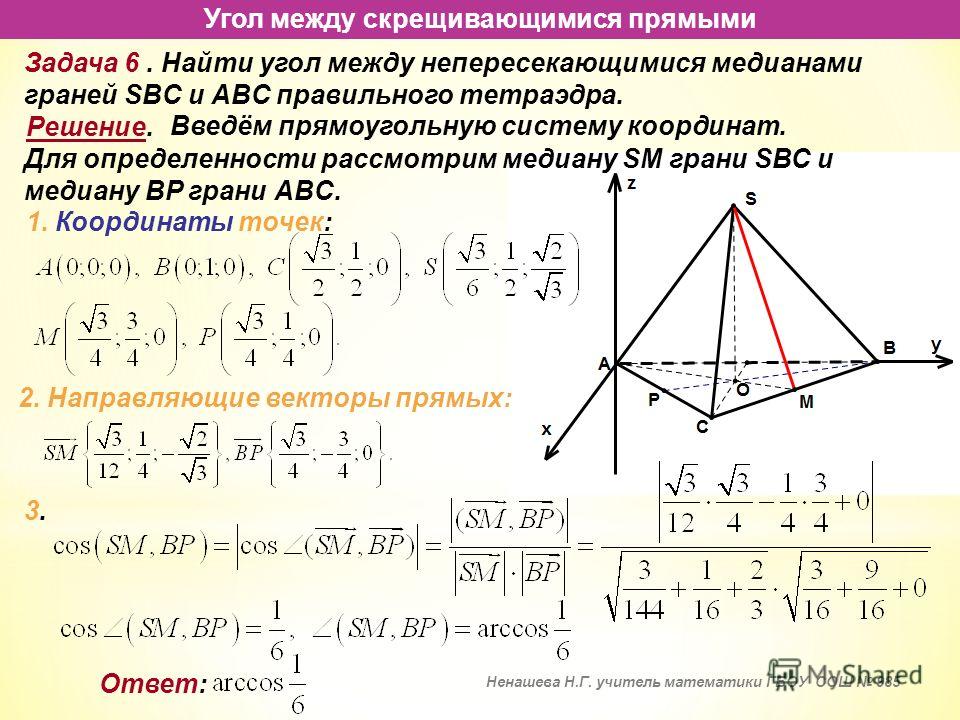
Чтобы найти компоненты этого вектора, нам нужно начать с определения его горизонтальной и вертикальной длины.
Как видите, длина по горизонтали равна 12, а по вертикали — 10. Когда мы разлагаем вектор на его компоненты, мы всегда получаем одно значение по горизонтали и одно по вертикали. Длины, которые мы измерили, являются величинами компонентов вектора.
Как видите, компонентами этого вектора являются два вектора, горизонтальный и вертикальный, с величинами 12 и 10.
Можем ли мы разложить вектор на его компоненты, если мы не можем измерить его горизонтальная и вертикальная длина? Да, можем, но давайте посмотрим, как это делается.
Рис. 3. Вектор v и его компоненты. Источник: Огулкан Тезкан, StudySmarter.
Если мы знаем угол градиента вектора, мы можем определить величину его горизонтальной и вертикальной составляющих. Для приведенного выше вектора v угол градиента равен a. Затем мы можем определить соотношение между углом и величиной компонентов с помощью тригонометрии.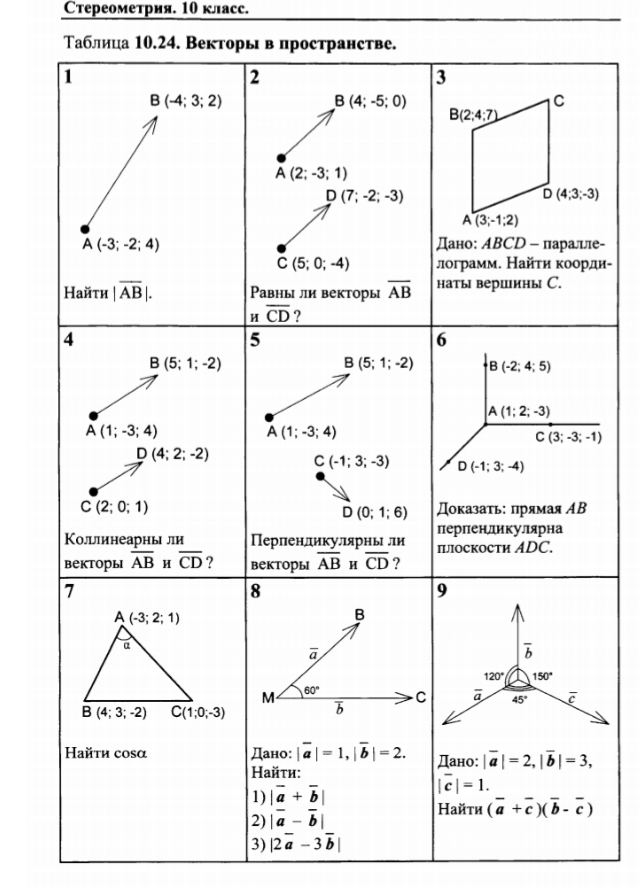
Определим величину горизонтальной составляющей v x . Мы знаем, что:
Если мы решим уравнение для v x , мы получим:
Теперь определим величину вертикальной составляющей v y . Опять же, мы знаем, что:
Если мы решим уравнение для v y , мы получим:
Сложение векторов вместе
Сложение двух векторов вместе называется нахождением их равнодействующей. Есть два способа сложения векторов. Первый включает с использованием масштабных диаграмм , а второй использует тригонометрию .
Определение результирующих векторов с помощью масштабных диаграмм
Чтобы найти результирующие векторы с помощью масштабных диаграмм, нам нужно нарисовать масштабную диаграмму векторов, которые мы хотим сложить вместе, соединяя векторы ‘ кончик к хвосту ‘.
Следующий пример иллюстрирует концепцию.
Человек сначала проходит на северо-восток 11,40 м, затем продолжает идти на восток 6,6 м и, наконец, проходит на северо-запад 21,26 м, прежде чем остановиться. Определить полное перемещение человека.
Определить полное перемещение человека.
Чтобы определить полное перемещение человека, нам нужно указать длины, которые он прошел, в виде векторов, каждый из которых имеет правильное направление и величину. Назовем его первое движение вектором А, второе — вектором В, а третье — вектором С.
Рисунок 4. Общее перемещение человека. Источник: Огулкан Тезкан, StudySmarter.
Если вы измерите линейкой общее перемещение, то увидите, что оно составляет 23,094 метра в северном направлении, хотя человек прошел 390,26 метра. Давайте докажем это математически, разложив векторы на их компоненты. В этом конкретном примере нам нужны только вертикальные компоненты, поскольку общее смещение является только вертикальным.
Рис. 5. Компоненты вектора. Источник: Огулкан Тезкан, StudySmarter.
Чтобы определить A y , , мы применяем уравнение для разложения векторов на их компоненты:
Нам не нужно определять компоненты B, так как этот пример не включает вертикальную компоненту . Для определения C y , мы применяем то же уравнение.
Для определения C y , мы применяем то же уравнение.
Полное перемещение равно сумме A y и C y , которое можно рассчитать следующим образом: другой, мы можем найти равнодействующую с помощью тригонометрии. Давайте снова посмотрим на пример.
Двое друзей толкают коробку. Две силы, которые они прикладывают, перпендикулярны друг другу. Один из друзей прикладывает силу в 3 ньютона (F 1 ) в восточном направлении, а другой прикладывает силу в 4 ньютона (F 2 ) в северном направлении. Определите результирующий вектор полной силы, действующей на коробку.
Рис. 6. Две перпендикулярные силы, воздействующие на коробку. Источник: Огулкан Тезкан, StudySmarter.
Две силы, F 1 и F 2 , перпендикулярны друг другу, а это означает, что модуль F в сумме равен гипотенузе треугольника, образованного этими векторами.
Задачи векторов — основные выводы
- В физике векторы используются для выражения любой величины, имеющей направление и величину.

- Чтобы разложить вектор на его компоненты, нам нужно измерить горизонтальную и вертикальную длины вектора и выразить их как два отдельных вектора.
- Чтобы сложить векторы вместе, мы можем использовать масштабные диаграммы или тригонометрию.
- Чтобы определить результирующие векторы с помощью масштабных диаграмм, нам нужно соединить векторы «кончик к хвосту».
- Если два вектора перпендикулярны друг другу, мы можем найти равнодействующую, используя теорему Пифагора.
Векторы и наборы задач со снарядами
Калькулятор, версия 2
Вы просматриваете устаревшую версию Калькулятора. Недавно мы переработали и улучшили Калькулятор. Версия 2 уже доступна! Мы увеличили количество задач более чем в три раза, разбили каждую часть на несколько небольших однотематических наборов задач и использовали генератор случайных чисел для предоставления числовой информации по каждой задаче. Ответы учащихся оцениваются автоматически, а обратная связь осуществляется мгновенно. И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
И мы сохранили такое же обязательство предоставлять помощь через ссылки на существующие ресурсы. В то время как БЕСПЛАТНАЯ версия делает все вышеперечисленное, учителя с подпиской на Task Tracker могут пойти еще дальше. Они могут модифицировать наши готовые наборы задач, писать свои собственные задачи с помощью нашего простого в использовании Конструктора задач и использовать планшет для разработки собственной программы, выражающей их акцент на использовании математики в физике.
Вернитесь на главную страницу, чтобы перейти к Версии 2. Узнайте больше о Версии 2. Или посетите Магазин, чтобы совершить покупку в системе отслеживания задач.
Векторы и снаряды: набор задач
Задача 1:
Тренер Суини проходит 26 ярдов на север вдоль боковой линии, делает паузу и проходит 12 ярдов назад на юг.
а. Определить расстояние, на которое проехал Coach.
б. Определить результирующее перемещение кареты.
- Аудиоуправляемое решение
Задача 2:
а. Роза Лодка плывет вверх по течению со скоростью 1,25 м/с относительно воды в реке, скорость течения которой 0,50 м/с относительно берегов реки. Какова результирующая скорость лодки Розы (относительно берегов)?
Роза Лодка плывет вверх по течению со скоростью 1,25 м/с относительно воды в реке, скорость течения которой 0,50 м/с относительно берегов реки. Какова результирующая скорость лодки Розы (относительно берегов)?
б. Роза Лодка плывет вниз по течению со скоростью 1,25 м/с относительно воды в реке, которая течет со скоростью 0,50 м/с относительно берегов реки. Какова результирующая скорость лодки Розы (относительно берегов)?
- Аудиогид
Задача 3:
Скорость взлета военного самолета с авианосца составляет примерно 170 миль/ч относительно воздуха. Они приобретают эту скорость за счет комбинации катапультной системы, имеющейся на авианосце, и реактивной двигательной установки самолета. Распространенная стратегия — направить авианосец и самолет против ветра. Если самолет взлетает с авианосца, который движется со скоростью 40 миль в час при встречном ветре со скоростью 20 миль в час, то какую скорость относительно палубы авианосца он должен иметь для взлета?
- Аудиогид
Задача 4:
Клэр де Иль делает покупки. Она проходит 16 м до конца прохода. Затем она поворачивает направо и проходит 21 метр по последнему проходу. Определите величину результирующего смещения Клэр.
Она проходит 16 м до конца прохода. Затем она поворачивает направо и проходит 21 метр по последнему проходу. Определите величину результирующего смещения Клэр.
- Аудиогид
Задача 5:
Джим Назиум идет с обеда на урок физкультуры. Он выходит из столовой и проходит 43 м на запад. Затем он поворачивается и проходит 72 метра на север по коридору, ведущему в раздевалку. Определите величину и направление результирующего смещения Джима.
- Аудиогид
Задача 6:
По пути из дома в школу Карла едет по трем улицам после выезда с подъездной дорожки. Она проезжает 1,85 мили на юг, 2,43 мили на восток и 0,35 мили на север. Определите величину результирующего смещения Карлы.
- Аудиогид
Задача 7:
Шейла — капитан университетской команды по кроссу. Во вторник во время внеклассной тренировки она вела команду на следующий забег из школы в ближайший парк, где они встретились с тренером для встречи: 0,68 мили, север; 1,09миль на восток; 1,56 мили к северу; 0,32 мили, запад. Определите величину и направление результирующего смещения команды.
Определите величину и направление результирующего смещения команды.
- Аудиогид
Задача 8:
Во время лабораторной работы по сложению векторов Мак и Тош начинают у дверей класса и проходят 40,0 м на север, 32,5 м на восток, 15,5 м на юг, 68,5 м на запад и 2,5 м на север. Определить величину и направление равнодействующего смещения Мака и Тоша.
- Аудиогид
Задача 9:
Эйвери, защитник футбольной команды Университета Юга, сделал самый потрясающий пас в игре «Возвращение домой» против соперника из города Норта. Он бросил передачу из точного центра поля в угол зачетной зоны, где Джамаал поймал ее на победный счет. Если футбольное поле имеет ширину 160 футов (от боковой линии до боковой линии) и расстояние от центра поля до задней части зачетной зоны составляет 60 ярдов, то какое расстояние пролетел мяч от рук Эйвери до рук Джамаала.
- Аудиогид
Задача 10:
Рассмотрим карту Соединенных Штатов ниже.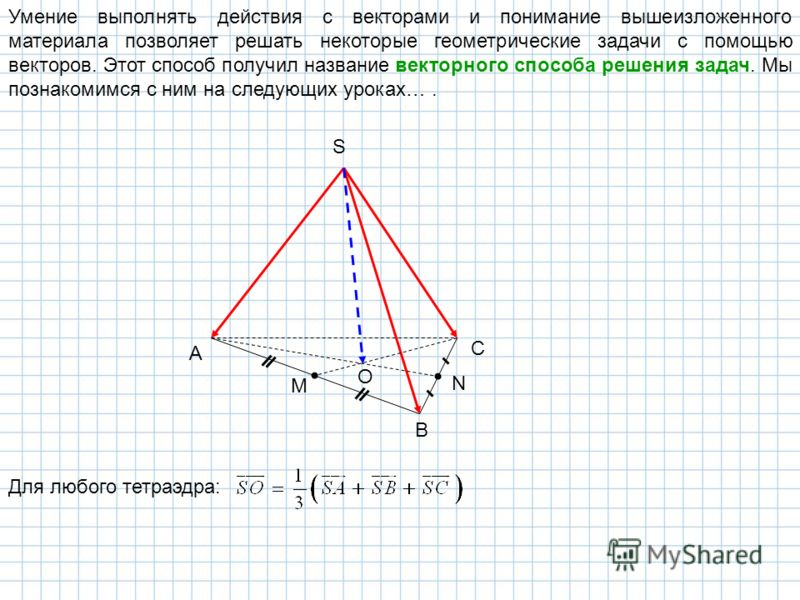 Учитывая масштаб, что 1 см = 340 км, можно использовать транспортир и линейку для определения величины и направления для следующих поездок. Все направления выражены против часовой стрелки с востока. Для каждого рейса используйте функции синуса, косинуса и тангенса, чтобы определить горизонтальную и вертикальную составляющие смещения. Обязательно укажите E, W, N или S в качестве направления для каждого компонента.
Учитывая масштаб, что 1 см = 340 км, можно использовать транспортир и линейку для определения величины и направления для следующих поездок. Все направления выражены против часовой стрелки с востока. Для каждого рейса используйте функции синуса, косинуса и тангенса, чтобы определить горизонтальную и вертикальную составляющие смещения. Обязательно укажите E, W, N или S в качестве направления для каждого компонента.
| Поездка | Рабочий объем | Гориз. Деталь | Вертик. Деталь |
| Чикаго — Денвер | 1430 км, 187° | ||
| Рино в Майами | 4030 км, 341° | ||
| Сиэтл — Вашингтон | 3480 км, 344° | ||
| Хьюстон — Солт-Лейк-Сити | 2040 км, 143° |
- Решение с аудиогидом
Проблема 11:
Пилот самолета, летящего прямо на север, получает от диспетчера полетов уведомление о том, что второй самолет летит на юг примерно на той же высоте и находится в том же районе. Пилоту сообщают, что самолет, летящий на юг, в настоящее время находится на расстоянии 13,5 км, 102° от его собственного самолета.
Пилоту сообщают, что самолет, летящий на юг, в настоящее время находится на расстоянии 13,5 км, 102° от его собственного самолета.
а. Сколько километров на север второй самолет?
б. Сколько километров западнее второго самолета?
г. Если оба самолета имеют воздушную скорость 290. км/ч, то сколько времени пройдет, прежде чем самолеты окажутся рядом ?
- Аудиогид
Задача 12:
Спелеолог (человек, исследующий пещеры) определяет, что вход в пещеру находится в 349 м, 253° от его текущего положения. Как далеко на юг и как далеко на запад от ее нынешнего положения находится вход в пещеру?
- Аудиогид
Задача 13:
Эйвери, квотербек Саута, делает пас на 36,5 ярда на 21° з. д. от южной широты, прежде чем его ловит Митчелл ловлей в прыжке. Если предположить, что поле проходит с севера на юг и что Эйвери сделал пас с расстояния 7,2 ярда за линией схватки, сколько ярдов было выиграно в игре?
- Аудиогид
Задача 14:
Миа Андер выходит из парадной двери своего дома и идет по пути, показанному на схеме справа (не в масштабе). Шаг состоит из четырех шагов со следующими величинами:
Шаг состоит из четырех шагов со следующими величинами:
A = 88 м
B = 272 м
C = 136 м
D = 183 м
Определите величину и направление результирующего смещения Мии.
- Аудиогид
Задача 15:
Дора исследует пещеру. Она начинается у входа и совершает следующие прямолинейные движения:
68 м, юг
112 м, 25° к северу от запада (155° против часовой стрелки)
34 м, юг CCW)
Определите положение Доры относительно входа в пещеру. То есть, как далеко и в каком направлении находится Дора от входа в пещеру?
- Аудиогид
Задача 16:
Тейлор и Дрю заканчивают последний урок за день до весенних каникул и решают спонтанно отправиться в путешествие. Их путешествие включает в себя следующие перемещения:
42 мили, 67° к северу от запада (113° против часовой стрелки)
61 миля, запад
23 мили, 17° к западу от юга (253° против часовой стрелки)
Машина Тейлора ломается после последней поездки.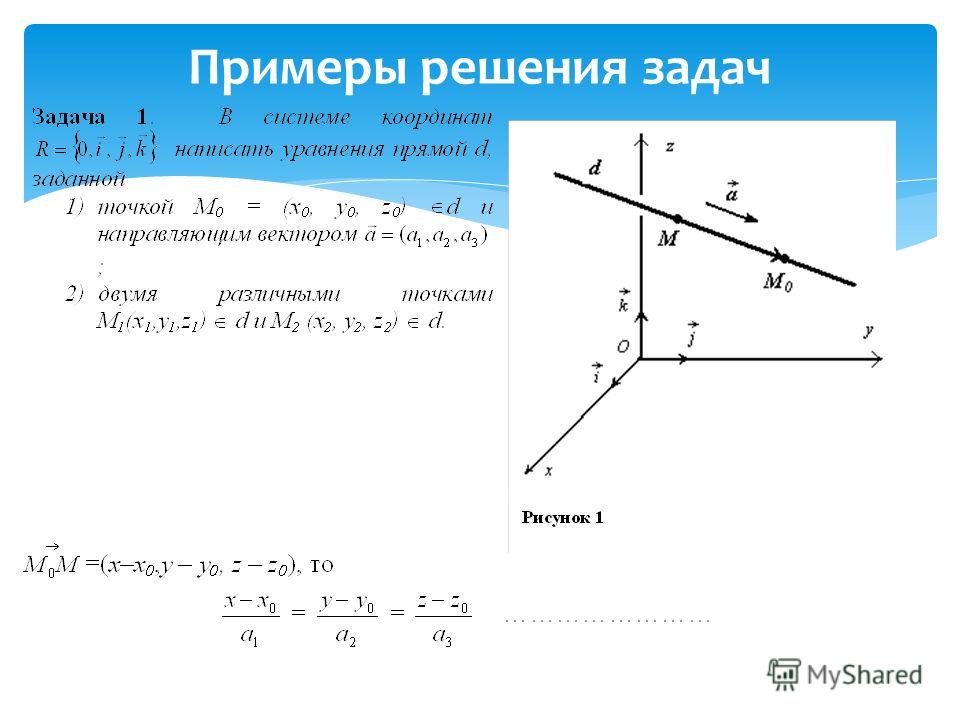 этап поездки. Как далеко и в каком направлении находятся Тейлор и Дрю от кампуса?
этап поездки. Как далеко и в каком направлении находятся Тейлор и Дрю от кампуса?
- Аудиогид
Задача 17:
В метеосводке указано, что в 12 км к югу и в 23 км к западу от вашего города был замечен торнадо. Сообщается, что шторм движется прямо к вашему городу со скоростью 82 км/ч.
а. На каком расстоянии от вашего города был замечен торнадо?
б. Приблизительно сколько времени (в минутах и часах) пройдет, прежде чем сильный шторм обрушится на ваш город?
- Решение для аудиогида
Задача 18:
Самолет отправляется в Канаду из пункта назначения, расположенного в 450 км к югу от границы. Самолет летит по прямолинейному пути со скоростью 189 миль в час в направлении 20,5 градусов к западу от севера. Определить количество минут до пересечения границы самолетом. Предположим, что граница проходит прямо с востока на запад в районе, где происходит полет.
- Аудиогид
Задача 19:
Гленда и Гарольд пытаются пересечь реку на каяке. Река течет прямо на восток на отметке 1,9РС. Гленда и Гарольд идут на каяке прямо на север и гребут со скоростью 2,4 м/с (относительно воды). Ширина реки в этом месте 38 м.
Река течет прямо на восток на отметке 1,9РС. Гленда и Гарольд идут на каяке прямо на север и гребут со скоростью 2,4 м/с (относительно воды). Ширина реки в этом месте 38 м.
а. Определите результирующую скорость лодки — как величину, так и направление.
б. Определите время, когда Гленда и Гарольд переправятся через реку.
г. Как далеко по течению будет лодка, когда Гленда и Гарольд достигнут противоположного берега?
- Аудиогид
Задача 20:
Тай Ридлегс садится в байдарку и направляется на запад прямо через реку. Река течет на юг со скоростью 48 см/с. Тай гребет на лодке со скоростью 98 см/с.
а. Определите результирующую скорость лодки — как величину, так и направление.
б. Если ширина реки в этом месте 22 м, то сколько времени потребуется Таю, чтобы пересечь реку? Предположим, что Тай держит свою байдарку на запад.
г. Как далеко вниз по течению будет Тай, когда он достигнет другого берега реки?
Как далеко вниз по течению будет Тай, когда он достигнет другого берега реки?
- Аудиогид
Задача 21:
Дилан и София гуляют по озеру Блюберд в совершенно безветренный день. Дилан, полный решимости произвести впечатление на Софию своей способностью прыгать через камни, берет самый плоский камень, который только может найти, и запускает его из пистолета с кромки воды. Скала приобретает полностью горизонтальную скорость 26 м/с с высоты 0,45 м над поверхностью воды.
а. Сколько времени потребуется камню, чтобы упасть на поверхность воды?
б. На какое расстояние от кромки воды пролетит камень, прежде чем совершит первый прыжок?
- Аудиогид
Задача 22:
Пытаясь создать всплеск, похожий на пушечное ядро, восьмилетний Мэтью сбегает с края доски хайдайвера со скоростью 4,6 м/с и падает с высоты 2,3 м в воду.
а. Определите время, за которое Мэтью упадет с высоты 2,3 м в воду.
Определите время, за которое Мэтью упадет с высоты 2,3 м в воду.
б. На каком расстоянии по горизонтали от края доски Мэтью погрузится в воду?
г. С какой скоростью Мэтью входит в воду?
- Аудиогид
Задача 23:
Има Пеоде хочет сбросить 2,8-килограммовую тыкву горизонтально с крыши школы, чтобы попасть в машину мистера Х. Автомобиль припаркован на расстоянии 13,4 м от основания здания ниже точки, где стоит Има. Крыша здания имеет высоту 10,4 м. Предполагая отсутствие сопротивления воздуха, с какой горизонтальной скоростью Има должен бросить тыкву, чтобы попасть в машину мистера Х.
- Аудиогид
Задача 24:
Водолазы Ла-Кебрада устраивают ежедневные развлечения для толпы в Акапулько, Мексика. Группа профессиональных хайдайверов ныряет со скалы Ла-Кебрада и падает с высоты 45,1 м (148 футов) в воду. Дайверы со скалы должны рассчитать время своего погружения не просто как проявление храбрости, а так, чтобы они достигли воды, когда прибудет гребень набегающей волны. Определите скорость, с которой Педро должен сбежать с обрыва, чтобы приземлиться в воду на расстоянии 17,8 м по горизонтали от края обрыва.
Определите скорость, с которой Педро должен сбежать с обрыва, чтобы приземлиться в воду на расстоянии 17,8 м по горизонтали от края обрыва.
- Аудиогид
Задача 25:
Самолет экстренной помощи сбрасывает пакет помощи группе медицинских работников, работающих в агентстве по оказанию помощи в африканской деревне. Пакет предназначен для приземления в небольшом озере, надувания прикрепленного плота при ударе и, наконец, всплытия на поверхность плотом вниз. Самолет будет двигаться горизонтально со скоростью 59,1 м/с. Посылка будет сброшена с горизонтального расстояния 521 м от намеченной цели. На какой высоте над водоемом должен лететь самолет, чтобы успешно совершить этот подвиг?
- Аудиогид
Задача 26:
Ресторан Choo Choo в ДесПлейнсе, штат Иллинойс, представляет собой закусочную в стиле 50-х годов, печально известную тем, что еду из кухни в столовую доставляют с помощью модели поезда O-масштаба. Обеденные корзины, наполненные хот-догами, гамбургерами, картофелем фри и т. п., устанавливаются на крыши вагонов-платформ и транспортируются на столешницы. На пятый день рождения Мэтью картофель фри скатился с вершины кучи на крутом повороте, двигаясь со скоростью 1,25 м/с, и упал на пол.
п., устанавливаются на крыши вагонов-платформ и транспортируются на столешницы. На пятый день рождения Мэтью картофель фри скатился с вершины кучи на крутом повороте, двигаясь со скоростью 1,25 м/с, и упал на пол.
а. Определите время, за которое картофель фри упадет с высоты 113 см от вершины кучи на пол.
б. Определить горизонтальное смещение мальков от края следа.
г. Определите скорость картофеля фри при ударе об пол.
- Аудиогид
Задача 27:
Аарон Эгин и Бад Дерфенгер — партнеры по лаборатории, которые в прошлом году заработали репутацию за то, что разбивали мензурки, проливали кислоту, смешивали неправильные химические вещества, разбивали термометры и случайно поджигали волосы Софии с помощью горелки Бунзена. И теперь, к радости класса физики, мистер Х. совершил ошибку, снова позволив им стать партнерами. В недавней лаборатории, в которой использовались дорогие гусеницы и тележки, Аарон и Бад оправдали свою репутацию. Несмотря на строгие предупреждения г-на Х., они позволили тележке скатиться с рельсов, а затем со стола со скоростью 208 см/с. Падение тележки на пол на горизонтальном расстоянии 96,3 см от края стола заставили весь класс замолчать. Используйте эту информацию, чтобы определить высоту лабораторных столов в лаборатории мистера Х.
Несмотря на строгие предупреждения г-на Х., они позволили тележке скатиться с рельсов, а затем со стола со скоростью 208 см/с. Падение тележки на пол на горизонтальном расстоянии 96,3 см от края стола заставили весь класс замолчать. Используйте эту информацию, чтобы определить высоту лабораторных столов в лаборатории мистера Х.
- Аудиогид
Задача 28:
Шэрон Стеди и Эл Вейскачон выиграли недавний конкурс Юга по бросанию яиц, который проводился во время недели возвращения домой. В своем победном броске Шэрон подбросила яйцо исподтишка, выпустив его со скоростью 8,06 м/с под углом 30° к горизонтали. К удовольствию публики, Эл поймал яйцо на той же высоте, что и бросок, даже не повредив скорлупу.
а. Рассчитайте горизонтальную и вертикальную составляющие начальной скорости.
б. Рассчитайте время, за которое яйцо достигнет середины траектории.
г. Рассчитайте общее время, в течение которого яйцо находится в воздухе.
д. Вычислите расстояние по горизонтали, пройденное яйцом от Шарона до Эла.
эл. Рассчитайте высоту яйца (относительно точки выпуска), когда оно находилось на пике своей траектории.
- Аудиогид
Задача 29:
Знаменитый китайский прыгун с трамплина Ли Пин Фар сходит с трапа с начальной скоростью 34,9 м/с под углом 35°.
а. Определить общее время полета.
б. Определить горизонтальное смещение.
г. Определите высоту пика (относительно начальной высоты). Предположим, что Ли приземляется на той же высоте, что и вершина пандуса, и что Ли является снарядом.
- Аудиогид
Задача 30:
Теннисистка вытягивается, чтобы достать мяч, едва находящийся над землей, и успешно перебрасывает его через голову соперника. Мяч брошен со скоростью 18,7 м/с под углом 65,1 градуса.
а. Определить время, в течение которого мяч находится в воздухе.
б. Определите максимальную высоту, на которую поднимается мяч.
г. Определите расстояние, которое мяч проходит по горизонтали до приземления.
- Аудиогид
Задача 31:
В канун Нового 2007 года Робби Мэддисон установил мировой рекорд по самому длинному прыжку на мотоцикле, преодолев 98,3 м по воздуху от рампы к рампе. (С тех пор рекорд был несколько раз побит самим Мэддисионом.) Предполагая, что угол запуска составляет 45 °, незначительное сопротивление воздуха и место приземления на той же высоте, что и высота запуска, определите скорость, с которой Мэддисон покинул рампу.
- Аудиогид
Задача 32:
Г-н Удади берет троих своих детей в парк для летнего отдыха. Олив Удади любит качаться и прыгать. В одном прыжке Олив покидает мах под углом 30° к горизонту со скоростью 2,2 м/с. Она приземляется на землю на горизонтальном расстоянии 1,09 м от места запуска.
а. Определите горизонтальную и вертикальную составляющие начальной скорости.
Определите горизонтальную и вертикальную составляющие начальной скорости.
б. Определите время, в течение которого Олив находится в воздухе.
г. Определите высоту по вертикали (относительно места приземления), с которой Олив прыгает с качелей.
- Аудиогид
Задача 33:
В явном стремлении заслужить участие в шоу Уничтожено за секунды Калеб пытается совершить велосипедный маневр, в котором он прыгает между двумя пандусами, приподнятые края которых расположены на расстоянии 1,8 метра друг от друга. Пандусы расположены под углом 35° и расположены на одной высоте. Определите скорость (в м/с и милях/ч), которую должен развить Калеб, чтобы выполнить этот трюк. (Дано: 1,00 м/с = 2,24 мили/ч)
- Аудиогид
Задача 34:
Альберт — лучший игрок южной футбольной команды. Его лучшее время зависания в прошлом сезоне было для плоскодонки, которую он нанес под углом 74° над горизонталью. Время зависания плоскодонки составило 6,2 секунды.
Время зависания плоскодонки составило 6,2 секунды.
а. Определить скорость, с которой мяч был отброшен.
б. Определите горизонтальное расстояние, пройденное мячом.
- Аудиогид
Вернуться к обзору
Просмотреть аудиоуправляемое решение проблемы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34
13 задач и решение для практики Вектор в физике
Мы представляем 13 задач с решениями, которые помогут вам изучить вектор в физике. Мы также предоставляем изображения, которые помогут вам лучше понять проблемы и решения. Удачной учебы.
Baca juga Vector Fisika: Operasi penjumlahan, Pengurangan, notasi \hat{i} dan \hat{j}, dan penguraian
1. Вектор смещения
Сдвиньте изображение выше
Сабрина прошла 75 метров на восток .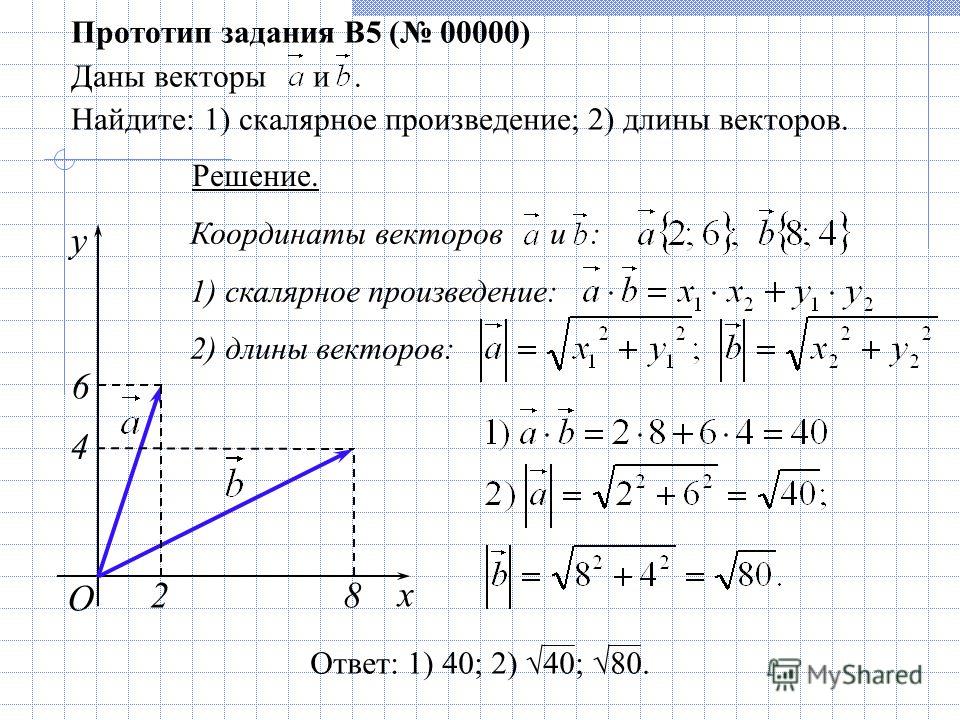 Затем она повернулась на 30 градусов влево и прошла 25 метров. Определите величину вектора смещения Сабрины.
Затем она повернулась на 30 градусов влево и прошла 25 метров. Определите величину вектора смещения Сабрины.
Решение:
Сдвиньте изображение выше, чтобы увидеть результирующий вектор. Результирующий расчет величины вектора выглядит следующим образом. 9{\circ}}}\\ =&97.46 \;\text{метр} \end{aligned}
Исходя из приведенных выше расчетов, водоизмещение «Сабрины» составляет 97,46 метра.
2. Найдите результирующую величину \overrightarrow{A}-\overrightarrow{B}
Сдвиньте изображение выше
«Сатуан» — это слово на индонезийском языке. С английского переводится как «единица».
Посмотрите на изображение выше. \overrightarrow{A} имеет величину 45 единиц. В то же время \overrightarrow{B} составляет 30 единиц. Определите величину \overrightarrow{A}-\overrightarrow{B}. 9{\circ}}}\\ \приблизительно&\;57\;\text{единица измерения} \end{aligned}
Итак, величина \overrightarrow{A}-\overrightarrow{B} составляет около 57 единиц. {\circ}
\end{выровнено} 9{\circ} и \left | R \right |= 40.98\;\text{единицы}
{\circ}
\end{выровнено} 9{\circ} и \left | R \right |= 40.98\;\text{единицы}
4. Найдите x-компоненту и y-компоненту вектора и запишите их, используя обозначения \hat{i} и \hat{j}
Посмотрите на предыдущую задачу и найдите x-компоненту и y-компоненту \overrightarrow{R}. Затем напишите \overrightarrow{R} в нотации \hat{i} и \hat{j}.
Решение:
Мы можем найти y-компоненту
\begin{aligned} R_y=&40,98 \times \cos(66,53)\\ =&16.32 \;\text{единицы} \end{выровнено}
Затем найдите x-компоненту
\begin{align} R_x=&40,98 \times \sin(66,53)\\ =&37.59 \;\text{единицы}\\ \end{aligned}
Обратите внимание, что \overrightarrow{R} указывает влево и вниз, что означает, что единичные векторы будут (-\hat{i}) и (-\hat{j}). Мы можем записать вектор \overrightarrow{R} следующим образом.
\begin{выровнено} \overrightarrow{R}=&R_x(-\шляпа{i})+R_x(-\шляпа{j})\\ =&-37,59\;\шляпа{i}+-16,32\;\шляпа{j} \end{aligned}
Итак, имеем R_x=37,59ед. , R_y=16,32 ед., и пишем \overrightarrow{R}=-37,59 \;\hat{i}+R_x-16,32\;\hat{j}
, R_y=16,32 ед., и пишем \overrightarrow{R}=-37,59 \;\hat{i}+R_x-16,32\;\hat{j}
5. Результат трех векторов
- \ стрелка вправо{A}=4\шляпа{i}+5\шляпа{j}
- \overrightarrow{B}=9\шляпа{i}-7\шляпа{j}
- \overrightarrow{C}=-3\шляпа{i}+2\шляпа{j}
Найдите результат \overrightarrow{A}-\overrightarrow{B}+\overrightarrow{C}. Определить результирующую величину.
Решение:
Во-первых, мы работаем с использованием обозначений \hat{i} и \hat{j}. 92}\\ =&16.12\; \text{единицы} \end{aligned}
По нашим расчетам результирующая длина \overrightarrow{A}-\overrightarrow{B}+\overrightarrow{C} составляет 16,12 единиц.
На изображении ниже показан весь вектор, которым мы оперируем.
6. Нахождение углов вектора
Найдите угол результирующего вектора из предыдущей задачи.
Решение:
Сначала мы вычисляем угол между отрицательной осью x и \overrightarrow{R} 9{\ circ} от положительной оси x.
7. Нахождение углов между двумя векторами одинаковой величины
Известно, что векторы \overrightarrow{A} и \overrightarrow{B} имеют одинаковую величину, и это L. Пусть R_1 равнодействующая \overrightarrow{A}+\overrightarrow{B}, а R_2 является результатом \overrightarrow{A}-\overrightarrow{B}. Если \frac{R_1}{R_2}=\sqrt{3}, определите угол между \overrightarrow{A} и \overrightarrow{B}.
9{\circ}
Кнопка «Поделиться»
8. Результат двух векторов в квадрате
Посмотрите на рисунок выше. Определите результирующий вектор \overrightarrow{A}+\overrightarrow{B}.
Решение:
Еще раз взгляните на картинку. Голова \overrightarrow{A} находится в центре правой стороны квадрата. Это означает, что \overrightarrow{A} имеет y-компоненту длины 6 единиц и x-компоненту 12 единиц. Мы можем записать вектор A, используя обозначения \hat{i} и \hat{j}. 92}\\ \примерно&\;25,46\; \text{units}\end{aligned}
Таким образом, результирующий вектор имеет длину 25,46 единиц.
9. Вычислите равнодействующую 3-х векторов, 2 из которых симметричны
Результирующий векторСдвиньте изображение выше
Посмотрите на картинку выше. Есть 3 вектора одинаковой длины, равной 30 единицам. Определите результирующую величину сложения этих трех векторов.
Решение:
Более подробно рассмотрите \overrightarrow{A} и \overrightarrow{B}. Y-компоненты двух векторов имеют одинаковую величину, но противоположные направления, поэтому они компенсируют друг друга. Таким образом, результат \overrightarrow{A}+\overrightarrow{B} представляет собой просто сложение x-компоненты двух векторов и точек влево. 92}\\ =&36,.47\; \text{единицы} \end{aligned}
Основываясь на проведенных нами вычислениях, результирующая величина сложения трех векторов составляет 36,35 единицы.
10. Результирующая кулоновских сил
На точечный заряд действуют 3 разные силы, а именно \overrightarrow{F_1}, \overrightarrow{F_2} и \overrightarrow{F_3}, как показано на рисунке выше. Определить результирующую силу, действующую на точечный заряд.
Определить результирующую силу, действующую на точечный заряд.
Baca juga : Гая Кулон (Листрик) и Соал Пембахасан Гая Кулон
Решение:
Мы описываем все векторы на x-компоненту и y-компоненту. Вы можете увидеть расчет в таблице ниже.
После описания F_1, F_2 и F_3 мы складываем эти компоненты, чтобы получить компоненты x и y результирующего вектора. Расчеты приведены в последней строке таблицы выше. При добавлении компонентов будьте осторожны со знаком (-)(+). Помните, что отрицательное значение означает, что сила направлена влево/вниз, а положительное означает, что сила направлена вправо/вверх. 9{\ круг}. Затем мяч совершает параболическое движение и достигает точки C за 0,328 секунды. Найдите расстояние (расстояния) между точками B и C.
Решение:
Параболическое движение представляет собой комбинацию двух движений одновременно, а именно движения с постоянной скоростью и движения с постоянным ускорением.
В этом случае, когда мяч движется, свет сверху заставит мяч отбрасывать тень на стол. Что ж, несмотря на то, что мяч движется по параболе, его тень на самом деле движется по прямой из точки B в точку C со скоростью v_x=v \cos{40}.
Чтобы найти расстояние (расстояния), мы делаем расчет ниже.
\begin{выровнено} S=&v_x \times t\\ =&v \cos{40} \times 0,328\\ =&2,5 \times \cos{40} \times 0,328\\ =&0,628 \; \текст{метр}\\ \приблизительно&63\; \текст{см} \end{aligned}
Мы сделали расчет, согласно которому расстояние (d) между B и C составляет около 63 см.
12. Нахождение вектора ускорения объекта
На объект действуют 2 силы, как показано выше. Определите направление (\theta) и величину ускорения объекта. 9{\ circ} от отрицательной оси Y.
13. Анализ закона Ньютона с помощью векторов
Сдвиньте изображение выше
На объект действует множество сил, как показано выше. Если объект остается в покое, определите величину F_2 и N (нормальная сила).
Решение:
Говорят, что объект покоится, если он удовлетворяет двум условиям.
Первое условие состоит в том, что сила справа равна силе слева. Посмотрите на второй слайд изображения выше. В этом случае сила справа равна F_1, а сила слева равна F_{2x}. Итак, чтобы выполнить первое условие, мы должны написать следующее. 9{\circ}}}\\ =&\frac{40}{3}\sqrt{3}\;\text{Ньютон} \end{aligned}
Второе условие: направленная вверх сила должна быть равна направленной вниз силе. Сдвиньте изображение выше и посмотрите. В этом случае есть 2 направленные вверх силы, а именно F_{2y} и N (нормальная сила). Пока есть одна нисходящая сила, а именно w(вес). Чтобы выполнить условие, что восходящая сила равна направленной вниз силе, мы должны написать следующее математическое уравнение.
N \;+\;F_{2y}=\;W
Мы можем оперировать приведенным выше уравнением далее
\begin{выровнено} N \;+\;F_{2y}=&\;W\\ Н\;+\; F_2 \;\sin{30}=&\;50\\ Н\;+\; \frac{40}{3}\sqrt{3}\times \frac{1}{2}=&\;50\\ N=&50 – \frac{40}{6}\sqrt{3}\\ =&38,45 \; \text{Ньютон} \end{align}
Итак, F_2=\frac{40}{3}\sqrt{3} ньютонов и N=38,45 ньютонов.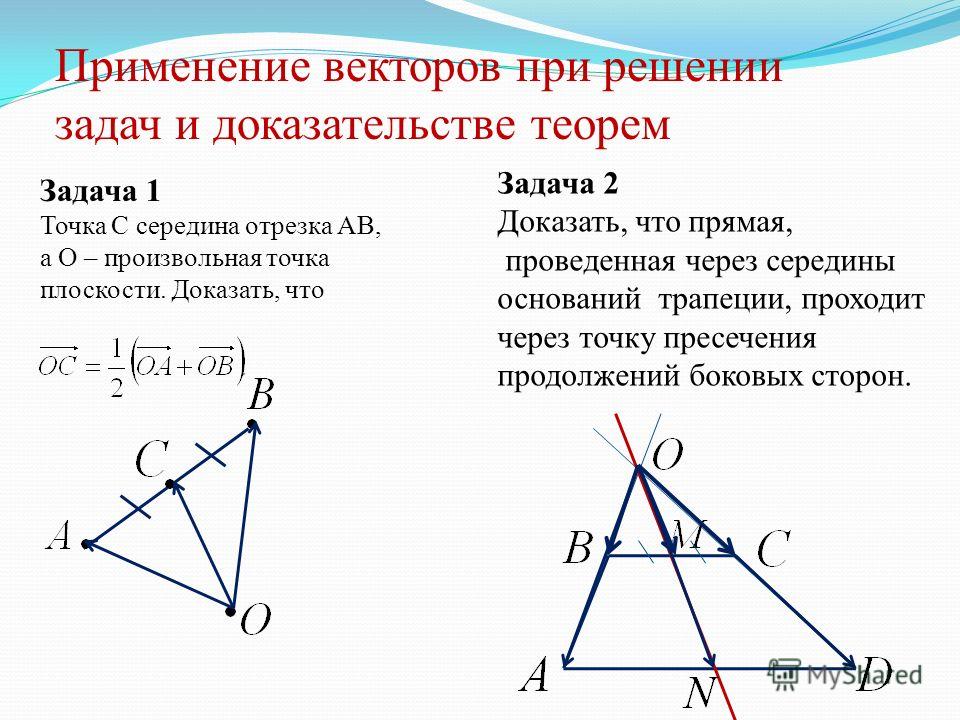
Кнопка «Поделиться»
Векторное разрешение и компоненты — Практика — Гиперучебник по физике
[закрыть]
практическая задача 1
Направлен лазерный луч 15.95° над горизонтом на расстоянии 11 648 м от зеркала. Он отскакивает от зеркала и продолжает движение еще 8570 м на высоте 11,44° над горизонтом, пока не достигнет цели. Каково результирующее смещение луча к цели?
раствор
Необходимо обработать векторы, расположенные не под правильным углом. Разбейте их на составляющие.
| x 1 = r 1 cos θ 1 x 1 = (11 648 м)cos(15,95°) x 1 = 11 200 м |
| y 1 = r 1 sin θ 1 y 1 = (11,648 m)sin(15.95°) y 1 = 3200 m |
| x 2 = R 2 COS θ 2 154. |
| y 2 = r 2 sin θ 2 y 2 = (8,570 m)sin(11.44°) y 2 = 1700 m |
Сложение векторов в одном направлении с «обычным» сложением.
| x = 11 200 м + 8 400 м x = 19,600 м |
| г = 3200 м + 1700 м г = 4900 м |
Добавить векторы под прямыми углами с комбинацией пифагорской теоремы для величины…
| R = √ (1 x 2 +13332 7 2 7 2 7 2 7 2 7 2 7 2 +1. 2 +1. 2 + 2 + 2 + 2 + . 19 600 м) 2 + (4 900 м) 2 ] r = 20 200 м |
и тангенс для направления.
| тангенс θ = | г | = | 4900 м | |
| х | 19 600 м | |||
| θ = | 14,04° | |||
Не забудьте ответить на вопрос.
Цель лазерного луча находится на расстоянии 20 200 м под углом места 14,04° .
Ах да, и не забудьте сделать рисунок. Я, наверное, должен был сказать тебе сделать это раньше. Мне неловко, что я сделал это дважды в разделах о векторах. Я должен подать лучший пример. Позвольте мне исправить это, предоставив вам анимированный рисунок.
Если у вас возникнет чувство дежавю , не пугайтесь. Матрица в порядке. Я переработал решение этой проблемы из более раннего. Идея заключалась в том, чтобы показать общий метод решения задач, используемый в физике. Всякий раз, когда это возможно, возьмите сложную проблему, которую вы еще не решили, и уменьшите ее до той, которую вы решили.
Как сложить параллельные векторы? Просто — добавьте их. Как сложить антипараллельные векторы? Тоже просто — вычесть их. Как сложить векторы под прямым углом. Разумно просто — используйте теорему Пифагора и тангенс. Как сложить векторы, которые не равны 0°, 180° или 9?0°? До безобразия просто — разложить их на составляющие. Не позволяйте векторам заставлять вас работать больше. Сделайте так, чтобы они указывали в удобном для вас направлении. Сделайте их в более простых векторах.
А потом студенты узнали, что на самом деле не существует такого понятия, как «плохой» вектор, и все живут долго и счастливо. Конец.
практическая задача 2
На точку действуют три силы: 3 Н под углом 0°, 4 Н под углом 90° и 5 Н под углом 217°. Что такое чистая сила?
раствор
Разложить векторы на их компоненты вдоль x и и оси. (Следите за знаками.) Затем добавьте компоненты вдоль каждой оси, чтобы получить компоненты равнодействующей. Используйте их, чтобы получить величину и направление равнодействующей. Задачи с большим количеством компонентов легче решать, когда значения записываются в виде таблицы, например:
Задачи с большим количеством компонентов легче решать, когда значения записываются в виде таблицы, например:
| величина | направление | x-компонент | Y-компонент | |
|---|---|---|---|---|
| первая сила | 3 Н | 0° | +3 с.ш. | 0 Н |
| вторая сила | 4 Н | 90° | 0 N | +4 с.ш. |
| третья сила | 5 С | 217° | −4 с.ш. | −3 с.ш. |
| результат | 1,4 Н | 135° | −1 с.ш. | +1 N |
Может оказаться полезным рисунок или анимация.
практическая задача 3
Велосипедист едет прямо на запад по прямой дороге. Ветер дует с 248° со скоростью 10 м/с.
- Этот ветер больше похож на встречный или попутный?
- Какова скорость встречного/попутного ветра?
- Какова скорость бокового ветра?
раствор
Начните с диаграммы. Вы можете нарисовать этого велосипедиста сверху, как это сделал я, но в этом нет необходимости. Однако нарисуйте стрелку, направленную вправо, чтобы обозначить направление велосипедиста. Направление ветра измеряется по часовой стрелке с севера. Север — 0°, восток — 90°, юг 180°, запад 270°. Ветер дует с 248°, что находится где-то между югом и западом. Нарисуйте стрелку из нижнего левого угла в верхний правый угол, чтобы обозначить ветер. Угол между двумя стрелками равен…
270° − 248° = 22°
Добавьте эту информацию на диаграмму.
Вот почему вам нужна диаграмма. Это позволяет легко увидеть ответ. Этот ветер больше похож на встречный ветер , чем на попутный.
Встречный ветер задается компонентом «x».

v x = v cos θ
v x = (10 m/s)cos(22°)
v x = 9.2 m/sБоковой ветер задается компонентом «y».
v y = v sin θ
v y = (10 м/с)sin(22°)4
40253 г = 3,7 м/с
практическая задача 4
В один злополучный зимний день я случайно поскользнулся на обледенелой рампе под углом 37° к горизонтали. Найдите мое ускорение вниз по рампе, учитывая, что ускорение свободного падения направлено прямо вниз и имеет значение 9,8 м/с 2 . (Предположим, что лед совершенно лишен трения.)
раствор
Это пример задачи о наклонной плоскости — обычное дело на вводных уроках физики. Решение…
Начните с диаграммы. Нарисуйте диагональную линию, чтобы представить пандус.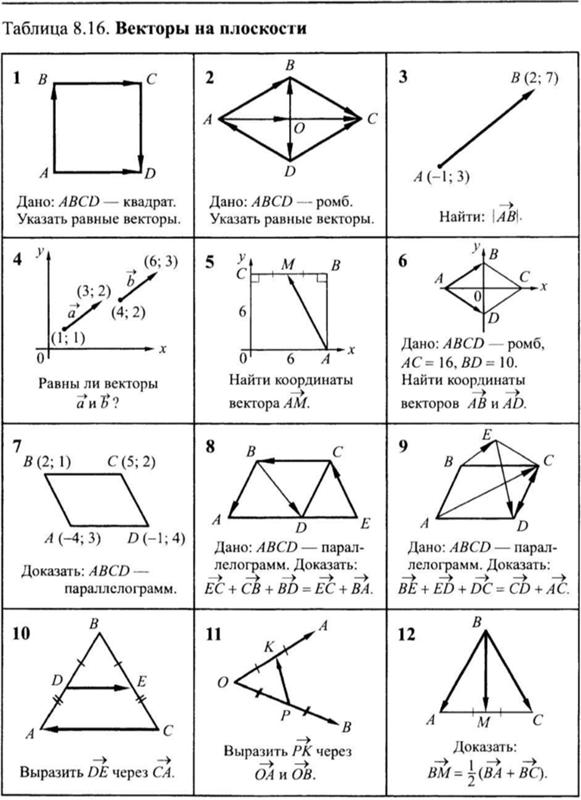


 : Просвещение, 2006.
: Просвещение, 2006.

 0253 2 = (8 570 м)cos(11,44°)
0253 2 = (8 570 м)cos(11,44°) 