Векторы. Скалярное и векторное произведения векторов.
Главная
» Информационные системы
» Компьютерная геометрия и графика
» Векторы. Скалярное и векторное произведения векторов.
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
Обозначение: .
Теорема. (Свойства скалярного произведения.)
1). Скалярное произведение подчиняется закону коммутативности:
, .
2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:

3). Скалярный квадрат вектора равен квадрату его модуля:
.
4). .
Доказательство. Все свойства очевидны из определения и их доказательства предоставляются читателям.
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложения векторов:
, .
2) Скалярный множитель можно выносить за знак скалярного произведения:
, , .
Доказательство. По свойству 4 предыдущей теоремы и по свойству проекции вектора на вектор (на ось) имеем:
.
Второе свойство доказывается аналогично.
Теорема доказана.
Замечание. Скалярное произведение можно рассматривать как числовую функцию от двух переменных, определенную на декартовом квадрате множества векторов :
,
т.е. , .
Тогда, свойства теоремы могут быть записаны так:
1) , ;
2) , , .
Первое из этих свойств называется свойством аддитивности функции f по первому аргументу, а второе – свойством однородности по первому аргументу. Если выполняются оба свойства, то говорят, что функция f линейна по первому аргументу. Отсюда происходит и название этих свойств скалярного произведения.
В силу коммутативности, скалярное произведение как функция двух переменных линейна и по второму аргументу, т.е. справедливы еще два свойства:
3) , ;
4) , , .
Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.
Другими словами, пусть , . Тогда
. (1)
Доказательство. Учитывая, что скалярное произведение ортогональных векторов равно нулю, а скалярный квадрат единичного вектора равен 1 , получаем:
, ч.т.д.
Теорема доказана.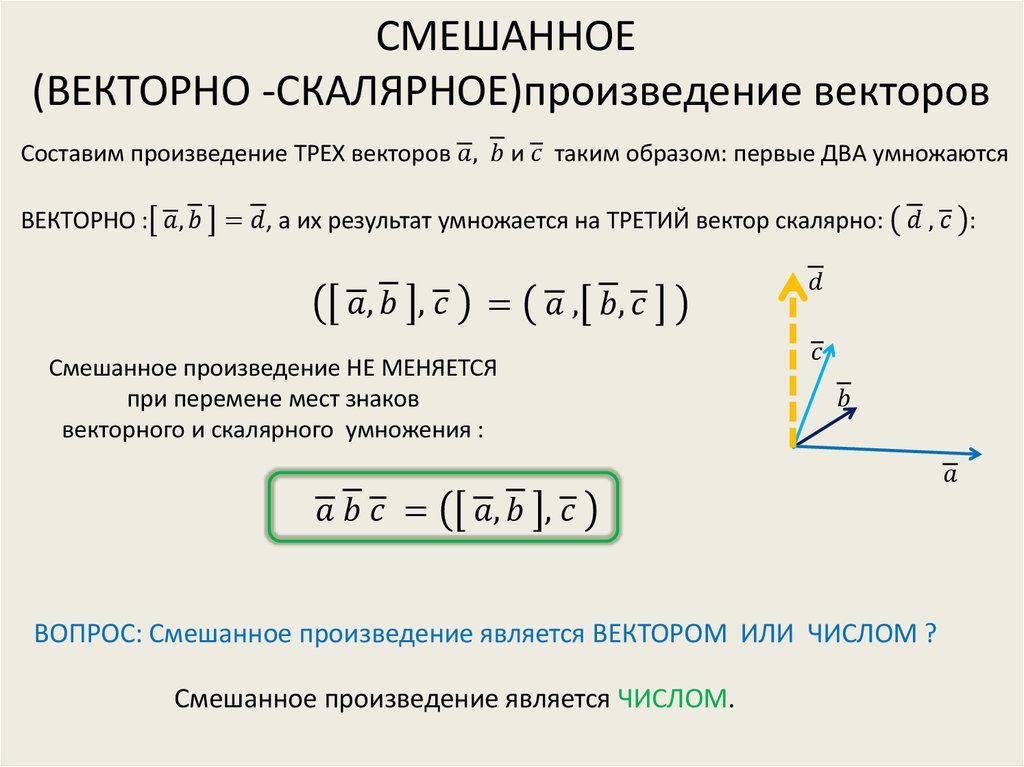
Следствие 1. Пусть . Тогда .
Доказательство. Эта формула нам уже известна. Здесь ее можно получить, используя равенство (1), в котором положим :
,
откуда и следует доказываемая формула.
Следствие доказано.
Следствие 2. Пусть , . Тогда
.
Доказательство. Очевидно.
п.5. Смешанное и векторное произведения векторов в координатной форме.
Теорема. Пусть , , . Тогда:
1) ;
2) .
Доказательство. 1) Используем свойство линейности векторного произведения:
.
Далее, заметим, что векторные произведения коллинеарных векторов равны нулевому вектору:
.
Рассмотрим другие векторные произведения базисных векторов:
рис.4.
, , .
Эти равенства легко устанавливаются с помощью рис.4.
Отсюда следует:
, ч.т.д.
2) Воспользуемся только что доказанной формулой:
.
Теперь, по теореме о скалярном произведении векторов в координатной форме, получаем:
, ч.т.д.
Теорема доказана.
Замечание. Векторное произведение часто записывают в форме определителя:
.
Разумеется это не определитель, а лишь форма записи векторного произведения. Она компактна и удобна для запоминания.
Следствие. Определитель не изменяется при круговой перестановке строк (столбцов) определителя. При транспозиции двух строк (столбцов) определитель меняет знак.
Доказательство. С одной стороны,
.
С другой стороны,
.
Но, , откуда и следует утверждение. Далее, т.к. , то
.
Так как определитель не изменяется при транспонировании, то доказанное свойство справедливо и для столбцов определителя.
Следствие доказано.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Скалярные и векторные величины
Даны определения и приведены примеры скалярных и векторных величин. Описаны математические операции над векторными величинами.
Физические величины бывают скалярными и векторными
Скалярные величины
Скалярная величина (от лат. scalaris – ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом.
Примеры скалярных величин: масса тела, время, температура, длина, путь, площадь.
Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:
Биомеханика опорно-двигательного аппарата человека
Векторные величины
Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. То есть вектор определяется численным значением и направлением.
Примеры векторных величин: перемещение, скорость, ускорение, сила, момент силы, импульс тела.
Обозначение векторных величин
На рисунках и схемах вектор отображается отрезком прямой со стрелкой на одном конце. Длина отрезка в выбранном масштабе выражает числовое значение векторной величины (его модуль), а стрелка указывает ее направление.
На рисунках, схемах и в тексте векторные величины обозначают несколькими способами:
1 способ. Векторная величина обозначается строчной или заглавной буквой со стрелкой или чертой над ней (рис. 1).
Рис.1. Вектор и его обозначение2 способ. Векторная величина обозначается заглавными буквами, обозначающими начало и конец вектора с чертой или стрелками над ними (рис. 1).
3 способ. Иногда векторные величины в формулах обозначаются жирным шрифтом, а скалярные — обычным. Например: F=ma
Операции над векторными величинами (векторами)
Над векторными величинами возможны следующие математические операции:
- Сложение и вычитание векторов.
- Умножение вектора на скаляр.

- Произведение векторов (скалярное и векторное).
Литература
- Петров В.А., Гагин Ю.А. Механика спортивных движений. – М: Физкультура и спорт, 1974. – 232 с.
С уважением, А.В. Самсонова
Похожие записи:
Сила тяжести
Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…
Сила
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Способ определения положения центров масс (центров тяжести) звеньев тела человека
Описан способ определения положения центров масс (центров тяжести, ЦТ) звеньев тела человека по Вильгельму Брауне и…
Распределение масс в теле человека
Описаны особенности распределения масс в теле человека. Дано понятие геометрии масс тела человека. Показано, что на…
Дано понятие геометрии масс тела человека. Показано, что на…
Центр масс и центр тяжести тела
Описаны: центр масс (ЦМ) и центр тяжести (ЦТ) твердого тела. Приведены различные определения ЦМ и ЦТ тела. Показано…
скаляров и векторов
Скаляры и векторыМатематика — это язык физики. С его помощью мы можем количественно описать мир вокруг нас. В механике мы будем использовать два типа величин, чтобы представлять такие понятия, как сила, масса и время в числовом виде. Эти два типа известны как скаляры и векторы.
Цели
- Изучите определения скаляров и векторов.
- См. несколько примеров векторных и скалярных величин.
- Преобразование векторов в их компоненты и обратно.
- Узнайте, как складывать, вычитать и умножать векторы.
Определения
Скаляр:
Скаляры используются для описания одномерных величин, то есть количества, для полного описания которых требуется только одно число. их. Примеры скалярных величин:
их. Примеры скалярных величин:| Температура Время Скорость Масса Расположение вдоль линии (1D) |
Вектор:
Векторы используются для описания многомерных количества. Многомерные величины – это те, которые требуют более чем одно число, чтобы полностью описать их. Векторы, в отличие от скаляров, имеют два характеристики, величина и направление. Примеры векторных величин:| Расположение в плоскости (2D) Местоположение в космосе (3D) Скорость Ускорение Сила |
Примечание:
Рисунки на этой странице содержат множество векторных диаграмм. Мы будет использовать цвета, чтобы различать, что представляет каждый вектор. Таблица ниже показывает цветовую схему, которую мы будем использовать с этого момента.| Векторный цвет | Значение |
|---|---|
| | Произвольные векторы (Красный) |
| | Векторы в направлении X (Синий) |
| | Векторы в направлении Y (Зеленый) |
| | Результирующие векторы (черный) |
| | Координатные оси (Серый) |
Векторные диаграммы
Мы используем векторные диаграммы для визуализации того, что происходит в физической системе. Несмотря на то, что мы можем решить большинство задач алгебраически, картинка может помочь.
указать на тонкости проблемы. Первый шаг при решении любой проблемы
в физике нарисовать картину.
Несмотря на то, что мы можем решить большинство задач алгебраически, картинка может помочь.
указать на тонкости проблемы. Первый шаг при решении любой проблемы
в физике нарисовать картину.Следующая диаграмма иллюстрирует два момента. Во-первых, это концепция кончик и хвост вектора. С векторами направление очень важно, поэтому мы ставим стрелку в направлении вектора идущий. Это иногда называют вершиной вектора. Другой конец обычно называют хвостом.
Вторая концепция, которую показывает диаграмма, состоит в том, что два вектора с одинаковая величина и направление одинаковы
Выражение векторов с помощью компонентов
Векторы могут быть выражены через их величину и направление или через с точки зрения их компонентов. Возможность перевода между двумя представление является важным навыком в физике. Величина вектора
его длина. Направление обычно задается через некоторый угол.
Величина вектора
его длина. Направление обычно задается через некоторый угол.При работе с векторами обычно гораздо удобнее их разбивать. в составные векторы. Векторы компонентов — это векторы, которые идут параллельно координатные оси. Например, двумерный вектор имеет две компоненты векторов, один в направлении X и один в направлении Y. Диаграмма ниже показывает двумерный вектор и его компоненты.
Длина и компоненты для вектора A и угол Ø ( «Phi» ) вычисляются как:
Сложение векторов Следующая диаграмма иллюстрирует векторную сумму. Обратите внимание, что мы можем перемещать хвост второго вектора к кончику первого вектора, чтобы получить результирующий вектор. Неважно, какой вектор перемещается, главное, чтобы кончик к хвосту друг с другом.
Как только векторы выражены как их независимые компоненты,
можно их добавить. Поскольку каждый компонент является скаляром, они могут быть добавлены
обычно к тому же компоненту другого вектора. Концептуально это выглядит
как на следующей схеме.
Концептуально это выглядит
как на следующей схеме.
Умножение вектора на скаляр
Вектор можно умножить на скаляр путем умножения каждого из его компоненты по этому номеру. Обратите внимание, что вектор не меняет направление, только длина. ЕслиЧастным случаем векторного умножения является умножение вектора на -1 . Это заставляет вектор изменить направление. Мы будем использовать это свойство для выполнения векторного вычитания.
Вычитание векторов Разность векторов работает так же, как сложение векторов, за исключением того, что мы умножьте вектор, который мы вычитаем, на
-1 . Это очень похоже вычитание двух чисел: A — B = A + (-B) . Диаграмма ниже иллюстрирует векторное вычитание в стиле от кончика к хвосту. Оригинал Вектор B показан пунктирной линией.
Помните, что важен порядок вычитания векторов. Если вы получите их назад, результирующая будет в противоположном направлении. т.е. А — В = -(В — А)
Пример 1
Путешественник проходит 2,5 км под углом 53,1 градуса к северу от востока, затем 2,0 км строго на восток. Каково ее полное перемещение от начальной точки, если вы измерите расстояние по прямой?
Пример 2
Несущий кабель телефонного столба мешает некоторым строителям. Для того, чтобы работа продолжалась, кабель необходимо переместить на 2 метра ближе к полюс. Если столб имеет высоту 10 метров и кабель в настоящее время закреплен до земли 8 метров от столба, сколько потребуется рабочим отрезать от кабеля, когда его двигают?Решения
Скаляры и векторы – определение, примеры, обозначения, различия и часто задаваемые вопросы
Скалярные и векторные величины используются для описания движения объекта. Скалярные величины определяются как физические величины, имеющие только величину или размер. Например, расстояние, скорость, масса, плотность и т. д. Однако векторные величины — это те физические величины, которые имеют как величину, так и направление, такие как перемещение, скорость, ускорение, сила, масса и т. д. Следует отметить, что при изменении векторной величины его величина и направление также меняются аналогичным образом, когда изменяется скалярная величина, изменяется только ее величина.
Скалярные величины определяются как физические величины, имеющие только величину или размер. Например, расстояние, скорость, масса, плотность и т. д. Однако векторные величины — это те физические величины, которые имеют как величину, так и направление, такие как перемещение, скорость, ускорение, сила, масса и т. д. Следует отметить, что при изменении векторной величины его величина и направление также меняются аналогичным образом, когда изменяется скалярная величина, изменяется только ее величина.
Что такое скалярная и векторная величина?
Скалярные величины — это величины, с которыми связана только величина или размер. Эти величины могут быть полностью выражены одним числом. Вот некоторые примеры скалярных величин: масса объекта, расстояние между двумя точками и т. д. Для выполнения операций со скалярными величинами работают обычные правила алгебры. Эти величины можно складывать и вычитать так же, как складывают и вычитают числа. Но только числа с одной и той же единицей измерения могут использовать процесс для скалярной величины.
Examples of Scalar Quantities
There exist many forms of scalar quantities some of them are listed below:
- Mass
- Speed
- Distance
- Time
- Area
- Volume
- Density
- Energy
- Температура
- Электрический заряд
- Гравитационная сила
С другой стороны, векторы — это величины, с которыми связано направление. Для сложения и вычитания эти величины подчиняются треугольному закону сложения векторов. Некоторые примеры векторных величин включают скорость, ускорение и т. д. При описании скорости необходимо указывать направление.
Любая векторная величина a может быть представлена в векторной форме как , которое представляет направление и величину вектора a. В случае единственной величины |a| обозначает величину.
Примеры векторных величин
В повседневной жизни существует бесчисленное множество примеров векторных величин.
Список некоторых из них ниже!
- Скорость
- Сила
- Давление
- Перемещение
- Ускорение
- Тяга
- Линейный импульс
- Электрическое поле
- Поляризация
- Вес
Векторное обозначение
, как показано ниже:
Разница между скалярной и векторной величиной
Скалярная | 4Векторная0033 |
| Скалярные величины имеют только величину или размер. | Векторные величины имеют как величину, так и направление. |
| Известно, что каждый скаляр существует только в одном измерении. | Векторные величины могут существовать в одном, двух или трех измерениях. |
| Всякий раз, когда происходит изменение скалярной величины, это также может соответствовать изменению ее величины. | Любое изменение векторной величины может соответствовать изменению либо ее величины, либо направления, либо того и другого. |
| Эти величины нельзя разложить на составляющие. | Эти величины можно разложить на составляющие, используя синус или косинус прилежащего угла. |
| Любой математический процесс, включающий более двух скалярных величин, дает только скаляры. | Математические операции над двумя или более векторами могут дать в результате либо скаляр, либо вектор. Например, скалярное произведение двух векторов дает только скаляр, тогда как перекрестное произведение, сумма или вычитание двух векторов дает вектор. |
Some examples of Scalar quantities are:
| Some examples of Vector quantities are:
|
Два вектора считаются равными, если они имеют одинаковую величину и направление.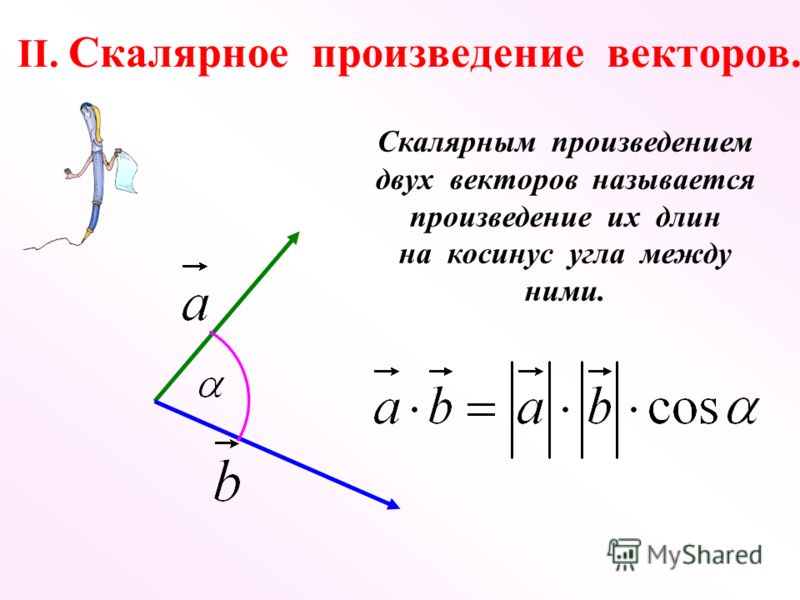 На рисунке ниже показаны два равных вектора, обратите внимание, что эти векторы параллельны друг другу и имеют одинаковую длину. На второй части рисунка показаны два неравных вектора, которые хотя и имеют одинаковую величину, но не равны, потому что имеют разные направления.
На рисунке ниже показаны два равных вектора, обратите внимание, что эти векторы параллельны друг другу и имеют одинаковую длину. На второй части рисунка показаны два неравных вектора, которые хотя и имеют одинаковую величину, но не равны, потому что имеют разные направления.
Умножение векторов на скаляр
Умножение вектора a на постоянный скаляр k дает вектор, направление которого остается тем же, но величина изменяется в k раз. На рисунке показан вектор до и после умножения на константу k. В математических терминах это можно переписать как
, если k > 1, величина вектора увеличивается, а уменьшается, когда k < 1.
Сложение векторов
Векторы нельзя складывать обычными алгебраическими правилами. При добавлении двух векторов необходимо учитывать величину и направление векторов. Закон треугольника используется для сложения двух векторов, на диаграмме ниже показаны два вектора «a» и «b», а результирующая вычисляется после их сложения. Сложение векторов следует коммутативному свойству, это означает, что результирующий вектор не зависит от порядка добавления двух векторов.
Сложение векторов следует коммутативному свойству, это означает, что результирующий вектор не зависит от порядка добавления двух векторов.
Треугольный закон сложения векторов– (Переместительное свойство)
Рассмотрим векторы, указанные на рисунке выше. Линия PQ представляет вектор «p», а QR представляет вектор «q». Линия QR представляет результирующий вектор. AC направлен от A к C.
Закон параллелограмма сложения векторовЛиния AC представляет собой
Величина результирующего вектора определяется выражением
θ представляет собой угол между двумя векторами. Пусть φ будет углом между результирующим вектором и вектором p.
Приведенная выше формула известна как закон сложения векторов треугольника.
Этот закон представляет собой еще один способ понимания сложения векторов. Этот закон гласит, что если два вектора, действующие в одной и той же точке, представлены сторонами параллелограмма, то результирующий вектор этих векторов представлен диагоналями параллелограмма. На рисунке ниже показаны эти два вектора, представленные на стороне параллелограмма.
На рисунке ниже показаны эти два вектора, представленные на стороне параллелограмма.
Также проверьте:
- Векторная алгебра
- Точечное и векторное произведение векторов
Решенные примеры на скаляре и векторе
901
Решение:
|v| =
а = 1, б = 4
|v| =
|v| =
|v| = √17
Пример 2. Вектор задается выражением v = i + 4j. Найдите модуль вектора, когда он масштабируется на константу 5.
Решение:
|v| =
5|v| = |5v|
а = 1, б = 4
|5v|
|5(i + 4j)|
|5i + 20j|
|в| =
|v| =
|v| = √425
Пример 3. Вектор задается выражением v = i + j. Найдите модуль вектора, когда он масштабируется на константу 0,5.
Решение:
|v| =
0,5|v| = |0,5 В|
а = 1, б = 1
|0,5v|
|0,5(i + j)|
|0,5i + 0,5j|
|в| =
|v| =
|v| = √0,5
Пример 4. Два вектора с величиной 3 и 4. Между этими векторами угол 90°. Найдите величину результирующих векторов.
Два вектора с величиной 3 и 4. Между этими векторами угол 90°. Найдите величину результирующих векторов.
Решение:
Пусть два вектора заданы p и q. Тогда результирующий вектор «r» определяется как
|p| = 3, |q| = 4 и
|r| = 5
Пример 5. Два вектора с величиной 10 и 9. Эти векторы имеют между собой угол 60°. Найдите величину результирующих векторов.
Решение:
Пусть два вектора заданы p и q. Тогда результирующий вектор «r» определяется как
|p| = 10, |q| = 9 и
Часто задаваемые вопросы о скалярах и векторах
Вопрос 1. Что вы подразумеваете под скалярами и векторами в физике?
Ответ:
Скаляры — это физические величины, которые имеют только величину или размер.
В то время как векторы — это физические величины, которые имеют как величину, так и направление.
Вопрос 2: Приведите несколько примеров векторов.
Ответ:
Вот несколько важных примеров векторов:
- Скорость
- Сила
- Давление
- Смещение
- Ускорение
- Тяга
Вопрос 3: Listarcal вниз количества важно s.
ОТВЕТ:
Вот несколько важных примеров скаляров:
9
- MASS
- СКОРОСТЬ
- Расстояние
- Область
- объем
Область объем 9Область объем 9. Количество векторов? Ответ:
Поскольку сила является физической величиной, которая имеет как величину, так и направление.


 Список некоторых из них ниже!
Список некоторых из них ниже!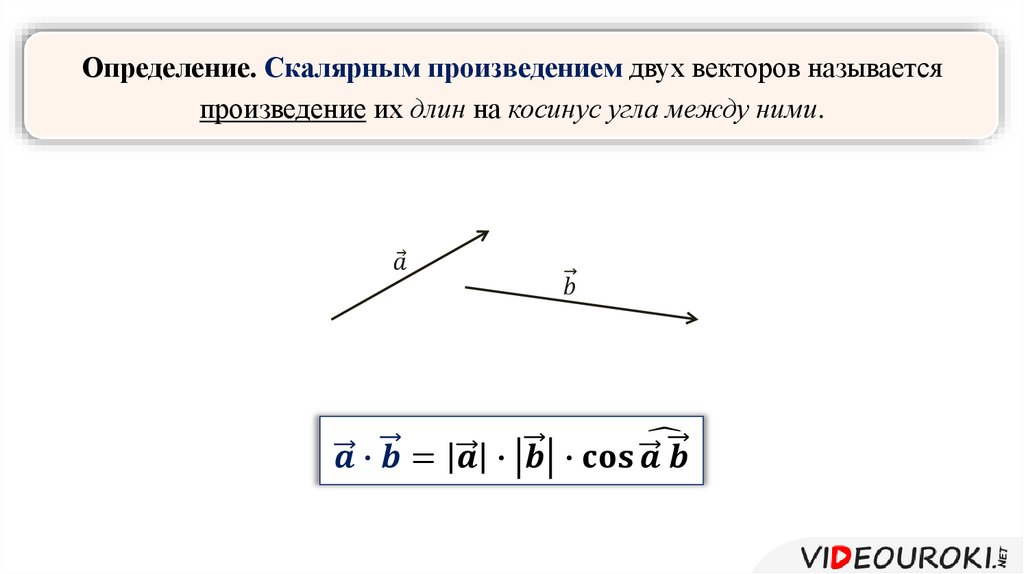 В то время как векторы — это физические величины, которые имеют как величину, так и направление.
В то время как векторы — это физические величины, которые имеют как величину, так и направление.