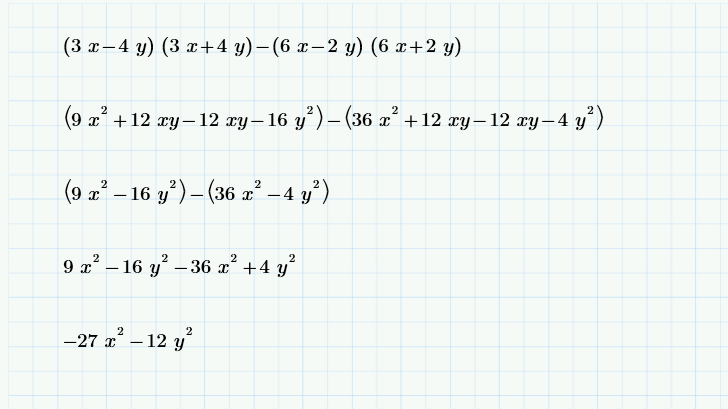X 3 x y 1 0: X+y=-3 x-y=1 система уравнений найти координаты

23-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

(10 баллов) Уравнение xy 1 = x + y2 определяет функцию y = f(x) в окрестности (-1,0).

Определите f (-1), fx (-1) fxx (-1) и второй полином Тейлора Tz (x), основанный на x = -1.

Вопрос

(10 баллов) Уравнение xy _ 1 = x + y2 определяет функцию y = f(x) в окрестности (-1,0). Определите f (-1), fx (-1) fxx (-1) и второй полином Тейлора Tz (x), основанный на x = -1.

Мгновенное решение:

Шаг 1/3
Сначала нам нужно найти функцию f(-1). Мы можем сделать это, взяв производную от y по x: у’ = f'(x)dx Теперь нам нужно найти точки, в которых эта производная обращается в нуль. Мы можем сделать это, взяв производную y по x в этих точках: у’ = 0 В точке (-1,0) производная становится равной нулю, поскольку y = 0.

---

Рекомендация видео с лучшим совпадением:

Решено проверенным экспертом

У нас нет заданного вами вопроса, но вот рекомендуемое видео, которое может помочь.

Вопрос о наилучшем совпадении

Пошаговые ответы

В упражнениях $1-10,$ используйте формулу Тейлора для $f(x, y)$ в начале координат, чтобы найти квадратичное и кубическое приближения $f$ вблизи начала координат .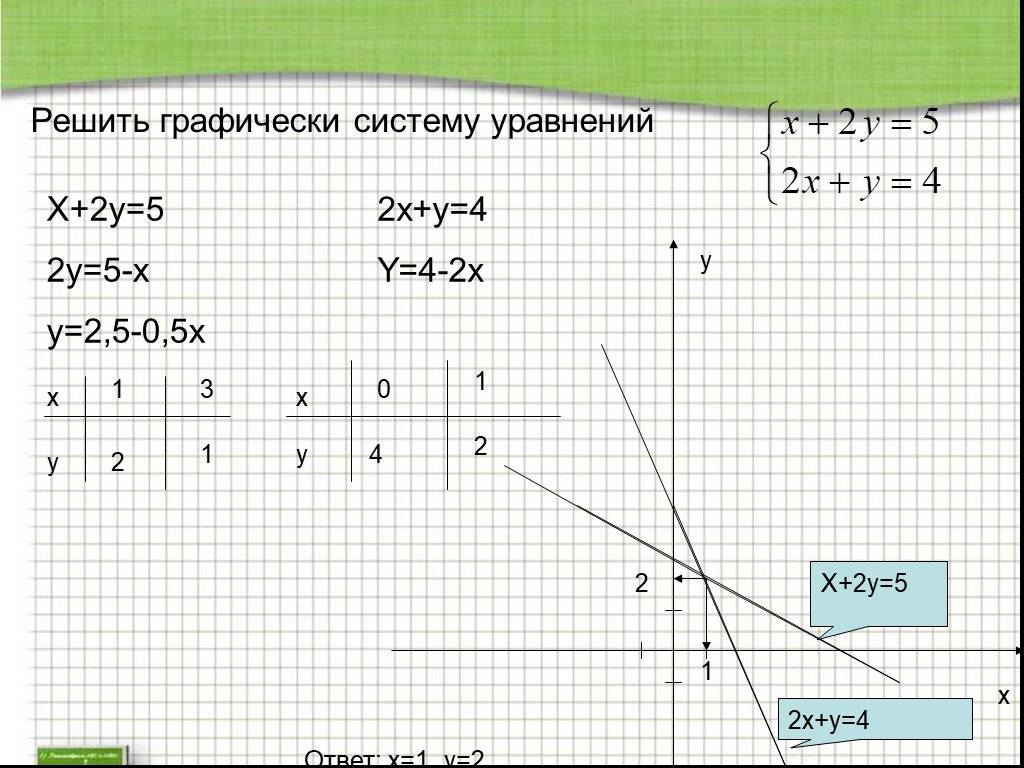

$$f(x, y)=\ln (2 x+y+1)$$

Рекомендуемые видеоролики

Стенограмма

Zehr используется для оценки значения функции в точке. Поскольку это функция двух переменных, вам нужно найти третьи частные производные включительно, чтобы найти полином Тейлора. Давайте продолжим и сделаем это. Сначала до двух с половиной. Да, 1/2 X, y и один. У нас всего несколько. Мы будем думать об этом как о чем-то в отрицательной степени, чтобы легче было взять производную. Отрицательное четыре на два X и почему плюс один в квадрате — это то, что вы получите. Следующий будет результатом этого негатива. Было более двух x плюс y и один квадрат. Один минус один на два х плюс. Причина в том, что большинство одной квадратной трети частичное. Теперь у нас есть и это. Это также. И отрицательная четверка. Отрицательное 16 на 2 х плюс. Кроме того, одна симпатичная часть X y по отношению к X. У нас также есть негатив к этому. Кроме того, это тоже. Эм, негатив. Это хорошая идея, чтобы дать положительный ответ.

Что случилось с последним? Должен был быть положительным. Это 8/2 X плюс у и один. Это мило. Давайте попробуем исправить это. Есть положительные ощущения. Это там. Производная от этого берется нами. У нас есть несколько. Ах, плохой. Это так позитивно. Положительный. А, негатив. 2Х плюс 1Х. Это мило. Последний был отрицательным. Тоже такой позитив. Больше двух плюс один. Это мило. Хорошо, хорошо. Далее, тогда. Эллен двух x плюс y плюс один был бы равен нулю, если бы мы подставили полином Тейлора. Я оставил место для этого, поэтому мы поместим его туда. Далее будет слишком негативно. Тоже четыре минуса. Один не положительный. Третьи 16 84 и два. Просто подставьте их в формулу, и вы получите X y. Это близко к константе, равной нулю. Коэффициенты y и X следующие. Итак, два х плюс один и 1/2 факториального умножения. На этот раз коэффициенты не положительные. Четыре к одному минус. Это отрицательная четверка. Извини за это. X квадрат плюс минус два раза два x y и минус один раз y в квадрате.