НОУ ИНТУИТ | Лекция | Скалярное произведение векторов. Свойства. Векторное произведение векторов. Свойства. Смешанное произведение векторов. Свойства
< Лекция 6 || Лекция 7: 123 || Лекция 8 >
Аннотация: В лекции рассматриваются линейные операции над векторами, и дается практическое использование этих операций при решении различных задач
Ключевые слова: операции, вектор, длина, модуль, компланарность, коллинеарность, Произведение, базисными векторами, ПО, Главная диагональ, произведение вектора, равенство, векторное произведение, антисимметричность, координаты, разность, направляющие косинусы, аргумент, площадь
Умножение
Различают несколько видов операции умножения.
1. Умножение вектора на скалярную величину. При умножении вектора на скаляр получают новый вектор , длина (модуль) которого изменяется в раз, а направление совпадает с направлением исходного вектора , если , или противоположно исходному вектору, если .
В координатной форме, если a = (ax;ay;az), то b = a= . Следовательно, операция умножения вектора на скаляр не влияет на компланарность (коллинеарность) векторов. Поэтому если несколько векторов до умножения на скаляр были компланарны (коллинеарны), то после умножения компланарность (коллинеарность) между ними сохранится.
Заметим, что любой вектор может быть представлен как произведение единичного, коллинеарного ему вектора на модуль рассматриваемого вектора, т.е.
2. Скалярное произведение векторов.
Определение 14. Скалярным произведением двух векторов и называется число S, равное .
Эта операция обозначается или
В частности, скалярный квадрат вектора равен квадрату его длины, т.е.
Если один из перемножаемых векторов единичный, то:
В этом случае результат представляет собой проекцию вектора на направление единичного вектора . Следовательно, любой вектор можно представить как , где a x,ay,az — проекции вектора соответственно на оси 0х, 0у и 0z.
Если вектор представлен через проекции на базисные векторы, то говорят о разложении вектора по ортогональному базису. Из рис. 6.1 видно, что в этом случае вектор является главной диагональю прямоугольного параллелепипеда, ребра которого параллельны осям координат и равны длинам проекций вектора на эти оси. Из этого же рисунка следует, что модуль вектора численно будет равен .
Рис.
6.1.
Из определения скалярного произведения следует, что любой вектор, независимо от типа, можно представить в виде:
где , и есть скалярное произведение вектора с ортами осей координат. Тогда из последнего равенства имеем
где , и — углы, которые составляет вектор соответственно с осями 0х, 0у и 0z.
Можно заметить, что скалярное произведение коммутативно и дистрибутивно, т.е. и . Можно убедиться самостоятельно в том, что всегда выполняется равенство
Замечание 1. Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны. Действительно, если ни один из векторов не нулевой, то, по определению скалярного произведения, последнее может быть равно нулю только тогда, когда
intuit.ru/2010/edi»>Замечание 2. , где — единичные векторы (орты) осей координат 2При этом оси координат могут быть взаимноперпендикулярны (ортогональны), хотя это и не обязательно. Данное замечание выполняется и для произвольной системы координат (косоугольной, криволинейной).Замечание 3. .
Замечание 4. Скалярное произведение векторов в координатной форме
Замечание 5. Используя формулу скалярного произведения векторов и , можно найти выражение косинуса угла между этими векторами через их проекции на орты:
Если , то это значит, что угол между векторами больше 90 , т.е. тупой, а если , то угол острый.
Замечание 6. Механический смысл скалярного произведения векторов.
Дальше >>
< Лекция 6 || Лекция 7: 123 || Лекция 8 >
Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число.  4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2.  Свойства скалярного произведения.3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки.  3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы.  § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов.  4. Центр системы параллельных векторов. |
Свойства вектора — равенство, сложение векторов, вычитание и умножение
В терминологии физики вы, должно быть, слышали о скалярных и векторных величинах. Мы часто определяем любую физическую величину по величине. Следовательно, физическая величина, характеризуемая величиной, называется скалярной величиной. Вот и все! Но есть и физические величины, которые наряду с направлением имеют определенную конкретную величину. Такая физическая величина, представленная ее величиной и направлением, называется векторной величиной. Таким образом, по определению вектор есть величина, характеризующаяся величиной и направлением. Сила, импульс, скорость, вес и т. д. являются типичными примерами векторной величины. В отличие от скалярной величины, о векторной величине нужно многое узнать.
Перед тем, как узнать о векторных величинах и их свойствах, давайте проведем различие между скалярными величинами и векторными величинами.
Скалярные величины
Это величины, которые имеют только величину и не имеют направления.
Скалярные величины одномерны.
С изменением величины изменяются и скалярные величины.
Математическая операция, выполняемая между двумя или более скалярными величинами, приводит к скалярной величине.
Простые алфавиты используются для обозначения скалярных величин.
Пример — скорость, время, масса, объем и т.д.
Векторные величины
Эти величины имеют как величину, так и направление.
Они могут быть одно-, двух- и трехмерными.
Векторные величины изменяются при изменении как величины, так и направления.
Результат двух или более векторных величин является векторной величиной при применении математических операций.
Для обозначения этих величин над буквами ставится стрелка.
Пример — перемещение, сила, скорость, ускорение и т. д.
Векторы обозначаются стрелкой над обозначающим символом. Например,
\[\overrightarrow{a}\] или \[ \overrightarrow{b}\] \[ \overrightarrow{b}\]
Величина вектора \[\overrightarrow{a}\] и \[\overrightarrow{b}\] обозначается через ∥a∥ и ∥b∥ соответственно.
Примерами вектора являются сила, скорость и т. д. Ниже показано, как он представлен. }\]
Линейный импульс:
\[\overrightarrow{p}\]
Вектор ускорения:
\[\overrightarrow{a}\]
Сила является вектором, поскольку сила является величиной интенсивности или силы, применяемой в каком-либо направлении. Скорость — это вектор, где его скорость — это величина, с которой объект движется по определенному пути.
Классификация векторов
В физике и математике используются различные типы векторов. Ниже приведены имена и описания этих векторов:
Нулевой вектор — это тип вектора, величина которого равна нулю.
Вектор положения. Вектор, описывающий положение точки в декартовой системе относительно начала координат, называется вектором положения.
Единичный вектор — Величина этого вектора равна единице.
Подобные векторы. Подобные векторы — это векторы, имеющие одинаковое направление.
В отличие от векторов — это векторы, имеющие противоположные направления.
Совместно-начальные векторы — Совместно-начальные векторы имеют одну и ту же начальную точку.
Равные векторы. Говорят, что векторы, имеющие одинаковую величину и направление, равны.
Копланарные векторы. Копланарные векторы — это векторы, параллельные одной плоскости или лежащие в одной плоскости.
Коллинеарные векторы.
Это векторы, параллельные друг другу, независимо от их величины и направления, называемые коллинеарными векторами.Отрицательный вектор. Два вектора, имеющие одинаковую величину, но разные направления (противоположные направления), называются отрицательными векторами друг друга.
Вектор смещения — это вектор, представляющий смещение точки из одного положения в другое.
Это векторы, параллельные друг другу, независимо от их величины и направления, называемые коллинеарными векторами.Двумерные векторы Описание
Двумерные векторы могут быть представлены в двух формах, т. е. в геометрической форме, прямоугольной записи и полярной записи.
1. Геометрическое изображение векторов
Простыми словами, линия со стрелкой — это вектор, где длина линии — величина вектора, а стрелка указывает направление вектора.
(изображение скоро будет загружено)
2.
Прямоугольное изображение
В этой форме вектор размещается в системе координат x и y, как показано на рисунке
(изображение будет загружено в ближайшее время)
Прямоугольное обозначение координат для этого вектора: \] = (6,3). Альтернативное обозначение — это использование двуединичных векторов î = (1,0) и ĵ = (0,1), так что v = 6î + 3ĵ.
3. Полярное изображение
В полярных обозначениях мы указываем модуль вектора r, r≥0 и угол θ с положительной осью x.
Теперь мы прочитаем различные свойства векторов, описанные ниже.
Равенство векторов
Если сравнить два вектора с одинаковой величиной и направлением, это равные векторы. Следовательно, если вы переводите вектор в положение без изменения его направления или вращения, т.е. параллельного переноса, вектор не меняет исходный вектор. Оба вектора до и после изменения положения являются равными векторами.
Тем не менее, было бы лучше, если бы вы помнили, что векторы одной и той же физической величины следует сравнивать вместе. Например, было бы целесообразно приравнять вектор силы 10 Н по положительной оси x и вектор скорости 10 м/с по положительной оси x.
Сложение векторов
Представьте себе два вектора a и b, их сумма будет равна a + b.
(изображение скоро будет загружено)
На изображении показана сумма двух векторов, образованных размещением векторов «голова к хвосту».
Сложение векторов следует двум законам, т. е. коммутативному закону и ассоциативному закону.
A. Коммутативный закон — порядок
, в котором добавляются два вектора, не имеет значения. Этот закон также называют законом параллелограмма. Рассмотрим параллелограмм, два смежных ребра обозначены как a + b, а другой дуэт ребер обозначен как b + a. Обе суммы равны, а значение равно величине диагонали параллелограмма
(изображение будет загружено в ближайшее время)
Изображение показывает, что закон параллелограмма, который доказывает, что сложение векторов не зависит от порядка векторов, т.
е. сложение векторов является коммутативным
B. Ассоциативный закон — сложение трех векторов не зависит от пара векторов добавлена первой.
(а+б)+с=а+(б+с).
Вычитание векторов
Сначала разберемся с вектором -a. Это вектор с равным значением a, но в противоположном направлении.
(изображение будет загружено в ближайшее время)
На изображении показаны два вектора в противоположном направлении, но одинаковой величины.
Таким образом, вычитание двух векторов определяется как сложение двух векторов в противоположном направлении.
x — y = x + (-y)
Умножение вектора на скалярное число
Рассмотрим вектор \[\overrightarrow{a}\] с величиной ∥a∥ и числом ‘n’. Если a умножается на n, то мы получаем новый вектор b. Покажи нам. Вектор \[\overrightarrow{b}\]= n \[\overrightarrow{a}\] Величина вектора \[\overrightarrow{b}\] равна ∥na∥.
Направление вектора \[\overrightarrow{b}\] совпадает с направлением вектора a \[\overrightarrow{a}\]
Если вектор \[\overrightarrow{a}\] находится в положительное направление x, вектор b \[\overrightarrow{b}\] также будет указывать в том же направлении, то есть в положительном направлении x.
Предположим, мы умножаем вектор на отрицательное число n, значение которого равно -1. Вектор \[\overrightarrow{b}\] будет в направлении, противоположном вектору \[\overrightarrow{a}\]
Произведение векторов
Перекрестное произведение двух векторов равно произведению модуля двух заданных векторов на синус угла между этими векторами. Векторное произведение представлено как
A x B = |A| |Б| sin θ nˆ
Где
A и B — два вектора
|A| = величина вектора A
|B| = величина вектора B
θ = угол между векторами A и B
\[\hat{n}\] = единичный вектор, перпендикулярный плоскости, содержащей два вектора
Некоторые свойства векторного произведения обсуждаются ниже:
A x B ≠ B x A
Но, A x B = (-B) x A
A x (B + C) = A x B + A x C
Когда векторы перпендикулярны друг другу, векторное произведение максимально.
Из-за параллельных и антипараллельных векторов векторное произведение становится равным нулю.
Когда вектор умножается сам на себя, получается нулевой вектор.
Векторы ортогональных единиц показывают перекрестный продукт следующим образом,
I x i = j x j = k x k = 0
i x j = k, j x k = i, k x i = j
j x i = -k, k x j = k = k x i = j
j x i = -k, k x j = k x i = j
j x i = -k, k x j = i, k x i = j
j x i = -k, k x j = i, k x i = j
j x i = -k, k x x -i, i x k = -j
Интересные факты
Знаете ли вы скалярное представление векторных величин, таких как скорость, вес — это скорость, а масса соответственно?
Скалярное умножение вектора выполняет многие функции обычного арифметического умножения, такие как законы распределения
a(x + y) = xa + xb(a + b)y = ay + by 1x = x(−1)x = -x 0 a = 0
Объяснение урока: Свойства операций над Векторы
В этом объяснителе мы узнаем, как использовать свойства сложения и умножения векторов.
Начнем с того, что вспомним, что вектор — это величина, имеющая как величину, так и направление. Вектор может быть представлен в подходящем пространстве направленным отрезком линии определенной длины. Это означает, что мы можем думать о векторах как о определяющих движениях, путешествующих в заданном направлении на заданное расстояние.
Эта идея позволяет нам сложить два вектора вместе; если оба вектора можно рассматривать как движение в заданном направлении на заданное расстояние, то их сумму можно рассматривать как комбинацию обоих объединенных движений.
В двух измерениях мы можем выбрать пространство, где мы можем представить величину и направление в терминах горизонтального и вертикального изменения. В этом пространстве вектор (𝑎,𝑏) имеет горизонтальную составляющую 𝑎 и вертикальную составляющую 𝑏. Мы можем думать об этом как о смещении на 𝑎 единиц по горизонтали и смещении на 𝑏 единиц по вертикали.
Это означает, что мы можем сложить два вектора вместе, учитывая их компоненты.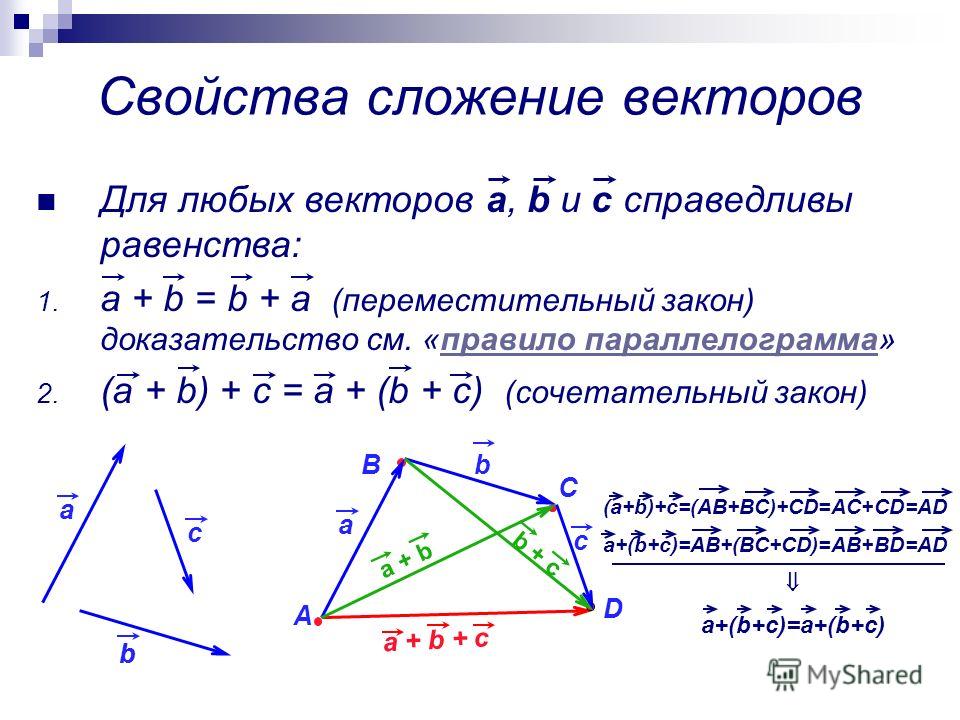
Графически сумма двух векторов ⃑𝑢 и ⃑𝑣 представляет собой комбинированное перемещение. Следовательно, мы можем нарисовать конечную точку первого вектора как начальную точку второго вектора. Затем сумма векторов имеет начальную точку первого вектора и конечную точку второго вектора, как показано на следующей диаграмме.
Поскольку вектор ⃑𝑢+⃑𝑣 представляет смещение как ⃑𝑢, так и ⃑𝑣, он будет иметь горизонтальную составляющую, равную сумме горизонтальных составляющих ⃑𝑢 и ⃑𝑣, и вертикальную составляющую, равную сумме вертикальных составляющих ⃑𝑢 и ⃑𝑣 . Это дает нам следующее.
Теорема: сложение векторов в двух измерениях
Для любых двух векторов в двух измерениях ⃑𝑢=(𝑢,𝑢) и ⃑𝑣=(𝑣,𝑣), ⃑𝑢+⃑𝑣=(𝑢+𝑣,𝑢+𝑣).
Поскольку сумма любых двух векторов в двух измерениях также является двумерным вектором, мы можем сказать, что сложение векторов в двух измерениях замкнуто. Это иногда называют свойством замыкания сложения векторов.
Эта идея распространяется на более высокие измерения; однако в этом объяснении мы будем работать только в двух измерениях.
Мы также можем определить скалярное умножение вектора как скалярное умножение его компонентов. Графически скалярное умножение вектора на скаляр 𝑘 представляет собой расширение вектора на коэффициент 𝑘.
Теорема: скалярное умножение векторов в двух измерениях
Для любых векторов ⃑𝑢=(𝑢,𝑢) и скаляра 𝑘, 𝑘⃑𝑢=(𝑘𝑢,𝑘𝑢).
Давайте рассмотрим пример использования этих определений для ответа на вопрос, связанный со свойством сложения векторов.
Пример 1: Коммутативность сложения векторов
Выполните следующие действия: (1,9)+(5,2)=(5,2)+(,).
Ответ
Начнем с упрощения левой части уравнения. Чтобы найти сумму пары векторов, вспомним, что ⃑𝑢=(𝑢,𝑢) и ⃑𝑣=(𝑣,𝑣).
Тогда, ⃑𝑢+⃑𝑣=(𝑢+𝑣,𝑢+𝑣).
В нашем случае ⃑𝑢=(1,9) и ⃑𝑣=(5,2); поэтому, (1,9)+(5,2)=(1+5,9+2)=(6,11).
Это равно правой части данного уравнения, поэтому мы будем называть недостающий вектор ⃑𝑤=(𝑤,𝑤).
Тогда мы можем упростить правую часть данного уравнения:
(5,2)+(𝑤,𝑤)=(5+𝑤,2+𝑤).
Приравнивая это к правой части уравнения, получаем (6,11)=(5+𝑤,2+𝑤).
Чтобы два вектора были равны, их соответствующие компоненты должны быть равны. Если соответствующие компоненты равны, мы получаем два уравнения: 6=5+𝑤,11=2+𝑤.
Мы можем решить их, чтобы увидеть 𝑤=1 и 𝑤=9, поэтому недостающий вектор равен ⃑𝑤=(1,9).
Есть второй способ показать это. Начнем со сложения векторов в левой части уравнения: (1,9)+(5,2)=(1+5,9+2).
Затем воспользуемся коммутативным свойством сложения: (1+5,9+2)=(5+1,2+9).
Наконец, мы можем использовать сложение векторов: (5+1,2+9)=(5,2)+(1,9).
Следовательно, пропущенный вектор равен (1,9).
Второй метод из приведенного выше вопроса можно обобщить на любые два вектора: (𝑢,𝑢)+(𝑣,𝑣)=(𝑢+𝑣,𝑢+𝑣)=(𝑣+𝑢,𝑣+𝑢)=(𝑣,𝑣)+(𝑢,𝑢).
Другими словами, для любых векторов в двух измерениях ⃑𝑢 и ⃑𝑣, ⃑𝑢+⃑𝑣=⃑𝑣+⃑𝑢.
Это известно как коммутативность сложения векторов. Графическая интерпретация этого свойства показана на следующей диаграмме.
Если ⃑𝑢 и ⃑𝑣 отличны от нуля, то мы можем изобразить эти векторы как стороны параллелограмма. Тогда вектор диагонали этого параллелограмма может быть представлен как ⃑𝑢+⃑𝑣, так и ⃑𝑣+⃑𝑢, поэтому эти выражения должны быть равны.
Нам необходимо рассмотреть случай, когда один или оба из этих векторов являются нулевыми. Если ⃑𝑢=(𝑢,𝑢), то мы можем показать, что (𝑢,𝑢)+⃑0=(𝑢,𝑢)+(0,0)=(𝑢+0,𝑢+0)=(𝑢,𝑢).
Следовательно, ⃑𝑢+⃑0=⃑𝑢.
Это называется свойством аддитивной идентичности, поскольку добавление нулевого вектора не меняет вектор.
Мы также можем продемонстрировать свойства, связанные со скалярным умножением. Например, для любого вектора ⃑𝑢=(𝑢,𝑢), 1⃑𝑢=1(𝑢,𝑢)=(1𝑢,1𝑢)=(𝑢,𝑢)=⃑𝑢.
Следовательно, 1⃑𝑢=⃑𝑢.
Это называется свойством мультипликативной идентичности, поскольку умножение вектора на скаляр 1 не влияет на его величину или направление.
Существует множество свойств сложения векторов и скалярного умножения в двух измерениях.
Мы не будем доказывать все это; однако все они могут быть получены путем рассмотрения компонентов векторов.
Теорема: свойства векторного сложения и скалярного умножения в двух измерениях
Для любых векторов скаляров 𝑛 и 𝑚 рассмотрим следующее.
- Свойства сложения векторов: ⃑𝑢+⃑𝑣 = ⃑𝑣+⃑𝑢⃑𝑢+⃑𝑣+⃑𝑤 = ⃑𝑢+⃑𝑣+⃑𝑤⃑𝑢+⃑0 = ⃑𝑢⃑𝑢+ -⃑𝑢 = ⃑0⃑𝑢+⃑𝑣 = ⃑𝑢+⃑𝑤, ⃑𝑣 = ⃑𝑤. (CommutativeProperty) (AssociativeProperty )(additiveidentityproperty)(additiveinverseproperty)Ifthen(eliminationproperty)
- Свойства скалярного умножения векторов: 𝑛⃑𝑢+⃑𝑣 = 𝑛⃑𝑢+𝑛⃑𝑣 (𝑛+𝑚) ⃑𝑢 = 𝑛⃑𝑢+𝑚⃑𝑢1⃑𝑢 = ⃑𝑢 (𝑛𝑚) ⃑𝑢 = 𝑛𝑚⃑𝑢𝑛⃑𝑢 = 𝑛⃑𝑣, ⃑𝑢 = ⃑𝑣. (DistributiveProperty) (DistributiveProperty) (MultiplicativeIdentityProperty) (AssociativeProperty )Ifthen(свойство устранения)
Все эти свойства верны для векторов размерностей выше двух и доказуемы алгебраически. Давайте теперь посмотрим на пример того, как
мы можем использовать эти свойства для вычисления выражения, включающего векторы.
Пример 2. Упрощение векторного выражения с использованием свойств векторных операций
Учитывая, что ⃑𝑎=(1,5) и ⃑𝑏=(6,2), найти ⃑𝑎+⃑𝑏+−⃑𝑎.
Ответ
Мы можем ответить на этот вопрос напрямую, используя свойства сложения векторов. Во-первых, мы воспользуемся коммутативным свойством сложения векторов, чтобы переупорядочить выражение. Это говорит о том, что для любых векторов ⃑𝑢 и ⃑𝑣 ⃑𝑢+⃑𝑣=⃑𝑣+⃑𝑢.
Применение этого выражения к нашему выражению дает ⃑𝑎+⃑𝑏+−⃑𝑎=⃑𝑎+−⃑𝑎+⃑𝑏.
Далее мы воспользуемся аддитивным обратным свойством сложения векторов, чтобы упростить выражение. Это говорит нам о том, что для любого вектора ⃑𝑢 ⃑𝑢+−⃑𝑢=⃑0.
Применяя это к нашему выражению вместе с ассоциативным свойством сложения векторов, получаем ⃑𝑎+−⃑𝑎+⃑𝑏=⃑0+⃑𝑏.
Наконец, мы будем использовать свойство аддитивной идентичности, которое говорит, что для любого вектора ⃑𝑢, ⃑𝑢+⃑0=⃑𝑢.
Следовательно, ⃑0+⃑𝑏=⃑𝑏=(6,2).
Второй метод заключается в работе с компонентами ⃑𝑎 и ⃑𝑏:
⃑𝑎+⃑𝑏+−⃑𝑎=(1,5)+(6,2)+(−(1,5)).
Распределим минус по вектору, умножив все его компоненты на −1: (1,5)+(6,2)+(-(1,5))=(1,5)+(6,2)+(-1,-5).
Теперь мы найдем сумму векторов, сложив вместе их соответствующие компоненты: (1,5)+(6,2)+(-1,-5)=(1+6-1,5+2-5)=(6,2).
В нашем следующем примере мы увидим демонстрацию того, как применять ассоциативное свойство сложения векторов. Метод сложения этих векторов вместе путем нахождения суммы их соответствующих компонентов можно обобщить, чтобы показать, что свойство ассоциативности верно для произвольных векторов.
Пример 3. Проверка ассоциативности сложения векторов в двух измерениях
Учтите, что ⃑𝑎=(1,6), ⃑𝑏=(3,7) и ⃑𝑐=(6,3).
- Найти ⃑𝑎+⃑𝑏+⃑𝑐.
- Найти ⃑𝑎+⃑𝑏+⃑𝑐.
- Равен ⃑𝑎+⃑𝑏+⃑𝑐 ⃑𝑎+⃑𝑏+⃑𝑐?
Ответ
Часть 1
Чтобы найти сумму этих векторов, складываем соответствующие компоненты: ⃑𝑎+⃑𝑏+⃑𝑐=(1,6)+((3,7)+(6,3)).
Вычисление выражения в круглых скобках дает
(1,6)+((3,7)+(6,3))=(1,6)+(3+6,7+3)=(1,6)+(9,10).
Сложение соответствующих компонентов этих векторов дает (1,6)+(9,10)=(1+9,6+10)=(10,16).
Часть 2
Для начала, ⃑𝑎+⃑𝑏+⃑𝑐=((1,6)+(3,7))+(6,3).
Вычисление выражения в круглых скобках дает ((1,6)+(3,7))+(6,3)=(1+3,6+7)+(6,3)=(4,13)+(6,3).
Сложение соответствующих компонентов этих векторов дает (4,13)+(6,3)=(4+6,13+3)=(10,16).
Часть 3
Мы показали, что оба этих выражения упрощаются и дают один и тот же вектор: (10,16). Это пример ассоциативного свойства сложения векторов. Мы можем использовать этот пример, чтобы обобщить это свойство.
Пусть ⃑𝑢=(𝑢,𝑢), ⃑𝑣=(𝑣,𝑣), и ⃑𝑤=(𝑤,𝑤).
Тогда, ⃑𝑢+⃑𝑣+⃑𝑤=((𝑢,𝑢)+(𝑣,𝑣))+(𝑤,𝑤)=(𝑢+𝑣,𝑢+𝑣)+(𝑤,𝑤)=((𝑢+𝑣) +𝑤,(𝑢+𝑣)+𝑤).
Затем мы можем использовать ассоциативное свойство сложения, чтобы переписать этот вектор: ((𝑢+𝑣)+𝑤,(𝑢+𝑣)+𝑤)=(𝑢+(𝑣+𝑤),𝑢+(𝑣+𝑤))=⃑𝑢+⃑𝑣+⃑𝑤.
Следовательно, для любых векторов в двух измерениях ⃑𝑢, ⃑𝑣 и ⃑𝑤
⃑𝑢+⃑𝑣+⃑𝑤=⃑𝑢+⃑𝑣+⃑𝑤.
В нашем следующем примере мы опишем свойство скалярного умножения и докажем, что это свойство выполняется для произвольных векторов и произвольного скаляра.
Пример 4. Описание свойства скалярного умножения
Какое свойство показывает, что 𝑐⃑𝑎+⃑𝑏=𝑐⃑𝑎+𝑐⃑𝑏?
Ответ
Это свойство называется распределительным свойством скалярного умножения над векторным сложением. Он утверждает, что для любых векторов ⃑𝑎=(𝑎,𝑎) и ⃑𝑏=(𝑏,𝑏) и скаляр 𝑐, 𝑐⃑𝑎+⃑𝑏=𝑐⃑𝑎+𝑐⃑𝑏.
Мы можем доказать это, рассмотрев компоненты ⃑𝑎 и ⃑𝑏: 𝑐⃑𝑎+⃑𝑏=𝑐((𝑎,𝑎)+(𝑏,𝑏))=𝑐(𝑎+𝑏,𝑎+𝑏).
Затем, чтобы умножить вектор на скаляр 𝑐, мы умножаем каждый компонент на 𝑐, что дает нам 𝑐(𝑎+𝑏,𝑎+𝑏)=(𝑐(𝑎+𝑏),𝑐(𝑎+𝑏)).
Далее, мы знаем, что умножение является дистрибутивным по отношению к сложению: (𝑐(𝑎+𝑏),𝑐(𝑎+𝑏))=(𝑐𝑎+𝑐𝑏,𝑐𝑎+𝑐𝑏).
Наконец, мы можем переписать это как
(𝑐𝑎+𝑐𝑏, 𝑐𝑎+𝑐𝑏) = (𝑐𝑎, 𝑐𝑎)+(𝑐𝑏, 𝑐𝑏) = 𝑐 (𝑎, 𝑎)+𝑐 (𝑏, 𝑏) = 𝑐⃑𝑎+𝑐⃑𝑏.
Это свойство известно как распределительное свойство скалярного умножения над скалярным сложением.
В следующем примере мы будем использовать свойства векторов, чтобы помочь нам определить недостающий вектор из векторного уравнения.
Пример 5. Проверка распределительного свойства скалярного умножения при сложении векторов
Выполните следующие действия: 2((2,5)+(5,1))=(,)+(10,2).
Ответ
Начнем с упрощения левой части уравнения. Во-первых, мы используем тот факт, что скалярное умножение является дистрибутивным по сравнению с векторным сложением: 2((2,5)+(5,1))=2(2,5)+2(5,1).
Затем мы можем вычислить скалярное умножение: 2(2,5)+2(5,1)=(2×2,2×5)+(2×5,2×1)=(4,10)+(10,2).
Приравнивая это к левой части уравнения, получаем (4,10)+(10,2)=(,)+(10,2).
Затем мы можем упростить это уравнение, используя свойство исключения сложения векторов, которое говорит нам, что если ⃑𝑢+⃑𝑣=⃑𝑢+⃑𝑤, то ⃑𝑣=⃑𝑤.
Чтобы было понятно, воспользуемся коммутативным свойством сложения векторов, чтобы переписать наше уравнение в виде
(10,2)+(4,10)=(10,2)+(,).
Затем мы исключаем вектор (10,2), что дает нам (4,10)=(,).
Следовательно, пропущенный вектор равен (4,10).
В нашем последнем примере мы докажем аддитивное свойство, обратное сложению векторов.
Пример 6. Описание свойства аддитивных инверсий для сложения векторов
Какое свойство сложения показывает, что ⃑𝑎+−⃑𝑎=⃑0?
Ответ
Это свойство называется аддитивным обратным свойством сложения векторов. Мы можем доказать это свойство, рассматривая компоненты вектора ⃑𝑎. Сначала пусть ⃑𝑎=(𝑎,𝑎).
Тогда, −⃑𝑎=(−1)(𝑎,𝑎)=(−𝑎,−𝑎).
Затем мы можем подставить это в наше выражение и вычислить: ⃑𝑎+−⃑𝑎=(𝑎,𝑎)+(−𝑎,−𝑎)=(𝑎−𝑎,𝑎−𝑎)=(0,0)=⃑0.
Это аддитивное обратное свойство состояний сложения векторов для любого вектора ⃑𝑎=(𝑎,𝑎), ⃑𝑎+−⃑𝑎=⃑0.
Давайте закончим повторением некоторых важных моментов этого объяснения.
Ключевые моменты
- Мы можем использовать свойства векторного сложения и скалярного умножения для упрощения выражений с участием векторов.
