Верхнетреугольная матрица: Верхнетреугольная матрица | это… Что такое Верхнетреугольная матрица?

Верхнетреугольная матрица | это… Что такое Верхнетреугольная матрица?

ТолкованиеПеревод

Верхнетреугольная матрица

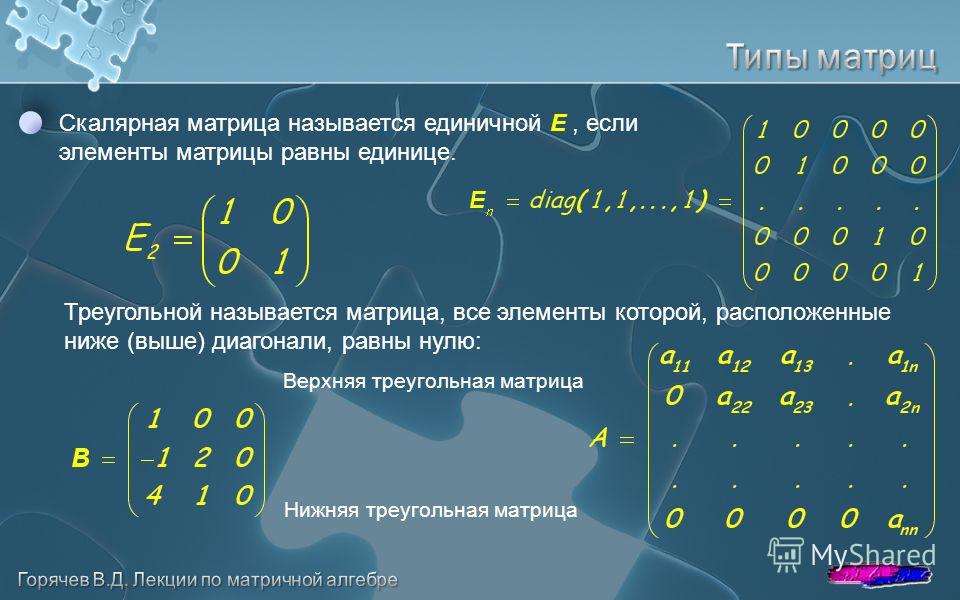
Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.

Пример верхнетреугольной матрицы

Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.

Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.

Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:

Любую ненулевую матрицу путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.

Свойства

• Определитель треугольной матрицы равен произведению элементов на её главной диагонали .
• Определитель унитреугольной матрицы равен единице.
• Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается UT(n, k) или UT_n (k).
• Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT(n, k) или LT_n (k).
• Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT_n (k
  ) по умножению, которая обозначается SUT(n, k) или SUT_n (k). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLT_n (k).
• Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
• Группа UT_n разрешима, а её унитреугольная подгруппа SUT_n нильпотентна.

См. также

• Система линейных алгебраических уравнений
• Элементарные преобразования матрицы

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

• Верхнетериберская ГЭС
• Верхнеудинский забайкальский казачий полк

Полезное

Верхняя треугольная матрица | это… Что такое Верхняя треугольная матрица?

ТолкованиеПеревод

Верхняя треугольная матрица

Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.

Пример верхнетреугольной матрицы

Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.

Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.

Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:

Любую ненулевую матрицу путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.

Свойства

• Определитель треугольной матрицы равен произведению элементов на её главной диагонали .
• Определитель унитреугольной матрицы равен единице.
• Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается UT(n, k) или UT_n (k).
• Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT(n, k) или LT_n (k).
• Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT_n (k) по умножению, которая обозначается SUT(n, k) или SUT_n (k). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLT_n (k).
• Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.
• Группа UT_n разрешима, а её унитреугольная подгруппа
  SUT_n нильпотентна.

См. также

• Система линейных алгебраических уравнений
• Элементарные преобразования матрицы

Wikimedia Foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

• Верхняя губа
• Верхняя улица

Полезное

Треугольная матрица

— нижняя и верхняя треугольная матрица, примеры

LearnPracticeDownload

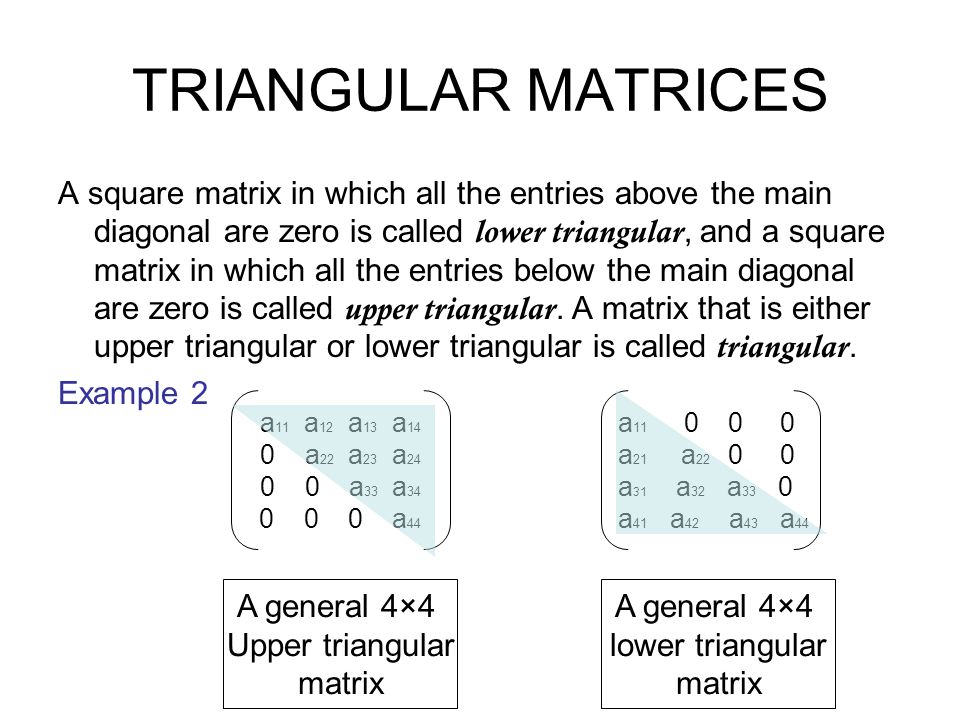
Треугольная матрица — это квадратная матрица, в которой все элементы ниже и/или выше диагонали равны нулю. У нас есть в основном два типа треугольных матриц.

• Квадратная матрица, все элементы которой выше главной диагонали равны нулю, называется нижней треугольной матрицей .
• Квадратная матрица, все элементы которой ниже главной диагонали равны нулю, называется верхняя треугольная матрица .

В этой статье давайте рассмотрим различные типы треугольных матриц, включая верхнюю треугольную матрицу и нижнюю треугольную матрицу, их определения и свойства. Мы также решим несколько примеров на основе треугольной матрицы для лучшего понимания концепции.

1.	Что такое треугольная матрица?
2.	Типы треугольных матриц
3.	Верхняя треугольная матрица
4.	Нижняя треугольная матрица
5.	Свойства треугольной матрицы
6.	Часто задаваемые вопросы о треугольной матрице

Что такое треугольная матрица?

Треугольная матрица — это особый вид квадратной матрицы в наборе матриц. Существует два типа треугольных матриц: нижняя треугольная матрица и верхняя треугольная матрица.

• Квадратная матрица называется нижней треугольной матрицей, если все элементы над ее главной диагональю равны нулю.
• Квадратная матрица называется верхнетреугольной, если все элементы ниже главной диагонали равны нулю.

Ниже приведен пример треугольной матрицы:

\(A = \left[\begin{array}{ccc} 2 & -1 & 3 \\ 0 & 5 & 2\\ 0 & 0 & -2 \end{array}\right]\) (верхний треугольник)

\(B = \left[\begin{array}{ccc} 2 & 0 & 0 \\ 1 & 5 & 0 \\ 1 & -1 & -2 \end{массив}\right]\) (нижний треугольник)

Типы треугольных матриц

Мы изучаем различные типы треугольных матриц. Ниже приведен список некоторых специальных типов треугольных матриц:

• Верхняя треугольная матрица: Говорят, что треугольная матрица является верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
• Нижняя треугольная матрица: треугольная матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
• Строго треугольная матрица: треугольная матрица называется строго треугольной, если все элементы главной диагонали равны нулю.
• Строго нижняя треугольная матрица: Нижняя треугольная матрица называется строго нижней треугольной матрицей, если все элементы главной диагонали равны нулю.
• Строго верхнетреугольная матрица: Верхняя треугольная матрица называется строго верхнетреугольной матрицей, если все элементы главной диагонали равны нулю.
• Единичная треугольная матрица: говорят, что треугольная матрица является единичной треугольной матрицей, если все элементы главной диагонали равны 1.
• Единичная нижняя треугольная матрица: Нижняя треугольная матрица называется единичной нижней треугольной матрицей, если все элементы главной диагонали равны 1.
• Единичная верхняя треугольная матрица: Верхняя треугольная матрица называется единичной верхней треугольной матрицей, если все элементы главной диагонали равны 1.

В следующих разделах мы в основном исследуем два типа треугольных матриц, а именно верхнюю и нижнюю треугольную матрицу.

Верхняя треугольная матрица

Квадратная матрица размера n × n A = [a _ij ] называется верхней треугольной матрицей тогда и только тогда, когда a _ij = 0 для всех i > j. Это означает, что все элементы ниже главной диагонали квадратной матрицы равны нулю в верхней треугольной матрице. Общее обозначение верхнетреугольной матрицы U = [u _ij для i ≤ j, 0 для i > j]. Пример верхней треугольной матрицы приведен ниже:

\(U = \left[\begin{array}{ccc} 6 & 0 & 8 \\ 0 & 10 & -12\\ 0 & 0 & 2 \end {массив}\справа]\)

Нижняя треугольная матрица

Квадратная матрица размера n × n A = [a _ij ] называется нижней треугольной матрицей тогда и только тогда, когда a _ij = 0 для всех i < j. Это означает, что все элементы выше главной диагонали квадратной матрицы равны нулю в нижней треугольной матрице. Общее обозначение нижней треугольной матрицы: L = [l _ij для i ≥ j, 0 для i < j]. Ниже приведен пример нижней треугольной матрицы:

\(L = \left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & -8 & 0 \\ 3 & -4 & 2 \конец{массив}\справа]\)

Свойства треугольной матрицы

Поскольку мы поняли смысл треугольной матрицы, давайте рассмотрим некоторые ее важные свойства. Ниже приведен список свойств треугольной матрицы:

• Транспонирование треугольной матрицы является треугольным.
• Транспонирование нижней треугольной матрицы равно n верхней треугольной матрице и наоборот.
• Произведение двух треугольных матриц есть треугольная матрица.
• Треугольная матрица обратима тогда и только тогда, когда все элементы главной диагонали отличны от нуля.
• Произведение двух нижних (верхних) треугольных матриц есть нижняя (верхняя) треугольная матрица.
• Обратная треугольная матрица является треугольной.
• Определитель треугольной матрицы является произведением элементов главной диагонали.

Важные замечания о треугольной матрице

• Обратимая матрица может быть записана как произведение нижней треугольной и верхней треугольной матриц тогда и только тогда, когда ее старшие главные миноры отличны от нуля. Это также известно как разложение LU.
• В матрице есть как верхняя, так и нижняя треугольная, тогда она называется диагональной матрицей.

Темы, связанные с треугольной матрицей

• Калькулятор матриц
• Формула матрицы

 

Примеры треугольной матрицы

1. Пример 1: Определите, является ли данная матрица треугольной. Также определите его тип.

   \(A = \left[\begin{array}{ccc} -1 & 0 \\ \\ 9 & -8 \end{array}\right]\)

   Решение:

   Элемент выше диагональ ₁₂ = 0, а ниже диагонали ₂₁ = 9.

   Следовательно, данная матрица является нижней треугольной матрицей, так как элемент выше главной диагонали равен нулю.

   Ответ: Следовательно, матрица A является нижней треугольной матрицей.

2. Пример 2: Найдите значения ‘a’ и ‘b’ в заданной матрице B такие, что B является строго верхней треугольной матрицей.

   \(B = \left[\begin{array}{ccc} 2a & 3 \\ \\ b & 0 \end{array}\right]\)

   Решение:

   Предположим, что B — строго верхняя треугольная матрица, элементы под диагональю равны нулю, а элементы главной диагонали равны нулю.

   Следовательно, мы должны иметь 2a = 0 и b = 0.

   Теперь 2a = 0 ⇒ a = 0

   Ответ: Следовательно, a = 0 и b = 0.

3. Пример 3: Найдите определитель матрицы A = \(\left[\begin{array}{ccc}
   2 & 0 & 0 \
   0&а&0\
   1 и 4 и б
   \end{массив}\right]\).

   Решение:

   Данная матрица является треугольной матрицей (нижней), так как все ее элементы выше диагонали равны нулю.

   Следовательно, его определитель есть произведение диагональных элементов.

   Итак, det A = (2)(a)(b) = 2ab.

   Ответ: 2аб.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.

Часто задаваемые вопросы о треугольной матрице

Что такое треугольная матрица в линейной алгебре?

Треугольная матрица — это особый тип квадратной матрицы в линейной алгебре, элементы которой ниже и выше диагонали имеют форму треугольника. Элементы выше и/или ниже главной диагонали треугольной матрицы равны нулю.

Каковы свойства треугольной матрицы?

Некоторые из важных свойств треугольных матриц:

• Транспонирование треугольной матрицы является треугольным.
• Произведение двух треугольных матриц есть треугольная матрица.
• Определитель треугольной матрицы равен произведению элементов главной диагонали.

Как называется матрица, если она одновременно и верхняя, и нижняя треугольная?

Если матрица одновременно нижнетреугольная и верхнетреугольная, то все ее недиагональные элементы равны нулю. В этом случае она называется диагональной матрицей.

Когда треугольная матрица обратима?

Треугольная матрица (нижняя или верхняя) обратима тогда и только тогда, когда все элементы главной диагонали отличны от нуля.

Что такое верхнетреугольная матрица?

Квадратная матрица размера n × n A = [a _ij ] называется верхнетреугольной матрицей тогда и только тогда, когда a _ij = 0 для всех i > j. Это означает, что все элементы ниже главной диагонали квадратной матрицы равны нулю в верхней треугольной матрице.

Что такое обратная нижняя треугольная матрица?

Обратная нижняя треугольная матрица также является нижней треугольной матрицей.

Как найти определитель треугольной матрицы?

Определитель треугольной матрицы можно найти, взяв произведение элементов главной диагонали.

Каковы собственные значения треугольной матрицы?

Собственные значения треугольной матрицы (верхние или нижние) — это элементы главной диагонали треугольной матрицы.

Скачать БЕСПЛАТНЫЕ учебные материалы

ЛИСТКИ

Рабочие листы по математике и визуальные учебные программы

Треугольная матрица — нижняя и верхняя треугольная матрица с примерами

Матрица определяется как прямоугольный массив чисел, которые расположены в строках и столбцах. Размер матрицы можно определить по количеству строк и столбцов в ней. Говорят, что матрица представляет собой матрицу «m на n», если она имеет «m» строк и «n» столбцов и записана как матрица «m × n». Например, матрица порядка «5 × 6» имеет пять строк и шесть столбцов. У нас есть различные типы матриц, такие как прямоугольные, квадратные, треугольные, симметричные, сингулярные и т. д.

Что такое треугольная матрица?

Треугольная матрица — это частный случай квадратной матрицы, в которой все элементы выше или ниже главной диагонали равны нулю. Верхняя треугольная матрица — это квадратная матрица, все элементы которой ниже главной диагонали равны нулю. Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю. Матрицы на изображении, приведенном ниже, являются верхней треугольной и нижней треугольной матрицами порядка «4 × 4».

 

Типы треугольных матриц

Существуют различные типы матриц, которые обсуждаются ниже в этой статье:

• Верхняя треугольная матрица: Верхняя треугольная матрица представляет собой квадратную матрицу, все элементы которой ниже главной диагонали равны нулю. .

• Нижняя треугольная матрица: Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю.

• Строго треугольная матрица: Треугольная матрица называется строго треугольной, если все элементы главной диагонали равны нулю.
• Строго нижняя треугольная матрица: Нижняя треугольная матрица называется строго нижней треугольной матрицей, если все элементы главной диагонали равны нулю.

• Строго верхнетреугольная матрица: Верхнетреугольная матрица называется строго верхнетреугольной матрицей, если все элементы главной диагонали равны нулю.

• Единичная треугольная матрица: Треугольная матрица называется единичной треугольной матрицей, если все элементы главной диагонали равны единице.
• Единичная нижняя треугольная матрица: Нижняя треугольная матрица называется единичной нижней треугольной матрицей, если все элементы главной диагонали равны единице.

• Единичная верхняя треугольная матрица: Верхняя треугольная матрица называется единичной верхней треугольной матрицей, если все элементы главной диагонали равны единице.

Верхняя треугольная матрица

Верхняя треугольная матрица — это квадратная матрица, все элементы которой ниже главной диагонали равны нулю. Квадратная матрица «A = [a _ij ]» называется верхней треугольной матрицей, когда _ij = 0 для всех i > j.

Если U _n,n является квадратной матрицей порядка «n × n», а u _ij представляет собой элемент в i ^-й -й строке и j ^-м -м столбце данной матрицы, то

Примеры верхней треугольной матрицы

Приведенная ниже матрица представляет собой верхнюю треугольную матрицу порядка «2 × 2». Мы видим, что элементы ниже главной диагонали равны нулям.

Приведенная ниже матрица является верхней треугольной матрицей порядка «3 × 3».

Нижняя треугольная матрица

Нижняя треугольная матрица — это квадратная матрица, все элементы которой выше главной диагонали равны нулю. Квадратная матрица «A = [a _ij ]» называется нижней треугольной матрицей, когда a _ij = 0 для всех i < j.

Если L — квадратная матрица порядка «n × n», а l _ij представляет собой элемент i ^th строк и j ^-й -й столбец данной матрицы, то условие того, что данная матрица является нижней треугольной матрицей, задается следующим образом:

элемент в i-й строке и j-м столбце данной матрицы, то условие того, что данная матрица является нижней треугольной матрицей, задается следующим образом:

 

Примеры нижней треугольной матрицы нижняя треугольная матрица порядка «2 × 2».

Приведенная ниже матрица представляет собой нижнюю треугольную матрицу порядка «3 × 3». Мы видим, что элементы выше главной диагонали являются нулями.

Свойства треугольной матрицы

Различные свойства треугольной матрицы обсуждаются ниже в этой статье:

• Транспонирование верхней треугольной матрицы является нижней треугольной матрицей, т. , а транспонированием нижней треугольной матрицы является верхняя треугольная матрица, т. е. L ^T = U.
• Определитель треугольной матрицы любого порядка равен произведению элементов главной диагонали.
• Обратная треугольная матрица также будет треугольной матрицей.
• Треугольная матрица обратима тогда и только тогда, когда все элементы главной диагонали отличны от нуля.
• При перемножении двух треугольных матриц результирующая матрица также будет треугольной.
• При перемножении двух верхних (нижних) треугольных матриц результирующая матрица также является верхней (нижней) треугольной матрицей.
• При добавлении двух верхних (нижних) треугольных матриц результирующая матрица также является верхней (нижней) треугольной матрицей.

Также проверьте

• Миноры и сомножители определителей
• Определитель квадратной матрицы
• Сопряженная квадратная матрица

Решенные примеры на треугольной матрице 5 Пример 1. Вычисление определителя матрицы нижеприведенный.

Решение:

Можно заметить, что данная матрица является верхней треугольной матрицей.

Мы знаем, что определитель верхнетреугольной матрицы любого порядка равен произведению элементов главной диагонали.

Итак, |А| = 1 × 7 × 8 = 56

Следовательно, определитель данной матрицы равен 56.

Пример 2: Докажите, что матрица, обратная обратной нижней треугольной матрице, также будет нижней треугольной матрицей.

Решение:

Рассмотрим нижнюю треугольную матрицу порядка «2 × 2», чтобы доказать, что матрица, обратная обратной нижней треугольной матрице, также будет нижней треугольной матрицей.

L ^-1 = Adj L/ |L|

|Л| = 5 × 8
    = 40

Мы видим, что обратная матрица также является нижней треугольной матрицей.

Значит, доказано.

Пример 3. Докажите, что транспонирование верхней треугольной матрицы является нижней треугольной матрицей.

Решение:

Чтобы доказать, что транспонирование верхней треугольной матрицы является нижней треугольной матрицей, рассмотрим верхнюю треугольную матрицу.

Теперь

Мы можем заметить, что результирующая матрица является нижней треугольной матрицей.

Отсюда доказано.

Пример 4: Найдите значения «a» и «b» в заданной матрице P, если P — единичная нижняя треугольная матрица.

Решение:

Мы знаем, что нижняя треугольная матрица называется единичной нижней треугольной матрицей, если все элементы главной диагонали равны единице.

Итак, 2а + 5 = 1

2а = 1 — 5 = -4

а = -4/2 = -2

3b — 2 = 1

3b = 1 + 2 = 3

3/3
   = 1

Следовательно, значения «a» и «b» равны −2 и 1 соответственно.

Часто задаваемые вопросы о треугольной матрице

Вопрос 1: Что подразумевается под треугольной матрицей?

Ответ:

Треугольная матрица является частным случаем квадратной матрицы, в которой все элементы выше или ниже главной диагонали равны нулю.

Вопрос 2: Что такое верхняя треугольная матрица?

Ответ:

Верхней треугольной матрицей называется квадратная матрица, все элементы которой ниже главной диагонали равны нулю. Квадратная матрица «A = [a _ij ]» называется верхней треугольной матрицей, когда _ij = 0 для всех i > j.

Вопрос 3: Что такое определитель верхней треугольной матрицы?

Ответ:

Определитель верхней треугольной матрицы любого порядка равен произведению элементов главной диагонали.

No related posts.