Как посчитать вероятность события. Формула вероятности события
«Случайности не случайны»… Звучит так, словно сказал философ, но на деле изучать случайности удел великой науки математики. В математике случайностями занимается теория вероятности. Формулы и примеры заданий, а также основные определения этой науки будут представлены в статье.
Что такое теория вероятности?
Теория вероятности — это одна из математических дисциплин, которая изучает случайные события.
Чтобы было немного понятнее, приведем небольшой пример: если подкинуть вверх монету, она может упасть «орлом» или «решкой». Пока монета находится в воздухе, обе эти вероятности возможны. То есть вероятность возможных последствий соотносится 1:1. Если из колоды с 36-ю картами вытащить одну, тогда вероятность будет обозначаться как 1:36. Казалось бы, что здесь нечего исследовать и предугадывать, тем более при помощи математических формул. Тем не менее, если повторять определенное действие много раз, то можно выявить некую закономерность и на ее основе спрогнозировать исход событий в других условиях.
Если обобщить все вышесказанное, теория вероятности в классическом понимании изучает возможность возникновения одного из возможных событий в числовом значении.
Со страниц истории
Теория вероятности, формулы и примеры первых заданий появились еще в далеком Средневековье, когда впервые возникли попытки спрогнозировать исход карточных игр.
Изначально теория вероятности не имела ничего общего с математикой. Она обосновывалась эмпирическими фактами или свойствами события, которое можно было воспроизвести на практике. Первые работы в этой сфере как в математической дисциплине появились в XVII веке. Родоначальниками стали Блез Паскаль и Пьер Ферма. Длительное время они изучали азартные игры и увидели определенные закономерности, о которых и решили рассказать обществу.
Такую же методику изобрел Христиан Гюйгенс, хотя он не был знаком с результатами исследований Паскаля и Ферма. Понятие «теория вероятности», формулы и примеры, что считаются первыми в истории дисциплины, были введены именно им.
Немаловажное значение имеют и работы Якоба Бернулли, теоремы Лапласа и Пуассона. Они сделали теорию вероятности больше похожей на математическую дисциплину. Свой теперешний вид теория вероятностей, формулы и примеры основных заданий получили благодаря аксиомам Колмогорова. В результате всех изменений теория вероятности стала одним из математических разделов.
Базовые понятия теории вероятностей. События
Главным понятием этой дисциплины является «событие». События бывают трех видов:
- Достоверные. Те, которые произойдут в любом случае (монета упадет).
- Невозможные. События, что не произойдут ни при каком раскладе (монета останется висеть в воздухе).
- Случайные. Те, что произойдут или не произойдут. На них могут повлиять разные факторы, которые предугадать очень трудно. Если говорить о монете, то случайные факторы, что могут повлиять на результат: физические характеристики монеты, ее форма, исходное положение, сила броска и т.
 д.
д.
Все события в примерах обозначаются заглавными латинскими буквами, за исключением Р, которой отведена другая роль. Например:
- А = «студенты пришли на лекцию».
- Ā = «студенты не пришли на лекцию».
В практических заданиях события принято записывать словами.
Одна из важнейших характеристик событий — их равновозможность. То есть, если подбросить монету, все варианты исходного падения возможны, пока она не упала. Но также события бывают и не равновозможными. Это происходит, когда кто-то специально воздействует на исход. Например, «меченые» игральные карты или игральные кости, в которых смещен центр тяжести.
Еще события бывают совместимыми и несовместимыми. Совместимые события не исключают появления друг друга. Например:
- А = «студентка пришла на лекцию».
- В = «студент пришел на лекцию».
Эти события независимы друг от друга, и появление одного из них не влияет на появление другого. Несовместимые события определяются тем, что появление одного исключает появление другого. Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.
Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.
Действия над событиями
События можно умножать и складывать, соответственно, в дисциплине вводятся логические связки «И» и «ИЛИ».Сумма определяется тем, что может появиться или событие А, или В, или два одновременно. В случае когда они несовместимы, последний вариант невозможен, выпадет или А, или В.
Умножение событий заключается в появлении А и В одновременно.
Теперь можно привести несколько примеров, чтобы лучше запомнились основы, теория вероятности и формулы. Примеры решения задач далее.
Задание 1 : Фирма принимает участие в конкурсе на получение контрактов на три разновидности работы. Возможные события, которые могут произойти:
- А = «фирма получит первый контракт».
- А 1 = «фирма не получит первый контракт».
- В = «фирма получит второй контракт».
- В 1 = «фирма не получит второй контракт»
- С = «фирма получит третий контракт».

- С 1 = «фирма не получит третий контракт».
С помощью действий над событиями попробуем выразить следующие ситуации:
- К = «фирма получит все контракты».
В математическом виде уравнение будет иметь следующий вид: К = АВС.
- М = «фирма не получит ни одного контракта».
М = А 1 В 1 С 1 .
Усложняем задание: H = «фирма получит один контракт». Поскольку не известно, какой именно контракт получит фирма (первый, второй или третий), необходимо записать весь ряд возможных событий:
Н = А 1 ВС 1 υ АВ 1 С 1 υ А 1 В 1 С.
А 1 ВС 1 — это ряд событий, где фирма не получает первый и третий контракт, но получает второй. Соответственным методом записаны и другие возможные события. Символ υ в дисциплине обозначает связку «ИЛИ». Если перевести приведенный пример на человеческий язык, то фирма получит или третий контракт, или второй, или первый. Подобным образом можно записывать и другие условия в дисциплине «Теория вероятности».
Собственно, вероятность
Пожалуй, в этой математической дисциплине вероятность события — это центральное понятие. Существует 3 определения вероятности:
- классическое;
- статистическое;
- геометрическое.
Каждое имеет свое место в изучении вероятностей. Теория вероятности, формулы и примеры (9 класс) в основном используют классическое определение, которое звучит так:
- Вероятность ситуации А равняется отношению числа исходов, что благоприятствуют ее появлению, к числу всех возможных исходов.
Формула выглядит так: Р(А)=m/n.
А — собственно, событие. Если появляется случай, противоположный А, его можно записывать как Ā или А 1 .
m — количество возможных благоприятных случаев.
n — все события, которые могут произойти.
 Соответственно, формула решения задания будет иметь вид:
Соответственно, формула решения задания будет иметь вид:Р(А)=9/36=0,25.
В итоге вероятность того, что из колоды вытянут карту червовой масти, составит 0,25.
К высшей математике
Теперь стало немного известно, что такое теория вероятности, формулы и примеры решения заданий, которые попадаются в школьной программе. Однако теория вероятностей встречается и в высшей математике, которая преподается в вузах. Чаще всего там оперируют геометрическими и статистическими определениями теории и сложными формулами.
Очень интересна теория вероятности. Формулы и примеры (высшая математика) лучше начинать изучать с малого — со статистического (или частотного) определения вероятности.
Статистический подход не противоречит классическому, а немного расширяет его. Если в первом случае нужно было определить, с какой долей вероятности произойдет событие, то в этом методе необходимо указать, как часто оно будет происходить. Здесь вводится новое понятие «относительная частота», которую можно обозначить W n (A). Формула ничем не отличается от классической:
Формула ничем не отличается от классической:
Если классическая формула вычисляется для прогнозирования, то статистическая — согласно результатам эксперимента. Возьмем, к примеру, небольшое задание.
Отдел технологического контроля проверяет изделия на качество. Среди 100 изделий нашли 3 некачественных. Как найти вероятность частоты качественного товара?
А = «появление качественного товара».
W n (A)=97/100=0,97
Таким образом, частота качественного товара составляет 0,97. Откуда взяли 97? Из 100 товаров, которые проверили, 3 оказались некачественными. От 100 отнимаем 3, получаем 97, это количество качественного товара.
Немного о комбинаторике
Еще один метод теории вероятности называют комбинаторикой. Его основной принцип состоит в том, что если определенный выбор А можно осуществить m разными способами, а выбор В — n разными способами, то выбор А и В можно осуществить путем умножения.
Например, из города А в город В ведет 5 дорог. Из города В в город С ведет 4 пути. Сколькими способами можно доехать из города А в город С?
Сколькими способами можно доехать из города А в город С?
Все просто: 5х4=20, то есть двадцатью разными способами можно добраться из точки А в точку С.
Усложним задание. Сколько существует способов раскладывания карт в пасьянсе? В колоде 36 карт — это исходная точка. Чтобы узнать количество способов, нужно от исходной точки «отнимать» по одной карте и умножать.То есть 36х35х34х33х32…х2х1= результат не вмещается на экран калькулятора, поэтому его можно просто обозначить 36!. Знак «!» возле числа указывает на то, что весь ряд чисел перемножается между собой.
В комбинаторике присутствуют такие понятия, как перестановка, размещение и сочетание. Каждое из них имеет свою формулу.
Упорядоченный набор элементов множества называют размещением. Размещения могут быть с повторениями, то есть один элемент можно использовать несколько раз. И без повторений, когда элементы не повторяются. n — это все элементы, m — элементы, которые участвуют в размещении. Формула для размещения без повторений будет иметь вид:
A n m =n!/(n-m)!
Соединения из n элементов, которые отличаются только порядком размещения, называют перестановкой.
Сочетаниями из n элементов по m называют такие соединения, в которых важно, какие это были элементы и каково их общее количество. Формула будет иметь вид:
A n m =n!/m!(n-m)!
Формула Бернулли
В теории вероятности, так же как и в каждой дисциплине, имеются труды выдающихся в своей области исследователей, которые вывели ее на новый уровень. Один из таких трудов — формула Бернулли, что позволяет определять вероятность появления определенного события при независимых условиях. Это говорит о том, что появление А в эксперименте не зависит от появления или не появления того же события в ранее проведенных или последующих испытаниях.
Уравнение Бернулли:
P n (m) = C n m ×p m ×q n-m .
Вероятность (р) появления события (А) неизменна для каждого испытания. Вероятность того, что ситуация произойдет ровно m раз в n количестве экспериментов, будет вычисляться формулой, что представлена выше. Соответственно, возникает вопрос о том, как узнать число q.
Если событие А наступает р количество раз, соответственно, оно может и не наступить. Единица — это число, которым принято обозначать все исходы ситуации в дисциплине. Поэтому q — число, которое обозначает возможность ненаступления события.
Теперь вам известна формула Бернулли (теория вероятности). Примеры решения задач (первый уровень) рассмотрим далее.
Задание 2: Посетитель магазина сделает покупку с вероятностью 0,2. В магазин зашли независимым образом 6 посетителей. Какова вероятность того, что посетитель сделает покупку?
Решение: Поскольку неизвестно, сколько посетителей должны сделать покупку, один или все шесть, необходимо просчитать все возможные вероятности, пользуясь формулой Бернулли.
А = «посетитель совершит покупку».
В этом случае: р = 0,2 (как указано в задании). Соответственно, q=1-0,2 = 0,8.
n = 6 (поскольку в магазине 6 посетителей). Число m будет меняться от 0 (ни один покупатель не совершит покупку) до 6 (все посетители магазина что-то приобретут). В итоге получим решение:
В итоге получим решение:
P 6 (0) = C 0 6 ×p 0 ×q 6 =q 6 = (0,8) 6 = 0,2621.
Ни один из покупателей не совершит покупку с вероятностью 0,2621.
Как еще используется формула Бернулли (теория вероятности)? Примеры решения задач (второй уровень) далее.
После вышеприведенного примера возникают вопросы о том, куда делись С и р. Относительно р число в степени 0 будет равно единице. Что касается С, то его можно найти формулой:
C n m = n! / m!(n-m)!
Поскольку в первом примере m = 0, соответственно, С=1, что в принципе не влияет на результат. Используя новую формулу, попробуем узнать, какова вероятность покупки товаров двумя посетителями.
P 6 (2) = C 6 2 ×p 2 ×q 4 = (6×5×4×3×2×1) / (2×1×4×3×2×1) × (0,2) 2 × (0,8) 4 = 15 × 0,04 × 0,4096 = 0,246.
Не так уж и сложна теория вероятности. Формула Бернулли, примеры которой представлены выше, прямое тому доказательство.
Формула Пуассона
Уравнение Пуассона используется для вычисления маловероятных случайных ситуаций.
Основная формула:
P n (m)=λ m /m! × e (-λ) .
При этом λ = n х p. Вот такая несложная формула Пуассона (теория вероятности). Примеры решения задач рассмотрим далее.
Задание 3 : На заводе изготовили детали в количестве 100000 штук. Появление бракованной детали = 0,0001. Какова вероятность, что в партии будет 5 бракованных деталей?
Как видим, брак — это маловероятное событие, в связи с чем для вычисления используется формула Пуассона (теория вероятности). Примеры решения задач подобного рода ничем не отличаются от других заданий дисциплины, в приведенную формулу подставляем необходимые данные:
А = «случайно выбранная деталь будет бракованной».
р = 0,0001 (согласно условию задания).
n = 100000 (количество деталей).
m = 5 (бракованные детали). Подставляем данные в формулу и получаем:
Р 100000 (5) = 10 5 /5! Х е -10 = 0,0375.
Так же как и формула Бернулли (теория вероятности), примеры решений с помощью которой написаны выше, уравнение Пуассона имеет неизвестное е. По сути его можно найти формулой:
По сути его можно найти формулой:
е -λ = lim n ->∞ (1-λ/n) n .
Однако есть специальные таблицы, в которых находятся практически все значения е.
Теорема Муавра-Лапласа
Если в схеме Бернулли количество испытаний достаточно велико, а вероятность появления события А во всех схемах одинакова, то вероятность появления события А определенное количество раз в серии испытаний можно найти формулой Лапласа:
Р n (m)= 1/√npq x ϕ(X m).
X m = m-np/√npq.
Чтобы лучше запомнилась формула Лапласа (теория вероятности), примеры задач в помощь ниже.
Сначала найдем X m , подставляем данные (они все указаны выше) в формулу и получим 0,025. При помощи таблиц находим число ϕ(0,025), значение которого 0,3988. Теперь можно подставлять все данные в формулу:
Р 800 (267) = 1/√(800 х 1/3 х 2/3) х 0,3988 = 3/40 х 0,3988 = 0,03.
Таким образом, вероятность того, что рекламная листовка сработает ровно 267 раз, составляет 0,03.
Формула Байеса
Формула Байеса (теория вероятности), примеры решения заданий с помощью которой будут приведены ниже, представляет собой уравнение, которое описывает вероятность события, опираясь на обстоятельства, которые могли быть связаны с ним. Основная формула имеет следующий вид:
Основная формула имеет следующий вид:
Р (А|B) = Р (В|А) х Р (А) / Р (В).
А и В являются определенными событиями.
Р(А|B) — условная вероятность, то есть может произойти событие А при условии, что событие В истинно.
Р (В|А) — условная вероятность события В.
Итак, заключительная часть небольшого курса «Теория вероятности» — формула Байеса, примеры решений задач с которой ниже.
Задание 5 : На склад привезли телефоны от трех компаний. При этом часть телефонов, которые изготавливаются на первом заводе, составляет 25%, на втором — 60%, на третьем — 15%. Известно также, что средний процент бракованных изделий у первой фабрики составляет 2%, у второй — 4%, и у третьей — 1%. Необходимо найти вероятность того, что случайно выбранный телефон окажется бракованным.
А = «случайно взятый телефон».
В 1 — телефон, который изготовила первая фабрика. Соответственно, появятся вводные В 2 и В 3 (для второй и третьей фабрик).
В итоге получим:
Р (В 1) = 25%/100% = 0,25; Р(В 2) = 0,6; Р (В 3) = 0,15 — таким образом мы нашли вероятность каждого варианта.
Теперь нужно найти условные вероятности искомого события, то есть вероятность бракованной продукции в фирмах:
Р (А/В 1) = 2%/100% = 0,02;
Р(А/В 2) = 0,04;
Р (А/В 3) = 0,01.
Теперь подставим данные в формулу Байеса и получим:
Р (А) = 0,25 х 0,2 + 0,6 х 0,4 + 0,15 х 0,01= 0,0305.
В статье представлена теория вероятности, формулы и примеры решения задач, но это только вершина айсберга обширной дисциплины. И после всего написанного логично будет задаться вопросом о том, нужна ли теория вероятности в жизни. Простому человеку сложно ответить, лучше спросить об этом у того, кто с ее помощью не единожды срывал джек-пот.
- Вероя́тность — степень (относительная мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным.
 Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности.
Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности.Исследование вероятности с математической точки зрения составляет особую дисциплину — теорию вероятностей. В теории вероятностей и математической статистике понятие вероятности формализуется как числовая характеристика события — вероятностная мера (или её значение) — мера на множестве событий (подмножеств множества элементарных событий), принимающая значения от
{\displaystyle 0}
{\displaystyle 1}
Значение
{\displaystyle 1}
Соответствует достоверному событию. Невозможное событие имеет вероятность 0 (обратное вообще говоря не всегда верно). Если вероятность наступления события равна
{\displaystyle p}
То вероятность его ненаступления равна
{\displaystyle 1-p}
В частности, вероятность
{\displaystyle 1/2}
Означает равную вероятность наступления и ненаступления события.

Классическое определение вероятности основано на понятии равновозможности исходов. В качестве вероятности выступает отношение количества исходов, благоприятствующих данному событию, к общему числу равновозможных исходов. Например, вероятность выпадения «орла» или «решки» при случайном подбрасывании монетки равна 1/2, если предполагается, что только эти две возможности имеют место и они являются равновозможными. Данное классическое «определение» вероятности можно обобщить на случай бесконечного количества возможных значений — например, если некоторое событие может произойти с равной вероятностью в любой точке (количество точек бесконечно) некоторой ограниченной области пространства (плоскости), то вероятность того, что оно произойдет в некоторой части этой допустимой области равна отношению объёма (площади) этой части к объёму (площади) области всех возможных точек.
Эмпирическое «определение» вероятности связано с частотой наступления события исходя из того, что при достаточно большом числе испытаний частота должна стремиться к объективной степени возможности этого события.
 В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.Вероятностное описание тех или иных явлений получило широкое распространение в современной науке, в частности в эконометрике, статистической физике макроскопических (термодинамических) систем, где даже в случае классического детерминированного описания движения частиц детерминированное описание всей системы частиц не представляется практически возможным и целесообразным. В квантовой физике сами описываемые процессы имеют вероятностную природу.
Хотите узнать, какие математические шансы на успех вашей ставки? Тогда для вас есть две хорошие новости. Первая: чтобы посчитать проходимость, не нужно проводить сложные расчеты и тратить большое количество времени. Достаточно воспользоваться простыми формулами, работа с которыми займёт пару минут. Вторая: после прочтения этой статьи вы с лёгкостью сможете рассчитывать вероятность прохода любой вашей сделки.
Вторая: после прочтения этой статьи вы с лёгкостью сможете рассчитывать вероятность прохода любой вашей сделки.
Чтобы верно определить проходимость, нужно сделать три шага:
- Рассчитать процент вероятности исхода события по мнению букмекерской конторы;
- Вычислить вероятность по статистическим данным самостоятельно;
- Узнать ценность ставки, учитывая обе вероятности.
Рассмотрим подробно каждый из шагов, применяя не только формулы, но и примеры.
Быстрый переход
Подсчёт вероятности, заложенной в букмекерские коэффициентыПервый шаг – необходимо узнать, с какой вероятностью оценивает шансы на тот или иной исход сам букмекер. Ведь понятно, что кэфы букмекерские конторы не ставят просто так. Для этого пользуемся следующей формулой:
P Б =(1/K)*100%,
где P Б – вероятность исхода по мнению букмекерской конторы;
K – коэффициент БК на исход.
Допустим, на победу лондонского Арсенала в поединке против Баварии коэффициент 4. Это значит, что вероятность его виктории БК расценивают как (1/4)*100%=25%. Или же Джокович играет против Южного. На победу Новака множитель 1.2, его шансы равны (1/1.2)*100%=83%.
Это значит, что вероятность его виктории БК расценивают как (1/4)*100%=25%. Или же Джокович играет против Южного. На победу Новака множитель 1.2, его шансы равны (1/1.2)*100%=83%.
Так оценивает шансы на успех каждого игрока и команды сама БК. Осуществив первый шаг, переходим ко второму.
Расчёт вероятности события игрокомВторой пункт нашего плана – собственная оценка вероятности события. Так как мы не можем учесть математически такие параметры как мотивация, игровой тонус, то воспользуемся упрощённой моделью и будем пользоваться только статистикой предыдущих встреч. Для расчёта статистической вероятности исхода применяем формулу:
P И =(УМ/М)*100%,
где P И – вероятность события по мнению игрока;
УМ – количество успешных матчей, в которых такое событие происходило;
М – общее количество матчей.
Чтобы было понятней, приведём примеры. Энди Маррей и Рафаэль Надаль сыграли между собой 14 матчей. В 6 из них был зафиксирован тотал меньше 21 по геймам, в 8 – тотал больше. Необходимо узнать вероятность того, что следующий поединок будет сыгран на тотал больше: (8/14)*100=57%. Валенсия сыграла на Месталье против Атлетико 74 матча, в которых одержала 29 побед. Вероятность победы Валенсии: (29/74)*100%=39%.
В 6 из них был зафиксирован тотал меньше 21 по геймам, в 8 – тотал больше. Необходимо узнать вероятность того, что следующий поединок будет сыгран на тотал больше: (8/14)*100=57%. Валенсия сыграла на Месталье против Атлетико 74 матча, в которых одержала 29 побед. Вероятность победы Валенсии: (29/74)*100%=39%.
И это все мы узнаем только благодаря статистике предыдущих игр! Естественно, что на какую-то новую команду или игрока такую вероятность просчитать не получится, поэтому такая стратегия ставок подойдет только для матчей, в которых соперники встречаются не первый раз. Теперь мы умеем определять букмекерскую и собственную вероятности исходов, и у нас есть все знания, чтобы перейти к последнему шагу.
Определение ценности ставкиЦенность (валуйность) пари и проходимость имеют непосредственную связь: чем выше валуйность, тем выше шанс на проход. Рассчитывается ценность следующим образом:
V= P И *K-100%,
где V – ценность;
P И – вероятность исхода по мнению беттера;
K – коэффициент БК на исход.
Допустим, мы хотим поставить на победу Милана в матче против Ромы и подчитали, что вероятность победы «красно-черных» 45%. Букмекер предлагает нам на это исход коэффициент 2.5. Будет ли такое пари ценным? Проводим расчёты: V=45%*2.5-100%=12.5%. Отлично, перед нами ценная ставка с хорошими шансами на проход.
Возьмём другой случай. Мария Шарапова играет против Петры Квитовой. Мы хотим заключить сделку на победу Марии, вероятность которой по нашим расчетам 60%. Конторы предлагают на этот исход множитель 1.5. Определяем валуйность: V=60%*1.5-100=-10%. Как видим, ценности эта ставка не представляет и от неё следует воздержаться.
Фактически формулы (1) и (2) это краткая запись условной вероятности на основе таблицы сопряженности признаков. Вернемся к примеру, рассмотренному (рис. 1). Предположим, что нам стало известно, будто некая семья собирается купить широкоэкранный телевизор. Какова вероятность того, что эта семья действительно купит такой телевизор?
Рис. 1. Поведение покупателей широкоэкранных телевизоров
1. Поведение покупателей широкоэкранных телевизоров
В данном случае нам необходимо вычислить условную вероятность Р (покупка совершена | покупка планировалась). Поскольку нам известно, что семья планирует покупку, выборочное пространство состоит не из всех 1000 семей, а только из тех, которые планируют покупку широкоэкранного телевизора. Из 250 таких семей 200 действительно купили этот телевизор. Следовательно, вероятность того, что семья действительно купит широкоэкранный телевизор, если она это запланировала, можно вычислить по следующей формуле:
Р (покупка совершена | покупка планировалась) = количество семей, планировавших и купивших широкоэкранный телевизор / количество семей, планировавших купить широкоэкранный телевизор = 200 / 250 = 0,8
Этот же результат дает формула (2):
где событие А заключается в том, что семья планирует покупку широкоформатного телевизора, а событие В — в том, что она его действительно купит. Подставляя в формулу реальные данные, получаем:
Дерево решений
На рис. 1 семьи разделены на четыре категории: планировавшие покупку широкоэкранного телевизора и не планировавшие, а также купившие такой телевизор и не купившие. Аналогичную классификацию можно выполнить с помощью дерева решений (рис. 2). Дерево, изображенное на рис. 2, имеет две ветви, соответствующие семьям, которые планировали приобрести широкоэкранный телевизор, и семьям, которые не делали этого. Каждая из этих ветвей разделяется на две дополнительные ветви, соответствующие семьям, купившим и не купившим широкоэкранный телевизор. Вероятности, записанные на концах двух основных ветвей, являются безусловными вероятностями событий А и А’ . Вероятности, записанные на концах четырех дополнительных ветвей, являются условными вероятностями каждой комбинации событий А и В . Условные вероятности вычисляются путем деления совместной вероятности событий на соответствующую безусловную вероятность каждого из них.
1 семьи разделены на четыре категории: планировавшие покупку широкоэкранного телевизора и не планировавшие, а также купившие такой телевизор и не купившие. Аналогичную классификацию можно выполнить с помощью дерева решений (рис. 2). Дерево, изображенное на рис. 2, имеет две ветви, соответствующие семьям, которые планировали приобрести широкоэкранный телевизор, и семьям, которые не делали этого. Каждая из этих ветвей разделяется на две дополнительные ветви, соответствующие семьям, купившим и не купившим широкоэкранный телевизор. Вероятности, записанные на концах двух основных ветвей, являются безусловными вероятностями событий А и А’ . Вероятности, записанные на концах четырех дополнительных ветвей, являются условными вероятностями каждой комбинации событий А и В . Условные вероятности вычисляются путем деления совместной вероятности событий на соответствующую безусловную вероятность каждого из них.
Рис. 2. Дерево решений
Например, чтобы вычислить вероятность того, что семья купит широкоэкранный телевизор, если она запланировала сделать это, следует определить вероятность события покупка запланирована и совершена , а затем поделить его на вероятность события покупка запланирована . Перемещаясь по дереву решения, изображенному на рис. 2, получаем следующий (аналогичный предыдущему) ответ:
Перемещаясь по дереву решения, изображенному на рис. 2, получаем следующий (аналогичный предыдущему) ответ:
Статистическая независимость
В примере с покупкой широкоэкранного телевизора вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор при условии, что она планировала это сделать, равна 200/250 = 0,8. Напомним, что безусловная вероятность того, что случайно выбранная семья приобрела широкоэкранный телевизор, равна 300/1000 = 0,3. Отсюда следует очень важный вывод. Априорная информация о том, что семья планировала покупку, влияет на вероятность самой покупки. Иначе говоря, эти два события зависят друг от друга. В противоположность этому примеру, существуют статистически независимые события, вероятности которых не зависят друг от друга. Статистическая независимость выражается тождеством: Р(А|В) = Р(А) , где Р(А|В) — вероятность события А при условии, что произошло событие В , Р(А) — безусловная вероятность события А.
Обратите внимание на то, что события А и В Р(А|В) = Р(А) . Если в таблице сопряженности признаков, имеющей размер 2×2, это условие выполняется хотя бы для одной комбинации событий А и В , оно будет справедливым и для любой другой комбинации. В нашем примере события покупка запланирована и покупка совершена не являются статистически независимыми, поскольку информация об одном событии влияет на вероятность другого.
Рассмотрим пример, в котором показано, как проверить статистическую независимость двух событий. Спросим у 300 семей, купивших широкоформатный телевизор, довольны ли они своей покупкой (рис. 3). Определите, связаны ли между собой степень удовлетворенности покупкой и тип телевизора.
Рис. 3. Данные, характеризующие степень удовлетворенности покупателей широкоэкранных телевизоров
Судя по этим данным,
В то же время,
Р (покупатель удовлетворен) = 240 / 300 = 0,80
Следовательно, вероятность того, что покупатель удовлетворен покупкой, и того, что семья купила HDTV-телевизор, равны между собой, и эти события являются статистически независимыми, поскольку никак не связаны между собой.
Правило умножения вероятностей
Формула для вычисления условной вероятности позволяет определить вероятность совместного события А и В . Разрешив формулу (1)
относительно совместной вероятности Р(А и В) , получаем общее, правило умножения вероятностей. Вероятность события А и В равна вероятности события А при условии, что наступило событие В В :
(3) Р(А и В) = Р(А|В) * Р(В)
Рассмотрим в качестве примера 80 семей, купивших широкоэкранный HDTV-телевизор (рис. 3). В таблице указано, что 64 семьи удовлетворены покупкой и 16 — нет. Предположим, что среди них случайным образом выбираются две семьи. Определите вероятность, что оба покупателя окажутся довольными. Используя формулу (3), получаем:
Р(А и В) = Р(А|В) * Р(В)
где событие А заключается в том, что вторая семья удовлетворена своей покупкой, а событие В — в том, что первая семья удовлетворена своей покупкой. Вероятность того, что первая семья удовлетворена своей покупкой, равна 64/80. Однако вероятность того, что вторая семья также удовлетворена своей покупкой, зависит от ответа первой семьи. Если первая семья после опроса не возвращается в выборку (выбор без возвращения), количество респондентов снижается до 79. Если первая семья оказалась удовлетворенной своей покупкой, вероятность того, что вторая семья также будет довольна, равна 63/79, поскольку в выборке осталось только 63 семьи, удовлетворенные своим приобретением. Таким образом, подставляя в формулу (3) конкретные данные, получим следующий ответ:
Однако вероятность того, что вторая семья также удовлетворена своей покупкой, зависит от ответа первой семьи. Если первая семья после опроса не возвращается в выборку (выбор без возвращения), количество респондентов снижается до 79. Если первая семья оказалась удовлетворенной своей покупкой, вероятность того, что вторая семья также будет довольна, равна 63/79, поскольку в выборке осталось только 63 семьи, удовлетворенные своим приобретением. Таким образом, подставляя в формулу (3) конкретные данные, получим следующий ответ:
Р(А и В) = (63/79)(64/80) = 0,638.
Следовательно, вероятность того, что обе семьи довольны своими покупками, равна 63,8%.
Предположим, что после опроса первая семья возвращается в выборку. Определите вероятность того, что обе семьи окажутся довольными своей покупкой. В этом случае вероятности того, что обе семьи удовлетворены своей покупкой одинаковы, и равны 64/80. Следовательно, Р(А и В) = (64/80)(64/80) = 0,64. Таким образом, вероятность того, что обе семьи довольны своими покупками, равна 64,0%. Этот пример показывает, что выбор второй семьи не зависит от выбора первой. Таким образом, заменяя в формуле (3) условную вероятность Р(А|В) вероятностью Р(А) , мы получаем формулу умножения вероятностей независимых событий.
Этот пример показывает, что выбор второй семьи не зависит от выбора первой. Таким образом, заменяя в формуле (3) условную вероятность Р(А|В) вероятностью Р(А) , мы получаем формулу умножения вероятностей независимых событий.
Правило умножения вероятностей независимых событий. Если события А и В являются статистически независимыми, вероятность события А и В равна вероятности события А , умноженной на вероятность события В .
(4) Р(А и В) = Р(А)Р(В)
Если это правило выполняется для событий А и В , значит, они являются статистически независимыми. Таким образом, существуют два способа определить статистическую независимость двух событий:
- События А и В являются статистически независимыми друг от друга тогда и только тогда, когда Р(А|В) = Р(А) .
- События А и B являются статистически независимыми друг от друга тогда и только тогда, когда Р(А и В) = Р(А)Р(В) .

Если в таблице сопряженности признаков, имеющей размер 2×2, одно из этих условий выполняется хотя бы для одной комбинации событий А и B , оно будет справедливым и для любой другой комбинации.
Безусловная вероятность элементарного события
(5) Р(А) = P(A|B 1)Р(B 1) + P(A|B 2)Р(B 2) + … + P(A|B k)Р(B k)
где события B 1 , B 2 , … B k являются взаимоисключающими и исчерпывающими.
Проиллюстрируем применение этой формулы на примере рис.1. Используя формулу (5), получаем:
Р(А) = P(A|B 1)Р(B 1) + P(A|B 2)Р(B 2)
где Р(А) — вероятность того, что покупка планировалась, Р(В 1) — вероятность того, что покупка совершена, Р(В 2) — вероятность того, что покупка не совершена.
ТЕОРЕМА БАЙЕСА
Условная вероятность события учитывает информацию о том, что произошло некое другое событие. Этот подход можно использовать как для уточнения вероятности с учетом вновь поступившей информации, так и для вычисления вероятности, что наблюдаемый эффект является следствием некоей конкретной причины. Процедура уточнения этих вероятностей называется теоремой Байеса. Впервые она была разработана Томасом Байесом в 18 веке.
Процедура уточнения этих вероятностей называется теоремой Байеса. Впервые она была разработана Томасом Байесом в 18 веке.
Предположим, что компания, упомянутая выше, исследует рынок сбыта новой модели телевизора. В прошлом 40% телевизоров, созданных компанией, пользовались успехом, а 60% моделей признания не получили. Прежде чем объявить о выпуске новой модели, специалисты по маркетингу тщательно исследуют рынок и фиксируют спрос. В прошлом успех 80% моделей, получивших признание, прогнозировался заранее, в то же время 30% благоприятных прогнозов оказались неверными. Для новой модели отдел маркетинга дал благоприятный прогноз. Какова вероятность того, что новая модель телевизора будет пользоваться спросом?
Теорему Байеса можно вывести из определений условной вероятности (1) и (2). Чтобы вычислить вероятность Р(В|А), возьмем формулу (2):
и подставим вместо Р(А и В) значение из формулы (3):
Р(А и В) = Р(А|В) * Р(В)
Подставляя вместо Р(А) формулу (5), получаем теорему Байеса:
где события B 1 , В 2 , … В k являются взаимоисключающими и исчерпывающими.
Введем следующие обозначения: событие S — телевизор пользуется спросом , событие S’ — телевизор не пользуется спросом , событие F — благоприятный прогноз , событие F’ — неблагоприятный прогноз . Допустим, что P(S) = 0,4, P(S’) = 0,6, P(F|S) = 0,8, P(F|S’) = 0,3. Применяя теорему Байеса получаем:
Вероятность спроса на новую модель телевизора при условии благоприятного прогноза равна 0,64. Таким образом, вероятность отсутствия спроса при условии благоприятного прогноза равна 1–0,64=0,36. Процесс вычислений представлен на рис. 4.
Рис. 4. (а) Вычисления по формуле Байеса для оценки вероятности спроса телевизоров; (б) Дерево решения при исследовании спроса на новую модель телевизора
Рассмотрим пример применения теоремы Байеса для медицинской диагностики. Вероятность того, что человек страдает от определенного заболевания, равна 0,03. Медицинский тест позволяет проверить, так ли это. Если человек действительно болен, вероятность точного диагноза (утверждающего, что человек болен, когда он действительно болен) равна 0,9. Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?
Если человек здоров, вероятность ложноположительного диагноза (утверждающего, что человек болен, когда он здоров) равна 0,02. Допустим, что медицинский тест дал положительный результат. Какова вероятность того, что человек действительно болен? Какова вероятность точного диагноза?
Введем следующие обозначения: событие D — человек болен , событие D’ — человек здоров , событие Т — диагноз положительный , событие Т’ — диагноз отрицательный . Из условия задачи следует, что Р(D) = 0,03, P(D’) = 0,97, Р(T|D) = 0,90, P(T|D’) = 0,02. Применяя формулу (6), получаем:
Вероятность того, что при положительном диагнозе человек действительно болен, равна 0,582 (см. также рис. 5). Обратите внимание на то, что знаменатель формулы Байеса равен вероятности положительного диагноза, т.е. 0,0464.
Краткая теория
Для количественного сравнения событий по степени возможности их
появления вводится числовая мера, которая называется вероятностью события. Вероятностью случайного события называется число, являющееся выражением меры объективной
возможности появления события.
Величины, определяющие, насколько значительны объективные основания рассчитывать на появление события, характеризуются вероятностью события. Необходимо подчеркнуть, что вероятность есть объективная величина, существующая независимо от познающего и обусловленная всей совокупностью условий, которые способствуют появлению события.
Объяснения, которые мы дали понятию вероятности, не являются математическим определением, так как они не определяют это понятие количественно. Существует несколько определений вероятности случайного события, которые широко применяются при решении конкретных задач (классическое, аксиоматическое, статистическое и т. д.).
Классическое определение вероятности события сводит это понятие к более элементарному понятию равновозможных событий, которое уже не подлежит определению и предполагается интуитивно ясным. Например, если игральная кость — однородный куб, то выпадения любой из граней этого куба будут равновозможными событиями.
Пусть достоверное
событие
распадается на
равновозможных случаев
, сумма
которых дает событие
. То есть случаи из
, на которые распадается
, называются благоприятствующими для
события
, так как появление одного из них
обеспечивает наступление
.
То есть случаи из
, на которые распадается
, называются благоприятствующими для
события
, так как появление одного из них
обеспечивает наступление
.
Вероятность события будем обозначать символом .
Вероятность события равна отношению числа случаев , благоприятствующих ему, из общего числа единственно возможных, равновозможных и несовместных случаев к числу , т. е.
Это есть классическое определение вероятности. Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число n, число случаев m, благоприятствующих данному событию, и затем выполнить расчет по вышеприведенной формуле.
Вероятность события, равная отношению числа благоприятных событию исходов опыта к общему числу исходов опыта называется классической вероятностью случайного события.
Из определения вытекают следующие свойства вероятности:
Свойство
1. Вероятность достоверного события равна единице.
Вероятность достоверного события равна единице.
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Свойство 4. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 5. Вероятность наступления противоположного события определяется так же, как и вероятность наступления события A.
Число случаев, благоприятствующих появлению противоположного события . Отсюда вероятность наступления противоположного события равна разнице между единицей и вероятностью наступления события A:
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
При выполнении комплекса условий
достоверное событие обязательно произойдет, а невозможное обязательно не
произойдет. Среди событий, которые при создании комплекса условий могут произойти,
а могут не произойти, на появление одних можно рассчитывать с большим основанием,
на появление других с меньшим основанием. Если, например, в урне белых шаров
больше, чем черных, то надеяться на появление белого шара при вынимании из урны
наудачу больше оснований, чем на появление черного шара.
Если, например, в урне белых шаров
больше, чем черных, то надеяться на появление белого шара при вынимании из урны
наудачу больше оснований, чем на появление черного шара.
Пример решения задачи
Пример 1
В ящике находится 8 белых, 4 черных и 7 красных шаров. Наудачу извлечены 3 шара. Найти вероятности следующих событий: – извлечен по крайней мере 1 красный шар, – есть по крайней мере 2 шара одного цвета, – есть по крайней мере 1 красный и 1 белый шар.
Решение задачи
Общее число исходов испытания найдем как число сочетаний из 19 (8+4+7) элементов по 3:
Найдем вероятность события – извлечен по крайней мере 1 красный шар (1,2 или 3 красных шара)
Искомая вероятность:
Пусть событие – есть по крайней мере 2 шара одного цвета (2 или 3 белых шара, 2 или 3 черных шара и 2 или 3 красных шара)
Число исходов, благоприятствующих событию:
Искомая вероятность:
Пусть событие – есть по крайней мере один красный и 1 белый шар
(1 красный, 1 белый, 1 черный или 1 красный, 2 белых или 2 красных, 1 белый)
Число исходов, благоприятствующих событию:
Искомая вероятность:
Ответ: P(A)=0. 773;P(C)=0.7688; P(D)=0.6068
773;P(C)=0.7688; P(D)=0.6068
Пример 2
Брошены две игральные кости. Найти вероятность того, что сумма очков не меньше 5.
Решение
Пусть событие – сумма очков не меньше 5
Воспользуемся классическим определением вероятности:
Общее число возможных исходов испытания
Число испытаний, благоприятствующих интересующему нас событию
На выпавшей грани первого игрального кубика может появиться одно очко, два очка…, шесть очков. аналогично шесть исходов возможны при бросании второго кубика. Каждый из исходов бросания первой кости может сочетаться с каждым из исходов второй. Таким образом, общее число возможных элементарных исходов испытания равно числу размещений с повторениями (выбор с размещениями 2 элементов из совокупнности объема 6):
Найдем вероятность противоположного события – сумма очков меньше 5
Благоприятствовать событию будут следующие сочетания выпавших очков:
| № | 1-я кость | 2-я кость | 1 | 1 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | 4 | 3 | 1 | 5 | 1 | 3 |
Изложено геометрическое определение вероятности и приведено решение широко известной задачи о встрече.
Теория вероятностей: формулы, виды событий, алгебра событий и решение задач
Теория вероятностей (разг. сокр. “тервер”) — это раздел математики, который занимается анализом случайных событий. С её помощью можно вычислить вероятность события — оно показывает насколько вероятно, что какое-то событие произойдёт. Это число всегда находится в интервале между 0 и 1, где 0 — означает невозможность, а 1 — оно точно произойдёт (достоверное событие).
Например: в мешке есть 6 шаров: 3 красных, 2 жёлтых и 1 синий. Какова вероятность вытащить красный?
Вероятность считается так: количество красных шаров поделить на общее количество шаров в мешке, т. е. 3/6 = 1/2.
Основные формулы теории вероятностей
Теоремы сложения и умножения вероятностей
| Применение | Формула |
|---|---|
| Сложение противоположных событий | P(A) + P(A̅) = 1 |
| Сложение несовместных событий | P(A + B) = P(A) + P(B) |
| Сложение совместных событий | P(A + B) = P(A) + P(B) — P(AB) |
| Умножение независимых событий | P(AB) = P(A) × P(B) |
Основные формулы вычисления
| Название | Формула | Применение/Пояснение |
|---|---|---|
| Классическое определение вероятности | Где m — количество элементарных событий, благоприятствующих событию А, и n — число всех элементарных событий данного испытания. | |
| Комбинаторика — Размещение | Соединения, в которых каждое содержит m элементов (без повторений между ними), взятых из числа данных n элементов. | |
| Комбинаторика — Размещения с повторениями | Число размещений с повторениями из n элементов по m элементов; соединения могут отличаться только порядком расположения элементов, но из m каких угодно и как угодно повторяющихся элементов. | |
| Комбинаторика — Сочетания | , где 0 ≤ m ≤ n | Соединения, в которых каждое содержит m элементов, взятых из числа данных n элементов; применяется когда порядок безразличен. |
| Перестановки | Соединения содержат все n элементов, отличие лишь в порядке их расположения. |
Виды событий
В теории вероятностей события бывают невозможными, случайными и достоверными.
Невозможное событие
Это то, которое уже известно, что в ходе испытания НЕ произойдёт, т. е. вероятность данного события равна нулю. Например: при бросании одной игральной кости (один раз), какова вероятность того, что выпадет 7 очков?
Случайное событие
Это событие может произойти или нет, обычно оно именно случайное. Например: при бросании игральной кости, какова вероятность того, что выпадет чётное число очков?
Достоверное событие
Это то, которое в ходе испытания обязательно произойдёт, т. е. вероятность данного события равна 1. Например: при бросании игральной кости, какова вероятность того, что она не останется в воздухе, а упадёт?
Совместные и несовместные события
Несовместные события — это когда появление одного исключает появление другого (в одном и том же испытании). Например: при бросании одной игральной кости выпадет одновременно и «2» и «3»?
Совместные события могут произойти одновременно. Например: два спортсмена плывут одновременно, два студента сдают экзамен.
Например: два спортсмена плывут одновременно, два студента сдают экзамен.
Противоположные события
Это два несовместимых события, которые образуют полную группу событий (третьего не существует). Например:
- А — при подбрасывании монеты выпадет орёл, A̅ — при подбрасывании монеты выпадет решка;
- D — из колоды карт будет извлечена дама, D̅ — из колоды карт будет извлечена не дама.
Алгебра событий
Логическое ИЛИ означает, что нужно произвести операцию сложения (сумма событий). Т. е. считаем возможность или событие А, или событие В, или оба (одновременно).
Логическое И — операция умножения (произведение событий). Т. е. считаем возможность и событие А, и событие В.
Задачи
Пример 1
В классе 27 учеников. Из них:
17 изучали немецкий язык,
6 — английский,
2 — оба языка.
Найти вероятность того, что случайно выбранный ученик изучал хотя бы один язык.
Что мы знаем:
𝑃(N) = 17/27,
𝑃(A) = 6/27,
𝑃(N ∙ A) = 2/27.
Значит вместе это будет:
𝑃(N + A) = 𝑃(N) + 𝑃(A) − 𝑃(N ∙ A) = 17/27 + 6/27 − 2/27 = 21/27 = 7/9.
Пример 2
Лотерейные билеты пронумерованы от 1 до 100. Какова вероятность того, что в выбранном билете будет стоять число больше 40 или чётное число?
Что мы знаем:
P(>40) = 60/100 = 6/10 = 3/5
P(Ch) = ½ = 5/10
Логическое ИЛИ означает, что нам нужно произвести операцию сложения (т. е. сумма событий).
Нам понадобится формула сложения совместных событий P(A + B) = P(A) + P(B) — P(AB).
Для этого нам нужно узнать сколько будет P(>40 . Ch), для этого используем формулу P(AB) = P(A) . P(B).
P(>40 . Ch) = P(>40) . P(Ch) = ⅗ . ½ = 3/10
Теперь можем подставить всё в формулу P(A + B) = P(A) + P(B) — P(AB):
P(>40 + Ch) = P(>40) + P(Ch) — P(>40.Ch) = 6/10 + 5/10 — 3/10 = 8/10 = ⅘.
Пример 3
В финале международного турнира по стрельбе из лука участвовали 8 спортсменов: 3 американца, 1 англичанин, 1 немец, 1 француз и 2 русских. Какова вероятность того, что хотя бы один русский попадёт в тройку лучших, учитывая, что все спортсмены имеют равные условия для получения медали (золотой, серебряной и бронзовой).
Какова вероятность того, что хотя бы один русский попадёт в тройку лучших, учитывая, что все спортсмены имеют равные условия для получения медали (золотой, серебряной и бронзовой).
Что мы знаем:
Когда в вопросе появляется «хотя бы один», можно «пойти от противного» — мы должны найти вероятность того, что этого не произойдёт (на пьедестале русских не будет), а затем вычесть это из 1.
P (никакой русский не выиграет золото) = 6/8 = 3/4
P (никакой русский не выиграет серебро) = 5/7 (убираем золотую медаль)
P (никакой русский не выиграет бронзу) = 4/6 = 2/3 (убираем золотую и серебряную медали)
P (на пьедестале не будет русских) = 3/4 x 5/7 x 2/3 = 30/84 = 5/14
P (хотя бы один русский на пьедестале) = 1 – 5/14 = 14/14 – 5/14 = 9/14.
Кто придумал теорию вероятностей
Основателями теории вероятностей являются два французских математика Блез Паскаль и Пьер Ферма. В 1654 г. французский писатель Антуан Гомбо (известный как Шевалье де Мере), интересовавшийся игрой и азартными играми, вызвал заинтересованность Паскаля насчёт популярной в то время игры в кости.
Кости бросались 24 раза, а вопрос стоял в том, стоит ли ставить деньги на выпадение хотя бы одной «двойной шестёрки». В то время считалось, что это было выгодно, но последующие расчёты показали прямо противоположное.
Узнайте про Метод Крамера, Интегралы, Корреляции, Математическое ожидание, Стандартное отклонение и Космологию.
Теория вероятности простым языком: пособие для чайников
Теория вероятности простым языком (сокр. «тервер») — это особый раздел математики, который ищет закономерности в случайных событиях. Математика — это точная наука цифр, поэтому она придает более точную возможность рассчитать исход случайного события.
Математика — это расчеты и формулы. Но так как наша статья называется «Теория вероятности простым языком», то мы постараемся обойтись без них. Для тех, кто хочет «глубже» понять, что это такое — тервер, можем посоветовать книгу «Теория вероятности и математическая статистика» В. Е. Гмурман.
Для чего нужна теория вероятности?
Знать хотя бы основы теории вероятности нужно каждому человеку.
Мы живем в непостоянном мире, где все построено на вероятностях и случайностях. Поэтому для развития правильного мировоззрения нужно хотя бы понимать, что и как может произойти.
Люди по натуре своей не сильно любят случайности. Большинству людей предпочтительнее постоянство, справедливость, определенность и объяснение всего происходящего. К примеру, в более ранние времена, люди не настолько были образованы и технологически подкованы, поэтому много чего происходящего они не способны были объяснить — так рождались суеверия и предрассудки. А подкрепляла их закономерность совпадений, так получилось и с «черной кошкой». Люди просто стали замечать частотные совпадения между неприятностью и черным котом, перешедшим дорогу.
Тервер — это то, что актуально как в быту, так и в точных науках: математике, химии, генетике, программировании и т. д.
Если простым языком, то теория вероятности изучает весь наш быт и окружающий мир:
случайность событий;
случайность величин;
случайность процессов;
свойство и возможность контролировать эти случайности.
Главным словом в теории вероятности является само слово «вероятность». Люди очень часто в обычной жизни употребляют это слово, даже не обращая на него внимания:
«Вечером, вероятно, будет дождь»;
«На выходных, вероятно, я буду работать»;
«Невероятно, как это получилось?»;
«Есть вероятность, что мне не хватит денег»;
и др.
То есть, употребляя подобные фразы, люди интуитивно уже используют теорию вероятности, пытаясь предположить о том, что произойдет или не произойдет какое-то событие. Теория вероятности как математический раздел дает такую же оценку случайностям, но только используя цифры, формулы и закономерности.
Несколько примеров использования теории вероятности:
экономика современных государств базируется на ней;
выпуск товаров в продажу сопровождается расчетом вероятных рисков и объемов продаж;
фондовые рынки и биржи;
предсказание погоды;
вероятность курса валют;
вероятность в кибернетике;
в автомобилестроении;
при разработке и отправке космических кораблей;
и т.
д.
Люди привыкли решать все эмоционально. К примеру, многие до сих пор боятся летать на самолетах, считают, что это очень опасно. Мужчины с годами превращаются в чёрствых и унылых людей, которым тяжело все – работа, отдых с родными, ремонт дома. Это случается из-за постоянной неудовлетворенности невозможностью реализовать свои сексуальные желания. Многие любители продажного секса в Уфе каждый раз встречаются с новой девушкой, не успевая утратить интерес к одной партнерше. Среди их контактов милая малышка, которая делает горловой минет, властная леди, которая умело обращается с плеткой, скромная студентка, краснеющая при первых прикосновениях. В то же время теория вероятности и статистические данные говорят об обратном. Вероятность погибнуть в авиакатастрофе равна около 1 на 8 000 000. В таком случае, если человек в каждый день будет летать на разных случайных самолетах, ему необходимо будет «налетать» 21 000 лет, чтобы умереть в авиакатастрофе. Вот и получается, что при полете на самолете самое опасное — это добираться до аэропорта на такси, потому что автомобиль куда опасней самолета.
Еще один пример эмоционального решения — это акулы. В год от нападения акул погибает около 12-15 человек, при этом от падения кокосов с пальмы погибает около 140 человек. Но кого люди больше боятся: акул или кокосов? Про кого снимают фильмы: про акул-убийц или про кокосов-убийц?
Миром управляют вероятность и расчеты. Поэтому нельзя упускать знания о теории вероятности и не использовать их в своей жизни. Нужно пытаться учитывать возможные вероятности и стремиться строить свою жизнь качественно.
Теория вероятности простым языком
Есть несколько подходов для исчисления теории вероятности. Самые простые из них мы с вами разберем, чтобы сформировать понимание о том, что такое тервер.
Вероятность и зависимые события
Этот метод используется, когда нужно определить вероятность в событиях, которые взаимосвязаны и зависят от исходов друг друга. Приведем простой пример.
Вы решили подарить другу на день рождения торт. Заказали курьерскую доставку торта, указали улицу, дом, подъезд, этаж, но забыли точный номер квартиры. Поэтому перед доставщиков торта будет выбор среди 3-х дверей. Теперь можно рассчитать, какова вероятность, что курьер попадет к другу с первого же раза.
Со стороны доставщика имеем 3 вероятных события:
Доставщик постучит в 1-ю дверь;
Доставщик постучит во 2-ю дверь;
Доставщик постучит в 3-ю дверь.
Но в нашу статистику включается еще и друг. Он тоже добавляет 3 вероятных события:
Друг может оказаться за 1-й дверью;
Друг может оказаться за 2-й дверью;
Друг может оказаться за 3-й дверью.
Вот и получается, что у нас может быть 9 вариантов развития событий: 3*3=9. Из них положительных вариантов, когда курьер позвонит в дверь к другу, — 3. Поэтому если отследить вероятность, что с первого раза курьер попадет в нужную дверь, то получается: 3/9 или 1/3.
Идем дальше. Доставщик торта звонит в первую дверь, а там не друг, а хорошенькая девушка в коротеньком халате. Доставщика такой «исход событий» удовлетворит, но вас и вашего друга — вряд ли. Поэтому нужно посчитать другую вероятность положительного исхода, внеся корректировки:
Доставщик постучит в 1-ю дверь;
Доставщик постучит во 2-ю дверь.
С другом тоже история повторяется:
Друг находится за 1-й дверью;
Друг находится за 2-й дверью.
Считаем по уже известной формуле и выходим на то, что шанс у доставщика постучать в нужную дверь вырос до ½.
И так дальше, если доставщик ошибется еще одной дверью, то на третий раз вероятность будет равна 1 или 100%.
Вероятность и независимые события
В данной ситуации искомая вероятность не зависит от благоприятного исхода событий и, соответственно, события не имеют влияния между собой.
Данный вид вероятности получается, когда решения принимаются с помощью монеты. То есть, загадывая на «орла», шанс, что выпадет именно он, равен 50% или ½.
Если бросков несколько подряд, то вероятность, что очередной раз выпадет «орел», уменьшается. Это происходит, потому что вступает в бой вероятность последовательности. То есть когда вы бросаете один раз, то вариантов два: «орел» или «решка», или ½, как мы уже говорили. Но если бросаете 5 раз подряд, то вариантов куда больше и шанс, что выпадет: «орел», «орел», «орел», «орел», «орел» — невелик. Рассчитывается так: ½ * ½ * ½ * ½ * ½ = 1/10.
Условные вероятности
Условные вероятности возникают в том случае, когда шанс, что наступит какое-то событие, зависит от какого-то условия.
Это очень хорошо видно, когда стоит вопрос о погоде:
Есть ли вероятность, что идет дождь, когда вы слышите громовые раскаты?
Есть ли вероятность, что идет дождь, когда вы видите, что на улице солнце?
Тут хорошо прослеживается, что если слышны/видны определенные условия, то вероятность становится больше/меньше.
Заключение
Теория вероятности, если простым языком, всегда требует наличия случая, убеждения, теории, условия и результата. Она присутствует во всех сферах нашей жизни, но в то же время ее использование в собственной жизни не всегда оправдывает ожидания.
Тервер — это то, что изучается еще с 16 века, но у чего до сих пор нет четкого определения. Она широко применяется в точных науках, но в то же время не всегда ей доверяют отдельные люди. В любом случае выбор всегда остается за вами и ответственность за свой выбор несете вы сами, а не монетка, которую вы подбрасываете вверх.

Вероятность против статистики
Вероятность против статистикиДалее: Джай-Алайские игроки и бейсбол Up: 6. Это бомж Предыдущий: 6. Это бомж
Вероятность и статистика — родственные области математики, которые заниматься анализом относительной частоты событий. Тем не менее, есть принципиальные различия в том, как они видят мир:
- Вероятность занимается предсказанием вероятности будущих событий, пока статистика предполагает анализ частоты прошлых событий.
- Вероятность — это прежде всего теоретическая область математики, который изучает следствия математических определений. Статистика — это прежде всего прикладная область математики, который пытается осмыслить наблюдения в реальном мире.
Обе темы важны, актуальны и полезны.
Но они разные, и понимание различия имеет решающее значение в
правильно интерпретировать релевантность математических доказательств. Многие игроки отправились в холодную и одинокую могилу за то, что не смогли заработать.
правильное различие между вероятностью и статистикой.
Многие игроки отправились в холодную и одинокую могилу за то, что не смогли заработать.
правильное различие между вероятностью и статистикой.
Это различие, возможно, станет яснее, если мы проследим мыслительный процесс математика, столкнувшегося со своей первой игрой в кости:
- Если бы этот математик был вероятностным, она бы увидела кости и подумать: «Шестигранная игральная кость? Предположительно, каждая грань игральных костей с одинаковой вероятностью выпадет лицевой стороной вверх. Теперь , предполагая , что каждая грань появляется с вероятностью 1/6, Я могу понять, каковы мои шансы на провал».
- Если бы вместо этого мимо проходил статистик,
она видела кости и думала: «Эти кости могут выглядеть хорошо,
но как мне знают что они не грузятся?
Я понаблюдаю некоторое время и буду отслеживать, как часто каждое число
подходит.
Затем я могу решить, согласуются ли мои наблюдения с предположением
равновероятностных граней.
Как только я буду достаточно уверен, что кости верны, я вызову вероятностного специалиста.
 чтобы сказать мне, как играть.»
чтобы сказать мне, как играть.»
Таким образом, теория вероятностей позволяет нам найти последствия данного идеального мира, в то время как статистическая теория позволяет нам чтобы измерить, насколько наш мир идеален.
Современная теория вероятностей возникла из игральных костей. Франции в 1654 году. Шевалье де Мере, французский дворянин, интересно, игрок или дом имел преимущество в варианте следующего игра со ставками. 6.1 В базовой версии игрок бросает четыре кубика и выигрывает при условии среди них нет шестерки. Заведение получает ставку на равные деньги, если выпадает хотя бы одна шестерка.
Де Мере обратил внимание на эту проблему французских математиков.
Блез Паскаль
и Пьер де Ферма,
наиболее известен как источник Великой теоремы Ферма.
Вместе эти люди разработали основы теории вероятностей,
попутно устанавливая, что дом выигрывает основную версию с вероятностью ,
где вероятность p = 0,5 означает честную игру, в которой дом выигрывает ровно в половине случаев. Мир джай-алаи нашего моделирования методом Монте-Карло предполагает, что
мы определяем исход очка между двумя командами, переворачивая
монета с соответствующим уклоном.
Если бы этот мир был реальностью, наша симуляция рассчитает
правильная вероятность каждого возможного исхода пари.
Но все игроки, конечно, не созданы равными.
Проведя статистическое исследование результатов всех матчей
с участием конкретного игрока, мы можем определить соответствующую сумму
сместить монету.
Мир джай-алаи нашего моделирования методом Монте-Карло предполагает, что
мы определяем исход очка между двумя командами, переворачивая
монета с соответствующим уклоном.
Если бы этот мир был реальностью, наша симуляция рассчитает
правильная вероятность каждого возможного исхода пари.
Но все игроки, конечно, не созданы равными.
Проведя статистическое исследование результатов всех матчей
с участием конкретного игрока, мы можем определить соответствующую сумму
сместить монету.
Но такие вычисления имеют смысл только в том случае, если наш смоделированный мир джай-алаи является моделью, соответствующей реальному миру. Джон фон Нейман однажды сказал, что «оценка покерной комбинации может быть чистой математикой». Мы должны свести нашу оценку пелотари к чистой математике.
Надеюсь, вам понравился этот отрывок из Расчетные ставки: компьютеры, азартные игры и математическое моделирование для
Win!, Стивен Скиена,
совместно опубликовано
Издательство Кембриджского университета
и
Математическая ассоциация Америки. Это книга о системе азартных игр, которая работает. Это говорит рассказ о том, как автор использовал компьютерное моделирование и методы математического моделирования для прогнозирования результатов матчи джай-алаи и успешно делать на них ставки, увеличивая первоначальная ставка более чем на 500% за год! Его метод может работать для всех: в конце книги он рассказывает, как лучше всего смотреть джай-алай и как на него делать ставки. С юмором и энтузиазмом Скиена рассказывает о своей жизни. увлечение компьютерным прогнозированием спортивных событий. Попутно он обсуждает другие игровые системы, как удачные и неудачные, для таких игр как лото, рулетка, блэкджек и фондовый рынок. Действительно, он показывает, как его Система джай-алай работает как миниатюрная торговая площадка. система. Хотите узнать о программных торговых системах, будущем азартных игр в Интернете, и настоящая причина, по которой брокерские конторы не предлагайте взаимные фонды, которые инвестируют в ипподромы и фронтоны? Как математические модели используются в политической опрос? Разница между корреляцией и причинно-следственной связью? Если вам интересны азартные игры и математика, шансы это книга для вас! Эта книга доступна в обоих твердый переплет
а также мягкая обложка. |
Далее: Джай-Алайские игроки и бейсбол Up: 6. Это бомж Предыдущий: 6. Это бомж Стив Скиена
04.06.2001
Вероятность | Основы математики
Марко Табога, доктор философии
Эта лекция определяет понятие вероятности и знакомит с ее основными характеристики.
Цель состоит в том, чтобы обеспечить строгое введение в математику вероятность, хотя и постепенно, с большим количеством пояснений и Примеры.
Table of contents
Definition of probability
Sample space, sample points and events
Space of events
Probability is defined by three properties
Old definitions of probability
Классическое определение вероятности
Частотное определение вероятности
Субъективистское определение вероятности
Other properties of probability
The probability of the empty set is 0
A sigma-additive function is additive
Probability of the complement
Probability of a union
Монотонность вероятности
Строгие определения
Более строгое определение события
A more rigorous definition of probability
Solved exercises
Exercise 1
Exercise 2
Exercise 3
Definition of probability
Было бы неплохо начать курс теории вероятностей с краткого,
простое и интуитивно понятное, но математически строгое определение вероятности. К сожалению, это невозможно.
К сожалению, это невозможно.
С одной стороны, строгое определение вероятности требует сложного математический аппарат и довольно неинтуитивен.
С другой стороны, простые определения часто вводят в заблуждение или, в лучшем случае, тавтологический.
Например, мы могли бы сказать, что вероятность — это число, которое количественно определяет вероятность данного события, когда еще неизвестно, произойдет ли это событие случиться или нет. Это определение носит круговой характер, поскольку в нем используется концепция вероятность, которая является синонимом вероятности. Тем не менее, мы можем использовать его как отправная точка. Он подчеркивает два важных факта:
Разрабатывая эти два факта, мы дадим (почти полностью) строгое
определение вероятности. Для этого введем понятие события.
в следующем разделе. Тогда мы определим вероятность как функцию, которая
привязывает числа к событиям и удовлетворяет определенным «интуитивным» свойствам.
На протяжении всей этой лекции мы предполагаем, что вы знакомы с основами теории множеств. Если нет, вы можете пересмотреть основы здесь.
Пространство выборки, точки выборки и события
Первое, что мы делаем, когда начинаем думать о Вероятность события состоит в том, чтобы перечислить ряд вещей, которые, возможно, случаться.
С математической точки зрения вещи в этом списке образуют множество, которое мы обозначать через .
Мы требуем удовлетворять следующим двум свойствам:
Взаимоисключающие результаты . Только одна из вещей в может случиться. То есть, если случается, то ни одна из вещей в наборе может случиться.
Исчерпывающие результаты . По крайней мере, одна из вещей в случится.
Если
удовлетворяет этим двум свойствам, оно называется пространством выборки ,
или пространство всех возможных исходов. Более того,
Более того,
элемент называется точкой выборки или возможной исход.
когда мы узнаем, что случилось, называется реализованным результатом .
подмножество называется событием (мы кратко объясним ниже, что не каждое подмножество выборочного пространства, строго говоря, событие; однако при первом чтении вы можете быть довольны это определение).
Вот пример примерного пространства.
Пример
Предположим, что мы бросаем кубик. Шесть чисел от 1 до 6 могут быть изображены лицевой стороной вверх, но
мы еще не знаем, какой из них появится. Пример пространства
isEach
из шести чисел является точкой отсчета. Результаты взаимоисключающие
потому что только одно число одновременно может появиться лицевой стороной вверх. Результаты также
исчерпывающим, потому что по крайней мере одно из шести чисел появится лицевой стороной вверх после
мы бросаем кубик.
Определять
событие (подмножество
).
Это можно описать как «нечетное число появляется лицевой стороной вверх». В настоящее время
определить также
это событие, и его можно описать как «цифра 6 появляется лицевой стороной вверх».
Результаты также
исчерпывающим, потому что по крайней мере одно из шести чисел появится лицевой стороной вверх после
мы бросаем кубик.
Определять
событие (подмножество
).
Это можно описать как «нечетное число появляется лицевой стороной вверх». В настоящее время
определить также
это событие, и его можно описать как «цифра 6 появляется лицевой стороной вверх».
Обратите внимание, что пространство выборки само по себе является событием, потому что каждое множество является подмножеством самого себя. Это называется конечно событие.
Также пустой набор является событием, потому что его можно рассматривать как подмножество . Это называется невозможным событием.
Пространство событий
Теперь, когда мы определили понятие события, мы можем подумать о
вероятность события
как число, прикрепленное к
что говорит нам о том, насколько вероятно, что
случится.
К сожалению, это еще не настоящее определение, потому что «вероятно» является синонимом. из «вероятного». Мы снова работаем по кругу! Но мы ближе к определению чем раньше. Чтобы стать еще ближе, нам нужно ввести еще одно математическое понятие пространства событий.
Пространство событий , которое мы обозначаем через , представляет собой набор подмножеств . Другими словами, каждый элемент является событием.
Пример Рассмотрим то же выборочное пространство, введенное в предыдущем примере (бросок умереть): определить в событияThe сеть пространство событий (помните, что а также являются событиями).
В строгой теории вероятностей требуется, чтобы пространство событий удовлетворяло
определенными свойствами (требуется, чтобы она была сигма-алгеброй). На данный момент мы
не обсуждаем эти свойства, но кратко расскажем о них
ниже, после определения вероятности.
Вероятность определяется тремя свойствами
Теперь мы готовы определить вероятность.
Определение Обозначим через функция из пространства событий множеству действительных чисел, т. е. функции, присваивающей число к каждому событию . Функция это вероятностная мера тогда и только тогда, когда она удовлетворяет следующие три свойства:
Диапазон : за любое событие .
Конечно :
Сигма-аддитивность (или счетная аддитивность): за любая последовательность взаимоисключающих событий (т. е. таких, что если ).
Когда вероятностная мера
присваивает номер
к событию
,
тогда
называется вероятностью
.
Мы наконец закончили! Мы определили вероятность! Теперь нам нужно убедиться что мы полностью понимаем определение.
Напомним основные шаги, сделанные на данный момент:
мы определили понятие события;
мы создали коллекцию событий, называемую пространством событий;
мы создали функцию в пространстве событий, которая присваивает номер каждое событие;
мы сказали, что если такая функция удовлетворяет определенным свойствам, то она вероятностная мера.
Последний пункт необходимо пояснить. Но прежде чем пытаться понять, почему три вышеприведенных математических свойства используются для определения вероятности, давайте проанализируйте их более подробно.
Свойство Range говорит само за себя. Это просто означает, что вероятность
событие — это действительное число от 0 до 1. Это можно рассматривать как
соглашение: мы решаем, что вероятность должна быть положительным числом и что
события могут иметь вероятность не более 1.
Это можно рассматривать как
соглашение: мы решаем, что вероятность должна быть положительным числом и что
события могут иметь вероятность не более 1.
Свойство «Наверняка» говорит о том, что должна быть максимально возможная вероятность. присваивается определенному событию (помните, что демонстрационное пространство должен быть исчерпывающим, поэтому, безусловно, одна из вещей в случится).
Свойство сигма-аддитивности немного более громоздко. Можно доказать (см. ниже), что если имеет место сигма-аддитивность, то и следующий вмещает:
Последнее свойство, называемое конечной аддитивностью , хотя и очень аналогичен сигма-аддитивности, его легче интерпретировать. Там сказано, что если два события не пересекаются, то вероятность того, что произойдет одно или другое равна сумме их индивидуальных вероятностей.
Для конкретности приведем простой пример, иллюстрирующий свойства
вероятности.
Пример Предположим, что мы подбрасываем монету. Возможные исходы: либо решка () или голова (), что есть, учтите пространство События Следующее назначение вероятностей удовлетворяет перечисленным свойствам превыше всего эти вероятности находятся в диапазоне от 0 до 1, поэтому свойство диапазона выполняется. , поэтому верное свойство удовлетворено. Также выполняется сигма-аддитивность потому чтои четыре пары , , , являются единственными четырьмя возможными парами непересекающихся множеств.
Теперь, когда мы познакомились с тремя свойствами вероятности, Остается ответить на фундаментальный вопрос: почему эти свойства были выбран для определения вероятности?
В основном, по историческим причинам. Перед Андреем Колмогоровым, видным
русский математик придумал это определение, статистики
предложены другие определения (см. следующий раздел). Эти определения имели
недостатки, но все они могут быть использованы для доказательства того, что вероятность должна удовлетворять
три свойства выше.
Эти определения имели
недостатки, но все они могут быть использованы для доказательства того, что вероятность должна удовлетворять
три свойства выше.
Колмогоров предложил отказаться от прежних определений и вместо них использовать три свойства в качестве определения. Этот подход уже доказал свою эффективность в разделе математики, называемом теорией меры. Собственно, Колмогоров понял, что вероятность — это особая мера (ограниченная 1), и адаптировал определение меры, которое очень похоже на определение вероятности приведено выше.
В следующем разделе мы сообщаем о некоторых старых определениях вероятности. Несмотря на свои недостатки, они могут помочь улучшить наше понимание концепции. вероятности.
Старые определения вероятности
В этом разделе кратко обсуждаются некоторые старые определения вероятности. Несмотря на то что
ни один из них не является полностью строгим и последовательным, а также достаточным сам по себе, чтобы
разъясняют значение вероятности, все они затрагивают важные аспекты.
Классическое определение вероятности
Согласно классическому определению, когда все возможные исходы эксперимента равновероятны, вероятность события есть отношение между числом исходов, благоприятствующих событию, и общим количество возможных исходов. Хотя это определение интуитивно понятно, оно имеет два основных недостатки:
он круговой, потому что он использует понятие вероятности для определения вероятность: она основана на предположении о «равновероятных» исходах, где равновероятно означает «имеющий одинаковую вероятность»;
она ограничена по объему, потому что не позволяет нам определить вероятность, когда возможные исходы не равновероятны.
Частотное определение вероятности
Согласно частотному определению, вероятность события – это
относительная частота самого события, наблюдаемая в течение большого количества
повторения одного и того же эксперимента. Другими словами, это предел, до которого
в
соотношение: сходится
когда число повторений опыта стремится к бесконечности. Несмотря на
своей интуитивной привлекательности, также это определение имеет ряд важных недостатков:
Другими словами, это предел, до которого
в
соотношение: сходится
когда число повторений опыта стремится к бесконечности. Несмотря на
своей интуитивной привлекательности, также это определение имеет ряд важных недостатков:
предполагается, что все вероятностные эксперименты можно повторять много раз, что неверно;
он также несколько цикличен, потому что неявно опирается на Закон больших чисел, который можно вывести только после определения вероятности.
Субъективистское определение вероятности
Согласно субъективистскому определению, вероятность события равна
связанные с готовностью человека принимать ставки на это событие.
Предположим, что лотерейный билет приносит 1 доллар в случае, если событие происходит, и 0 в случае его возникновения.
случае, когда событие не происходит. Человеку предлагается установить цену за это
лотерейный билет, в котором ей должно быть безразлично, быть покупателем или
продавец билета. Субъективная вероятность события определяется как
равна цене, установленной таким образом индивидуумом. Также это определение имеет некоторые
недостатки:
Субъективная вероятность события определяется как
равна цене, установленной таким образом индивидуумом. Также это определение имеет некоторые
недостатки:
разные люди могут устанавливать разные цены, тем самым предотвращая объективная оценка вероятностей;
цена, которую человек готов заплатить за участие в лотерее, может быть под влиянием других факторов, не имеющих ничего общего с вероятностью; за например, на поведение человека при размещении ставок может влиять его предпочтения.
Прочие свойства вероятности
В следующих подразделах обсуждаются другие математические свойства, которыми обладают вероятность.
Вероятность пустого набора 0
Здесь мы доказываем, что .
Доказательство
Определить
последовательность событий следующая:
последовательность — это последовательность непересекающихся событий, потому что пустое множество не пересекается
из любого другого набора. Затем,
который
подразумевает и
.
Затем,
который
подразумевает и
.
Сигма-аддитивная функция является аддитивной
Сигма-аддитивная функция также добавка:
Proof
Определите последовательность событий следующим образом: последовательность — это последовательность непересекающихся событий, потому что пустое множество не пересекается из любого другого набора. Тогда
Вероятность дополнения
Позволять быть событием и его дополнение (т. е. множество всех элементов которые не принадлежат ). Затем
Доказательство
Примечание это и что а также являются непересекающимися множествами. Затем, используя свойство уверенности и конечное аддитивность, мы получитькакой подразумевает
Другими словами, вероятность того, что событие не произойдет, равна единице. минус вероятность того, что это произойдет.
Вероятность союза
Мы уже видели, как вычислить
в частном случае, когда
а также
два непересекающихся события. В более общем случае, когда они не
обязательно непересекающиеся, формула
is
В более общем случае, когда они не
обязательно непересекающиеся, формула
is
Доказательство
Это доказывается следующим образом. Первая заметка это так чтоКроме того событие можно записать как следует: и три события в правой части не пересекаются. Таким образом,
Монотонность вероятности
Если два события а также таковы, что , затем
Доказательство
Это легко доказать, используя аддитивность:где последнее неравенство является следствием того, что (по дальностному свойству вероятности).
Другими словами, если встречается реже, чем , поскольку последний предполагает больше событий, то вероятность должна быть меньше вероятности .
Строгие определения
В этом разделе мы даем совершенно строгие определения события и вероятность.
Более строгое определение события
Определение события, данное выше, не совсем строго.
Часто статистики работают с вероятностными моделями, в которых некоторые подмножества пример пространства не считаются событиями.
Это происходит в основном по следующим двум причинам:
иногда выборочное пространство представляет собой действительно сложный набор; делать вещи проще, внимание ограничивается только некоторыми подмножествами выборочного пространства;
иногда можно последовательно присвоить вероятности только некоторым подмножества выборочного пространства; в этих случаях только те подмножества, к которым вероятности могут быть назначены считаются событиями.
Обозначим через пространство событий, то есть множество подмножеств которые считаются событиями. В строгой теории вероятностей пространство события должны быть сигма-алгеброй.
Определение является сигма-алгебра на если это множество подмножеств удовлетворяющие следующим трем свойствам:
Полный набор.
 .
.Закрытие при дополнении. Если тогда также (дополнение это множество всех элементов которые не принадлежат ).
Замыкание по счетным объединениям. Если представляет собой последовательность подмножеств принадлежащий , затем
Почему для удовлетворения этих свойств требуется пространство событий?
Помимо ряда математических причин кажется довольно интуитивным, что они должны быть удовлетворены (и действительно лучший способ приблизиться к сигма-алгебрам для первый раз — запомнить их свойства и убедить себя, что они разумный). Давайте посмотрим, почему.
Свойство 1) означает, что пространство событий должно включать событие «что-то случится», вполне тривиальное требование!
Свойство 2) означает, что если «одна из вещей множества
будут
произойти» считается событием, то и «ни одно из
вещи в комплекте
будут
случиться» считается событием. Это вполне естественно: если вы
учитывая возможность того, что событие произойдет, то по необходимости вы
должны также одновременно учитывать возможность того, что одно и то же событие
не случится.
Это вполне естественно: если вы
учитывая возможность того, что событие произойдет, то по необходимости вы
должны также одновременно учитывать возможность того, что одно и то же событие
не случится.
Свойство 3) немного сложнее. Однако следующее свойство, вытекающее из 3), наверное, проще интерпретировать: это означает, что если «одна из вещей в будут случиться» и «одна из вещей в будут произойти» считаются двумя событиями, то также «одним из вещи в или же одна из вещей в будут произойти» должно считаться событием. Это просто означает, что если вы в состоянии отдельно оценить возможность возникновения двух событий, то вы должен быть в состоянии оценить возможность хотя бы одного из них. Свойство 3) расширяет это интуитивное свойство до счетная коллекция событий: расширение необходимо по математическим причинам, чтобы вывести определенную непрерывность свойства вероятностных мер.
Сделаем последнее замечание по терминологии:
Более строгое определение вероятности
Приведенное выше определение вероятности не было вполне строгим. Теперь, когда
мы определили сигма-алгебры и пространства событий, мы можем сделать это полностью
тщательный.
Теперь, когда
мы определили сигма-алгебры и пространства событий, мы можем сделать это полностью
тщательный.
Определение Позволять быть сигма-алгеброй на выборочном пространстве . Функция является вероятностной мерой тогда и только тогда, когда она удовлетворяет следующие два свойства:
Конечно вещь. .
Сигма-аддитивность. Позволять любая последовательность элементов такой, что подразумевает . Тогда
Ничего нового не было добавлено к определению вероятности, данному в
предыдущие разделы. Это более строгое определение лишь уточняет, что
Вероятностная мера — это функция, определенная на сигма-алгебре событий. Следовательно,
невозможно правильно говорить о вероятности для подмножеств выборки
пространство
которые не принадлежат сигма-алгебре
(т. е. для неизмеримых подмножеств).
е. для неизмеримых подмножеств).
Тройной называется вероятностным пространством .
Решаемые упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Из урны с цветными шарами случайным образом вынимают шар. Шарики могут быть либо красным, либо синим (другие цвета невозможны). Вероятность нарисовать синий шар . Какова вероятность того, что вытащите красный шар?
Решение
Образец пространства можно представить как объединение двух непересекающихся событий а также :куда событие можно описать как «вынут красный шар», а событие можно описать как «вынут синий шар». Обратите внимание, что является дополнением :
Мы знаем , вероятность вытянуть синий мяч:
Нам нужно найти , вероятность вытащить красный шар. Используя формулу для вероятности из дополнение:
Упражнение 2
Рассмотрим пример пространства состоящая из трех возможных исходы:
Предположим, что вероятности, присвоенные трем возможным исходам
Можно ли найти событие, вероятность которого равна ?
Решение
Есть два события, вероятность которых
.
Первый это
Используя формулу вероятности объединения непересекающихся событий, находим получить
Второй это
Используя снова формулу вероятности объединения непересекающихся событий, мы получить
Упражнение 3
Рассмотрим пример пространства состоящий из четырех возможных исходы:
Рассмотрим три события , а также определяется как следует:
Предположим, что их вероятности
Теперь рассмотрим четвертое событие определяется как следует:
Находить .
Решение
Обратите внимание, аддитивность:
Следовательно, для вычисления , нам нужно вычислить а также .
находится с помощью аддитивности :так что
находится с использованием того факта, что один минус вероятность события равна вероятность его дополнения и тот факт, что :
Как следствие,
Как цитировать
Пожалуйста, указывайте как:
Taboga, Marco (2021). «Математика вероятностей», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-probability/probability.
«Математика вероятностей», Лекции по теории вероятностей и математической статистике. Прямая публикация Kindle. Онлайн приложение. https://www.statlect.com/fundamentals-of-probability/probability.
Каковы шансы? — Scientific American
Поделиться в Facebook
Поделиться в Twitter
Поделиться на Reddit
Поделиться на LinkedIn
Поделиться по эл. Соберите несколько чисел и подбросьте несколько монет, чтобы узнать! Предоставлено: Джордж Рецек
Ключевые понятия
Математика
Вероятность
Фракции
ПроцентыВведение
Вы когда-нибудь слышали, чтобы кто-нибудь говорил, что вероятность того, что что-то случится, равна «50 на 50»? Что это на самом деле означает? Эта фраза как-то связана с вероятностью. Вероятность говорит вам, насколько вероятно, что событие произойдет. Это означает, что для определенных событий вы можете рассчитать вероятность того, что они произойдут. В этом упражнении вы выполните эти расчеты, а затем проверите их, чтобы увидеть, соответствуют ли они действительности!
В этом упражнении вы выполните эти расчеты, а затем проверите их, чтобы увидеть, соответствуют ли они действительности!Фон
Вероятность позволяет нам количественно оценить вероятность того, что событие произойдет. Возможно, вы знакомы со словами, которые мы используем, говоря о вероятности, такими как «определенно», «вероятно», «маловероятно», «невозможно» и так далее. Вы, наверное, также знаете, что вероятность того, что событие произойдет, варьируется от невозможного, что означает, что это событие не произойдет ни при каких обстоятельствах, до уверенности, что означает, что событие произойдет без сомнения. В математике эти экстремальные вероятности выражаются как 0 (невозможно) и 1 (верно). Это означает, что число вероятности всегда представляет собой число от 0 до 1. Вероятность также может быть записана в виде процента, то есть числа от 0 до 100 процентов. Чем выше число вероятности или процент события, тем более вероятно, что событие произойдет.Вероятность возникновения определенного события зависит от количества возможных исходов события.
 Если событие имеет только один возможный исход, вероятность этого исхода всегда равна 1 (или 100 %). Однако, если существует более одного возможного результата, это меняется. Простой пример — подбрасывание монеты. Если вы подбрасываете монету, возможны два исхода (орел или решка). Пока с монетой не манипулировали, теоретические вероятности обоих исходов одинаковы — они равновероятны. Сумма всех возможных исходов всегда равна 1 (или 100 %), потому что наверняка произойдет один из возможных исходов. Это означает, что при подбрасывании монеты теоретическая вероятность выпадения орла или решки составляет 0,5 (или 50 процентов).
Если событие имеет только один возможный исход, вероятность этого исхода всегда равна 1 (или 100 %). Однако, если существует более одного возможного результата, это меняется. Простой пример — подбрасывание монеты. Если вы подбрасываете монету, возможны два исхода (орел или решка). Пока с монетой не манипулировали, теоретические вероятности обоих исходов одинаковы — они равновероятны. Сумма всех возможных исходов всегда равна 1 (или 100 %), потому что наверняка произойдет один из возможных исходов. Это означает, что при подбрасывании монеты теоретическая вероятность выпадения орла или решки составляет 0,5 (или 50 процентов).С шестигранным кубиком все сложнее. В этом случае, если вы бросите кубик, возможны 6 исходов (1, 2, 3, 4, 5 или 6). Можете ли вы выяснить, какова теоретическая вероятность для каждого числа? Это 1/6 или 0,17 (или 17 процентов). В этом упражнении вы проверите свои расчеты вероятностей. Интересная часть вероятностей заключается в том, что знание теоретической вероятности определенного результата не обязательно говорит вам что-либо об экспериментальных вероятностях, когда вы на самом деле пытаетесь это сделать (за исключением случаев, когда вероятность равна 0 или 1).
 Например, результаты с очень низкой теоретической вероятностью на самом деле имеют место в реальности, хотя и очень маловероятны. Так как же ваши теоретические вероятности соответствуют вашим экспериментальным результатам? Вы узнаете, бросив монету и бросив кубик в этом упражнении.
Например, результаты с очень низкой теоретической вероятностью на самом деле имеют место в реальности, хотя и очень маловероятны. Так как же ваши теоретические вероятности соответствуют вашим экспериментальным результатам? Вы узнаете, бросив монету и бросив кубик в этом упражнении.Материалы
- Монета
- Шестигранная матрица
- Бумага
- Ручка или карандаш
Подготовка- Подготовьте счетную ведомость, чтобы подсчитать, сколько раз монета выпадала орлом или решкой.
- Подготовьте второй счетный лист, чтобы подсчитать, как часто вы бросали каждое число на кубике.
Процедура- Рассчитайте теоретическую вероятность того, что монета выпадет орлом или решкой соответственно. Запишите вероятности в виде дроби. Какова теоретическая вероятность для каждой стороны?
- Теперь приготовьтесь бросить монету.
 Как часто из 10 бросков вы ожидаете выпадение орла или решки?
Как часто из 10 бросков вы ожидаете выпадение орла или решки? - Подбросьте монету 10 раз. После каждого броска запишите, выпали ли вы орлом или решкой в своем листе подсчета.
- Подсчитайте, как часто выпадали орлы и решки. Запишите результаты в виде дроби. Например, 3 решки из 10 бросков будут 3/10 или 0,3. (Знаменатель всегда будет количеством раз, когда вы подбрасываете монету, а числитель будет результатом, который вы измеряете, например, сколько раз монета падает решкой.) Вы также можете выразить те же результаты, глядя на выпадение орла. за те же 10 бросков. Таким образом, это будет 7 орлов из 10 бросков: 7/10 или 0,7. Соответствуют ли ваши результаты вашим ожиданиям?
- Подбросьте еще 10 монет. Вы ожидаете таких же результатов? Почему или почему нет?
- Сравните свои результаты второго раунда с результатами первого раунда. Они одинаковые? Почему или почему нет?
- Продолжайте подбрасывать монету.
 На этот раз бросьте его 30 раз подряд. Запишите свои результаты для каждого броска в свой счетный лист. Каких результатов вы ожидаете на этот раз?
На этот раз бросьте его 30 раз подряд. Запишите свои результаты для каждого броска в свой счетный лист. Каких результатов вы ожидаете на этот раз? - Посмотрите на свои результаты 30 подбрасываний монеты и преобразуйте их в дробную форму. Чем они отличаются от ваших предыдущих результатов для 10 подбрасываний монеты?
- Подсчитайте, сколько орлов и решек вы получили за общее количество бросков монеты на данный момент, что должно быть 50. Опять же, запишите свои результаты в виде дроби (с количеством бросков в качестве знаменателя (50) и результатом, который вы подсчитали, как числитель). Совпадает ли ваша экспериментальная вероятность с вашей теоретической вероятностью с первого шага? (Простым способом преобразования этой дроби в проценты является умножение знаменателя и числителя на 2, поэтому 50 x 2 = 100. И после умножения числителя на 2 вы получите число, выходящее за пределы 100. — и процент.)
- Рассчитайте теоретическую вероятность выпадения каждого числа на шестигранной игральной кости.
 Запишите вероятности в виде дроби. Какова теоретическая вероятность каждого числа?
Запишите вероятности в виде дроби. Какова теоретическая вероятность каждого числа? - Возьмите кости и бросьте их 10 раз. После каждого броска запишите, какое число вы получили в свой счетный лист. Как часто из 10 бросков вы ожидаете получить каждое число?
- После 10 бросков сравните свои результаты (записанные в форме дробей) с вашими прогнозами. Насколько они близки?
- Сделайте еще 10 бросков кубика, записывая результат каждого броска. Ваши результаты меняются?
- Теперь бросьте кости 30 раз подряд (записывая результат после каждого броска). Как часто вы выбрасывали каждое число на этот раз?
- Подсчитайте, как часто вы выбрасывали каждое число из всех 50 бросков. Запишите результаты в виде дроби. Совпадает ли ваша экспериментальная вероятность с вашей теоретической вероятностью? (Используйте ту же формулу, что и для подбрасывания монеты, умножив знаменатель и числитель на 2, чтобы получить процентное значение.
 )
) - Сравните рассчитанные числа вероятностей с вашими фактическими данными для обоих действий (монеты и кости). Что ваши объединенные результаты говорят вам о вероятности?
- Дополнительно: Еще больше увеличьте количество подбрасываний монет и бросков костей. Как ваши результаты соотносятся с рассчитанными вероятностями при увеличении количества событий (бросков или бросков)?
- Дополнительно: Посмотрите, как вероятности могут быть представлены деревьями вероятностей. Можете ли вы нарисовать дерево вероятностей для подбрасывания монеты и броска костей?
- Дополнительно: Если вас интересуют более сложные расчеты вероятности, узнайте, как можно рассчитать вероятность повторяющегося события, например: Насколько вероятно, что при подбрасывании монеты выпадет два орла подряд?
Наблюдения и результаты
Вычислить вероятность подбрасывания монеты довольно просто. Подбрасывание монеты имеет только два возможных исхода: орел или решка. Оба исхода равновероятны. Это означает, что теоретическая вероятность выпадения орла или решки равна 0,5 (или 50%). Вероятности всех возможных исходов должны составлять в сумме 1 (или 100 процентов), что и происходит. Однако, когда вы подбрасывали монету 10 раз, вы, скорее всего, не получили пять орлов и пять решек. На самом деле ваши результаты могли быть 4 орла и 6 решек (или другой результат, отличный от 5 и 5). Эти числа будут вашими экспериментальными вероятностями. В этом примере они составляют 4 из 10 (0,4) для головы и 6 из 10 (0,6) для решки. Когда вы повторили 10 подбрасываний монеты, вы, вероятно, получили другой результат во втором раунде. То же самое, вероятно, верно и для 30 бросков монеты. Даже когда вы просуммируете все 50 бросков монеты, вы, скорее всего, не получите абсолютно равной вероятности выпадения орла и решки. Таким образом, ваши экспериментальные вероятности, вероятно, не соответствовали вашим расчетным (теоретическим) вероятностям.
Подбрасывание монеты имеет только два возможных исхода: орел или решка. Оба исхода равновероятны. Это означает, что теоретическая вероятность выпадения орла или решки равна 0,5 (или 50%). Вероятности всех возможных исходов должны составлять в сумме 1 (или 100 процентов), что и происходит. Однако, когда вы подбрасывали монету 10 раз, вы, скорее всего, не получили пять орлов и пять решек. На самом деле ваши результаты могли быть 4 орла и 6 решек (или другой результат, отличный от 5 и 5). Эти числа будут вашими экспериментальными вероятностями. В этом примере они составляют 4 из 10 (0,4) для головы и 6 из 10 (0,6) для решки. Когда вы повторили 10 подбрасываний монеты, вы, вероятно, получили другой результат во втором раунде. То же самое, вероятно, верно и для 30 бросков монеты. Даже когда вы просуммируете все 50 бросков монеты, вы, скорее всего, не получите абсолютно равной вероятности выпадения орла и решки. Таким образом, ваши экспериментальные вероятности, вероятно, не соответствовали вашим расчетным (теоретическим) вероятностям.

 д.
д.
 Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности.
Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность (и невероятность) бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднительна. Возможны различные градации «уровней» вероятности.
 В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
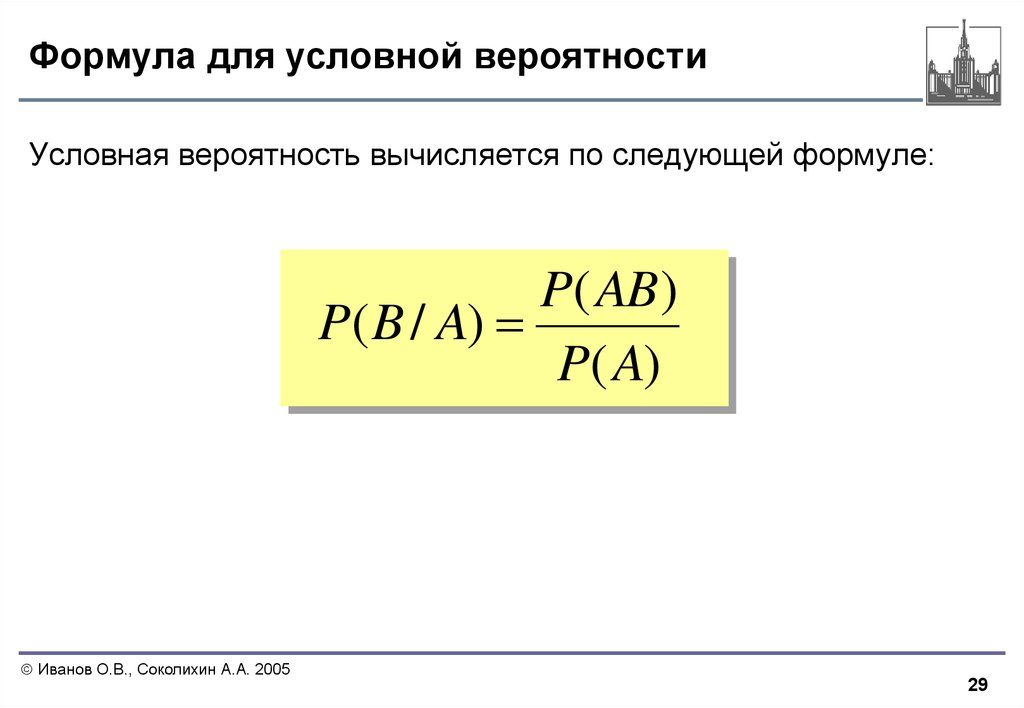 Мы живем в непостоянном мире, где все построено на вероятностях и случайностях. Поэтому для развития правильного мировоззрения нужно хотя бы понимать, что и как может произойти.
Мы живем в непостоянном мире, где все построено на вероятностях и случайностях. Поэтому для развития правильного мировоззрения нужно хотя бы понимать, что и как может произойти.
 д.
д.


 И так дальше, если доставщик ошибется еще одной дверью, то на третий раз вероятность будет равна 1 или 100%.
И так дальше, если доставщик ошибется еще одной дверью, то на третий раз вероятность будет равна 1 или 100%. Это очень хорошо видно, когда стоит вопрос о погоде:
Это очень хорошо видно, когда стоит вопрос о погоде:
 чтобы сказать мне, как играть.»
чтобы сказать мне, как играть.»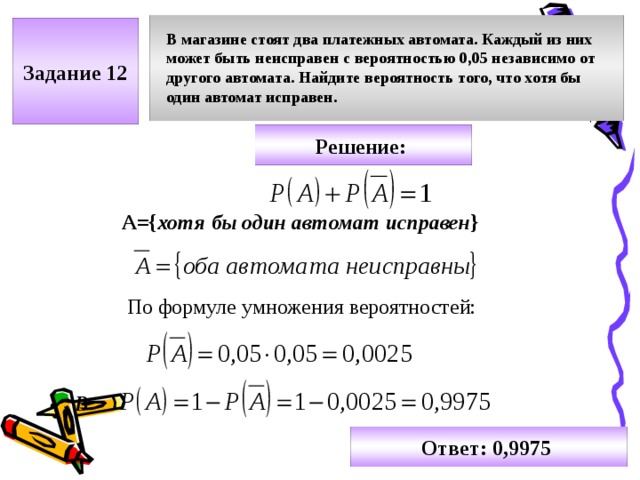
 .
. В этом упражнении вы выполните эти расчеты, а затем проверите их, чтобы увидеть, соответствуют ли они действительности!
В этом упражнении вы выполните эти расчеты, а затем проверите их, чтобы увидеть, соответствуют ли они действительности! Если событие имеет только один возможный исход, вероятность этого исхода всегда равна 1 (или 100 %). Однако, если существует более одного возможного результата, это меняется. Простой пример — подбрасывание монеты. Если вы подбрасываете монету, возможны два исхода (орел или решка). Пока с монетой не манипулировали, теоретические вероятности обоих исходов одинаковы — они равновероятны. Сумма всех возможных исходов всегда равна 1 (или 100 %), потому что наверняка произойдет один из возможных исходов. Это означает, что при подбрасывании монеты теоретическая вероятность выпадения орла или решки составляет 0,5 (или 50 процентов).
Если событие имеет только один возможный исход, вероятность этого исхода всегда равна 1 (или 100 %). Однако, если существует более одного возможного результата, это меняется. Простой пример — подбрасывание монеты. Если вы подбрасываете монету, возможны два исхода (орел или решка). Пока с монетой не манипулировали, теоретические вероятности обоих исходов одинаковы — они равновероятны. Сумма всех возможных исходов всегда равна 1 (или 100 %), потому что наверняка произойдет один из возможных исходов. Это означает, что при подбрасывании монеты теоретическая вероятность выпадения орла или решки составляет 0,5 (или 50 процентов). Например, результаты с очень низкой теоретической вероятностью на самом деле имеют место в реальности, хотя и очень маловероятны. Так как же ваши теоретические вероятности соответствуют вашим экспериментальным результатам? Вы узнаете, бросив монету и бросив кубик в этом упражнении.
Например, результаты с очень низкой теоретической вероятностью на самом деле имеют место в реальности, хотя и очень маловероятны. Так как же ваши теоретические вероятности соответствуют вашим экспериментальным результатам? Вы узнаете, бросив монету и бросив кубик в этом упражнении. Как часто из 10 бросков вы ожидаете выпадение орла или решки?
Как часто из 10 бросков вы ожидаете выпадение орла или решки?  На этот раз бросьте его 30 раз подряд. Запишите свои результаты для каждого броска в свой счетный лист. Каких результатов вы ожидаете на этот раз?
На этот раз бросьте его 30 раз подряд. Запишите свои результаты для каждого броска в свой счетный лист. Каких результатов вы ожидаете на этот раз?  Запишите вероятности в виде дроби. Какова теоретическая вероятность каждого числа?
Запишите вероятности в виде дроби. Какова теоретическая вероятность каждого числа?  )
)  Подбрасывание монеты имеет только два возможных исхода: орел или решка. Оба исхода равновероятны. Это означает, что теоретическая вероятность выпадения орла или решки равна 0,5 (или 50%). Вероятности всех возможных исходов должны составлять в сумме 1 (или 100 процентов), что и происходит. Однако, когда вы подбрасывали монету 10 раз, вы, скорее всего, не получили пять орлов и пять решек. На самом деле ваши результаты могли быть 4 орла и 6 решек (или другой результат, отличный от 5 и 5). Эти числа будут вашими экспериментальными вероятностями. В этом примере они составляют 4 из 10 (0,4) для головы и 6 из 10 (0,6) для решки. Когда вы повторили 10 подбрасываний монеты, вы, вероятно, получили другой результат во втором раунде. То же самое, вероятно, верно и для 30 бросков монеты. Даже когда вы просуммируете все 50 бросков монеты, вы, скорее всего, не получите абсолютно равной вероятности выпадения орла и решки. Таким образом, ваши экспериментальные вероятности, вероятно, не соответствовали вашим расчетным (теоретическим) вероятностям.
Подбрасывание монеты имеет только два возможных исхода: орел или решка. Оба исхода равновероятны. Это означает, что теоретическая вероятность выпадения орла или решки равна 0,5 (или 50%). Вероятности всех возможных исходов должны составлять в сумме 1 (или 100 процентов), что и происходит. Однако, когда вы подбрасывали монету 10 раз, вы, скорее всего, не получили пять орлов и пять решек. На самом деле ваши результаты могли быть 4 орла и 6 решек (или другой результат, отличный от 5 и 5). Эти числа будут вашими экспериментальными вероятностями. В этом примере они составляют 4 из 10 (0,4) для головы и 6 из 10 (0,6) для решки. Когда вы повторили 10 подбрасываний монеты, вы, вероятно, получили другой результат во втором раунде. То же самое, вероятно, верно и для 30 бросков монеты. Даже когда вы просуммируете все 50 бросков монеты, вы, скорее всего, не получите абсолютно равной вероятности выпадения орла и решки. Таким образом, ваши экспериментальные вероятности, вероятно, не соответствовали вашим расчетным (теоретическим) вероятностям.