Sin 2x sin2x: Решить уравнение sin^2x-sin2x=0 — ответ на Uchi.ru

Лучший ответ по мнению автора

Итак, как только вы дойдете до конца средней школы или начала старшей школы, вы обнаружите этот раздел математики, который мы называем тригонометрией. 2(2x). 92(2x), давайте рассмотрим несколько основных моментов, которые помогут нам понять производные. Итак, мы должны знать, что это за термины и каковы их отношения. Рассмотрим относительно угла x. Поэтому считайте x углом в треугольнике между основанием и гипотенузой. Итак, sin x равен отношению перпендикуляра к гипотенузе треугольника. Далее, cos x — это отношение между основанием треугольника и гипотенузой. Кроме того, tan x — это отношение перпендикуляра треугольника к основанию. Однако остальные 3 являются просто обратными значениями первых 3. Читайте также: Что такое правило частного и произведения?

Следовательно, cosec x совпадает с 1/sin x, sec x совпадает с 1/cos x, а cot x совпадает с 1/cot x.

Содержание

Существуют различные функции, объединяющие их. Кроме того, углы могут также измениться. Вместо x может быть 2x или 3x. Для каждого из них предусмотрены различные расчеты. Однако в этой статье мы увидим только производную от sin^x и производную от sin^2x одну за другой. 2x. Итак, производная f’(x) будет равна2x)

Следовательно, dq/ dx = -2cosxsinx (как производная от cos x = – sin x)

Следовательно, теперь, если мы добавим p и q, мы получим исходную функцию f(x)

Итак, складывая dp/ dx и dq/ dx, мы можем получить производную исходной функции f(x) или f'(x).

Следовательно, f'(x) = 2sinx * cosx – 2cosx * sinx

Итак, f'(x) = 0.

Теперь, если вы попытаетесь вычислить сумму другим способом, мы также найдем то же самое причина.

Итак, по законам тригонометрии мы знаем, что 92

Итак, мы применим здесь цепное правило дифференцирования. Более того, мы уже знаем, что производная от sin x равна cos x.

Следовательно, f’(x) равно 2sin 2x * d/dx (sin2x)

Теперь вычислим вторую часть отдельно.

Итак, d/dx (sin 2x) = cos 2x * d/dx (2x)

Таким образом, мы снова применяем цепное правило.

Следовательно, d/ dx (sin 2x) = 2cos2x

Итак, f'(x) = 2 sin2x * 2 cos2x

Или f'(x) = 4 sin2x * cos2x

Теперь мы уже знаем sin 2x = 2sinx * cosx 92(2x) равно 2sin4x. Тем не менее, следуйте двум разделам выше, чтобы получить конкретное представление о происхождении.

Ответ. Итак, производная от 2sin2x равна 4cos2x.

Ответ. Итак, производная от 2x равна 2. Это потому, что производная от x унитарна.

Ответ. Производная только от 2 равна 0. Итак, это потому, что производная любой константы равна 0, а 2 определенно равна единице.

Ответ. Итак, производная от 2cos2x равна – 4sin2x.

Sin2X açılımı nedir? Trigonometri sin2x açılımı konu anlatımı

Oluşturulma Tarihi: Nisan 26, 2022 02:09

Yunanca da trigōnon «üçgen» + metron «ölçmek anlamına gelen trigonometri matematiğin bir dalıdır. Üçgenlerin açıları ve kenarları arasındaki bağıntıları konu edinmektedir.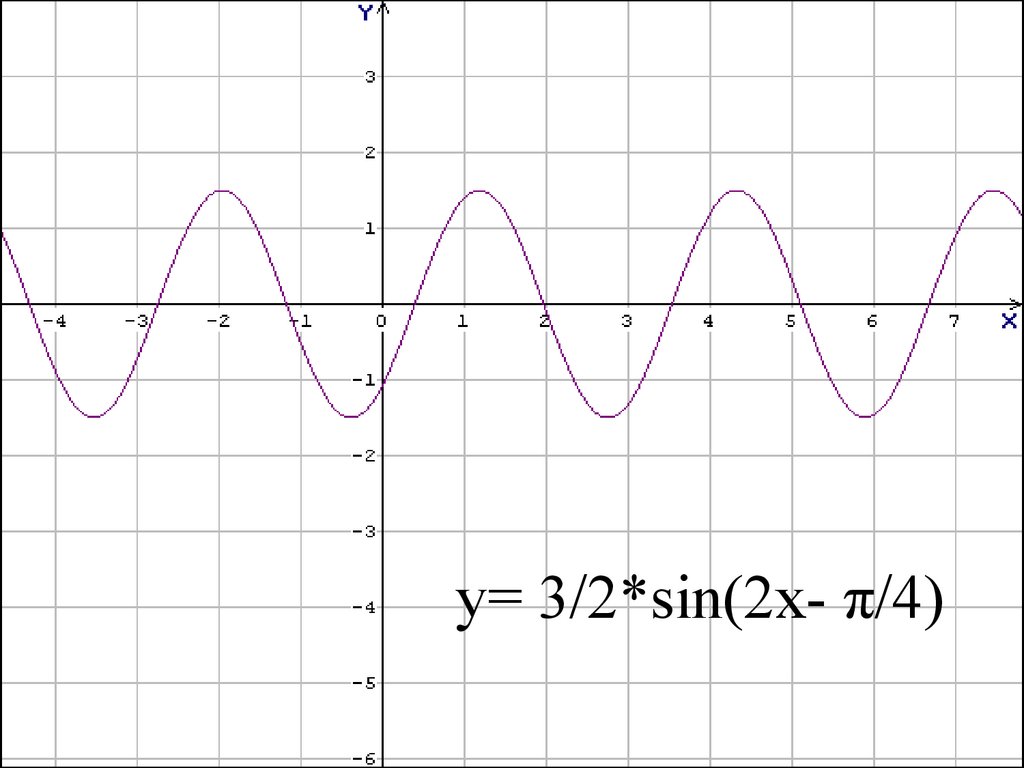

Хаберин Девами

class=’medianet-inline-adv’>

Тригонометрия синуса, косинус гиби тригонометрик fonksiyonlar kullanılmaktadır. Günümüzde özellikle fizik ve mühendislik konularında sıkça kullanılmaktadır.

  Sin2x Açılımı Недир?  

 Тригонометрия matematiğin alanında en önemli konuların başında gelmektedir. Bu nedenle trigonometri derslerinde öğrencilerin çok işine yarayacak bir açılım olan sin2x açılımı oldukça önemli olmaktadır. Ayrica Sin2x açılımı olan yarım açı formülleri trigonometri alanında hayat kurtarıcı olabilmektedir.

  Тригонометрия Sin2x Açılımı Konu Anlatımı  

 Sin2x = 2.sinx.cosx denklemine eşittir. Bu açılım da her bir açının yarısını alacak biçimde kullanıldığı anlatılmaktadır. En basit olarak Sin40 = 2.sin20.cos20 olarak karşımıza çıkar. Bu formül bazı sorularda bir açı verilip onun yarısının ya da iki katının sinus değeri arandığı durumlarda rahatlıkla kullanılmaktadır.

Хаберин Девами

class=’medianet-inline-adv’>

 Sin2x açılımının bilimsel olarak birden fazla ispatını yapmak mümkündür. Ancak önemli olan sin2x açılımını çok iyi anlamaktır.

  Sin2x Açılımı  

 Trigonometri elbette matematiğin en önemli konularından biridir. Sin2x özellikle öğrencilerin işine çok yarayacak bir açılım olmaktadır. Sin2x=2.sinx.cosx şeklinde ifade edilir. Bu açılım ile mühendislik, fizik ve matematik alanında çalışan herkes içli dışlı olmaktadır.

  Sin2x Açılımının İspatları nelerdir?  

 Sin2x açılımının birden çok ispatı bulunmaktadır. Fakat bu konuda önemli olan husus sin2x açılımını çok iyi ögrenmek ve kavramak olmaktadır.

Испат .

 İlk olarak basit yoldan anlatmak gerekirse, bildiğimiz değerlerden ispat yöntemi uygulanabilir. 30, 45, 60 gibi düz ölçülerin trigonometrik degerleri aşağıdaki gibidir.

 Sin60 = √3/2 ile Sin30 = 1/2 ve Cos30 = √3/2 olmaktadır.

 Açılımlara göre sin60 = 2.sin30.cos30 şeklinde ifade edilmelidir. O halde √3/2 = 2.(1/2).√3/2 açılımı olmalıdır. İşlemler yapıldığı zaman bunun ispat edildigini ve sağlandığını rahatlıkla görmekteyiz.

Aynı Zamanda Bu Ispatı 90 VE 45 DERECE ölçüleri Ile Denemek Konuyu Yeterince anlayabilmek iCin Sizlere Fayda Sağlayacaktır.

İspat  

Haberin Devamı

class=’medyanet-inline-adv’>

  ​​​​​ Toplam ve fark formüllerini bilen herkes bu ispatı da kolaylıkla kullanılabilir. Bilindiği gibi sin(a + b) = sina.cosb + cosa.sinb açılımı sinüsün toplama formülü olmaktadır.

 Bu formül üzerinden gidildiği zaman a ve b’nin ikisi yerine de x yazılırsa sin(x + x) = sin2x = sinx.cosx + cosx. sinx = 2.sinx.cosx şeklinde bulunur.

 Bu 2. ispat yöntemi takip edilerek aynı şekilde cos2x açılımını da kolaylıkla sizde Elde edebilirsiniz. Trigonometri konularında bu şekilde ispat yapıldığı zaman hem formülü çok daha iyi kavramaya hem de formülün biri unutulduğu taktirde diğerini elde ederek bulmaya yardımcı olmaktadır.

 Geometri dalını kullanarak da sin2x açılım formülünün ispatını yapmak mümkün olmaktadır. Ancak yine де verdiğimiz бу 2 ispat yöntemi soruların çözümünde Yeterli olacaktır.

Haberin Devamı

class=’medyanet-inline-adv’>

  Trigonometri de Sin2x Açılımı İle ilgili Örnekler  

 Birkaç soru ile Sin2x açılımını tam kavramak ve öğrenmek daha mümkün hale gelir. Bu örnek sorular konuyu pekiştirme de yardımcı olabilir.

 Soru1: Sin80/(sin40.cos40) ifadesinin trigonometri de eşiti nedir?

 Çözüm: ilk olarak Sin80 ifadesini 40 derece olacak şekilde açalım.