Параллелограмм — что это такое (определение), свойства, признаки и периметр параллелограмма
Обновлено 22 июля 2021 Просмотров: 168 896 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
В этой статье мы подробно расскажем о таком термине, как ПАРАЛЛЕЛОГРАММ.
С этой фигурой каждый из нас познакомился еще в школе – на уроках геометрии в 8 классе. Но если кто проболел в то время, прогулял занятия или просто не усвоил материал – мы поможем закрыть этот пробел.
Определение параллелограмма
Итак,
Параллелограмм – это геометрическая фигура, которая является разновидностью четырехугольника. У него противоположные стороны лежат на параллельных линиях, а соответственно, являются параллельными по отношению друг к другу.
Выглядит эта фигура вот так:
Это классический вид параллелограмма, который в учебниках приводят всегда в первую очередь. В данной фигуре сторона AD параллельна стороне ВС, а АВ параллельна CD.
Интересно, что более известные всем нам фигуры – квадрат, прямоугольник и ромб – также являются параллелограммами.
Можно даже дать такие определения:
- Квадрат – это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
- Прямоугольник – это параллелограмм, у которого стороны пересекаются под прямым углом, но при этом они не равны между собой.
- Ромб – это параллелограмм, у которого все стороны равны между собой, но при этом они не пересекаются под прямым углом.
Происхождение термина «параллелограмм»
Как и многие термины в математике, слово ПАРАЛЛЕЛОГРАММ пришло к нам из Древней Греции. И легко предположить, что оно как-то связано с самым известным в истории математиком – Евклидом.
Действительно, так и есть. Слово ПАРАЛЛЕЛОГРАММ впервые можно найти именно в трудах Эвклида, которые называются «Начала». Оно состоит из двух греческих слов – «Parallelos», что, естественно, означает «параллельный», и «Gramme» — «линия».
Таким образом, ПАРАЛЛЕЛОГРАММ можно перевести как «параллельные линии». Этот принцип и заложен в определении геометрической фигуры.
Еще любопытный факт, что именно Евклид поделил все четырехугольники на две большие категории. Первая – это параллелограммы, у которых противоположные стороны параллельны. И трапеции (что это?), у которых параллельна только одна пара сторон.
Свойства и признаки параллелограмма
Как понять, что перед нами ПАРАЛЛЕЛОГРАММ? Есть целый ряд признаков, который характерен только для этой геометрической фигуры.
Возьмем в качестве примера еще раз нашу фигуру:
Чтобы этот четырехугольник ABCD можно было считать параллелограммом, должно выполняться одно из следующих условий:
- Две противоположные стороны попарно параллельны.
- Две противоположные стороны попарно равны между собой.
- Две противоположные стороны и равны, и параллельны. В данном случае можно брать только одну пару сторон.
AD II BC и AD =BC.
 Или AB II CD и AB = CD
Или AB II CD и AB = CD - Противоположные углы попарно равны между собой.
- Диагонали пересекаются в центре фигуры и делятся точкой пересечения на две равные части.
- Если сложить два соседних угла, то получится 180 градусов.
∠А + ∠В = ∠В + ∠С = ∠С + ∠D = ∠D + ∠А = 180
Это самые простые признаки параллелограмма. Есть еще некоторые признаки, смысл которых поясняется в этом видео:
Причем, для того чтобы удостовериться в подлинности фигуры, достаточно доказать только одно из них.
Правило действует и в обратную сторону – если хоть один из признаков параллелограмма верен, то автоматически верны и все остальные, и они не нуждаются в отдельном доказательстве.
Соответственно, если хоть один признак не получил подтверждения, то фигуру нельзя считать параллелограммом. И все остальное также не совпадет.
Как посчитать периметр параллелограмма
Для подсчетов длины периметра четырехугольников обычно просто складывают длины его сторон. Но в случае с параллелограммом все несколько проще, так как стороны у него попарно равны.
Снова возьмем для примера нашу фигуру:
Только для удобства обозначим стороны по-другому. AD и ВС будет просто «а», а АВ и CD – «b». Получится вот так:
Чтобы рассчитать периметр, надо просто сложить все стороны:
P = a + b + a + b
Но эту же формулу можно переиначить и по-другому:
P = 2a +2b
Или совсем просто:
P = (a + b) * 2
Это и есть формула периметра параллелограмма, которая записана во всех учебниках.
Как рассчитать площадь параллелограмма
С площадью геометрических фигур всегда чуть сложнее, чем с периметрами. Но параллелограмм в какой-то мере уникален, потому что для расчета его площади существует сразу несколько формул.
- Вычисление площади параллелограмма по высоте.
Напомним, высотой называют линию, которая выходит из вершины геометрической фигуры и идет под прямым углом к противоположному основанию.
- Вычисление площади параллелограмма по углам. Если известны длины сторон и хотя бы один угол, то можно применить следующую формулу.
- Вычисление площади параллелограмма по диагоналям. Для этого надо знать не только длину диагоналей, но и величину угла между ними. И тогда можно применять следующую формулу.
Вот и все, что мы хотели рассказать о ПАРАЛЛЕЛОГРАММЕ. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Фигура параллелограмм. Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.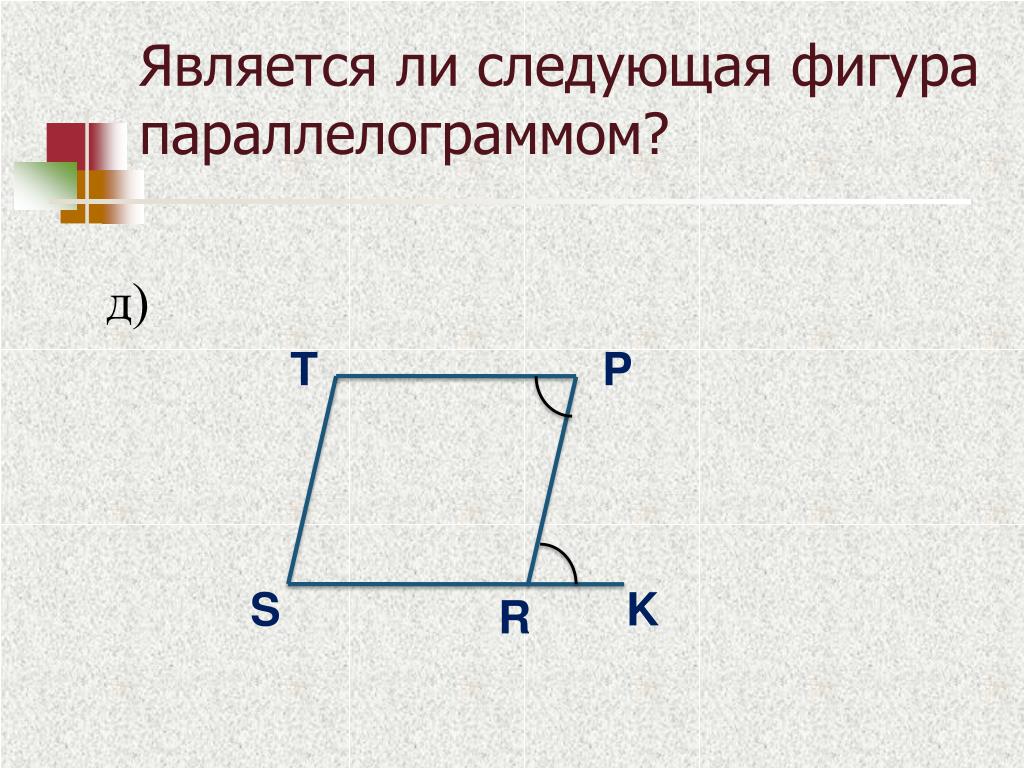 Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны.
Первым делом проведем диагональ \(AC \) . Получаются два треугольника: \(ABC \) и \(ADC \) .
Так как \(ABCD \) — параллелограмм, то справедливо следующее:
\(AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.
\(AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.
Следовательно, (по второму признаку: и \(AC \) — общая).
И, значит, \(\triangle ABC = \triangle ADC \) , то \(AB = CD \) и \(AD = BC \) .
2. Противоположные углы тождественны.
Согласно доказательству свойства 1 мы знаем, что \(\angle 1 = \angle 2, \angle 3 = \angle 4 \)
. Таким образом сумма противоположных углов равна: \(\angle 1 + \angle 3 = \angle 2 + \angle 4 \)
. Учитывая, что \(\triangle ABC = \triangle ADC \)
получаем \(\angle A = \angle C \)
, \(\angle B = \angle D \)
.
3. Диагонали разделены пополам точкой пересечения.
По свойству 1 мы знаем, что противоположные стороны тождественны: \(AB = CD \) . Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \(\triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \(BO = OD \) (напротив углов \(\angle 2 \) и \(\angle 1 \) ) и \(AO = OC \) (напротив углов \(\angle 3 \) и \(\angle 4 \) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
\(AB = CD \)
; \(AB || CD \Rightarrow ABCD \)
— параллелограмм.
Рассмотрим подробнее. Почему \(AD || BC \) ?
\(\triangle ABC = \triangle ADC \) по свойству 1 : \(AB = CD \) , \(\angle 1 = \angle 2 \) как накрест лежащие при параллельных \(AB \) и \(CD \) и секущей \(AC \) .
Но если \(\triangle ABC = \triangle ADC \) , то \(\angle 3 = \angle 4 \) (лежат напротив \(AD || BC \) (\(\angle 3 \) и \(\angle 4 \) — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.
\(AB = CD \) , \(AD = BC \Rightarrow ABCD \) — параллелограмм.
Рассмотрим данный признак. Еще раз проведем диагональ \(AC \) .
По свойству 1 \(\triangle ABC = \triangle ACD \) .
Из этого следует, что: \(\angle 1 = \angle 2 \Rightarrow AD || BC \) и \(\angle 3 = \angle 4 \Rightarrow AB || CD \) , то есть \(ABCD \) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.
 {\circ} \)
. Но \(\alpha \)
и \(\beta \)
являются внутренними односторонними при секущей \(AB \)
.
{\circ} \)
. Но \(\alpha \)
и \(\beta \)
являются внутренними односторонними при секущей \(AB \)
.Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
Свойства параллелограмма
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.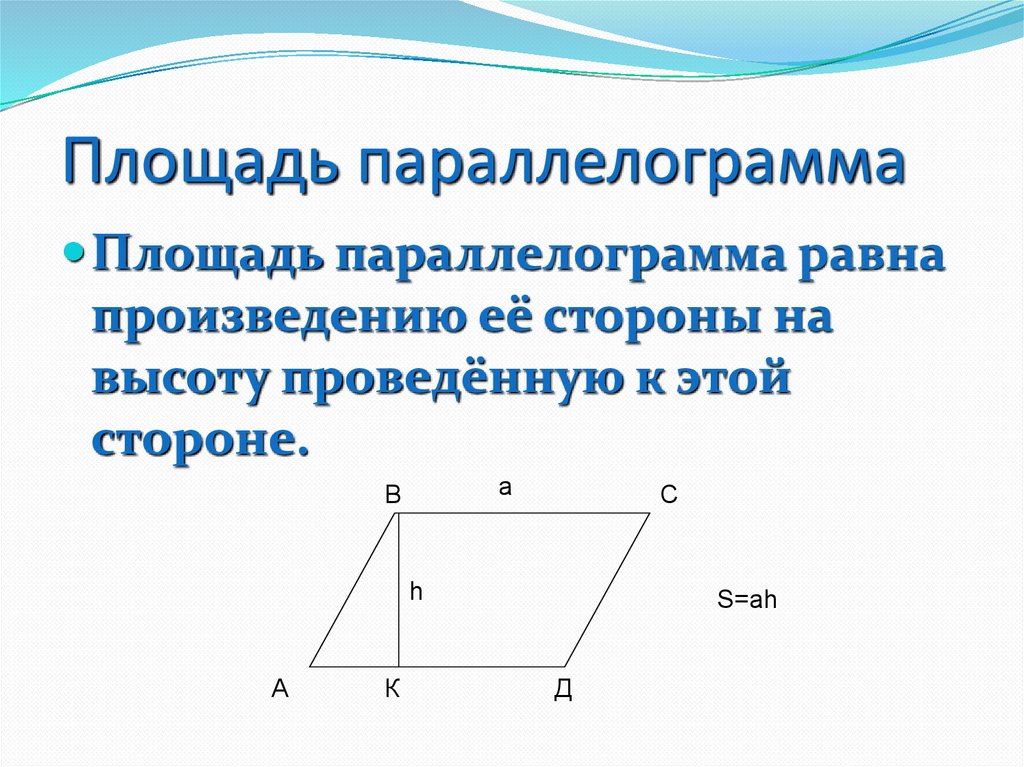
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
Все основные свойства проиллюстрированы на следующих трех рисунках.
При-зна-ки па-рал-ле-ло-грам-ма
1. Определение и основные свойства параллелограмма
Нач-нем с того, что вспом-ним опре-де-ле-ние па-рал-ле-ло-грам-ма.
Опре-де-ле-ние. Па-рал-ле-ло-грамм — че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 1).
Рис. 1. Па-рал-ле-ло-грамм
Вспом-ним ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :
Для того, чтобы иметь воз-мож-ность поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть уве-рен-ным, что фи-гу-ра, о ко-то-рой идет речь, — па-рал-ле-ло-грамм.
2. Первый признак параллелограмма
Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .
Рис. 2. Пер-вый при-знак па-рал-ле-ло-грам-ма
До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 2), она раз-би-ла его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках:
по пер-во-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.
Из ра-вен-ства ука-зан-ных тре-уголь-ни-ков сле-ду-ет, что по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. Имеем, что:
До-ка-за-но.
3. Второй признак параллелограмма
Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .
.
Рис. 3. Вто-рой при-знак па-рал-ле-ло-грам-ма
До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 3), она раз-би-ва-ет его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках, ис-хо-дя из фор-му-ли-ров-ки тео-ре-мы:
по тре-тье-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.
Из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что и по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. По-лу-ча-ем:
па-рал-ле-ло-грамм по опре-де-ле-нию. Что и тре-бо-ва-лось до-ка-зать.
До-ка-за-но.
4. Пример на применение первого признака параллелограмма
При-мер 1. В вы-пук-лом че-ты-рех-уголь-ни-ке Найти: а) углы че-ты-рех-уголь-ни-ка; б) сто-ро-ну .
Ре-ше-ние. Изоб-ра-зим Рис. 4.
па-рал-ле-ло-грамм по пер-во-му при-зна-ку па-рал-ле-ло-грам-ма.
А. по свой-ству па-рал-ле-ло-грам-ма о про-ти-во-по-лож-ных углах, по свой-ству па-рал-ле-ло-грам-ма о сумме углов, при-ле-жа-щих к одной сто-роне.
Б. по свой-ству ра-вен-ства про-ти-во-по-лож-ных сто-рон.
ре-тий при-знак па-рал-ле-ло-грам-ма
5. Повторение: определение и свойства параллелограмма
На-пом-ним, что па-рал-ле-ло-грамм — это че-ты-рёх-уголь-ник, у ко-то-ро-го про-ти-во-по-лож-ные сто-ро-ны по-пар-но па-рал-лель-ны. То есть, если — па-рал-ле-ло-грамм, то (см. Рис. 1).
Па-рал-ле-ло-грамм об-ла-да-ет целым рядом свойств: про-ти-во-по-лож-ные углы равны (), про-ти-во-по-лож-ные сто-ро-ны равны (). Кроме того, диа-го-на-ли па-рал-ле-ло-грам-ма в точке пе-ре-се-че-ния де-лят-ся по-по-лам, сумма углов, при-ле-жа-щих к любой сто-роне па-рал-ле-ло-грам-ма, равна и т.д.
Но для того, чтобы поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть аб-со-лют-но уве-рен-ны-ми в том, что рас-смат-ри-ва-е-мый че-ты-рёх-уголь-ник — па-рал-ле-ло-грамм. Для этого и су-ще-ству-ют при-зна-ки па-рал-ле-ло-грам-ма: то есть те факты, из ко-то-рых можно сде-лать од-но-знач-ный вывод, что че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.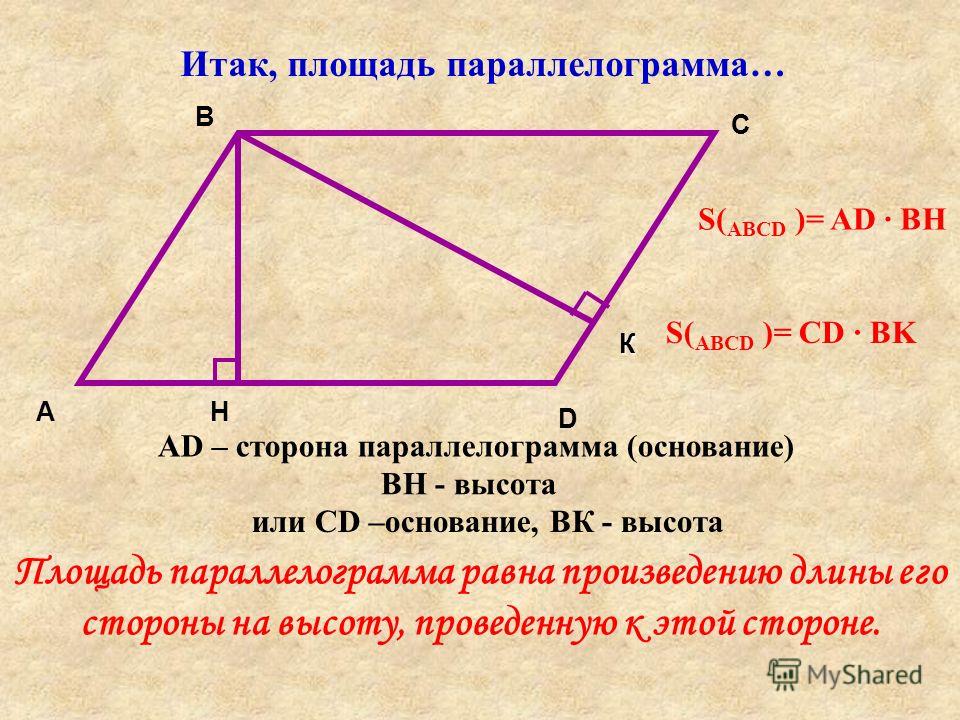 На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.
На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.
6. Третий признак параллелограмма и его доказательство
Если в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам, то дан-ный че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.
Дано:
Че-ты-рёх-уголь-ник; ; .
До-ка-зать:
Па-рал-ле-ло-грамм.
До-ка-за-тель-ство:
Для того чтобы до-ка-зать дан-ный факт, необ-хо-ди-мо до-ка-зать па-рал-лель-ность сто-рон па-рал-ле-ло-грам-ма. А па-рал-лель-ность пря-мых чаще всего до-ка-зы-ва-ет-ся через ра-вен-ство внут-рен-них на-крест ле-жа-щих углов при этих пря-мых. Таким об-ра-зом, на-пра-ши-ва-ет-ся сле-ду-ю-щий спо-соб до-ка-за-тель-ства тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма: через ра-вен-ство тре-уголь-ни-ков .
До-ка-жем ра-вен-ство этих тре-уголь-ни-ков. Дей-стви-тель-но, из усло-вия сле-ду-ет: . Кроме того, по-сколь-ку углы — вер-ти-каль-ные, то они равны. То есть:
То есть:
(пер-вый при-знак ра-вен-ства тре-уголь-ни-ков — по двум сто-ро-нам и углу между ними).
Из ра-вен-ства тре-уголь-ни-ков: (так как равны внут-рен-ние на-крест ле-жа-щие углы при этих пря-мых и се-ку-щей ). Кроме того, из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что . Зна-чит, мы по-лу-чи-ли, что в че-ты-рёх-уголь-ни-ке две сто-ро-ны равны и па-рал-лель-ны. По пер-во-му при-зна-ку па-рал-ле-ло-грам-ма: — па-рал-ле-ло-грамм.
До-ка-за-но.
7. Пример задачи на третий признак параллелограмма и обобщение
Рас-смот-рим при-мер на при-ме-не-ние тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма.
При-мер 1
Дано:
— па-рал-ле-ло-грамм; . — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на (см. Рис. 2).
До-ка-зать: — па-рал-ле-ло-грамм.
До-ка-за-тель-ство:
Зна-чит, в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам.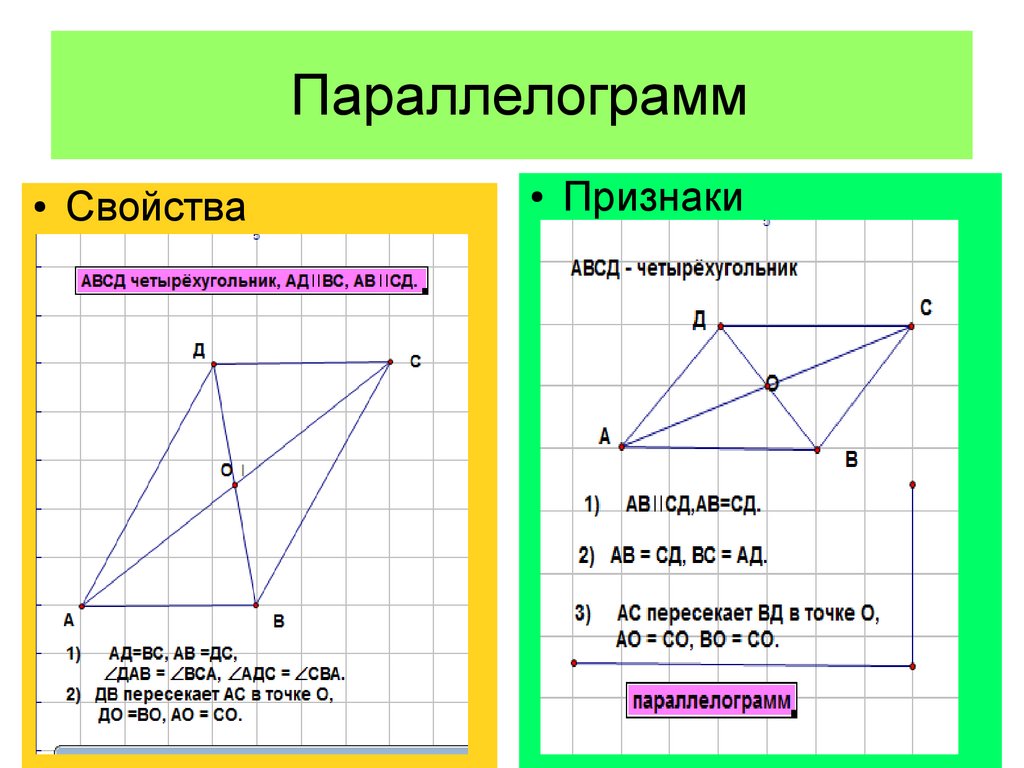 По тре-тье-му при-зна-ку па-рал-ле-ло-грам-ма из этого сле-ду-ет, что — па-рал-ле-ло-грамм.
По тре-тье-му при-зна-ку па-рал-ле-ло-грам-ма из этого сле-ду-ет, что — па-рал-ле-ло-грамм.
До-ка-за-но.
Если про-ве-сти ана-лиз тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма, то можно за-ме-тить, что этот при-знак со-от-вет-ству-ет свой-ству па-рал-ле-ло-грам-ма. То есть, то, что диа-го-на-ли де-лят-ся по-по-лам, яв-ля-ет-ся не про-сто свой-ством па-рал-ле-ло-грам-ма, а его от-ли-чи-тель-ным, ха-рак-те-ри-сти-че-ским свой-ством, по ко-то-ро-му его можно вы-де-лить из мно-же-ства че-ты-рёх-уголь-ни-ков.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma
http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg
http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg
http://wwww.tepka.ru/geometriya/16.1.gif
Доказательство
Первым делом проведем диагональ AC
. Получаются два треугольника: ABC
и ADC
.
Получаются два треугольника: ABC
и ADC
.
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).
И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD
.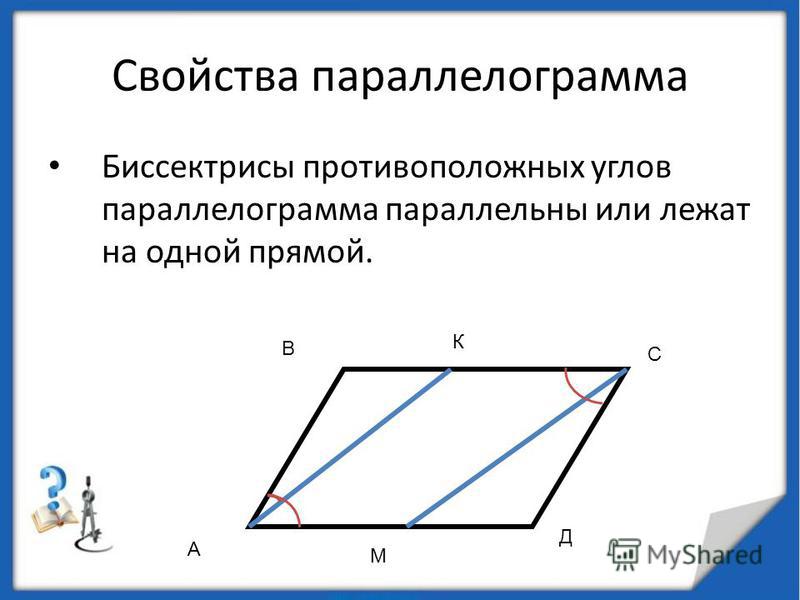 Еще раз отметим накрест лежащие равные углы.
Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).
Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC ?
\triangle ABC = \triangle ADC
по свойству 1 : AB = CD
, AC
— общая и \angle 1 = \angle 2
как накрест лежащие при параллельных AB
и CD
и секущей AC
. {\circ}
говорит и о том, что AD || BC
.
{\circ}
говорит и о том, что AD || BC
.
При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.
AO = OC ; BO = OD \Rightarrow параллелограмм.
Доказательство
BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .
Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .
Четвертый признак верен.
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠
ОАD=∠
ОСВ и ∠
ОDА=∠
ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠
А=∠
С и ∠
В=∠
D. Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон. Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам.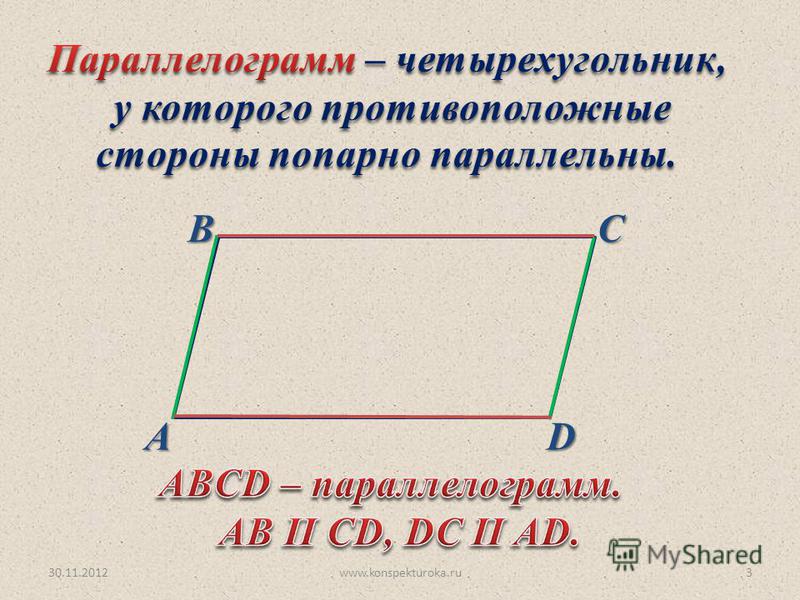 Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
Как доказать что геометрическая фигура параллелограмм. Параллелограмм
Параллелограмм. Признаки параллелограмма
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
Теорема.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство.
Пусть ABCD – данный параллелограмм, O – точка пересечения диагоналей данного параллелограмма.
Δ AOD = Δ COB по первому признаку равенства треугольников (OD = OB, AO = OC по условию теоремы, ∠ AOD = ∠ COB, как вертикальные углы). Следовательно, ∠ OBC = ∠ ODA. А они являются внутренними накрест лежащими для прямых AD и BC и секущей BD. По признаку параллельности прямых прямые AD и BC параллельны. Так же доказываем, что AB и DC тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.
Так же доказываем, что AB и DC тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.
Теорема.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Пусть ABCD – данный четырехугольник. AD параллельно BC и AD = BC.
Тогда Δ ADB = Δ CBD по первому признаку равенства треугольников (∠ ADB = ∠ CBD, как внутренние накрест лежащие между прямыми AD и BC и секущей DB, AD=BC по условию, DB – общая).
Следовательно, ∠ ABD = ∠ CDB, а эти углы являются внутренними накрест лежащими для прямых AB и CD и секущей DB. По теореме признаке параллельности прямых AB и CD параллельны. Значит, ABCD – параллелограмм. Теорема доказана.
Теорема.
Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.
I. Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.
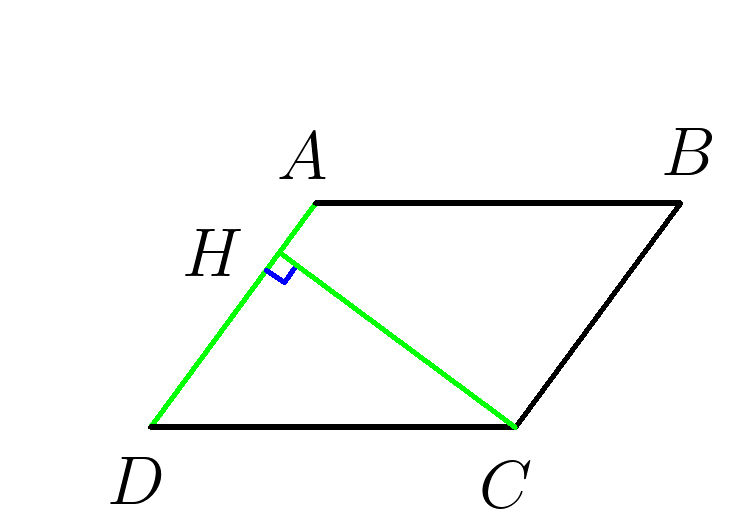
Задача 1. Из вершин В и D параллелограмма АBCD, у которого АВ≠ ВС и угол А — острый, проведены перпендикуляры BK и DM к прямой АС. Докажите, что четырехугольник BMDK — параллелограмм.
Доказательство.
Так как ВК и DM перпендикулярны одной и той же прямой АС, то ВК II DM. Кроме того, ВК и DM являются высотами, проведенными в равных треугольниках Δ АВС и Δ CDA из вершин равных углов ∠B и ∠D к одной и той же стороне АС, следовательно, ВК = DM. Имеем: две стороны ВК и DM четырехугольника BMDK параллельны и равны, значит, BMDK – параллелограмм, что и требовалось доказать.
Кроме того, ВК и DM являются высотами, проведенными в равных треугольниках Δ АВС и Δ CDA из вершин равных углов ∠B и ∠D к одной и той же стороне АС, следовательно, ВК = DM. Имеем: две стороны ВК и DM четырехугольника BMDK параллельны и равны, значит, BMDK – параллелограмм, что и требовалось доказать.
II. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
Задача 2. На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственно точки M, N, P и Q так, что AM=CP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD и MNPQ — параллелограммы.
Доказательство.
1. По условию в четырехугольнике ABCD противоположные стороны состоят из равных отрезков, поэтому равны, т.е. AD=BC, AB=CD. Следовательно, ABCD – параллелограмм.
2. Рассмотрим Δ MBN и Δ PDQ. BM=DP и BN=DQ по условию. ∠B =∠D как противолежащие углы параллелограмма ABCD. Значит, Δ MBN = Δ PDQ по двум сторонам и углу между ними (1-й признак равенства треугольников). А в равных треугольниках против равных углов лежат равные стороны. Отсюда MN=PQ. Мы доказали, что противоположные стороны MN и PQ четырехугольника MNPQ равны. Аналогично, из равенства треугольников Δ MAQ и Δ PCN следует равенство сторон MQ и PN, которые являются противоположными сторонами четырехугольника MNPQ. Имеем: противоположные стороны четырехугольника MNPQ попарно равны. Следовательно, четырехугольник MNPQ – параллелограмм. Задача решена.
А в равных треугольниках против равных углов лежат равные стороны. Отсюда MN=PQ. Мы доказали, что противоположные стороны MN и PQ четырехугольника MNPQ равны. Аналогично, из равенства треугольников Δ MAQ и Δ PCN следует равенство сторон MQ и PN, которые являются противоположными сторонами четырехугольника MNPQ. Имеем: противоположные стороны четырехугольника MNPQ попарно равны. Следовательно, четырехугольник MNPQ – параллелограмм. Задача решена.
III. Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Задача 3. Диагонали параллелограмма ABCD пересекаются в точке O, Докажите, что четырехугольник MNPQ, вершинами которого являются середины отрезков OA, OB, OC и OD, — параллелограмм.
Доказательство.
По свойству диагоналей параллелограмма ABCD его диагонали AC и BD точкой пересечения делятся пополам, т.е. ОА=ОС и ОВ=OD. Диагонали четырехугольника MNPQ так же пересекаются в точке О, которая будет серединой каждой их них. Действительно, так как вершины четырехугольника MNPQ по условию являются серединами отрезков ОА, ОС, ОВ и OD, то BN=ON=OQ=DQ и AM=OM=OP=CP. Следовательно, диагонали MP и NQ четырехугольника MNPQ в точке пересечения делятся пополам, следовательно, четырехугольник MNPQ – параллелограмм, что и требовалось доказать.
Действительно, так как вершины четырехугольника MNPQ по условию являются серединами отрезков ОА, ОС, ОВ и OD, то BN=ON=OQ=DQ и AM=OM=OP=CP. Следовательно, диагонали MP и NQ четырехугольника MNPQ в точке пересечения делятся пополам, следовательно, четырехугольник MNPQ – параллелограмм, что и требовалось доказать.
Теорема: Четырехугольник является параллелограммом, если:
- противоположные его углы равны;
- противоположные его стороны попарно равны;
- его диагонали точкой пересечения делятся пополам;
- две его противоположные стороны параллельны и равны.
Доказательство:
A. Пусть в четырехугольнике KLMN углы К и М равны друг другу и равны а, пусть также равны друг другу и равны р углы L и N (рисунок). Учитывая, что сумма углов четырехугольника равна 360°, получаем, что 2α + 2β = 360°, или α + β = 180°. Учитывая, что углы К и L, равные соответственно аир, являются внутренними односторонними углами при прямых KN и LM, пересеченных прямой KL, заключаем, что стороны KN и LM параллельны.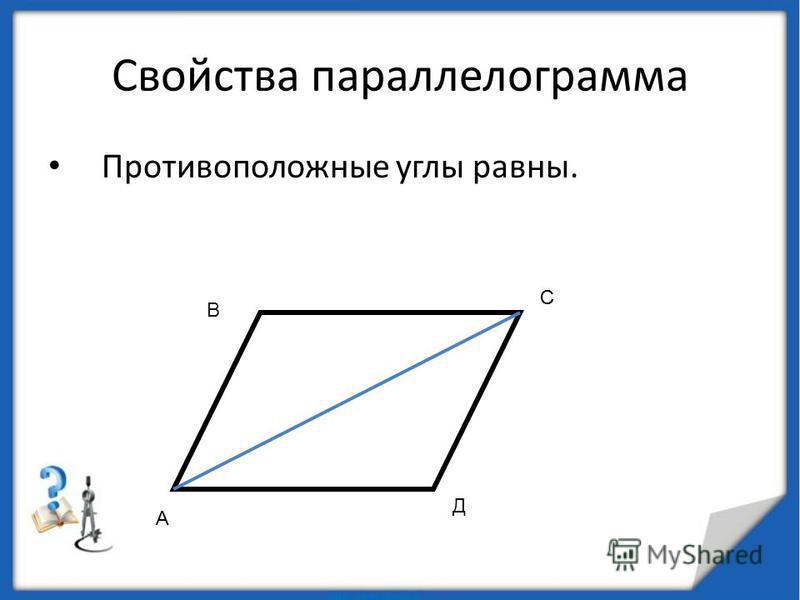 Также по углам К и N заключаем, что стороны KL и NM параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник KLMN — параллелограмм.
Также по углам К и N заключаем, что стороны KL и NM параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник KLMN — параллелограмм.
B. Пусть в четырехугольнике CDEF стороны CD и FE, а также CF и DE попарно равны (рисунок). Проведем одну из диагоналей четырехугольника, например СЕ. Треугольники CDE и EFC равны по трем сторонам. Поэтому углы DEC и FCE равны. Поскольку эти углы являются внутренними накрест лежащими при прямых DE и CF, пересеченных прямой СЕ, то стороны DE и CF параллельны. Также из равенства углов DCE и FEC получаем, что стороны CD и FE параллельны. Теперь по определению параллелограмма утверждаем, что четырехугольник CDEF — параллелограмм.
C. Пусть точка В пересечения диагоналей IL и КМ четырехугольника IKLM делит эти диагонали пополам: IB = BL и KB = ВМ (рисунок). Тогда треугольники KBL и MBI равны по двум сторонам и углу между ними. Это позволяет утверждать, что углы 1MB и LKB равны, а значит, стороны IM и KL параллельны. Аналогично из равенства треугольников KBI и MBL делаем вывод о параллельности сторон IK и LM.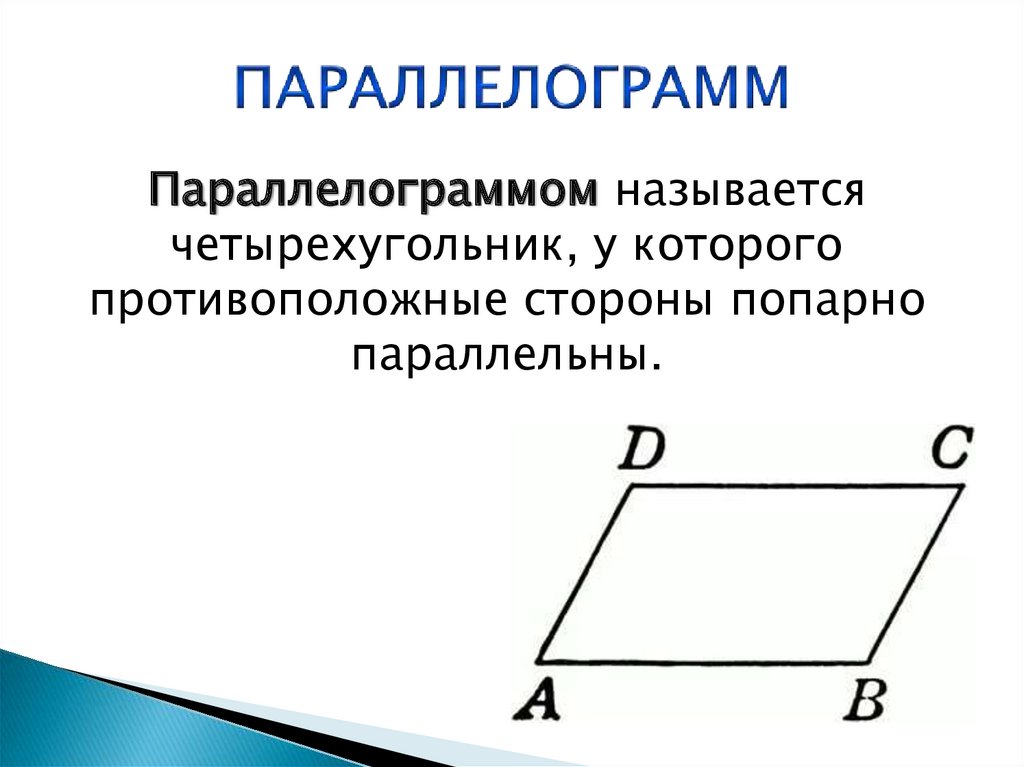 Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
Теперь по определению параллелограмма можем утверждать, что четырехугольник IKLM — параллелограмм. Очень часто это надо знать при решении олимпиадных задачах на школьных олимпиадах.
D. Пусть в четырехугольнике OPQR противоположные стороны ОР и RQ параллельны и равны (рисунок). Проведем диагональ OQ. Полученные углы POQ и RQO равны, так как они являются внутренними накрест лежащими при параллельных прямых ОР и RQ, пересеченных прямой OQ. Поэтому треугольники OPQ и RQO равны по двум сторонам и углу между ними. Значит, их соответствующие углы PQO и ROQ равны.
А поскольку они являются внутренними накрест лежащими углами при прямых PQ и OR, пересеченных прямой OQ, то стороны PQ и OR параллельны. Учитывая параллельность сторон ОР и RQ, по определению параллелограмма утверждаем, что четырехугольник OPQR — параллелограмм.
Это четырёхугольник, противоположные стороны которого попарно параллельны.
Свойство 1
. Любая диагональ параллелограмма делит его на два равных треугольника.
Доказательство . По II признаку (накрест лежащие углы и общая сторона).
Теорема доказана .
Свойство 2 . В параллелограмме противолежащие стороны равны, противолежащие углы равны.
Доказательство
.
Аналогично,
Теорема доказана .
Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.
Доказательство .
Теорема доказана .
Свойство 4 . Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. — вершину — два равнобедренных?-ка).
Доказательство
.
Теорема доказана .
Свойство 5 . В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.
Доказательство .
Теорема доказана .
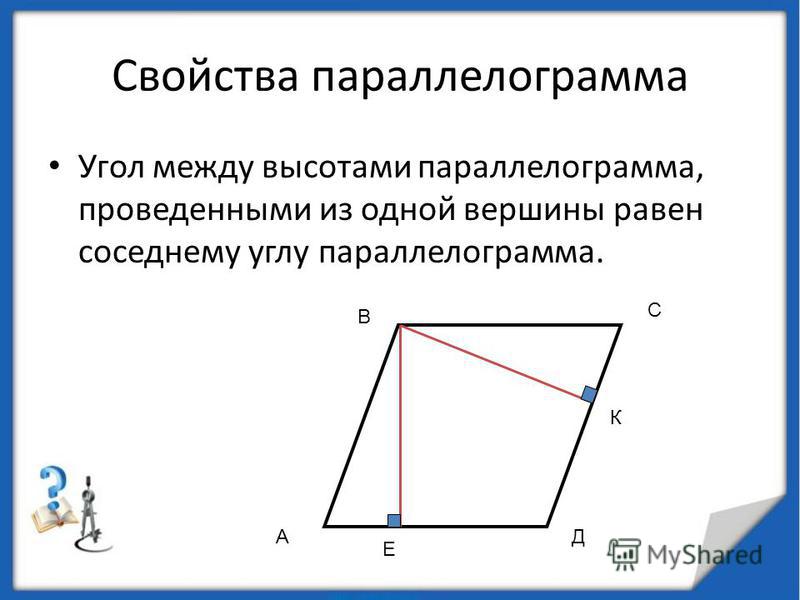
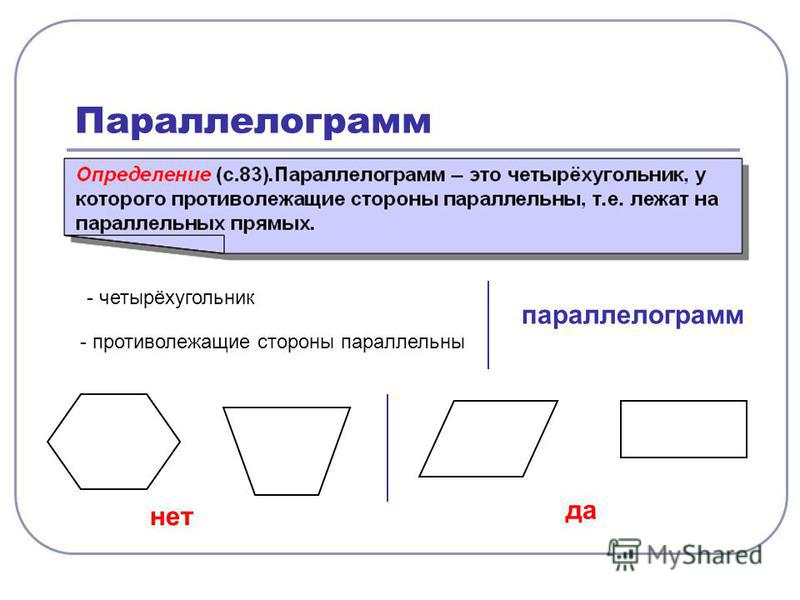
Свойство 6 . Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.
Доказательство
.
Теорема доказана .
Свойство 7 . Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
Доказательство .
Теорема доказана .
Построение биссектрисы угла. Свойства биссектрисы угла треугольника.
1) Построить произвольный луч DE.
2) На данном луче построить произвольную окружность с центром в вершине и такую же
с центром в начале построенного луча.
3) F и G — точки пересечения окружности со сторонами данного угла, H — точка пересечения окружности с построенным лучом
Построить окружность с центром в точке H и радиусом, равным FG.
5) I — точка пересечения окружностей построенного луча.
6) Провести прямую через вершину и I.
IDH — требуемый угол.
)
Свойство 1 . Биссектриса угла треугольника разбивает противоположную сторону пропорционально прилежащим сторонам.
Доказательство
. Пусть x, y-отрезки стороны c. Продолжим луч BC. На луче BC отложим от C отрезок CK, равный AC.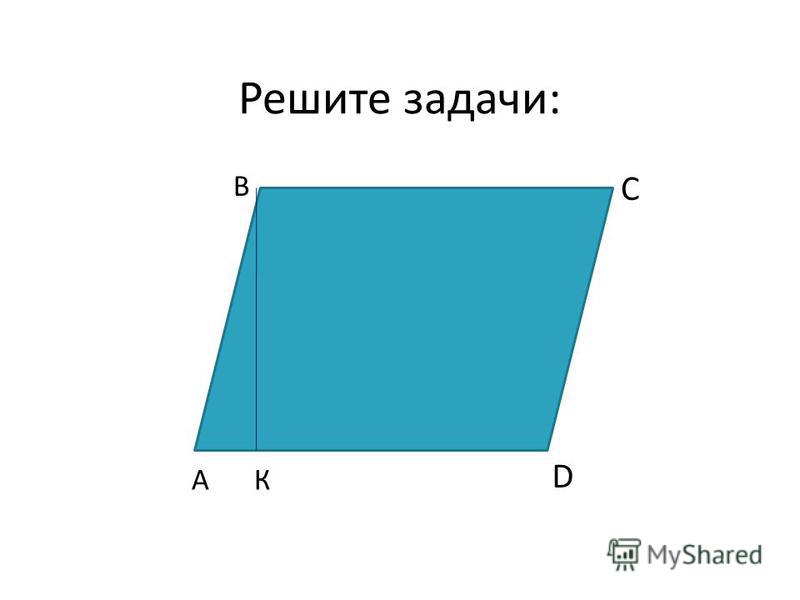
При-зна-ки па-рал-ле-ло-грам-ма
1. Определение и основные свойства параллелограмма
Нач-нем с того, что вспом-ним опре-де-ле-ние па-рал-ле-ло-грам-ма.
Опре-де-ле-ние. Па-рал-ле-ло-грамм — че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 1).
Рис. 1. Па-рал-ле-ло-грамм
Вспом-ним ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :
Для того, чтобы иметь воз-мож-ность поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть уве-рен-ным, что фи-гу-ра, о ко-то-рой идет речь, — па-рал-ле-ло-грамм. Для этого необ-хо-ди-мо знать такие факты, как при-зна-ки па-рал-ле-ло-грам-ма. Пер-вые два из них мы се-год-ня и рас-смот-рим.
2. Первый признак параллелограмма
Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .
Рис.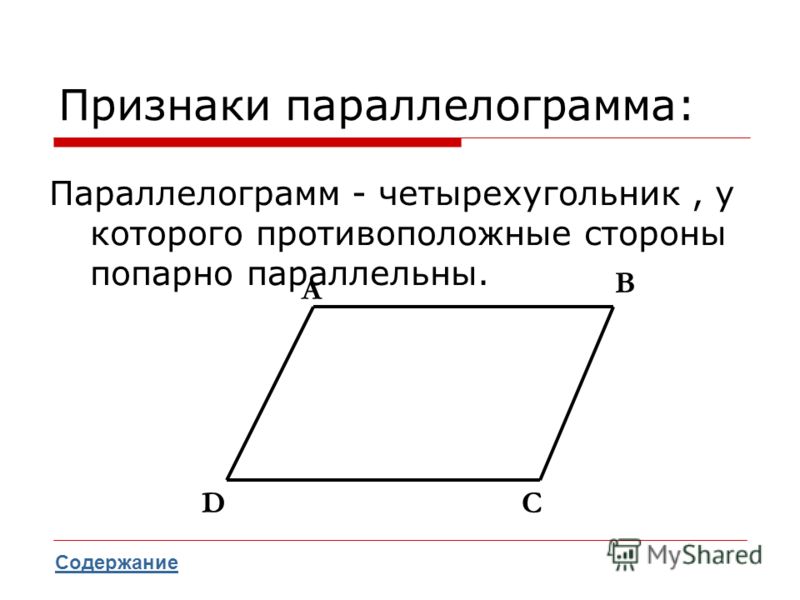 2. Пер-вый при-знак па-рал-ле-ло-грам-ма
2. Пер-вый при-знак па-рал-ле-ло-грам-ма
До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 2), она раз-би-ла его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках:
по пер-во-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.
Из ра-вен-ства ука-зан-ных тре-уголь-ни-ков сле-ду-ет, что по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. Имеем, что:
До-ка-за-но.
3. Второй признак параллелограмма
Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны, то этот че-ты-рех-уголь-ник — па-рал-ле-ло-грамм . .
Рис. 3. Вто-рой при-знак па-рал-ле-ло-грам-ма
До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 3), она раз-би-ва-ет его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках, ис-хо-дя из фор-му-ли-ров-ки тео-ре-мы:
по тре-тье-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.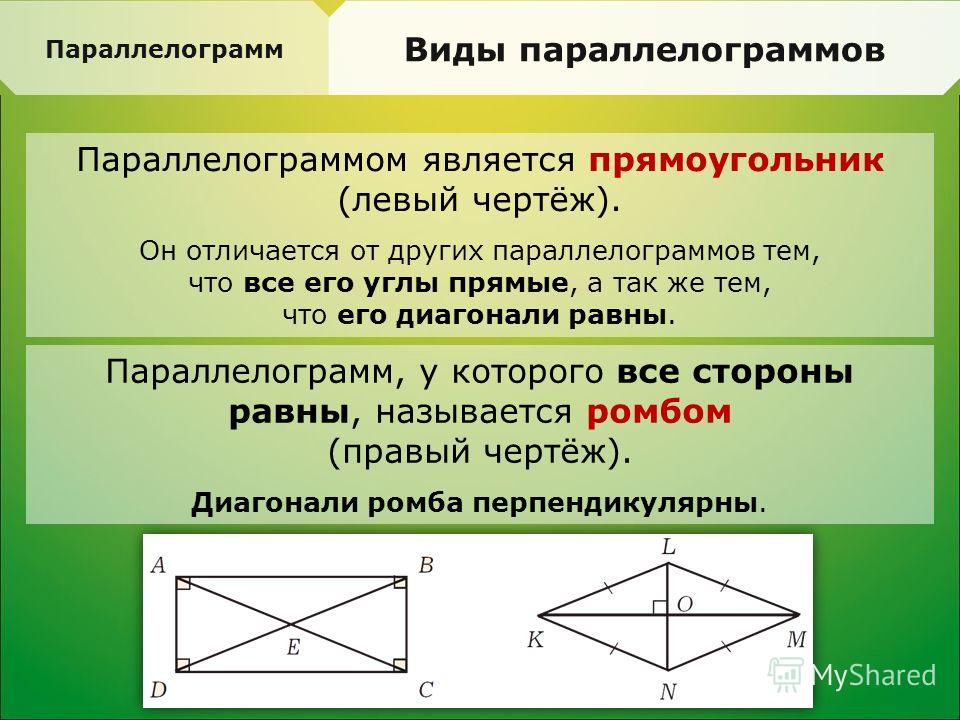
Из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что и по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. По-лу-ча-ем:
па-рал-ле-ло-грамм по опре-де-ле-нию. Что и тре-бо-ва-лось до-ка-зать.
До-ка-за-но.
4. Пример на применение первого признака параллелограмма
Рас-смот-рим при-мер на при-ме-не-ние при-зна-ков па-рал-ле-ло-грам-ма.
При-мер 1. В вы-пук-лом че-ты-рех-уголь-ни-ке Найти: а) углы че-ты-рех-уголь-ни-ка; б) сто-ро-ну .
Ре-ше-ние. Изоб-ра-зим Рис. 4.
па-рал-ле-ло-грамм по пер-во-му при-зна-ку па-рал-ле-ло-грам-ма.
А. по свой-ству па-рал-ле-ло-грам-ма о про-ти-во-по-лож-ных углах, по свой-ству па-рал-ле-ло-грам-ма о сумме углов, при-ле-жа-щих к одной сто-роне.
Б. по свой-ству ра-вен-ства про-ти-во-по-лож-ных сто-рон.
ре-тий при-знак па-рал-ле-ло-грам-ма
5. Повторение: определение и свойства параллелограмма
На-пом-ним, что па-рал-ле-ло-грамм — это че-ты-рёх-уголь-ник, у ко-то-ро-го про-ти-во-по-лож-ные сто-ро-ны по-пар-но па-рал-лель-ны.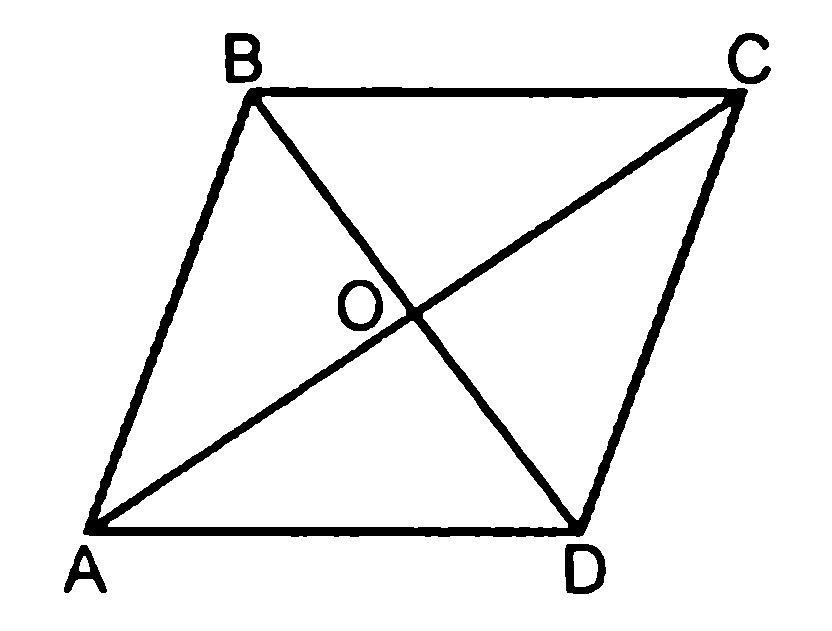 То есть, если — па-рал-ле-ло-грамм, то (см. Рис. 1).
То есть, если — па-рал-ле-ло-грамм, то (см. Рис. 1).
Па-рал-ле-ло-грамм об-ла-да-ет целым рядом свойств: про-ти-во-по-лож-ные углы равны (), про-ти-во-по-лож-ные сто-ро-ны равны (). Кроме того, диа-го-на-ли па-рал-ле-ло-грам-ма в точке пе-ре-се-че-ния де-лят-ся по-по-лам, сумма углов, при-ле-жа-щих к любой сто-роне па-рал-ле-ло-грам-ма, равна и т.д.
Но для того, чтобы поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть аб-со-лют-но уве-рен-ны-ми в том, что рас-смат-ри-ва-е-мый че-ты-рёх-уголь-ник — па-рал-ле-ло-грамм. Для этого и су-ще-ству-ют при-зна-ки па-рал-ле-ло-грам-ма: то есть те факты, из ко-то-рых можно сде-лать од-но-знач-ный вывод, что че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом. На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.
6. Третий признак параллелограмма и его доказательство
Если в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам, то дан-ный че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.
Дано:
Че-ты-рёх-уголь-ник; ; .
До-ка-зать:
Па-рал-ле-ло-грамм.
До-ка-за-тель-ство:
Для того чтобы до-ка-зать дан-ный факт, необ-хо-ди-мо до-ка-зать па-рал-лель-ность сто-рон па-рал-ле-ло-грам-ма. А па-рал-лель-ность пря-мых чаще всего до-ка-зы-ва-ет-ся через ра-вен-ство внут-рен-них на-крест ле-жа-щих углов при этих пря-мых. Таким об-ра-зом, на-пра-ши-ва-ет-ся сле-ду-ю-щий спо-соб до-ка-за-тель-ства тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма: через ра-вен-ство тре-уголь-ни-ков .
До-ка-жем ра-вен-ство этих тре-уголь-ни-ков. Дей-стви-тель-но, из усло-вия сле-ду-ет: . Кроме того, по-сколь-ку углы — вер-ти-каль-ные, то они равны. То есть:
(пер-вый при-знак ра-вен-ства тре-уголь-ни-ков — по двум сто-ро-нам и углу между ними).
Из ра-вен-ства тре-уголь-ни-ков: (так как равны внут-рен-ние на-крест ле-жа-щие углы при этих пря-мых и се-ку-щей ). Кроме того, из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что . Зна-чит, мы по-лу-чи-ли, что в че-ты-рёх-уголь-ни-ке две сто-ро-ны равны и па-рал-лель-ны. По пер-во-му при-зна-ку па-рал-ле-ло-грам-ма: — па-рал-ле-ло-грамм.
Зна-чит, мы по-лу-чи-ли, что в че-ты-рёх-уголь-ни-ке две сто-ро-ны равны и па-рал-лель-ны. По пер-во-му при-зна-ку па-рал-ле-ло-грам-ма: — па-рал-ле-ло-грамм.
До-ка-за-но.
7. Пример задачи на третий признак параллелограмма и обобщение
Рас-смот-рим при-мер на при-ме-не-ние тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма.
При-мер 1
Дано:
— па-рал-ле-ло-грамм; . — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на , — се-ре-ди-на (см. Рис. 2).
До-ка-зать: — па-рал-ле-ло-грамм.
До-ка-за-тель-ство:
Зна-чит, в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам. По тре-тье-му при-зна-ку па-рал-ле-ло-грам-ма из этого сле-ду-ет, что — па-рал-ле-ло-грамм.
До-ка-за-но.
Если про-ве-сти ана-лиз тре-тье-го при-зна-ка па-рал-ле-ло-грам-ма, то можно за-ме-тить, что этот при-знак со-от-вет-ству-ет свой-ству па-рал-ле-ло-грам-ма. То есть, то, что диа-го-на-ли де-лят-ся по-по-лам, яв-ля-ет-ся не про-сто свой-ством па-рал-ле-ло-грам-ма, а его от-ли-чи-тель-ным, ха-рак-те-ри-сти-че-ским свой-ством, по ко-то-ро-му его можно вы-де-лить из мно-же-ства че-ты-рёх-уголь-ни-ков.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/priznaki-parallelogramma
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/tretiy-priznak-parallelogramma
http://www.uchportfolio.ru/users_content/675f9820626f5bc0afb47b57890b466e/images/46TThxQ8j4Y.jpg
http://cs10002.vk.me/u31195134/116260458/x_56d40dd3.jpg
http://wwww.tepka.ru/geometriya/16.1.gif
Определение, типы, формулы, примеры задач, часто задаваемые вопросы
Термин «параллелограмм» происходит от греческого «parallelogrammon», означающего «ограниченный параллельными линиями». Итак, параллелограмм – это четырехугольник, окруженный параллельными прямыми. Он имеет ту же форму, что и параллельные противоположные стороны. Форма параллелограмма бывает трех основных типов: квадратная, прямоугольная и ромбовидная, каждая из которых обладает уникальными свойствами. Давайте узнаем больше о свойствах параллелограмма, площади и периметра параллелограмма, а также их примерах, подробно.
Параллелограмм является одним из особых видов четырехугольника. Углы между соседними сторонами параллелограмма могут быть разными, но чтобы он был параллелограммом, противоположные стороны должны быть параллельны. Четырехугольник является параллелограммом, если его противоположные стороны параллельны и равны. Следовательно, параллелограмм определяется как четырехугольник, у которого две пары противоположных сторон параллельны и равны. Ниже приведена схема параллелограмма ABCD, имеющего смежные стороны «a» и «b» и высоту «h».
Свойства параллелограмма
Четырехугольник обладает особыми свойствами, если их применить, то получится параллелограмм. Давайте посмотрим на свойства параллелограмма,
- Противоположные стороны параллелограмма параллельны и равны.
- Противоположные углы параллелограмма равны.
- Если сказано, то один из углов параллелограмма равен 90°. Тогда все углы равны 90°, и он становится прямоугольником.
- Диагонали параллелограмма делят друг друга пополам.

- Последовательные углы параллелограмма являются дополнительными.
Типы параллелограммов
Параллелограммы можно разделить на несколько типов в зависимости от их свойств. Основываясь на свойствах параллелограмма, сторонах и углах, параллелограмм подразделяется на три типа:
Прямоугольник
Прямоугольник — это параллелограмм с двумя парами равных параллельных противоположных сторон и четырьмя прямыми углами. Изучите прямоугольник ABCD и свяжите его со следующими свойствами:
- Две пары параллельных сторон. Здесь АВ || DC и AD || BC
- Четыре прямых угла ∠A = ∠B = ∠C = ∠D = 90°.
- Противоположные стороны имеют одинаковую длину, где AB = DC и AD = BC.
- Две равные диагонали, где AC = BD.
- Диагонали, которые делят друг друга пополам.
Квадрат
Параллелограмм с четырьмя равными сторонами и четырьмя равными углами называется квадратом. Обратите внимание на квадрат ACDB и свяжите его со следующими свойствами:
- Четыре равные стороны AB = BC = CD = DA.

- Прямые углы равны ∠A = ∠B = ∠C = ∠D = 90°.
- Две пары параллельных сторон. Здесь АВ || DC и AD || ДО Н.Э.
- Две одинаковые диагонали, где AD = BC.
- Диагонали перпендикулярны и делят друг друга пополам; AD перпендикулярна BC.
Ромб
Параллелограмм с четырьмя равными сторонами и равными противоположными углами называется ромбом. Рассмотрим ромб ABCD и присвоим ему следующие атрибуты
- На данном рисунке четыре равные стороны AB = CD = BC = AD.
- Две пары параллельных сторон AB || КД и БК || ОБЪЯВЛЕНИЕ.
- Противоположные углы равны ∠A = ∠B и ∠C = ∠D.
- Здесь диагонали (AC и BD) перпендикулярны друг другу и делятся пополам под прямым углом.
Все 2D-фигуры имеют две основные формулы для площади и периметра. Давайте обсудим эти две формулы параллелограмма в этом разделе.
Площадь параллелограмма
Площадь параллелограмма – это пространство между четырьмя сторонами параллелограмма.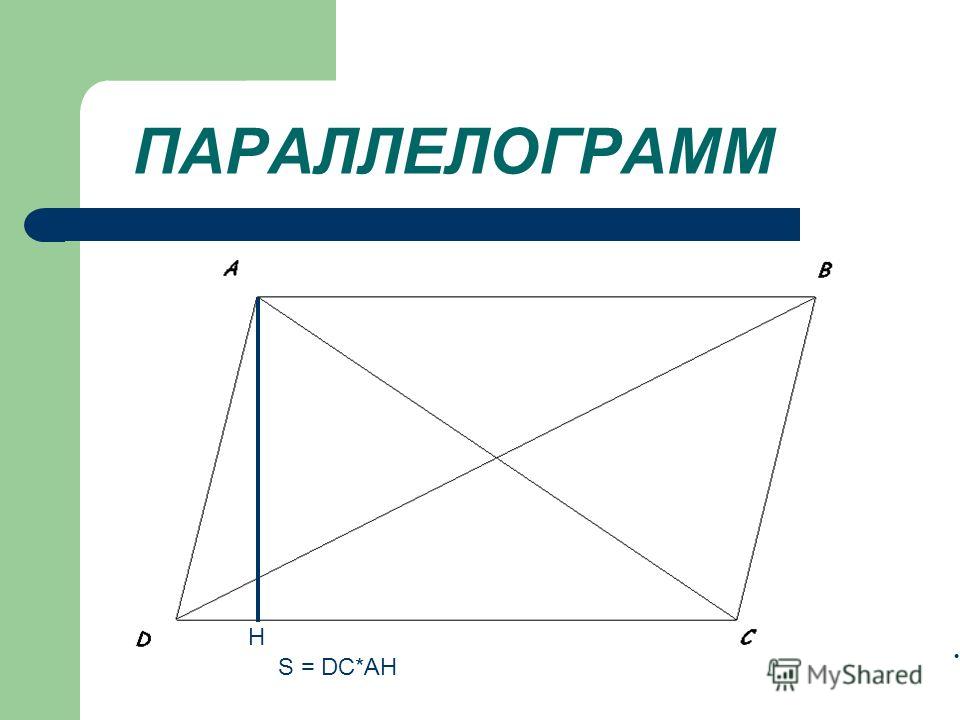 Его можно рассчитать, зная длину основания и высоту параллелограмма и измерив их в квадратных единицах, таких как см 2 , м 2 или дюйм 2 . Обратите внимание на следующий параллелограмм, представляющий основание и высоту.
Его можно рассчитать, зная длину основания и высоту параллелограмма и измерив их в квадратных единицах, таких как см 2 , м 2 или дюйм 2 . Обратите внимание на следующий параллелограмм, представляющий основание и высоту.
Рассмотрим параллелограмм ABCD с основанием (b) и высотой (h). Площадь параллелограмма вычисляется по формуле:
Площадь параллелограмма = основание (b) × высота (h)
Площадь параллелограмма без высоты
Когда высота параллелограмма неизвестна, но площадь параллелограмма может быть найдена при условии угол нам известен. Формула площади параллелограмма без учета высоты:
Площадь параллелограмма = ab Sinθ
Где a и b — стороны параллелограмма, а θ — угол между ними.
Периметр параллелограмма
Периметр параллелограмма — это длина его контура, поэтому он равен сумме всех сторон.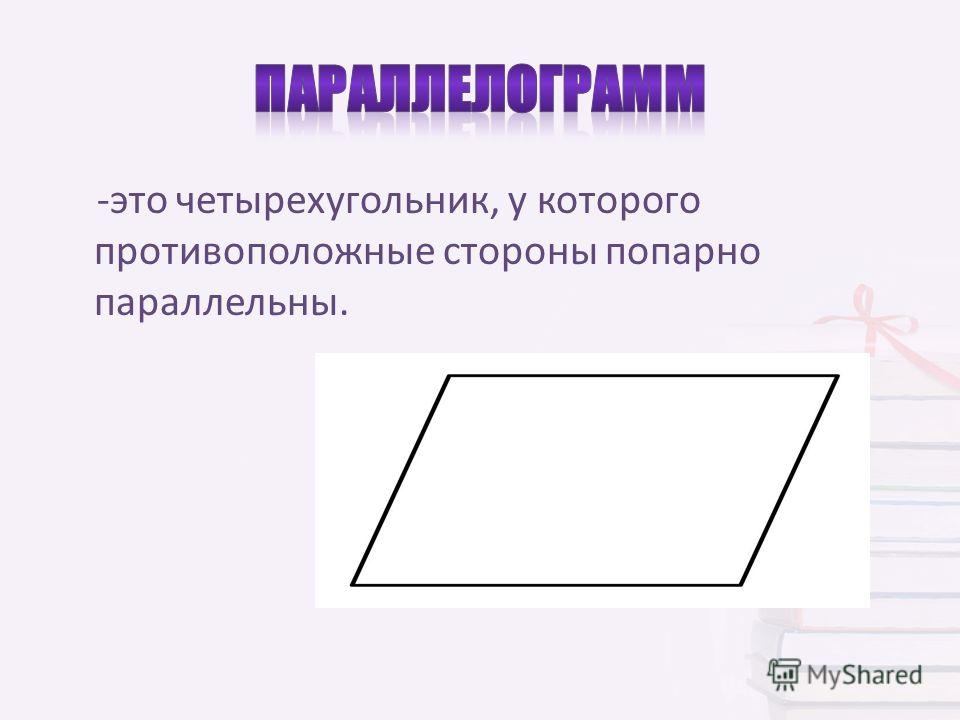 В параллелограмме противоположные стороны равны. Допустим стороны равны a и b. Следовательно, периметр (P) параллелограмма с ребрами выражается в единицах P = 2 (a + b).
В параллелограмме противоположные стороны равны. Допустим стороны равны a и b. Следовательно, периметр (P) параллелограмма с ребрами выражается в единицах P = 2 (a + b).
Периметр параллелограмма = 2 (a + b)
Теорема о параллелограмме
Теорема: Параллелограммы на одном основании и между одинаковыми параллелями имеют одинаковую площадь.
Доказательство: Предположим, что есть два параллелограмма ABCD и ABEF с одинаковым основанием DC и между одинаковыми параллельными прямыми AB и FC
Доказать: Площадь параллелограмма ABCD = Площадь параллелограмма ABEF
На рисунке ниже , два параллелограмма ABCD и ABEF лежат между одними и теми же параллельными прямыми и имеют одно и то же основание. Площадь ABDE является общей для обоих параллелограммов. Если присмотреться к двум треугольникам, △BCD и △AEF могут оказаться конгруэнтными.
BC = AE (противоположные стороны параллелограмма),
∠BCD = ∠AEF (это соответствующие углы, поскольку BC || AE и CE являются поперечными).
∠BDC = ∠AFE (это соответствующие углы, потому что BD || AF и FD являются секущими).
Таким образом, по критерию конгруэнтности треугольников ASA. Эти два треугольника конгруэнтны, и их площади должны быть равны.
площадь (BCD) = площадь (AEF)
⇒ площадь (BCD) + площадь (ABDE) = площадь (AEF) + площадь (ABDE)
⇒ площадь(ABCD) = площадь(ABEF)
Следовательно, параллелограммы, лежащие между одними и теми же параллельными прямыми и имеющие общее основание, имеют одинаковую площадь.
Разница между прямоугольником и параллелограммом
Прямоугольник и параллелограмм являются четырехугольниками, а прямоугольник является параллелограммом, поскольку он обладает всеми свойствами параллелограмма и даже больше. Однако параллелограмм не всегда является прямоугольником. Ниже приведены различия в свойствах прямоугольника и параллелограмма.
Properties | Parallelogram | Rectangle |
| Sides | The opposite sides of a parallelogram are equal.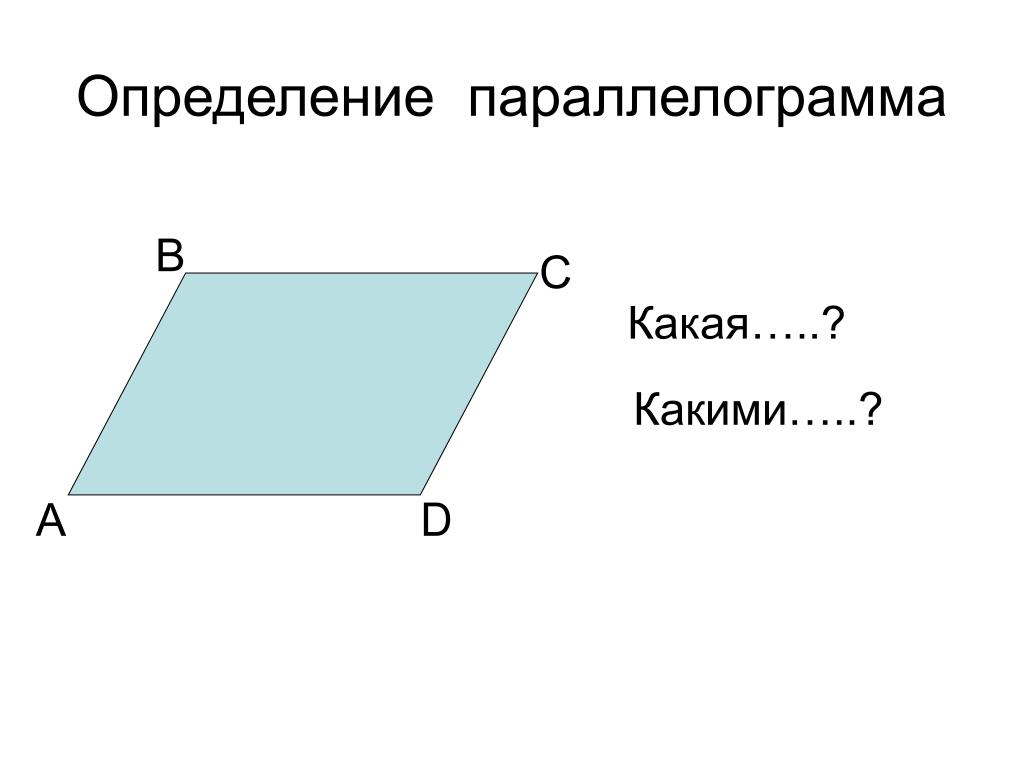 | Противоположные стороны прямоугольника равны. |
| Диагонали | Диагонали параллелограмма делятся пополам, но диагонали не равны. | Диагонали прямоугольника делят друг друга пополам, и диагонали также равны друг другу. |
| Углы | Противоположные углы параллелограмма равны, а прилежащие углы смежные. | Все углы прямоугольника равны между собой и равны 90°. |
Решенные примеры на параллелограмме
Пример 1: Найдите длину другой стороны параллелограмма с основанием 12 см и периметром 60 см.
Решение:
Дан периметр параллелограмма = 60см.
Длина основания данного параллелограмма = 12 см.
P = 2 единицы (a + b)
Где b = 12 см, а P = 40 см.
60 = 2 (а + 12)
60 = 2а + 24
2а = 60-24
2а = 36
а = 18см
Следовательно, длина другой стороны параллелограмма равна 18см
.
Пример 2: Найдите периметр параллелограмма с длиной основания и стороны 15 см и 5 см соответственно.
Решение:
Длина основания данного параллелограмма = 15 см
Длина стороны данного параллелограмма = 5 см
Подставив значения, получим
P = 2(15 + 5)
P = 2(20)
P = 40 см
Следовательно, периметр параллелограмма будет 40 см.
Пример 3: Угол между двумя сторонами параллелограмма равен 90°. Если длины двух параллельных сторон равны 5 см и 4 см соответственно, найдите площадь.
Решение:
Если один угол параллелограмма равен 90°. Тогда остальные углы также равны 90°. Следовательно, параллелограмм становится прямоугольником. Площадь прямоугольника равна длине, умноженной на ширину.
Площадь параллелограмма = 5 × 4
Площадь параллелограмма = 20 см 2
Вопрос 4: Какова площадь параллелограмма, если диагонали равны 8 см, а угол между диагонали составляет 60°.
Решение:
Чтобы найти площадь параллелограмма, необходимо знать основание и высоту, сначала найдем основание параллелограмма, применяя закон косинусов,
b 2 = 4 2 + 5 2 – 2(5)(4)cos(120°)
b 2 = 16 + 25 – 40(0,8)
b см 2 0 900 30 = 30 9 90 90 86
Нахождение высоты параллелограмма,
4/sinθ = b/sin120
4/sinθ = 3/-0,58
sinθ = -0,773
θ = 50 °
Теперь, чтобы найти высоту,
Sinθ = H/10
0,76 = H/10 0003
H = 7,6 см
Площадь параллелограмма = 1/2 × 3 × 7,6
= 11,4 см 2
Пример 5. Докажите, что параллелограмм, описанный вокруг окружности, является ромбом.
Решение:
Дано:
- Параллелограмм ABCD
- Circle PQRS
Доказать: ABCD — ромб.
Доказательство:
Мы знаем, что касательные, проведенные из внешней точки к окружности, равны друг другу. Следовательно:
AP = AS ⇢ (1)
BP = BQ ⇢ (2)
DS = DR ⇢ (3)
CR = CQ ⇢ (4)
Сложение левой и правой частей уравнений 1, 2 , 3 и 4:
AP + BP + DS + CR = AS + BQ + DR + CQ
AB + DR + CR = AS + DS + BC
AB + CD = AD + BC
Так как противоположные углы параллелограмма равны:
2AB = 2BC
AB = BC, и аналогично CD = AD.
Следовательно: AB = CD = BC = AD.
Поскольку все стороны равны, ABCD — ромб.
Часто задаваемые вопросы о параллелограмме
Вопрос 1: Является ли ромб параллелограммом?
Ответ:
Да, ромб — это параллелограмм. Ромб обладает всеми свойствами параллелограмма и даже больше.
Вопрос 2: Чем параллелограмм отличается от четырехугольника?
Ответ:
Все параллелограммы являются четырехугольниками, но не все четырехугольники обязательно являются параллелограммами.
Например, трапеция — это четырехугольник, а не параллелограмм. Чтобы четырехугольник был параллелограммом, все противоположные стороны должны быть параллельны и равны.
Вопрос 3. Является ли трапеция параллелограммом? Чем трапеция отличается от параллелограмма?
Ответ:
Трапеция отличается от параллелограмма тем, что все противоположные стороны трапеции не параллельны друг другу. У трапеции есть только пара противоположных граней, которые параллельны друг другу.
Вопрос 4. Равны ли диагонали параллелограмма?
Ответ:
Нет, диагонали параллелограмма не равны. Однако диагонали параллелограмма делят друг друга пополам.
Вопрос 5: Каждый ромб является параллелограммом. Правда или ложь?
Ответ:
Верно. Каждый ромб является параллелограммом.
Однако параллелограмм не всегда соответствует определению ромба, а значит, и наоборот.
Вопрос 6. Является ли квадрат параллелограммом?
Ответ:
Да, квадрат является параллелограммом, поскольку он обладает всеми свойствами параллелограмма и даже больше, так как квадрат обладает некоторыми дополнительными свойствами (например, все углы прямые и т. д.), все параллелограммы не квадраты.
Вопрос 7. Является ли прямоугольник параллелограммом?
Ответ:
Да, прямоугольник — это параллелограмм. Прямоугольник — это параллелограмм, поскольку он обладает всеми свойствами параллелограмма и даже больше. Однако параллелограмм не всегда является прямоугольником.
Похожие статьи
- Ромб
- Прямоугольник
- Квадрат
2.1: Параллелограммы — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 39635
- Иллюстративная математика
- OpenUp Resources
Lesson
Давайте исследуем особенности и площади параллелограммов.
Упражнение \(\PageIndex{1}\): Особенности параллелограмма
Фигуры A, B и C представляют собой параллелограммов . Фигуры D, E и F представляют собой 90 543, а не 90 544 параллелограмма.
Рисунок \(\PageIndex{1}\)Изучите примеры и не примеры. На что вы обращаете внимание:
- сколько сторон у параллелограмма?
- противоположных сторон параллелограмма?
- противоположных углов параллелограмма?
Упражнение \(\PageIndex{2}\): Площадь параллелограмма
- Найдите площадь параллелограмма и объясните свои рассуждения.
- Измените параллелограмм, перетащив зеленые точки в его вершинах. Найдите его площадь и объясните свои рассуждения.
- Если вы использовали многоугольники сбоку, чем они вам помогли? Если нет, то могли бы вы использовать один или несколько многоугольников, чтобы показать другой способ нахождения площади параллелограмма?
Упражнение \(\PageIndex{3}\): множество параллелограммов
Найдите площадь каждого параллелограмма. Покажите свои рассуждения.
Покажите свои рассуждения.
Резюме
Параллелограмм представляет собой четырехугольник (у него четыре стороны). Противоположные стороны параллелограмма параллельны. Также верно, что противоположные стороны параллелограмма имеют одинаковую длину, и противоположные углы параллелограмма имеют одинаковую меру.
Рисунок \(\PageIndex{4}\): два параллелограмма с указанными углами и длинами сторон. Слева верхняя и нижняя стороны = 5 единиц. Левая и правая стороны = 4,24 единицы. Верхний левый и нижний правый углы = 135 градусов. Верхний правый и нижний левый углы = 45 градусов. Справа верхняя и нижняя стороны = 90,34 единицы. Левая и правая стороны = 4 единицы. Верхний левый и нижний правый углы = 27,2 градуса. Верхний правый и нижний левый углы = 152,8 градуса.Существует несколько стратегий нахождения площади параллелограмма .
- Мы можем разложить и перестроить параллелограмм так, чтобы получился прямоугольник.
 Вот три способа:
Вот три способа:
- Мы можем заключить параллелограмм, а затем вычесть площадь двух треугольников в углу.

Оба эти способа будут работать для любого параллелограмма. Однако для некоторых параллелограммов процесс разложения и перестановки требует гораздо больше шагов, чем если бы мы заключили параллелограмм в прямоугольник и вычли объединенную площадь двух треугольников в углах.
Рисунок \(\PageIndex{7}\): заштрихованный параллелограмм на сетке. База из трех единиц. Наклонные стороны, которые наклоняются на 6 единиц по вертикали по сравнению с 9 единицами по горизонтали. Параллелограмм, разложенный штриховыми отрезками на шесть равных прямоугольных треугольников. Каждый треугольник имеет вертикальную сторону, равную 2 единицам, и горизонтальную сторону, равную 3 единицам. Стрелки идут влево от каждого из 5 нижних треугольников. Получившаяся фигура представляет собой прямоугольник, высота которого равна 6 единицам, а ширина — 3 единицам.
Стрелки идут влево от каждого из 5 нижних треугольников. Получившаяся фигура представляет собой прямоугольник, высота которого равна 6 единицам, а ширина — 3 единицам.Glossary Entries
Определение: Параллелограмм
Параллелограмм — это тип четырехугольника, у которого две пары параллельных сторон.
Вот два примера параллелограмма.
Рисунок \(\PageIndex{8}\): два параллелограмма с указанными углами и длинами сторон. Слева верхняя и нижняя стороны = 5 единиц. Левая и правая стороны = 4,24 единицы. Верхний левый и нижний правый углы = 135 градусов. Верхний правый и нижний левый углы = 45 градусов. Справа верхняя и нижняя стороны = 90,34 единицы. Левая и правая стороны = 4 единицы. Верхний левый и нижний правый углы = 27,2 градуса. Верхний правый и нижний левый углы = 152,8 градуса.Определение: Четырехугольник
Четырехугольник — это тип многоугольника, который имеет 4 стороны. Прямоугольник является примером четырехугольника. Пятиугольник не является четырехугольником, потому что у него 5 сторон.
Практика
Упражнение \(\PageIndex{4}\)
Выберите все параллелограммов. Для каждой цифры, которая равна , а не 9Выбрано 0544, объясните, откуда вы знаете, что это не параллелограмм.
Фигура Е — прямоугольный треугольник.Упражнение \(\PageIndex{5}\)
- Разложите и переставьте этот параллелограмм так, чтобы получился прямоугольник.
- Какова площадь параллелограмма? Объясните или ваши рассуждения.
Упражнение \(\PageIndex{6}\)
Найдите площадь параллелограмма.
Рисунок \(\PageIndex{11}\)Упражнение \(\PageIndex{7}\)
Объясните, почему этот четырехугольник , а не параллелограмм.
Рисунок \(\PageIndex{12}\): Четырехугольник на сетке. Длина нижней стороны 8 ед. Длина верхней стороны 4 ед. Левая сторона поднимается на 5 единиц при перемещении вправо на 13 единиц, а правая сторона поднимается на 5 единиц при перемещении вправо на 9 единиц.
Упражнение \(\PageIndex{8}\)
Найдите площадь каждой фигуры. Покажите свои рассуждения.
Рисунок \(\PageIndex{13}\): фигура с восемью сторонами, нарисованная на сетке. Четыре стороны прямые и простираются влево, вправо, вверх и вниз на 2 единицы каждая. Остальные стороны представляют собой угловые стороны, соединяющие каждую из прямых сторон со следующей. Фигура имеет в общей сложности 6 единиц в высоту и 6 единиц в ширину. Рисунок \(\PageIndex{14}\)(из модуля 1.1.3)
Упражнение \(\PageIndex{9}\)
Найдите площадь прямоугольника с каждым набором длин сторон.
- \(5\) в и \(\frac{1}{3}\) в
- \(5\) в и \(\frac{4}{3}\) в
- \(\frac{5}{2}\) в и \(\frac{4}{3}\) в
- \(\frac{7}{6}\) в и \(\frac{6}{7}\) в
(из блока 1.1.1)
Эта страница под названием 2.1: Parallelograms распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Illustrative Mathematics с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Иллюстративная математика
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Метки
- источник!@https://access.openupresources.org/curricula/our6-8math/en/grade-6/index.html
- источник@https://access.openupresources.
 org/curricula/our6-8math/en/grade-6/index.html
org/curricula/our6-8math/en/grade-6/index.html
Параллелограммы: значение, примеры и свойства
Подумайте о разметке на пешеходном переходе. Это замкнутые 4-сторонние фигуры с противоположными сторонами, которые равны и параллельны. Такие фигуры называются параллелограммами.
Четырехсторонняя плоская фигура известна как четырехугольник . В этой статье мы рассмотрим особый тип четырехугольника, известный как параллелограмм .
Определение параллелограмма
Четырехугольник с двумя парами противоположных параллельных сторон называется параллелограмм .
Мы знаем, что у четырехугольника 4 стороны. В параллелограмме эти 4 стороны состоят из 2 пар противоположных параллельных сторон.
На следующей диаграмме показан параллелограмм.
Иллюстрация параллелограмма — StudySmarter Originals
На приведенном выше рисунке:
- AB // CD
- AC // BD
Свойства параллелограммов
В дополнение к вышесказанному мы можем определить различные свойства параллелограммов.
Мы будем использовать следующий параллелограмм ABDC с диагоналями d 1 =BC и d 2 =AD для иллюстрации свойств.
Параллелограмм с диагоналями d1 и d2 — StudySmarter Originals
В параллелограмме противоположные стороны равны.
Это означает, что в приведенном выше параллелограмме AB=CD и AC=BD.
В параллелограмме противоположные углы равны.
Это означает, что в приведенном выше параллелограмме , ∠CAB=∠CDB и ∠ACD=∠ABD
В параллелограмме последовательные углы являются дополнительными.
В любом параллелограмме можно выделить 4 пары последовательных углов. Они всегда являются дополнительными (что означает, что сумма углов составляет 180 градусов). In the above parallelogram:
∠CAB + ∠ABD = 180,
∠ABD + ∠BDC = 180,
∠BDC + ∠DCA = 180,
∠DCA + 50 40CAB 9
Если любой угол в параллелограмме прямой, это означает, что все 4 внутренних угла прямые.

Это прямое следствие вышеуказанного свойства. Если какой-либо угол в параллелограмме прямой, то прилежащий к нему угол равен 180-90=90 (согласно указанному выше свойству). В свою очередь, следующий смежный угол будет прямым и так далее. Следовательно, в любом параллелограмме, если вы идентифицируете любой угол как прямой, вы можете прямо заключить, что все 4 угла прямые.
Диагонали параллелограмма делят друг друга пополам.
В приведенном выше параллелограмме точка O является серединой обеих диагоналей d 1 и d 2 .
Каждая диагональ параллелограмма делит параллелограмм на два равных треугольника .
В приведенном выше параллелограмме диагональ d 1 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABC и ΔBCD. Точно так же диагональ d 2 разделила бы параллелограмм на два конгруэнтных треугольника, ΔABD и ΔACD.
Площадь параллелограммы
Рассмотрим следующую параллелограмму:Параллелограмма с базой B и высотой h — StudySmarter Originals
.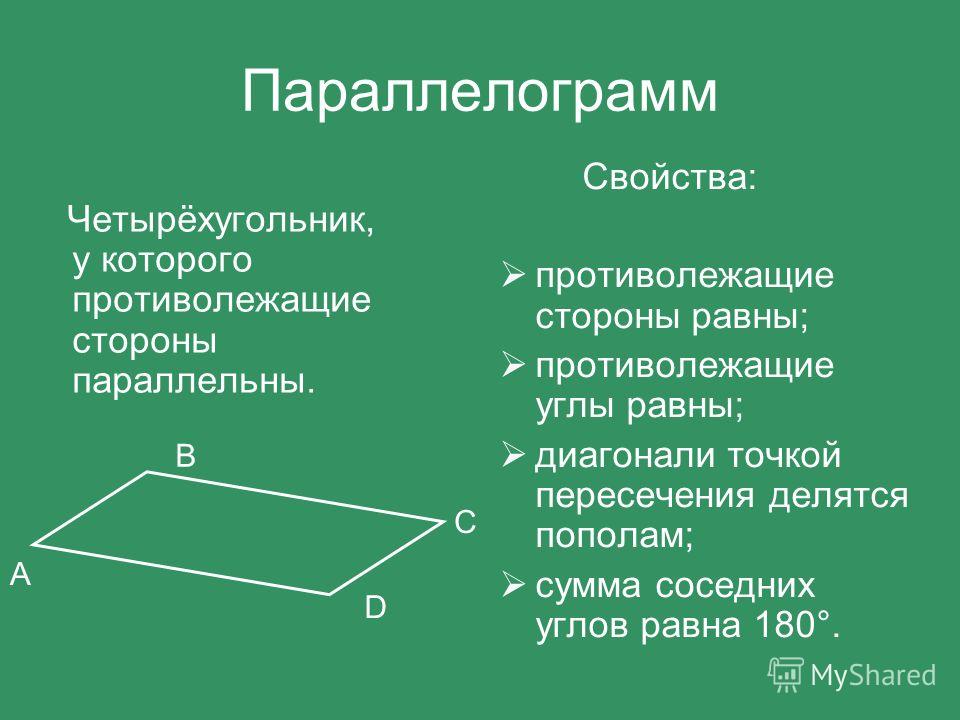 × h
× h
где b = основание, h = высота
Теперь значение b — это длина стороны AB, которая здесь считается основанием. Условно за основание принимают одну из длинных сторон параллелограмма. Значение h является высотой параллелограмма. Его также иногда называют высотой. Высота – это длина линии, проведенной от основания к противоположной стороне. Высота перпендикулярна основанию.
Параллелограмм: Примеры задач
В этом разделе мы рассмотрим примеры математических задач, которые могут возникнуть в связи с параллелограммами и их свойствами.
Параллелограмм с основанием 8 футов имеет площадь 20 футов 2 . Какова высота параллелограмма?
В следующем параллелограмме ∠ABD = 47°, ∠CBD = 72°. Найдите ∠CDA.
Иллюстрация параллелограмма — StudySmarter Originals
∠ABC = ∠ABD + ∠CBD
= 47 + 72 = 119.
Противоположные углы параллелограмма равны. Следовательно,
∠CDA = ∠ABC = 119°
Различные типы параллелограммов
В этом разделе мы выделим 3 специальных типа параллелограммов, каждый из которых имеет свои характеристики и свойства:
Ромб
9Прямоугольник
Квадрат
Ромб
Ромб – четырехугольник, все 4 стороны которого равны по длине0098 равносторонний ).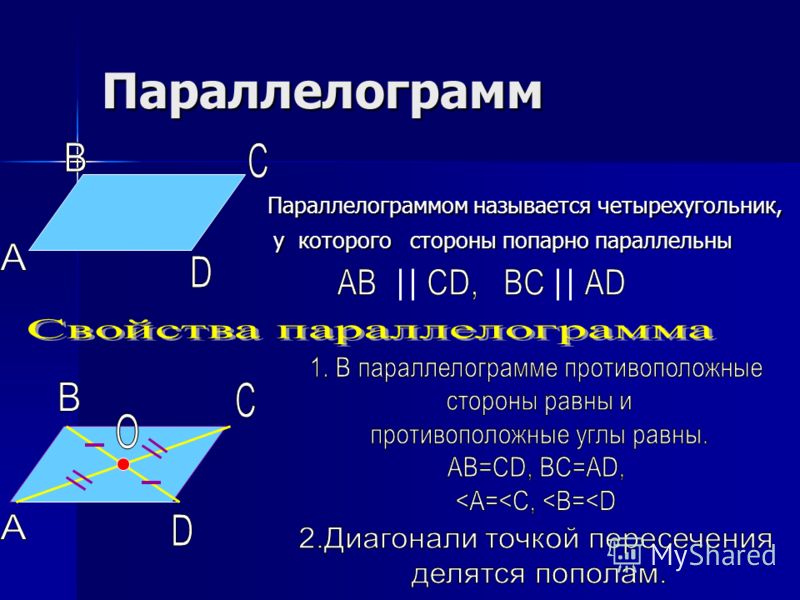 Оказывается, противоположные пары сторон ромба всегда параллельны. Это делает каждый ромб параллелограммом. И наоборот, мы можем сказать, что равносторонний параллелограмм является ромбом. Диагонали ромба всегда пересекаются под прямым углом.
Оказывается, противоположные пары сторон ромба всегда параллельны. Это делает каждый ромб параллелограммом. И наоборот, мы можем сказать, что равносторонний параллелограмм является ромбом. Диагонали ромба всегда пересекаются под прямым углом.
Поскольку ромб является особым типом параллелограмма, ромб также обладает всеми свойствами параллелограмма.
Прямоугольник
Прямоугольник — это параллелограмм, все внутренние углы которого прямые. Так как в прямоугольнике все углы равны, то равноугольный .
Поскольку прямоугольник представляет собой особый тип параллелограмма, он также обладает всеми свойствами параллелограмма.
Квадрат
Квадрат – это четырехугольник, у которого все 4 стороны равны, а все углы прямые. Это делает квадрат типом параллелограмма, типом ромба и типом прямоугольника! Таким образом, квадрат демонстрирует все свойства параллелограмма, ромба и прямоугольника.
Параллелограммы — ключевые выводы
- Четырехугольник с двумя парами противоположных параллельных сторон называется параллелограммом.


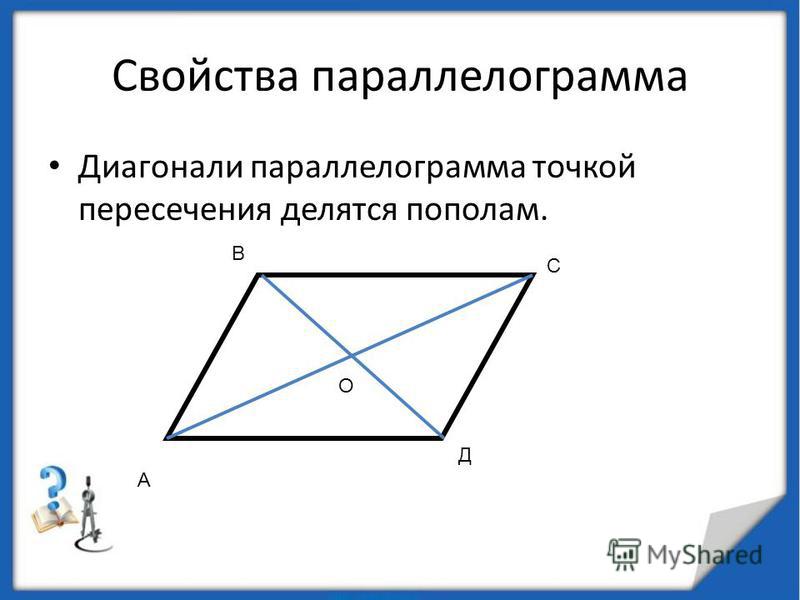 Или AB II CD и AB = CD
Или AB II CD и AB = CD
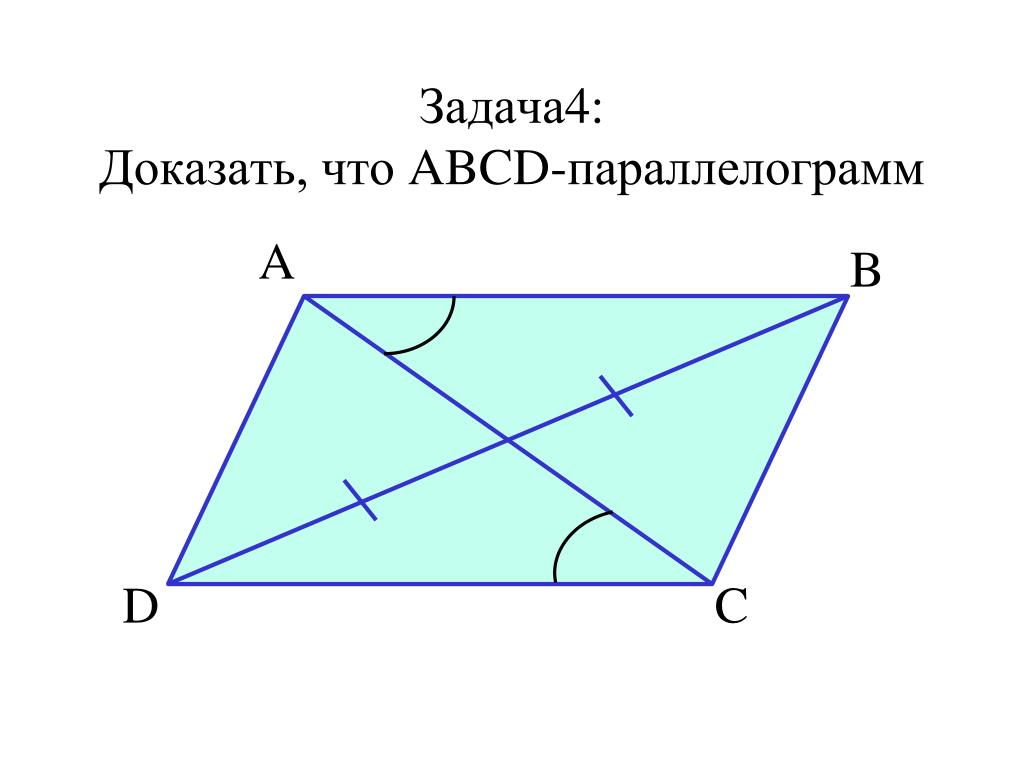

 Например, трапеция — это четырехугольник, а не параллелограмм. Чтобы четырехугольник был параллелограммом, все противоположные стороны должны быть параллельны и равны.
Например, трапеция — это четырехугольник, а не параллелограмм. Чтобы четырехугольник был параллелограммом, все противоположные стороны должны быть параллельны и равны. Однако параллелограмм не всегда соответствует определению ромба, а значит, и наоборот.
Однако параллелограмм не всегда соответствует определению ромба, а значит, и наоборот.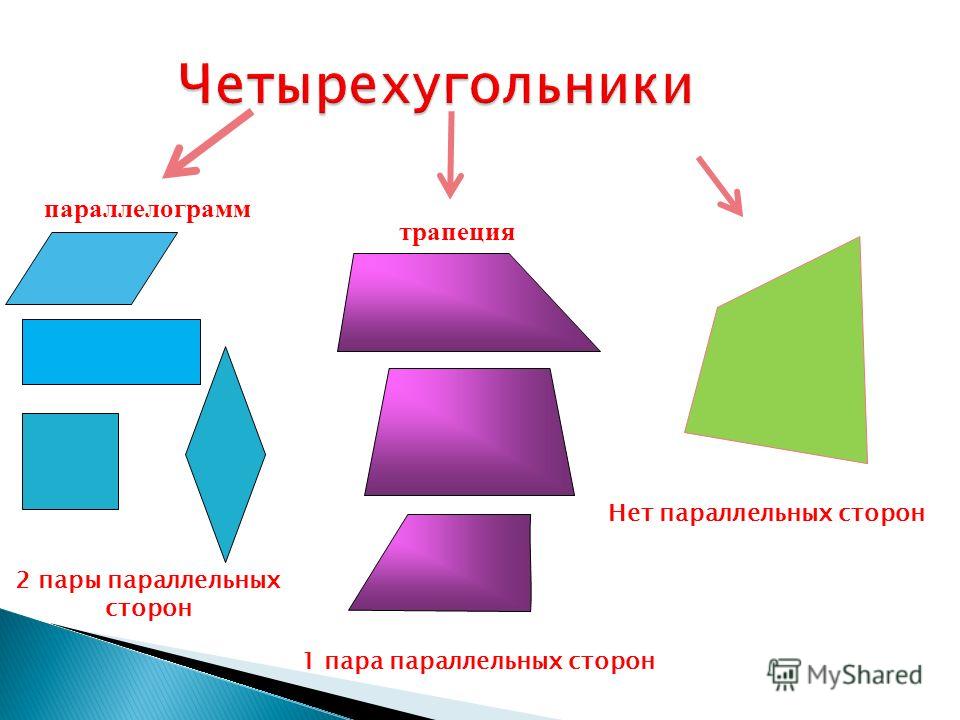 Вот три способа:
Вот три способа: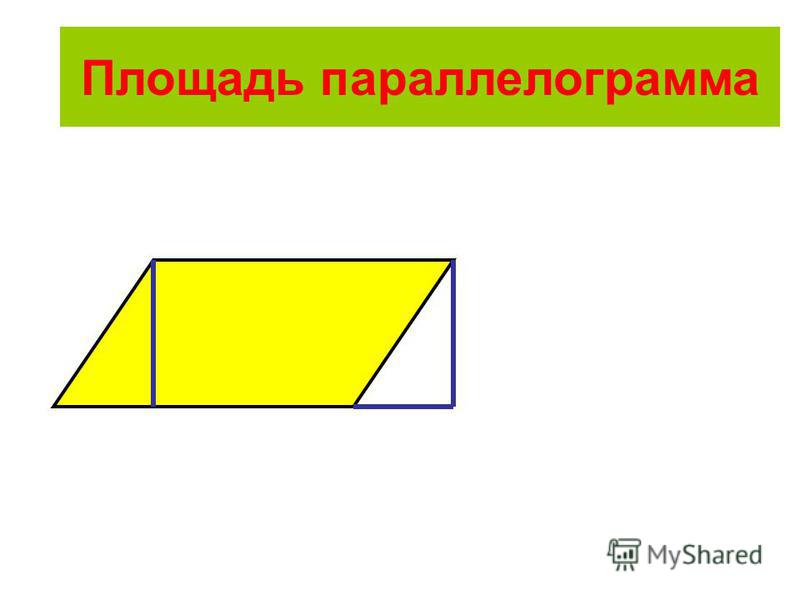
 org/curricula/our6-8math/en/grade-6/index.html
org/curricula/our6-8math/en/grade-6/index.html
