Вертикальные асимптоты найти онлайн: Найти вертикальные асимптоты онлайн

2*arctgh(x)*arcctgh(x)

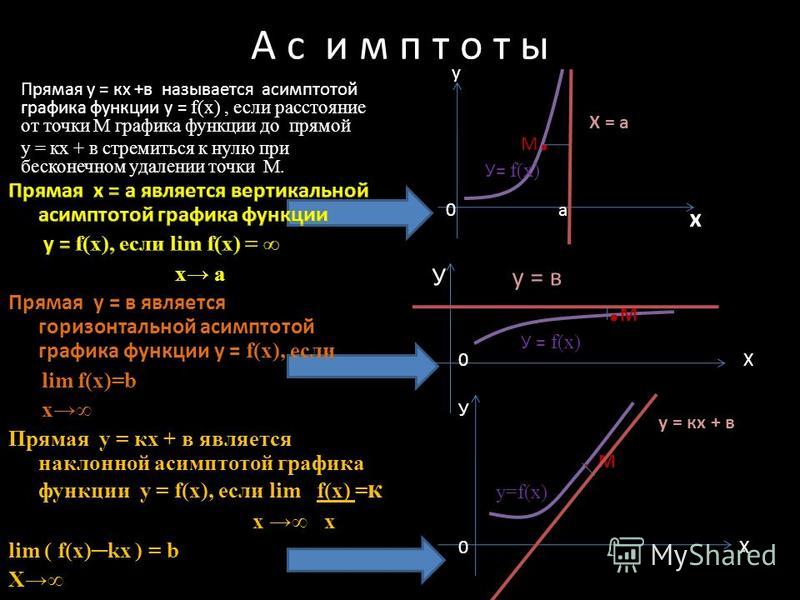
Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да
• Минимум и максимум функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

5. Асимптоты.

Вертикальная асимптота.

Если выполнено хотя бы одно из условий

, ,

то прямую называют вертикальной асимптотой графика функции .

Невертикальная асимптота.

Прямую

называют невертикальной асимптотой графика функции при , если

.

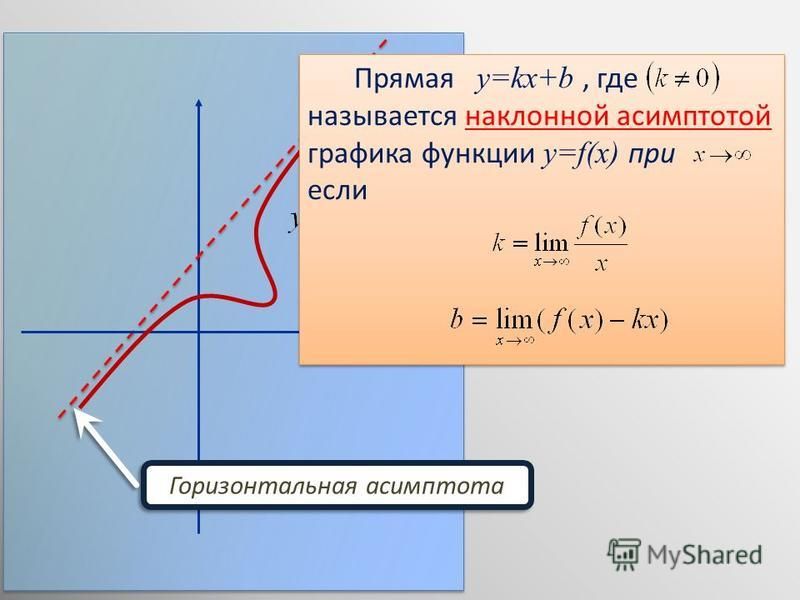
Если , то асимптоту называют наклонной, а если , то асимптоту называют горизонтальной.

Аналогично вводится понятие асимптоты при .

Для того чтобы прямая была асимптотой графика функции при , необходимо и достаточно, чтобы существовали конечные пределы

,

.

Аналогично находится асимптота при .

Исследование асимптот при и при как правило проводят отдельно.

В некоторых частных случаях возможно совместное исследование асимптот при и при , например, для

1) рациональных функций;

2) четных и нечетных функций, для графиков которых исследование можно проводить на части области определения.

Следует отметить, что метод вычисления пределов для нахождения асимптот не позволяет оценить взаимное расположение графика функции и его асимптоты. Для определения взаимного положения графика и асимптоты можно пользоваться следующими правилами.

1) Если функция имеет асимптоту при , дифференцируема и строго выпукла вниз на луче , то график функции лежит выше асимптоты.

2) Если функция имеет асимптоту при , дифференцируема и строго выпукла вверх на луче , то график функции лежит ниже асимптоты.

3) Могут быть другие случаи поведения графика функции при стремлении к асимптоте. Например, возможно, что, график функции бесконечное число раз пересекает асимптоту.

Аналогичное утверждение справедливо и при .

До исследования свойств выпуклости графика функции взаимное расположения графика функции и его асимптоты можно определить по знаку в методе выделения главной части.

Метод выделения главной части. Для нахождения асимптоты выделяем главную часть функции при . Аналогично при .

Главную часть дробно рациональной функции удобно находить, выделяя целую часть дроби.

Главную часть иррациональной функции при решении практических примеров удобно находить используя методы представления функции формулой Тейлора при .

Главную часть иррациональных функций вида и удобно находить соответственно методом выделения полного квадрата или полного куба подкоренного выражения.

5.1. Найти асимптоты графика функции

.

 Прямая — вертикальная асимптота.

Наклонная асимптота. Найдем угловой коэффициент и свободный член по формулам

,

Таким образом, прямая — наклонная асимптота.

Найдем асимптоту методом выделения главной части дробно-рациональной функции. Выполняя деление «столбиком», получаем

То есть, .

Таким образом, прямая — наклонная асимптота. 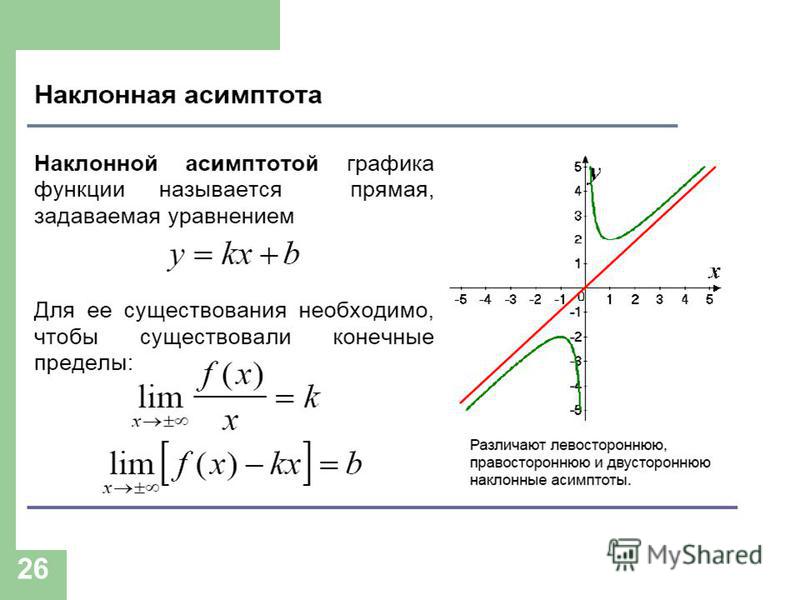

5.2. Найти асимптоты линии: .

 Вертикальных и горизонтальных асимптот нет.

Выражая уравнение линии в явном виде :.

Тогда

,

.

В итоге имеем 2 наклонных асимптоты: .

5.3. Найти асимптоты линии: .

 Выразим уравнение линии в явном виде: .

Так как ,

то прямая — наклонная асимптота.

5.4. Найти асимптоты функции:

Так как функция не определена в точках =1, то — вертикальные асимптоты.

Найдём наклонную асимптоту: угловой коэффициент прямой и число найдём, применяя формулы:

; .

.

Получили: — наклонная асимптота. 

5.5. Найти наклонную асимптоту графика функции .

 Так как

,

то по формуле Тейлора получаем

и прямая является искомой асимптотой. ◄

5.6. Найти наклонные асимптоты графика функции при и .

 В подкоренном выражении выделим полный квадрат

.

Так как график функции симметричен относительно прямой и

то при . Значит, прямая является асимптотой при , а прямая — асимптотой при . ◄

Как найти вертикальную асимптоту функции

Вертикальная асимптота:

Это вертикальная линия , которая не является частью графика функции, но направляет ее для значений y «далеко» вверх и/или «далеко» вниз.

График может пересечь ее, но в конце концов, для достаточно больших или достаточно малых значений y, то есть

y —-> ±∞

Всегда график будет приближаться к горизонтальной асимптоте, не касаясь ее .

На приведенной выше диаграмме x = k является горизонтальной асимптотой. Потому что график становится все ближе и ближе к x = k, не касаясь его, поскольку y —-> ±∞.

Мы сможем найти вертикальные асимптоты функции, только если это рациональная функция.

То есть функция должна быть в виде

f(x) = g(x)/h(x)

Рациональная функция. Пример:

Шаг 1:

Пусть f(x) — заданная рациональная функция. Приравняйте знаменатель к нулю.

Шаг 2 :

Когда мы приравняем знаменатель к нулю, предположим, мы получаем x = a и x = b.

Шаг 3 :

Уравнения вертикальной асимптоты:

Решение:

Шаг 1:

В данной рациональной функции знаменатель равен

x + 6

Шаг 2:

Приравняйте знаменатель к нулю и найдите x.

х + 6 = 0

х = — 6

Шаг 3 :

Уравнение вертикальной асимптоты:

x = — 6

Пример 2 :

f(x) = (x ² + 2x — 3)/(x ² 6  — 9×0 + 0 3)

Решение :

Шаг 1 :

В данной рациональной функции знаменатель равен

x ²  — 5x + 6

Шаг 2 :

Приравняем знаменатель к x и решим нуль знаменателя для x.

x ²  — 5x + 6 = 0

(x — 2)(x — 3) = 0

x — 2 = 0 или x — 3 = 0

x = 2 или x = 3

Шаг 3 :

Уравнения двух вертикальных асимптот

x = 2 и x = 3

93002 Пример :

f(x) = (2x — 3)/(x ² — 4)

Решение :

Шаг 1 :

В данной рациональной функции знаменатель равен

2

x 29007 4

Шаг 2:

Приравняйте знаменатель к нулю и найдите x.

x ²  — 4 = 0

x ²  — 2 ²  = 0

(x + 2)(x — 2) = 0

x = 9002 3 2 9002 шаг 2 90 или x0 = 0 :

Уравнения двух вертикальных асимптот:

Шаг 1 :

В данной рациональной функции знаменатель равен

x ²  + 4

Шаг 2 :

Приравняйте знаменатель к нулю и найдите x.

x ² + 4 = 0

x ² = -4

x = ± √ -4

x = ± 2i

x = 2i или x = -2i (воображаемая)

. 3 :

Когда мы приравниваем знаменатель к нулю, мы не получаем реальных значений x.

Итак, вертикальной асимптоты нет.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Калькулятор асимптот — Онлайн-калькулятор асимптот

Прямая линия называется асимптотой кривой y = f (x), если, говоря простым языком, кривая касается линии на бесконечности.

Что такое калькулятор асимптот?

«Калькулятор асимптот Cuemath» — это онлайн-инструмент, который помогает рассчитать асимптотический график для заданной функции. Калькулятор асимптот Cuemath поможет вам найти асимптотический график для заданной функции за несколько секунд.

Как пользоваться калькулятором асимптот?

Чтобы использовать калькулятор, выполните следующие действия:

• Шаг 1: Введите функцию относительно одной переменной в заданных полях ввода.
• Шаг 2: Нажмите кнопку  «Вычислить» , чтобы найти асимптотический график для заданной функции
• Шаг 3:  Нажмите кнопку  «Сброс» , чтобы очистить поля и найти асимптотический график для различных функций.

 

Как найти асимптоты?

Асимптота определяется как линия, к которой приближается кривая, но не пересекает ее бесконечно, или можно сказать, что асимптота — это линия, к которой сходится кривая. Асимптота никогда не пересекает кривую, даже если они бесконечно близки.

Существует три типа асимптот: 1. Горизонтальная асимптота 2. Вертикальная асимптота 3. Наклонная асимптота

1. Горизонтальная асимптота: функции.

• Если оба многочлена имеют одинаковую степень, разделите коэффициенты членов с наибольшими степенями. Это ваша асимптота!
• Если степень числителя меньше знаменателя, то асимптота находится при y=0.
• Если степень числителя больше знаменателя, то горизонтальной асимптоты нет!

2.

Вертикальная асимптота: Вертикальная асимптота встречается в рациональных функциях в точках, когда знаменатель равен нулю, а числитель не равен нулю. Мы можем найти вертикальную асимптоту, приравняв знаменатель рациональной функции к нулю.

 

Хотите находить сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Заказать бесплатный пробный урок

Решено Пример:

Найти асимптоту заданной функции f(x) = (x + 5) / (x — 3)

Решение: 

Найти асимптоту по вертикали , приравняйте знаменатель рациональной функции к нулю.

x — 3 = 0

x = 3

Итак, существует вертикальная асимптота при x = 3

\(\lim _{x \rightarrow 3+} f(x)=\pm \infty, \ quad \lim _{x \rightarrow 3-} f(x)=\pm \infty\)

В этом случае у нас есть горизонтальная асимптота в точке y=1, поскольку она попадает в случай -1.

No related posts.