Свойства секущей и параллельных прямых: Свойства параллельных прямых. Аксиома параллельных прямых — урок. Геометрия, 7 класс.

признаки при пересечении секущей, определение

Содержание:

• Что такое параллельные прямые
• Свойства параллельных прямых с доказательством
• Признаки при пересечении секущей
• Свойства углов при параллельных прямых и секущей

Содержание

• Что такое параллельные прямые
• Свойства параллельных прямых с доказательством
• Признаки при пересечении секущей
• Свойства углов при параллельных прямых и секущей

Что такое параллельные прямые

Определение

Параллельные прямые — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.

Основные признаки:

1. В случае, если две прямые параллельны третьей, они являются параллельными между собой. Так, если а || c и также b || c, то и a || b.
2. Если они перпендикулярны по отношению к третьей, то они не пересекаются: т.е., если а ⊥ с  и  b ⊥ c,  то  a || b.

   

Свойства параллельных прямых с доказательством

Определение

Свойства параллельных прямых — это утверждения, являющиеся обратными по отношению к признакам, упомянутым ранее.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Они обладают следующими свойствами:

1. Через любую точку, которая, что немаловажно, не лежит на прямой, можно провести параллель, притом лишь одну. Данное утверждение является Евклидовой аксиомой. 
2. Если прямая, лежащая на плоскости, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой: если  a || b  и  c ⊥ a,  то  c ⊥ b.

 

Дано:  a || b  и  c ⊥ a

Доказать: c ⊥ b

Доказательство:

1. с пересекает а, следовательно, с пересекает также прямую, параллельную а, т.е. b.
2. Исходя из этого, можно утверждать, что с — это секущая по отношению к а и b.
3. При секущей с ∠1 и ∠2 являются накрест лежащими.
4. Из свойств углов при параллельных прямых, пересеченных секущей, нам известно о равенстве накрест лежащих углов: следовательно, ∠1 = ∠2.
5. Как следствие, ∠2 = 90 градусов, что означает, что c ⊥ b. Что и требовалось доказать.

Признаки при пересечении секущей

Определение

Секущей называется прямая, пересекающая:

• кривую в двух точках;
• или две прямые, которые лежат в этой же плоскости, в двух разных точках.

Рассмотрим признаки, которые характерны для параллельных прямых при пересечении их секущей.

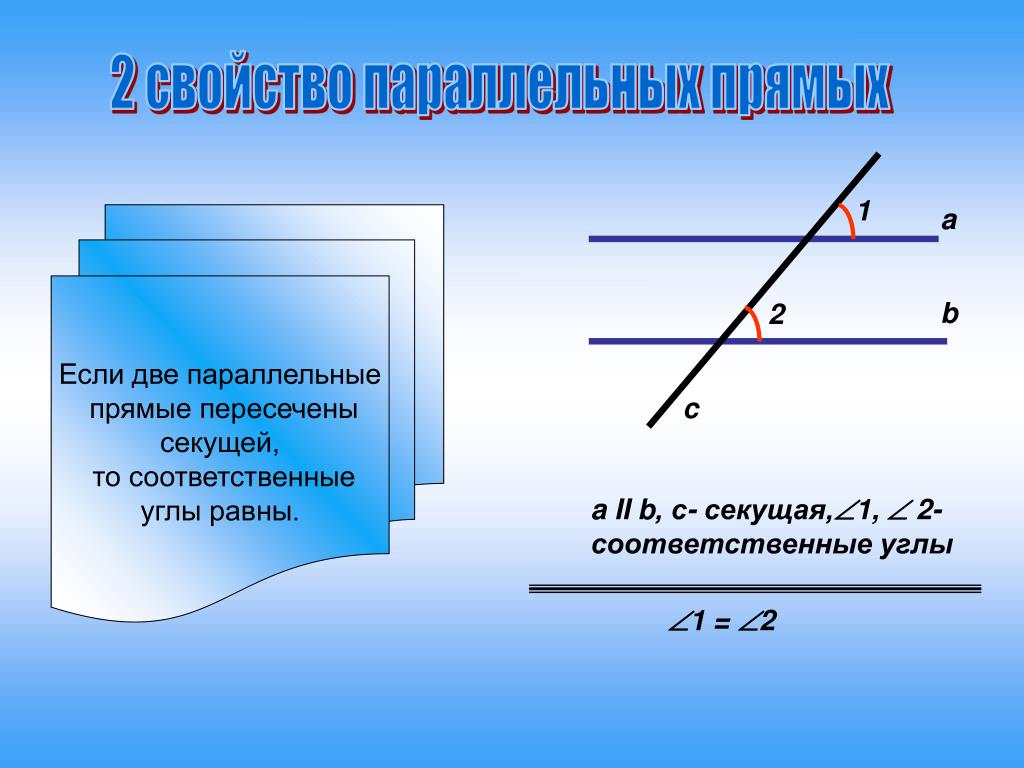
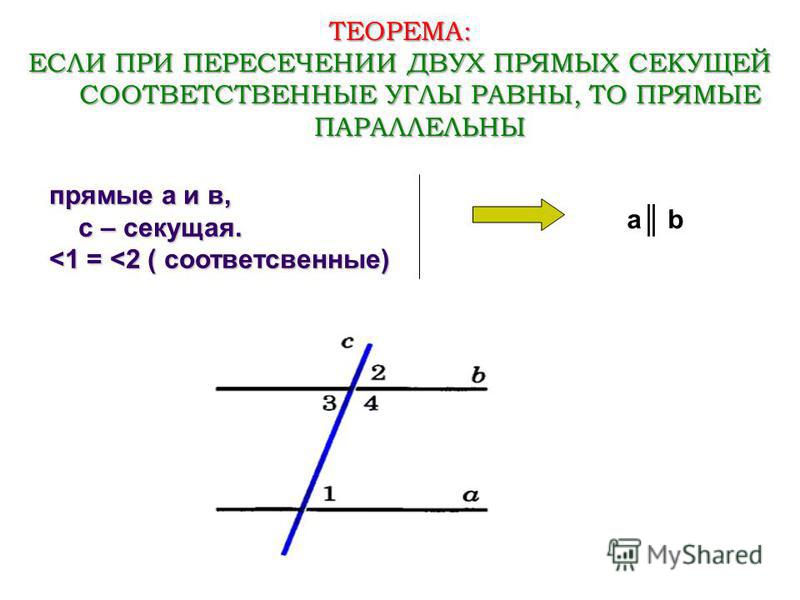
Если соответственные углы равны, то прямые не пересекаются. Если ∠2 = ∠4,  следовательно,  a || b.

 

Если сумма внутренних односторонних углов равняется 180 градусам, то прямые являются параллельными. Если  ∠1 + ∠2 = 180°,  следовательно,  a || b.

 

Если внутренние накрест лежащие углы равны, то прямые также являются параллельными. Если  ∠1 = ∠3,  следовательно,  a || b.

 

Свойства углов при параллельных прямых и секущей

Кроме того, следует охарактеризовать основные свойства углов, образованных при пересечении секущей прямой. Данные свойства являются обратными рассмотренным выше признакам.

При пересечении двух параллельных прямых третьей, сумма внутренних односторонних углов, образованных ими, равняется 180 градусам: если  a || b,  то  ∠1 + ∠2 = 180°.

 

В случае, когда две параллельные прямые пересечены третьей, соответственные углы, образованные ими, равны: если  a || b,  то  ∠2 = ∠4.

 

Если две параллельные прямые пересекаются третьей, накрест лежащие углы, образованные ими, равны: если  a || b,  то  ∠1 = ∠3.

 

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Свойство параллельных прямых

2/9/20

Свойства параллельных прямых

Параллельные прямые.

Определение.

а

b

Две прямые на плоскости называются

ПАРАЛЛЕЛЬНЫМИ , если они не пересекаются.

2/9/20

Пары углов, образованные

при пересечении прямых

секущей.

с

2

1

3

4

а

6

5

7

8

b

Накрест лежащие углы

Односторонние углы

Соответственные углы

2/9/20

Признак параллельности

двух прямых

по накрест лежащим углам.

с

a ıı b

2

1

а

3

4

b

Если при пересечении двух прямых секущей

НАКРЕСТ ЛЕЖАЩИЕ углы равны,

то прямые параллельны

2/9/20

Признак параллельности

двух прямых

по соответственным углам.

с

a ıı b

2

1

3

4

а

6

5

7

8

b

Если при пересечении двух прямых секущей

СООТВЕТСТВЕННЫЕ углы равны.

то прямые параллельны

2/9/20

Признак параллельности

двух прямых

по односторонним углам.

с

a ıı b

2

1

а

3

4

b

Если при пересечении двух прямых секущей

сумма ОДНОСТОРОННИХ углов равна 180 0

,

то прямые параллельны

2/9/20

то, что дано требуется

доказать

Теорема

Условие

Заключение

Теорема, обратная данной –такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.

2/9/20

Теорема, обратная данной

то, что дано требуется

доказать

Заключение

Условие

2/9/20

Признаки параллельных прямых

СВОЙСТВА

То (заключение)

Если (условие)

прямые параллельны

накрест лежащие углы равны

соответственные углы равны

прямые параллельны

сумма односторонних углов равна 180 градусов

прямые параллельны

получили

2/9/20

9

Сравнительная таблица.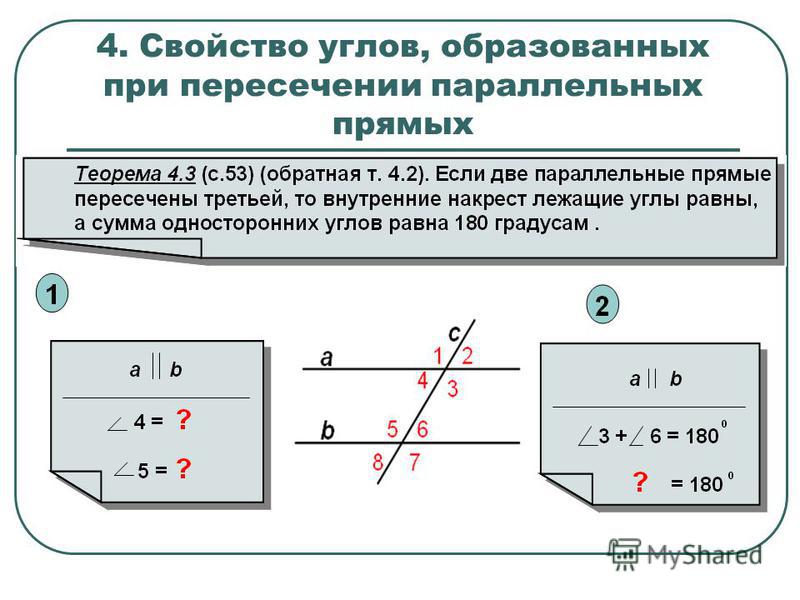

Название теоремы

Признак параллельности прямых

Формули-ровка теоремы

Свойства параллельных прямых

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Условие

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

(дано)

Заключе-ние

a||b

(доказать)

 1=  2

Прямые a, b, c – их секущая,  1,  2 – накрест лежащие углы;  1=  2

Прямые a, b, c – их секущая,  1,  2 – накрест лежащие углы; a||b

2/9/20

Замечание .

Если доказана некоторая теорема, то отсюда еще не следует справедливость обратного утверждения.

Более того, обратное утверждение не всегда верно. Например, « вертикальные углы равны ».

Обратное утверждение: « если углы равны, то они вертикальные»

— конечно же, неверно.

2/9/20

Свойства параллельных прямых.

с

2

1

а

3

4

b

Если две параллельные прямые пересечены

секущей, то НАКРЕСТ ЛЕЖАЩИЕ углы равны.

2/9/20

Свойства параллельных прямых.

с

2

1

3

4

а

6

5

7

8

b

Если две параллельные прямые пересечены

секущей, то СООТВЕТСТВЕННЫЕ углы равны.

2/9/20

Свойства параллельных прямых.

с

2

1

а

3

4

b

Если две параллельные прямые пересечены секущей,

то сумма ОДНОСТОРОННИХ углов равна 180 0 .

Свойство параллельных прямых.

Если две параллельные прямые пересечены

секущей, то НАКРЕСТ ЛЕЖАЩИЕ углы равны.

P

Дано: прямые a ∥ b ,

секущая MN;  1 и  2 – накрест лежащие;

Доказать:  1 =  2;

M

а

1

2

в

N

Доказательство.

• Допустим, что  1 ≠  2;
• Отложим от луча MN ∠PMN =  2, так чтобы ∠PMN и  2 были накрест лежащими углами при пересечении прямых MP и b секущей MN;

• По построению эти накрест лежащие углы равны, поэтому MP ∥ b.
• Мы получили, что через точку М проходят 2 прямые параллельные прямой b. Но это противоречит аксиоме параллельных прямых.
• Значит, наше допущение неверно и  1 =  2

2/9/20

Следствие.

Если прямая перпендикулярна к одной из двух

параллельных прямых, то она перпендикулярна и к другой .

с

M

Дано: прямые a ∥ b ,

c  a

Доказать: c  b

а

1

2

в

N

2/9/20

Решение задач.

УСТНО

с

4

Дано: прямые a ∥ b ,

 1 = 75 ⁰

Найти:  2,  3, ∠4 .

2

а

3

1

в

2/9/20

Решение задач.

УСТНО

Дано: прямые a ∥ b ,

 1 + ∠2 = 160 ⁰

Найти:  3,  4, ∠5 , ∠6.

с

2

4

а

3

1

5

в

6

2/9/20

Дано: aǁb;

Найти:

c 1 2

3

• Дано: qǁz

t 3

Найти:

Аксиома параллельных прямых.

а

А

b

Через точку, не лежащую на данной прямой,

проходит только одна прямая,

параллельная данной.

2/9/20

Следствие из аксиомы

параллельных прямых.

1 0

a ıı b

с

а

b

Если прямая пересекает одну из двух

параллельных прямых, то она

пересекает и другую.

2/9/20

Следствие из аксиомы

параллельных прямых.

2 0

a ıı b

а

с

b

Если две прямые параллельны третьей прямой,

то они параллельны.

2/9/20

Секанс окружности — определение, формула, свойства, теоремы и примеры

Секущая окружности — это линия, пересекающая окружность в двух различных точках. Секан происходит от латинского слова secare , что означает резать. Его также можно понимать как продолжение хорды окружности, выходящей за пределы окружности.

1.	Что такое секанс окружности?
2.	Секан окружности Примеры
3.	Секущие теоремы
4.	Тангенс и секанс окружности
5.	Часто задаваемые вопросы о секущей окружности

Что такое секанс окружности?

Секущая окружности — это линия, пересекающая окружность и пересекающая окружность в 2 различных точках. В приведенном ниже круге PQ — это секущая линия, которая пересекает окружность в двух точках A и B.

Разница между хордой и секущей

Когда секущая пересекает окружность в двух точках, мы получаем хорду в двух точках пересечения. Хорда окружности – это отрезок, концы которого лежат на дуге окружности. В показанном выше круге AB — это хорда, являющаяся частью секущей QP. Другими словами, хорда — это отрезок, соединяющий две точки на окружности окружности, и если эту хорду продолжить в обе стороны, она станет секущей. Секущая, проходящая через центр круга, дает диаметр. Таким образом, секущая линия определяет хорду или диаметр окружности.

Секущая окружности Примеры

В реальной жизни мы сталкиваемся с секущей окружности во многих местах, где бы ни были задействованы окружности или кривые. Например, при строительстве изогнутых мостов, при определении расстояния между вращающейся вокруг Луны и различными точками на Земле и так далее. Есть много интересных свойств секущих, которые помогают в непонятных геометрических построениях. Существует множество теорем о кругах, основанных на секущих и пересекающихся секущих круга.

Теоремы о секущих

Теорема о пересекающихся секущих утверждает, что когда две секущие пересекаются во внешней точке, произведение одного целого секущего и его внешнего сегмента равно произведению другого целого секущего и его внешнего сегмента. Это также известно как теорема о секущих или теорема о секущих степенях.

На приведенном выше рисунке видно, что AB и AC — два секущих отрезка, пересекающихся в точке A. AD — внешний секущий всего секущего AB, а AE — внешний секущий сегмент AC. Таким образом, согласно теореме имеем AB × AD = AC × AE

Секущие и меры угла

Две секущие могут пересекаться внутри или снаружи круга. В кругах, показанных ниже, мы находим, что пересекающиеся секущие внутри и снаружи создают углы x и y в точках пересечения соответственно. В первом круге секущие пересекаются внутри круга, а большая дуга AD и малая дуга BD пересекаются с секущими. Во втором круге секущие пересекаются вне круга, а большая дуга PT и малая дуга QS пересекаются с секущими.

Существуют две теоремы, основанные на этом свойстве секущих. Согласно теореме имеем:

• Угол, образованный двумя секущими, пересекающимися внутри круга, равен половине суммы дуг, на которые они опираются.
• Угол, образованный двумя секущими, пересекающимися вне круга, равен половине разности дуг, на которые они опираются.

Тангенс и секанс окружности

Касательные и секущие — это линии, которые пересекают окружность и бесконечно тянутся в обоих направлениях. Основное различие между ними состоит в том, что секущая пересекает окружность в двух точках, а касательная — в одной. Касательная перпендикулярна радиусу в точке касания.

Теорема о касательной секущей

Согласно теореме о касательной секущей, если секущая и касательная проведены к окружности из общей внешней точки, то произведение длины всей секущей и внешней секущей равно квадрат длины касательного отрезка.

На приведенном выше рисунке видно, что:

• Секущая AC и касательная CD проведены из одной и той же внешней точки. Секущие сегменты АВ (внутренний) и ВС (внешний). Произведение секущей на ее внешний отрезок равно квадрату касательного отрезка. АС × ВС = CD ²
• Угол, образуемый касательной и секущей снаружи, равен половине разности большой дуги и малой дуги, пересекаемой ими. \(\alpha = \dfrac{1}{2}[\overline{\rm AD} — \overline{\rm BD}]\)

Ознакомьтесь с несколькими интересными темами, связанными с секущей окружности:

• Формула наклона секущей
• Сегмент круга
• Все формулы круга
• Длина окружности

Важные примечания

Вот несколько моментов, которые следует помнить при изучении секущей окружности:

• Секущей окружности называется линия, соединяющая две различные точки на кривой.
• Теорема о пересекающихся секущих утверждает, что если мы проведем две секущие из внешней точки окружности, произведение одной секущей и ее внешнего отрезка будет равно произведению другой секущей и ее внешнего отрезка.
• Правило секущей-тангенса гласит, что когда секущая и касательная проводятся из общей внешней точки, произведение секущей и ее внешнего сегмента равно квадрату касательного сегмента.

Часто задаваемые вопросы о секущей окружности

Что такое секущая окружности?

Прямая, пересекающая окружность ровно в двух различных точках, называется секущей окружности. Секущая линия включает хорду и всегда выходит за пределы круга. Другими словами, если хорда расширена в обе стороны, она становится секущей.

Секущая окружности и хорда окружности — одно и то же?

Нет, секанс и аккорд разные. Хорда – это часть секущей, конец которой лежит на секущей. Сеанс получается бесконечным продолжением хорды в обоих направлениях. Хорда лежит внутри круга, тогда как секущая выходит за пределы круга.

Что такое теорема о касательной секущей?

Согласно теореме о касательной и секущей, когда секущая и касательная проведены к окружности и если они пересекаются во внешней точке окружности, они связаны таким образом, что квадрат касательной равен произведению весь секущий сегмент и внешний секущий сегмент.

Что такое теорема о пересекающихся секущих?

Согласно теореме о пересекающихся секущих, когда две секущие пересекаются во внешней точке, произведение одной целой секущей и ее внешней части равно произведению другой целой секущей и ее внешней части.

Всегда ли секущая окружности является хордой?

Сеанс никогда не может быть аккордом, но он содержит аккорд. Продолжение хорды в обе стороны является секущей окружности.

Сколько секущих может быть в круге?

В круге может быть бесконечное количество секущих. Каждая секущая пересекает окружность в двух точках.

6.19: Теорема о пересекающихся секущих — K12 LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5044

Докажите и используйте теоремы о прямых, пересекающих окружность в двух точках.

Отрезки от секущих

Когда две секущие пересекаются за пределами окружности , окружность делит секущие на пропорциональные друг другу сегменты.

Две секущие отрезки Теорема : Если две секущие проведены из общей точки вне круга и отрезки помечены, как показано ниже, то \(a(a+b)=c(c+d)\).

Рисунок \(\PageIndex{1}\)

Что если вам дан круг с двумя секущими, которые пересекаются вне круга? Как можно использовать длину некоторых отрезков, образованных их пересечением, для определения длин неизвестных отрезков?

Пример \(\PageIndex{1}\)

Найти \(x\). Упростите любые радикалы.

Рисунок \(\PageIndex{2}\)

Решение

Используйте теорему о двух секущих отрезках.

\(\begin{выровнено} 8(8+x)&=6(6+18) \\ 64+8x&=144 \\ 8x&=80 \\ x&=10\end{выровнено}\)

Пример \(\PageIndex{2}\)

Найти \(x\). Упростите любые радикалы.

Рисунок \(\PageIndex{3}\)

Решение

Используйте теорему о двух секущих отрезках.

\(\begin{align} 15(15+27)&=x\cdot45 \\ 630&=45x \\ x&=14 \end{align}\)

Пример \(\PageIndex{3}\)

Найдите значение \(x\).

Рисунок \(\PageIndex{4}\)

Решение

Используйте теорему о двух секущих отрезках.

\(\begin{align}18\cdot(18+x)&=16\cdot(16+24) \\ 324+18x&=256+384 \\ 18x&=316 \\ x&=17\dfrac{5 {92&=144 \\ x&=12,\: x\neq −12 (\text{длина неотрицательна})\end{выровнено}\)

Пример \(\PageIndex{5}\)

Верно или неверно : Две секущие всегда пересекаются вне круга.

Решение

Ложь. Если две секущие параллельны, они никогда не пересекутся. Также возможно, что две секущие пересекаются внутри круга.

Обзор

Заполните поля для каждой проблемы ниже. Затем найдите недостающий сегмент.

1. Рисунок \(\PageIndex{6}\)

\(3(\text{______}+\text{______})=2(2+7)\)

2. Рисунок \(\PageIndex{7}\)

\(x\cdot\text{______}=8(\text{______}+\text{______})\)

Найдите x на каждой диаграмме ниже. Упростите любые радикалы.

3. Рисунок \(\PageIndex{8}\)
4. Рисунок \(\PageIndex{9}\)
5. Рисунок \(\PageIndex{10}\)

6. Заполните пропуски в доказательстве теоремы о двух секущих отрезках. Рисунок \(\PageIndex{11}\)

Дано : Секущие \(\overline{PR}\) и \(\overline{RT}\)

Докажите : \(a(a+b)=c(c+d)\)

Выписка	Причина
1. Секанты \(\overline{PR}\) и \(\overline{RT}\) с отрезками \(a\), \(b\), \(c\) и \( д\).	1. Дано
2. \(\угол R\угол \угол R\)	2. Рефлексивная PoC
3. \(\угол QPS\cong \угол STQ\)	3. Конгруэнтность вписанных углов Теорема
4. \(\Delta RPS\sim \Delta RTQ\)	4. Постулат подобия АА
5. \(ac+d=ca+b\)	5. Соответственные части подобных треугольников пропорциональны
6. \(а(а+b)=с(с+d)\)	6. Перекрестное умножение

Найдите неизвестную переменную.

7. Рисунок \(\PageIndex{12}\)
8. Рисунок \(\PageIndex{13}\)
9. Рисунок \(\PageIndex{14}\)
10. Рисунок \(\PageIndex{15}\)
11. Рисунок \(\PageIndex{16}\)
12. Рисунок \(\PageIndex{17}\)
13. Рисунок \(\PageIndex{18}\)
14. Рисунок \(\PageIndex{19}\)
15. Рисунок \(\PageIndex{12}\)

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 9. 10.

Словарь

Срок	Определение
центральный угол	Угол, образованный двумя радиусами, вершина которого находится в центре окружности.
хорда	Отрезок, концы которого лежат на окружности.
круг	Набор всех точек, находящихся на одинаковом расстоянии от определенной точки, называемой центром .
диаметр	Хорда, проходящая через центр окружности. Длина диаметра в два раза больше длины радиуса.
Вписанный угол	Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол равен половине дуги, на которую опирается.
перехваченная дуга	Дуга внутри вписанного угла, концы которой лежат на этом угле.
точка касания	Точка, в которой касательная касается окружности.
радиус	Расстояние от центра до внешнего края круга.
АА Постулат подобия	Если два угла одного треугольника равны двум углам другого треугольника, то эти два треугольника подобны.
Конгруэнтность	Конгруэнтные фигуры одинаковы по размеру, форме и размеру.
Рефлексивное свойство конгруэнтности	\(\overline{AB}\cong \overline{AB}\) или \(\angle B\cong \angle B\)
Секущая	Секанс угла прямоугольного треугольника — это величина, которая получается путем деления длины гипотенузы на длину стороны, примыкающей к данному углу. Отношение секущей обратно пропорционально отношению косинуса.
секущая линия	Секущая — это линия, соединяющая две точки на кривой.
Касательная	Касательная линия — это линия, которая «просто касается» кривой в одной точке и ни в какой другой.
Теорема о двух секущих отрезках	Теорема о двух секущих отрезках утверждает, что если у вас есть точка вне круга и вы проводите из нее две секущие линии, между образующимися отрезками существует взаимосвязь. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт