|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Оснащения врачебно-сестринской бригады. Интересное: Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
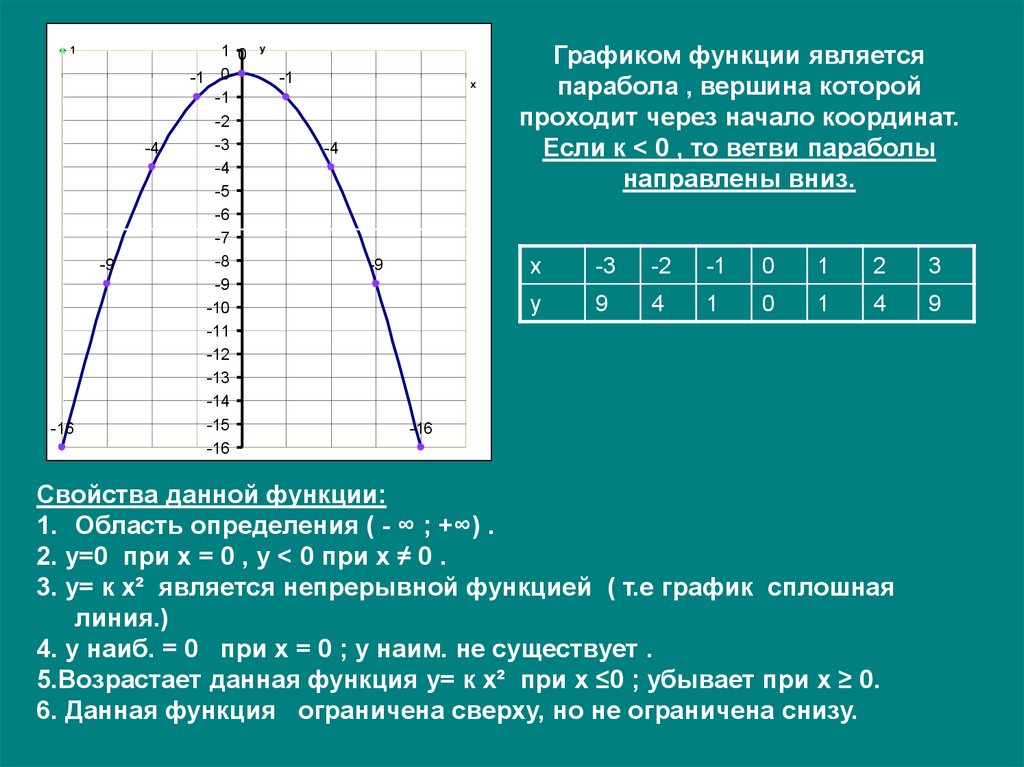
⇐ ПредыдущаяСтр 2 из 2 Парабола. Вспоминаем некоторые свойства функции . Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: . Область определения любой функции стандартно обозначается через или . Буква обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R). Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае: – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через или . Функция является чётной. Если функция является чётной, то ее график симметричен относительно оси. Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Функция не ограничена сверху. Аналитически свойство записывается так: . Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси (влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх на «плюс бесконечность». При изучении пределов функций желательно понимать геометрический смысл предела.Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций. Пример 2 Построить график функции . В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю: Если с производными плохо, следует ознакомиться с уроком Итак, решение нашего уравнения: – именно в этой точке и находится вершина параболы. Почему это так, можно узнать из теоретической статьи о производной и урока об экстремумах функции. А пока рассчитываем соответствующее значение «игрек»: Таким образом, вершина находится в точке Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция – не является чётной, но, тем не менее, симметричность параболы никто не отменял. В каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы: Данный алгоритм построения образно можно назвать «челноком» или принципом «туда-сюда» Выполним чертеж:
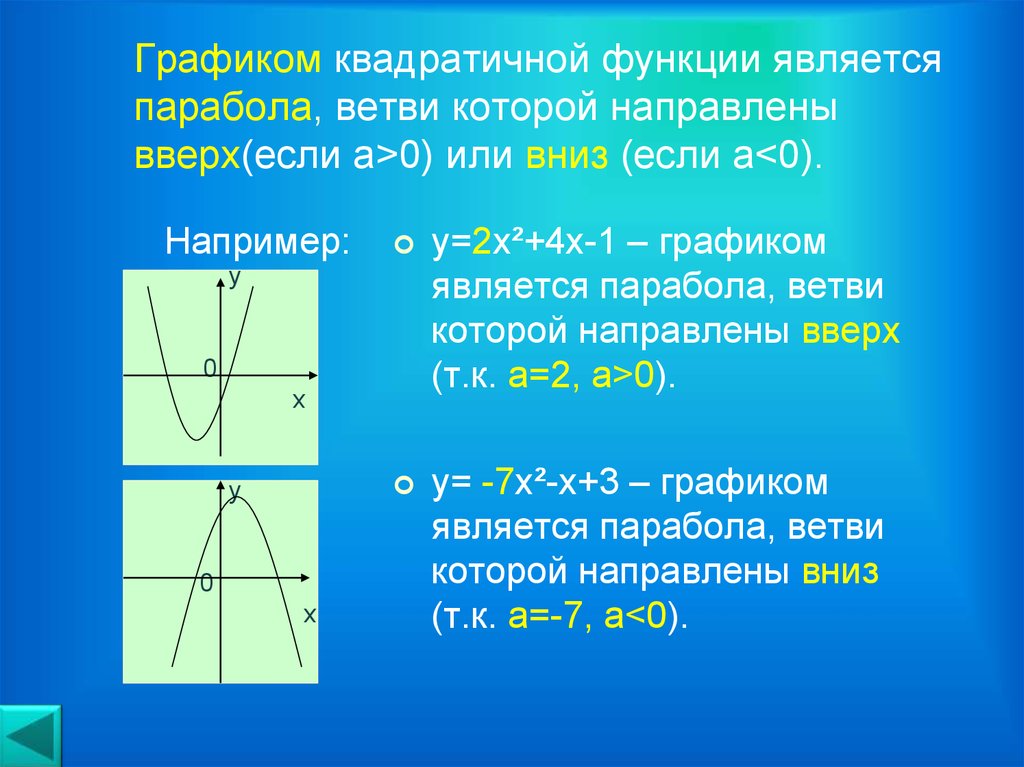
Для квадратичной функции ( ) справедливо следующее: Если, то ветви параболы направлены вверх. Если, то ветви параболы направлены вниз. Углублённые знания о кривой можно получить на уроке Гипербола и парабола.
Кубическая парабола Кубическая парабола задается функцией . Вот знакомый со школы чертеж:
Область определения – любое действительное число: . Область значений – любое действительное число: . Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: Функция не ограничена. На языке пределов функции это можно записать так: , Кубическую параболу тоже удобнее строить с помощью алгоритма «челнока»: Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении уже не нужно ничего считать, автоматом записываем, что . Эта особенность справедлива для любой нечетной функции. А теперь поговорим о графиках функций-многочленов высоких степеней чуть более подробно. График функции ( ) принципиально имеет следующий вид:
Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:
График функции Он представляет собой одну из ветвей параболы. Выполним чертеж:
Область определения: . Область значений: . То есть, график функции полностью находится в первой координатной четверти. Функция не ограничена сверху. Или с помощью предела: При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело: На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже. Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде приходиться строить значительно чаще. Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе.
График гиперболы Опять же вспоминаем тривиальную «школьную» гиперболу . Выполним чертеж: Область определения: . Область значений: . Запись обозначает: «любое действительное число, исключая ноль» В точке функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись обозначает, что мы бесконечно близко приближаемся по оси к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись обозначает, что мы бесконечно близко приближаемся по оси к нулю справа. При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: . Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой. В данном случае ось является вертикальной асимптотой для графика гиперболы при . Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой. Также односторонние пределы , говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу. Исследуем функцию на бесконечности: , то есть, если мы начнем уходить по оси влево (или вправо) на бесконечность, то «игреки» стройным шагом будут Таким образом, ось является горизонтальной асимптотой для графика функции , если «икс» стремится к плюс или минус бесконечности. Функция является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: . График функции вида() представляет собой две ветви гиперболы. Если, то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше). Если, то гипербола расположена во второй и четвертой координатных четвертях. Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков. Пример 3 Построить правую ветвь гиперболы Используем поточечный метод построения, при этом, значения выгодно подбирать так, чтобы делилось нацело: Выполним чертеж:
Детальную геометрическую информацию о рассмотренной линии можно найти в статьеГипербола и парабола.
⇐ Предыдущая12 Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Квадратичная функция
Квадратичной называется функция вида , где , – любые действительные числа.
График функции при называется параболой.
Свойства квадратичной функции:
1).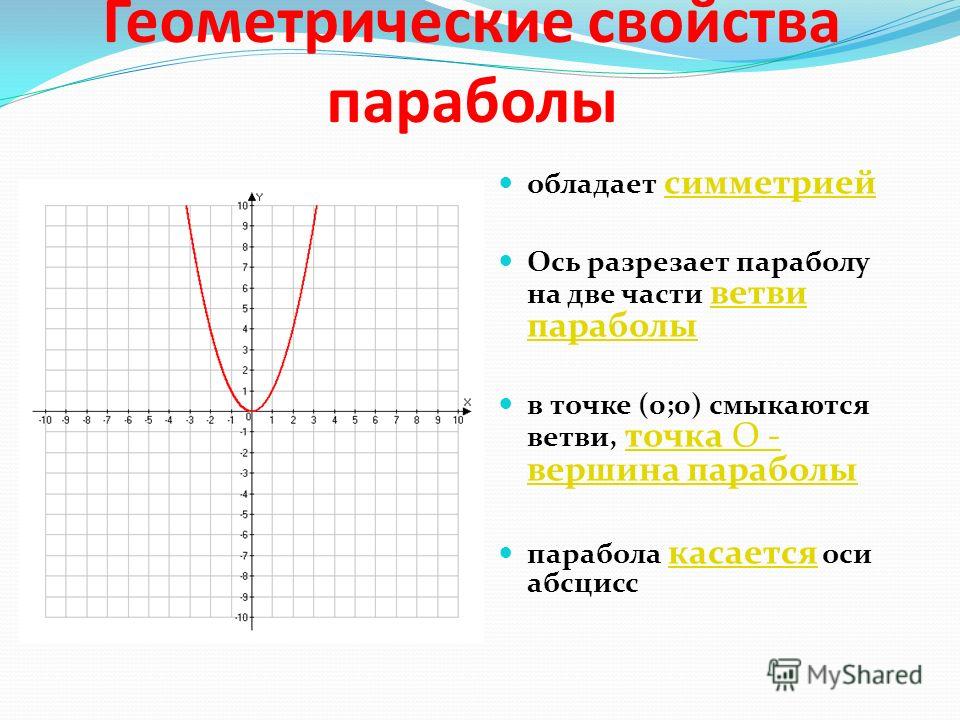 Область определения
функции: .
Область определения
функции: .
2). Область значений: .
3). Координаты вершины параболы : , .
4). Если , то ветви параболы направлены вниз. Если – вверх.
5). Прямая является осью симметрии графика квадратичной функции.
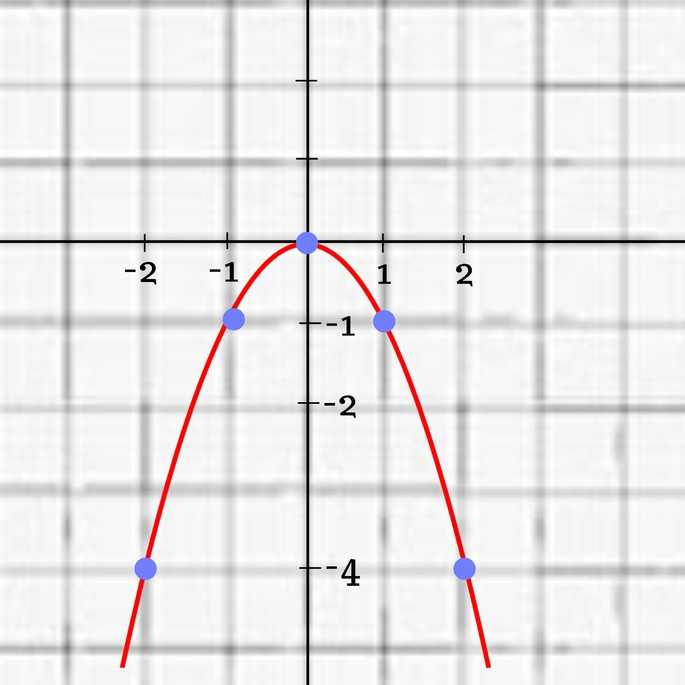
Пример квадратичной функции :
Гипербола
Функция вида , где , ( — коэффициент обратной пропорциональности) называется функцией обратной пропорциональности.
График функции , называется гиперболой.
Свойства функции обратной пропорциональности:
1). Область определения функции: .
2). Область значений: .
3).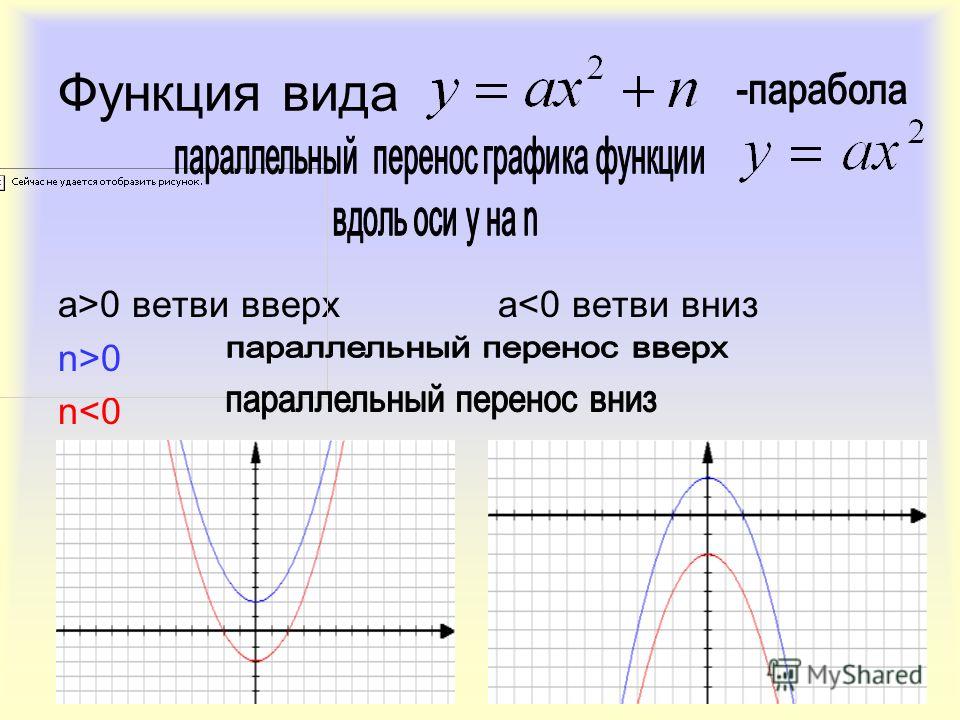 Функция нечетна.
Функция нечетна.
4). Функция не пересекает координатные оси.
5). При , при
6). Функция убывает на промежутках и .
7). Прямые и являются асимптотами (при и соответственно).
Степенная функция с натуральным показателнм.
Степенной функцией с натуральным показателем называется функция .
При получаем прямую пропорциональность: ; при – квадратную параболу; при – обратную пропорциональность или гиперболу.
Свойства степенной функции:
1). Область определения функции:
2). Для любых график функции проходит через точку .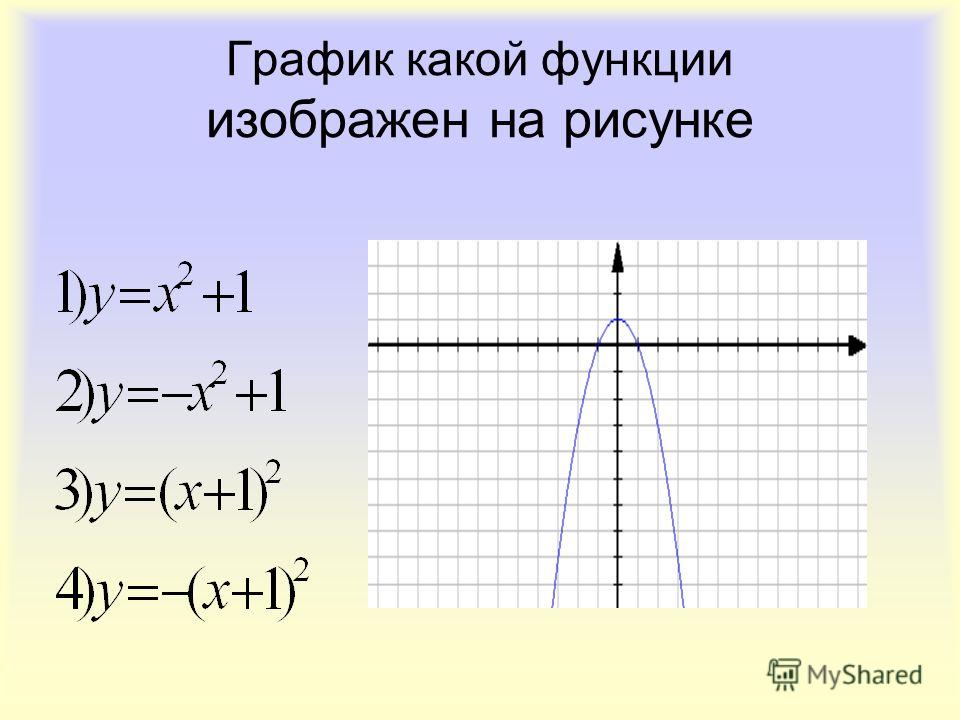
3). Для любых график функции проходит через точку .
Степенные функции имеют смысл и при , но их графики имеют различный вид в зависимости от того, является ли чётным числом или нечётным.
Функция четная:
| Функция нечетная: |
При | При ; при |
Функция возрастает на Функция убывает на | Функция возрастает на |
График функции аналогичен графику функции (парабола) | График функции аналогичен графику функции (кубическая парабола) |
Пример степенных функций и :
Функция .

Свойства функции корня:
При четном функция обладает теми же свойствами, что и функция :
1). Область определения: луч . Это следует из, того что выражение определено лишь при .
2). Функция ни четна, ни нечетна
3). Функция возрастает на луче .
4). График функции напоминает график функции :
При нечетном функция обладает теми же свойствами, что и функция :
1). Область определения функции – вся числовая прямая.
2). Функция нечетна.
3). Функция возрастает на всей числовой прямой.
4). График функции напоминает график функции :
Показательная функция
Функция вида ,
при называется показательной функцией с
основанием .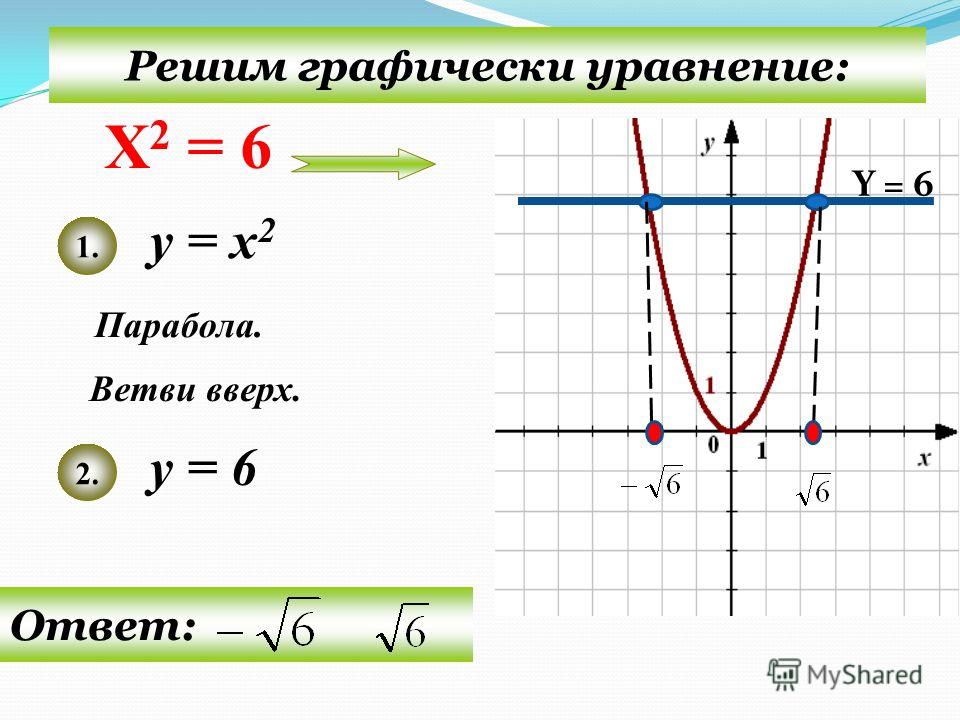
Свойства показательной функции:
1). Область определения функции:
2). Область значений: .
3). Если , то и если , то .
4). При функция строго монотонно возрастает на всей числовой прямой.
При функция строго монотонно убывает на всей числовой прямой.
Примеры показательных функций и :
ГИА. Квадратичная функция. Урок «Функция y=ax2, ее график и свойства Как называется график функции y ax2
Вывод о симметричности графиков функций y=ax 2 и y=-ax2 (при ≠0) относительно оси абсцисс отдельно выделен на слайде 12 для запоминания и наглядно отображен на соответствующем графике. Далее понятие о графике квадратичной функции y=x 2 распространяется на более общий случай функции y=ax 2 , утверждая, что такой график также будет называться параболой.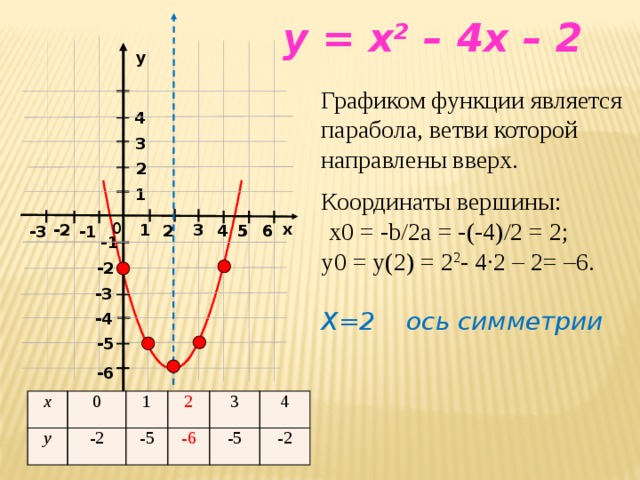
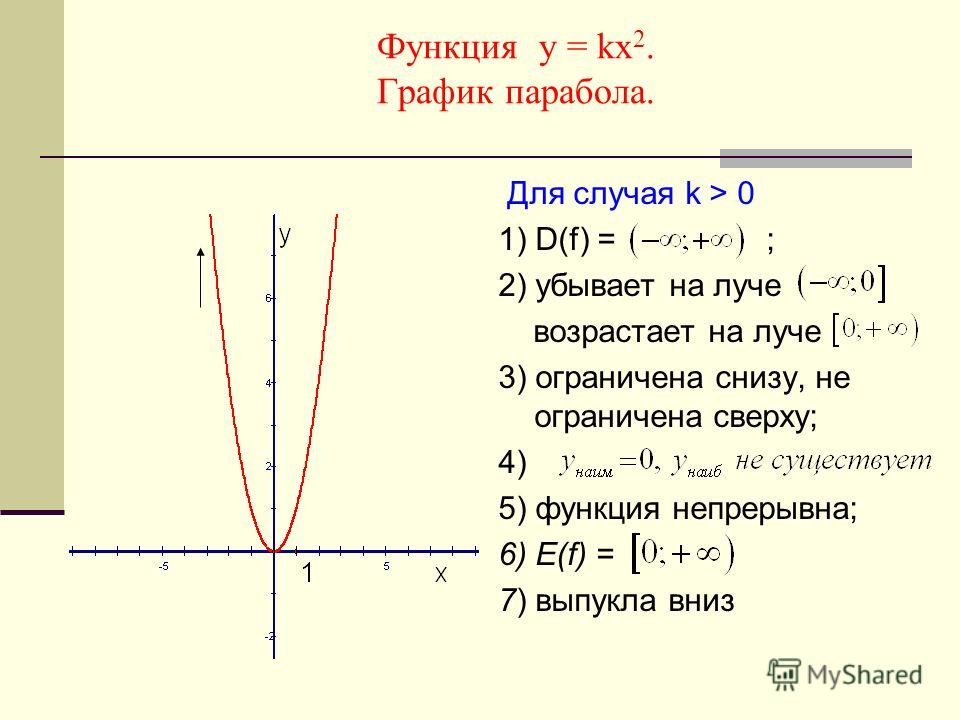
На слайде 14 рассматриваются свойства квадратичной функции y=ax 2 при положительном. Отмечается, что ее график проходит через начало координат, а все точки, кроме, лежат в верхней полуплоскости. Отмечена симметричность графика относительно оси ординат, уточняя, что противоположным значениям аргумента соответствуют одинаковые значения функции. Указано, что промежуток убывания данной функции (-∞;0], а возрастание функции выполняется на промежутке. Значения данной функции охватывают всю положительную часть действительной оси, нулю она равна в точке, а наибольшего значения не имеет.
На слайде 15 описываются свойства функции y=ax 2 , если отрицательный. Отмечается, что ее график также проходит через начало координат, но все его точки, кроме, лежат в нижней полуплоскости. Отмечена симметричность графика относительно оси, и противоположным значениям аргумента соответствуют равные значения функции. Возрастает функция на промежутке, убывает на. Значения данной функции лежат в промежутке, нулю она равна в точке, а наименьшего значения не имеет.
Обобщая рассмотренные характеристики, на слайде 16 выводится, что ветви параболы направлены вниз при, а вверх — при. Парабола симметрична относительно оси, а вершина параболы располагается в точке ее пересечения с осью. У параболы y=ax 2 вершина — начало координат.
Также важный вывод о преобразованиях параболы отображается на слайде 17. На нем представлены варианты преобразований графика квадратичной функции. Отмечено, что график функции y=ax 2 преобразуется симметричным отображением графика относительно оси. Также возможно сжатие или растяжение графика относительно оси.
На последнем слайде делаются обобщающие выводы о преобразованиях графика функции. Представлены выводы о том, что график функции получается симметрическим преобразованием относительно оси. А график функции получается из сжатием или растяжением исходного графика от оси. При этом растяжение от оси в раз наблюдается в случае, когда. Сжатием к оси в 1/a раз график образуется в случае.
Презентация «Функция y=ax 2 , ее график и свойства» может быть использована учителем в качестве наглядного пособия на уроке алгебры.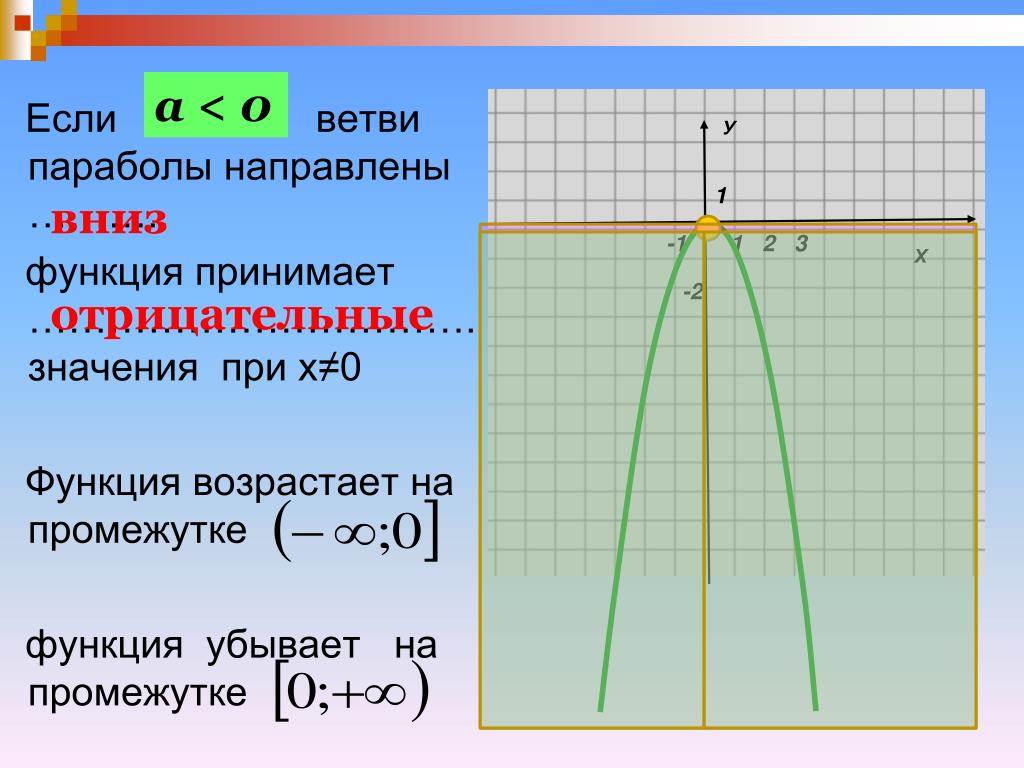 Также данное пособие хорошо раскрывает тему, давая углубленное понимание предмета, поэтому может быть предложена для самостоятельного изучения учениками. Также данный материал поможет учителю дать объяснение в ходе дистанционного обучения.
Также данное пособие хорошо раскрывает тему, давая углубленное понимание предмета, поэтому может быть предложена для самостоятельного изучения учениками. Также данный материал поможет учителю дать объяснение в ходе дистанционного обучения.
Рассмотрим выражение вида ах 2 +вх+с, где а, в, с — действительные числа, а отлично от нуля. Это математическое выражение известно как квадратный трехчлен.
Напомним, что ах 2 — это старший член этого квадратного трехчлена, а — его старший коэффициент.
Но не всегда у квадратного трехчлена присутствуют все три слагаемые. Возьмем для примера выражение 3х 2 + 2х, где а=3, в=2, с=0.
Перейдем к квадратичной функции у=ах 2 +вх+с, где а, в, с — любые произвольные числа. Эта функция является квадратичной, так как содержит член второй степени, то есть х в квадрате.
Довольно легко построить график квадратичной функции, например, можно воспользоваться методом выделения полного квадрата.
Рассмотрим пример построения графика функции у равно -3х 2 — 6х + 1.
Для этого первое, что вспомним, схему выделения полного квадрата в трехчлене -3х 2 — 6х + 1.
Вынесем -3 у первых двух слагаемых за скобки. Имеем -3 умножить на сумму х квадрат плюс 2х и прибавить 1. Добавив и отняв единицу в скобках, получаем формулу квадрата суммы, которую можно свернуть. Получим -3 умножить на сумму (х+1) в квадрате минус 1 прибавить 1. Раскрывая скобки и приводя подобные слагаемые, выходит выражение: -3 умноженное на квадрат суммы (х+1) прибавить 4.
Построим график полученной функции, перейдя к вспомогательной системе координат с началом в точке с координатами (-1; 4).
На рисунке из видео эта система обозначена пунктирными линиями. Привяжем функцию у равно -3х 2 к построенной системе координат. Для удобства возьмем контрольные точки. Например, (0;0), (1;-3), (-1;-3), (2;-12), (-2;-12). При этом отложим их в построенной системе координат. Полученная при построении парабола является необходимым нам графиком. На рисунке это красная парабола.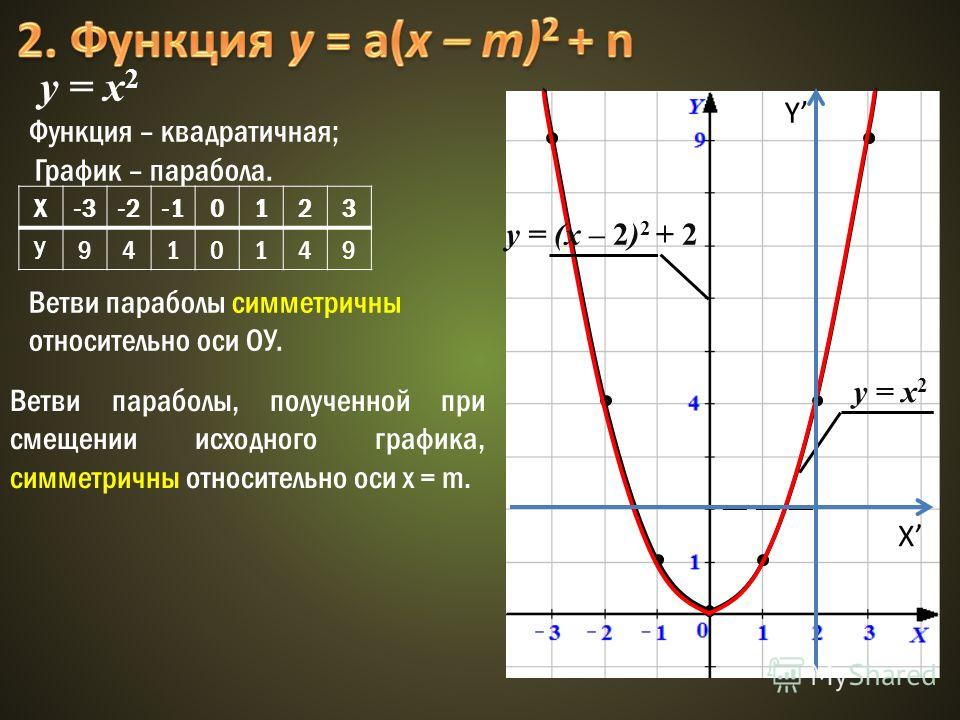
Применяя метод выделения полного квадрата, мы имеем квадратичную функцию вида: у = а*(х+1) 2 + m.
График параболы у = ах 2 + bx + c легко получить из параболы у=ах 2 параллельным переносом. Это подтверждено теоремой, которую можно доказать, выделив полный квадрат двучлена. Выражение ах 2 + bx + c после последовательных преобразований превращается в выражение вида: а*(х+l) 2 + m. Начертим график. Выполним параллельное перемещение параболы у = ах 2 , совмещая вершину с точкой с координатами (-l;m). Важно то, что х= -l, а значит -b/2а. Значит эта прямая является осью параболы ах 2 + bx + c, ее вершина находится в точке с абсциссой х нулевое равно минус в, деленное на 2а, а ордината вычисляется по громоздкой формуле 4ас — b 2 /. Но эту формулу запоминать не обязательно. Так как, подставив значение абсциссы в функцию, получим ординату.
Для определения уравнения оси, направления ее ветвей и координат вершины параболы, рассмотрим следующий пример.
Возьмем функцию у = -3х 2 — 6х + 1.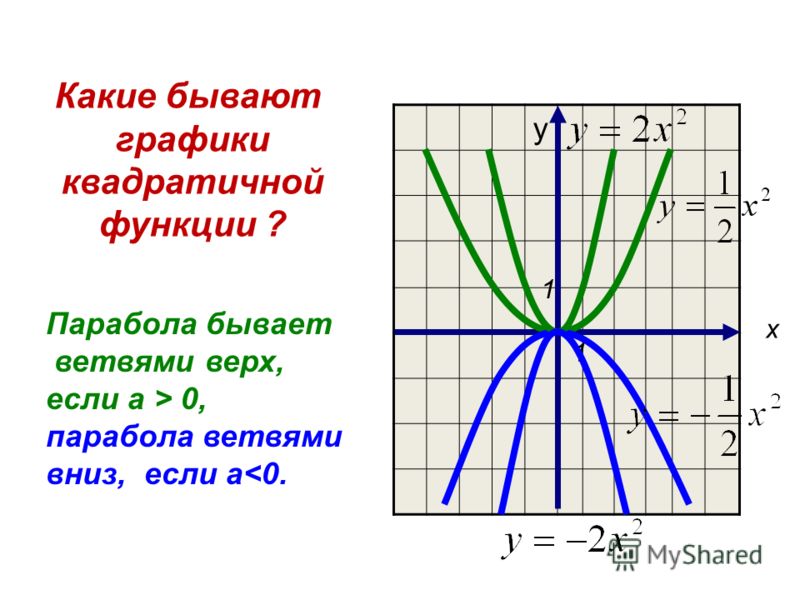 Составив уравнение оси параболы, имеем, что х=-1. А это значение является координатой х вершины параболы. Осталось найти только ординату. Подставив значение -1 в функцию, получим 4. Вершина параболы находится в точке (-1; 4).
Составив уравнение оси параболы, имеем, что х=-1. А это значение является координатой х вершины параболы. Осталось найти только ординату. Подставив значение -1 в функцию, получим 4. Вершина параболы находится в точке (-1; 4).
График функции у = -3х 2 — 6х + 1 получен при параллельном переносе графика функции у = -3х 2 , значит, и ведет себя аналогично. Старший коэффициент отрицателен, поэтому ветви направлены вниз.
Мы видим, что для любой функции вида y = ах 2 + bx + c, самым легким является последний вопрос, то есть направление веток параболы. Если коэффициент а положительный, то ветви — вверх, а если отрицательный, то — вниз.
Следующим по сложности идет первый вопрос, потому что требует дополнительных вычислений.
И самый сложный второй, так как, кроме вычислений, еще необходимы знания формул, по которым находятся х нулевое и у нулевое.
Построим график функции у = 2х 2 — х + 1.
Определяем сразу — графиком является парабола, ветви направлены вверх, так как старший коэффициент равен 2, а это положительное число.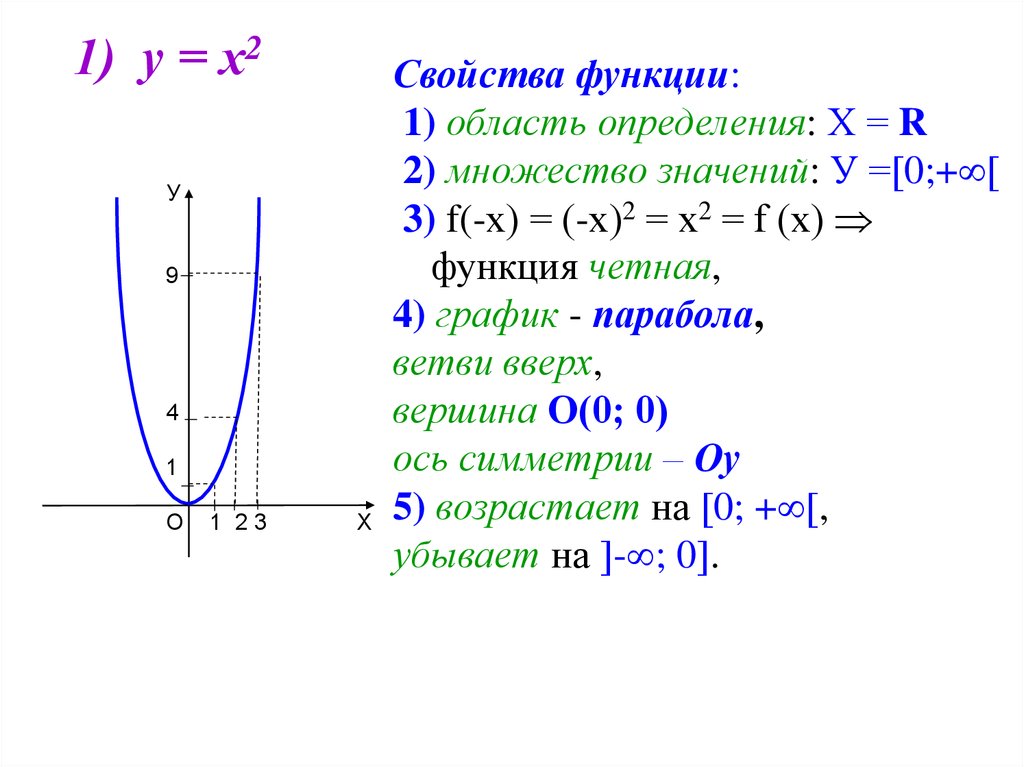 По формуле находим абсциссу х нулевое, она равна 1,5. Для нахождения ординаты вспомним, что у нулевое равно функции от 1,5, при вычислении получим -3,5.
По формуле находим абсциссу х нулевое, она равна 1,5. Для нахождения ординаты вспомним, что у нулевое равно функции от 1,5, при вычислении получим -3,5.
Вершина — (1,5;-3,5). Ось — х=1,5. Возьмем точки х=0 и х=3. у=1. Отметим данные точки. По трем известным точкам строим искомый график.
Для построения графика функции ах 2 + bx + c необходимо:
Найти координаты вершины параболы и отметить их на рисунке, потом провести ось параболы;
На оси ох взять две симметричные, относительно оси, параболы точки, найти значение функции в этих точках и отметить их на координатной плоскости;
Через три точки построить параболу, при необходимости можно взять еще несколько точек и строить график по ним.
В следующем примере мы научимся находить наибольшее и наименьшее значения функции -2х 2 + 8х — 5 на отрезке .
По алгоритму: а=-2, в=8, значит х нулевое равно 2, а у нулевое — 3, (2;3) — вершина параболы, а х=2 является осью.
Возьмем значения х=0 и х=4 и найдем ординаты этих точек. 2+4x-3$ на отрезке $[-5;2]$.
2+4x-3$ на отрезке $[-5;2]$.
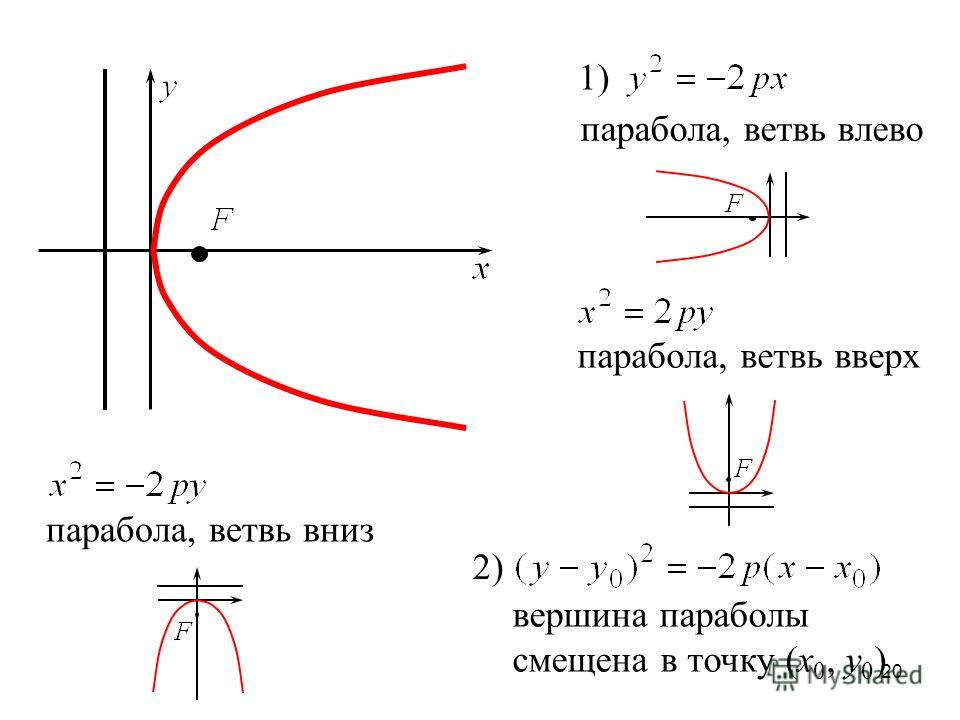
парабола
Слово
«парабола» относится
к параллельности конического сечения и касательной к конической мантии. Также
притча 1) была выведена
от греческого «парабола».
Параболу можно рассматривать как эллипс с одним фокусом в
бесконечность. Это означает, что параллельный световой пучок в параболическом зеркале сойдется вместе.
в одну точку. Было сказано, что Архимед действительно использовал параболическое зеркало в
военное дело. Именно во время осады Сиракуз (214–212 гг. до н. э.) римлянами Архимед построены отражающие пластины примерно в форме параболы. Эти пластины использовались для
направить солнечный свет на римские корабли и поджечь их. Хотя это событие
обсуждается некоторыми историками, недавно была доказана осуществимость плана Архимеда 2) .
Другими технологическими объектами в форме параболы являются параболический микрофон и параболический микрофон.
антенна, используемая для фокусировки звуковых и электромагнитных волн соответственно.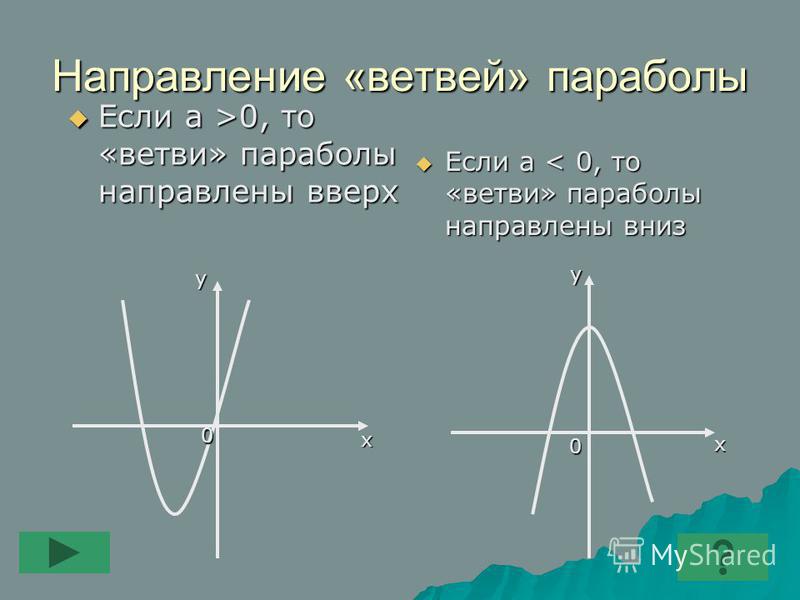
Менаихмос (350 г. до н.э.) нашел параболу при попытке продублировать
куб: нахождение куба с площадью, вдвое большей площади данного куба 3) . На самом деле он пытался решить уравнение x 3 = 2. Менеихм решил уравнение как пересечение парабол y = x 2 и х = у 2 .
Евклид (ок. 300 г. до н. э.) писал о параболе в своем трактате «Конические сечения» (утерян).
Аполлоний (200 г. до н.э.) также написал о параболе в четырех книгах с таким же названием, вероятно, используя работу Евклида.
Именно он дал название параболе.
Гипатия (355-415), первая известная женщина-математик, писала «о кониках Аполлония»,
популяризация творчества Аполлония. После Гипатии кажется, что кониками пренебрегали
до семнадцатого века.
Рен Декарт (1596-1650) выбрал параболу в своей работе «Гомтри» (1637) для иллюстрации своей работы по аналитической геометрии.
Блез Паскаль (1623-1662) рассматривал кривую как проекцию окружности.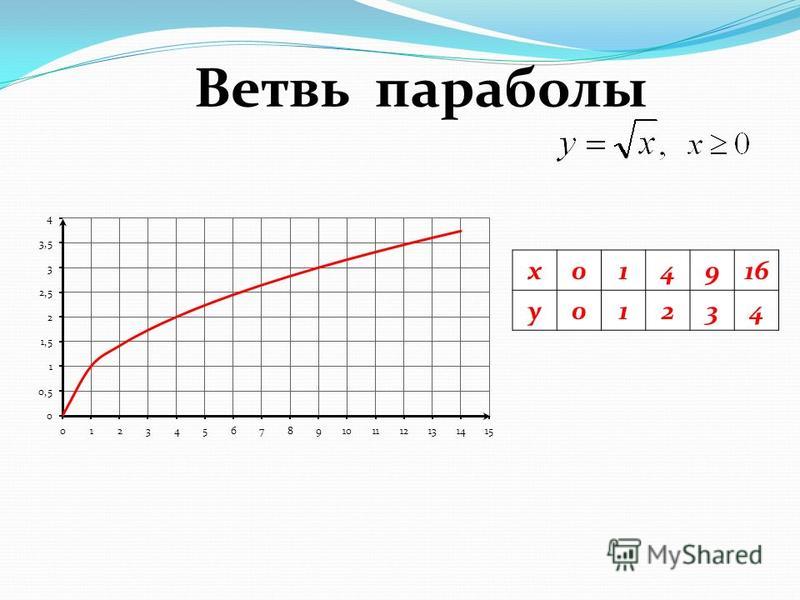
Пьер де Ферма писал в 1636 г. в письме к Робервалю, что он нашел обобщение кривой,
который позже получил название параболы Ферма, 7 лет назад.
Как видите, парабола — одна из наиболее изученных кривых.
В кривой параболы парабола (вершиной вниз) повторяется бесконечно.
Некоторые свойства параболы:
- парабола является эвольвентой полукубической параболы
- траектория параболы образуется, когда эвольвента круг катится по линии
- кривая представляет собой образец синусоидальной спирали
- это педаль куба Чирнхаузена
Кроме того, из параболы можно вывести следующие кривые:
| вид производной кривой | кривая |
| катакаустическая лучи, перпендикулярные оси | Кубик Чирнхаузена |
| изоптический | гипербола |
| ортоптический | директриса параболы |
| обратная полярность фокус как центр инверсии | кардиоидная |
| обратная полярность вершина как центр инверсии | циссоид |
| рулетка парабола катится по другой (равной) параболе | циссоида: путь вершины |
| рулетка парабола катится по линии | Контактная сеть: путь фокус |
Педали параболы даны:
| и | педаль | педаль параболы |
| 0 | вершина | циссоид (Диокла) |
| 1 | фут — пересечения оси и — директрисы | (справа) строфоид |
| 3 | отражение фокуса в директрисе | трисектриса Маклорена |
| — | на директрисе | косой строфоид |
| — | фокус | строка |
Итальянец Лука Валерио определил площадь параболы в 1606 г.
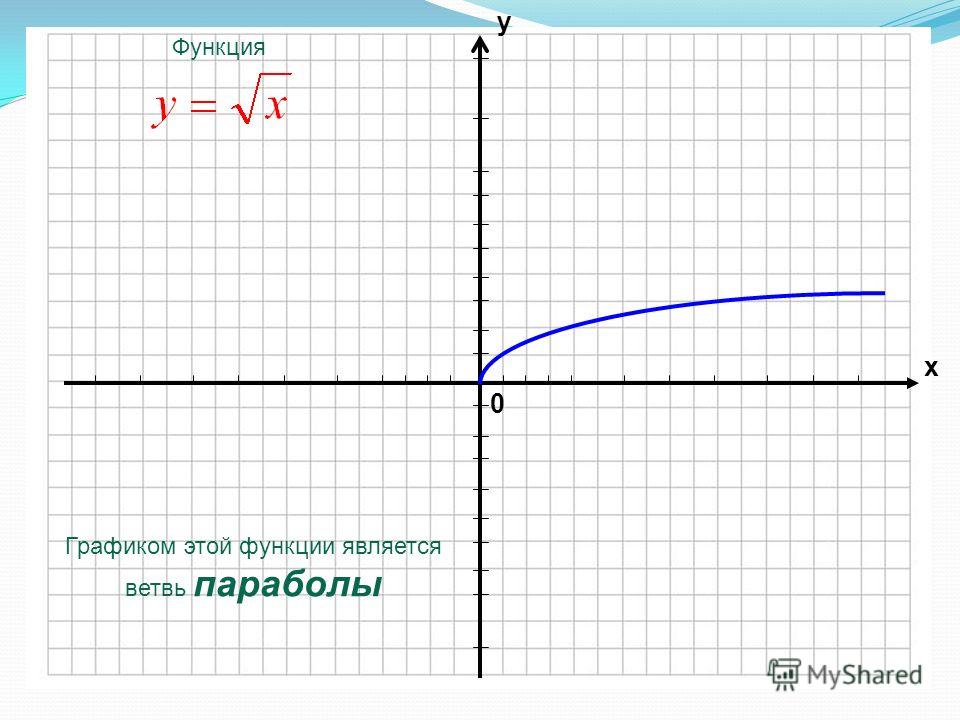 ; была названа квадратурой параболы. Но было Архимед кто
впервые нашел значение этой площади. В своей работе «Квадратура параболы» он
сформулировал площадь как 2/3 от произведения основания и высоты параболы
сектор 3) .
; была названа квадратурой параболы. Но было Архимед кто
впервые нашел значение этой площади. В своей работе «Квадратура параболы» он
сформулировал площадь как 2/3 от произведения основания и высоты параболы
сектор 3) . В конце Средневековья пушка вошла в обиход на
поле битвы. Поэтому было важно предсказать точное место, где
снаряд приземлился бы. На этот вопрос пытались ответить многие ученые, и Галилео Галилей (1564-1642), который нашел отношение первым.
Что траектория снаряда — пренебрегая эффектами
трения — имеет форму параболы, легко понять следующим образом: координата х пропорциональна прошедшему времени,
координата y квадратична (из-за постоянной силы гравитации).
Собственно говоря, это отношение уже в 15 веке было известно как «квадратичный закон».
При учете трения о воздух заторможенный
возникает парабола, которая на самом деле является разновидностью экспоненциальной кривой.
Параболическая скорость — это минимальная скорость, при которой можно избежать (сил гравитации)
небесный объект.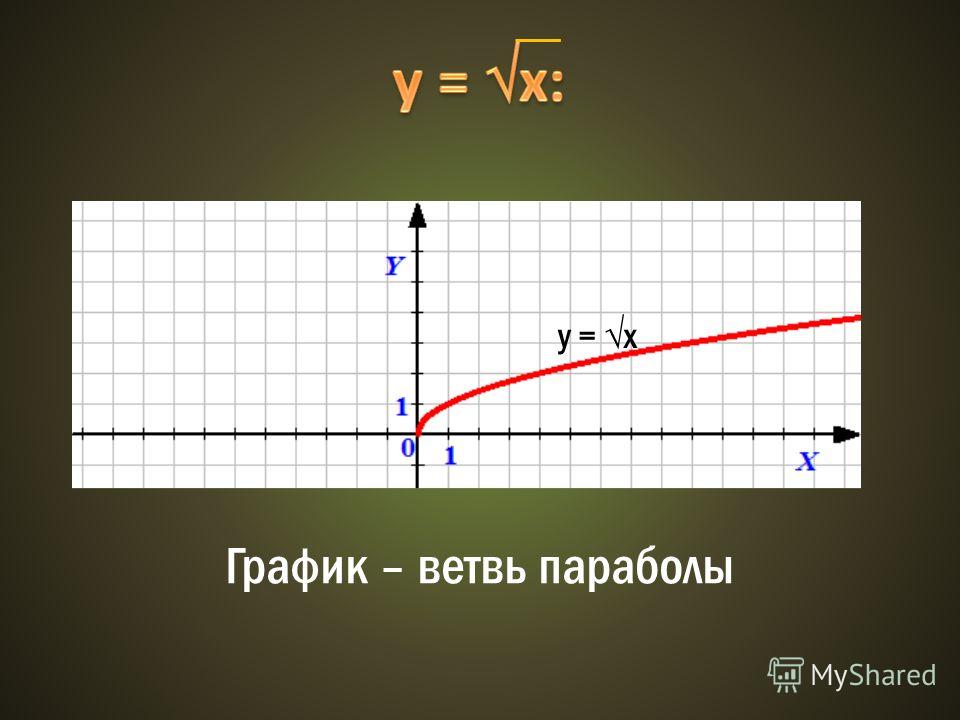
А арка (например, каменная) называется параболической, когда ее форма имеет вид ….
Теперь пришло время для эксперимента: повесьте на горизонтальный пояс несколько светильников, на равных
расстояния. Если пренебречь весом пояса по сравнению с светильниками, точки подвеса
лампа образует параболу 4) . Эта форма
не зависит от веса ламп, а также от расстояния между лампами. в
В случае хорды без ламп вместо параболы образуется контактная сеть.
Юнгиус (1669) доказал, что Галилео был неправ, указав эту кривую
быть параболой.
В отпуске на голландском пляже Северного моря можно увидеть дюны в форме параболы
(параболическая дюна), образованная песком, разбрасываемая ветром, но удерживаемая растениями дюны.
При экспериментировании часто встречаются квадратичные соотношения между переменными. Так и есть
кинетическая энергия тела пропорциональна квадрату скорости. В другом филиале
математики находим повторную параболу, изученную впервые (в 60-е годы) Мирберг . В случае сходимости говорят об аттракторе . И тепло
уравнение, дифференциальное уравнение в частных производных второго порядка, также называется параболическим уравнением .
дифференциальное уравнение . Причиной является сходство отношений 5) .
В случае сходимости говорят об аттракторе . И тепло
уравнение, дифференциальное уравнение в частных производных второго порядка, также называется параболическим уравнением .
дифференциальное уравнение . Причиной является сходство отношений 5) .
примечания
1) Para = рядом, bole (Гр.) = бросить, parabole = то, что брошено дальше к (для сравнения).
2) Мюллер 1985 с. 111.
3) искали куб, содержащий удвоенный объем данного куба: Waerden 1950 p. 88.
4) с благодарностью Крису Рорресу (Университет Дрекселя).
5) Это следует из обнуления импульса силы, действующей на низшую точку
аккорда.
6).
Дом — INTEF
Últimas noticias
Primeras Jornadas nacionales sobre el modelo curricular, competencial e inclusivo
El plazo de inscripción finaliza el 21 de octubre de 2022.
Premios Nacionales a Experiencias Educativas Inspiradoras para el aprendizaje (1.ª edición)
El plazo de participación en el concurso estará abierto hasta el 8 de octubre de 2022.
Comienza el MOOC Diseña el Plan Digital de tu center (4.ª Edición)
Se inicia el el 13 de septiembre y finaliza el 20 de octubre de 2022. ¡Inscribete!
El 15 de octubre se celebará el I Congreso Nacional de Radio Escolar
Este encuentro, dirigido a profesorado de los niveles previos a la Universidad, está promovido por el Ministryio de Educación y Formación Profesional y la Fundación COPE.
El Plan Digital de Centro. Ун Марко пара ла интеграции де лас tecnologías.
Эль-усо-де-лос-медиос-дигиталис для артикуляционного образования и проезда по образовательным центрам.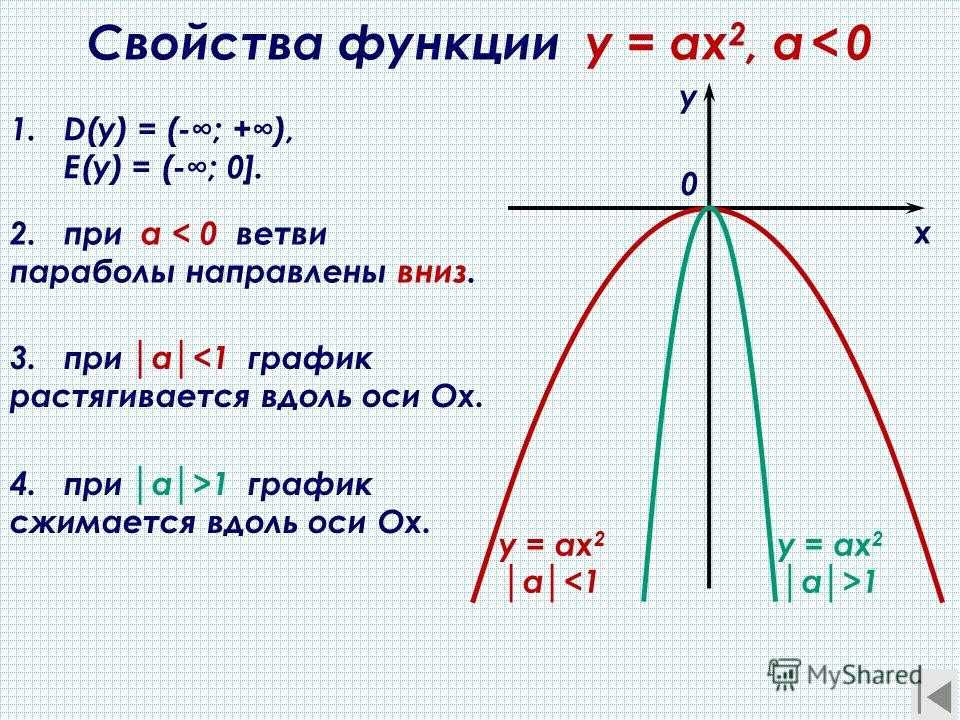 El Plan Digital de Centro proporciona un marco para que las tecnologías enriquezcan y mejoren el proceso de aprendizaje del a…
El Plan Digital de Centro proporciona un marco para que las tecnologías enriquezcan y mejoren el proceso de aprendizaje del a…
Participa en la CodeWeek 2022
По почте, в которой представлены активы puestas en Marcha en torno a la Semana de la Programación de la Unión Europea.
EDUcharla «Образовательная оценка II: формирование и включение»
Este miércoles 28 сентября, до 16:00 часов, continuaremos hablando sobre la Evaluación educativa, en una nueva EDUcharla. Siguiendo con la temática …
Evento en directo. Учебная программа El Nuevo Marco: Desde la Norma al Centro
Ретрансляция по каналу YouTube del INTEF martes 20 сентября в 16:30.
Calendario formación abierta 1er trimestre curso 2022/23
Se desarrollarán un total de diez cursos en modalidad NOOC y dos cursos en format MOOC.
Más noticias
Lo más buscado
- Recursos educativos
- Recursos de aprendizaje en linea
- Convocatoria de cursos de formación 2022
- Recursos de imagegenes y sonidos
Повестка дня
- MOOC «Diseña el Plan Digital de tu center» (4-е издание).

- Ver todos los eventos
Видео Семена
Твиты пользователя educaINTEF
/nfs-netapp/mercurio/intef.es
Fecha CRON: 2022-10-06 0:47:39am
Вневременный момент 35 лет INJUVE
Посещение выставки «Вневременный момент». 35 лет INJUVE». Una retrospectiva que Presenta la selección de algunos de los trab…
InShot:
Этот артикул представляет собой InShot , который является средством редактирования видео, которое может быть использовано для создания контента для просмотра… 3
- Aprendizaje en línea
- Competencia Digital Educativa
- eTwinning
- Estancias profesionales
- Cursos de verano
- Scientix
- Otros proyectos
- Educharlas
- ConectaTIC
- Mecanismo de Recuperación y Resiliencia
- ExeLearning
- Procomún
- La aventura de aprender
- Proyecto EDIA
- Experiencias educativas inspiradoras
- Banco de imágenes y sonidos
- Educación digital de calidad
- Recursos Educativos para el Aprendizaje en Línea
- Escuela de Pensamiento computacional e Inteligencia Artificial
- Aula del futuro
- Observatorio de tecnología educativa
- AbiesWeb
- Escuelas conectadas
- Samsung Smart School
- Seguridad del menor en internet
Коносенос
Recursos orientados menores de edad, familias y educadores, para hacer de Internet y las redes sociales un medio más seguro.
Aprendizaje en línea пункт уна цифрового преобразования де ла educación. Participa, comparte, conecta.
El CEDEC tiene como finalidad el diseño, la promoción y el desarrollo de materiales educativos digitales a través del software libre que estén disposición de toda la comunidad educativa.
eTwinning es una acción para centros escolares no universitarios, con el objetivo de facilitar el contacto y el trabajo colaborativo entre docentes y alumnado europeo con la ayuda de las tecnologías.Infórmate y regístrate.
Recursos educativos abiertos, formación y soluciones technológicas para ayudar los docentes incorporar el pensamiento computacional, la robotica y la programación en el aula.
Веб-сайт с информацией, содержащей различные типы учебных материалов (материалы, формы, платформы, приложения и т. д.) для обучения на расстоянии.
ConectaTIC es un espacio de apoyo y colaboración para la educación digital que ofrece una selección de materiales formativos, un entorno profesional de comunicación para el intercambio de experiencias y una vía para realizar consultas sobre la educación en linea.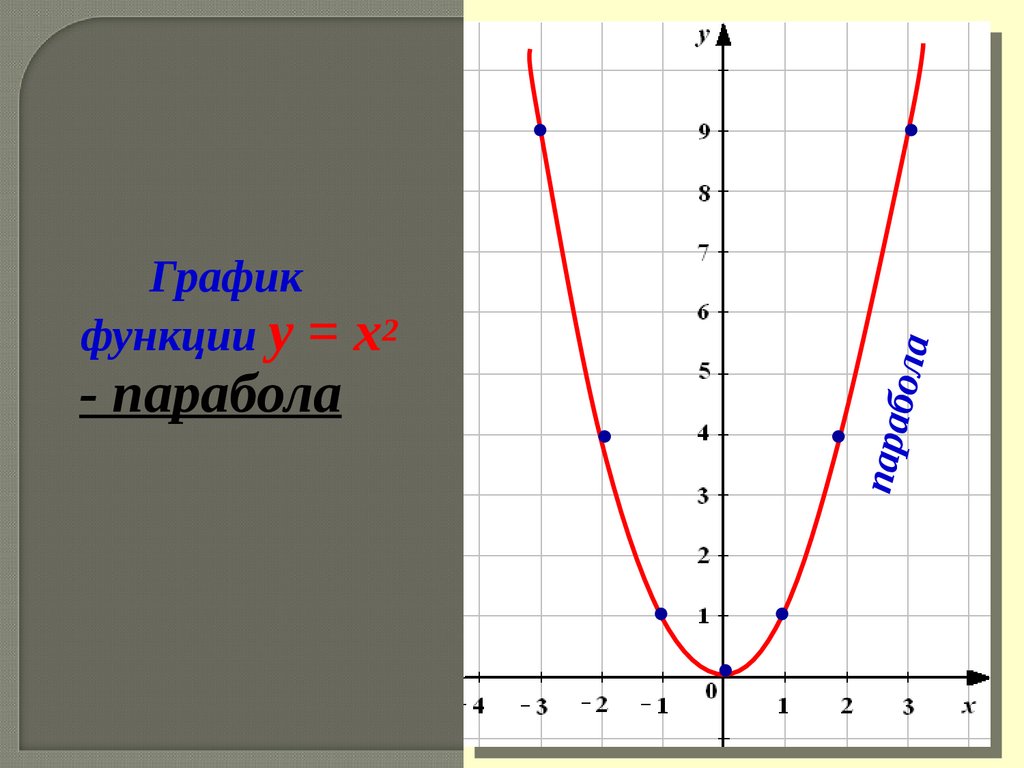
Основы параболы (Видео и практические вопросы)
TranscriptPractice
Парабола представляет собой отчетливую форму квадратного уравнения при графическом отображении. В этом видео мы дадим вам некоторые подсказки, найденные в квадратных уравнениях, которые могут рассказать вам больше о параболах, которые они рисуют .
Итак, симметрия параболы обусловлена квадратом члена в квадратном уравнении. Однако есть одна точка на параболе, которая не имеет «зеркального отражения». Эта точка называется вершиной и обозначается упорядоченной парой (h,k). Вершина представляет собой либо максимальное значение , либо минимальное значение параболы, в зависимости от того, в каком направлении открывается парабола.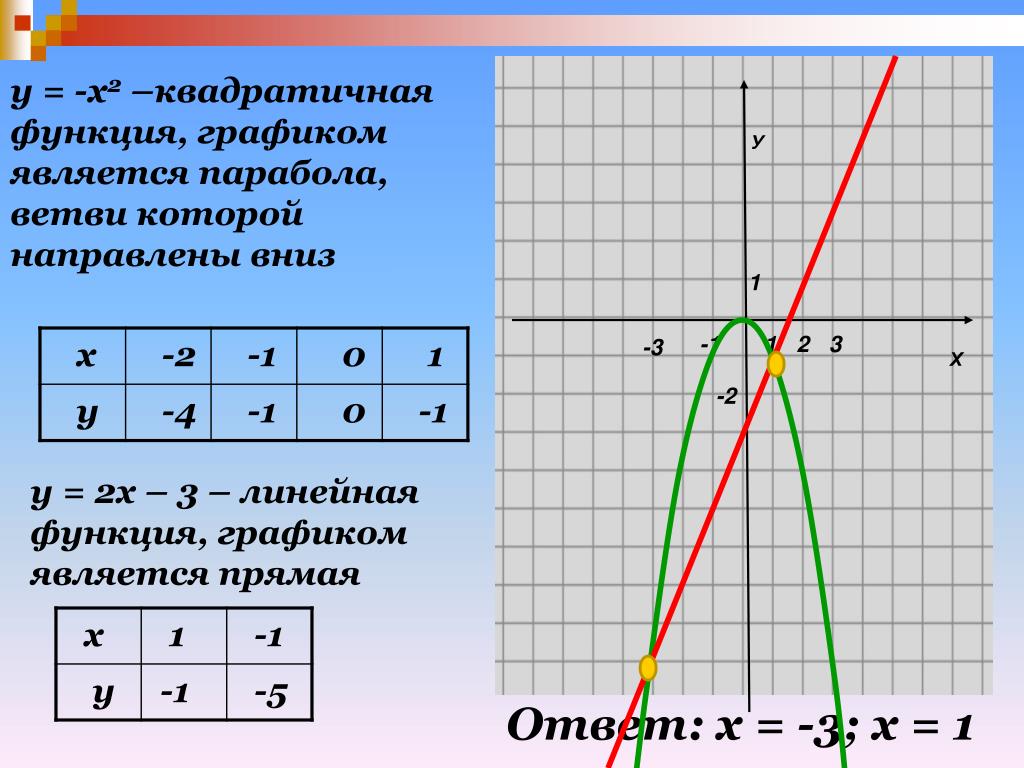
Когда переменная x возведена в квадрат в квадратном уравнении, парабола «откроется» либо вверх, либо вниз . Представьте себе две симметричные ветви графа, отходящие от вершины в одном направлении; либо вверх, к положительной бесконечности по оси y, либо вниз, к отрицательной бесконечности по оси y.
Однако, когда y-переменная возведена в квадрат в квадратном уравнении, парабола «откроется» либо вправо , поскольку обе ветви простираются от вершины к положительной бесконечности по оси x, либо к слева от , в сторону отрицательной бесконечности по оси x.
Чтобы лучше понять это, нам нужно посмотреть, как записываются квадратных уравнения . Они записываются в двух основных формах:
- 1. Стандартная форма квадратного уравнения записывается как y=ax 2 +bx+c, где «a» представляет собой коэффициент квадрата переменной, «b» коэффициент линейного члена, а «с» представляет собой константу.
 Поскольку переменная x возведена в квадрат, это квадратичная функция, которая открывается либо вверх, либо вниз.
Поскольку переменная x возведена в квадрат, это квадратичная функция, которая открывается либо вверх, либо вниз.Квадратное уравнение в этой форме с квадратом переменной y будет записано как x=ay 2 +by+c. Парабола, построенная по этому соотношению, развернулась бы либо влево, либо вправо.
- 2. Квадратичная функция, имеющая форму вершины , записывается как y=a(x-h) 2 +k, где «a» — коэффициент квадратного бинома, который в данном примере содержит x- переменная. Вершина параболы находится в упорядоченной паре (h,k). Если изобразить эту параболу на графике, она откроется либо вверх, либо вниз. Уравнение для открывающейся влево или вправо параболы в форме вершины будет записано как x=a(y-k) 2 +ч.
Как видите, значение «а» является общим элементом в обеих формах квадратного уравнения. Это значение содержит ключ к тому, в каком направлении будет раскрываться парабола.
Если значение «а» положительное, уравнения с квадратом переменной x будут отображаться в виде парабол, открывающихся ВВЕРХ.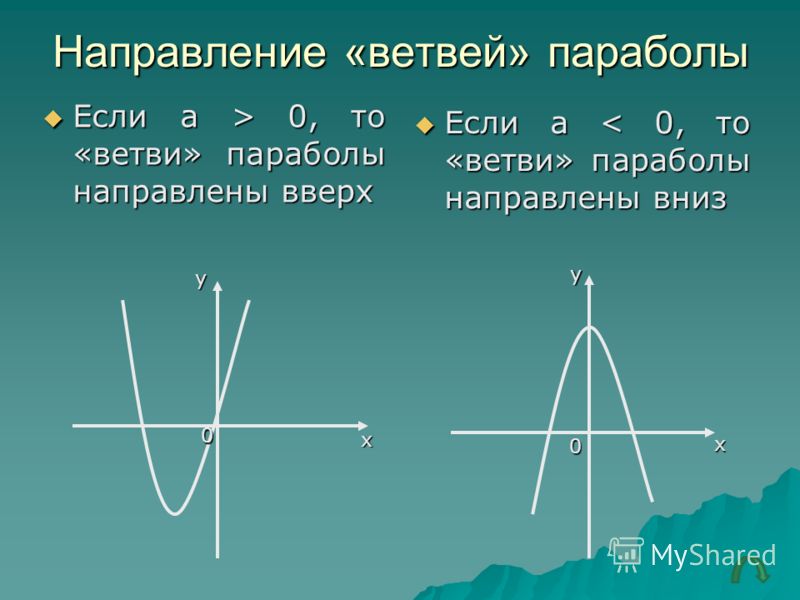 Уравнения с квадратом переменной y будут отображаться как параболы, открывающиеся ВПРАВО.
Уравнения с квадратом переменной y будут отображаться как параболы, открывающиеся ВПРАВО.
Если значение «a» отрицательное, уравнения с квадратом переменной x будут отображаться в виде парабол, открывающихся ВНИЗ. Уравнения с квадратом переменной y будут графически изображаться в виде парабол, открывающихся НАЛЕВО.
Чтобы свести воедино всю эту информацию, давайте рассмотрим несколько примеров квадратных уравнений:
- 1. y=2×2+3x-6
Это квадратное уравнение стандартной формы с квадратом переменной x и =2. Поскольку a>0, парабола откроется «вверх».
- 2. y=-4(x-3)2+2
Это квадратное уравнение вершинной формы с квадратом переменной x, вершиной в упорядоченной паре (3,2) и a=-4. Потому что а3. x=3y2-2y-1
Это квадратное уравнение стандартной формы с квадратом переменной y и a=3. Поскольку a>0, парабола откроется «направо». 92\) член определяет направление раскрытия параболы, в этом случае, поскольку коэффициент равен 2 и уравнение параболы выражено в терминах y , то парабола раскрывается в восходящем направлении.
Скрыть ответ
Вопрос №4:
В каком направлении открывается график параболы \(x=-y²+y+1\)?
Вправо
Влево
Вверх
Вниз
Показать ответ
Ответ: 92–2х–5\)?
\((-1,-6)\)
\((-1,6)\)
\((1,-6)\)
\((1,6)\)
Показать ответ
Ответ:
Поскольку уравнение параболы не представлено в вершинной форме, мы можем либо построить уравнение, либо преобразовать его в вершинную форму, чтобы найти вершину. График уравнения показывает, что вершина — это точка, расположенная в \((1,-6)\).
Чтобы преобразовать уравнение в вершинную форму, мы сначала переместим константу в другую часть уравнения, а затем спросим, какой коэффициент даст нам идеальный квадрат? Не забывайте, вы не можете добавить что-то к одной стороне, не добавив при этом и к другой стороне.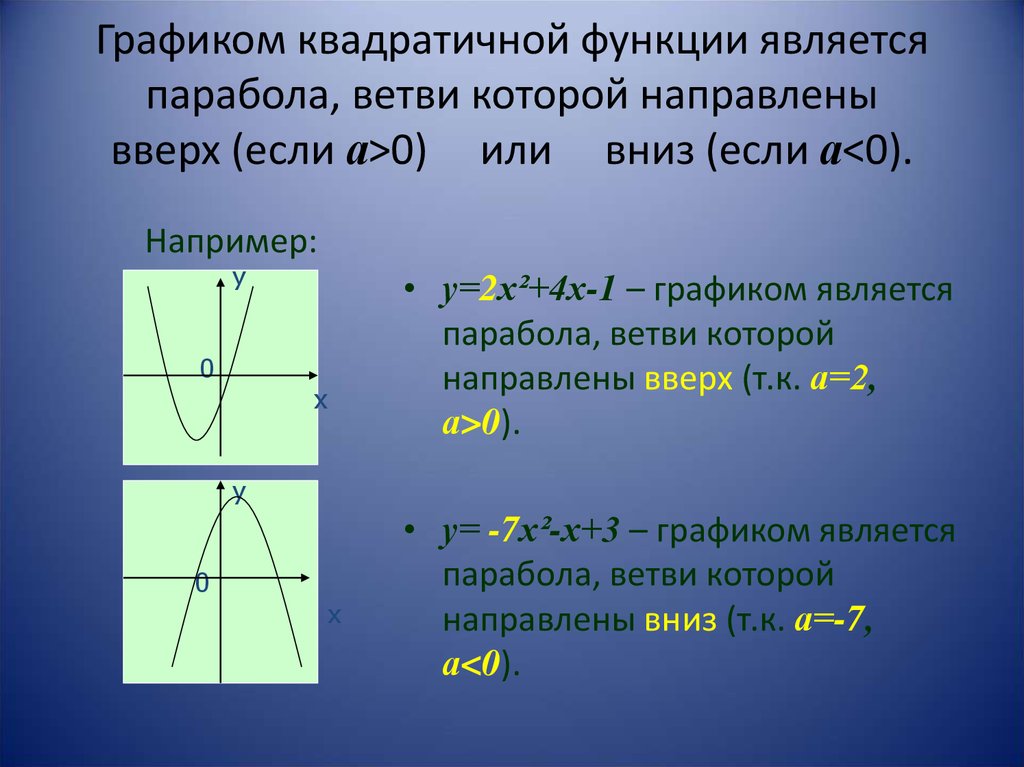


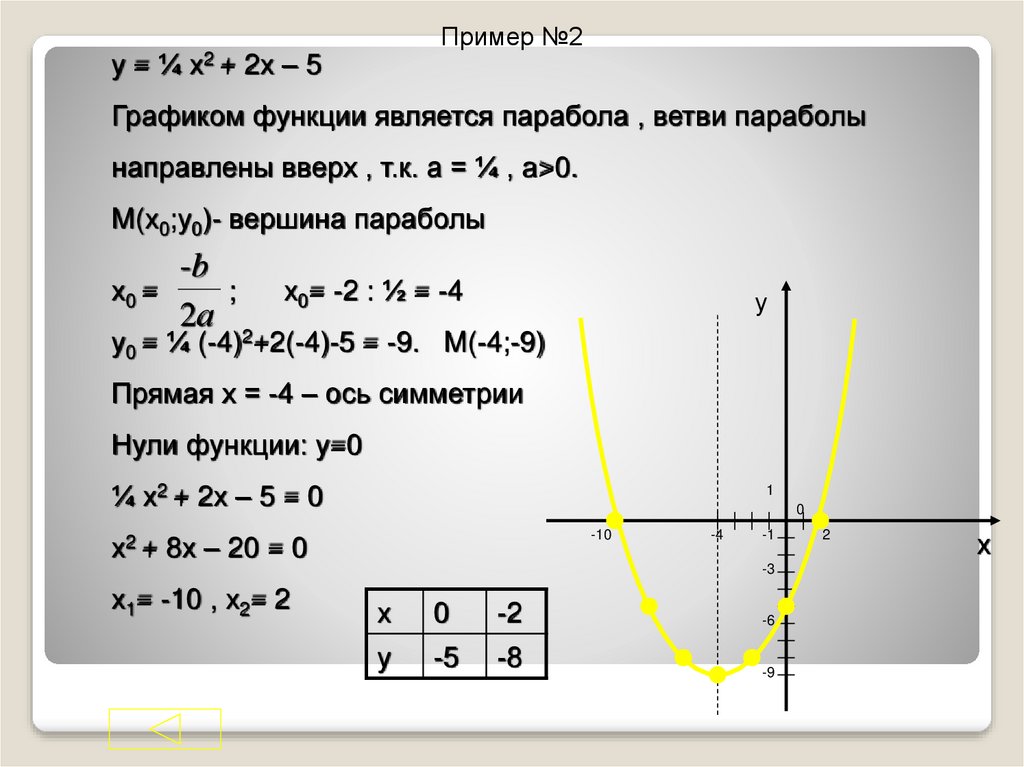 График квадратичной функции ( ) представляет собой параболу. Рассмотрим знаменитый случай:
График квадратичной функции ( ) представляет собой параболу. Рассмотрим знаменитый случай: Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно вместоподставить в уравнение . В случае с параболой проверка выглядит так: , значит, функция является четной.
Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно вместоподставить в уравнение . В случае с параболой проверка выглядит так: , значит, функция является четной.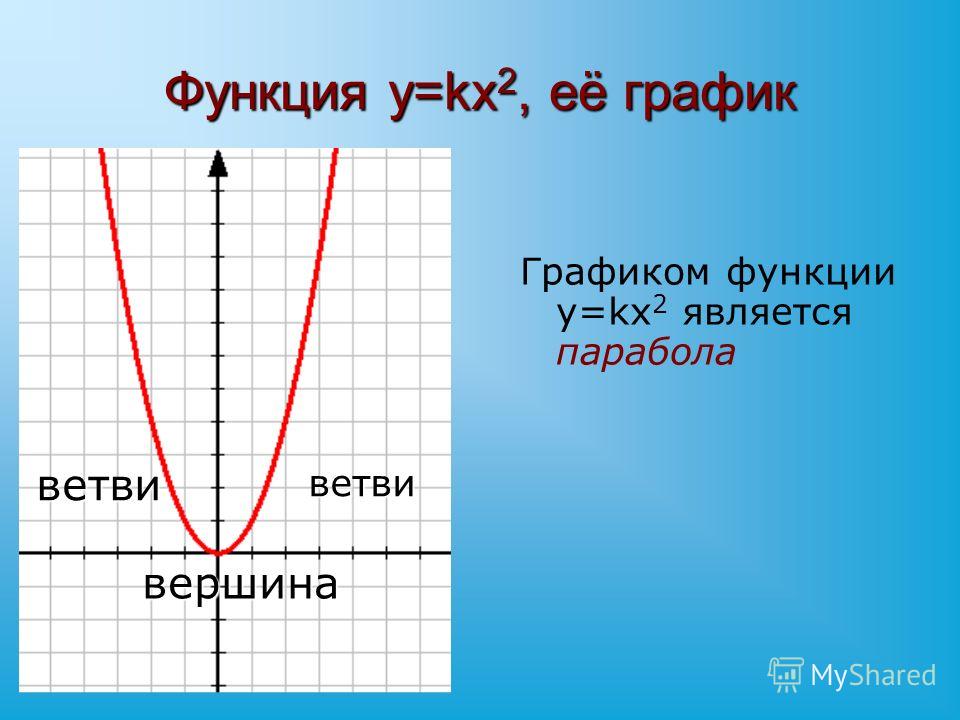 Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.
Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.