Таблицы сложения и умножения
Таблицы сложения и умноженияДвоичная система счисления
| 1+0=1 | 1*0=0 |
| 1+1=10 | 1*1=1 |
Троичная система счисления
| Таблица сложения | Таблица умножения | ||
| 1+1=2 | 1*1=1 | ||
| 1+2=10 | 2+2=11 | 1*2=2 | 2*2=11 |
Восьмеричная система счисления
| Таблица сложения | ||||||
| 1+1=2 | ||||||
| 1+2=3 | 2+2=4 | |||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=10 | |||
| 1+5=6 | 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | ||
| 1+6=7 | 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | |
| 1+7=10 | 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
| Таблица умножения | ||||||
| 1*1=2 | ||||||
| 1*2=2 | 2*2=4 | |||||
| 1*3=3 | 2*3=6 | 3*3=11 | ||||
| 1*4=4 | 2*4=10 | 3*4=14 | 4*4=20 | |||
| 1*5=5 | 2*5=12 | 3*5=17 | 4*5=24 | 5*5=31 | ||
| 1*6=6 | 2*6=14 | 3*6=22 | 4*6=30 | 5*6=36 | 6*6=44 | |
| 1*7=7 | 2*7=16 | 3*7=25 | 4*7=34 | 5*7=43 | 6*7=52 | 7*7=61 |
Шестнадцатеричная система счисления
| Таблица сложения | ||||||||||||||
| 1+1=2 | ||||||||||||||
| 1+2=3 | 2+2=4 | |||||||||||||
| 1+3=4 | 2+3=5 | 3+3=6 | ||||||||||||
| 1+4=5 | 2+4=6 | 3+4=7 | 4+4=8 | |||||||||||
| 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | 5+5=A | ||||||||||
| 1+6=7 | 2+6=8 | 3+6=9 | 4+6=A | 5+6=B | 6+6=C | |||||||||
| 1+7=8 | 2+7=9 | 3+7=A | 4+7=B | 5+7=C | 6+7=D | 7+7=E | ||||||||
| 1+8=9 | 2+8=A | 3+8=B | 4+8=C | 5+8=D | 6+8=E | 7+8=F | 8+8=10 | |||||||
| 1+9=A | 2+9=B | 3+9=C | 4+9=D | 5+9=E | 6+9=F | 7+9=10 | 8+9=11 | 9+9=12 | ||||||
| 1+A=B | 2+A=C | 3+A=D | 4+A=E | 5+A=F | 6+A=10 | 7+A=11 | 8+A=12 | 9+A=13 | A+A=14 | |||||
| 1+B=C | 2+B=D | 3+B=E | 4+B=F | 5+B=10 | 6+B=11 | 7+B=12 | 8+B=13 | 9+B=14 | A+B=15 | B+B=16 | ||||
| 1+C=D | 2+C=E | 3+C=F | 4+C=10 | 5+C=11 | 6+C=12 | 7+C=13 | 8+C=14 | 9+C=15 | A+C=16 | B+C=17 | C+C=18 | |||
| 1+D=E | 2+D=F | 3+D=10 | 4+D=11 | 5+D=12 | 6+D=13 | 7+D=14 | 8+D=15 | 9+D=16 | A+D=17 | B+D=18 | C+D=19 | D+D=1A | ||
| 1+E=F | 2+E=10 | 3+E=11 | 4+E=12 | 5+E=13 | 6+E=14 | 7+E=15 | 8+E=16 | 9+E=17 | A+E=18 | B+E=19 | C+E=1A | D+E=1B | E+E=1C | |
| 1+F=10 | 2+F=11 | 3+F=12 | 4+F=13 | 5+F=14 | 6+F=15 | 7+F=16 | 8+F=17 | 9+F=18 | A+F=19 | B+F=1A | C+F=1B | D+F=1C | E+F=1D | F+F=1E |
| Таблица умножения | ||||||||||||||
| 1*1=1 | ||||||||||||||
| 1*2=2 | 2*2=4 | |||||||||||||
| 1*3=3 | 2*3=6 | 3*3=9 | ||||||||||||
| 1*4=4 | 2*4=8 | 3*4=C | 4*4=10 | |||||||||||
| 1*5=5 | 2*5=A | 3*5=F | 4*5=14 | 5*5=19 | ||||||||||
| 1*6=6 | 2*6=C | 3*6=12 | 4*6=18 | 5*6=1E | 6*6=24 | |||||||||
| 1*7=7 | 2*7=E | 3*7=15 | 4*7=1C | 5*7=23 | 6*7=2A | 7*7=31 | ||||||||
| 1*8=8 | 2*8=10 | 3*8=18 | 4*8=20 | 5*8=28 | 6*8=30 | 7*8=38 | 8*8=40 | |||||||
| 1*9=9 | 2*9=12 | 3*9=1B | 4*9=24 | 5*9=2D | 6*9=36 | 7*9=3F | 8*9=48 | 9*9=51 | ||||||
| 1*A=A | 2*A=14 | 3*A=1E | 4*A=28 | 5*A=32 | 6*A=3C | 7*A=46 | 8*A=50 | 9*A=5A | A*A=64 | |||||
| 1*B=B | 2*B=16 | 3*B=21 | 4*B=2C | 5*B=37 | 6*B=42 | 7*B=4D | 8*B=58 | 9*B=63 | A*B=6E | B*B=79 | ||||
| 1*C=C | 2*C=18 | 3*C=24 | 4*C=30 | 5*C=3C | 6*C=48 | 7*C=54 | 8*C=60 | 9*C=6C | A*C=78 | B*C=84 | C*C=90 | |||
| 1*D=D | 2*D=1A | 3*D=27 | 4*D=34 | 5*D=41 | 6*D=4E | 7*D=5B | 8*D=68 | 9*D=75 | A*D=82 | B*D=8F | C*D=9C | D*D=A9 | ||
| 1*E=E | 2*E=1C | 3*E=2A | 4*E=38 | 5*E=46 | 6*E=54 | 7*E=62 | 8*E=70 | 9*E=7E | A*E=8C | B*E=9A | C*E=A8 | D*E=B6 | E*E=C4 | |
| 1*F=F | 2*F=1E | 3*F=2D | 4*F=3C | 5*F=4B | 6*F=5A | 7*F=69 | 8*F=78 | 9*F=87 | A*F=96 | B*F=A5 | C*F=B4 | D*F=C3 | E*F=D2 | F*F=E1 |
Задачи
Контрольная работа
К оглавлению
Таблицы сложения, вычитания, умножения, деления
Таблицы сложения, вычитания, умножения, деления
Сложение, вычитание, умножение и деление относятся к математическим действиям, точнее, к арифметическим действиям. Таблица сложения, таблица вычитания, таблица умножения и таблица деления наглядно демонстрируют результаты этих математических действий.
Таблица сложения, таблица вычитания, таблица умножения и таблица деления наглядно демонстрируют результаты этих математических действий.
При сложении чисел получается новое число. Числа, которые складываются, называются «слагаемые», результат сложения называется «сумма». Обозначают сложение чисел знаком «плюс» +. При сложении сумма всегда больше любого из слагаемых. Результаты сложения можно записать в виде таблицы сложения.
Математическим действием, обратным сложению, является вычитание. Вычитание также называют отниманием чисел. Число, из которого вычитают, называется «уменьшаемое». Число, которое вычитают, называется «вычитаемое». Результат вычитания называется «разность». Обозначают вычитание чисел знаком «минус» -. При вычитании уменьшаемое всегда больше разности. Для проверки правильности полученного результата при вычитании нужно сложить разность и вычитаемое. В результате сложения должно получиться уменьшаемое. Результаты вычитания можно записать в виде таблицы вычитания.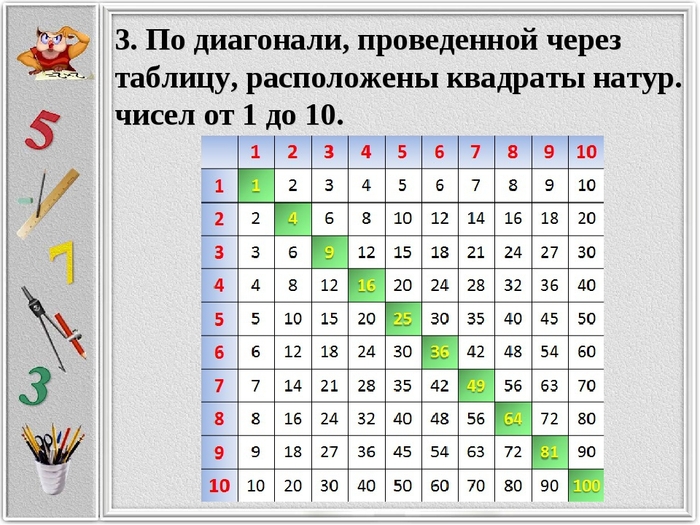 Эта таблица не является арифметической таблицей вычитания, поскольку в ней представлены отрицательные числа. Отрицательные числа не являются натуральными числами и изучаются алгеброй, а не арифметикой. Перед отрицательными числами ставится знак минус.
Эта таблица не является арифметической таблицей вычитания, поскольку в ней представлены отрицательные числа. Отрицательные числа не являются натуральными числами и изучаются алгеброй, а не арифметикой. Перед отрицательными числами ставится знак минус.
Числа, которые умножаются, называются «сомножители», результат умножения называется «произведение». Обозначают умножение чисел знаком «умножение» х. При умножении положительных чисел произведение всегда положительное и больше любого из сомножителей. При умножении положительного числа на отрицательное результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При умножении двух отрицательных чисел результат получается положительным – минус на минус дает плюс. Результаты умножения можно записать в виде таблицы умножения.
При умножении двух отрицательных чисел результат получается положительным – минус на минус дает плюс. Результаты умножения можно записать в виде таблицы умножения.
Математическим действием, обратным умножению, является деление. Иногда при обозначении деления употребляется выражение «частное двух чисел». Обозначают деление знаком «деление» : или дробной чертой. Число, которое делится, называется «делимое». Если число записывается в виде дроби, делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делитель». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частное». При делении положительных чисел частное всегда положительно. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Результаты деления можно записать в виде таблицы деления. Таблицу деления можно представить правильными дробями или десятичными дробями.
Результаты деления можно записать в виде таблицы деления. Таблицу деления можно представить правильными дробями или десятичными дробями.
Немного от себя.
Иметь калькулятор — это хорошо, но знать таблицу умножения — это выгодно! Тогда в любой ситуации продавцам будет гораздо труднее вас обсчитывать. «Пять у два — пятнадцать, плюс двенадцать — сорок семь, а всего с вас семьдесят!» — бойко лопочет продавщица, клацая по клавишам калькулятора. Я тупо смотрю на приготовленные три десятки в руках и прикидываю, могли ли так резко подскочить цены на товары. «А почём же у вас …?» — удивленно спрашиваю я. «Ой, я, наверное, ошиблась…» — продавщица снова клацает по калькулятору, берет у меня приготовленную сумму и дает мне сдачи.
В помощь посетителям добавлю маленькую рубрику вопрос-ответ. Все вопросы взяты из поисковых запросов посетителей этого сайта, ответы на вопросы — мои.
Как Петр 1 называл сложение, вычитание, умножение и деление? — Петр 1 называл их адиция (по-английски сложение будет addition), субстракция (в английском языке пишется substraction и переводится как фундамент, основание; вычитание в английском языке пишется deduction) мультипликация (на английском языке multiplication означает умножение) и дивизия (по-английски деление будет division; моё любимое «деление на ноль» будет division by zero). Так было сказано в одной из книг о Петре 1, что он должен был знать адицию, субстракцию, мультипликацию и дивизию. То ли кто-то что-то напутал (в смысле спутал основы знаний с банальным вычитанием), то ли царь Петр не шибко вникал в то, что он говорил. Оно и понятно, это подданным нельзя ошибаться, а царям — всё можно.
Умножение и деление на 1 — при умножении или делении числа на единицу это число не изменяется. Например, восемнадцать умноженное (или деленное) на один равняется восемнадцать. Если отрицательное число умножить или разделить на один, в результате получится точно такое же отрицательное число.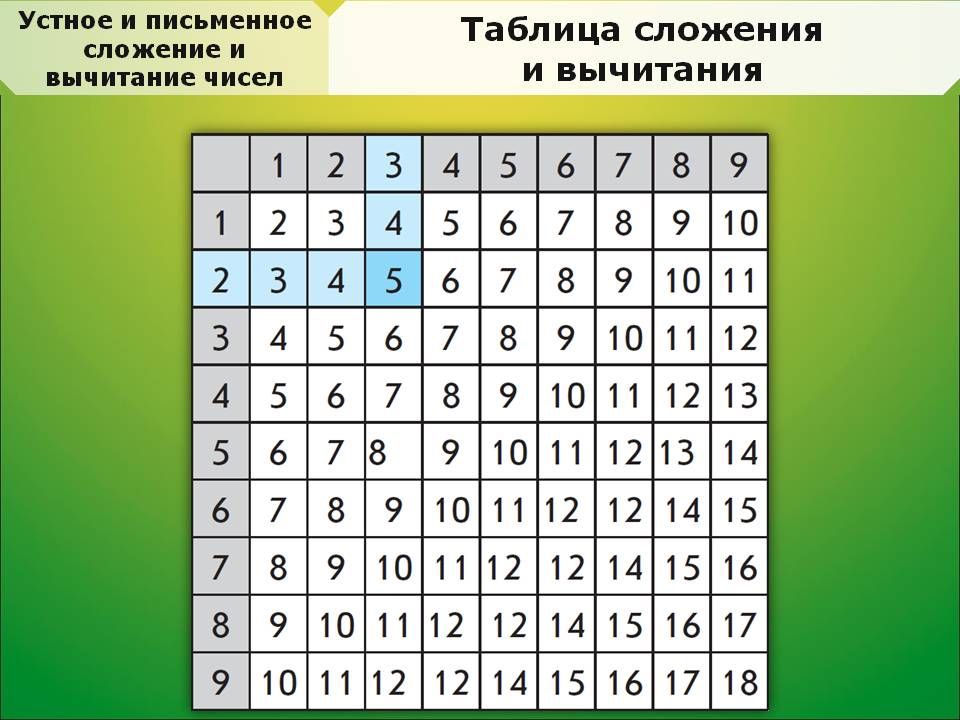
Как называются числа при сложении? — при сложении числа называются слагаемыми. Слагаемых может быть два или больше.
Частное — это деление или умножение? — частное — так называется результат деления.
Как делить отрицательные числа? — точно так же, как и положительные. Только не забывайте ставить знак минус перед результатом деления. Если отрицательное число разделить на положительное — в результате будет отрицательное число.
Минус умножить на минус — при умножении минуса на минус будет плюс.
Деление минус на минус — при делении минуса на минус будет плюс.
Деление отрицательных дробей, деление отрицательной дроби на отрицательную — при делении двух отрицательных дробей результат будет положительным. Результат деления может быть как дробным, так и целым числом.
Деление на минус, деление на отрицательное число — при делении положительного числа (плюс) в результате получается отрицательное число (минус), при делении отрицательного числа (минус) в результате будет положительное число (плюс).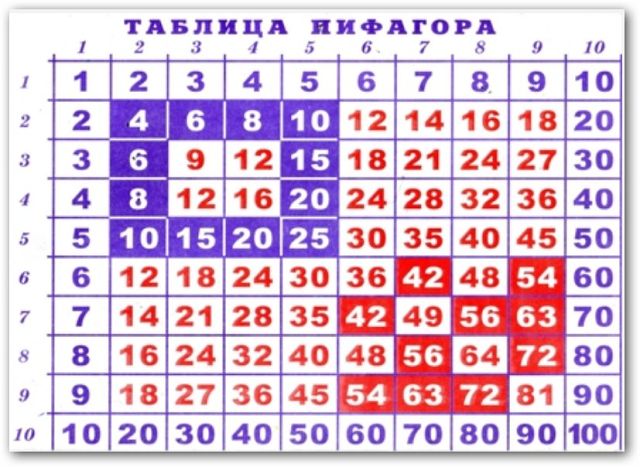
Деление положительного числа на отрицательное — дает в результате отрицательное число.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
19 ноября 2008 года — 28 февраля 2017 года.
© 2006 — 2017 Николай Хижняк. Все права защишены.
Таблица умножения | это… Что такое Таблица умножения?
Табли́ца умноже́ния, она же табли́ца Пифаго́ра — таблица, где строки и столбцы озаглавлены множителями, а в ячейках таблицы находится их произведение. Используется для обучения школьников умножению.
Содержание
|
Изучение
В своё время введение заучиваемой наизусть таблицы умножения революционизировало устный и письменный счёт. До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.
До этого использовались разные хитрые способы вычисления произведений однозначных чисел, которые сильно замедляли весь процесс и служили источником дополнительных ошибок.
В российских школах значения традиционно доходят до 10×10. В Великобритании до 12×12, что связано в том числе с единицами английской системой мер длины (1 фут = 12 дюймов) и денежного обращения (существовавшей до 1971 г.: 1 фунт стерлингов = 20 шиллингам, 1 шиллинг = 12 пенсам).
В Советском Союзе таблицу умножения обычно «задавали на лето» после 1-го класса, а закрепляли на занятиях во 2-м классе (в возрасте 8 лет). В российских школах чаще всего проходят во 2-м классе. По стандартам английского школьного образования таблица умножения должна быть выучена к возрасту 11 лет (планируется ужесточение требования до 9 лет).[1]
Обычное представление
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как найти результат по таблице умножения
Чтобы узнать результат произведения 4×8 по таблице умножения , нужно найти четвёрку в левом столбце и восьмёрку в верхней строке, провести от 4 горизонтальную линию и от 8 вертикальную. Клетка, на которой линии встречаются, является произведением (в данном случае 32).
Клетка, на которой линии встречаются, является произведением (в данном случае 32).
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
Применение
Помимо широко известного применения классической таблицы умножения для выработки практических навыков умножения натуральных чисел, её можно использовать в некоторых математических доказательствах, например, при выводе формулы суммы кубов натуральных чисел или получении подобного выражения для суммы квадратов[2].
Обобщения
Наряду с таблицей умножения, в некоторых случаях бывают удобны таблицы сложения.
Таблица Кэли
Таблица Кэли — в абстрактной алгебре, таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Названа в честь английского математика Артура Кэли. Имеет важное значение в дискретной математике, в частности, в теории групп, в которой в качестве операций рассматриваются умножение и сложение. Таблица позволяет определить, является ли группа абелевой, найти центр группы и обратные элементы по отношению к другим элементам в этой группе.
В высшей алгебре таблицы Кэли могут также использоваться для определения бинарных операций в полях, кольцах и других алгебраических структурах. Также они удобны при проведении действий в данных структурах.
Модулярная арифметика
Все остатки от деления на натуральное число образуют кольцо, а от деления на простое число — поле. Это иллюстрируется таблицами умножения:
Таблица умножения в кольце вычетов по модулю 8
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 0 | 2 | 4 | 6 |
| 3 | 0 | 3 | 6 | 1 | 4 | 7 | 2 | 5 |
| 4 | 0 | 4 | 0 | 4 | 0 | 4 | 0 | 4 |
| 5 | 0 | 5 | 2 | 7 | 4 | 1 | 6 | 3 |
| 6 | 0 | 6 | 4 | 2 | 0 | 6 | 4 | 2 |
| 7 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Таблица умножения в поле вычетов по модулю 5
| × | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
См.
 также
также- Умножение
- Деление (математика)
- Сложение
- Вычитание
Примечания
- ↑ Children must learn times tables by age nine… // Daily Mail, 17.12.2011
- ↑ Роу С. Геометрические упражнения с куском бумаги. — 2-е изд. — Одесса: Матезис, 1923. — С. 68—72.
Ссылки
- Способ Пифагора
Таблицы сложения и умножения
Таблицы сложения и умножения| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 0 | |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 0 | 1 1 | |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 0 | 1 1 | 1 2 | |
| 4 | 5 | 6 | 7 | 8 | 9 | 1 0 | 1 1 | 1 2 | 1 3 | |
| 5 | 6 | 7 | 8 | 9 | 1 0 | 1 1 | 1 2 | 1 3 | 1 4 | |
| 6 | 7 | 8 | 9 | 1 0 | 1 1 | 1 2 | 1 3 | 1 4 | 1 5 | |
| 7 | 8 | 9 | 1 0 | 1 1 | 1 2 | 1 3 | 1 4 | 1 5 | 1 6 | |
| 8 | 9 | 1 0 | 1 1 | 1 2 | 1 3 | 1 4 | 1 5 | 1 6 | 1 7 | |
| 9 | 1 0 | 1 1 | 1 2 | 1 3 | 1 4 | 1 5 | 1 6 | 1 7 | 1 8 |
. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 2 | 2 | 4 | 6 | 8 | 1 0 | 1 2 | 1 4 | 1 6 | 1 8 | |
| 3 | 3 | 6 | 9 | 1 2 | 1 5 | 1 8 | 2 1 | 2 4 | 2 7 | |
| 4 | 4 | 8 | 1 2 | 1 6 | 2 0 | 2 4 | 2 8 | 3 2 | 3 6 | |
| 5 | 5 | 1 0 | 1 5 | 2 0 | 2 5 | 3 0 | 3 5 | 4 0 | 4 5 | |
| 6 | 6 | 1 2 | 1 8 | 2 4 | 3 0 | 3 6 | 4 2 | 4 8 | 5 4 | |
| 7 | 7 | 1 4 | 2 1 | 2 8 | 3 5 | 4 2 | 4 9 | 5 6 | 6 3 | |
| 8 | 8 | 1 6 | 2 4 | 3 2 | 4 0 | 4 8 | 5 6 | 6 4 | 7 2 | |
| 9 | 9 | 1 8 | 2 7 | 3 6 | 4 5 | 5 4 | 6 3 | 7 2 | 8 1 |
Творческий проект для классов К-8
|
Урок Планы
- 1869 Задача вступительного экзамена MIT
- Проблема «3N+1»
- Корзина, полная яиц
- Геометрическое доказательство теоремы Пифагора «вырезать и вставить»
- Проблема для Молодые и старые ученики
- Проблема от русского Олимпиада по математике
- Доказательство Пифагора теорема с использованием подобных треугольников
- Головоломка с целыми числами от одного до шестнадцати
- Головоломка с числом 1089
- «Струнный рисунок», который мы можем нарисовать: ромб внутри шестиугольника
- Трехсторонний кот для рисования
- Путешественник на сетке 6 на 6
- Дополнительная плата
- Прибавление в детском саду и первый класс
- Арифметический вундеркинд из 1899 года
- Старый купец и его четверо детей
- Древний узел
- Анимации на TI
- Углы треугольника: геометрическое свойство посредством складывания бумаги
- Районы и границы
- Площадь и Периметр
- Арифметика с манипуляциями
- Средний балл за тест
- Мяч в коробке
- Банан
- Бочки, Бочки и другие фигурные контейнеры
- Большие числа АКА Зерна риса на шахматная доска
- Блочные дома
- Сборка собачьей будки в масштабе
- Построение ящика со скелетом в соответствии с к Спецификации
- Свечи
- Корзины для конфет
- Емкость
- Наутилус с камерой
- Проверка, является ли число простым номер
- Коробка с китайским календарем
- Аккорды по кругу
- Круг, квадрат и треугольник
- Часы и время
- Монеты
- Раскрашивание линий в шестиугольнике
- Красочный Треугольники
- Конгруэнтность Треугольники
- Подсчет
- Счетная доска для детей учащиеся
- Счет до 100
- Бумага для биговки По кривым
- кубики
- Куб со срезанным краем
- Кухня полоски
- Вырезание прямоугольника
- Разрезание треугольника
- Разрезание треугольника на две части куски равной площади и равного периметра
- Разрезание равностороннего треугольника
- Резка многогранников
- Цилиндр и конус с одинаковой высотой и диаметром основания
- Вывод формулы для площадь треугольника
- Диагональ площади
- Разделение квадрата
- Деление с остатком на ТИ-108: Два экземпляра
- Собаки, кошки и мыши
- Точка за точкой
- Удвоение и деление пополам
- Рисунок прямоугольник
- Рисование простой фигуры из устных указаний
- Рисование треугольников
- Легкие квадраты
- Яичная дилемма (Часть 1)
- Возведение в степень
- Факторинг
- фантазии Конверты
- Нахождение дроби между двумя дроби
- Пятиконечный 3D звезда
- Перелистывание монеты
- Сложенный бумажный цветок С шестью лепестками
- Четыре жука
- Четыре карты
- Четыре кубика
- От одного миллиарда до нуля
- От одного до одного триллиона
- Игра кругов и звезд
- Игра в десятки
- Гигантская энчилада
- Шляпа для Хэллоуина
- Орел или решка?
- Шестиугольная головоломка
- Праздник Орнамент
- Лошадь на продажу
- Как работает Калькулятор Вычислить квадратный корень из числа?
- Сколько пентамино?
- Сколько клеток на шахматной доске?
- Сколько треугольников? (Части 1 и 2)
- Сколько треугольников в этом треугольнике?
- Как измерить угол без транспортира
- Как преобразовать прямоугольник в другой прямоугольник
- Гиперболы и Эллипсы
- Я могу угадать твой возраст!
- Я могу угадать ваш возраст и номер дома!
- Невозможный объект
- Вписанный треугольник
- Проценты
- Введение в измерения (первый класс)
- Неправильные многоугольники
- Юлекурв АКА Валентайн Корзина
- Прыжок: игра в пасьянс с десятью жетонами
- Воздушные змеи
- Умножение решетки
- Дырявая крыша
- Ушастые твари
- Волшебные бобы
- Волшебный складной кубик
- Магический квадрат
- Создание животных Резка полигональных пазлов
- Создание блоков из четырех Кубики
- Изготовление коробок
- Изготовление эвольвенты
- Лабиринт
- Мини-слот-машина
- Луны
- Больше задач с точками
- Больше старых задач со словами
- Умножения «Готово по Адаму Рису»
- Натан подбрасывает монету 20 раз
- Игра с числами Кости
- Головоломка с числами
- Воля старого пастуха
- Олимпийские кольца
- Одна треть
- Покраска домов (и другие «рабочие» задачи)
- Парадокс средних
- Разделение квадрата
- Пентагон Пазлы
- Алгебра телефонных номеров
- Копилка
- Игра с фигурами
- Powerball 55
- Красивая подарочная коробка
- Простые числа: сито Эратосфена
- Свойства коробки
- Тыквы
- Пазл с камешками
- Пирамида на четверти
- Пирамида кубов
- Пирамида из мрамора
- Четырехугольники
- Прямоугольники
- Правильные многоугольники с равными Районы
- Связанные проблемы
- Прямоугольный треугольник
- Последовательности составных номера: конкурс
- Фигуры цифр
- Формы чисел с использованием треугольники
- Делиться хлебом
- Овца: Старая головоломка
- Шесть пирамид
- Шестнадцать Квадратные дюймы
- Печать Соломона
- Игра «Сортировка»
- Спираль (марки К-4)
- Спираль (5-8 классы)
- Спираль Феодора на Калькуляторе ТИ-83/84
- Квадратные и кубические единицы
- Квадрат в треугольнике
- Соломенные многогранники
- Алгоритм вычитания
- Вычитание со счетчиками
- Сумма всех 100 чисел в таблице умножения
- Сумма первых N целых чисел
- Сумма двух квадратов
- Выживший на шестиугольном острове
- Татами
- Чайные коробки
- Преобразование температуры
- Мозаика круга
- Задача о лестнице и ящике
- Сыр «Смеющаяся корова» Клиновые контейнеры
- Практическая ценность Доказательства
- Рейнберд Зуни
- Три четверти
- Круг из трех частей Пазл
- Бросание одного кубика
- Треугольник в квадрат: A шарнирный разборный
- Превращение прямоугольника в квадрат путем вскрытия
- Двенадцать простых фигур
- Двадцать четыре кубика
- Две старые проблемы
- Два брата пастуха
- Понимание Длинная дивизия
- Необычный Контейнеры
- Что дальше?
- Что это за прямоугольник?
- Инь Ян
Отрыв
| Примечания | Кредиты
| Альбом | НМСУ
Курсы для учителей | Контакт
США
последнее изменение:
2 февраля 2022 г.
разговор по таблице умножения
разговор по таблице умножения| РАЗГОВОР ПО ТАБЛИЦЕ УМНОЖЕНИЯ |
Что такое умножение?
Умножение на самом деле повторяющееся сложение .
Итак, 4 раза 3 говорит нам, что к нужно добавить четыре тройки , а 2 раза 5 говорит нам, что к нужно добавить две пятерки .
4 × 3 = 3 + 3 + 3 + 3
2 × 5 = 5 + 5
И, как сложение, умножение равно коммутативный — порядок не имеет значения. Произведение 7 × 3 точно такое же, как произведение 3 × 7. Мы можем умножать в прямом или обратном порядке и получать тот же ответ.
Однако нахождение сумм, а не произведений, не очень эффективно, когда мы хотим 36 умножить на 9.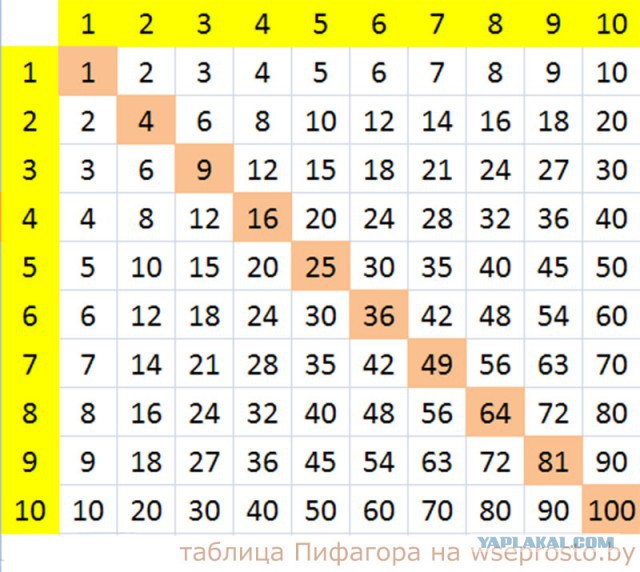 Прежде всего, нам пришлось бы перевернуть нашу бумагу боком, чтобы написать тридцать шесть девяток и все эти знаки плюс, тогда нам потребовалось бы долго искать сумму. Итак, вместо того, чтобы усложнять себе жизнь, мы учим таблицу умножения и учим ее хорошо.
Прежде всего, нам пришлось бы перевернуть нашу бумагу боком, чтобы написать тридцать шесть девяток и все эти знаки плюс, тогда нам потребовалось бы долго искать сумму. Итак, вместо того, чтобы усложнять себе жизнь, мы учим таблицу умножения и учим ее хорошо.
Таблица умножения
Чтобы найти произведение любых двух чисел в таблице, найдите ячейку или квадрат , где строка одного числа пересекается со столбцом другого числа. Таблица показывает нам, что 4 × 7 = 28 , потому что мы видим 28 в ячейке, где 4-я строка пересекает 7-й столбец .
ТАБЛИЦА УМНОЖЕНИЯ
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Вспомогательные устройства памяти для умножения
С тех пор, как люди начали изучать математику, ученики жаловались, когда приходило время запоминать таблицы умножения от 1 до 9. Итак, давайте посмотрим на таблицу произведений, чтобы найти информацию, которая поможет нам научиться умножать без особых страданий и жалоб. .
Итак, давайте посмотрим на таблицу произведений, чтобы найти информацию, которая поможет нам научиться умножать без особых страданий и жалоб. .
1. Есть НЕЧЕТНЫЕ и ЧЕТНЫЕ номера.
ЧЕТНОЕ × ЛЮБОЕ ЧИСЛО равно ЧЕТНОМУ .
НЕЧЕТНЫЙ × НЕЧЕТНЫЙ является НЕЧЕТНЫМ
Все продукты под номерами 2, 4, 6 и 8 в таблице являются четными . Кроме того, продукты под номером 8 — это double продукты под номером 4 , которые являются double продуктами под номером 2 . Итак, если мы выучим таблицу умножения на 2, мы сможем вычислить числа 4 и 8, удвоив (умножив на 2).
ТАБЛИЦА УМНОЖЕНИЯ
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
2. Если мы знаем таблицу умножения на 3, мы знаем числа 6 и 9.
Если мы знаем таблицу умножения на 3, мы знаем числа 6 и 9.
В соответствии с 6 продукты представляют собой двойных троек , а до 9 они тройных (3 раза) t он 3 .
3. Теперь 5 и 7 — оба простые числа.
До 5 каждое нечетное кратное оканчивается на 5, каждое четное на 0.
Поскольку мы знаем таблицы умножения на 2 и умножения на 3, мы знаем таблицы умножения на 5 и 7.
Распределительное свойство говорит, что мы можем распределить умножение следующим образом:
3 × 5 = 3 × ( 2 + 3 ) = (3 × 2 ) + (3 × 3 ).
Итак, , чтобы найти 5-кратные произведения ,
мы добавляем продуктов в 2- и 3-кратные таблицы .
4 × 5 = 4 × (2 + 3) = 8 + 12 = 20
и
чтобы найти 7-кратные продукты ,
мы добавляем продукты в т он 3-х и 4-х кратные столы .
5 × 7 = 5 × (3 + 4) = 15 + 20 = 35
.
Ярлыки умножения
1) Распределить множитель
Поскольку умножение представляет собой повторяющееся сложение, оно обладает теми же свойствами, что и сложение. Это означает, что оба коммутативных и дистрибутивных свойств применимы к . Итак, мы можем умножить в прямом или обратном направлении и получить тот же результат, и мы можем распределить или раздать множитель в виде суммы. Мы можем использовать этот подход, когда мы умножаем числа любого размера на единицу или даже двухзначное число.
Примеры:
1) 3 × 207 = 3 × ( 200 + 7 ) = (3 × 200 ) + (3 × 7 ) = 621
2) 7 х 53 = 7 х ( 50 + 3 ) = (7 х 50 ) + (7 х 3 ) = 350 + 21 = 371
3) 15 х 21 = 15 х ( 20 + 1 ) = (15 х 20 ) + (15 х 1 ) = 300 + 15 = 315
2) Подход к продукту колонки
Когда мы умножаем на 1-значный номер , мы можем использовать подход, подобный подходу суммы столбцов к сложению, который называется подходом Column Product Approach .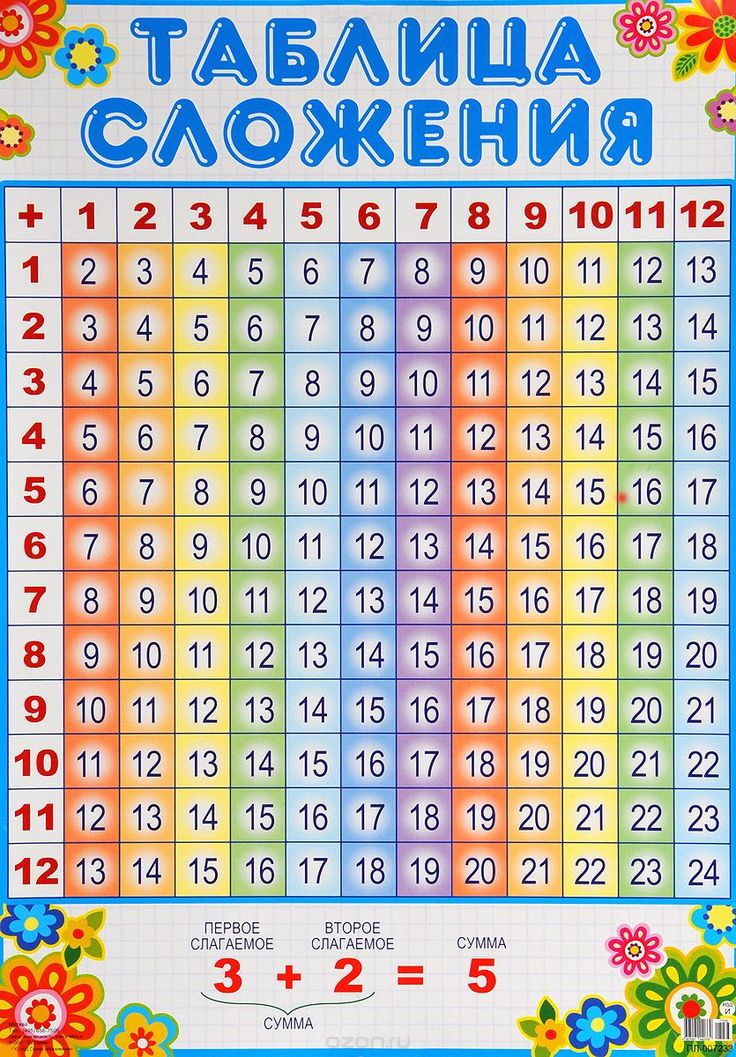 Мы записываем произведение множителя с в каждом столбце — правильно выровняли — и затем мы добавляем к ним . При таком подходе лучше всего начать с самого большого столбца значений слева, чтобы мы могли правильно выстроить места.
Мы записываем произведение множителя с в каждом столбце — правильно выровняли — и затем мы добавляем к ним . При таком подходе лучше всего начать с самого большого столбца значений слева, чтобы мы могли правильно выстроить места.
Пример:
.
Теперь возьмите карандаш, ластик и блокнот, перепишите вопросы,
выполните практические упражнения, затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем повторите попытку.
.
Практическое упражнение
1) Используйте метод распределительного свойства для умножения:
| а) | б) | в) | г) |
( таблица умножения )
2) Используйте метод колоночного произведения , чтобы умножить:
| а) | б) | в) | г) |
.