Ветвь параболы функция ее свойства и график: Свойства квадратичной функции y = ax² — урок. Алгебра, 8 класс.

Конспект урока « График и свойства функции у =ах2″

Конспект  урока  «График и свойства функции y = ax²»

 

Цель урока:

1.    Формирование знаний обучающихся о графике и свойствах функции у = ах^2.

2.    Формирование представления о влиянии коэффициента а на свойство и вид графика у = ах².

3.     Формирование навыков построения графиков данной функции.

4.       Воспитание сознательного отношения к учебному труду. Образовательные задачи:

1.    Актуализировать знания по теме: «Функция у = х²«

2.     Изучить свойство функции у = ах², при а > 0, а < 0.

3.   Рассмотреть влияние коэффициента а на свойства и вид графика у = ах². Развивающие задачи:

1. Развивать логическое мышление через построение графиков функций. Воспитательные задачи:

1. Отрабатывать навыки аккуратности и точности построения графиков. Формы работы на уроке:

·        коллективная;

·        индивидуальная;

·        фронтальная.

Методы обучения:

·        словесный;

·        наглядный;

·        практический.

Ход урока:

I.   Организационный момент.

II.  Постановка цели урока:

Мы продолжаем изучение темы «Квадратичная функция». И сегодня мы должны с вами повторить все, что мы знаем о функции у = х² а затем рассмотрим новую функцию у = ах² ее свойства и график.

III.   Повторение:

(Актуализация знаний)

 Среди изображенных графиков функций найдите график функции у = х²

 

 

 

 

·        Как называется график данной функции?

·        Как называется точка пересечения графика функции с осью ординат?

·        Назовите основные свойства функции у = х².

(Приглашается 1 ученик к доске и работает с графиком функции у = х²).

Свойства функции у = х

2:

1.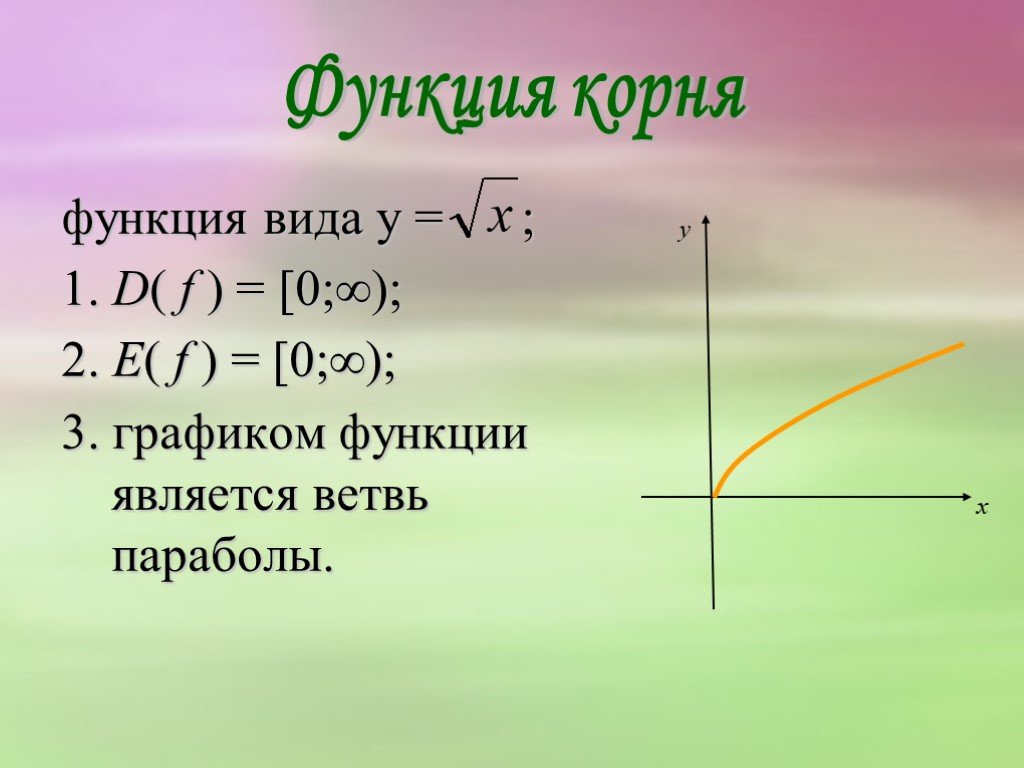      При х=0, у=0

При значении х=0, значение функции равно нулю.

2.     При х > 0; х< 0; у > 0.

При любом значении х, кроме нуля значение функции положительно.

3.     График функции у = х² симметричен относительно оси ординат. Ось ординат является осью симметрии параболы.

4.     Функция у = х² возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0.

·        При каких условиях функция возрастает?

·        При каких условиях функция убывает?

Возрастает: большему значению х соответствует большее значение у.

Убывает: большему значению х соответствует меньшее значение у.

·        Какие новые математические понятия вы узнали при изучении темы у = х²?

·        парабола;

·        ветвь параболы;

·        вершина параболы.

IV.                                                  Объяснение нового материала.

Итак, мы повторили свойства функции у = ах².

·        Открываем тетради, записываем число, тему урока «Свойства и график функции у = ах². «

1)    Рассмотрим график и свойства функции у = ах², когда а > 0. Для этого в одной системе координат построим графики функций:

у = х²

у = 2х²

у = х²

Для экономии времени у вас на рабочих листах №1 и здесь на координатной плоскости построен уже график функции у = х². Обучающиеся строят на рабочих листах графики функций у = 2х² и у = х².

Анализ построенных графиков позволяет сделать вывод:

1.     Графиками всех трех функций является парабола.

2.     Ветви парабол направлены вверх.

3.     Вершины парабол находятся в начале координат.

4.     Графики функций симметричны оси ОУ.

Выясним,  как  коэффициент а влияет на вид параболы в зависимости от коэффициента а.

Сравним две функции:

у = 2х²

у = х²

При одних и тех же значениях х, значение функции у = 2х² увеличивается в 2 раза, т. е. ординаты этой функции становятся больше в 2 раза. И наша парабола растягивается от оси ОХ вдоль оси ОУ.

 

А теперь сравним функции:

у = х²

у = х²

 

При одних и тех же значениях х, значение функции у = х² уменьшается в

2 раза, а значит ординаты этой функции становятся меньше в 2 раза. И наша парабола сжимается к оси ОХ вдоль оси ОУ и становится шире. Итак, если у функции у = ах² коэффициент а > 1 то происходит растяжение парабол от оси ОХ вдоль оси ОУ.

Если  коэффициент а < 1, то происходит сжатие парабол к оси ОХ вдоль оси ОУ. А теперь по графикам данных функций запишем свойства функции у = ах², при а > 0.

1.  х = 0; у = 0

При значении х = 0, значение функции равно 0.

2.   При х>0 и х<0, у>0. При любом значении х, кроме х = 0, функция принимает только положительные значения.

3.   График функции симметричен относительно оси ординат.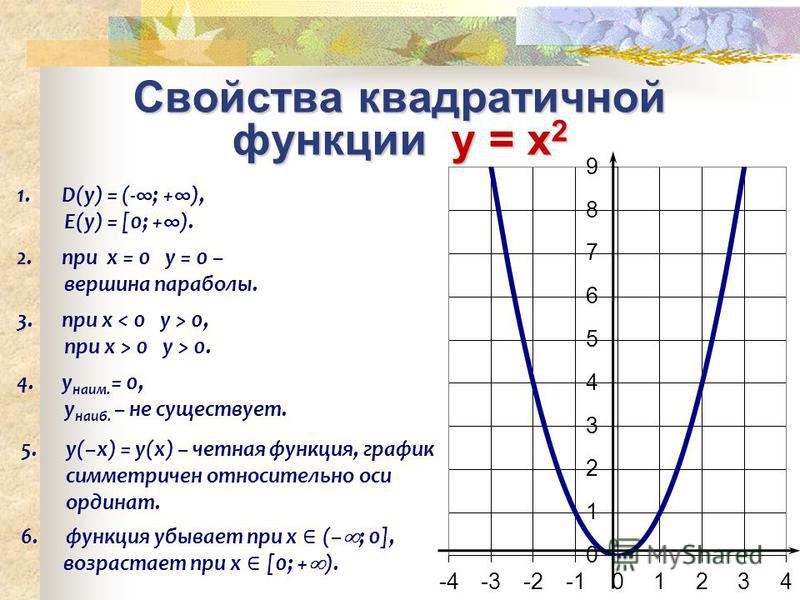 Ось ординат является осью симметрии.

4.   Функция  возрастает  на промежутке х ≥ 0 убывает на промежутке х ≤ 0.

Рассмотрим функцию у = ах,  когда  а < 0.

В одной системе координат построим графики функций:

у = -х²

у = -2х²

у = х²

После построения графиков делаем вывод: если а < 0, то

1)  Графиками этих функций является парабола.

2)  Ветви параболы направлены вниз.

3)  Вершина параболы находится в начале координат.

Рассмотрим свойства функции у = ах² при а < 0

1. При значении х = 0, значение функции равно 0.

2.  При любых значениях х, кроме х = 0, значение функции отрицательно. При х > 0 и х < 0, у < 0.

3.   Графики функций симметричны оси ОУ. ОУ — ось симметрии параболы.

4.   На промежутке х ≤ 0 функция возрастает, на промежутке х ≥ 0 функция убывает.

Выводы: мы рассматривали с вами функцию у = ах², при коэффициенте а > 0 и а < 0, еще раз проговорим свойства данной функции. Если коэффициент  а > 0, то

1.   Графиком данной функции является парабола, ветви которой направлены вверх.

2.    Вершина параболы находится в точке начала координат.

3.   График функции симметричен оси ординат, которая является осью симметрии параболы.

4.    Значение функции при любом значении х, кроме х = 0, положительно.

5.    Функция возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0. Если коэффициент  а < 0, то

1.Графиком функции является парабола ветви которой направлены вниз.

            2.Вершина параболы находится в точке начала координат.

3.График функции симметричен относительно оси ОУ. Ось ОУ является осью симметрии параболы.

Закрепление:

1. Определите направление ветвей параболы данных функций:

1.у = — 0,1х²   у = х²

   у = — 2,2 х²  у = 5,7 х²

2.На каком промежутке функция у = -5х² возрастает? (х ≤ 0)

3.На каком промежутке функция у = 7х² убывает? (х ≤ 0)

4. Что произойдет с графиком функции у = х², если коэффициент а увеличим в 5 раз (произойдет растяжение параболы от оси ОХ вдоль оси ОУ в 5 раз). 5.Что произойдет с графиком функции у = х

2, если коэффициент а уменьшить в 5 раз? (произойдет сжатие параболы к оси ОХ вдоль оси ОУ в 5 раз).

Диагностика знаний обучающихся. Работа по карточкам.

1.По графикам определить знак коэффициента а функции у = ах²

 Предлагается несколько видов графиков  функции у = ах², изображенных на таблицах.

Ответ:                                                                                  Ответ:

2.Определить направление ветвей парабол следующих функций:

а) у = -0,8х²                                               б) у = — 0,1х²

Ответ:                                                   Ответ:

3. а)  график функции  у = 4х²  получается                                    графика функции у = х²  от оси                             вдоль оси                           

 в                 раза.

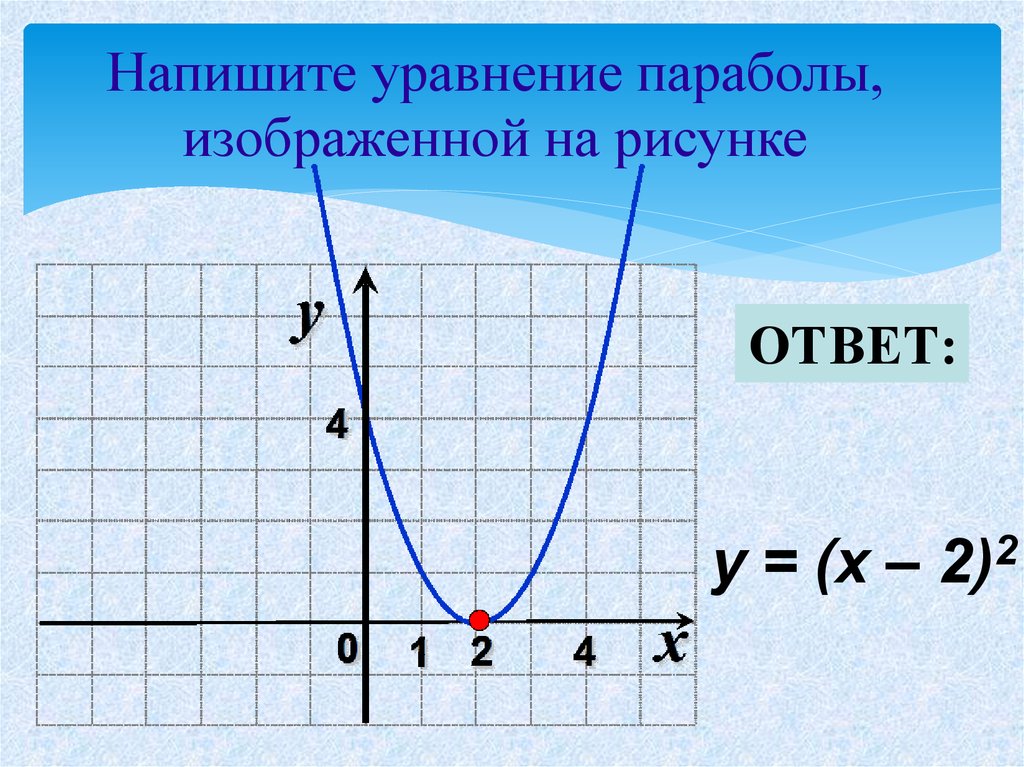
    б) график функции  у = х²  получается                                      графика функции у = х²  к оси                 вдоль оси                     в                 раза.

4. Функция у = -3х² возрастает на промежутке х                  .

5. Функция у = 1,2 х² убывает на промежутке х                   .

6. Какая из функций у = -0,1 х² и у = 0,1 х² возрастает на промежутке х≤0.

 

Ответ:

 

Критерии оценивания работы:

За 6 правильных ответов оценка «отлично».

За 5 или 4 правильных ответа оценка «хорошо».

За 3 правильных ответа оценка «удовлетворительно».

Ответы диагностики:

1.  а) а > 1 б) а < 1

2.   а) вниз б) вниз

3.а) растяжением от оси ОХ вдоль оси ОУ в 4 раза,

   б) сжатием к оси ОХ вдоль оси ОУ в 4 раза.

4.х ≤0

5.x ≤0

6.у = -0,1 х²

Для слабых обучающихся выдается алгоритм выполнения заданий диагностики.

1,2. Если ветви параболы направлены вверх, то а > 0.

       Если ветви параболы направлены вниз, то а < 0.

3. Если  а > 1, то парабола растягивается от оси ох вдоль оси оу  в а раз.         Если  а < 1, то парабола сжимается к оси ох вдоль оси  оу.

4.Если а < 0, то функция у = ах² возрастает при х ≤ 0.

5,6. Если а > 0, то функция у = ах² убывает при х ≤0.

После работы с карточками дети сверяют свои ответы с ответами на доске. Выставляют себе оценки и сдают работы.

VII. Итоги урока.

Сегодня мы рассмотрели с вами функцию у = ах²

,  ее свойства и график. Выяснили как коэффициент а влияет на свойства и график функции у = ах².

После изучения новой темы, МЫ ДОЛЖНЫ ЗНАТЬ:

·        Свойства графика функции у = ах², при а > 0 и а < 0.

·        Направление ветвей параболы в зависимости от коэффициента а.

·      Название графика функции.

МЫ ДОЛЖНЫ УМЕТЬ:

·        По графику функции определить знак коэффициента а.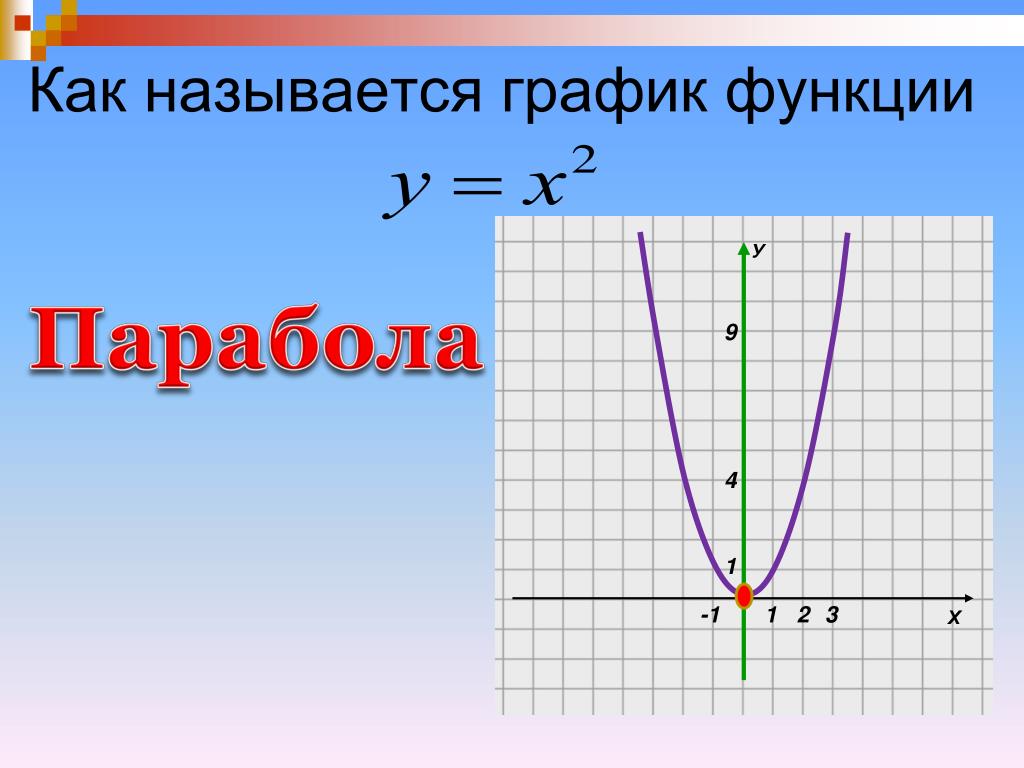 2, её график и свойства»

Определение:

Квадратичной называют функцию вида:

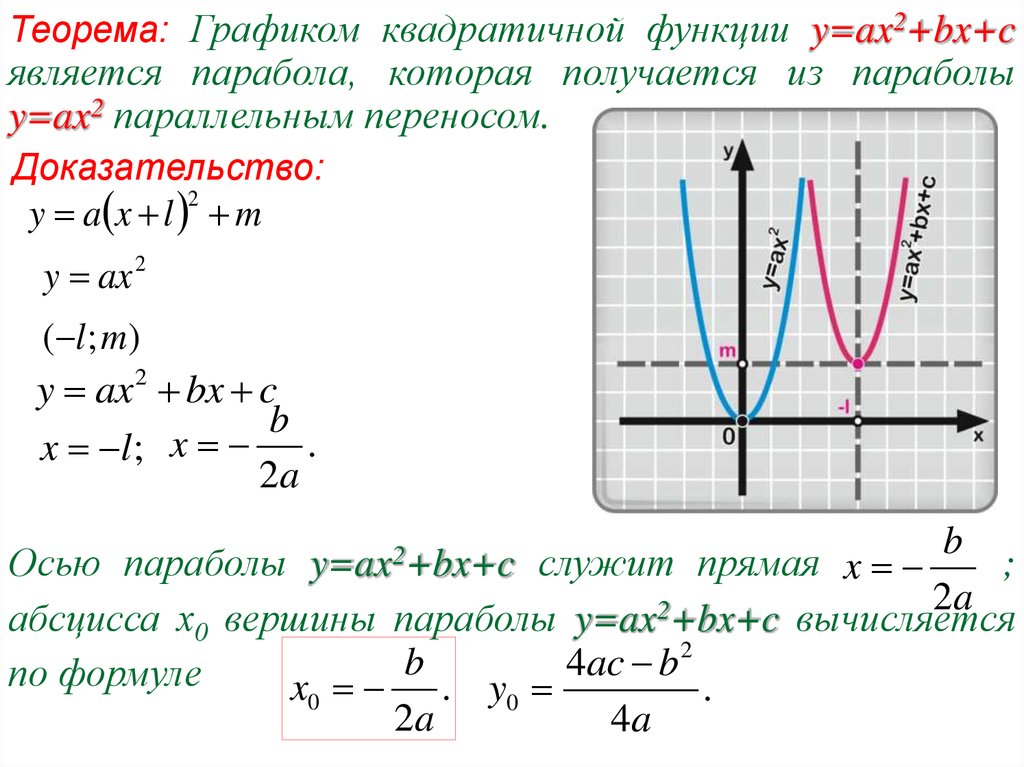
Графиком квадратичной функции является парабола. Она состоит из двух ветвей и имеет вершину.

Ветви могут быть направлены вверх:

Ветви могут быть направлены вниз:

Квадратичная функция имеет свои свойства. Поговорим о них. В своей вершине квадратичная функция сменяет своё поведение с убывания на возрастание и с возрастания на убывание. Понятно, что областью определения в обоих случаях будет множество всех действительных чисел. Если говорим о нулях функции, то мы имеем ввиду те значения, при которых функция у=0. Когда находят нули функции по графику, то ищут точки пересечения графика с осью х. Если же находят нули функции по уравнению, то значение функции принимают равное 0. Тем самым получаем квадратное уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно, график может иметь 2 точки пересечения с осью х, 1 точку пересечения с осью х или не пересекать её. Понятно, что нулями квадратичной функции являются корни соответствующего квадратного уравнения. По графику удобно находить промежутки знакопостоянства и промежутки монотонности функции.

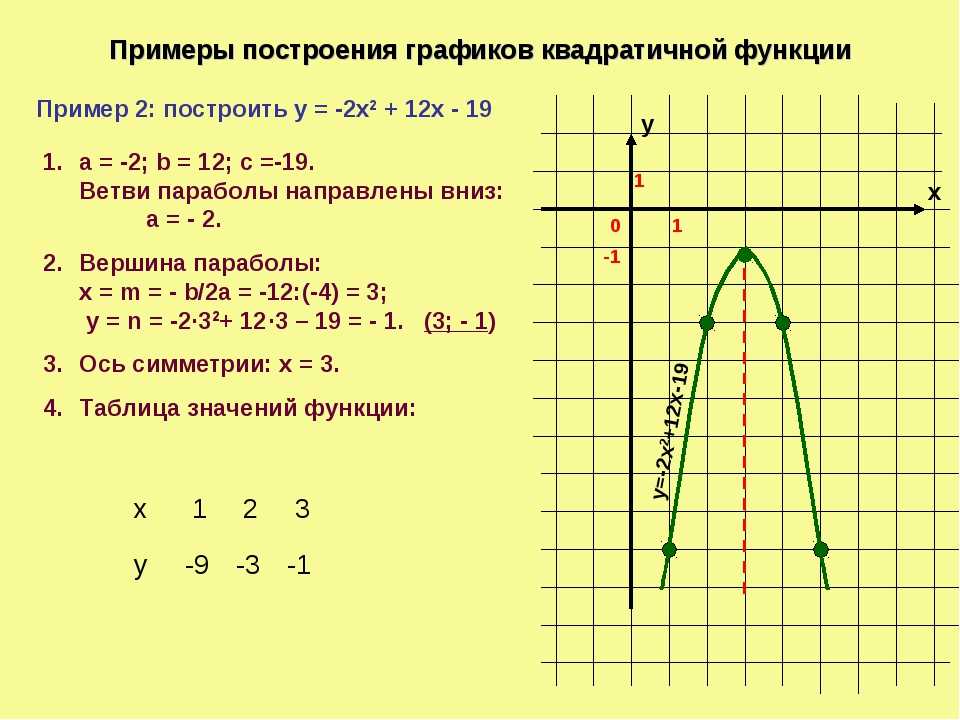
Пример: по графику квадратичной функции опишите её свойства.

На рисунке изображена парабола, ветви которой направлены вверх, значит a>0. Опишем её свойства.

Областью определения и областью значений являются:

Нулями функции являются:

Промежутки знакопостоянства:

Промежутки монотонности:

Заметим, что описать свойства функции по её графику проще, чем по формуле. Поэтому очень важно уметь изображать график функции.

Рассмотрим частный случай квадратичной функции:

Изобразим график этой функции схематично и обратим внимание на некоторые её свойства. Возможны два случая изображения графика.

Областью определения в обоих случаях является:

Область значений:

Функция такого вида обращается в ноль только при х=0, график будет пересекать ось х в одной точке. Первым свойством мы запишем, что если:

Другими словами график такой функции всегда проходит через точку начала координат. Причём эта точка является вершиной параболы.

Если же

то график расположен выше или ниже оси Х.

Если взять противоположные значения аргумента, то видно, что им соответствуют одинаковые значения функции. Противоположным значениям аргумента соответствуют равные значения функции. Другими словами график функции симметричен относительно оси у.

Промежутки монотонности:

Заметим, что:

Пример.

В одной координатной плоскости изобразим графики функций:

Составим таблицу значений для первой функции.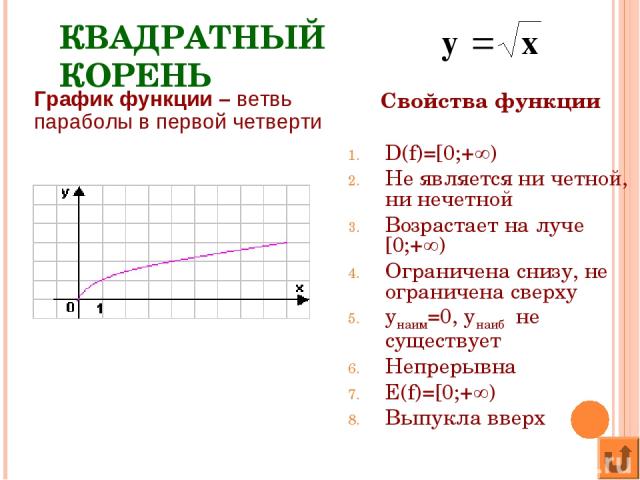

Составим таблицу значений для второй функции

Получим два графика, они симметричны относительно оси х.

Рассмотрим пример: изобразим в одной координатной плоскости графики функции:

Составим таблицу значений для функции:

Составим таблицу значений для функции:

Составим таблицу значений для функции:

Изобразим графики этих функций:

График функции у=ах² можно получить из параболы у=х² растяжением от оси х в а раз, если а>0, и сжатием к оси х в 1/а раз к оси х, если 0<а<1.

Предыдущий урок 4 Разложение квадратного трёхчлена на множители

Следующий урок 6 График функции y=ax^2 +n

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Парабола — свойства, компоненты и график

Параболы — это первая коника, с которой мы познакомимся на наших занятиях по алгебре. Эти коники, открывающиеся вверх или вниз, представляют собой квадратичных функции . Это также то, что делает параболы особенными — их уравнения содержат только один член в квадрате.

Параболы — это U-образные коники, представляющие квадратичные выражения. Это результат разрезания конуса по диагонали плоскостью.

Параболы используются для моделирования движения снарядов и формы отражателей. Эти коники имеют широкое применение в физике, архитектуре, технике и многом другом. Вот почему понимание свойств и компонентов парабол необходимо при изучении конических сечений .

В этой статье мы подробно узнаем о параболах, включая следующее:

• Познакомившись с различными стандартными формами парабол.

• Знание того, когда параболы открываются вертикально или горизонтально.

• Узнайте, как строить графики парабол по их компонентам или уравнениям.

Давайте начнем с понимания того, как получаются параболы и их различные возможные формы. Со временем мы узнаем, как мы можем применять их в реальных приложениях, решая некоторые текстовые задачи.

Что такое парабола?

Параболы — это конические сечения, полученные в результате разрезания конусов (или двойных конусов) наклонной плоскостью с одной и той же стороны конуса, как показано на модели ниже.

На этом изображении видно, что результирующее пересечение вернет U-образную секцию . Когда это происходит, образующаяся коника представляет собой параболу .

При срезе под определенным углом парабола может быть симметричной в горизонтальном или вертикальном направлении. Теперь, когда мы можем представить себе, как формируются параболы, пришло время погрузиться в их формальное определение.

Это включает в себя построение графика, знание различных компонентов параболы и немедленное определение ориентации параболы.

Формальное определение параболы

Параболы — это кривые, содержащие точки, в которых их расстояния от фокуса и их расстояния от директрисы всегда будут равны.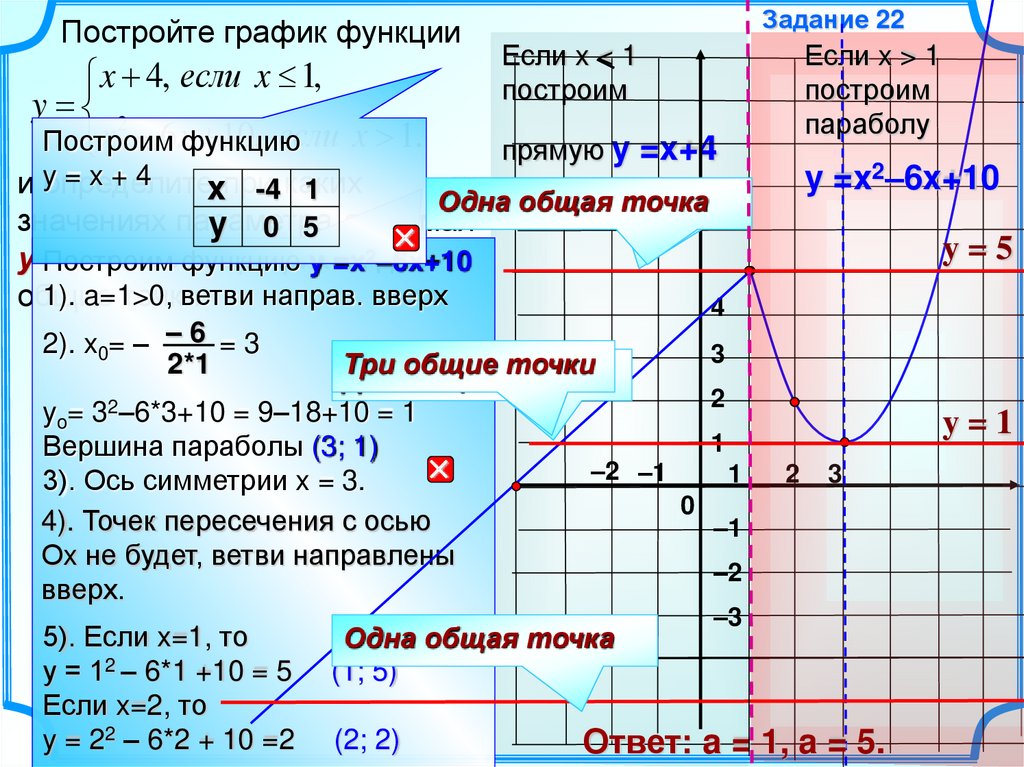 Приведенная ниже модель может помочь нам визуализировать значение этого определения.

Парабола будет содержать три важных элемента: фокус, директрису и вершину. Эта парабола, которая открывается вверх, показывает, что все точки $P$ вдоль кривой параболы будут иметь одинаковое расстояние от фокуса и директрисы.

Это означает, что расстояние от фокуса до $P$ и $P$ от директрисы будет постоянным независимо от положения $P$.

Имейте в виду, что это относится и к вершине – расстояние между вершиной и фокусом будет таким же, как расстояние между вершиной и директрисой.

Как найти уравнение параболы?

Как мы упоминали в предыдущем разделе, параболы могут раскрываться вверх, вниз, вправо и влево. Уравнения, представляющие эти уравнения, также будут различаться, поэтому нам нужно выучить четыре стандартные формы, представляющие параболы.

Формула параболы

Стандартная форма параболы зависит от двух факторов: вершины параболы и ориентации параболы.

• Вершина графика параболы может быть $(0, 0)$ или $(h, k)$.

• Знак $p$ и то, какой из членов возводится в квадрат, будут определять, будет ли график открываться вверх, вниз, влево или вправо.

• Эти варианты приведут к четырем вариантам стандартной формы параболы.

Ниже приведены стандартные формы параболы с учетом этих условий.

Center	Orientation	Sign of $\boldsymbol{p}$	Equation
\begin{aligned}( 0, 0) \end{align}	Открытие вверх, Открытие вниз 92 &= 4p(x – h) \end{aligned}

Из этого мы можем видеть, что есть четыре стандартные формы, которые мы можем иметь в виду, и отметить, что значение $p$ поможет нам определить, является ли парабола открывается вверх или вниз.

Мы можем использовать эту диаграмму, чтобы найти вершину, директрису и фокус параболы независимо от ее ориентации, а переводы выполняются на параболе.

Как найти вершину параболы?

Вершина параболы представляет собой среднюю точку фокуса и директрисы параболы. Для парабол, симметричных по вертикали, вершина представляет собой точку минимума $y$. Между тем, параболы, симметричные по горизонтали, будут иметь вершину, отражающую точку минимума $x$.

Зная график параболы, легко определить ее вершину, как показано на графиках выше. Ось симметрии параболы также проходит через ее вершину, поэтому ось симметрии будет либо $y = k$, либо $x = h$, в зависимости от того, является ли $k$ или $h$ крайней (минимальной или максимальной) точкой. $y$ или $x$ соответственно. 92$ центр находится в начале координат, так что вершина будет равна $(0,0)$.

Если мы сможем найти правильный квадратный трехчлен, то уравнение будет иметь вершину $(h, k)$.

Используйте стандартные формы уравнения параболы (см. таблицу выше) для определения значений $h$ и $k$.

Как найти направляющую параболы?

Директриса – это фиксированная линия, проходящая вне параболы. Зная кривую параболы, мы можем найти ее, отодвинув от вершины на $p$ единиц.

• Если парабола открывается вверх , то директриса находится на $p$ единиц ниже вершины.

• Если парабола открывается вниз , то директриса находится на $p$ единиц над вершиной .

• Если парабола открывается влево , то директриса находится на $p$ единиц справа от вершины .

• Если парабола раскрывается вправо , директриса находится на $p$ единиц левее вершины .

Уравнение вершины будет зависеть от значения $p$ из стандартной формы уравнения параболы.

Orientation	Sign of $\boldsymbol{p}$	Equation of the Directrix
Parabola is symmetric vertically	$ P> 0 $	$ Y = P $
	$ P <0 $	$ y = -p $
Parabola ISMICMTALLALALLALLY
	Parabola ISMTARIZONTALLALLY
. $ P> 0 $		$ x = P $
	$ P <0 $	$ x = -p

. или горизонтальная пунктирная линия. Уравнение директрисы также покажет нам расстояние $p$ вершины от фокуса и директрисы.

Как найти фокус параболы?

У параболы только один фокус, он расположен на расстоянии $p$ единиц от вершины и находится внутри отверстия параболы.

Зная значение $p$, мы можем отсчитать $p$ единиц от вершины, чтобы определить положение фокуса.

Если нам дано уравнение параболы, мы можем добавить $p$ к координате $x$ или $y$ вершины в зависимости от ее положения. Таблица ниже может помочь вам найти координату фокуса. 92 = 4p(y – k)$

$(h, k + p)$

Конечно, когда $p < 0$, мы упрощаем вычитание $p$ из $h$ или $ к$. Просто обязательно учитывайте его отрицательный знак всякий раз, когда это необходимо.

Когда вы застряли или вам нужно быстро запомнить эти свойства, хорошим подходом является использование вершины , найденной в середине фокуса, и направляющей .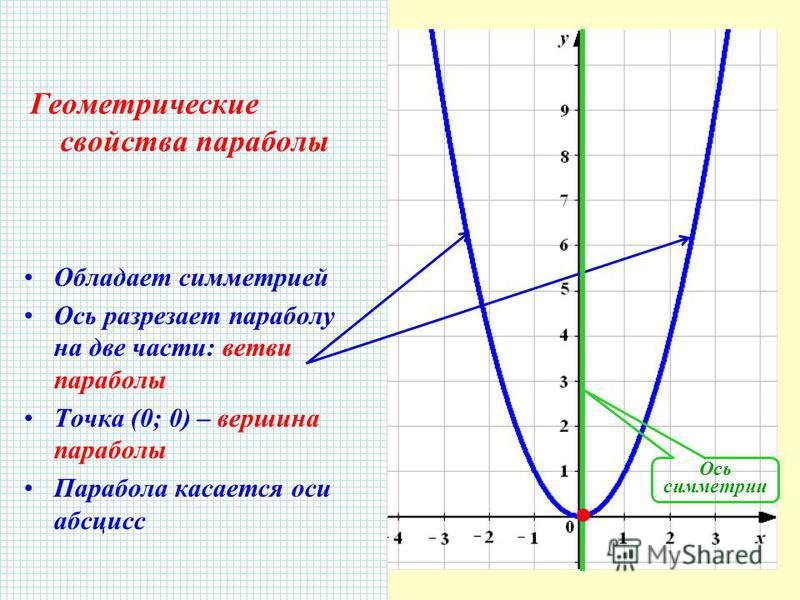

Теперь, когда мы понимаем каждый компонент параболы и их уравнения в стандартной форме, пришло время объединить все это и начать строить параболы на $xy$-плоскостях. Не забудьте быстро повторить эти компоненты, так как мы будем широко использовать их в следующем разделе.

Как построить параболу?

Как мы упоминали в предыдущих разделах, параболы могут раскрываться вверх, вниз, влево или вправо. Это означает, что параболы будут выглядеть так же, как &-образные кривые, но каждый график может иметь другую вершину или ориентацию.

Когда вам дают уравнение параболы, убедитесь, что вы всегда записываете его в стандартной форме, чтобы его было легче изобразить в виде графика, поскольку мы можем сразу найти важные компоненты.

92$.

Найдите значение $4p$, затем найдите $p$.

Постройте вершину и фокус параболы.

Также укажите расположение направляющей.

Нарисуйте кривую параболы после (использование дополнительных точек в качестве ориентира необязательно). 2$.

Постройте вершину, найдя значения $h$ и $k$.

Вынесите константу из линейного выражения и приравняйте константу к $4p$.

Найдите $p$, затем используйте это, чтобы найти фокус и направляющую.

Нарисуйте кривую параболы после (использование дополнительных точек в качестве ориентира необязательно).

Как видно из четырех графиков, показанных выше, мы видим, что это помогает понять свойства параболы, чтобы определить местонахождение фокуса и директрисы, учитывая вершину параболы.

Не беспокойтесь; вы сможете изобразить параболы в приведенных ниже примерах. Прежде чем погрузиться в эти проблемы, обязательно просмотрите свои заметки и ознакомьтесь с важными указателями.

Пример 1

Давайте воспользуемся приведенным ниже графиком и нашими знаниями о параболах, чтобы ответить на следующие вопросы.

а. Какова стандартная форма уравнения параболы?
б. Если $4p = 36$, каковы координаты фокуса?
с. Используя значение $p$ из 1b, каково уравнение его направляющей? 92 = 4py$.

Разделите обе части уравнения, $4p = 36$, на $4$, чтобы найти $p$. Это представляет собой расстояние фокуса и директрисы от вершины параболы.

\begin{aligned}4p &= 36\\ p &= 9\end{aligned}

Мы ожидаем, что фокус будет на $p = 9$ выше начала координат, поэтому координат фокуса будут быть $ (0, 0 + 9) = (0, 9) $.

Поскольку график направлен вверх, мы ожидаем, что направляющая параболы будет расположена на $p$ единиц ниже начала координат. Эта парабола симметрична по вертикали, поэтому мы ожидаем, что направляющая будет иметь уравнение вида $y = -p$. 92 = 4px$. Для этих типов парабол известны следующие свойства их компонент:

• Вершина будет находиться в точке $(0, 0)$.

• Кроме того, фокус будет находиться в $(p, 0)$, а его направляющая будет равна $x = -p$.

Поскольку $4p = 32$, мы имеем $p = 8$.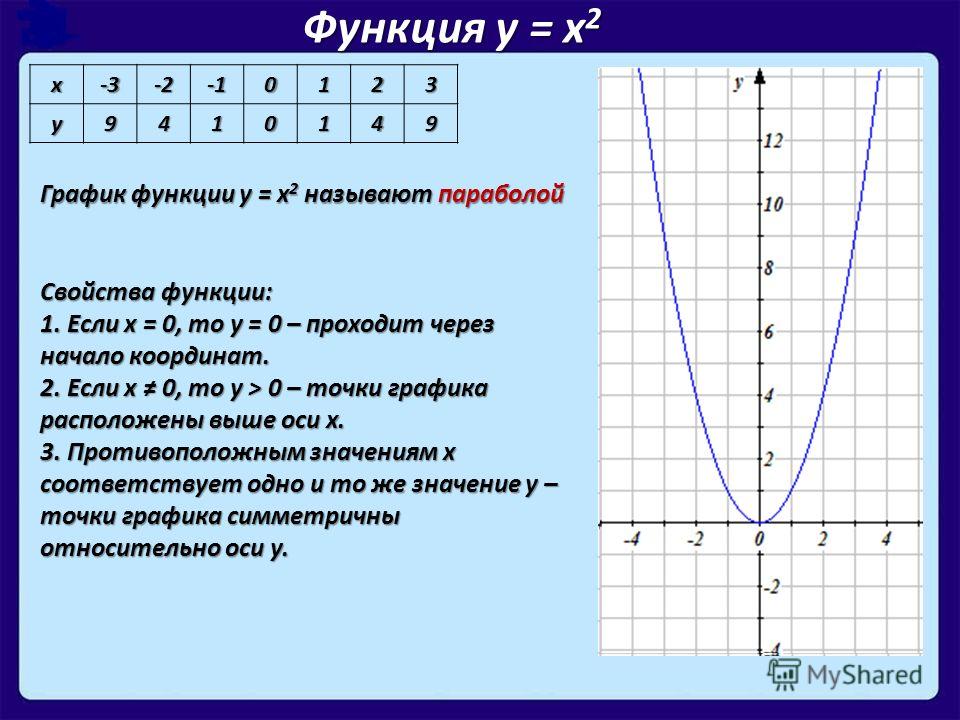 2$ в правой части. 92 &= -\dfrac{1}{2}y\end{aligned}

Это уравнение имеет такой же общий вид со второй параболой. Мы применим аналогичный процесс, но на этот раз у нас есть $4p = -\dfrac{1}{2}$, поэтому $p = -\dfrac{1}{8}$.

• Четвертый фокус параболы будет находиться в точке $\left(0, -\dfrac{1}{8}\right)$.

• Кроме того, уравнение направляющей параболы имеет вид $y = -\dfrac{1}{8}$.

Пример 92 = 16x$ с фокусом в точке $(4, 0)$ и директрисой $x = -4$.

Пример 5

Найдите уравнения в стандартной форме для следующих парабол, которые удовлетворяют приведенным ниже условиям.

а. Парабола с фокусом в точке $(-6, 0)$ и директриса в точке $x = 6$.
б. Парабола с вершиной в точке $(3,-8)$ и фокусом в точке $(3,-6)$.
с. Парабола с фокусом в точке $(6, -2)$ и уравнение направляющей $x = 92 = -12(х – 6)$.

Для четвертой параболы, поскольку у нас есть $x = 4$ в качестве направляющей, мы можем видеть, что парабола открывается либо влево, либо вправо.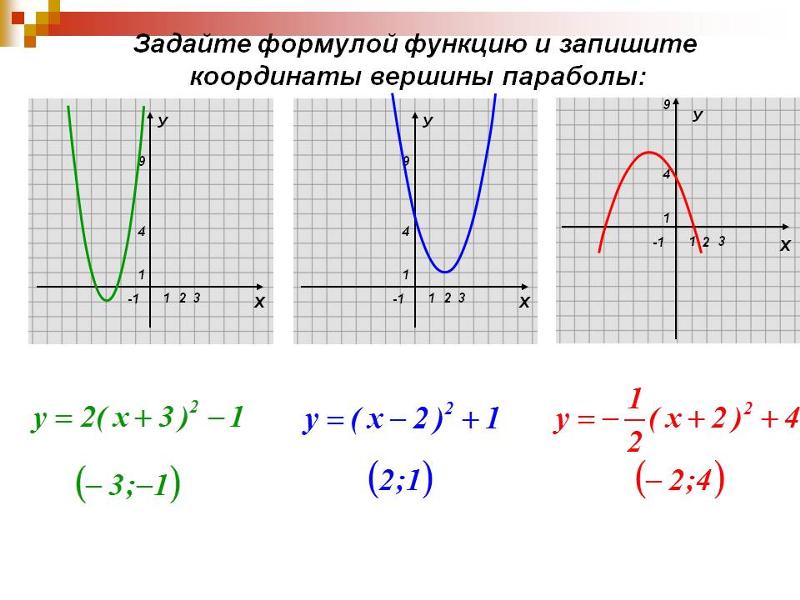

Точки параболы равноудалены от точки $(0, 4)$, поэтому эта точка фактически является фокусом. Зная это, мы можем подтвердить, что кривая открывается вправо.

Расстояние между вершиной $(h, k)$ и фокусом будет таким же, как и у директрисы. Мы видим, что директриса и фокус отстоят друг от друга на $4$ единиц, поэтому фокус находится на $\dfrac{4}{2} = 2$ справа от фокуса. 92 = 4p(x – h)$, где $(h, k)$ равно $(2, -4)$ и $4p = 8$.

\begin{aligned} 4p&=8 \\p&=2\end{aligned}

Так как это $(y + 4)$ в квадрате, мы ожидаем, что парабола будет симметричной по горизонтали с фокусом и директрисой $p = 2$ единиц от вершины.

• Это означает, что парабола имеет фокус в точке $(2 + 2, -4) = (4, -4)$.

• Он также имеет направляющую в точке $x =h – p$ или $x = 0$.

92 &= 8(x – 2)\\ &= 8(4 – 2)\\&= 16\\\\ y + 4&= \pm \sqrt{16}\\y&=-4 \pm 4\\ &= \{0, -8\}\end{aligned}

Это означает, что парабола проходит через точки $(4, -8)$ и $(4, 0)$. 2 = 8(x – 2)$ с фокусом в точке $(4, -4)$, вершиной в точке $(2, -4)$ и направляющей. $x = 0$. 92 + 16x – 8y + 16 = 0$ в стандартной форме.

а. Определите вершину параболы, директрису и фокус.

б. Нарисуйте кривую параболы и включите компоненты в 6a.

в. По графику найдите область определения и диапазон параболы.

д. Что представляет собой вершина параболы?

Решение

Сначала перепишем уравнение, чтобы выполнить следующие шаги в стандартной форме.

• Разделив обе части уравнения на $2$. 92 &= 4(y + 2)\end{aligned}

  Теперь, когда уравнение приведено в стандартную форму, теперь мы можем определить важные компоненты параболы.

  • Вершина параболы расположена в точке $(-4, -2)$.

  • Поскольку $4p = 4$, расстояние вершины от фокуса до директрисы равно $p = 1$ единице.

  • Так как $p$ положительно и квадрат $(x + 4)$, парабола открыта u, поэтому фокус равен $(-4, -2+1) = (-4, -1)$ и 92 = 4(y + 2)$ с фокусом, вершиной и директрисой параболы.

    Давайте посмотрим на окончательный график, чтобы определить область и диапазон параболы.

    • Мы видим, что граф простирается по обе стороны от $x$, так что домен будет состоять из всех действительных чисел или $\{x|x \in \mathbb{R}\}$.

    • Нижняя точка показанной параболы является ее вершиной, поэтому диапазон может быть любым значением $y$ , которое больше или равно $-1$ или алгебраически, \{y|y \geq-1\}.

    Как упоминалось в предыдущем пункте, вершина $(-4, -2)$ является нижней точкой параболы и, следовательно, минимальным значением функции .

    Пример 8

    Джеймс руководит компанией, которая устанавливает спутниковые антенны с параболической поверхностью, открывающейся вверх. Диаметр тарелки составляет 25 долларов США футов, а глубина — 5 долларов США футов. Если приемник спутника действует как фокус параболической спутниковой антенны:

    а. На каком расстоянии приемник от основания спутниковой антенны?

    б. 2 = 4py$. Однако на этот раз мы будем использовать $(10, 25)$, поэтому мы ожидаем новое значение для $p$. 92 &= 4p(25)\\ 100 &= 100p\\ p&= 1\end{aligned}

    Отсюда видно, что из $p_{\text{old}} = \dfrac{1}{4 }$ и $p_{\text{новый}} = 1$. Приемник теперь будет расположен на $1$ футе выше вершины.

    б. Это означает, что высота приемника от спутниковой антенны равна , умноженная на в четыре раза, и теперь равна $1$ футу.

    Определение, уравнение, свойства, типы, примеры и часто задаваемые вопросы

    Парабола — это график квадратного уравнения. Частный случай квадратичной функции называется параболической функцией. Движение различных объектов называется параболическим движением, например движение камня, брошенного под действием силы тяжести. В этой статье мы выведем формулу параболы, различные формы параболы и ее свойства.

    Что такое парабола?

    Парабола — это уравнение конкретной кривой, при котором точка на кривой всегда равноудалена от фиксированной точки и фиксированной линии. Неподвижная точка является фокусом параболы, а неподвижная линия является направляющей параболы. Геометрическое место точки, равноудаленной от данной точки (фокуса) и данной прямой (директрисы), называется параболой.

    Геометрия — это область математики, изучающая размеры, положение, формы, углы и размеры различных объектов. Двухмерная геометрия включает в себя такие формы, как квадраты, круги, треугольники, шестиугольники и т. д. Двухмерные фигуры имеют только 2 измерения. Трехмерная геометрия включает в себя такие формы, как кубы, цилиндры, конусы и т. д. Трехмерные фигуры имеют 3 измерения. Но все эти формы сделаны из линий.

    Конус является частью трехмерной геометрии и представляет собой трехмерную форму. Но даже несмотря на то, что это трехмерное твердое тело, множество кривых может быть получено путем пересечения плоскости и прямого кругового конуса под разными углами. Форма кривой изменяется при смещении положения плоскости сечения.

     

    Стандартное уравнение параболы

    Общая форма уравнения параболы имеет вид0973

    В этой форме направляющая параллельна оси Y.

    Если директриса параллельна оси абсцисс, , то стандартное уравнение параболы имеет вид их уравнение имеет вид y ² = -4ax и x ² = -4ay. Таким образом, даны четыре уравнения параболы:

    • y ² = 4ax
    • y ² = – 4ax
    • x ² = 4ay
    • x ² = – 4ay

    Parabola

    A Парабола — это уравнение кривой, при котором точка кривой равноудалена от фиксированной точки и фиксированной прямой. Неподвижная точка называется фокусом параболы, а неподвижная линия называется направляющей параболы.

    Парабола получается, когда прямой круговой конус разрезается секущей плоскостью под любым углом и параллельно наклонной высоте конуса.

    General equation of a parabola is:

      y = a(x-h) ² + k
    or
    x = a(y-k) ² +h , 

    where (h , k) представляет собой вершину.

    Важные термины, относящиеся к параболе

    • Фокус: Точка (a, 0) называется фокусом параболы
    • Директриса: Линия, проведенная перпендикулярно основной оси и проходящая через точку (-a , 0) — директриса параболы. Директриса всегда перпендикулярна оси параболы.
    • Фокальная хорда: Хорда, проходящая через фокус параболы, называется фокальной хордой параболы. Фокусная хорда всегда пересекает параболу в двух различных точках.
    • Фокусное расстояние: Расстояние от любой точки (x ₁ ,y ₁ ), лежащей на параболе, от фокуса параболы называется фокусным расстоянием. Фокусное расстояние равно перпендикулярному расстоянию данной точки от директрисы.
    • Широкая прямая кишка: Хорда, перпендикулярная оси параболы и проходящая через фокус параболы, называется прямой кишкой. Точками окончания широкой прямой кишки являются (а, 2а), (а, -2а), а их длину принимают за LL’ = 4а.
    • Эксцентриситет: Отношение расстояния точки от фокуса и расстояния точки от директрисы называется эксцентриситетом. Эксцентриситет параболы равен 1.

    Стандартное уравнение правильной параболы

      y ² = 4ax

    Для приведенного выше уравнения вершина равна (0,0)

    Фокус: для приведенного выше, (a,0)

    ^{9 Directrix линия, проведенная параллельно оси y и проходящая через (-a,0)} 

    Latus Rectum: Это фокальный шнур, проходящий через фокус параболы.

    Эксцентриситет: Это отношение расстояния между точкой от фокуса и расстоянием от той же точки до директрисы. Для параболы значение эксцентриситета равно 9.0972 1 .

    Вывод уравнения параболы

     

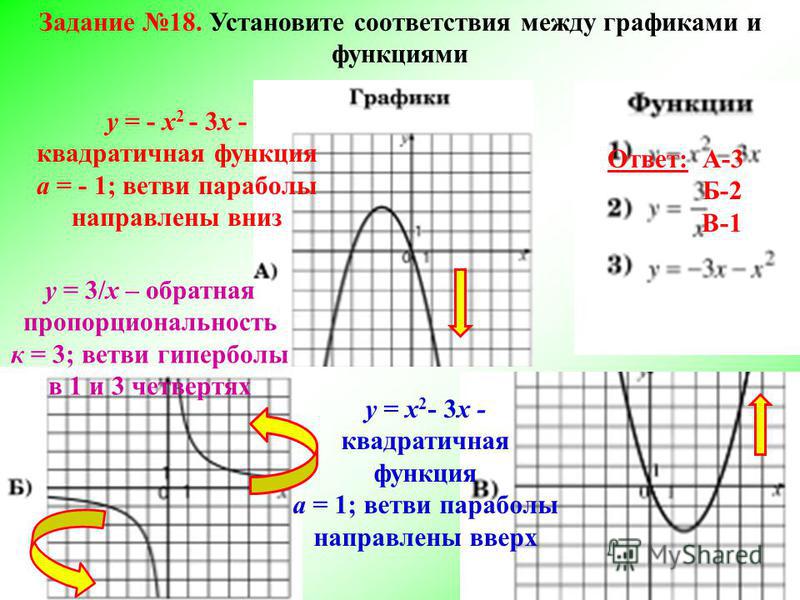
    Возьмем точку P с координатами (x,y) на параболе, лежащей в плоскости X-Y. По определению параболы расстояние любой точки параболы от фокуса и от директрисы равно. Теперь расстояние P от направляющей определяется как PB, где координаты точки B равны (-a, y), поскольку она лежит на направляющей, а расстояние P от фокуса равно PF, приравнивая PB, и PF мы получаем,

    Вывод Уравнение Параболы

    Согласно приведенному выше обсуждению имеем PF = PB

    Согласно формуле расстояния

    PF = √(x−a) ² +(y−0) ² = √{(x−a) ² +y ² }…..(1)

    PB = √{(x+a) ² }……(2)

    По уравнению (1) и (2)

    √{(x −a) ² +y ² } = √{(x+a) ² }

    Возведение обеих сторон в квадрат,

    (x – a) ² + y ^{2 x 909 a3 ) 2}

    x ² + ² – 2ax + y ² = x ² + a ² + 2ax

    y ² – 2ax = 2ax

    y ² = 4ax

    this is the required equation of the parabola

    Various forms of Parabola

     

    y ² = 4ax

    Equation of the axis is y = 0

    Equation of the directrix is ​​x = -a 

    Vertex of the parabola находится в  (0, 0)

    Фокус параболы -(a, 0)

    Длина латус -прямой кишки -4a

    y ² = -4ax

    Уравнения оси -y = 0

    Уравнения is x=a

    Вершина параболы находится в точке (0 , 0)

    Фокус параболы (-a , 0)

    Длина прямой кишки 4a

    x ^{34 90}

    Уравнения оси x = 0

    Уравнения директрисы y =-a

    Вершина параболы находится в точке (0 , 0)

    Фокус параболы (0 , a)

    Длина прямой кишки 4a

    02 x

    02 x

    02 ² = -4ay

    Уравнения оси x = 0

    Уравнения направляющей y = a

    Вершина параболы находится в точке (0, 0) -а)

    Длина прямой кишки 4а

    Параметрические координаты параболы

    Для параболы y ² = 4ax, если мы возьмем x = at ² и y = 2at для любого значения « t », они будут удовлетворять уравнению параболы, координаты (at ² , 2at) называются параметрическими координатами, а « t» называются параметрами.

    Таким образом, x = at ² и y = 2at называются параметрическими уравнениями параболы y ² = 4ax

    Аналогично, параметрическая форма параболы x ² = 4ay are x = 2at, y = at ²

    Общие уравнения параболы

    Общее уравнение параболы задается как y = a(x – h) ² + k или x = a( y – k) ² +h, где (h, k) обозначает вершину параболы

    (Правильная форма) y = a(x – h) ² + k

    (В сторону от) x = a( y – k) ² +h

    Уравнение касательной к параболе

    Касательные – это линии, которые касаются кривой только в одной точке. Таким образом, линия, касающаяся параболы ровно в одной точке, называется касательной к параболе. Существуют различные способы нахождения касательной параболы, которые обсуждаются ниже 9.0005

    Уравнение касательной в точечной форме

    Для данной параболы y ² = 4ax уравнение касательной в точке (x ₁ , y ₁ ) определяется как yy _{1 9109x+3 91(x 1 , y 1 ) 1} ). где (x ₁ , y ₁ ) — точка контакта между касательной и кривой.

    Уравнение касательной в параметрической форме

    Для заданной параболы y ² = 4ax уравнение касательной в точке (at ² , 2at) задается как ty = x + at ² , где (at ² , 2at) — точка контакта между касательной и кривой.

    Уравнение касательной в форме наклона

    Для заданной параболы y ² = 4ax с наклоном м уравнение касательной в точке (a/m ² , 2a/m) задается как y = mx + a/m, где (a/m ² , 2a/m) — точка контакта между касательной и кривой.

    Решенные примеры для уравнения параболы

    Пример 1: найти координаты фокуса, оси, уравнения направляющей и прямой линии параболы y ² = 16х.

    Решение:

    Уравнение параболы: y ² = 16x

    по сравнению со стандартной формой y ² = 4AX,

    4a = 16

    A = 4

    595595995995

    .

    5995995999 2

    .

    5995. коэффициент x положителен, поэтому парабола направлена ​​вправо.

    Кроме того, ось симметрии проходит вдоль положительной оси x.

    Следовательно,

    Фокус параболы равен (a, 0) = (4, 0).

    Уравнение направляющей x = -a, т.е. x = -4 

    Длина широкой прямой кишки = 4a = 4(4) = 16

    Пример 2: Найдите уравнение параболы, симметричной относительно оси y и проходящей через точку (3, -4).

    Решение:

    Учитывая, что парабола симметрична относительно оси Y и имеет вершину в начале координат.

    Таким образом, уравнение может иметь вид х ² = 4ау или х ² = -4ау, где знак зависит от того, направлена ​​ли парабола вверх или вниз.

    Поскольку парабола проходит через точку (3, -4), лежащую в четвертом квадранте, она должна открываться вниз.

    Итак, уравнение будет таким: x ² = -4ay

    Подставляя (3, -4) в приведенное выше уравнение,

    (3) ² = -4a(-4)

    9 = 16a

    A = 9/16

    Следовательно, уравнение параболы: x ² = -4 (9/16) y

    4x ² = -9y

    Пример 3: Найти координаты фокуса, оси и уравнения направителя и прямой кишки параболы y ² = 8x.

    Решение:

    Уравнение параболы: y ² = 8x

    по сравнению со стандартной формой Y ² = 4AX,

    4a = 8

    A = 2

    559559592 A = 2

    5595. коэффициент x положителен, поэтому парабола направлена ​​вправо.

    Кроме того, ось симметрии проходит вдоль положительной оси x.

    Следовательно,

    Фокус параболы равен (a, 0) = (2, 0).

    Уравнение направляющей x = -a, т.е. x = -2

    Длина широкой прямой кишки = 4a = 4(2) = 8

    Пример 4: Найти координаты фокуса, оси, уравнение директрисы и широкая прямая кишка параболы y ² = 52x.

    Решение:

    Данное уравнение параболы: y ² = 52x

    Сравнение со стандартной формой y ² = 4ax,

    4a = 52

    a = 13

    Коэффициент x положительный, поэтому парабола открывается вправо.

    Кроме того, ось симметрии проходит вдоль положительной оси x.

    Следовательно,

    Фокус параболы равен (a, 0) = (13, 0).

    Уравнение направляющей x = -a, т.е. x = -13

    Длина широкой прямой кишки = 4a = 4(13) = 52

    Пример 5: Найти координаты фокуса, оси, уравнение директрисы и широкая прямая параболы x ² = 16 лет.

    Решение:

    Уравнение параболы: x ² = 16y

    по сравнению со стандартной формой x ² = 4ay,

    4a = 16

    A = 4

    5595995

    595995

    95999999 гг. коэффициент x положителен, поэтому парабола направлена ​​вверх.

    Кроме того, ось симметрии проходит вдоль положительной оси x.

    Следовательно,

    Фокус параболы равен (0,a) = (0, 4).

    Уравнение направляющей y= -a, т.е. y = -4

    Длина широкой прямой кишки = 4a = 4(4) = 16

    Часто задаваемые вопросы по параболе

    Вопрос 1: Что понимается под сопряженной осью параболы?

    Ответ:

    Прямая, проходящая через вершину параболы и перпендикулярная ее поперечной оси, называется сопряженной осью параболы.

    Вопрос 2: Перечислите несколько вариантов использования Parabola.

    Ответ:

    Параболы используются для различных целей некоторые из них

    • Параболическая арка используется при строительстве различных памятников.
    • Параболические зеркала используются в отражающих телескопах, спутниках и т. д.
    • Параболы используются в различных математических расчетах, таких как отслеживание пути ракеты, траектории пули и т. д.

    Вопрос 3: Как график параболы?

    Ответ:

    График параболы имеет форму U.

    Вопрос 4: Что такое эксцентриситет параболы?

    Ответ:

    Эксцентриситет определяется как отношение расстояний любой точки конического сечения до его фокуса и соответствующей директрисы. Для параболы эксцентриситет равен 1 .

    No related posts.