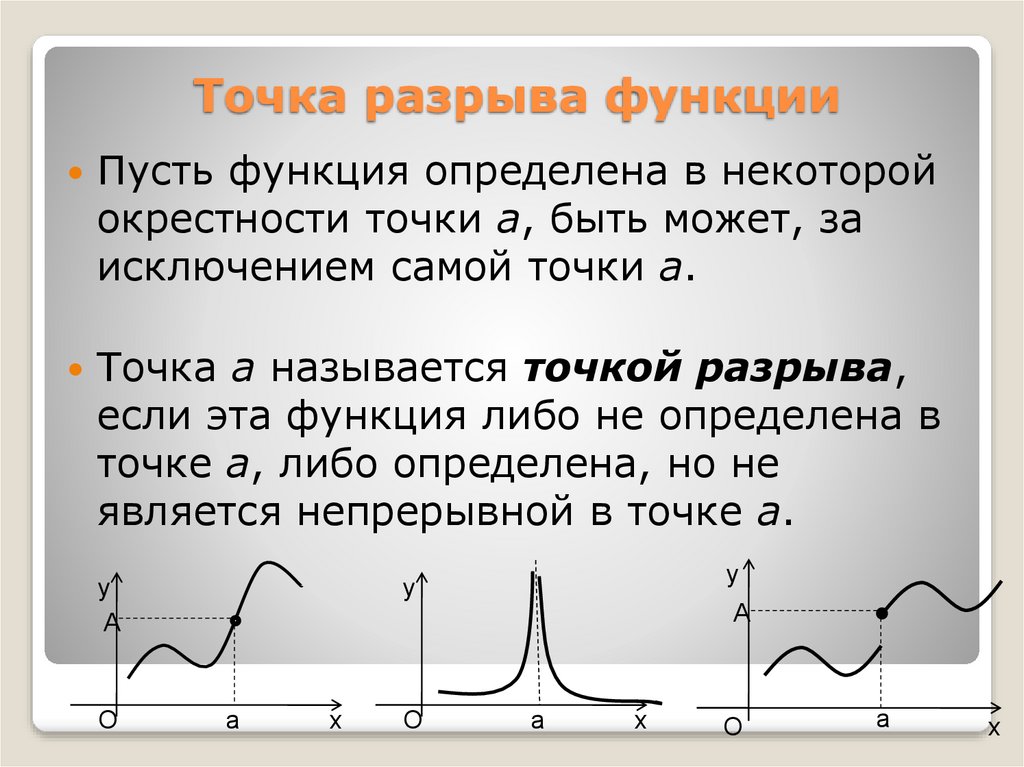
| (11 класс, модуль III, урок 4) Урок 4. Непрерывность обратных функций План урока 4.1. Множество значений непрерывной функции 4.2. Теорема о нуле непрерывной функции 4.3. Достаточное условие непрерывности для монотонной функции 4.4. Непрерывность арифметического корня 4.5. Непрерывность логарифмической функции 4.6. Непрерывность обратных тригонометрических функций 4.7. Заключительное замечание о непрерывности элементарных функций Тесты Домашнее задание Формулируются теоремы о множестве значений непрерывной на промежутке функции, доказывается теорема Больцано-Коши о нуле непрерывной функции. Формулируется и доказывается достаточное условие непрерывности для монотонной функции. Эти утверждения применяются для обоснования непрерывности широкого класса элементарных функций. 4.1. Множество значений непрерывной функции При доказательстве существования функции, обратной к заданной функции , нужно показать, что различным значениям из области определения соответствуют различные значения функции. В этом часто помогает монотонность. Например, функция на отрезке строго возрастает. Отсюда следует, что если , , и , то при будем иметь неравенство , а при — неравенство , то есть различным значениям из отрезка соответствуют различные значения функции . Вопрос. Как доказать, что функция , определенная при всех , имеет обратную функцию? Когда функция , рассматриваемая на множестве , имеет обратную, то для определения обратной функции нужно знать множество значений функции . В нахождении множества значений непрерывной функции часто помогает следующее утверждение. Теорема 11. Пусть функция непрерывна на отрезке и , . Эту теорему иногда называют теоремой о промежуточных значениях непрерывной функции. Теорему о промежуточных значениях непрерывной функции можно применять для доказательства существования корней некоторых уравнений. Пример 1. Доказательство. Функция непрерывна на всей числовой прямой. Рассмотрим отрезок . Функция непрерывна на этом отрезке, , , а число находится между числами и . Вопрос. Как доказать, что уравнение имеет корень m‘ интервале ? + 4.2. Теорема о нуле непрерывной функции Теорему 11 можно получить как следствие из теоремы о нуле непрерывной функции. Теорема 12. Пусть функция непрерывна на отрезке и принимает в концах значения разных знаков. Тогда найдется такое число из отрезка , что .Разберем доказательство теоремы 12, использующее метод деления пополам. Доказательство. I шаг. Разделим точкой отрезок на два равных отрезка и вычислим . Если , то теорема доказана и процесс заканчивается. Если , то обозначим , ; если же , то обозначим , . В результате получаем, что , . II шаг. Разделим точкой отрезок И так далее: получив на очередном шаге отрезок , делим его точкой пополам, вычисляем и, аналогично предыдущему, либо заканчиваем процесс, либо строим отрезок так, что , . В том случае, когда указанный процесс не заканчивается через конечное число шагов, появляется последовательность вложенных друг в друга отрезков, длина которых стремится к нулю. По условию функция непрерывна на отрезке , а поэтому непрерывна в точке . Следовательно, и . Но так как , то , откуда . С другой стороны, , а поэтому , откуда следует равенство . Тем самым теорема 11 доказана.Вопрос. Как с помощью теоремы 11 доказать теорему 10? (Приложение – портрет, рис. 1) Коши, Огюстен Луи (21.08.1789-23.05.1857) – французский математик. Труды Коши относятся к различным областям математики (преимущественно математического анализа) и математической физики. Его курсы анализа, основанные на понятии предела, послужили образцом для большинства курсов позднейшего времени. В них он, в частности, дал определение непрерывности функции, четкое построении теории сходящихся рядов, определение интеграла как предела интегральных сумм. (Приложение – портрет, рис. 2) Кантор, Георг (03.03.1845-06.01.1918) – немецкий математик. Разработал теорию бесконечных множеств и теорию трансфинитных чисел. Ввел понятие предельной точки, развил одну из теорий иррациональных чисел, сформулировал одну из аксиом непрерывности о последовательности вложенных друг в друга отрезков.  Идеи Кантора первоначально встретили резкое неприятие со стороны многих современников, но впоследствии оказали глубокое влияние на развитие математики.(Приложение – портрет, рис. 3) 4.3. Достаточное условие непрерывности для монотонной функции Для доказательства непрерывности функций, которые обратны к непрерывным функциям, будем использовать следующее свойство. Теорема 13. Пусть функция определена, монотонна на отрезке и принимает все промежуточные значения между и . Тогда функция непрерывна на Доказательство. Предположим для определенности, что функция является строго возрастающей. Возьмем произвольную точку . Вопрос. Как доказать, что функция принимает все значения из промежутка ? Напомним, что при любом натуральном функция , рассматриваемая на луче , строго возрастает и непрерывна. Теорема 11 из пункта 4.1 позволяет установить, что эта функция принимает все значения из промежутка . Поэтому обратная к ней функция определена на луче , строго возрастает и принимает все значения из промежутка .  Тогда по теореме 13 из пункта 4.3 можно сделать вывод, что функция непрерывна в каждой точке своей области определения.Вопрос. Как доказать, что ? Из теоремы 13 следует, что функция непрерывна в каждой точке своей области определения. Аналогично определяется логарифмическая функция при и доказывается ее непрерывность. Вопрос. Как доказать, что 4.6. Непрерывность обратных тригонометрических функций Аналогично доказывается непрерывность функций и на всей области определения. Вопрос. Как доказать непрерывность функции на всей области определения? Вопрос. Как доказать непрерывность функции на интервале ? Для этого возьмем произвольную точку и, обозначив через наименьшее расстояние от до концов промежутка , рассмотрим последовательности и . Предположим для определенности, что функция является строго возрастающей.
. Какие изменения нужно внести в рассуждения, если точка совпадает с одним из концов промежутка ? Как изменить полученное доказательство непрерывности монотонной функции, множество значений которой является промежутком, для случая строго убывающей функции? И наконец, докажите, что у произвольной монотонной функции точки разрыва могут быть только первого рода (см. 1. ; 2. ; 3. ; 4. ? (Правильный вариант: 1) Каково множество значений функции на отрезке : 1. ; 2. ; 3. ; 4. ? (Правильный вариант: 3) Каково множество значений функции на отрезке : 1. ; 2. ; 3. ; 4. ? (Правильный вариант: 2) Каково множество значений функции на отрезке : 1. ; 2. ; 3. ; 4. ? (Правильный вариант: 1) Какая из функций является обратной к функции , рассматриваемой на промежутке : 1. на промежутке ; 2. на промежутке ; 3. 4. на промежутке ? (Правильный вариант: 3) Какая из функций является обратной к функции , рассматриваемой на промежутке : 1. на промежутке ; 2. на промежутке ; 3. на промежутке ; 4. на промежутке ? (Правильный вариант: 4) Задание 2. Укажите все правильные варианты ответа. Какая из функций является обратной к функции , рассматриваемой на промежутке : 1. ; 2. ; 3. ; 4. ? (Правильные варианты: 1, 2) Какая из функций является обратной к функции , рассматриваемой на промежутке : 1. ; 2. ; 3. ; 4. ? (Правильные варианты: 3, 4) Домашнее задание 1. Найдите множество значений функции на отрезке , если: а) , , ; б) , , ; в) , , ; г) , , ; д) , , . 2. Найдите множество значений функции на отрезке , если: а) , , ; б) , , ; в) , , ; г) , , . 3.** Найдите множество значений функции на всей области определения: а) ; б) ; в) ; г) ; д) ; е) . 4.** С точностью до найдите: а) корень уравнения из интервала ; б) корень уравнения из интервала ; в) корень уравнения из интервала ; г) корень уравнения из интервала . 5. Докажите, что функция непрерывна в точке , если: а) и ; б) и ; в) и ; г) и . 6.* Найдите предел: а) ; б) ; в) ; г) ; д) ; е) . 7. Докажите, что функция непрерывна в точке , если: а) и ; б) и ; в) и ; г) и . 8. Найдите предел: а) ; б) ; в) . 9. Найдите предел: а) ; б) ; в) ; г) ; д) ; е) . 10.* Найдите предел: а) ; б) ; в) . 11.** Докажите, что . 12.** Докажите, что функция не имеет предела в нуле. Рисунки (названия файлов) Рисунок 2. – Cauchy.jpg Рисунок 3. – Cantor_2.jpg Каталог: file.php жүктеу/скачать 260.46 Kb. Достарыңызбен бөлісу: |
Тогда для каждого числа , заключенного между числами и , найдется такое число из отрезка , что . 
Поэтому по теореме 11 существует такое число из интервала , что . Следовательно, уравнение на отрезке имеет какой-то действительный корень.
Пусть, для определенности, и . Обозначим , . Тогда , . Далее шаг за шагом выполним следующие построения.
По аксиоме Кантора найдется единственная точка , общая для всех отрезков, причем , .
Много работал над логическими основами выдвинутой им арифметической теории действительных чисел (1817). В «Парадоксах бесконечного» (изд. 1851) явился предшественником Георга Кантора в исследованиях бесконечных множеств.
Для любого положительного числа рассмотрим числа и (если , то примем , если , то примем ). На промежутке найдутся такие числа и , что , . Пусть . Тогда в силу строгой монотонности функции для любого из -окрестности числа выполняются неравенства , откуда следует непрерывность функции в точке . В случае строго убывающей функции доказательство совершенно аналогично. Легко понять, как изменить доказательство, если точка является одним из концов промежутка .
Поэтому обратная к ней функция определена на отрезке , строго возрастает и принимает все значения из отрезка . Отсюда по теореме 13 получаем непрерывность функции в каждой точке своей области определения.
урок 2). 
на промежутке ;
Функция называется строго убывающей на множестве , если для любых чисел и из неравенство влечет неравенство . 
– Bolzano_3.jpgФункции одной независимой переменной
Уроки 1-2
Тема: « Функции одной независимой переменной. Пределы. Непрерывность функции.
План:
1. Определение функции. Свойства функций.
2. Способы задания функции.
3. График функции.
4. Предел функции.
5. Непрерывность функции.
1.Определение функции. Свойства функций.
Определений 1:
Если даны числовое множество Х и правило f , позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят , что задана функция y = f(x) с областью определения Х. Пишут y = f(x) , х € Х. Для области определения используют обозначение D(x). Переменную х называют независимой переменной. Или аргументом, а переменную у — зависимой переменной. Множество всех значений функции y = f(x) , х € Х называют областью значений функции и обозначают Е(f).
Пример
Свойства функций:
Определение 1.
Функцию y = f(x) называют возрастающей на множестве Х, если для любых точек х1 и х2 множества Х таких, что х1 < х2, выполняется неравенство f(x1)< f(x2).
Определение 2.
Функцию y = f(x) называют убывающей на множестве Х, если для любых точек х1 и х2 множества Х таких, что х1 > х2, выполняется неравенство f(x1)> f(x2).
возрастающая убывающая
Термины «возрастающая» и «убывающая» объединяют одним общим термином «Монотонная функция».
Определение 3.
Функцию y = f(x) называют ограниченной снизу на множестве Х, если все значения этой функции на множестве Х больше некоторого числа.
Определение 4.
Функцию y = f(x) называют ограниченной сверху на множестве Х, если все значения этой функции на множестве Х меньше некоторого числа.
Определение 5.
Функцию y = f(x) , х € Х.называют четной , если для любого значения х из множества Х выполняется равенство f(-x) = f(x)
Пример
Доказать, что y=x4 — четная функция.
Решение: Здесь f(x)=x4 , f(-x) = (-x4) = x4 значит для любого значения х выполняется равенство f(-x) = f(x), т. е. функция является четной.
Определение 6.
Функцию y = f(x) , х € Х.называют нечетной , если для любого значения х из множества Х выполняется равенство f(-x) = — f(x)
Пример
Доказать, что y=x3 — нечетная функция.
Решение: Здесь f(x)=x3 , f(-x) = (-x3) = -x3 значит для любого значения х выполняется равенство f(-x) = -f(x), т. е. функция является нечетной.
2. Способы задания функций
a. Табличный.
b. Аналитический.
с. Графический.
3. График функции
Если задана функция y = f(x), х € Х и на координатной плоскости отмечены все точки вида ( х ; у ), где х € Х, а y = f(x), то множество этих точек называют графиком функции
y = f(x), х € Х.
4.
a)Предел функции на бесконечности
Пусть дана функция y = f(x), в области определения которой содержится луч [ а; +∞ ) и пусть прямая у = b является горизонтальной асимптотой графика функции y = f(x), Для описания этой геометрической модели используется запись:
lim f(x) = b
x + ∞
( Читают: предел функции y = f(x), при стремлении х к плюс бесконечности равен b).
y
b y=f(x)
а x
0
Если же задана функция y = f(x), в области определения которой содержится луч (-∞; а] и прямая у = b является горизонтальной асимптотой графика функции y = f(x), Для описания этой геометрической модели используется запись:
lim f(x) = b
x -∞
y
b
Y=f(x)
а x
Если одновременно выполняются соотношения lim f(x) = b lim f(x) = b ,
х→+∞ х→ — ∞
то их можно объединить одной записью lim f(x) = b ,
х→∞
Для вычисления предела функции на бесконечности используют правила:
1)
2) если
, , то
a) Предел суммы равен сумме пределов:
b) Предел произведения равен произведению пределов:
с) Предел частного равен частному пределов, если с не равно 0:
d) Постоянный множитель выносится за знак предела:
b) Предел функции в точке
lim f(x) = b
х→а
Смысл приведенной записи заключается в следующем: если значения аргумента выбирать все ближе и ближе к а , то соответствующее значение функции все меньше и меньше будет отличаться от предельного значения b.
Для вычисления предела функции в точке , как и для вычисления предела функции на бесконечности используется теорема об арифметических операциях над пределами .
Теорема:
Если lim f(x) = b lim g(x) = c. То
х→a х→ a
При условии, что с≠0
5. Непрерывность функции
Определение 1
Функцию y = f(x) называют непрерывной в точке х = а, если выполняется соотношение lim f(x) = f(а)
х→ a
Определение 2
Функцию y = f(x) называют непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка.
Урок Видео: Непрерывность функций
Стенограмма видео
Непрерывность функций
В этом уроке мы узнаем, как
проверить непрерывность функции и определить интервал, на котором функция
является непрерывным.
Возможно, вы знакомы с нахождение непрерывности функции в точке и, действительно, различные типы прерывность, с которой мы сталкиваемся. Мы можем проверить, является ли функция непрерывной в точке, используя следующее формальное определение. Функция 𝑓 от 𝑥 непрерывна в точке, где 𝑥 равно 𝑎, если предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥, равно функции, оцененной в 𝑥 равно 𝑎.
Теперь так много подразумеваемого Требование к этому условию состоит в том, что обе эти вещи должны существовать. Для нормального предела существуют, левый и правый предел также должны существовать при приближении 𝑥 к 𝑎 и быть равными до некоторого значения 𝐿. При этом 𝑓 из 𝑎 должно быть определено, и оно должно быть равно левому, правому и нормальному пределу для непрерывность. Здесь мы сказали, что это значение равно 𝐿.
Теперь давайте подумаем о преемственности
через интервал.
Разговорное определение этого
может быть, если вы сможете нарисовать график функции на интервале без
поднимая ручку. Более строгий способ думать о
это означало бы, что функция 𝑓 от 𝑥 непрерывна на интервале, если
требование непрерывности в точке выполняется для всех значений 𝑥 в пределах
интервал. Теперь это может показаться очевидным, но один
Способ проверки непрерывности в течение интервала состоит в том, чтобы убедиться, что нет
разрывы в указанном интервале. Мы можем посмотреть на пару примеров
графики, чтобы получить наглядное представление об этом.
Определите, выполняются ли следующие утверждение истинно или ложно. Функция, представленная график является непрерывной функцией.
На этот вопрос нам дали
функция 𝑔 от 𝑥, которая определена для всех значений 𝑥 над действительными числами,
обозначены этими стрелками.
Теперь мы можем почти сразу увидеть
что наша функция 𝑔 от 𝑥 разрывна, так как при значении 𝑥 равном трем мы
есть пробел в нашем графике. На самом деле, мы можем признать это как
разрыв скачка, при этом 𝑔 из 𝑥 не определено в точке три, два, обозначено
полой точкой и определяется в точке три, один, обозначенный закрашенным
точка.
Если бы мы посмотрели на лево- и
правосторонних пределов, когда 𝑥 приближается к трем, мы обнаружим, что, хотя оба существуют,
их значения расходятся. А это будет означать, что нормальный
предела не существует. Здесь мы напомним наше определение для
непрерывность в точке, которая говорит, что предел, когда 𝑥 приближается к 𝑎, указанного
функция должна быть равна значению оцениваемой функции, где 𝑥 равно
𝑎. Теперь в нашем случае предел, как 𝑥
приближается к трем из 𝑔 из 𝑥, не равно 𝑔 из трех, так как предел не
существует.
Итак, мы доказали, что функция 𝑔 от 𝑥 имеет разрыв в точке 𝑥, равной трем. Наш ответ на вопрос, следовательно, ложно. Функция, представленная график не является непрерывной функцией. В заключение отметим, что наша функция может иметь разрыв, даже если она определена по всем реальным числа.
Теперь посмотрим на другое графическое изображение. Пример определения того, является ли функция непрерывной или нет.
Определить, работает ли функция представленный графом, является непрерывным или прерывистым.
На этот вопрос нам дали
функция 𝑓 от 𝑥, которая определяется, когда 𝑥 больше или равно нулю или
меньше или равно трем. Интересные моменты этого
возникают, когда 𝑥 равно единице и когда 𝑥 равно двум. Здесь мы видим резкое изменение
градиент. И мы можем признать, что это
означает, что наша функция не будет дифференцируема в этих точках.
В целях обеспечения непрерывности однако это не обязательно является причиной для беспокойства. Взяв точку, где 𝑥 равно например, мы видим, что и левосторонний, и правосторонний пределы приближаются такое же значение. И это будет там, где 𝑓 из 𝑥 равен единице. Отсюда следует, что нормальный предел, когда 𝑥 приближается к единице, примет то же значение. И это тоже хорошо видно 𝑓 единица также равна единице.
На самом деле, эти две вещи вместе
являются условием непрерывности. Так как у нас это нормально
предел, когда 𝑥 приближается к одному из 𝑓 из 𝑥, равен 𝑓 из одного. Та же логика будет следовать для
точка, где 𝑥 равно двум, и, собственно, для всех остальных точек вдоль нашего
домен функции. Это ставит нас в положение
ответьте на наш вопрос. Мы заключаем, что 𝑓 из 𝑥 является
непрерывная функция.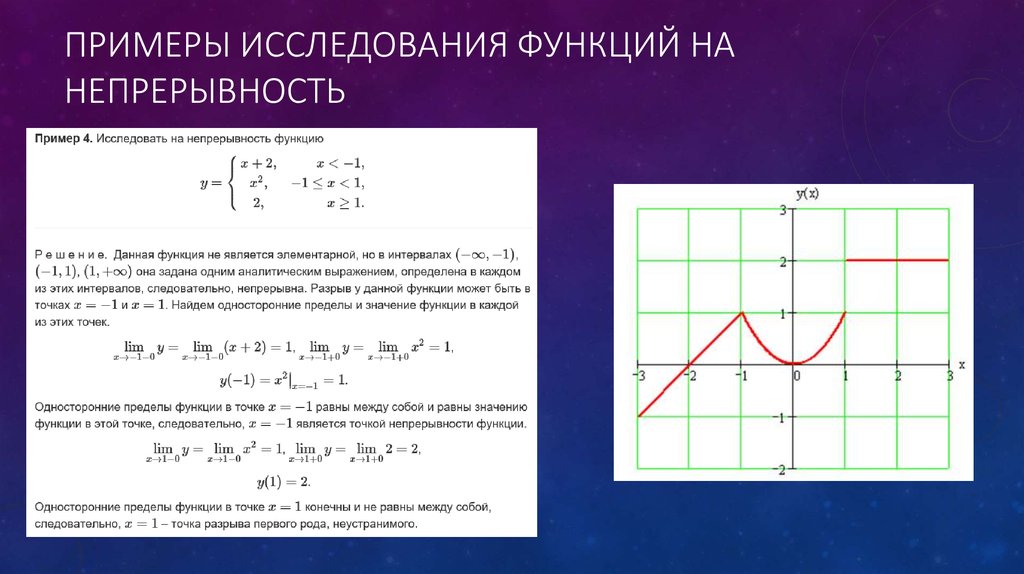
Теперь два предыдущих вопроса дал нам графические примеры функций, которые были непрерывными, и функций, которые не были. В нашем примере мы видели функцию со скачкообразным разрывом. Однако функции с любым другим разрывность, такая как устранимая или бесконечная, также не будет классифицироваться как непрерывные функции. И наоборот, существует множество типов функции, которые непрерывны. И мы рассмотрим несколько примеры их алгебраической оценки.
Следующие типы функций
непрерывны во всей своей области определения, полиномиальные функции, рациональные функции,
тригонометрические функции и экспоненциальные функции. Важным отличием здесь является
мы говорим, что эти функции непрерывны во всей своей области определения, а не
для всех значений 𝑥 над действительными числами. Мы вернемся к этому моменту
потом.
Но прежде чем мы это сделаем, еще одно важное
факт.
Суммы, разности, произведения, частные, а композиции непрерывных функций также непрерывны для всех точки, где 𝑥 определено правильно. Опять же, они находятся в доменах наших вновь созданных функций. Теперь доказательство непрерывности для все эти типы функций выходят за рамки этого видео, но мы можем перейти через один такой пример с использованием полиномиальной функции и следующий вопрос.
Что можно сказать о непрерывность функции 𝑥 в кубе плюс пять 𝑥 в квадрате минус два 𝑥 плюс два?
Учитывая общее правило, что
полиномиальная функция непрерывна в своей области определения и области определения нашей функции
— это все действительные числа, мы можем почти сразу дать следующий ответ. Функция непрерывна на ℝ,
действительные числа, потому что это многочлен.
Это, по сути, быстрый ответ
на наш вопрос.
Но вместо того, чтобы остановиться здесь, давайте рассмотрим полосатое доказательство того, почему это так.
Строительный блок, с которого мы начнем с является пределом, когда 𝑥 приближается к 𝑎, только некоторой постоянной 𝑘. Теперь ясно, что значение 𝑥 не имеет значения для нашего постоянного 𝑘. Итак, ответ на этот предел просто 𝑘. Здесь мы скажем, что 𝑘 настоящий количество. Далее переходим к случаю предел, когда 𝑥 приближается к 𝑎, функции, которая является просто 𝑥. Делая прямую замену приближение 𝑥 равно 𝑎, мы видим, что здесь ответ на наш предел просто 𝑎. А также мы должны здесь оговорить что 𝑎 также является одним из действительных чисел.
Далее добавляем мощность и берем
предел, когда 𝑥 приближается к 𝑎 из 𝑥, возведенному в некоторую степень 𝑛. В этом случае 𝑛 является одним из
натуральные числа, включая ноль.
Итак, ноль, один, два, три,
и так далее. С той же прямой заменой
аргумента, мы находим, что этот предел равен 𝑎 в степени 𝑛. А что, если мы добавим некоторые
постоянный 𝑘 перед нашим 𝑥 в степени 𝑛? Постоянный кратный закон позволяет нам
чтобы переместить нашу константу 𝑘 за пределы нашего предела следующим образом. Теперь мы видим предел, который мы ищем
for совпадает с предыдущей строкой, умноженной на 𝑘. Итак, наш ответ 𝑘 раз 𝑎
в степени 𝑛, опять же с подходом прямой замены.
Хорошо, теперь мы расширим
немного, добавив два новых термина к нашему пределу и различая разные
значения 𝑘 и 𝑛, где все значения 𝑘 и 𝑛 подчиняются тем же правилам. Теперь, используя законы сложения
пределы, мы можем разделить наш один предел на три отдельных предела следующим образом. Теперь вы можете заметить, что эти
первые два термина принимают ту же форму, что и предыдущая линия работы, которую мы только что
завершенный.
Таким образом, мы можем сказать, что они
являются 𝑘 один раз 𝑎 в степени 𝑛 один и 𝑘 два раза 𝑎 в степени 𝑛
два соответственно. Конечно, наш последний срок
константа, которую мы видели в нашем первом примере. Предел этой константы равен
конечно, всего 𝑘 три.
Теперь мы обнаружили, что наш предел 𝑘 один раз 𝑎 в степени 𝑛 один плюс 𝑘 два раза 𝑎 в степени 𝑛 два плюс 𝑘 три. Теперь, если мы вызовем функцию, которая мы создали здесь 𝑓 из 𝑥, мы должны увидеть, что предел, который у нас есть найдено, равно нашей функции, оцененной в точке, где 𝑥 равно 𝑎, в другими словами, 𝑓 из 𝑎.
Наш последний и решающий шаг в
узнавая форму функции 𝑓 от 𝑥, которую мы создали. Поскольку 𝑘 — действительное число, а 𝑛
— натуральное число, включающее ноль, каждый из этих членов дает нам вещественное число, кратное
𝑥 возводится в любую положительную целую степень или в ноль.
По предельному правилу сложения имеем
мы можем добавить в нашу функцию столько терминов, сколько захотим. Наряду с этим мы прикрыли
добавление стандартной вещественной константы 𝑘. Наша функция 𝑓 от 𝑥, следовательно,
представляет любой многочлен, который мы хотим построить.
Наконец, мы доказали, что предел, когда 𝑥 приближается к 𝑎, поскольку наша функция 𝑓 от 𝑥 равна 𝑓 от 𝑎. Поскольку 𝑓 из 𝑥 — это любой многочлен и 𝑎 — любое действительное число, мы только что доказали, что полиномиальная функция непрерывно по всему множеству действительных чисел, так как это действительно условие для непрерывности.
Теперь мы доказали нашу преемственность
условие для многочленов. И это доказательство можно расширить или
изменен, чтобы охватить другие функции, упомянутые ранее. Теперь, при классификации этих
функции были непрерывными, мы тщательно различали, что они
непрерывны по всему их домену, а не для всех действительных чисел.
Так получилось, что домен
многочлен — это действительные числа, однако это не обязательно так для других
функции, такие как рациональные числа. Давайте рассмотрим один такой пример, чтобы
проиллюстрировать это.
Найдите множество, на котором 𝑓 из 𝑥 что равно 𝑥 минус 22 по всему 𝑥 в квадрате минус два 𝑥 минус 63 равно непрерывный.
На этот вопрос у нас есть
рациональная функция в виде 𝑃 от 𝑥 над 𝑄 от 𝑥. Теперь мы знаем, что рациональное
функция непрерывна в своей области определения. И, следовательно, наш вопрос сводится к
нахождение области определения нашей функции 𝑓 of 𝑥. По сути, мы хотим найти значения
из 𝑥, что привело бы к тому, что наша функция либо не была бы определена, либо росла бы в сторону
положительная или отрицательная бесконечность. Глядя на форму нашего
функции, мы видим, что эти неприятные моменты возникнут, когда знаменатель
наше частное 𝑄 от 𝑥 равно нулю.
Мы можем двигаться вперед с нашим сначала задайте вопрос, разложив 𝑄 из 𝑥. Немного осмотревшись, мы видим что это квадратичное число разлагается на 𝑥 минус девять раз 𝑥 плюс семь, поскольку эти два числа имеют сумму отрицательных двух и произведение отрицательных 63. Из факторной теоремы мы можем затем посмотрите, что когда 𝑥 равно девяти или когда 𝑥 отрицательно семь, 𝑄 из 𝑥 будет оценивать до нуля. Помещая эту факторизованную версию 𝑄 из 𝑥 обратно в нашу функцию, мы можем сделать вывод, что 𝑥 равно девяти и 𝑥 равняется отрицательной семерке, не входит в область применения нашей функции. Это связано с тем, что при этих значениях знаменатель нашего частного был бы равен нулю. И, следовательно, 𝑓 из 𝑥 не даст нам числовую оценку.
Так как 𝑓 из 𝑥 ведет себя во всех остальных
реальных значений 𝑥, можно сказать следующее.
Область определения нашей функции 𝑓 of 𝑥
— это действительные числа за вычетом набора из девяти и отрицательных семи. Итак, 𝑓 из 𝑥 непрерывно над
действительные числа минус набор из девяти и минус семь. И вот, мы ответили на наш
вопрос.
В дополнение к нашему предыдущему
вопрос, вы можете вспомнить, что когда общий множитель может быть отменен на вершине и
нижняя половина частного, например, образующая рациональную функцию, это будет
соответствуют устранимой особенности на нашем графе. В этом случае, поскольку функция
undefined, где 𝑥 равно 𝑎, очевидно, что мы не можем выполнить критерии для
непрерывность. В случаях, когда общие факторы
не может быть отменено в верхней и нижней частях наших частных, мы ожидаем, что
чтобы увидеть асимптоты, где значения 𝑓 из 𝑥 будут приближаться к положительным или отрицательным
бесконечность.
При этих асимптотах, даже если левый и правый пределы должны были совпадать, как в этом случае, хотя мы можем выразить, что предел, когда 𝑥 приближается к 𝑎 из 𝑓 из 𝑥, равен бесконечности, это это просто особый способ сказать, что предела не существует. А на самом деле предела нет существуют на любой из этих асимптот. Теперь, поскольку у нас есть места, где наши предела не существует, опять же, мы не можем выполнить наши критерии непрерывности. И в этих точках 𝑓 из 𝑥 будет быть прерывистым.
Далее некоторые функции можно
определенные кусочно, ведут себя по-разному на разных интервалах. Применяются те же правила непрерывности
в интервалах нашей кусочной функции, но мы должны быть осторожны, когда
рассматривая границу между интервалами. Чтобы преемственность была
поддерживается над границей, конечными точками двух секций или подфункций,
должны присоединиться.
Лучше всего это иллюстрируется
пример.
Предположим, что 𝑓 из 𝑥 равно пять грех 𝑥 минус три больше 𝑥 минус три, если 𝑥 меньше трех и пяти 𝑥 в квадрате над девятью, если 𝑥 больше или равно трем. Найдите набор, на котором 𝑓 непрерывный.
Здесь у нас есть кусочная функция
определяется на двух интервалах. Граница двух наших интервалов
происходит в точке, где 𝑥 равно трем. И, следовательно, это важное
точка. Для нашей первой подфункции имеем
тригонометрическое выражение на верхней половине нашего частного и биномиальное на
нижняя половина. Поскольку мы знаем, что тригонометрический
функции и многочлены непрерывны в своих областях определения, а частные
непрерывные функции также непрерывны в своих областях определения, мы заключаем, что это
поэтому подфункция также непрерывна в своей области определения.
Теперь, здесь, нам нужно быть немного осторожно, так как при значениях, где 𝑥 равно трем, эта подфункция оценивается как ноль над нулем, что является неопределенной формой. К счастью для нас, 𝑓 из 𝑥 только определяется этой подфункцией при значениях 𝑥, строго меньших трех, не где 𝑥 равно трем. Вместо этого, когда 𝑥 больше или равно трем, 𝑓 из 𝑥 определяется пятью 𝑥 в квадрате над девятью.
Опять же, здесь стоит отметить, что
этот моном определен над и имеет область определения всех действительных чисел. Это означает, что домен нашего
функция 𝑓 от 𝑥 — это все действительные числа. Но мы должны быть осторожны, чтобы не
поспешно перескакивать к выводу, что 𝑓 из 𝑥 также непрерывно по всем действительным
числа. Вместо этого мы все равно должны проверить
критерии непрерывности на границе между нашими подфункциями или когда 𝑥 равно
равно трем.
Сначала найдем 𝑓 из трех по заменив на пять 𝑥 в квадрате над девятью. Это значение легко вычислить. И получаем ответ пять. Далее нам нужно проверить, что наш нормальный предел существует и также равен пяти. Если это не так, то мы разрыв в точке 𝑥 равен трем. Следовательно, наша функция не будет непрерывен в этот момент.
Чтобы двигаться вперед, мы сначала признаем
что любая сторона 𝑥 равна трем, наша функция определяется двумя разными
подфункции. Чтобы найти наш левый предел, или когда 𝑥
подходы с отрицательного направления, мы используем нашу первую подфункцию. Здесь мы уже показали, что
прямая замена 𝑥 равно трем приводит нас к неопределенной форме нуля
больше нуля, поэтому нам нужно использовать другой подход. Вместо этого мы используем правило, согласно которому
предел, когда 𝑥 приближается к нулю греха 𝑥 над 𝑥, равен единице.
Теперь наше выражение не в этом форма. И так, выполняем некоторые манипуляции, взяв коэффициент в пять раз выше нашего предела, используя постоянное множественное правило. Далее выполняем 𝑢-замена. Установив 𝑢 как 𝑥 минус три, мы получить следующее. Наш предел становится грехом 𝑢 сверх 𝑢. Однако мы не должны забывать изменить само предельное значение. 𝑢 плюс три равно 𝑥. Следовательно, 𝑢 плюс три подхода три с отрицательного направления или 𝑢 приближается к нулю с отрицательного направления направление.
Глядя на наше правило, мы знаем, что
если нормальный предел существует и равен единице, то лево- и правосторонний
пределы тоже существуют и тоже равны единице. Теперь мы можем использовать наше правило для оценки
что этот предел равен единице. Следовательно, левосторонний предел, как 𝑥
приближается к трем из 𝑓 из 𝑥, равно пятикратному единице, что, конечно, просто
пять.
Теперь наш правосторонний предел далеко
проще оценить. Для этого, поскольку мы приближаемся
𝑥 равно трем справа, мы берем предел, используя другую нашу подфункцию. Просто, путем прямой замены, мы
найти, что этот предел равен пяти.
Так как лево- и правосторонний пределы существуют и равны одному и тому же значению, поэтому мы можем заключить, что предел, когда 𝑥 приближается к трем из 𝑓 из 𝑥, также равен пяти. А раньше вы помните, что мы обнаружил, что 𝑓 из трех также равно пяти. Поскольку предел по мере приближения 𝑥 три из 𝑓 из 𝑥, равно 𝑓 из трех, мы заключаем, что 𝑓 из 𝑥 непрерывно когда 𝑥 равно трем.
Если бы вы подумали об этом
визуально это означает, что две конечные точки наших подфункций соединятся. А теперь вспомним, что ранее мы
пришел к выводу, что 𝑓 из 𝑥 непрерывно по всем действительным числам, кроме
три, которые мы должны были проверить.
И теперь, когда мы проверили три,
мы можем сказать, что наша функция 𝑓 от 𝑥 непрерывна на всех действительных
числа. И это ответ на наш
вопрос.
Чтобы подвести итоги, давайте пройдемся по несколько ключевых моментов. Функция непрерывна над интервал, если он непрерывен во всех точках указанного интервала. Функция, которую мы будем называть 𝑓 of 𝑥, непрерывна в точке, скажем, где 𝑥 равно 𝑎, если предел, как 𝑥 приближается к 𝑎 из 𝑓 из 𝑥, равно 𝑓 из 𝑎. Здесь мы отмечаем импликацию, во-первых, что этот предел существует и, во-вторых, что функция определена при 𝑥 равно 𝑎.
Полиномиальный, рациональный,
тригонометрические и экспоненциальные функции непрерывны в своих областях определения. И здесь отметим, что это не
обязательно все действительные числа. Кроме того, суммы, разности,
произведения, частные и композиции непрерывных функций также непрерывны в
точки, где 𝑥 определено правильно.
Неполадки функции могут часто можно найти, ища значения x, которые приводят к делению на ноль. И они могут быть съемными или существенные разрывы. Граница между интервалами кусочных функций следует проверить, чтобы убедиться, что концы подфункции объединяются. Если левостороннее и правостороннее пределы не совпадают в этих точках, то результатом будет скачок разрыв. Если левостороннее и правостороннее пределы совпадают, и они оба равны функции, оцененной в этой точке, тогда преемственность сохранится.
Непрерывность и дифференцируемость — Tutorialspoint
Исчисление используется во всех областях физических наук, актуарных наук, статистики, техники и в других областях, где проблема может быть математически смоделирована и требуется оптимальное решение. Непрерывность функций является одним из основные понятия топологии. Непрерывная функция — это функция, для которой достаточно небольшие изменения на входе приводят к сколь угодно малым изменениям на выходе, в то время как дифференцируемая функция одной действительной переменной — это функция, производная которой существует в каждой точке своей области.