Все формулы для векторов: Векторы — основные понятия и формулы

Содержание

основные понятия. Координаты вектора. Длина вектора

Понятие вектора
Координаты вектора в прямоугольной декартовой системой координат в пространстве
Условие коллинеарности векторов в координатах
Длина вектора и направляющие косинусы

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Тот факт, что вектор — это направленный отрезок, будет проще понять, остановившись на различиях между скалярными и векторными величинами.

В приведенной ниже таблице «Не векторы» — это скалярные величины или просто скаляры, а «Векторы» — векторные величины.

Не векторы	Векторы
Масса	Сила тяжести
Длина	Путь
Время	Ускорение
Плотность	Давление
Температура	Скорость
Объем
Площадь
Модуль вектора

Не векторы (скаляры) не имеют направления, а векторы имеют направление.

Вектор обязательно идёт от некоторой точки A по прямой к некоторой точке B. Числовое значение вектора — длина, а физическое и геометрическое — направление. Из этого и выводится первое, самое простое определение вектора. Итак, вектор — это направленный отрезок, идущий от точки A к точке B. Обозначается он так: .

А чтобы приступить к различным операциям с векторами, нам нужно познакомиться с ещё одним определением вектора.

Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.

Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.

Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.

Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.

Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.

Если A — начало вектора, а B — его конец, то вектор обозначается символом или одной строчной буквой . На рисунке конец вектора указывается стрелкой (рис. 1)

Длиной (или модулем) геометрического вектора называется длина порождающего его отрезка

Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.

В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. В курсе высшей математики векторы изучаются в разделе аналитической геометрии, где рассматриваются свободные векторы. Итак, если свободный вектор — это вектор, начало которого может быть в любой точке пространства, то все векторы одинакового направления и длины считаются равными.

Перейти к операциям над векторами

Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке, желательно открыть его в новом окне.

В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.

С произвольной точкой М пространства свяжем вектор

называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:

Числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).

Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси.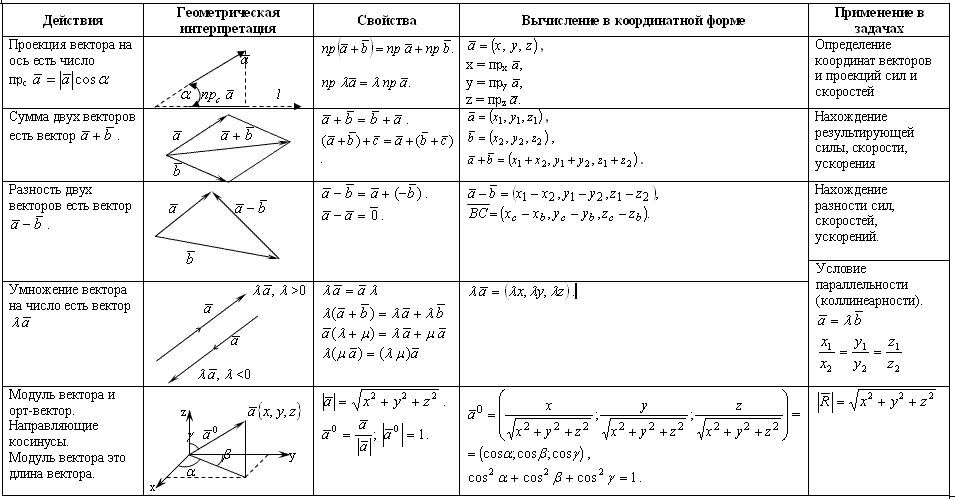 Обозначим через

Соответственно орты координатных осей Ox, Oy, Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей:

(2)

Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.

После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме

(3)

Представления вектора в виде (2) и (3) тождественны.

Векторы называются коллинеарными, если они связаны отношением

Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением

то есть, координаты векторов пропорциональны.

Пример 1. Даны векторы . Коллинеарны ли эти векторы?

Решение. Выясним соотношение координат данных векторов:

Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.

Перейти к операциям над векторами

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Векторы

Вследствие взаимной перпендикулярности координатных осей длина вектора

равна длине диагонали прямоугольного параллелепипеда, построенного на векторах

и выражается равенством

(4)

Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.

Пусть в заданной системе координат начало вектора находится в точке

а конец – в точке

(рис.8).

Тогда

Из равенства

следует, что

Отсюда

или в координатной форме

(5)

Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора

. Формула (4) в этом случае примет вид

(6)

Направление вектора определяют направляющие косинусы. Это косинусы углов, которые вектор образует с осями Ox, Oy и Oz. Обозначим эти углы соответственно α, β и γ. Тогда косинусы этих углов можно найти по формулам

Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора

или

Учитывая, что длина орта вектора равна одной единице, то есть

получаем следующее равенство для направляющих косинусов:

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 2. Найти длину вектора x = (3; 0; 4).

Решение. Длина вектора равна

Пример 3. Даны точки:

Выяснить, равнобедренный ли треугольник, построенный на этих точках.

Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:

Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.

Перейти к операциям над векторами

Пример 4. Найти длину вектора и его направляющие косинусы, если .

Решение. Координаты вектора даны:

Длина вектора равна квадратному корню из суммы квадратов координат вектора:

Находим направляющие косинусы:

Решить задачу на векторы самостоятельно, а затем посмотреть решение

Пример 5. Найти длину, направляющие косинусы и орт вектора , если , .

Правильное решение и ответ.

Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Перейти к операциям над векторами

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Векторы

Назад

Листать

Вперёд>>>

Поделиться с друзьями

Весь блок «Аналитическая геометрия»

Векторы

Понятие вектора, операции над векторами
Сложение векторов: длина суммы векторов и теорема косинусов
Скалярное произведение векторов, угол между двумя векторами
Линейная зависимость векторов
Базис системы векторов. Аффинные координаты
Векторное произведение векторов, смешанное произведение векторов

Плоскость

Уравнения плоскости, взаимное расположение плоскостей

Прямая на плоскости

Уравнение прямой с угловым коэффициентом
Общее уравнение прямой на плоскости
Уравнение прямой в отрезках
Каноническое уравнение прямой на плоскости
Параметрические уравнения прямой на плоскости
Нормальное уравнение прямой на плоскости, расстояние от точки до прямой

Как найти координаты вектора: формулы, примеры

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение координат вектора

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Нахождение координат вектора
Примеры задач

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора


Для плоских задач	AB = {B_x — A_x; B_y — A_y}
Для трехмерных задач	AB = {B_x — A_x; B_y — A_y; B_z — A_z}
Для n-мерных векторов	.. B<sub>n</sub> — A<sub>n</sub>}</em></span>» data-order=»<span class="math"><em><span style="text-decoration: overline;">AB</span> = {B<sub>1</sub> — A<sub>1</sub>; B<sub>2</sub> — A<sub>2</sub>; … B<sub>n</sub> — A<sub>n</sub>}</em></span>»>AB = {B₁ — A₁; B₂ — A₂; … B_n — A_n}

Примеры задач

Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).

Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.

Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB_x + A_x = 6 + 2 = 8.
B_y = AB_y + A_y = 14 + 5 = 19.

Таким образом, B = (8; 19).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Vectors — Mathematics A-Level Revision

Векторная величина имеет как величину, так и направление. Ускорение, скорость, сила и перемещение — все это примеры векторных величин. Скалярная величина имеет только величину (поэтому направление не имеет значения). Примеры включают скорость, время и расстояние.

Единичные векторы

Единичный вектор — это вектор, величина которого равна 1. Обычно используются три важных единичных вектора, и это векторы в направлении осей x, y и z. . Единичный вектор в направлении оси x равен i , единичный вектор в направлении оси Y равен j , а единичный вектор в направлении оси Z равен k .

Запись векторов в этой форме может упростить работу с векторами.

Величина вектора

Величина вектора может быть найдена с помощью теоремы Пифагора .

Обозначим величину вектора a через | и |

Векторы положения

Векторы положения — это векторы, определяющие положение точки относительно фиксированной точки (начала).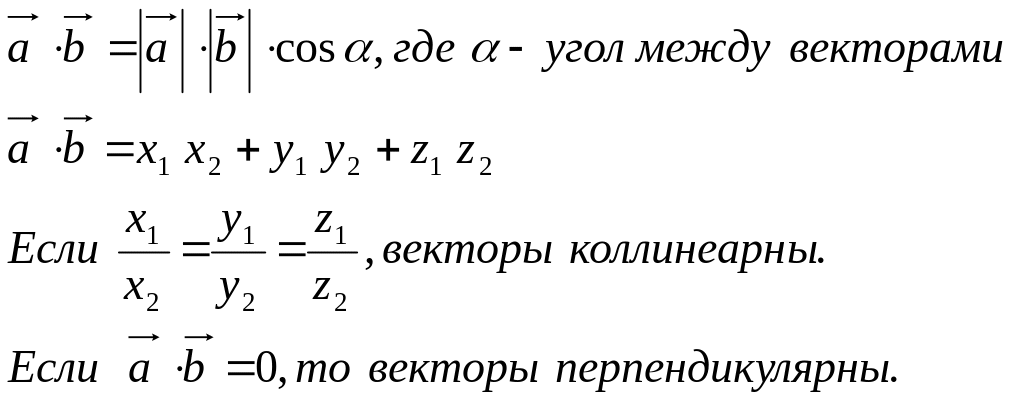

Например, точки A, B и C являются вершинами треугольника с векторами положения a , b и c соответственно:

Вы можете рисовать в начале координат, где хотите.

Обратите внимание, что = — a + b = b — a , потому что вы можете попасть из A в B, пройдя из A в O, а затем из O в B.

Векторное уравнение прямой

Векторное уравнение прямой, проходящей через точку a и в направлении d :

Это означает, что для любого значения t точка р — это точка на прямой.

Если нам даны векторные уравнения двух разных линий, мы можем выяснить, где пересекаются линии, исходя из их уравнений.

Пример

Найдите где линии с уравнениями r = i + j + t (3 i — j ) и r = — i + s ( j ) пересекаются.

При их пересечении можно приравнять уравнения: 0011 и )

Приравнивающие коэффициенты:
1 + 3t = -1 и 1 — t = s
Таким образом, t = -2/3 и s = 5/3 3 или s = 5/3 в одно из приведенных выше уравнений. Это дает — и +5 и /3 .

Скалярное произведение

Предположим, у нас есть два вектора:

a i + b j + c k и d 900 11 i + e j + f k , то их скалярное (или точечное) произведение: ad + be + fc. Итак, умножьте коэффициенты на вместе, коэффициенты на вместе и коэффициенты на вместе и сложите их все.

Обратите внимание, что это скалярное число (это не вектор).

Запишем скалярное произведение двух векторов a и b как a·b .

Пример

Если a = i + 4 j — 2 k и b 9001 2 = 2 i + 4 j + 6 k , тогда a ·b = 2 + 16 — 12 = 6

Угол между двумя векторами

Мы можем использовать скалярное произведение, чтобы найти угол между двумя векторами, благодаря следующей формуле:

Важным фактом является то, что два вектора перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю. Это потому, что если q = 90 градусов выше, то a·b = 0.

В этом видео рассматриваются векторы и скаляры.

Формула скалярного произведения через компоненты вектора
Геометрическое определение скалярного произведения гласит, что скалярное произведение двух векторов $\vc{a}$ и $\vc{b }$ это $$\vc{a} \cdot \vc{b} = \|\vc{a}\| \|\vc{b}\| \cos\тета,$$ где $\theta$ — угол между векторами $\vc{a}$ и $\vc{b}$. Хотя эта формула удобна для понимания свойств скалярного произведения, формула скалярного произведения в терминах компонентов вектора облегчила бы вычисление скалярного произведения между двумя заданными векторами.
В качестве первого шага рассмотрим скалярное произведение между стандартными единичными векторами, т. е. векторами $\vc{i}$, $\vc{j}$ и $\vc{k}$ длины один и параллельно осям координат.
Загрузка апплета
Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях, $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный), представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.
Дополнительная информация об апплете.
Поскольку стандартные единичные векторы ортогональны, мы немедленно заключаем, что скалярное произведение между парой различных стандартных единичных векторов равно нулю: \начать{выравнивать*} \vc{i} \cdot \vc{j} = \vc{i} \cdot \vc{k} = \vc{j} \cdot \vc{k}=0. \конец{выравнивание*} Скалярное произведение между единичным вектором и самим собой также просто вычислить. В этом случае угол равен нулю и $\cos\theta=1$. Учитывая, что все векторы имеют длину один, скалярные произведения равны \начать{выравнивать*} \vc{i} \cdot \vc{i} = \vc{j} \cdot \vc{j} = \vc{k} \cdot \vc{k}=1. \конец{выравнивание*}
Вторым шагом является вычисление скалярного произведения двух трехмерных векторов. \начать{выравнивать*} \vc{a} &= (a_1,a_2,a_3) = a_1\vc{i} + a_2\vc{j}+a_3\vc{k}\\ \vc{b} &= (b_1,b_2,b_3) = b_1\vc{i} + b_2\vc{j}+b_3\vc{k}. \конец{выравнивание*} Для этого мы просто утверждаем, что для любых трех векторов $\vc{a}$, $\vc{b}$ и $\vc{c}$ и любого скаляра $\lambda$ \начать{выравнивать*} (\lambda\vc{a}) \cdot \vc{b} &= \lambda(\vc{a}\cdot\vc{b}) = \vc{a} \cdot (\lambda\vc{b} )\\ (\vc{a}+\vc{b}) \cdot \vc{c} &= \vc{a} \cdot \vc{c} + \vc{b}\cdot \vc{c}. \конец{выравнивание*} (Эти свойства означают, что скалярное произведение является линейным.)
Учитывая эти свойства и тот факт, что скалярное произведение коммутативно, мы можем разложить скалярное произведение $\vc{a} \cdot \vc{b}$ по компонентам, \начать{выравнивать*} \vc{a} \cdot \vc{b} &= (a_1\vc{i} + a_2\vc{j}+a_3\vc{k}) \cdot (b_1\vc{i} + b_2\vc{j}+b_3\vc{k}) \\ &= a_1b_1 \vc{i} \cdot \vc{i} + a_2b_2\vc{j}\cdot\vc{j} + a_3b_3\vc{k}\cdot\vc{k} \\ &\quad + (a_1b_2+a_2b_1)\vc{i}\cdot\vc{j} + (a_1b_3+a_3b_1)\vc{i}\cdot\vc{k} \\ &\quad + (a_2b_3+a_3b_2)\vc{j}\cdot \vc{k}.
No related posts.