Все формулы круга и окружности: Формулы круга и окружности, формулы для расчета площади и периметра круга и окружности

Содержание

Окружность и круг | СПАДИЛО

Определения

Определение окружности

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Формула длины окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Определение

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Определение

Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

Касательная перпендикулярна радиусу, проведенному в точку касания. На рисунке 4 видно, что радиус АВ перпендикулярен касательной а.

Из одной точки можно провести две касательных к окружности. На рисунке показаны две касательные АХ и ВХ, которые проведены из точки Х.
Отрезки касательных, проведенные из одной точки, равны.
Углы, образованные касательными и отрезком, соединяющим центр окружности с точкой, из которой они идут, равны.
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
Угол, образованный касательной и хордой, измеряется половиной дуги, заключенной между его сторонами.
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть: СМ²=ВМ×АМ

Круг и его площадь

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR², где π=3,14.

Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S=π R2360..×α , где α – угол между радиусами.

Сегмент

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.

Даниил Романович | Просмотров: 2.5k

Бесплатные видеоуроки от проекта «Инфоурок»

Большая коллекция из 3243 видеоурока по 20 предметам и различным темам

УченикВероника

УчительЕвгения Вадимовна

Отличный учитель, который всегда вовлекает ученика в процесс, и сам проявляет заинтересованность в успехах ученика. Интересно слушать и работать!

УченикВероника

УчительДарья Максимовна

Дарья Максимовна замечательный, отзывчивый педагог!Обьясняет простым и доступным язык любую сложную тему- это большой плюс!! Спасибо большое моему репетитору, так как я уверена, что ОГЭ сдам на отлично !!

УченикДарья

УчительЕлизавета Владимировна

Очень качественные и продуктивные занятия. Занимаюсь не долго, но уже чувствуется прогресс. Очень милый и добрый преподаватель. Всё понятно объясняет. Мне, очень нравится заниматься математикой с Елизаветой Владимировной.

УченикКарина

УчительАндрей Юрьевич

Мне понравилось заниматься с Андреем Юрьевичем. Впервые встречаю репетитора, который прежде учить языку, рассказывает про его истоки – географию, культуру, историю. Мне очень откликается такой подход. Видно, что преподаватель с большим опытом. Я очень довольна первым занятием! Буду продолжать заниматься с данным преподавателем.

УченикМия

УчительТатьяна Александровна

Ответственная, настойчивая, харизматичная, пунктуальная, высокий уровень проф подготовки, терпеливая. Наша девочка довольна, проявляет явный интерес к урокам и продвинулась в изучаемой теме. Большое спасибо вам и преподавателю Татьяне Александровне.

УченикАлёна

УчительЕлена Петровна

Прекрасный преподаватель. После восьми занятий английский стал намного лучше, многое узнала. Все понятно в объяснении, уроки на позитиве. Благодарна за работу. Искренне рекомендую.

УченикКатя

УчительЕлена Александровна

Все понравилось приятно работать с учителем. Как по мне лучше чем Елена Александровна я еще не видела учителя по русскому языку.

УченикДиана

УчительДиана Михайловна

У Дианы Михайловны занимаются английским языком две дочери: Есения и Ксения. Девочкам очень нравится преподаватель и наполнение уроков, материал преподносится в очень интересной форме, а все объяснения понятны и доступны. Девочки уже показали успехи в изучении английского языка в школе.

УченикДмитрий

УчительСветлана Анатольевна

Дмитрий прошел со Светланой Анатольевной 4 занятия и уже виден прогресс! Мальчик по натуре немного застенчивый, поначалу был немногословен, но уже хорошо разговаривает на уроках, что говорит о профессионализме педагога.

УченикАрина

УчительИрина Сергеевна

Спасибо огромное. Очень рады, что нашли этот ресурс для занятий. Ирина Сергеевна объясняет все быстро, понятно и динамично. Всего за несколько занятий наверстали упущенное по химии и прошли дальше. Обязательно будем обращаться в дальнейшем.

УченикЕлизавета

УчительРимма Николаевна

У Елизаветы есть успехи, занимается с удовольствием и заинтересованностью. Римма Николаевна очень интересно преподносит материал. Очень нравится учитель, занимаемся с удовольствием.

УченикАртём

УчительНина Ивановна

Нам понравилась Нина Ивановна, хороший человек и прекрасный педагог. Очень ответственная, трудолюбивая и толковая. Сразу нашла подход к ученику. Доходчиво объяснит любую тему. Преподаватель, в отличии от многих репетиторов не просто отбывает время, а действительно помогает.

УченикЭдуард

УчительЖанна Сергеевна

Замечательный педагог, нашла подход с первых занятий. Все очень доходчиво и понятно объясняет. Ребенку очень нравится, просит дополнительные часы для занятий.

УченикЛюдмила

УчительРита Ивановна

Добрый день! Рита Ивановна очень профессионально оценила все пробелы моего сына и нам бы хотелось продолжить с ней обучение! Занятия очень хорошие, учитель понятно все объясняет, всем рекомендую.

УченикСветлана

УчительОльга Олеговна

Спасибо Ольге Олеговне за проведённый урок в праздничный день. Здоровья, процветания, побольше радостных событий в жизни, благополучия, успехов и удачи в таком не лёгком и таком нужном труде!!! Спасибо за урок, всё понравилось!

УченикИрина

УчительТатьяна Николаевна

Очень грамотный педагог, хорошо подходит к вопросам с которыми обращаемся, подход к ребенку очень понравился, буквально на 5-8 урок у ребенка был уже прогресс и теперь любит математику. На урок математики приходим с удовольствием, подтянули свои недочеты, решаем быстро примеры, а главное сами. Спасибо за знания!

УченикПолина

УчительСветлана Михайловна

Светлана Михайловна очень хороший учитель, за урок мы разбираем много вопросов и обсуждаем правила русского языка в каждом конкретном примере. Занимаюсь с удовольствием!

УченикМария

УчительДарья Александровна

Замечательный, приятный и внимательный преподаватель. Ребенок сначала засмущался от непривычного формата урока, но Дарья Александровна, в итоге, смогла завоевать внимание и доверие дочери. Обязательно будем продолжать обучение! Спасибо!

УченикАнтон

УчительСветлана Васильевна

Репетитор быстро оценила проблемы, порекомендовала способы восполнения пробелов. Продолжим заниматься дальше, так как Светлана Васильевна доступно объясняет материал, и все сразу становится понятным. Классный репетитор, советую!

УченикСофия

УчительГалина Михайловна

Добрый день! Галина Михайловна — замечательный педагог! Мне все было очень понятно и вообще было приятно общаться! Была непонятна тема : ,, Не /ни с глаголами ,,. После того, как Галина Михайловна объяснила, все трудности были сняты. Огромное спасибо !!! 🙏

УченикЛеонид

УчительЕлена Александровна

На уроке педагог работала по индивидуальной программе, выявила пробелы в знаниях и все доходчиво разъяснила. Сложные темы, объяснили легко и понятно, сыну все очень понравилось!

УченикГалина

УчительТамара Иосифовна

Замечательный педагог и очень доброжелательный человек!!! Тамара Иосифовна очень доходчиво объяснила непонятные для меня моменты, причем из разных тем, за один урок!!! Урок проходил в спокойной и дружественной обстановке. Спасибо большое!!! Очень понравилось!!!

УченикМария

УчительВладимир Григорьевич

Спасибо большое, Вы лучший преподаватель по информатике. Как хорошо, что есть такая замечательная платформа. Спасибо всем, кто ее организовал и Вам лично. Всем друзьям и знакомым буду рекомендавать! онлайн-уроки.

УченикОльга

УчительИрина Ивановна

Очень понравился урок! Ирина Ивановна с первых минут расположил к себе ребёнка так, что даже мой непоседливый и не очень настроенный на учебу пятиклассник увлекся так, что не заметил, как пролетели 45мин. Спасибо! С удовольствием продолжим занятия!

УченикФёдор

УчительНаталия Анатольевна

Как родитель могу сказать, что самое важное — это расположить к себе ребенка. Уже после первого занятия с Наталией Анатольевной я увидела желание заниматься в глазах своей дочери. Занятие проходило очень комфортно. Понравилось, как построена программа проверочного урока.

УченикПолина

УчительМарина Михайловна

Мне очень понравилось вводное занятие, спасибо большое. За пол часа Марина Михайловна с помощью разговора поняла все мои слабые места и помогла многие из них подправить и понять. Я хочу заниматься с ней и далее.

УченикАйсултан

УчительГалина Дмитриевна

Здравствуйте! У нас был пробный урок с Галиной Дмитриевной по математике. Занимались именно логическими задачами. Учитель имеет очень хороший подход к детям и у нее есть своя отработанная хорошая методика. Хорошо объясняет, приятная. Спасибо!

УченикВиктор

УчительЮлия Анатольевна

Спасибо большое учитель объясняет очень хорошо там где ты что либо не поймёшь педагог тебе всё объяснит как раз педагог сказала повторить всё то что мне говорил предыдущий репетитор СПАСИБО БОЛЬШОЕ !!!

УченикМаксим

УчительАлёна Юрьевна

Благодарим за интересное и познавательное занятие! Преподаватель четко и внимательно ведет занятие, обращает внимание на моменты, которые необходимо доработать. Профессионально! Приятно общаться.

УченикАлександр

УчительАнастасия Сергеевна

Добрый день! Мы безумно рады, что нам посчастливилось найти такого замечательного и удивительного педагога, как Анастасия Сергеевна! Она очень интересно проводит урок, ребёнок безумно рад. Сразу чувствуется, что человек талантливый. С нетерпением ждём новый урок.

УченикЕкатерина

УчительСергей Васильевич

Спасибо за урок! Занятие очень понравилось, Сергей Васильевич все понятно и интересно обьясняет, во время урока была доброжелательная атмосфера. Также учитель посоветовал некоторые книги и способы подготовки к экзамену. Спасибо!!!

УченикКарина

УчительГулез Гаджимурадовна

Нравятся все педагоги с которыми мы занмаемся, все обладают высоким уровнем профессионализма,используют интересные и современные методы и технологии обучения. Имеет хороший уровень научно-методической подготовки. Ребенок занимается с большим интересом. Будем заниматься с Вами до окончания школы, сейчас мы в 4 классе)

УченикФеона

УчительНаталия Михайловна

За 45 минут узнала и поняла больше, чем за полгода в школе. Учитель объясняет очень понятно, доходчиво, выше школьного уровня. Однозначно этот урок не последний. С Уважением, Феона.

УченикЕкатерина

УчительНаталья Васильевна

Спасибо, Наталья Васильевна! Профессионально, четко, по делу. Педагог очень терпеливая, спокойная, уверенная. Занятие очень понравилось и ребенку и мне, маме.

УченикМаксим

УчительАлександр Александрович

Спасибо большое Александру Александровичу. Очень быстро нашел подход к ребёнку , а так же увлек математикой! Ребёнку было комфортно общаться. Надеемся встретиться на следующих занятиях.

УченикМарина

УчительНиколай Васильевич

Николай Васильевич помог за короткий срок восполнить пробелы в знаниях, за что очень благодарны! Уроки очень интересные! Будем обращаться еще к нему.

УченикМарина

УчительАлександр Сергеевич

Занятия ребенку с Александром Сергеевичем очень нравятся. Все схватывает, доволен уроками. С репетитором нашли общий язык. Мы очень благодарны Александру Сергеевичу! Хороший педагог. Спасибо.

УченикЕлизавета

УчительАлёна Игоревна

Дети понимают всё, абсолютно. В школе не понимают ничего, а с Вашими репетиторами понимают всё. Сдвиги очень большие. Алёна Игоревна хороший педагог. Все занятия результативные.

УченикДжу Уван Ми

УчительГалина Михайловна

Плохо знаю русский язык, и постоянно делаю многие ошибки в тексте и в работе. Только благодаря достуным объяснениям учителя я мог самостоятельно находить ошибки. Большое спасибо за Вашу работу и сердечные помощи в изучении русского языка!

УченикРоман

УчительИрина Алексеевна

Мой сын занимался с Ириной Алексеевной, очень понравилось, всё спокойно и понятно было показано, рассказано. Очень профессионально и качественно выстроены занятия, учитель доброжелателен, ребенку интересно заниматься.

УченикЖеня

УчительОльга Сергеевна

Ольга Сергеевна — профессинал своего дела. Высококвалифицированный педагог. По английскому нужно было именно аудирование и речь, 100% подобрали репетитора по нашему запросу. Педагог строгий — то, что нужно моему ребёнку. Мы очень довольны!

УченикНикита

УчительСарвар Шодиевич

До этого никогда не занимался у репетиторов, думал что буду сидеть ничего не понимать и всё время уйдёт зря. Однако Сарвар Шодиевич очень понятно объясняет, не подчёркивает ваши «незнания» и до упора старается всё разъяснить. Могу с уверенностью посоветовать этого репетитора каждому, кто хочет разобраться в алгебре и геометрии.

УченикВиктор

УчительЮлия Анатольевна

УченикЭльмира

УчительЛюдмила Евгеньевна

Выражаю благодарность центру где есть такие сильные и ответственные учителя. Отдельная благодарность Людмиле Евгеньевне за опыт за знания.

УченикДарья

УчительОльга Александровна

Ольга Александровна отлично объясняет темы, с ребенком нашла общий язык моментально. Дочь занимается с удовольствием, пробелы подтянули за пару уроков. Спасибо Вам большое!

УченикОлеся

УчительГузалия Робертовна

Сыну очень понравилось заниматься с Гузалией Робертовной. Очень внимательный и доброжелательный педагог, который сразу видит слабые стороны. Всячески поощряет ребёнка и помогает поднять самооценку. Большое спасибо!

УченикДарья

УчительМария Никитична

Нравится, как преподает Мария Никитична (по программе школы + присутствует игровая минутка, ученице на занятиях не бывает скучно) Уровень знаний повысили до 5-ки, значительно расширили словарный запас. Все устраивает, рекомендует знакомым и в целом рада, что такая платформа существует.

УченикОлеся

УчительДаниил Станиславович

Спасибо. Урок понравился. Даниил Станиславович заинтересовал английским языком. Составили предположительные темы для занятий после новогодних праздников

УченикГеоргий

УчительЕкатерина Станиславовна

Грамотный, добрый, располагающий к себе педагог. С ребёнком Екатерина Станиславовна установила хороший контакт. Преподносит информацию очень доступно. Занятие проходит разнообразно, в том числе в игровой форме. Рекомендуем 5+

УченикНиколя

УчительАлла Валентиновна

Алла Валентиновна отличный преподаватель! Выявила все пробелы в знаниях Константина по русскому языку и работает над их устранением. Также помогает в работе над текущими темами урока. Уже прошли несколько занятий и продолжаем заниматься. нашла общий язык с сыном. Все нравится. Хотим заниматься дальше!

УченикПолина

УчительСветлана Григорьевна

Светлана Григорьевна просто супер учитель!!!! Все очень понятно и хорошо объясняет, прохожу с ней темы по географии 6 класса. На уроке с ней очень интересно. Уже 2 урока — одно удовольствие!!!

УченикНаталья

УчительСергей Александрович

Классный репетитор, все темы разбираются на 5+, будем обязательно продолжать обучение, также рекомендуем всем ученикам!

УченикМаксим

УчительНадежда Викторовна

Замечательный педагог, с которым нравится заниматься. Максим готовится к сдаче ОГЭ по русскому языку и занимается с репетитором с начала ноября прошлого года. За это время успели повторить пройденный материал и изучить несколько тем нового материала. Надежда Викторовна объясняет материал в доступной форме. Максим продолжит с ней занятия.

УченикАлександра

УчительИрина Борисовна

Отличный репетитор ! Ирина Борисовна обьясняет сложные темы простым и доступным языком ! Сердечно благодарю педагога за грамотность и профессионализм !!!!

УченикФеона

УчительЯнина Александровна

Преподаватель компетентный, объясняет понятно, выше школьного уровня. Быстро заполняет пробелы в знаниях. Будем сотрудничать. С Уважением, Феона.

УченикМадина

УчительМария Анатольевна

Очень чётко и понятно объяснила Мария Анатольевна. Спасибо вам. Не смотря первый раз, пробную занятия, она прям очень понравилась дочке и естественно мне💐. В дальнейшем обязательно будем заниматься с ней и подниматься.

УченикВероника

УчительЕвгения Вадимовна

УченикВероника

УчительДарья Максимовна

УченикДарья

УчительЕлизавета Владимировна

УченикКарина

УчительАндрей Юрьевич

Формула круга — Геометрия Формулы круга

Окружность представляет собой набор точек на плоскости, расположенных на одинаковом расстоянии от фиксированной точки (центра окружности).

Хорда окружности — это расстояние между двумя точками окружности. Наибольшая хорда называется диаметром окружности. Радиус круга равен половине диаметра.

Длина окружности — это расстояние по окружности. Если r — радиус окружности, то длина окружности равна 2πr, где π примерно равно 3,14. Площадь круга радиуса r равна πr ² .

В приведенном выше круге O — центр круга, AB и CD — хорды. АВ — диаметр, ОВ — радиус. Если OB = 5, то периметр круга или длина окружности равна 2π(5) = 10π, а площадь круга равна π(5) ² = 100π.

Дуга: Является частью круга. Большая дуга — это дуга, большая, чем полуокружность, а малая дуга — это дуга, меньшая, чем полуокружность.

Конгруэнтные окружности : Окружности с равными радиусами называются конгруэнтными окружностями.

Концентрические окружности : Окружности, имеющие один и тот же центр, называются концентрическими окружностями.

Касательные окружности : Окружности, лежащие в одной плоскости и соприкасающиеся снаружи в одной точке, называются касательными окружностями.

Линия, перпендикулярная диаметру или радиусу окружности в точке касания окружности, называется касательной. Прямая L касается окружности, а радиус OT перпендикулярен прямой L.

Если каждая вершина многоугольника лежит на окружности, то многоугольник вписан в окружность, а окружность называется описанной. Если каждая сторона многоугольника касается окружности, то многоугольник описан вокруг окружности, а окружность вписана в многоугольник.

На рисунке выше четырехугольник PQRS вписан в окружность, а шестиугольник ABCDEF описан вокруг окружности.

Если в окружность вписан треугольник, одна из сторон которого равна диаметру окружности, то треугольник прямоугольный. В приведенном выше круге XZ — диаметр, а мера угла XYZ — 90°.

Некоторые важные свойства окружностей:

Перпендикуляр из центра окружности к хорде окружности делит хорду пополам.

И наоборот, линия, соединяющая центр окружности и середину хорды, перпендикулярна хорде.
Конгруэнтные окружности или равные хорды равноудалены от центра.

И наоборот, две хорды окружности или конгруэнтных окружностей, равноудаленных от центра, равны. Две хорды PQ, RS пересекаются в точке, тогда CP × CQ = CR × CS

В круге или конгруэнтных кругах равные хорды образуют равные углы в центре.

И наоборот, хорды, стягивающие равные углы в центре конгруэнтных или одинаковых окружностей, равны.
Если две окружности касаются друг друга снаружи, расстояние между их центрами равно сумме их радиусов.

Если два круга касаются друг друга внутренне, расстояние между их центрами равно разнице их радиусов.
Вписанный угол равен половине длины дуги, на которую он опирается. (Теорема о вписанном угле). ∠ACB = ½ дуги (ADB) = ½ ∠AOB.

Стягивающие углы одинаковые отрезки равны:

∠AP ₁ B = ∠AP ₂ B. Угол, образуемый полуокружностью, равен 90°
, т. е. ∠AP ₁ B = 90° = ∠AP ₂ B

Угол, стягиваемый в малом сегменте, тупой, а в большом сегменте — острый.
∠AP ₁ B > 90° и ∠AP ₂ B < 90°
Для двух окружностей с центрами A и B RS и PQ — прямые общие касательные, а EF и CD — поперечные общие касательные.

(Возможны только две поперечные общие касательные и прямые общие касательные.)
Касательная всегда перпендикулярна линии, соединяющей центр и точку касания.

Две касательные из одной внешней точки имеют одинаковую длину. PA = PB

Если AB — хорда окружности, а PC — касательная (оба для внешней точки P), то PA × PB = PC ²
Длина прямой общей касательной = √(расстояние между центрами) ² — (r ₁ — r ₂ ) ²
Длина поперечной общей касательной = √(расстояние между центрами) ² — (р ₁ + р ₂ ) ²
Теорема об альтернативном отрезке:

Угол между любой хордой (в точке касания) и касательной равен углу, образуемому хордой в любой точке по другую сторону отрезка (альтернативного отрезка).
На рис. ∠CBP ₂ = ∠CAB = X° и ∠P ₁ BA = ∠ACB = Y°

Вписанные четырехугольники:

Четырехугольник называется вписанным, если противоположные углы четырехугольника являются дополнительными и все его вершины лежат на окружности. Точки, лежащие на окружности, называются коциклическими.

Противоположные углы вписанного четырехугольника дополнительные. И наоборот, если противоположные углы четырехугольника дополнительные, то это вписанный четырехугольник.

Внешний угол вписанного четырехугольника равен углу, противоположному прилежащему к нему внутреннему углу. ∠BCE = ∠DAC.

Для любого вписанного четырехугольника сумма произведения двух пар противоположных сторон равна произведению диагоналей.

PQ × RS + QR × SP = PR × SQ.

Площадь вписанного четырехугольника = √(s-a)(s-b)(s-c)(s-d), где s — полупериметр, а a, b, c и d — стороны четырехугольника.

Площадь вписанного в окружность четырехугольника, в который можно вписать окружность =√a×b×c×d , где a, b, c и d — стороны четырехугольника.

Секторы окружности:

Количество градусов дуги в окружности (или количество градусов в полном обороте) равно 360.

В показанной выше окружности с центром O длина дуги RS равна x/ 360 окружности круга; например, если x = 60°, то дуга RS имеет длину 1/6 длины окружности. Мы можем запомнить следующие формулы:

Предлагаемое действие:

Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас

Длина дуги RS = 2πr × x/360. ∵ Полный круг имеет 360 градусов, и любая его часть должна быть равна x/360.
Площадь сектора ORS = πr ² x/360. ∵ Полный круг имеет 360 градусов, и любая его часть должна быть равна x/360
Площадь сегмента круга (QSR) = r ² [(πθ / 360°) — (sinθ / 2)]
Периметр сегмента = 2πr(θ / 360°) + 2rsin(θ/2)

Круги в ACT Математика: геометрические формулы и стратегии

Одной из самых любимых фигур ACT является круг (по крайней мере, мы так предполагаем, учитывая, как часто круги встречаются в тесте). Вам не дадут никаких формул на ACT, поэтому вам нужно будет знать и запоминать все тонкости работы кругов до дня экзамена. И, учитывая, как часто появляются круги, решение задач с кругами определенно в ваших интересах.

Это будет ваше полное руководство по кругам ACT , включая площади, окружности, градусы, дуги и точки на окружности. Мы расскажем вам, что означают эти термины, как манипулировать и решать различные аспекты круга, а также как решать самые сложные вопросы круга ACT, которые вы можете увидеть в день экзамена.

Что такое круги?

Окружность образована из бесконечного числа точек, равноудаленных (на одинаковом расстоянии) от одной точки — центра окружности. Круг также является двумерной формой, что означает, что он абсолютно плоский.

Таким образом, любые прямые линии, проведенные из центра, точно попадут на край круга, если все линии имеют одинаковую длину.

Градусы и радианы

Окружность измеряется либо в градусах, либо в радианах. Оба являются способами выразить либо весь круг, либо части круга.

Полный круг имеет 360 градусов. Полукруг (половина круга) имеет $360/2 = 180$ градусов, поэтому прямая равна 180 градусам.

Чтобы найти часть круга, вы должны найти ее относительно 360 градусов. Таким образом, восьмая часть окружности составляет 360 долларов США (1/8) = 45 долларов США градусов, а треть окружности равна 360 долларов США (1/3) = 120 долларов США и т. д.

Так же, как круг имеет 360 градусов, вы также можете сказать, что он имеет $2π$ радиан. Вы находите радианную меру частей круга точно так же, как вы находили части круга, используя градусы.

Таким образом, восьмая часть окружности в радианах составляет $2π(1/8) = π/4$ радиан, а треть окружности в радианах составляет $2π(1/3) = {2π}/3$ радиан и т. д. (Для получения дополнительной информации о радианах ознакомьтесь с нашим руководством по тригонометрии ACT.)

Окружность

Окружность — это край круга. Он составлен из бесконечных точек, равноудаленных от центра.

Диаметр

Диаметр — это любая прямая линия, проведенная через центр круга, которая соединяет две противоположные точки на окружности круга.

Радиус

Радиус круга — это прямая линия, проведенная из центра в любую точку окружности. Это всегда половина диаметра.

Касание

Окружности часто называют касательными друг к другу. Это означает, что они соприкасаются ровно в одной точке на каждой окружности. Они могут быть внутри друг друга (как на этом рисунке) или касаться «снаружи» в одной точке.

π (пи)

Если вы посещали уроки геометрии, то, вероятно, вы также знакомы с π (пи). π — математический символ, представляющий отношение длины окружности любого круга к его диаметру. Обычно выражается как 3,14 (159), но его цифры продолжаются бесконечно. (Дополнительную информацию о соотношениях см. в нашем руководстве по соотношениям ACT.)

Допустим, у нас есть круг определенного диаметра (подойдет любой диаметр).

Теперь давайте выстроим этот же круг так, чтобы у нас была серия одинаковых измерений диаметра подряд.

Теперь, если мы выберем точку на окружности круга и выровняем ее в начале линии, мы сможем затем «развернуть» окружность, чтобы увидеть ее длину.

Как только мы развернем окружность и разложим ее, мы увидим, что ее размер чуть более чем в 3 раза больше диаметра окружности (в частности, 3,14159, или π, умноженное на диаметр).

Независимо от того, каков диаметр круга, длина окружности всегда будет в π раз больше диаметра. Итак, если диаметр круга равен 1, то его длина окружности равна π. А если его диаметр равен 2, то его окружность равна 2π и т. д.

Вы знаете все свои определения (ух!), и что теперь? Что ж, пришло время собрать кусочки в наши надежные формулы круга!

Формулы круга

Вам не дадут никаких формул на тесте , поэтому вам нужно будет выучить эти формулы круга ACT наизусть, чтобы решить свои круговые задачи. Давайте посмотрим на все формулы, которые вам понадобятся.

Окружность

$$c = πd$$

Поскольку π представляет собой отношение между диаметром окружности и ее окружностью, вы всегда можете найти длину окружности, если знаете ее диаметр (или радиус) с помощью формулы:

$c = πd$ или $c = π2r$

Поскольку участник должен бежать по кругу, он бежит по окружности. И нам говорят, что она сделает это 3 раза, чтобы завершить свою гонку.

Таким образом, петля с 1 дорожкой будет:

$c_{1 \loop} = π2r$ (нам говорят, что радиус равен «$R$», поэтому мы можем оставить его как есть.)

И 3 -track loop будет:

$c_{3 \loop} = (π2r) * 3$

$π6r$

Итак, наш окончательный ответ K 92$$

Вы также можете использовать π для нахождения площади круга, так как площадь круга тесно связана с его окружностью. (Почему? Потому что круг состоит из бесконечных точек, а значит, он, по существу, состоит из бесконечных треугольных клиньев — в основном пирога с бесконечным числом ломтиков. Высота каждого из этих клиньев будет радиусом круга, а совокупная основаниями будет длина окружности.)

Таким образом, вы сможете найти площадь круга, используя формулу: 92({\arc \степень}/360°)$$

Чтобы найти длину окружности дуги окружности (или площадь клина, сделанного из определенной дуги), вы должны умножить стандартные формулы окружности на дробь окружности, которую охватывает дуга.

Чтобы определить долю окружности, которую охватывает дуга, вы должны иметь градусную меру дуги и найти ее меру из полных 360 градусов окружности. Таким образом, если вы хотите найти длину окружности дуги, составляющей 90°, она будет равна $1/4$ общей площади круга. Почему? Потому что $360/90 = 4$ (другими словами, 90/360 = 1/4$).

Чтобы найти меру окружности дуги, мы должны иметь как градусную меру, так и радиус или диаметр окружности. К счастью, все это у нас есть.
Градусная мера дуги, как нам говорят, равна 45.
Верхняя диаграмма говорит нам, что диаметр окружности равен 24 футам.
Таким образом, длина окружности нашей дуги равна:
$c \arc = πd({\arc \degree}/360°)$
$c \arc = π24(45/360)$
$c = 3π$
Поскольку мы видим, что в нашем ответе не используются единицы измерения $π$, давайте преобразуем наш ответ в цифры, заменив $π$ на 3,14.
$3π = 3(3,14)$
$9,42$
Мы успешно нашли измерение нашей дуги, но мы еще не совсем закончили. Вопрос заключается в том, чтобы найти полную длину молнии , которая охватывает длину дуги, а также радиус окружности. Это означает, что мы должны найти наш радиус и добавить его к нашему измерению дуги.
Радиус круга равен 12. Почему 12? Потому что наш диаметр составляет 24 фута, а радиус круга всегда равен половине диаметра. $24/2 = 12$
Таким образом, если мы сложим нашу меру дуги и наш радиус вместе, мы получим:
$9,42 + 12 = 21,42$
И самый близкий ответ, соответствующий нашему измерению 21,42, — это вариант ответа G, 22.
Это означает, что наш окончательный ответ G , 22.

Обладая небольшим знанием формул (и, предположительно, некоторым глазом тритона), вы можете решить любые задачи с кругами. Магия!

Типичные вопросы с кругами в ACT
Задания с кругами в ACT могут быть одного из двух типов: задача с диаграммой или задача со словами. Давайте рассмотрим каждый тип.

Задача с диаграммой
Задача с диаграммой даст вам диаграмму, с которой можно работать. Вы должны использовать визуализацию, которую вам предоставили, и либо найти недостающую часть, либо найти эквивалентные размеры или различия.
Полезный совет: часто (хотя и не всегда) хитрость в решении задачи с кругом заключается в нахождении и понимании радиуса. Все линии, проведенные от центра к окружности, являются радиусами и, следовательно, равны, и это часто играет жизненно важную роль в решении всей проблемы.

Мы надеемся найти одно утверждение, которое НЕ соответствует действительности, поэтому давайте пройдемся по ним и посмотрим, какие из них верны, а какие неточны.
Вариант ответа F говорит о том, что угол TUM равен 65°. Итак, мы знаем, что угол TMU должен быть равен 50°, потому что это среднеквадратичное значение противоположного угла, а противоположные углы равны. (Подробнее об этом читайте в нашем руководстве по линиям и углам ACT.)
Мы также знаем, что линии TM и MU равны. Почему? Потому что они оба являются радиусами круга (линии от центра к окружности круга), и поэтому они должны быть равны. Это означает, что треугольник TMU является равнобедренным треугольником, а значит, углы MTU и TUM равны.
В треугольнике 180°, поэтому, если вычесть 50°, мы получим:
$180 — 50 = 130$
Это означает, что каждый из углов MTU и TUM в сумме равен 130. И, поскольку они равны, мы можем найти их меру, разделив 130° пополам.
$130/2 = 65$
Итак, F верно, угол TUM равен 65°.
Теперь рассмотрим вариант G, в котором говорится, что прямые RS и TU параллельны. Мы знаем, что это правда. Почему? Потому что вместе треугольники образуют два диаметра круга. И поэтому прямые линии вниз от того места, где эти диаметры касаются окружности круга, будут параллельны.
H говорит, что дуга TXU измеряет 50°. Мы уже знаем, что это так, потому что угол RMS равен 50°, а противоположный ему угол равен TMU, который также должен быть равен 50°. Поскольку дуга TXU содержит угол TMU и состоит из него, ее размер также должен быть равен 50°.
Вариант ответа J говорит о том, что строка RM = строка TM, что, как мы также знаем, верно. Почему? Потому что они оба являются радиусами окружности и поэтому должны быть равны.
Методом исключения это должно означать, что K неправильный (и, следовательно, наш окончательный выбор), но давайте удостоверимся.
K говорит, что линии RS и SM равны, но мы уже знаем, что это не может быть правдой. Почему? Поскольку RM и MS оба являются радиусами, они должны быть равны, а RMS угла равен 50°, что означает, что треугольник не является равносторонним. Поскольку это не равносторонний треугольник, линии RM и TM не могут быть равны. (Примечание: если этот вопрос вас смутил, ознакомьтесь с нашим руководством по треугольникам ACT)
Таким образом, наш окончательный ответ — K. каким-то образом вращается по кругу. Как вы видели ранее в разделе, посвященном площадям и окружностям, вопросы со словами часто будут немного более простыми, чем вопросы с диаграммами, поскольку картинка вам не дается.
Когда вам задают проблемный вопрос, рекомендуется сделать собственный быстрый набросок сцены. Это поможет вам сохранить все детали в порядке.
Поскольку это задача со словами, давайте создадим собственную картину этой сцены.
Во-первых, мы знаем, что у нас есть круглый стол. Нам говорят, что это 3 фута в диаметре (другими словами, 36 дюймов), поэтому давайте нарисуем его.
Теперь скатерть будет прямоугольной формы и будет свисать не менее чем на 5 дюймов из любой точки круглого стола.
Наконец, нам понадобится еще по 1 дюйму скатерти с каждой стороны (чтобы сшить в качестве последнего штриха).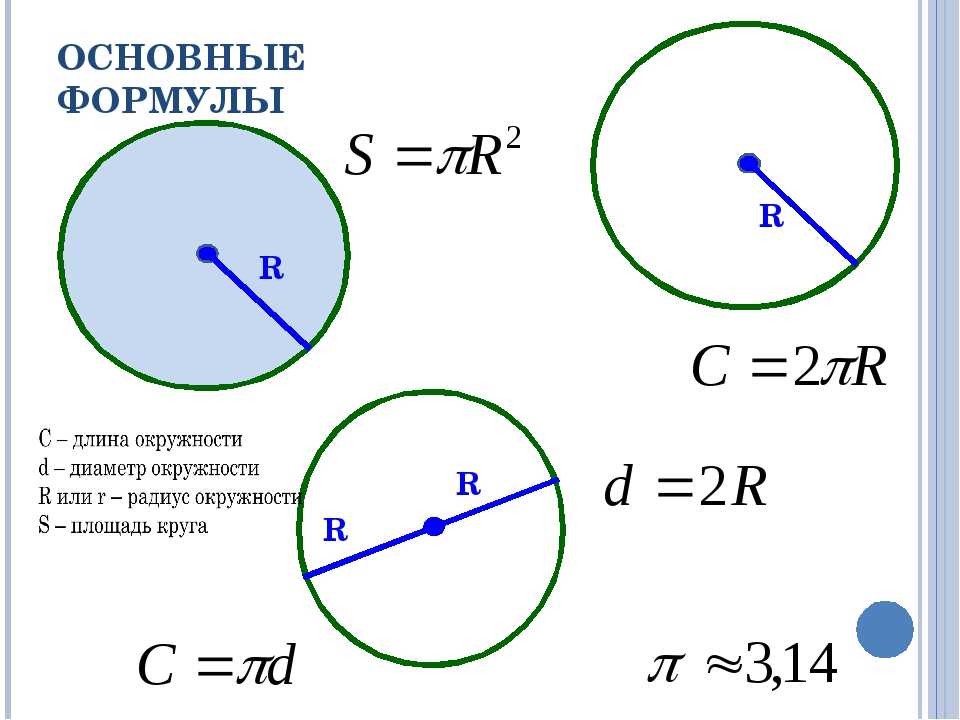
Теперь мы можем просто считать наши дюймы сверху вниз (или из стороны в сторону) по прямой линии. Это скажет нам минимальную длину, необходимую для ткани.
Если мы пройдем сверху вниз, то увидим, что нам потребуется:
1$ + 5 + 36 + 5 + 1$
48$ дюймов ткани.
Наш окончательный ответ: K, 48.

Реальные (и вкусные) применения окружностей и площадей.

Как решить задачу с кругом
При возникновении задачи с кругом не забудьте использовать следующие математические стратегии ACT: Как только вы откроете математический раздел ACT, выделите 20 секунд и запишите свои формулы. Таким образом, вы будете иметь их в качестве ориентира до конца отведенного вам времени, и вы не будете беспокоиться о том, чтобы забыть их в пылу момента, когда они понадобятся вам позже.
#2: Нарисуйте свои собственные диаграммы
Если вам не дали схему, нарисуйте ее сами! Создание собственного изображения не займет много времени, и это может избавить вас от горя и борьбы во время прохождения теста.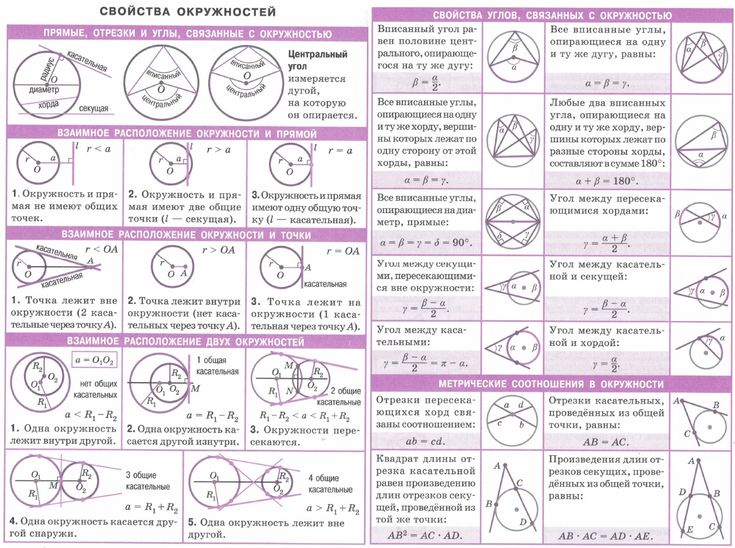 Может быть слишком легко сделать предположение или перепутать числа, когда вы пытаетесь выполнить математику в уме, поэтому не бойтесь уделить время и нарисовать свои собственные картинки.
А если тебе дадут схему, нарисуй и ее! Отметьте конгруэнтные линии и углы, запишите свои измерения радиуса или заданные вами углы. Отметьте любую информацию, которая вам нужна или которую вы получили. Причина, по которой не все отмечено на ваших диаграммах, заключается в том, что вопрос не будет слишком простым, поэтому всегда записывайте свою информацию самостоятельно.
#3: Проанализируйте, что на самом деле от вас требуется
Все формулы в мире не помогут вам, если вы думаете, что должны найти площадь, но на самом деле вас просят найти длину окружности . Всегда помните, что стандартизированные тесты пытаются заставить вас решать вопросы способами, которые вам, вероятно, незнакомы, поэтому внимательно читайте и обращайте пристальное внимание на вопрос, который вам на самом деле задают.
#4: Используйте свои формулы
После того, как вы проверили, что должны найти, большинство вопросов с кругами довольно просты. Вставьте свои данные в свои формулы, изолируйте недостающую информацию и решите. Вуаля!

Вкусный математический заговор?

Проверьте свои знания
А теперь давайте проверим свои знания по кругу на этих реальных математических задачах ACT.
1.

2.
3.
Ответы: B, B, H
Ответ Объяснения:
1. В порядке. мера части круговой диаграммы, мы должны определить долю (или процент) сектора, с которым мы работаем, по сравнению со всей величиной круга.
В этом случае мы хотим узнать, какая доля людей в целом проголосовала за Гомес, чтобы определить, какая часть круговой диаграммы должна быть отведена голосам Гомеса.
Если 40 человек из 200 проголосовали за Гомес, то голоса Гомес составляют:
$40/200$
$1/5$ от общего количества голосов.
Поскольку голоса Гомес составляют 1/5$ от общего числа голосов, они должны занимать 1/5$ на круговой диаграмме.
Окружность 360 градусов. Итак:
$(360)(1/5) = 72$
Дуговой сектор голосов Гомеса будет на круговой диаграмме под углом 72 градуса.
Итак, наш окончательный ответ B.
2. Нам дан диаметр 8 и нам нужно найти периметр всей фигуры из двух полукругов и квадрата.
Вместе два полукруга образуют полный круг диаметром 8, а их окружность составляет часть периметра. Это означает, что мы должны найти длину окружности, которую образуют два полукруга, сложенные вместе.
$c = πd$
$c = π(8)$
Таким образом, длина окружности, которую образуют две полуокружности, равна $8π$.
(Поскольку мы имеем дело с полукругами, вы также можете найти половину каждой из их окружностей, сказав: ${1/2}c = 8π$ => $4π$. Каждая из их окружностей будет равна $4π$, поэтому вместе они составят: $4π + 4π = 8π$ В любом случае общая длина окружности периметра составит $8π$.)
Теперь мы должны добавить это к остальной части периметра, которая образована частью квадрата. Две стороны квадрата (обе равны 8) составляют часть периметра, поэтому мы имеем:
$p = 8 + 8 + 8π$
$p = 16 + 8π$
Итак, наш окончательный ответ — B.
3. Поскольку мы работаем с окружностями, мы знаем, что линии PS и PT являются радиусами. Почему? P является центром окружности, а точки T и S лежат на окружности, поэтому мы знаем, что линии, соединяющие их, являются радиусами.
Поскольку PS и PT равны, а угол PST равен 30 градусам, это означает, что угол PTS также равен 30 градусам. Почему? Углы напротив равных прямых равны (подробнее об этом читайте в нашем руководстве по треугольникам ACT).
Это означает, что мы можем найти угол TPS, поскольку фигура представляет собой треугольник (всего 180 градусов).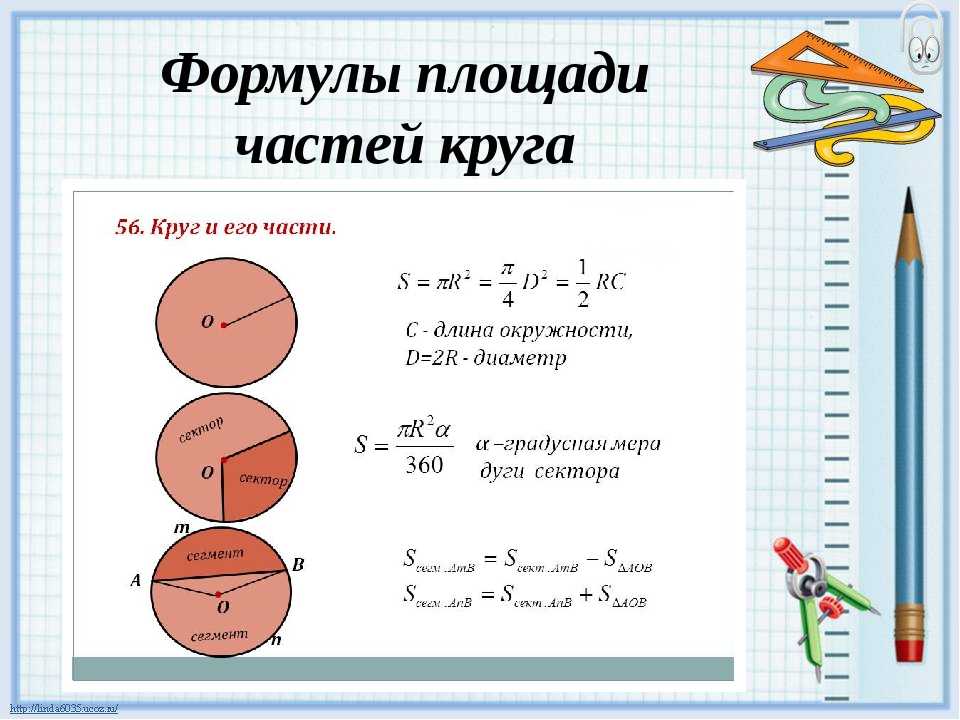
180$ — 30 — 30 = 120$
Таким образом, угол TPS = 120 градусов.
Теперь, когда мы нашли угол TPS, мы можем также найти угол RPS. Вместе два угла образуют прямую линию, а это значит, что они должны быть равны 180 градусам. (Почему? Потому что круг равен 360 градусам, а полуокружность — 180 градусам. Таким образом, прямая линия всегда будет равна 180 градусам.)
$180 — 120 = 60$
Это означает, что угол RPS = 60 градусов. А так как угол RPS образует нашу дугу, то наша дуга равна 60 градусам.
Итак, наш окончательный ответ H.

Щенки не умеют лгать; это научный факт. Вы решили свои математические задачи в ACT, и это действительно здорово.

Выводы
Задачи с кругами довольно распространены, но большинство из них представляют собой небольшие вариации на одни и те же темы площади и окружности. В ACT наиболее полезной частью любого круга, как правило, является радиус, и как только вы привыкнете к мысли, что все радиусы равны, вы часто сможете быстро справиться даже с самыми сложными проблемами круга ACT.
Помните свои формулы и сохраняйте ясную голову в отношении того, что от вас требуется, и вы сможете вынести значительную часть раздела геометрии ACT только с кругами.

Что дальше?
Теперь, когда вы знаете все, что нужно знать о кружках ACT, убедитесь, что вы в курсе всех других математических тем ACT. Если вам нужно освежить знания по объемной геометрии, тригонометрии, отношениям или целым числам, вы найдете то, что вам нужно, в наших руководствах по математике ACT.
Не хватает времени на математику ACT? Мы покажем вам советы и приемы, необходимые для того, чтобы бить время.
Ищете репетитора по математике?
Ознакомьтесь с нашими руководствами о том, как найти идеального репетитора ACT для ваших нужд.
Рыбалка, чтобы получить высший балл? Наш путеводитель по математике на 800 баллов (написанный лучшим бомбардиром) расскажет вам, как именно достичь этих целей к экзаменационному дню.
Хотите улучшить свой результат ACT на 4 балла?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к ACT. Мы гарантируем возврат ваших денег если вы не улучшите свой балл ACT на 4 балла или более.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравился этот урок математики, вам понравится и наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

Есть друзья, которым также нужна помощь в подготовке к экзамену? Поделись этой статьей!
Кортни Монтгомери
Об авторе
Кортни набрала 99-й процентиль по SAT в старшей школе и закончила Стэнфордский университет со степенью в области культурной и социальной антропологии.
No related posts.