О производных / Хабр
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я «предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения.
А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.
Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.
Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.
Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.
Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
Глянем вот на этот график:
Даша — стабильный середнячок.
Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.
К чему это я?
1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:
- А где работаешь?
- А кем?
- Сколько получаешь?
и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.
2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.
3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?
Каков знак Вашей производной?
Производные иерархии — SQL Server Master Data Services
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
Применимо к:SQL Server — только windows Управляемый экземпляр SQL Azure
Производная иерархия Master Data Services является производным от связей атрибутов на основе домена, которые уже существуют между сущностями в модели.
Можно создать производную иерархию, в которой выделяется любая из существующих связей атрибутов на основе домена в модели.
Конечные элементы группируют другие конечные элементы
В производной иерархии конечные элементы из одной сущности используются для группировки конечных элементов другой сущности. Производная иерархия основана на связи между этими сущностями. Явная иерархия, напротив, основана на элементах только из одной сущности и структурируется любым заданным способом.
Можно изменить структуру производной иерархии, не затрагивая базовые данные. Пока отношения существуют в модели, удаление производной иерархии не влияет на основные данные.
Явные иерархии или производные иерархии
В следующей таблице приведены некоторые различия между явными и производными иерархиями.
Примечание
Явные иерархии являются устаревшими в этом выпуске Master Data Services.
| Явные иерархии | Производные иерархии |
|---|---|
| Структура определяется пользователем | Структура образуется из связей между атрибутами на основе домена |
| Содержит элементы из одной сущности | Содержит элементы из нескольких сущностей |
| Использует консолидированные элементы для группировки других элементов | Использует конечные элементы одной сущности для группировки конечных элементов другой сущности |
Создание иерархии с изменяемой глубиной
Есть два проверенных способа создания иерархии с изменяемой глубиной.
Если необходимо, чтобы все уровни имели одинаковые атрибуты, создайте одну сущность и затем создайте рекурсивную иерархию для сущности с помощью доменного атрибута, основанного на сущности.
Если необходимо получить один набор атрибутов для конечных элементов и другой набор для верхних уровней, создайте две сущности для производной иерархии. Для конечной сущности используйте атрибут домена, который основывается на родительской сущности. Для родительской сущности используйте атрибут на основе домена, который основывается сам на себе.
Пример производной иерархии
В следующем примере конечные элементы сущности «Продукт» сгруппированы по конечным элементам сущности «Подкатегория», которые затем сгруппированы по конечным элементам сущности «Категория». Эта иерархия возможна, потому что у сущности «Продукт» есть атрибут «Подкатегория» на основе домена, а у сущности «Подкатегория» есть атрибут «Категория» на основе домена.
Структура иерархии показывает, как группируются элементы.
Сущность с наибольшим числом элементов располагается в самом низу.
В производной иерархии можно выделить связь между «Продуктом» и «Подкатегорией» и затем между «Подкатегорией» и «Категорией». При просмотре элементов в этой иерархии каждый уровень дерева содержит элементы из одной сущности.
Иерархия такого типа предотвращает перемещение элемента на недопустимый уровень. Например, можно переместить велосипед Road-650 из одной подкатегории, «Дорожные велосипеды», в другую, «Горные велосипеды». Нельзя перенести Road-650 напрямую внутри категории, например 1 {велосипеды}. Каждый раз при перемещении элемента в дереве иерархии значение атрибута на основе домена для элемента изменяется, отражая это перемещение.
Примечания
Все элементы в производном дереве иерархии сортируются по идентификатору. Нельзя менять порядок сортировки.
Если атрибут на основе домена для элемента пуст и атрибут используется в производной иерархии, то элемент не отображается в иерархии.
| Описание задачи | Раздел |
|---|---|
| Создание новой производной иерархии. | Создание производной иерархии (службы Master Data Services) |
| Скрытие или удаление уровней в существующей производной иерархии. | Скрытие или удаление уровней в производной иерархии (службы Master Data Services) |
| Изменение имени существующей производной иерархии. | Изменение имени производной иерархии (службы Master Data Services) |
| Удаление существующей производной иерархии. | Удаление производной иерархии (службы Master Data Services) |
См. также
Атрибуты на основе домена (Master Data Services)
Явные иерархии (службы основных данных)
Рекурсивные иерархии (службы Master Data Services)
Производные иерархии с явными ограничениями (службы Master Data Services)
Отображение связей «многие-ко-многим» в производных иерархиях (Master Data Services)
Коллекции (Master Data Services)
Все приемы и приемы
На этой странице вы найдете все, что вам нужно знать о решении производных.
Моя цель на этой странице – сделать из вас машину для решения производных :-).
Я расположил приемы, которые вам необходимо изучить, в таком порядке, чтобы вам было легче их понять. Эту страницу можно использовать как карту, которая поможет вам в изучении деривативов, или вы можете использовать ее для обзора всех методов решения деривативов.
Готовы? Пошли…
Основные правила
Использование определенияСамый простой способ расчета производных — использование определения. Это включает в себя расчет лимита. Вычислять производные таким образом — это навык.
Как и в случае с любым другим навыком, вы совершенствуетесь только с практикой. Мы подробно говорим о том, как использовать определение на странице вычисления производной по определению.
Цепное правило Цепное правило является наиболее важным правилом для получения деривативов. С его помощью вы сможете найти производную практически любой функции.
Чтобы узнать о цепном правиле, перейдите на эту страницу: Цепное правило.
Правило произведенияПравило произведения позволяет находить производные функций, которые являются произведениями других функций. Это очень полезный метод, и одна из немногих формул, которые вы должны запомнить в математическом анализе.
Чтобы узнать о правиле продукта, перейдите на эту страницу: Правило продукта.
Частное правилоЧастное правило — это частный случай правила произведения, поэтому вам не нужно запоминать другую формулу. Я покажу вам метод решения производных от частных с помощью правила произведения.
Чтобы узнать об этом методе, перейдите на эту страницу: Правило частного.
Неявное дифференцированиеНеявное дифференцирование позволяет находить производные функций, выраженных забавным образом, которые мы называем неявными. Ключ в понимании цепного правила.
Чтобы узнать о неявной дифференциации, перейдите на эту страницу: Неявная дифференциация.
Основные формулы
Производная тригонометрических функцийЧтобы начать накапливать знания о производных, нам понадобятся некоторые формулы. Двумя основными являются производные тригонометрических функций sin(x) и cos(x). Сначала нам нужно найти эти две производные, используя определение.
Имея их в своем наборе инструментов, вы можете решать производные с использованием тригонометрических функций, используя другие инструменты, такие как цепное правило или правило произведения.
Чтобы узнать о производных тригонометрических функций, перейдите на эту страницу: Производные тригонометрических функций.
Производная экспоненциальной функцииДобавим еще одну функцию в список тех, от которых мы умеем брать производную. Это действительно полезно и красиво. Чтобы узнать о производной экспоненциальной функции, перейдите на эту страницу.
Производная логарифмов Добавим в наш список еще одну формулу, снова используя определение производной.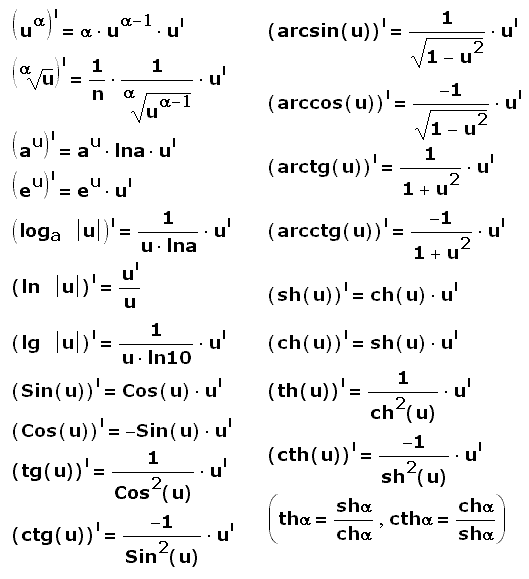
Результат довольно удивительный.
Чтобы узнать о производной натурального логарифма, перейдите на эту страницу: Производная от ln(x).
Производная обратных триггерных функцийЗдесь мы узнаем о производной arcsin(x), arccos(x) и других. Эти формулы довольно сложно запомнить, поэтому полезно знать, как доказать их самому себе. Перейти на эту страницу: производная обратных триггерных функций.
Другие часто задаваемые формулыЕсть некоторые формулы для производных, которые мне очень часто задают. Это:
- Производная от tan(x): не так хорошо известна, как производные от sin(x) и cos(x). Для его вычисления воспользуемся правилом отношения.
- Производная обратной функции: Как вообще найти производную обратной функции?
- Производная интеграла: вам нужно знать об интегралах, прежде чем увидеть это. Этот вопрос возникает всегда, и на этой странице мы неплохо развеиваем все сомнения.
И я думаю, что это суммирует основные методы решения производных.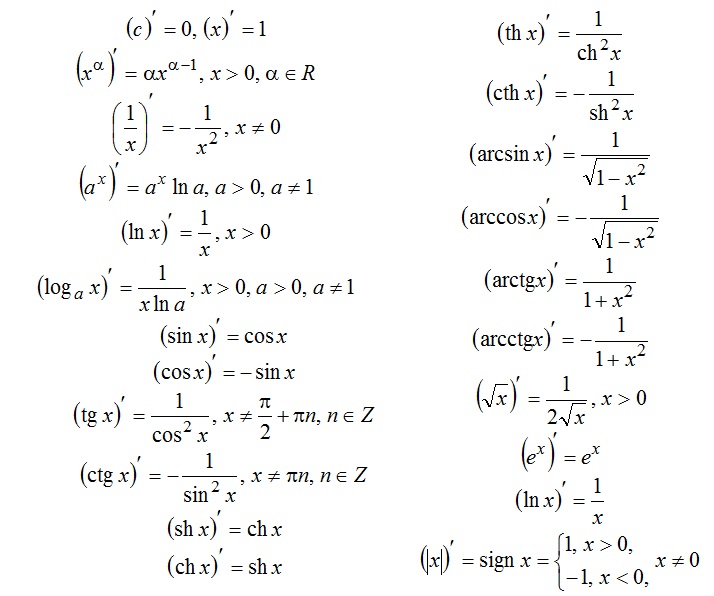
Если у вас есть какой-либо другой трюк или важный момент, который я, возможно, упустил, оставьте мне комментарий ниже, и мы сможем это обсудить.
Производная | Определение и факты
наклон линии
Просмотреть все СМИ
- Похожие темы:
- исчисление дифференциация частная производная частное правило вторая производная
Просмотреть весь связанный контент →
производная , в математике скорость изменения функции по отношению к переменной. Производные лежат в основе решения задач исчисления и дифференциальных уравнений. Как правило, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы получить скорость изменения некоторой интересующей нас переменной, включают эту информацию в некоторое дифференциальное уравнение и используют методы интегрирования для получения функции, которую можно использовать для предсказания поведения исходной переменной. системы в различных условиях.
Геометрически производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке. Его вычисление, по сути, происходит из формулы наклона прямой линии, за исключением того, что для кривых необходимо использовать процесс ограничения. Наклон часто выражается как «увеличение» над «пробегом» или, в декартовых терминах, как отношение изменения х к изменению х . Для прямой линии, показанной на рисунке, формула наклона имеет вид ( y 1 − y 0 )/( x 1 − x 0 ). Другой способ выразить эту формулу: 18 , если ч используется для х 1 − x 0 и f ( x ) для y . Это изменение в обозначениях полезно для перехода от идеи наклона линии к более общему понятию производной функции.
Викторина «Британника»
Числа и математика
Для кривой это отношение зависит от того, где выбраны точки, отражая тот факт, что кривые не имеют постоянного наклона.
Чтобы найти наклон в желаемой точке, выбор второй точки, необходимой для расчета отношения, представляет собой трудность, потому что, как правило, отношение будет представлять только средний наклон между точками, а не фактический уклон в любой точке ( см. рисунок). Чтобы обойти эту трудность, используется процесс ограничения, при котором вторая точка не фиксируется, а задается переменной, например ч в соотношении для прямой линии выше. Нахождение предела в этом случае — это процесс нахождения числа, к которому отношение приближается, когда ч приближается к 0, так что предельное отношение будет представлять фактический уклон в данной точке. Над частным [ f ( x 0 + h ) − f ( x 0 )]/ h так, чтобы его можно было переписать в форме, в которой предел, когда h приближается к 0, можно увидеть более непосредственно. Рассмотрим, например, параболу, заданную выражением x 2 .
При нахождении производной x 2 , когда x равно 2, частное равно [(2 + h ) 2 − 2 2 ]/ h . Расширяя числитель, частное становится (4 + 4 ч + ч 2 — 4)/ ч = (4 ч + ч 2 )/ ч . И числитель, и знаменатель по-прежнему приближаются к 0, но если ч на самом деле не ноль, а лишь очень близко к нему, то ч можно разделить, получив 4 + ч , что, как легко заметить, приближается к 4 как ч. приближается к 0.
Итак, производная от f ( x ) при x 0 , записанная как ф ′( х 0 ), ( д ф / д х )( х 0 ), или D f ( x 0 ), определяется так, как если бы этот предел существовал.
Дифференцирование, т.