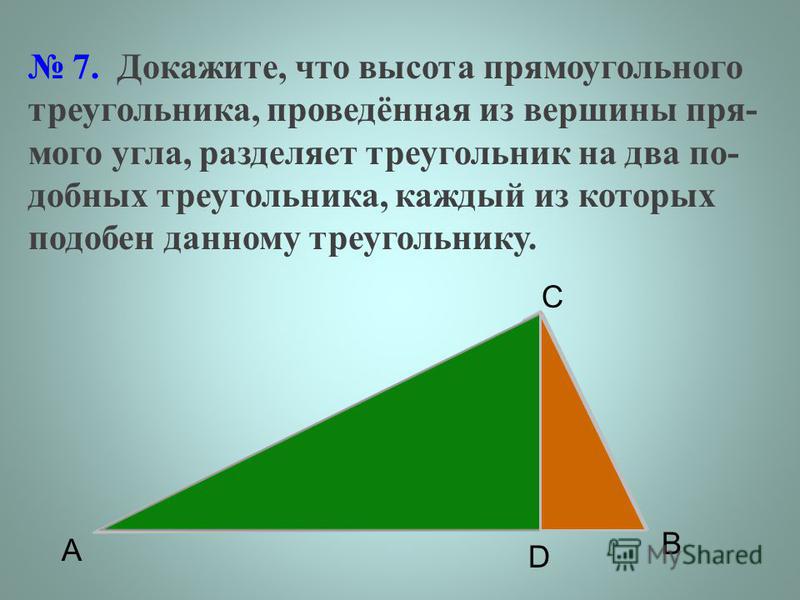
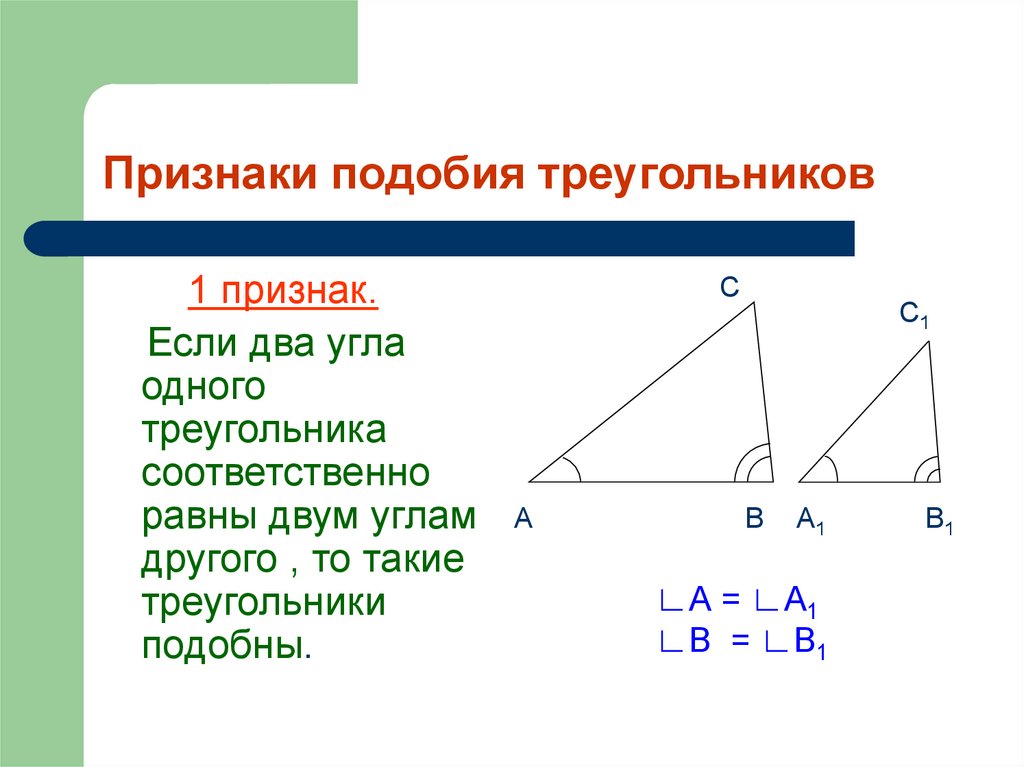
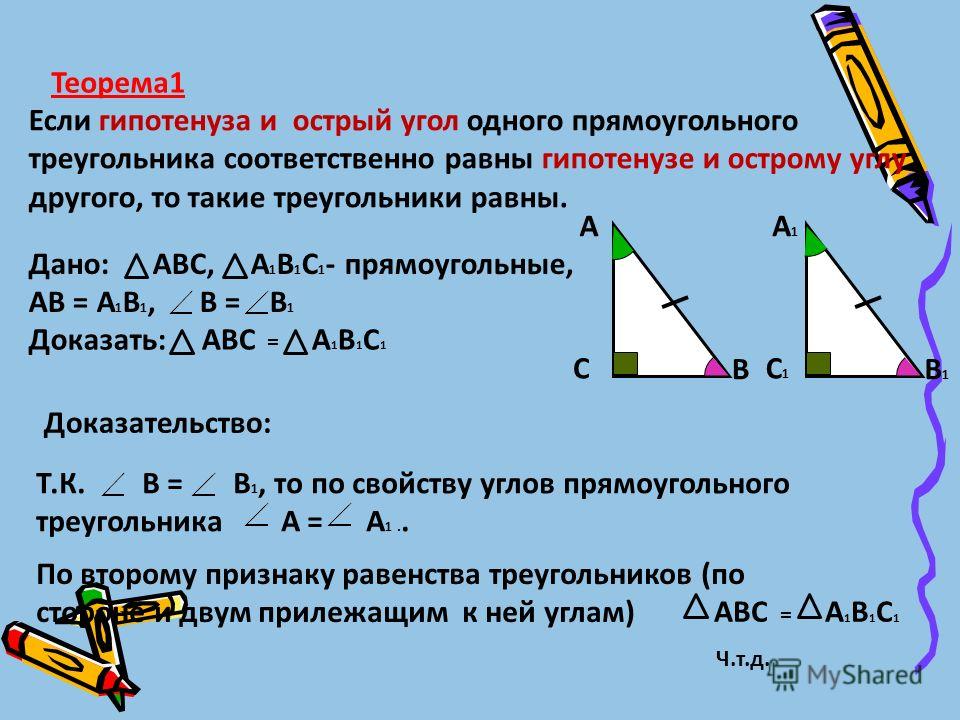
Какое из следующих утверждений верно? 1) Все прямоугольные треугольники подобны. 2) Через заданную точку плоскости модно провести провести единственную прямую. 3) Диагонали ромба точкой пересечения делятся пополам.
Последние вопросы
Математика
8 минут назад
№3 . Приведите дроби к общему знаменателю:
а) 1/4 и 1/12;
б) 3/16 и 5/12.
№4: Сократите дробь:
132132/312312
Математика
37 минут назад
Валера и Алина неправильно мокращают дробиМатематика
37 минут назад
Обчисліть: -2,7+(-5,3)Математика
37 минут назад
Позначте на координатній прямій числа, модуль яких дорівнює 4; 8; 2,5; 0; 2.
Математика
37 минут назад
приставте в виде неправенльной дроби 1 целая 3\7Математика
42 минут назад
Допоможіть будь ласка з 4,5,6 Даю 50 балів. СРОЧНООООМатематика
47 минут назад
Математика 4 классМатематика
48 минут назад
Памагите пж
- Математика
1 час назад
Помогите составить ВОДГУК по беларускому языку П.
 Трус «падають сняжынки»
Трус «падають сняжынки»По плану:1 абзац-уступ пра паэта
2абзац-галоуная думка,анализ верша,сваи адносины да тэмы и галоунай думки,мастацка вобразные сродки и з якой мэтай яны ужываюцца,прыклад творау на гэту тэму.
3 абзац- вывад,сваи адносины да верша.
Математика
1 час назад
1) Первая сторона треугольника равна 7см, вторая на 2см короче первой, а третья на 4см длиннее второй. Найти все стороны и периметр треугольника.
Помогите пожалуйста…. строчно
с решением..
Математика
1 час назад
7 Реши задачи. 6) Из гаража одновременно в одном направлении вышли две автомашины. Одна шла со скоростьо 80 км/час, а другая со скоростью 65 км/час. На каком расстоянии д будут эти машины через 3 часа?Математика
1 час назад
три пакета. В первый пакет насыпали 0.6 кг №1. Конфеты рассыпаны в три пакета. конфет, во второй — в 2,5 раза больше чем в первый, а в третий — в 1,5 раза меньше чем в первый. Сколько конфет в первом и третьем пакетах вместе? №2. Молоко разлили в три кувшина. В первый кувшин налили 1,5 литров молока, во второй — в 2,5 раза меньше чем в первый, а в третий в 1,4 раза больше чем в первый. Сколько литров молока налили во второй и третий кувшины? Додните действия: столбиком
В первый пакет насыпали 0.6 кг №1. Конфеты рассыпаны в три пакета. конфет, во второй — в 2,5 раза больше чем в первый, а в третий — в 1,5 раза меньше чем в первый. Сколько конфет в первом и третьем пакетах вместе? №2. Молоко разлили в три кувшина. В первый кувшин налили 1,5 литров молока, во второй — в 2,5 раза меньше чем в первый, а в третий в 1,4 раза больше чем в первый. Сколько литров молока налили во второй и третий кувшины? Додните действия: столбикомМатематика
1 час назад
(x + 5)(x-7)= x² — 2x — 35; даю 50 баллМатематика
1 час назад
хелп ми, 4 класс страница 106 номер 1Математика
2 часа назад
Учи ру математика
Все предметы
English
United States
Polski
Polska
Bahasa Indonesia
Indonesia
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Português
Brasil
Русский
Россия
How much to ban the user?
1 hour 1 day
1. |
В ответ запишите номер выбранного утверждения.
| |||||||||||||||||||||||
Как определить, подобны ли прямоугольные треугольники
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по базовой геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как определить, подобны ли прямоугольные треугольники
; угол прямой; ; ;
Найти .
Возможные ответы:
Правильный ответ:
Объяснение:
Так как и прямой угол, также прямой угол.
– гипотенуза первого треугольника; так как одна из его сторон составляет половину длины этой гипотенузы, то 30-60-90 с более короткой ногой и более длинной.
Поскольку эти два треугольника подобны, является гипотенузой второго треугольника и его более длинным катетом.
Следовательно, .
Сообщить об ошибке
Что из следующего является достаточным, чтобы сказать, что два прямоугольных треугольника подобны?
Возможные ответы:
Две стороны и один угол равны.
Два угла и одна сторона равны.
Две стороны одинаковые.
Все углы равны.
Правильный ответ:
Все углы равны.
Объяснение:
Если все три угла треугольника равны, а стороны нет, то один из треугольников является увеличенной копией другого. Когда это происходит, пропорции между сторонами остаются неизменными, что является критерием сходства.
Сообщить об ошибке
Какое из следующих утверждений относительно двух треугольников верно?
Возможные ответы:
Треугольники подобны по стороне-углу-стороне
Треугольники не подобны, потому что они не одного размера.
Треугольники подобны катету-гипотенузе
Треугольники подобны, потому что они оба прямоугольные.
У нас недостаточно информации, чтобы показать, что треугольники подобны.
Правильный ответ:
Треугольники подобны по стороне-углу-стороне
Пояснение:
Хотя мы должны немного поработать, мы можем показать, что эти треугольники подобны.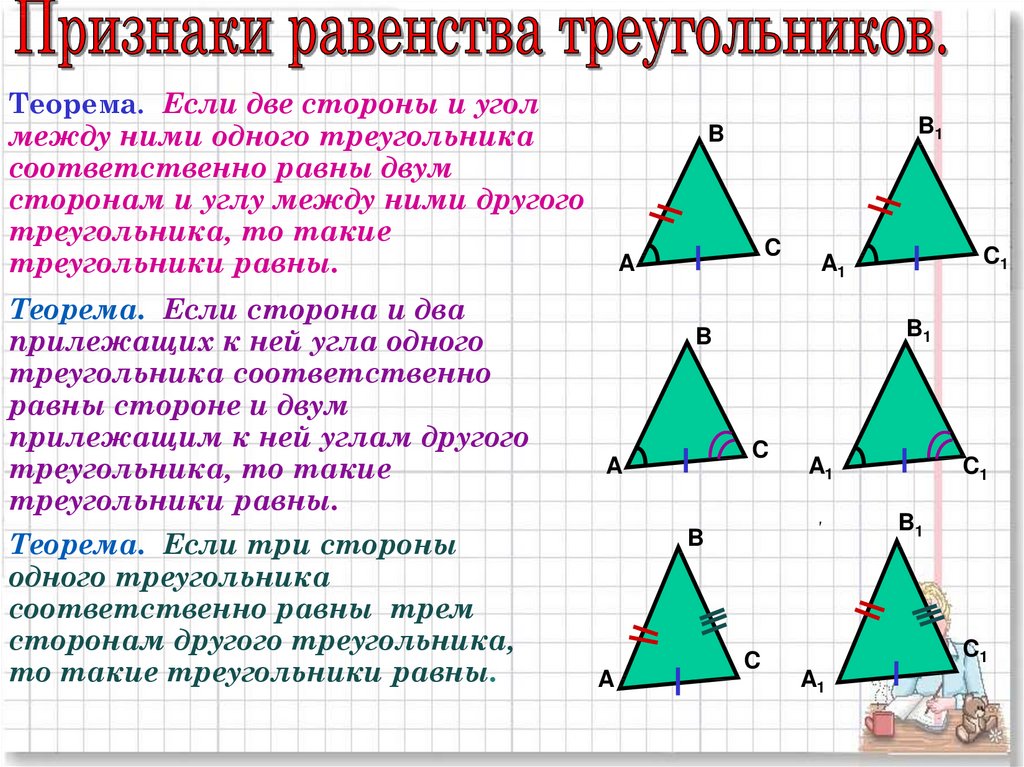 Во-первых, прямоугольные треугольники не обязательно всегда подобны. Они должны соответствовать необходимым критериям, как и любые другие треугольники; более того, нет теоремы о гипотенузе-ноге для сходства, а есть только конгруэнтность; следовательно, мы можем исключить два варианта ответа.
Во-первых, прямоугольные треугольники не обязательно всегда подобны. Они должны соответствовать необходимым критериям, как и любые другие треугольники; более того, нет теоремы о гипотенузе-ноге для сходства, а есть только конгруэнтность; следовательно, мы можем исключить два варианта ответа.
Однако мы можем использовать теорему Пифагора с меньшим треугольником, чтобы найти недостающую сторону. Это дает нам длину 48. Сравнивая отношение более коротких катетов в каждом треугольнике к соотношению более длинных катетов, мы получаем
В обоих случаях катет большего треугольника в два раза длиннее треугольника. соответствующий катет в меньшем треугольнике. Учитывая, что угол между двумя катетами является прямым углом в каждом треугольнике, эти углы равны. Теперь у нас есть достаточно доказательств, чтобы сделать вывод о сходстве по стороне-углу-стороне.
Сообщить об ошибке
Два треугольника и подобны, если:
Возможные ответы:
Их соответствующие углы равны И их соответствующие длины пропорциональны.
Их соответствующие углы равны.
Их соответствующие углы равны И их соответствующие длины равны.
Их соответствующие длины пропорциональны.
Правильный ответ:
Их соответствующие углы равны, И их соответствующие длины пропорциональны.
Объяснение:
Теорема о подобных фигурах утверждает, что подобные фигуры имеют равные соответствующие углы и пропорциональные соответствующие длины. Одного из этих условий недостаточно. Если две фигуры имеют равные соответствующие углы и равные соответствующие длины, то они конгруэнтны, а не подобны.
Сообщить об ошибке
и являются треугольниками.
Похожи ли?
Возможные ответы:
Да, потому что и оба треугольника прямоугольные.
Недостаточно информации для ответа на этот вопрос.
Нет, потому что и не одного размера.
Да, потому что и похожи.
Правильный ответ:
Недостаточно информации для ответа на этот вопрос.
Объяснение:
Теорема о подобных фигурах утверждает, что подобные фигуры имеют равные соответствующие углы и пропорциональные соответствующие длины. Другими словами, нам нужно знать как меры соответствующих углов, так и длины соответствующих сторон. В этом случае мы знаем только меры и . Мы не знаем меры каких-либо других углов или длины любой из сторон, поэтому мы не можем ответить на вопрос — они могут быть похожими, а могут и не быть.
Недостаточно знать, что обе фигуры являются прямоугольными треугольниками, и мы не можем предполагать, что углы являются одним и тем же измерением, потому что они кажутся одинаковыми.
Подобные треугольники не обязательно должны быть одного размера.
Сообщить об ошибке
и подобные треугольники.
Какова длина ?
Возможные ответы:
Правильный ответ:
Объяснение:
Так как и подобные треугольники, мы знаем, что они имеют пропорциональные соответствующие длины. Мы должны определить, какие стороны соответствуют. Здесь мы знаем, что соответствует , потому что оба отрезка лежат под противоположными углами и между углами и . Точно так же мы знаем, что соответствует , потому что оба отрезка лежат как против углов, так и между углами и . Мы можем использовать эту информацию, чтобы установить пропорцию и определить длину .
Подставьте известные значения.
Перемножить и упростить.
и из-за неправильной пропорции. получается из-за неправильного умножения и .
Сообщить об ошибке
Эти треугольники похожи? Дайте обоснование.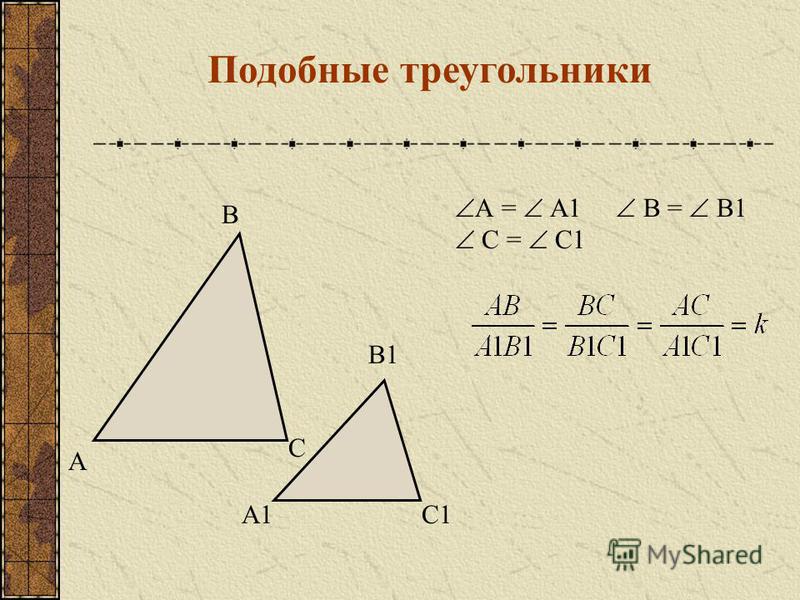
Возможные ответы:
Да — треугольники подобны по АА
Нет — углы не равны
Недостаточно информации — нам нужно знать хотя бы одну длину стороны в каждом треугольнике
Нет — длины сторон не пропорциональны
Да — они ВЫГЛЯДЯТ похожими
Правильный ответ:
Да — треугольники подобны по AA
Пояснение:
Эти треугольники были нарисованы намеренно, чтобы ввести в заблуждение. Просто взглянув на них, углы, которые кажутся соответствующими, получают разные угловые измерения, поэтому они не «выглядят» похожими. Однако, если мы вычтем, мы получим, что недостающий угол в треугольнике с углом 66 градусов должен быть 24 градуса, так как . Точно так же недостающий угол в треугольнике с углом 24 градуса должен быть равен 66 градусам. Это означает, что все 3 соответствующие пары углов равны, что делает треугольники подобными.
Сообщить об ошибке
Эти треугольники похожи? Если да, укажите масштабный коэффициент.
Возможные ответы:
Да -масштаб
№
Да — Масштабная коэффициент
Да — Масштабная коэффициент
не может быть определено — мы должны знать все три стороны обеих треугонов
Правильно — правильно ответ:
Да — коэффициент масштабирования
Пояснение:
Два треугольника подобны, но мы не можем быть в этом уверены, пока не сравним все три соответствующие пары сторон и не убедимся, что отношения одинаковы. Для этого нам сначала нужно найти недостающие стороны, используя теорему Пифагора.
В меньшем треугольнике отсутствует не гипотенуза с, а один из катетов, поэтому мы будем использовать формулу немного по-другому.
вычесть 36 из обеих сторон
Теперь мы можем сравнить все три отношения соответствующих сторон:
один из способов сравнения этих отношений состоит в их упрощении.
Мы можем упростить крайнее левое отношение, разделив верх и низ на 3 и получив .
Мы можем упростить среднее соотношение, разделив верх и низ на 4 и получив .
Наконец, мы можем упростить отношение справа, разделив верх и низ на 5 и получив .
Это означает, что треугольники определенно подобны, и является коэффициентом масштабирования.
Сообщить об ошибке
Эти прямоугольные треугольники подобны? Если да, укажите масштабный коэффициент.
Возможные ответы:
Недостаточно информации для определения
Нет — длины сторон не пропорциональны
Да — масштабный коэффициент
Да — масштабный коэффициент
Да — масштабный коэффициент
Правильный ответ:
Нет — длины сторон не пропорциональны
6
6
Пояснение: Чтобы сравнить эти треугольники и определить, подобны ли они, нам нужно знать длины всех трех сторон в обоих треугольниках. Чтобы получить недостающие, мы можем использовать теорему Пифагора:
Чтобы получить недостающие, мы можем использовать теорему Пифагора:
Возьмите квадратный корень
Другое треугольник отсутствует один из ног, а не гипотенуза, поэтому мы соответствующим образом скорректируем:
СПТРАТАЦИЯ 36 С обеих сторон
Сейчас. мы можем сравнить отношения соответствующих сторон:
Первое отношение упрощается до , но мы не можем упростить другие больше, чем они уже есть. Три соотношения явно не совпадают, значит, это не подобные треугольники.
Сообщить об ошибке
Дано: и .
и оба являются прямыми углами.
Правда или ложь: Из предоставленной информации следует, что .
Возможные ответы:
Верно
Неверно
Правильный ответ:
Верно
Объяснение:
Если мы хотим доказать это , то , и соответствуют , и соответственно.
Согласно теореме о сходстве сторон (SASS), если две стороны треугольника пропорциональны соответствующим сторонам другого треугольника, а прилежащие к ним углы равны, то треугольники подобны.
и , таким образом, Отдел имущества равенства, . Кроме того, и , соответствующие им углы, являются прямыми углами, поэтому . Условия SASS соблюдены, поэтому
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Learn by Concept
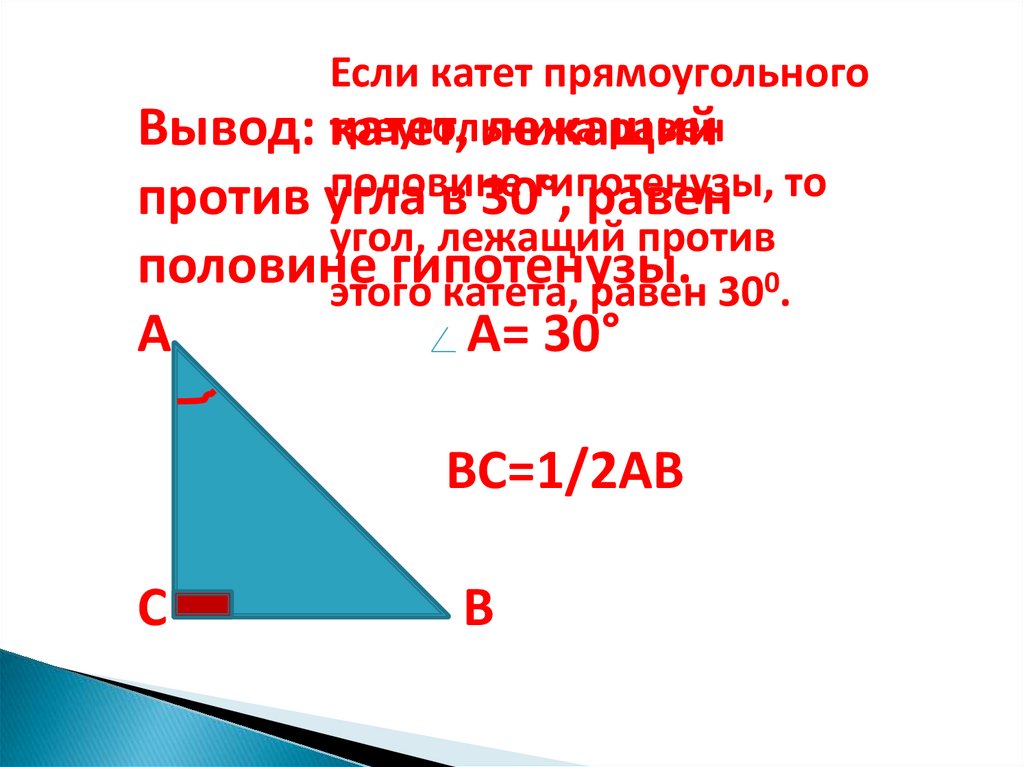
Интересные свойства прямоугольных треугольников
Добро пожаловать в мой блог о прямоугольных треугольниках и сходстве между ними! Прямоугольный треугольник — это тип треугольника, в котором один угол равен 90 градусов, а это означает, что сумма двух других углов должна составлять 90. Этот тип треугольника имеет много интересных свойств, но самое главное — все прямоугольные треугольники подобны.
Чтобы понять, почему все прямоугольные треугольники подобны, важно понять, что означает сходство. Когда две фигуры подобны, они имеют равные соответствующие углы и пропорциональные соответствующие длины. Это известно как теорема о подобных фигурах. Все прямоугольные треугольники следуют этой теореме, а это означает, что все они имеют равные соответствующие углы и пропорциональные соответствующие длины.
Из-за этого все прямоугольные треугольники имеют много общих свойств. Например, теорема Пифагора утверждает, что для любого прямоугольного треугольника со сторонами a, b и c (с гипотенузой) a2 + b2 = c2. Эта теорема работает для всех прямоугольных треугольников независимо от размера или формы из-за их сходства.
Прямоугольные треугольники также играют важную роль в тригонометрии. Из-за их сходства тригонометрические функции можно использовать для простого нахождения неизвестных сторон или углов в любом заданном треугольнике. Тригонометрия также позволяет нам использовать свойства синуса, косинуса и тангенса (известные как правило синусов) для вычисления углов и длин в любом прямоугольном треугольнике.
Наконец, важно отметить, что хотя все прямоугольные треугольники похожи, они могут различаться по размеру и форме в зависимости от длины их сторон. Например, равносторонний треугольник — это особый тип прямоугольного треугольника, в котором все три стороны равны по длине; тогда как равнобедренный треугольник — это особый тип прямоугольного треугольника, в котором две стороны равны по длине, а третья сторона отличается от обеих сторон по длине.
В заключение, все прямоугольные треугольники подобны, потому что они следуют теореме о подобных фигурах — это означает, что они имеют как равные соответствующие углы, так и пропорциональные соответствующие длины на каждой стороне треугольника — что делает их идеальными для использования в тригонометрии при вычислении углов или длины с заданным треугольником.
Два прямоугольных треугольника подобны?
Чтобы определить, подобны ли два прямоугольных треугольника, необходимо сравнить их соответствующие стороны. Если длины гипотенузы и катета одного треугольника пропорциональны соответствующим частям другого треугольника, то эти два треугольника можно считать подобными. Кроме того, если все три угла в обоих треугольниках конгруэнтны (равны), то они также подобны. Используя эти критерии, можно определить, подобны ли два прямоугольных треугольника.
Кроме того, если все три угла в обоих треугольниках конгруэнтны (равны), то они также подобны. Используя эти критерии, можно определить, подобны ли два прямоугольных треугольника.
Подобие прямоугольных треугольников
Прямоугольные треугольники всегда подобны, потому что они имеют общий угол 90 градусов. Этот общий угол одинаков для всех прямоугольных треугольников, а это означает, что их соответствующие углы всегда будут равны. Кроме того, соотношение длин их сторон всегда будет одинаковым, что делает их соответствующие длины пропорциональными. Следовательно, все прямоугольные треугольники подобны друг другу.
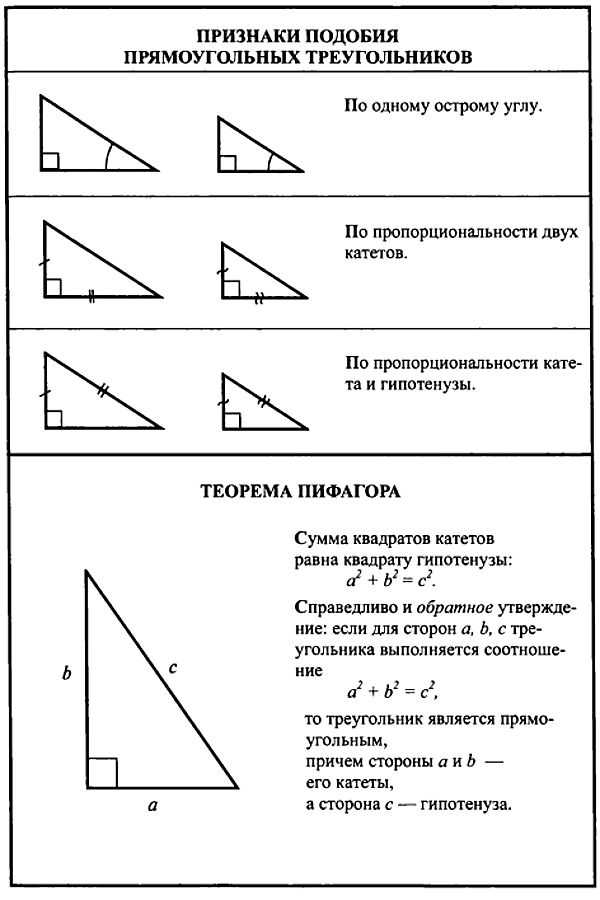
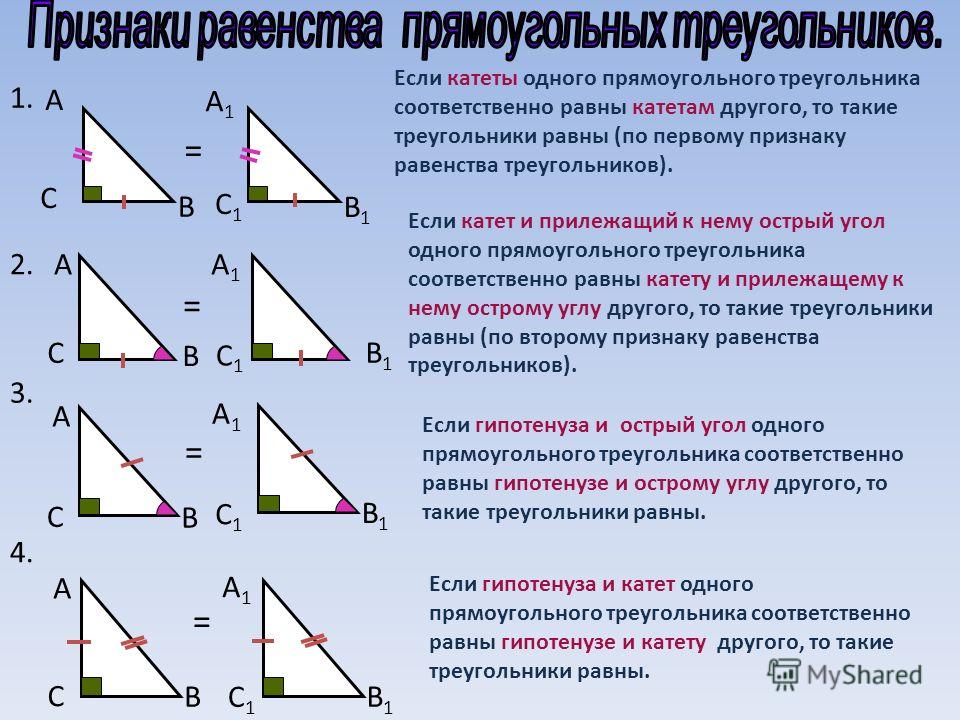
Правила доказательства подобия двух треугольников
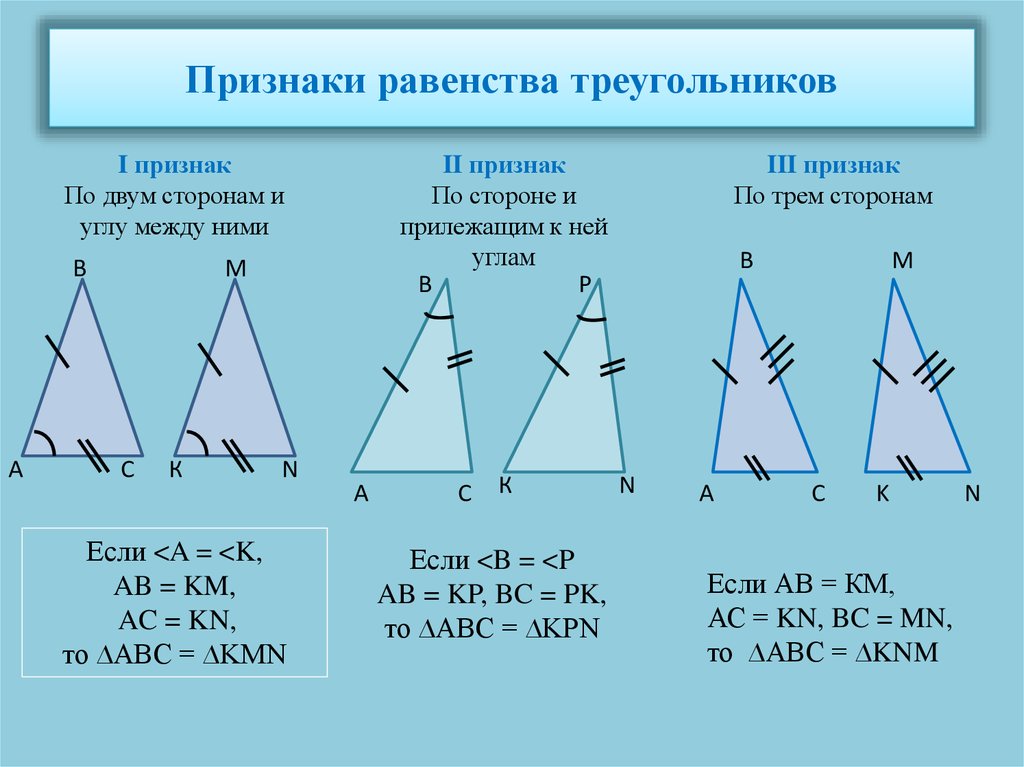
1. Первое правило подобия: соответствующие углы двух треугольников конгруэнтны, что означает, что их мера равна. Это означает, что если два треугольника имеют одинаковый угол в одном из углов, то два других угла также должны быть равны.
2. Второе правило подобия: длины соответствующих сторон пропорциональны, что означает, что все они находятся в одном и том же отношении. Если сторона одного треугольника в два раза длиннее стороны другого треугольника, то все соответствующие стороны должны иметь такое же отношение.
Если сторона одного треугольника в два раза длиннее стороны другого треугольника, то все соответствующие стороны должны иметь такое же отношение.
3. Третье правило подобия: Если два треугольника удовлетворяют как Первому, так и Второму Правилу подобия, то они подобны и любые оставшиеся углы или стороны также будут пропорциональны или конгруэнтны. Другими словами, если выполняются первые два правила, то все остальные измерения также должны соответствовать этому шаблону, чтобы доказать сходство.
Доказательство подобия двух треугольников
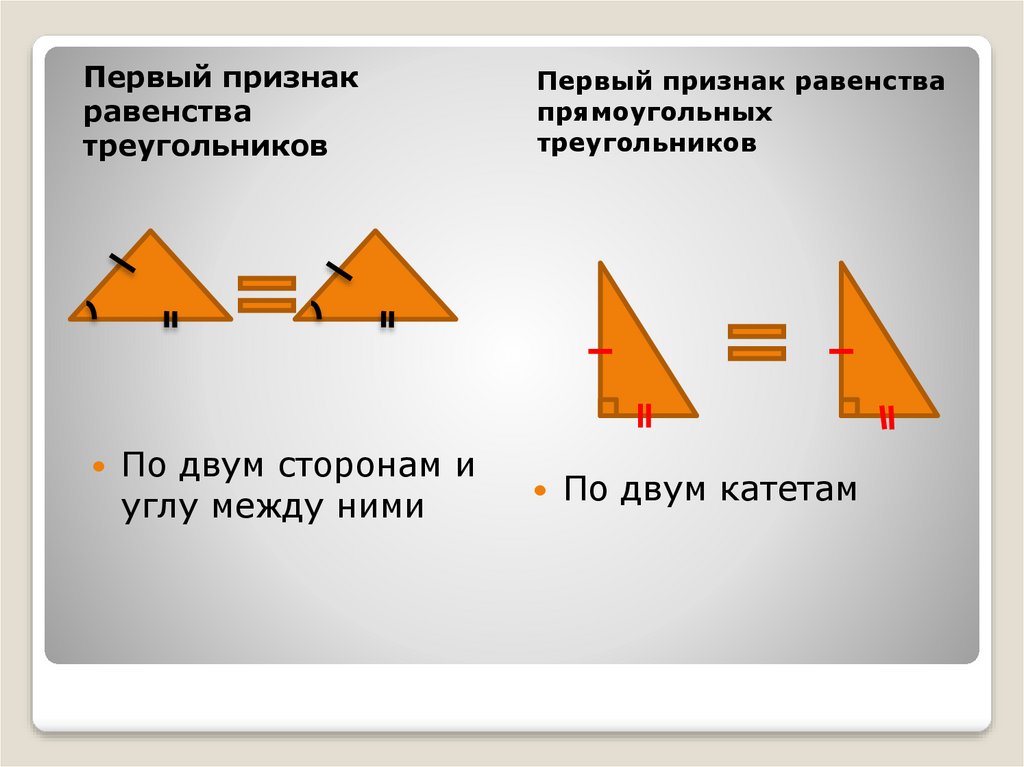
Три способа доказать, что два треугольника подобны: угол-угол (AA), сторона-угол-сторона (SAS) и сторона-сторона-сторона (SSS).
Угол-Угол (AA) утверждает, что если два угла одного треугольника равны двум углам другого треугольника, то эти два треугольника подобны. Например, если треугольник ABC имеет угол A = угол DEF, а угол B = угол EDF, то по теореме AA треугольник ABC подобен треугольнику DEF.
Side-Angle-Side (SAS) утверждает, что если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти два треугольника подобны. Например, если у треугольника ABC сторона AB = стороне DE, а угол B = углу E, то по теореме SAS треугольник ABC подобен треугольнику DEF.
Например, если у треугольника ABC сторона AB = стороне DE, а угол B = углу E, то по теореме SAS треугольник ABC подобен треугольнику DEF.
Наконец, Side-Side-Side (SSS) утверждает, что если три стороны одного треугольника равны трем сторонам другого треугольника, то эти два треугольника подобны. Например, если треугольник ABC имеет сторону AB = сторону DE, сторону BC = сторону EF и сторону AC = сторону DF, то по теореме SSS треугольник ABC подобен треугольнику DEF.
Используя эти три теоремы, вы можете легко определить, подобны ли два треугольника.
Похожи ли прямые углы?
Нет, два прямых угла не всегда подобны. Подобие — это отношение между двумя фигурами, которое сохраняет соотношение между соответствующими сторонами и углами. Следовательно, чтобы две фигуры были похожи, все их соответствующие стороны и углы должны иметь одинаковое отношение. Так как два прямых угла всегда будут иметь одинаковую угловую меру (90°), они могут быть подобны только в том случае, если они имеют одинаковое отношение сторон. Если один прямой угол имеет более длинные стороны, чем другой, то они не могут быть подобными.
Если один прямой угол имеет более длинные стороны, чем другой, то они не могут быть подобными.
Всегда ли прямые углы равны?
Нет, два прямых угла не всегда одинаковы. Сходство — это геометрическое понятие, при котором две фигуры имеют одинаковую форму и размер, но могут находиться в разных положениях. С другой стороны, конгруэнтность — это концепция, согласно которой две фигуры одинаковы как по размеру, так и по положению. Два прямых угла могут быть равными, но не обязательно подобными; они просто должны быть равны в меру.
Подобие всех треугольников
Равносторонние треугольники всегда подобны друг другу, то есть все три стороны и углы треугольника равны. Это означает, что если два равносторонних треугольника имеют одинаковый размер, они будут иметь одинаковую форму. Кроме того, любые два равносторонних треугольника можно идеально совместить, потому что у них равные стороны и углы. Кроме того, все равносторонние треугольники не только подобны друг другу, но и подобны любому другому треугольнику с тремя равными сторонами и тремя равными углами.
Подобие треугольников ААА
Да, треугольники ААА подобны. Это связано с теоремой «угол-угол-угол» (AAA), которая гласит, что если все три соответствующих угла двух треугольников равны по размеру, то эти два треугольника подобны. Эта теорема применима к любому типу треугольника, включая прямоугольные, тупоугольные и остроугольные треугольники. Следовательно, когда все три угла двух разных треугольников равны по размеру, эти два треугольника можно считать подобными.
Почему некоторые треугольники не похожи
Не все треугольники подобны, потому что углы и длины их сторон могут различаться. Все равносторонние треугольники имеют три равных угла и три равные длины сторон, что делает их подобными. Однако другие типы треугольников имеют разные углы и длины сторон, что может отличать их друг от друга. Например, у равнобедренного треугольника два равных угла и две равные длины сторон, тогда как у разностороннего треугольника нет равных сторон или углов. Кроме того, в тупоугольном треугольнике один угол больше 90 градусов, чего нет ни в равнобедренном, ни в разностороннем треугольнике. Следовательно, все треугольники не обязательно подобны из-за различных углов и длин сторон.
Следовательно, все треугольники не обязательно подобны из-за различных углов и длин сторон.
Источник: voovers.com
Почему некоторые треугольники не похожи?
Некоторые треугольники не подобны, потому что отношения соответствующих сторон в треугольниках не одинаковы. Чтобы два треугольника были подобны, у них должны быть три пары соответствующих сторон, имеющих одинаковое отношение. Если одно или несколько из этих соотношений различны, треугольники не будут подобны. Кроме того, если мы не знаем никаких угловых мер для двух треугольников, то мы можем использовать теорему подобия SSS, чтобы определить, подобны ли они. Эта теорема утверждает, что если два треугольника имеют три пары соответствующих сторон, имеющих одинаковую длину, то они также должны быть подобны.
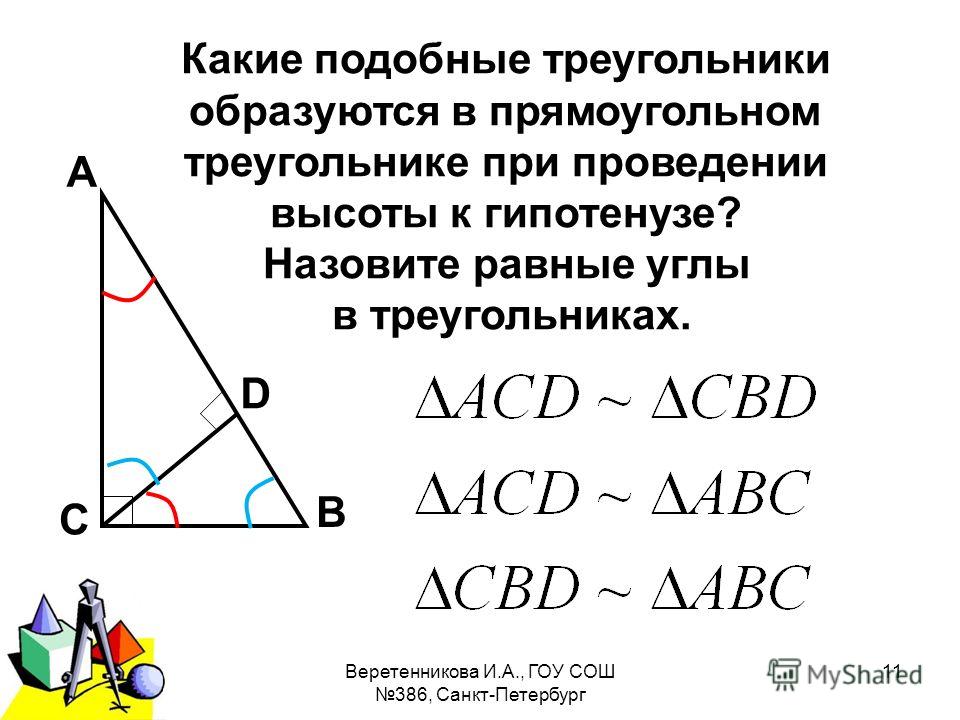
Похожи ли прямоугольные треугольники внутри прямоугольных треугольников?
Нет, прямоугольный треугольник внутри прямоугольного треугольника не обязательно подобен. Если внутренний прямоугольный треугольник имеет те же стороны, что и внешний прямоугольный треугольник, то он подобен. Однако, если внутренний прямоугольный треугольник имеет стороны, отличные от сторон внешнего прямоугольного треугольника, то он не подобен. Например, если одна сторона внешнего прямоугольного треугольника в два раза длиннее одной стороны внутреннего прямоугольного треугольника, то они не подобны.
Если внутренний прямоугольный треугольник имеет те же стороны, что и внешний прямоугольный треугольник, то он подобен. Однако, если внутренний прямоугольный треугольник имеет стороны, отличные от сторон внешнего прямоугольного треугольника, то он не подобен. Например, если одна сторона внешнего прямоугольного треугольника в два раза длиннее одной стороны внутреннего прямоугольного треугольника, то они не подобны.
Все ли прямоугольные треугольники конгруэнтны?
Нет, не все прямоугольные треугольники конгруэнтны. Два прямоугольных треугольника могут иметь одинаковые углы, но не быть конгруэнтными. Конгруэнтность требует, чтобы две фигуры были идентичны как по размеру, так и по форме, а это означает, что все соответствующие стороны и углы должны быть равны друг другу. Если длины всех сторон прямоугольного треугольника умножить на одно и то же число, то углы не изменятся, но треугольники не будут равны.
Правила для подобных треугольников
Правила для подобных треугольников следующие: Два треугольника считаются подобными, если они имеют одинаковую форму, но могут быть разными по размеру.
 Чтобы получить недостающие, мы можем использовать теорему Пифагора:
Чтобы получить недостающие, мы можем использовать теорему Пифагора:

 Кроме того, если все три угла в обоих треугольниках конгруэнтны (равны), то они также подобны. Используя эти критерии, можно определить, подобны ли два прямоугольных треугольника.
Кроме того, если все три угла в обоих треугольниках конгруэнтны (равны), то они также подобны. Используя эти критерии, можно определить, подобны ли два прямоугольных треугольника. Если сторона одного треугольника в два раза длиннее стороны другого треугольника, то все соответствующие стороны должны иметь такое же отношение.
Если сторона одного треугольника в два раза длиннее стороны другого треугольника, то все соответствующие стороны должны иметь такое же отношение. Например, если у треугольника ABC сторона AB = стороне DE, а угол B = углу E, то по теореме SAS треугольник ABC подобен треугольнику DEF.
Например, если у треугольника ABC сторона AB = стороне DE, а угол B = углу E, то по теореме SAS треугольник ABC подобен треугольнику DEF. Если один прямой угол имеет более длинные стороны, чем другой, то они не могут быть подобными.
Если один прямой угол имеет более длинные стороны, чем другой, то они не могут быть подобными.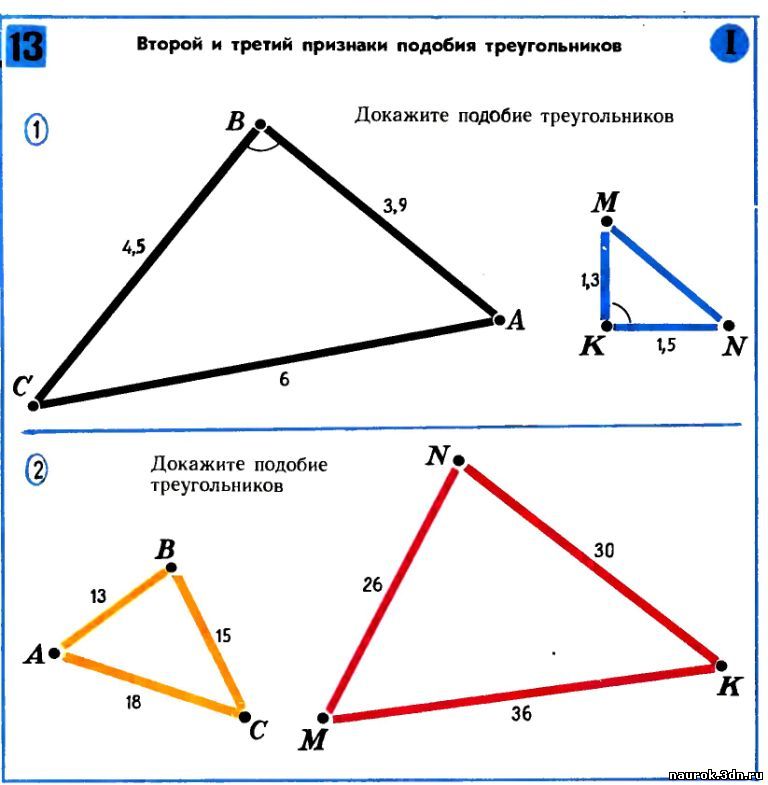
 Следовательно, все треугольники не обязательно подобны из-за различных углов и длин сторон.
Следовательно, все треугольники не обязательно подобны из-за различных углов и длин сторон.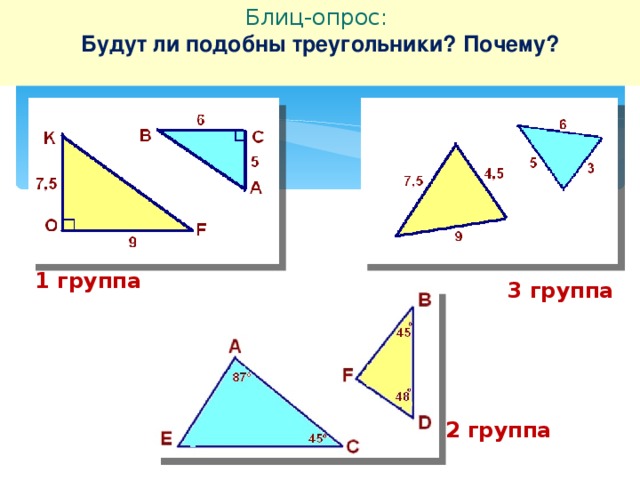 Если внутренний прямоугольный треугольник имеет те же стороны, что и внешний прямоугольный треугольник, то он подобен. Однако, если внутренний прямоугольный треугольник имеет стороны, отличные от сторон внешнего прямоугольного треугольника, то он не подобен. Например, если одна сторона внешнего прямоугольного треугольника в два раза длиннее одной стороны внутреннего прямоугольного треугольника, то они не подобны.
Если внутренний прямоугольный треугольник имеет те же стороны, что и внешний прямоугольный треугольник, то он подобен. Однако, если внутренний прямоугольный треугольник имеет стороны, отличные от сторон внешнего прямоугольного треугольника, то он не подобен. Например, если одна сторона внешнего прямоугольного треугольника в два раза длиннее одной стороны внутреннего прямоугольного треугольника, то они не подобны.


 Трус «падають сняжынки»
Трус «падають сняжынки»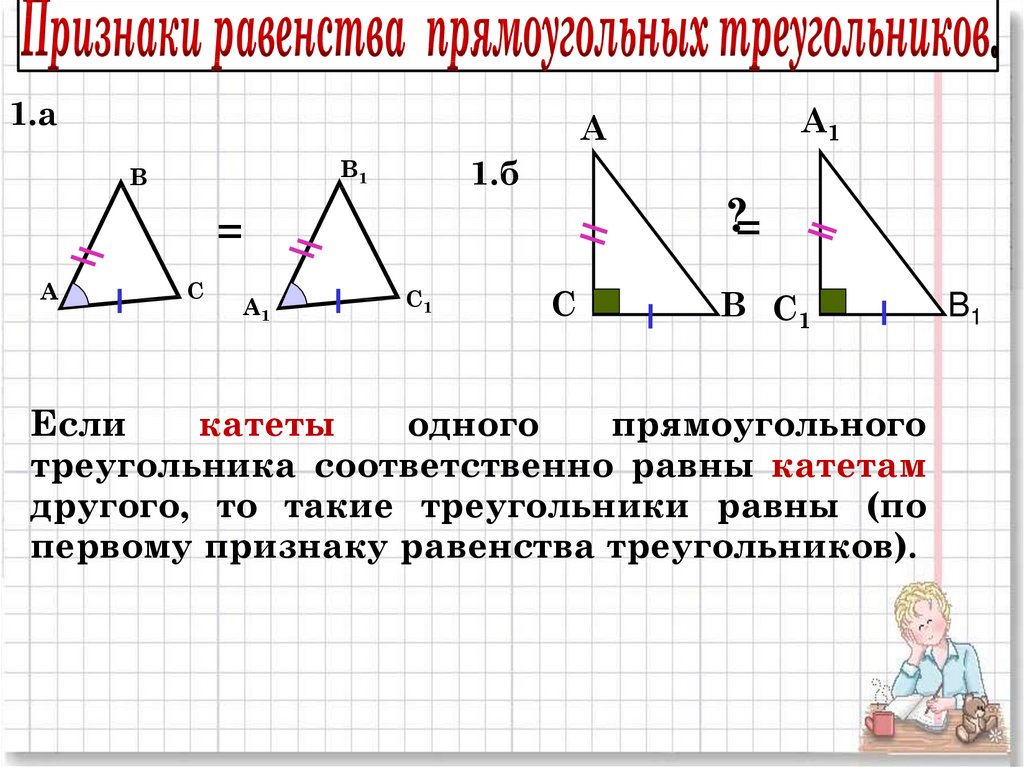 В первый пакет насыпали 0.6 кг №1. Конфеты рассыпаны в три пакета. конфет, во второй — в 2,5 раза больше чем в первый, а в третий — в 1,5 раза меньше чем в первый. Сколько конфет в первом и третьем пакетах вместе? №2. Молоко разлили в три кувшина. В первый кувшин налили 1,5 литров молока, во второй — в 2,5 раза меньше чем в первый, а в третий в 1,4 раза больше чем в первый. Сколько литров молока налили во второй и третий кувшины? Додните действия: столбиком
В первый пакет насыпали 0.6 кг №1. Конфеты рассыпаны в три пакета. конфет, во второй — в 2,5 раза больше чем в первый, а в третий — в 1,5 раза меньше чем в первый. Сколько конфет в первом и третьем пакетах вместе? №2. Молоко разлили в три кувшина. В первый кувшин налили 1,5 литров молока, во второй — в 2,5 раза меньше чем в первый, а в третий в 1,4 раза больше чем в первый. Сколько литров молока налили во второй и третий кувшины? Додните действия: столбиком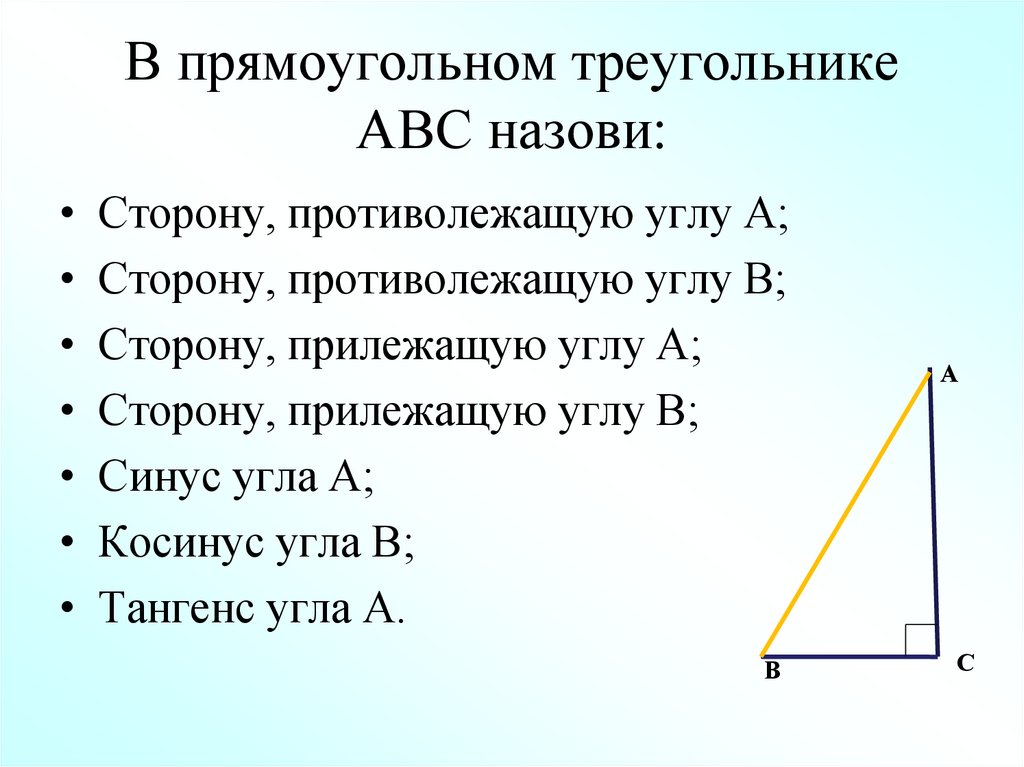 Какое из следующих утверждений верно?
Какое из следующих утверждений верно?



 Какое из следующих утверждений верно?
Какое из следующих утверждений верно?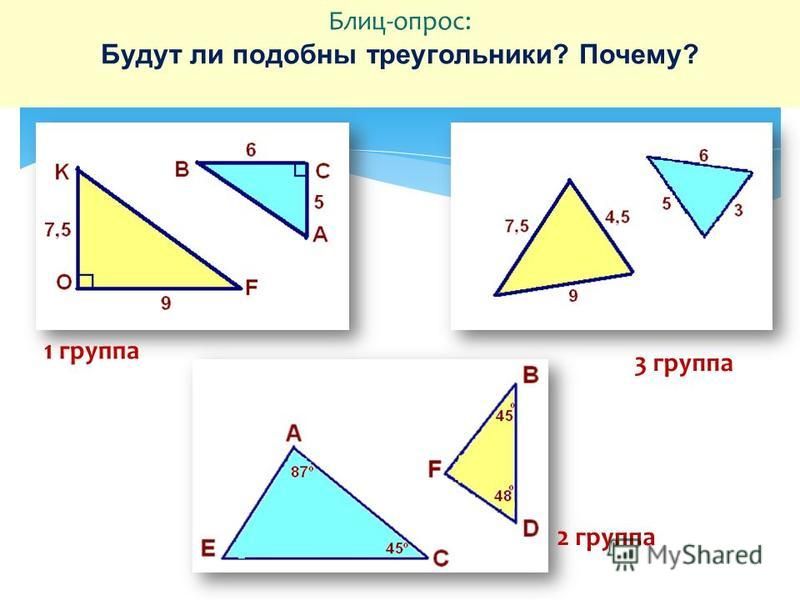

 Какие из следующих утверждений верны?
Какие из следующих утверждений верны?