Как записывается область определения функции: § Область определения функции

Что такое функция? 7 класс онлайн-подготовка на Ростелеком Лицей

Отношения между объектами

 

Любой объект (стул, стол, собака, человек) может быть предметом исследования. Но исследовать можно не только сами объекты, но и отношения между ними. Мы часто рассуждаем об отношениях между людьми – дружбе, ненависти, любви. На них непосредственно нельзя указать, они неосязаемы, но вместе с тем мы говорим о них, описываем, прекрасно друг друга понимаем, когда слышим: «Петя дружит с Васей».

 

В жизни мы вводим отношения не только между людьми. Например, на карте есть два города A и Б – это два объекта. А расстояние между A и Б – это отношение между ними. На него уже нельзя указать пальцем. Или фраза: «Плед лежит на стуле». Плед и стул – это объекты, а вот «лежит на» – это уже отношение между пледом и стулом. Оказывается, мы можем изучать не только сами объекты, но и отношения между ними. Этим мы сейчас и займёмся.

 

Определение функции

 

 

У каждого человека есть размер обуви. Людей очень много, а размеров обуви мало. Если с одной стороны отметить всех людей (например, в виде точек), а с другой – существующие размеры обуви, то можно от каждой точки провести стрелку к одному из размеров обуви (Рис. 1) (в математике используют такую терминологию: можно отобразить множество людей на множество размеров обуви). Или, говоря по-другому, между этими множествами можно установить соответствие.

 

 

Рис. 1. Отображение множества людей на множество размеров обуви

Можно установить и обратное соответствие: каждый размер обуви есть у некоторого подмножества людей (Рис. 2).

Рис. 2. Отображение множества размеров обуви на множество людей  

Другой пример: обычные часы. Каждому времени суток соответствует какое-то определённое положение стрелок на этих часах. И, наоборот, каждое положение стрелок соответствует какому-то времени суток. Обратите внимание: во всех примерах мы рассматриваем не сами объекты (люди и обувь, время суток и стрелки часов), а новое понятие – отношение между объектами.

Итак, как видим, примеров разных отношений очень много. А как говорить о них точно? Все ли нужно изучать? И как это делать? Все отношения задают между множествами какое-то соответствие. Некоторые из соответствий особенные, они каждому элементу из одного множества ставят в соответствие ровно один элемент из другого множества. Такие соответствия, которые называются функциями, мы и будем изучать.

 

В наших примерах: у человека может быть только один размер обуви, каждому времени суток соответствует только одно положение стрелок на часах. А вот, например, 36 размер обуви может быть у большого количества людей. Поэтому такие соответствия функциями не будут.

Дадим строгое определение функции. Функция – это соответствие между двумя множествами такое, что каждому элементу одного множества  ставится в соответствие единственный элемент другого множества . Первое множество называют областью определения функции, а второе – областью значений функции. Обозначают:  и  соответственно.

Пример 1: задана функция, которая ставит в соответствие каждому человеку размер его обуви. Область определения функции  – множество людей, область значений функции  –  множество размеров обуви.

Пример 2: задана функция, которая ставит в соответствие каждому дню месяца среднюю температуру воздуха. Область определения функции  – множество дней месяца, область значений функции  –  множество температур (Рис. 3).

 

Рис. 3. Соответствие между днями месяца и средней температурой воздуха  

 

Числовая функция

 

 

В математике мы чаще будем работать с одним из видов функций – числовыми функциями. Числовая функция – это функция, областью определения  и областью значений  которой являются числовые множества. Например, функция пройденного пути в зависимости от времени (при равномерном движении): . Такая функция является числовой.

 

Числовые функции можно задавать разными способами.

1. Словесный.
2. Аналитический.
3. Графический.
4. Табличный.

В рассмотренном выше примере мы задали функцию с помощью формулы, такое способ задания называется аналитическим. Рассмотрим другой пример. Каждому числу поставим в соответствие его квадрат. Это функция. На самом деле это будет функция площади квадрата в зависимости от длины его стороны:  (если мы оговорим, что ).

Мы будем изучать различные числовые функции. Что вообще можно в них изучать? У функций могут быть наибольшие и наименьшие значения – максимумы и минимумы, функции могут возрастать и убывать и т.д. Все эти свойства функций помогают решать конкретные прикладные задачи (например, нахождение оптимальных параметров, при которых та или иная величина достигает своего максимума – доход, эффективность и т.д., или минимума – расход, количество ошибок и т.д.). Но для того чтобы решать задачи, нужно выделить общие свойства функций и изучить их.

Повторим рассуждение, которое уже озвучивали в наших уроках. Есть заводы, которые создают различные инструменты. А дальше каждый сам использует созданные инструменты в своих целях: с помощью отвёртки можно закручивать и откручивать винты и шурупы, но можно ею же пытаться открыть дверь или забить гвозди. Так и математика – завод инструментальный, создаёт различные инструменты, которые потом могут использоваться в физике, экономике и других сферах для решения конкретных прикладных задач.

---

 

Естественные области определения и значений 

В примере с площадью квадрата мы сказали, что . Т.е. наложили некоторое ограничение на область определения функции: . Получается, что  и  – это две различные функции? Да, именно так, потому что первая функция определена при неположительных значениях переменной (Рис. 1), а вторая – нет (Рис. 2).

Рис. 1. График функции

Рис. 2. График функции

То есть для задания функции, вообще говоря, недостаточно просто задать формулу соответствия.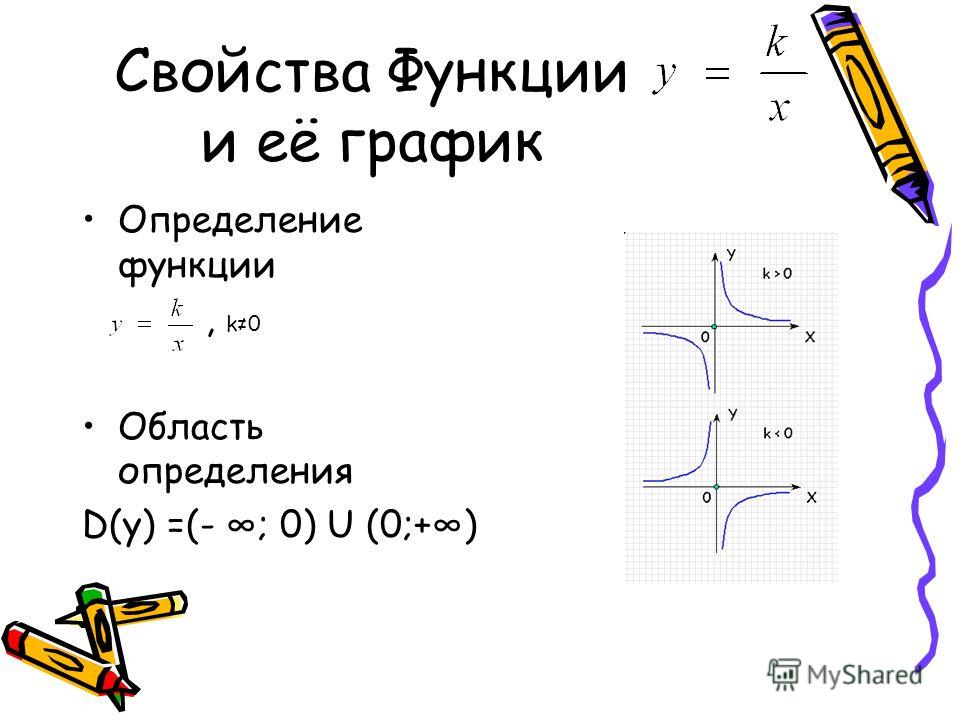 Необходимо ещё указать области определения и значений функции. Но чаще всего этого не делают, предполагая, что они естественные. Естественная область определения при аналитическом задании – это область допустимых значений выражения, которое записано в формуле.

Пример 1.

Область определения:

Записывают так:

Пример 2.

Область определения:

Отсюда:

Естественная область значений – это множество значений, которые может принимать функция. Например, естественная область значений функции  – это все числа больше либо равные . Записывают так:

---

 

 

Графический способ задания функции

 

 

Анализировать функцию иногда легче, если построен её график. По нему часто легко определить, на каких промежутках функция убывает или возрастает, где у неё максимум и минимум и т.д. Таким образом, у графического способа задания функции (задание функции с помощью графика) и аналитического разные цели. Если сказать грубо, то аналитический способ более точный, он позволяет вычислить значение функции в любой точке и выполнять с функцией различные преобразования. Графический способ более наглядный – по графику можно сделать вывод о тех или иных свойствах функции.

 

Рассмотрим графический способ подробнее. График функции представляет собой совокупность точек , где  и  – соответствующие значения из областей определения и значений (Рис. 4).

 

Рис. 4. График функции

График задает соответствие между множествами  и  или – что то же самое – задает функцию. При этом для изображения необходимо задать соответствующую систему координат. Чаще всего мы будем использовать декартову систему координат.

---

 

Область определения и область значений функции при графическом задании функции

Рассмотрим функцию, заданную следующим графическим образом (Рис.1).

Рис. 1. График функции

Область определения функции – это все значения, при которых определена функция.

Для рассматриваемой функции область определения функции – это все числа от  до  включительно (Рис. 2).

Рис. 2. Область определения рассматриваемой функции

Область значений функции – это все значения , которые принимает функция.

Для рассматриваемой функции область значений функции – это все числа от  до  включительно (см. рис. 3):

Рис. 3. Область значений рассматриваемой функции

Если строго, то область определения функции  – это проекция графика на ось абсцисс, а область значений функции – проекция графика на ось ординат. Проекция – понятие, которое нам знакомо из геометрии. Слово неслучайно созвучно со словом прожектор (оба от латинского projectio – «бросание вперёд») Если мы посветим на график функции прожектором следующим образом, то тень, которую мы увидим на экране,  – это проекция графика на ось , т.е. область значений функции (Рис. 4).

Рис. 4. Проекция графика на ось

Аналогично тень на  будет проекцией графика на ось  (Рис. 5), т.е. область определения функции.

Рис. 5. Проекция графика на ось

---

 

Словесный и табличный способы задания

Любую функцию можно задать различными способами. Рассмотрим на примере конкретной функции. Словесный способ: функция, которая ставит в соответствие каждому числу его квадрат. Табличный способ: при задании табличным способом указываются пары соответствующих значений.

При таком задании функции область определения функции и область задания функции – это множество значений переменных, которые указаны в таблице:

Аналитический способ: с помощью формулы: . Графический способ задания функции (Рис. 1).

Рис. 1. Графический способ задания функции

---

 

 

Линейные функции

 

 

Для задания числовых функций мы чаще всего будем использовать аналитический и графический методы, т.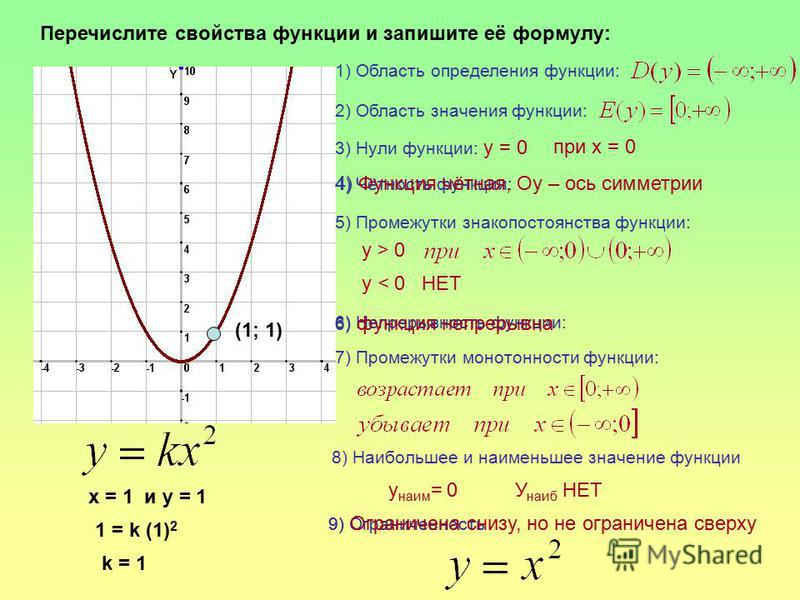 к. при использовании этих методов легче изучать свойства функций. Различные свойства функции мы будем изучать на протяжении всего курса алгебры, а сейчас рассмотрим несколько частных случаев функций.     Вернемся к функции пройденного пути при равномерном движении, т.е. , где  – путь,  – скорость,  – время. Например, при скорости  получим функцию . Если , то , если , то , если , то . Мы видим, что при одинаковом изменении аргумента , у нас одинаковое изменение значения функции – пройденного пути .     Функции, обладающие таким свойством,называются линейными, в общем виде их можно записать так: . Графиком таких функций будет прямая.     Пример линейной функции: пусть . Построим график этой функции. Нарисуем таблицу и заполним ее, т.е. при двух разных значениях  найдем, чему равен . И по полученным значениям построим прямую на координатной плоскости.  

 

Итак, точки  принадлежат графику функции. Отметим эти точки на плоскости и проведем через них прямую (Рис. 5). 

Рис. 5. График линейной функции  

Эта прямая и является графиком функции . Обратим внимание, что для построения графика линейной функции нам достаточно двух точек. Это связано с тем, что мы знаем: графиком будет прямая, а любая прямая на плоскости однозначно задаётся по двум точкам.

 

Нелинейные функции

 

 

Естественно, не все функции линейные. Например, мы знаем, что площадь квадрата зависит от его стороны следующим образом: . Попробуем приблизительно построить ее график по точкам. Поскольку сторона квадрата больше 0, то . Значит, точка  не принадлежит графику функции (точку  «выкалывают», на графике обводят в кружок).

 

Снова нарисуем таблицу, возьмем некоторые значения  и найдем значения  при этих фиксированных значениях .

Нарисуем эти точки на плоскости и посмотрим, какая линия через них проходит (Рис. 6).

Рис. 6. График нелинейной функции

 

Данная функция уже не является линейной, так как при увеличении  на 1,  увеличивался на разные величины, в зависимости от начального значения переменной .

Такие функции называются нелинейными. Рассмотренная функция является примером квадратичной функции.

Сторона квадрата не может быть отрицательной или равной 0, поэтому обобщим и построим график функции  для любых значений аргумента. Построим график данной функции по точкам. Снова нарисуем таблицу, заполним ее разными значениями  и посчитаем, чему равен  при каждом из этих значений .

 

Отметим эти точки на плоскости и проведем кривую, которая проходит через них (Рис. 7). Полученный график называют параболой.

Рис. 7. График квадратичной функции

В общем виде квадратичная функция записывается так: , где  – некоторые числа, .

 

---

 

Другие примеры нелинейных функций

Если рассмотреть зависимость времени на преодоление заданного расстояния в зависимости от скорости, то получим пример еще одного вида функций – обратной пропорциональности. Например, если расстояние между двумя городами равно , то , где  – время,  – это скорость (Рис.

1).

Рис. 1. График обратной пропорциональности

Рассмотрим, как выглядит график в общем виде (для любых допустимых значений аргумента). Функция имеет следующий вид: . Рассмотрим графики функции при  и  (Рис. 2).

Рис. 2. Графики функции  при  и

Рассмотрим ещё один пример. Объем куба зависит от его стороны: . Такая функция называется кубической (). Попробуем приблизительно построить ее график по точкам (Рис. 3).

Рис. 3. График функции

Сторона куба не может быть отрицательной или равной , поэтому обобщим и построим график функции  для любых значений аргумента (Рис. 4).

Рис. 4. График функции

---

 

Заключение

На этом уроке мы познакомились с понятием функция (отношение между множествами объектов).

Для того чтобы определить функцию, необходимо задать три вещи: область определения функции , область значений функции , правило, по которому каждому элементу из первого множества ставится в соответствие единственный элемент второго (Рис.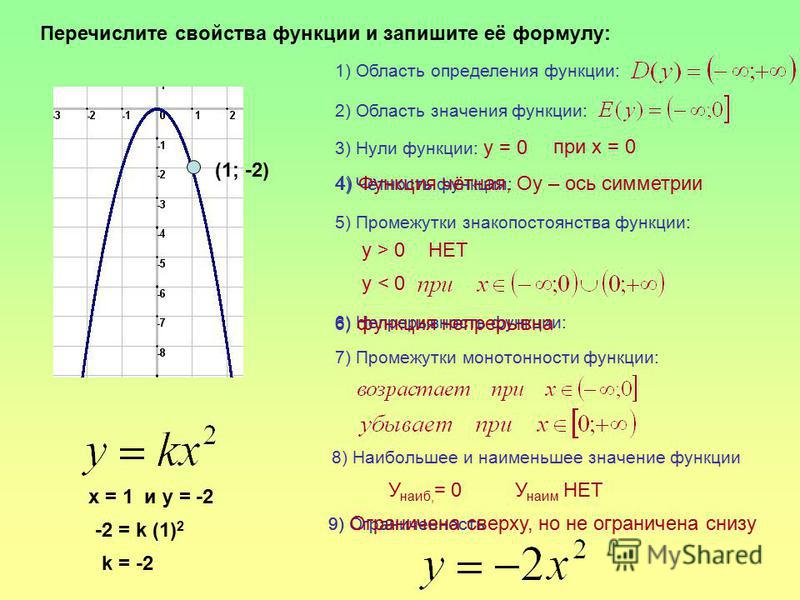 8).

Рис. 8. Вещи, необходимые для определения функции

Основные способы задания функции: аналитический, графический, словесный, табличный. На уроках математики мы чаще всего будем обращаться к аналитическому и графическому способам. На следующем уроке мы более подробно изучим свойства одного типа функций, а именно: линейной функции.

 

Список рекомендованной литературы

1. Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, издательство «Просвещение», 2017.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2014.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник, издательство «Просвещение», 2013

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «ege-study.ru» (Источник)

2. Интернет-портал «math-prosto. ru» (Источник)

3. Интернет-портал «algebraclass.ru» (Источник)

 

Домашнее задание

1. Площадь прямоугольника со сторонами  см и  см равна  . Выразить формулой зависимость  от . Для значения аргумента  найти соответствующее значение функции .

2. Функция задана формулой . Найти значение функции, соответствующее значению аргумента, равному .

3. Найти область определения функции: .

 

 

ФУНКЦИЯ • Большая российская энциклопедия

ФУ́НКЦИЯ (от лат. functio – ис­пол­не­ние, осу­ще­ст­в­ле­ние), од­но из ос­нов­ных по­ня­тий ма­те­ма­ти­ки, оз­на­чаю­щее за­ви­си­мость од­них пе­ре­мен­ных ве­ли­чин от дру­гих. Сло­во «ве­ли­чи­на» в этом оп­ре­де­ле­нии по­ни­ма­ет­ся в са­мом ши­ро­ком смыс­ле: это мо­жет быть име­но­ван­ное чис­ло, от­вле­чён­ное чис­ло (дей­ст­ви­тель­ное или ком­плекс­ное), неск. чи­сел (т. е. точ­ка про­стран­ст­ва) и во­об­ще эле­мент лю­бо­го мно­же­ст­ва.

Действительная функция одного действительного переменного

В про­стей­шем слу­чае, ко­гда ве­ли­чи­на – дей­ст­ви­тель­ное чис­ло, по­ня­тие «Ф. » оп­ре­де­ля­ет­ся сле­дую­щим об­ра­зом. Пусть ка­ж­до­му чис­лу $x$ из за­дан­но­го мно­же­ст­ва $E$ по­став­ле­но в со­от­вет­ст­вие чис­ло $y$, обо­зна­чае­мое $y=f(x)$ (чи­та­ет­ся «иг­рек ра­вен эф от икс»). То­гда го­во­рят, что на мно­же­ст­ве $E$ за­да­на функ­ция $y=f(x)$, $x∈E$. При этом упот­реб­ля­ют­ся сле­дую­щие тер­ми­ны: $x$ – не­за­ви­си­мое пе­ре­мен­ное, или ар­гу­мент; $y$ – за­ви­си­мое пе­ре­мен­ное, или функ­ция; $E$ – мно­же­ст­во зна­че­ний, ко­то­рые мо­жет при­ни­мать $x$, – об­ласть оп­ре­де­ле­ния, или об­ласть за­да­ния Ф. (об­ла­стью оп­ре­де­ле­ния Ф. мо­жет быть мно­же­ст­во всех дей­ст­ви­тель­ных чи­сел, ин­тер­вал, от­ре­зок и т. п.). Сло­ва «по­став­ле­но в со­от­вет­ст­вие» оз­на­ча­ют, что ука­зан оп­ре­де­лён­ный спо­соб, по ко­то­ро­му для ка­ж­до­го $x∈E$ на­хо­дит­ся зна­че­ние $y=f(x)$. Этот спо­соб в дан­ном слу­чае обо­зна­чен сим­во­лом $f$. Для обо­зна­че­ния Ф. при­ме­ня­ют­ся и др. бу­к­вы, напр. $y=g(x)$, $y=F(x)$, $s=h(t)$, $v=φ(s)$. {2m}.$$

Графический способ задания функции

Рас­про­стра­нён гра­фич. спо­соб за­да­ния Ф. Гра­фи­ком Ф. $y=f(x)$, $y∈E$, на­зы­ва­ет­ся мно­же­ст­во то­чек плос­ко­сти с пря­мо­уголь­ны­ми ко­ор­ди­на­та­ми $(x,y)$, где $x∈E$, $y=f(x)$. Гра­фич. спо­соб за­да­ния Ф. ши­ро­ко при­ме­ня­ет­ся на прак­ти­ке. Так, мн. про­цес­сы из­ме­не­ния од­ной ве­ли­чи­ны в за­ви­си­мо­сти от дру­гой ис­сле­ду­ют­ся с по­мо­щью кри­вых, за­пи­сан­ных с по­мо­щью са­мо­пи­шу­щих при­бо­ров. Хо­тя гра­фик Ф. и не да­ёт воз­мож­но­сти точ­но­го оп­ре­де­ле­ния чис­лен­ных зна­че­ний $x$ и $y$, он на­гляд­но от­ра­жа­ет ка­че­ст­вен­ное по­ве­де­ние Ф. (не­пре­рыв­ность, мо­но­тон­ность, мак­си­му­мы и ми­ни­му­мы, точ­ки пе­ре­ги­ба и т. д.) и по­это­му яв­ля­ет­ся важ­ным сред­ст­вом ис­сле­до­ва­ния функ­ции.

Табличный способ задания функции

При таб­лич­ном спо­со­бе за­да­ния Ф. за­да­ёт­ся в ви­де таб­ли­цы, в ко­то­рой для ка­ж­до­го зна­че­ния ар­гу­мен­та ука­зы­ва­ет­ся со­от­вет­ст­вую­щее ему зна­че­ние Ф. Та­кой спо­соб за­да­ния Ф. час­то при­ме­ня­ет­ся в тех слу­ча­ях, ко­гда об­ласть оп­ре­де­ле­ния со­сто­ит из ко­неч­но­го чис­ла зна­че­ний.

Действительная функция нескольких действительных переменных

Ф. от двух пе­ре­мен­ных оп­ре­де­ля­ет­ся сле­дую­щим об­ра­зом. Рас­смат­ри­ва­ет­ся мно­же­ст­во $E$ упо­ря­до­чен­ных пар чи­сел $(x,y)$. Ес­ли ка­ж­дой па­ре $(x,y)∈E$ по­став­ле­но в со­от­вет­ст­вие дей­ст­ви­тель­ное чис­ло $z$, то го­во­рят, что на мно­же­ст­ве $E$ оп­ре­де­ле­на Ф. $z=f(x,y)$ от двух пе­ре­мен­ных $x$ и $y$. Т. к. ка­ж­дой па­ре чи­сел $(x,y)$ со­от­вет­ст­ву­ет на плос­ко­сти точ­ка с ко­ор­ди­на­та­ми $(x,y)$, то Ф. $f(x,y)$ за­да­на на мно­же­ст­ве $E$ то­чек плос­ко­сти. Гра­фик Ф. $z=f(x,y)$ мож­но изо­бра­зить в трёх­мер­ном про­стран­ст­ве, где за­да­на пря­мо­уголь­ная сис­те­ма ко­ор­ди­нат $(x,y,z)$, в ви­де мно­же­ст­ва то­чек $(x,y,f(x,y))$, про­ек­ции ко­то­рых на плос­кость $(x,y)$ при­над­ле­жат мно­же­ст­ву $E$. Напр., гра­фик функ­ции $z=\sqrt{1-x^2-y^2},$ $x^2+y^2 ⩽ 1$, и име­ет­ся в ви­ду ариф­ме­тич. ко­рень, изо­бра­жа­ет­ся верх­ней по­ло­ви­ной ша­ро­вой по­верх­но­сти ра­диу­са 1 с цен­тром в на­ча­ле ко­ор­ди­нат.

Ана­ло­гич­но мож­но рас­смат­ри­вать мно­же­ст­во $E$, со­стоя­щее из упо­ря­до­чен­ных сис­тем $(x_1,x_2,…,x_n)$ из $n$ чи­сел, и Ф. $z=f(x_1,x_2,…,x_n)$ от $n$ пе­ре­мен­ных, оп­ре­де­лён­ную на мно­же­ст­ве $E$.

Общее понятие функции

Пусть за­да­ны мно­же­ст­ва $E$ и $E_1$ эле­мен­тов лю­бой при­ро­ды и пусть ка­ж­до­му эле­мен­ту $x∈E$ по­став­лен в со­от­вет­ст­вие эле­мент $y∈E_1$, обо­зна­чае­мый $y=f(x)$. То­гда го­во­рят, что за­да­на функ­ция $y=f(x)$, $x∈E$, что час­то за­пи­сы­ва­ет­ся как $f:\,E→E_1$.

При­ня­та сле­дую­щая тер­ми­но­ло­гия: $x$ – не­за­ви­си­мое пе­ре­мен­ное, или ар­гу­мент; $E$ – об­ласть оп­ре­де­ле­ния Ф., ка­ж­дый эле­мент $x∈E$ – зна­че­ние ар­гу­мен­та; $y$ – за­ви­си­мое пе­ре­мен­ное, или Ф., от ар­гу­мен­та $x$; $E_1$ – об­ласть зна­че­ний Ф., ка­ж­дый эле­мент $y∈E_1$ та­кой, что $y=f(x)$ для не­ко­то­ро­го зна­че­ния $x∈E$, на­зы­ва­ет­ся зна­че­ни­ем функ­ции. 2}$ ото­бра­жа­ет от­ре­зок $–1 ⩽ x ⩽ 1$ на от­ре­зок $0 ⩽ y ⩽ 1$.

Для Ф. $f(x)$ и $g(x)$ ес­те­ст­вен­ным об­ра­зом оп­ре­де­ля­ют­ся ариф­ме­тич. опе­ра­ции: это Ф., при­ни­маю­щие (в тех слу­ча­ях, ко­гда это име­ет смысл) зна­че­ния $f(x)±g(x)$, $f(x)g(x)$, $f(x)/g(x)$.

Тер­мин «Ф.» ча­ще все­го ис­поль­зу­ет­ся толь­ко для обо­зна­че­ния чи­сло­вой Ф. от од­но­го или не­сколь­ких пе­ре­мен­ных (дей­ст­ви­тель­ных или ком­плекс­ных). В др. слу­ча­ях, как пра­ви­ло, ис­поль­зу­ют­ся спец. тер­ми­ны: опе­ра­тор, ото­бра­же­ние, пре­об­ра­зо­ва­ние, функ­цио­нал.

См. так­же Мо­но­тон­ная функ­ция, Не­пре­рыв­ная функ­ция, Пе­рио­ди­че­ская функ­ция, Спе­ци­аль­ные функ­ции, Чёт­ные и не­чёт­ные функ­ции, Эле­мен­тар­ные функ­ции.

Исторический очерк

Как и ос­таль­ные по­ня­тия ма­те­ма­ти­ки, по­ня­тие Ф. сло­жи­лось не сра­зу, а про­шло дол­гий путь раз­ви­тия. По су­ще­ст­ву, речь о функ­цио­наль­ной за­ви­си­мо­сти и её гра­фич. изо­бра­же­нии идёт в ра­бо­те П.  Фер­ма «Вве­де­ние и изу­че­ние пло­ских и те­лес­ных мест» (1636, опубл. в 1679). Изу­че­ние ли­ний по их урав­не­ни­ям в «Гео­мет­рии» Р. Де­кар­та (1637) так­же ука­зы­ва­ет на яс­ное пред­став­ле­ние о вза­им­ной за­ви­си­мо­сти двух пе­ре­мен­ных ве­ли­чин. У англ. ма­те­ма­ти­ка И. Бар­роу («Лек­ции по гео­мет­рии», 1670) в гео­мет­рич. фор­ме ус­та­нав­ли­ва­ет­ся вза­им­ная об­рат­ность дей­ст­вий диф­фе­рен­ци­ро­ва­ния и ин­тег­ри­ро­ва­ния (ра­зу­ме­ет­ся, без упот­реб­ле­ния са­мих этих тер­ми­нов). Это сви­де­тель­ст­ву­ет о со­вер­шен­но от­чёт­ли­вом вла­де­нии по­ня­ти­ем Ф. В гео­мет­рич. и ме­ха­нич. ви­де это по­ня­тие мож­но най­ти и у И. Нью­то­на. Од­на­ко тер­мин «Ф.» впер­вые по­яв­ля­ет­ся лишь в 1692 у Г. Лейб­ни­ца, и при­том не со­всем в со­вре­мен­ном его по­ни­ма­нии. Лейб­ниц на­зы­ва­ет Ф. разл. от­рез­ки, свя­зан­ные с к.-л. кри­вой, напр. абс­цис­сы её то­чек. В пер­вом пе­чат­ном кур­се «Ана­ли­за бес­ко­неч­но ма­лых» франц. ма­те­ма­ти­ка Г. Ло­пи­та­ля (1696) тер­мин «Ф. » не упот­реб­ля­ет­ся.

Пер­вое оп­ре­де­ле­ние Ф. в смыс­ле, близ­ком к со­вре­мен­но­му, встре­ча­ет­ся у И. Бер­нул­ли (1718): «Функ­ция – это ве­ли­чи­на, со­став­лен­ная из пе­ре­мен­ной и по­сто­ян­ной». В ос­но­ве это­го не впол­не от­чёт­ли­во­го оп­ре­де­ле­ния ле­жит идея за­да­ния Ф. ана­ли­тич. фор­му­лой. Та же идея вы­сту­па­ет и в оп­ре­де­ле­нии Л. Эйле­ра, дан­ном им во «Вве­де­нии в ана­лиз бес­ко­неч­ных» (1748): «Функ­ция пе­ре­мен­но­го ко­ли­че­ст­ва есть ана­ли­ти­че­ское вы­ра­же­ние, со­став­лен­ное ка­ким-ли­бо об­ра­зом из это­го пе­ре­мен­но­го ко­ли­че­ст­ва и чи­сел или по­сто­ян­ных ко­ли­честв». На про­тя­же­нии 18 в. от­сут­ст­во­ва­ло до­ста­точ­но яс­ное по­ни­ма­ние раз­ли­чия ме­ж­ду Ф. и её ана­ли­тич. вы­ра­же­ни­ем. С нач. 19 в. уже всё ча­ще и ча­ще оп­ре­де­ля­ют по­ня­тие Ф. без упо­ми­на­ния о её ана­ли­тич. вы­ра­же­нии. Та­кие оп­ре­де­ле­ния встре­ча­ют­ся в ра­бо­тах Ж. Фу­рье (1822), Д. Ди­рих­ле (1829, 1837), Н. И. Ло­ба­чев­ско­го (1834). Так сло­жи­лось совр. по­ня­тие Ф., сво­бод­ное от упо­ми­на­ния о её ана­ли­тич. за­да­нии.

Flow & Scope • Программа Hello World

Интерпретатор Python читает программу точно так же, как вы читаете эту страницу: по одной строке, слева направо и сверху вниз. Интерпретатор выполняет операции и функции в том порядке, в котором он их встречает. Это называется потоком управления или потоком выполнения . В отличие от интерпретатора Python, когда мы что-то читаем и сталкиваемся со словом, которое не понимаем, мы не сходим с ума и не отключаемся (обычно). Мы продолжаем читать и либо угадываем определение слова, исходя из контекста, либо делаем паузу и сверяемся со словарем. Интерпретатор Python не такой гибкий. Вы не можете вызвать функцию до ее определения. Интерпретатор должен знать, что это за функция и что она делает до встречает эту функцию.

Написание функций Python: Flow

Например, следующая программа, too_soon.py:

 too_soon()
защита слишком_скоро():
    print("Не ставить тележку перед трубкозубом") 

… вернет эту ошибку:

 Трассировка (последний последний вызов):
  Файл "too_soon. py", строка 1, в 
    слишком_скоро()
NameError: имя 'too_soon' не определено 

Когда мы вызываем функцию, она считывает наши аргументы по одному слева направо. Затем он обрабатывает значения аргументов и по завершении возвращает значение. Попробуйте следующее в программе под названием flow.py: 9))

В приведенном выше примере, несмотря на то, что мы передали сначала переменную «слева», наша функция сначала напечатала «справа», потому что именно в этом порядке мы ее вызывали.

Написание функций Python: Область применения

Представьте, что ваша программа Python — это мир ( Hello World ), а ваша функция — это ваша группа друзей. Одним из соглашений программирования является объявление переменных в верхней части вашей программы. Эти переменные глобальные . Любые переменные, объявленные внутри функции, равны местный . Глобальные переменные доступны внутри или вне функции, но локальные переменные доступны только внутри функции, в которой они объявлены. Глобальные переменные подобны новостям или общеизвестным фактам: все знают имя президента США. Локальные переменные подобны секретам и внутренним шуткам: их понимаете только вы и ваши друзья; остальной мир понятия не имеет, о чем вы говорите. Это называется прицелом . Переменная, доступная любой функции в программе, имеет глобальная область . Переменная, доступная только внутри функции, имеет локальную область видимости . Давайте напишем программу, inventory.py:

 global_variable = "Сегодня 4 августа."
вечеринка защиты():
    local_variable = «Сегодня мой день рождения!»
    печать (глобальная_переменная)
    печать (локальная_переменная)
вечеринка()
печать (глобальная_переменная)
print(local_variable) 

Это вернет следующую ошибку:

 Traceback (последний вызов последний):
  Файл "invitation.py", строка 10, в 
    печать (локальная_переменная)
NameError: имя «local_variable» не определено 

Измените строку 10 на что-нибудь забавное и снова запустите программу:

 global_variable = «Сегодня 4 августа». 
вечеринка защиты():
    local_variable = «Сегодня мой день рождения!»
    печать (глобальная_переменная)
    печать (локальная_переменная)
вечеринка()
печать (глобальная_переменная)
print("Это моя вечеринка, и я высушу, если захочу...") 

Когда я вызываю функцию party(), мои друзья знают, что сегодня и 4 августа, и мой день рождения. Вызов глобальной переменной вне функции party возвращает дату, 4 августа, потому что у всех есть доступ к дате. Но вызов локальной переменной вне функции party() возвращает ошибку, потому что никто за пределами функции party() не знает, что у меня день рождения.

Говоря о вечеринке, в следующей главе будет торт.

Программирование на Lua: 6.1

Программирование на Lua: 6.1

Это первое издание было написано для Lua 5.0. Несмотря на то, что они по-прежнему актуальны для более поздних версий, есть некоторые отличия.
Четвертое издание предназначено для Lua 5.3 и доступно на Amazon и в других книжных магазинах.
Покупая книгу, вы также помогаете проекту Lua.

	Программирование на Луа
	Часть I. Язык Глава 6. Дополнительные сведения о функциях

---

Когда функция записывается внутри другой функции, он имеет полный доступ к локальным переменным из объемлющей функции; эта функция называется лексической областью видимости . Хотя это может показаться очевидным, это не так. Лексическая область видимости плюс первоклассные функции, мощная концепция языка программирования, но немногие языки поддерживают эту концепцию.

Начнем с простого примера. Предположим, у вас есть список имен учеников. и таблица, которая связывает имена с оценками; вы хотите отсортировать список имен, в соответствии с их оценками (сначала более высокие оценки). Вы можете выполнить это задание следующим образом:

    имена = {"Петр", "Павел", "Мария"}
    оценки = {Мэри = 10, Пол = 7, Питер = 8}
    table. sort (имена, функция (n1, n2)
      вернуть оценки[n1] > оценки[n2] -- сравнить оценки
    конец)
 

Теперь предположим, что вы хотите создать функцию для выполнения этой задачи:

    функция sortbygrade (имена, оценки)
      table.sort (имена, функция (n1, n2)
        вернуть оценки[n1] > оценки[n2] -- сравнить оценки
      конец)
    конец
 

Интересным моментом в примере является то, что анонимная функция, данная вроде обращается к параметру классов , который является локальным для включающей функции sortbygrade . Внутри этой анонимной функции оценок не является ни глобальной, ни локальной переменной. Мы называем это внешней локальной переменной , или upvalue . (Термин «повышенная стоимость» немного вводит в заблуждение, потому что оценивает как переменную, а не значение. Однако этот термин имеет исторические корни в Lua. и это короче, чем «внешняя локальная переменная».)

Почему это так интересно? Потому что функции являются первоклассными значениями. Рассмотрим следующий код:

    функция новыйСчетчик()
      местный я = 0
      функция возврата () -- анонимная функция
               я = я + 1
               вернуть я
             конец
    конец
    
    c1 = новыйСчетчик()
    печать (c1()) --> 1
    печать (с1()) --> 2
 

Теперь анонимная функция использует upvalue, i , сохранить свой счетчик. Однако к тому времени, когда мы вызовем анонимную функцию, и уже за рамками, потому что функция, которая создала эту переменную ( newCounter ) вернулся. Тем не менее, Lua правильно обрабатывает эту ситуацию, используя концепцию закрытия . Проще говоря, замыкание — это функция плюс все должен правильно получить доступ к своим значениям. Если мы снова вызовем newCounter , он создаст новую локальную переменную i , так что мы получим новое закрытие, воздействуя на эту новую переменную:

    c2 = новыйСчетчик()
    печать (с2()) --> 1
    печать (с1()) --> 3
    печать (c2()) --> 2
 

Итак, c1 и c2 — разные замыкания над той же функцией и каждый действует независимо создание локальной переменной i . С технической точки зрения, ценностью в Lua является замыкание, не та функция. Сама функция — это всего лишь прототип замыканий. Тем не менее, мы будем продолжать использовать термин «функция» для ссылайтесь на закрытие всякий раз, когда нет возможности путаницы.

Замыкания являются ценным инструментом во многих контекстах. Как мы видели, они полезны в качестве аргументов для функций более высокого порядка например вроде . Замыкания полезны для функций, которые строят другие функции. как наш пример newCounter ; этот механизм позволяет программам Lua включать причудливые техники программирования из функционального мира. Замыкания также полезны для функций обратного вызова . Типичный пример здесь происходит когда вы создаете кнопки в типичном наборе инструментов GUI. Каждая кнопка имеет функцию обратного вызова для вызова когда пользователь нажимает кнопку; вы хотите, чтобы разные кнопки выполняли разные действия при нажатии. Например, цифровому калькулятору нужно десять одинаковых кнопок, по одному на каждую цифру. Вы можете создать каждый из них с функцией, подобной следующей:

    функция digitButton (цифра)
      Кнопка возврата {метка = цифра,
                     действие = функция ()
                                add_to_display(цифра)
                              конец
                   }
    конец
 

В этом примере мы предполагаем, что Кнопка является функцией набора инструментов. который создает новые кнопки; метка — метка кнопки; а действие — это функция обратного вызова вызываться при нажатии кнопки. (На самом деле это закрытие, потому что он обращается к upvalue цифра .) Функция обратного вызова может быть вызвана долгое время после digitButton выполняла свою задачу и после того, как локальная переменная цифра вышла из области видимости, но он все еще может получить доступ к этой переменной.

Затворы ценны также в совсем другой контекст. Поскольку функции хранятся в обычных переменных, мы можем легко переопределить функции в Lua, даже предопределенные функции. Это средство — одна из причин, по которой Lua такой гибкий. Однако часто, когда вы переопределяете функцию, вам нужно исходная функция в новой реализации. Например, предположим, что вы хотите переопределить функцию грех до работают в градусах, а не в радианах. Эта новая функция должна преобразовать свой аргумент, а затем вызовите исходную функцию sin , чтобы выполнить реальную работу. Ваш код может выглядеть так

    старый грех = math.sin
    math.sin = функция (х)
      вернуть oldSin(x*math.pi/180)
    конец
 

Более чистый способ сделать это выглядит следующим образом:

    делать
      локальный oldSin = math.sin
      местное k = math.pi/180
      math.sin = функция (х)
        вернуть старый грех (х * к)
      конец
    конец
 

Теперь мы храним старую версию в приватной переменной; единственный способ получить к нему доступ через новую версию.

Вы можете использовать эту же функцию для создания безопасных сред, также называется песочницей . Безопасная среда необходима при запуске ненадежного кода, Например, код, полученный сервером через Интернет. Например, чтобы ограничить файлы, к которым может получить доступ программа, мы можем переопределить функцию open (из библиотеки io ) с использованием замыканий:

    делать
      локальный oldOpen = io.open
      io.open = функция (имя файла, режим)
        если access_OK(имя файла, режим) то
          вернуть oldOpen(имя файла, режим)
        еще
          вернуть nil, "доступ запрещен"
        конец
      конец
    конец
 

Чем хорош этот пример, так это тем, что после такого переопределения программа не может вызвать неограниченный открытый , кроме как через новую ограниченную версию. Он сохраняет небезопасную версию как закрытую переменную в замыкании, недоступен извне. С помощью этого средства вы можете создавать песочницы Lua в самом Lua, с обычным преимуществом: гибкостью. Вместо универсального решения, Lua предлагает вам метамеханизм, так что вы можете адаптировать свою среду для ваших конкретных потребностей безопасности.