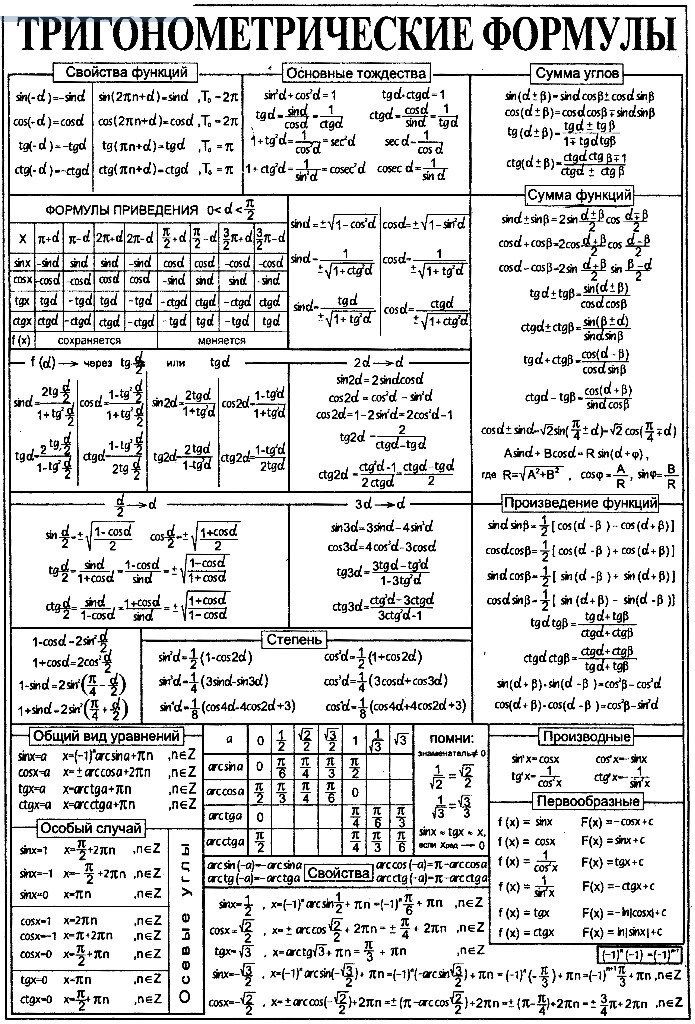
Тригонометрические тождества
Тригонометрические функции являются неотъемлемой частью тригонометрии, поэтому знание этих функций очень важно. Но на чем основываются эти функции? Конечно же, на тригонометрических тождествах.
Давайте разберемся, что же такое тождество вообще? Самое простое определение, это, конечно же, сходство. Если «копнуть» глубже, то мы можем говорить о том, что тождество – отношение между некоторыми предметами (реальными или абстрактными), что позволяет говорить об их неотличимости в каких-то характеристиках. На самом деле такое определение к тригонометрии подходит, ведь в каких-то характеристиках наши функции действительно схожи и неотъемлемы друг от друга.
Давайте подробнее рассмотрим каждое тригонометрическое тождество.
Соотношение синуса и косинуса одного и того же угла – именно это тригонометрическое тождество и является основным в тригонометрии. Выглядит это тождество следующим образом:
Sin2a +cos2a = 1
Попробуем объяснить, почему это тождество выглядит именно так. Изначально у нас есть прямоугольный треугольник с определенным углом а. Гипотенуза нашего треугольника равна 1. Один катет треугольника – это косинус, а другой – синус. Теперь применяем к нашему треугольнику теорему Пифагора и получаем наше тригонометрическое тождество.
Изначально у нас есть прямоугольный треугольник с определенным углом а. Гипотенуза нашего треугольника равна 1. Один катет треугольника – это косинус, а другой – синус. Теперь применяем к нашему треугольнику теорему Пифагора и получаем наше тригонометрическое тождество.
Теперь рассмотрим зависимость между тангенсом и котангенсом. Тут все просто. Произведение тангенса и котангенса равно 1.
Зависимость между тангенсом и косинусом угла выводится очень просто. Для начала берем наше основное тригонометрическое тождество и делим его на квадрат косинуса, потом упрощаем левую часть уравнения и получаем наше третье тождество (при это важно помнить, что деление возможно только в том случае. если косинус не равняется нулю).
Тригонометрические тождества
cos2α + sin2α = 1
|cosα| = √1 — sin2α
|sinα| = √1 — cos2α
tgα * ctgα = 1
| tgα = | 1 ctgα |
| ctgα = | 1 tgα |
| 1 + ctg2α = | 1 sin2α | = cosec2α |
| 1 + tg2α = | 1 cos2α | = sec2α |
Выражения одних тригонометрических функций через другие
| sin(x) = | ||
|---|---|---|
| через cos(x) | ±√1 — cos2x | |
| через tg(x) |
| |
| через ctg(x) |
| |
| через sec(x) |
| |
| через cosec(x) |
|
| cos(x) = | ||
|---|---|---|
| через sin(x) | ±√1 — sin2x | |
| через tg(x) |
| |
| через ctg(x) |
| |
| через sec(x) |
| |
| через cosec(x) |
|
| tg(x) = | ||
|---|---|---|
| через sin(x) |
| |
| через cos(x) |
| |
| через ctg(x) | ||
| через sec(x) | ±√sec2x — 1 | |
| через cosec(x) |
|
| ctg(x) = | ||
|---|---|---|
| через sin(x) |
| |
| через cos(x) |
| |
| через tg(x) | ||
| через sec(x) |
| |
| через cosec(x) | ±√cosec2x — 1 |
| sec(x) = | ||
|---|---|---|
| через sin(x) |
| |
| через cos(x) | ||
| через tg(x) | ±√1 + tg2x | |
| через ctg(x) |
| |
| через cosec(x) |
|
| cosec(x) = | ||
|---|---|---|
| через sin(x) | ||
| через cos(x) |
| |
| через tg(x) |
| |
| через ctg(x) | ±√1 + ctg2x | |
| через sec(x) |
|
Простейшие тригонометрические тождества.
 Тригонометрические тождества
Тригонометрические тождестваВ статье подробно рассказывается об основных тригонометрических тождествах.Эти равенства устанавливают связь между sin , cos , t g , c t g заданного угла. При известной одной функции можно через нее найти другую.
Тригонометрические тождества для рассмотрения в денной статье. Ниже покажем пример их выведения с объяснением.
sin 2 α + cos 2 α = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α
Yandex.RTB R-A-339285-1
Поговорим о важном тригонометрическом тождестве, которое считается основой основ в тригонометрии.
sin 2 α + cos 2 α = 1
Заданные равенства t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α выводят из основного путем деления обеих частей на sin 2 α и cos 2 α . После чего получаем t g α = sin α cos α , c t g α = cos α sin α и t g α · c t g α = 1 — это следствие определений синуса, косинуса, тангенса и котангенса.
Равенство sin 2 α + cos 2 α = 1 является основным тригонометрическим тождеством.
Пусть даны координаты точки А (1 , 0) , которая после поворота на угол α становится в точку А 1 . По определению sin и cos точка А 1 получит координаты (cos α , sin α) . Так как А 1 находится в пределах единичной окружности, значит, координаты должны удовлетворят условию x 2 + y 2 = 1 этой окружности. Выражение cos 2 α + sin 2 α = 1 должно быть справедливым. Для этого необходимо доказать основное тригонометрическое тождество для всех углов поворота α .
В тригонометрии выражение sin 2 α + cos 2 α = 1 применяют как теорему Пифагора в тригонометрии. Для этого рассмотрим подробное доказательство.
Используя единичную окружность, поворачиваем точку А с координатами (1 , 0) вокруг центральной точки О на угол α . После поворота точка меняет координаты и становится равной А 1 (х, у) . Опускаем перпендикулярную прямую А 1 Н на О х из точки А 1 .
На рисунке отлично видно, что образовался прямоугольный треугольник О А 1 Н. По модулю катеты О А 1 Н и О Н равные, запись примет такой вид: | А 1 H | = | у | , | О Н | = | х | . Гипотенуза О А 1 имеет значение равное радиусу единичной окружности, | О А 1 | = 1 . Используя данное выражение, можем записать равенство по теореме Пифагора: | А 1 Н | 2 + | О Н | 2 = | О А 1 | 2 . Это равенство запишем как | y | 2 + | x | 2 = 1 2 , что означает y 2 + x 2 = 1 .
По модулю катеты О А 1 Н и О Н равные, запись примет такой вид: | А 1 H | = | у | , | О Н | = | х | . Гипотенуза О А 1 имеет значение равное радиусу единичной окружности, | О А 1 | = 1 . Используя данное выражение, можем записать равенство по теореме Пифагора: | А 1 Н | 2 + | О Н | 2 = | О А 1 | 2 . Это равенство запишем как | y | 2 + | x | 2 = 1 2 , что означает y 2 + x 2 = 1 .
Используя определение sin α = y и cos α = x , подставим данные угла вместо координат точек и перейдем к неравенству sin 2 α + cos 2 α = 1 .
Основная связь между sin и cos угла возможна через данное тригонометрическое тождество. Таким образом, можно считать sin угла с известным cos и наоборот. Чтобы выполнить это, необходимо разрешать sin 2 α + cos 2 = 1 относительно sin и cos , тогда получим выражения вида sin α = ± 1 — cos 2 α и cos α = ± 1 — sin 2 α соответственно. Величина угла α определяет знак перед корнем выражения. Для подробного выяснения необходимо прочитать раздел вычисление синуса, косинуса, тангенса и котангенса с использованием тригонометрических формул.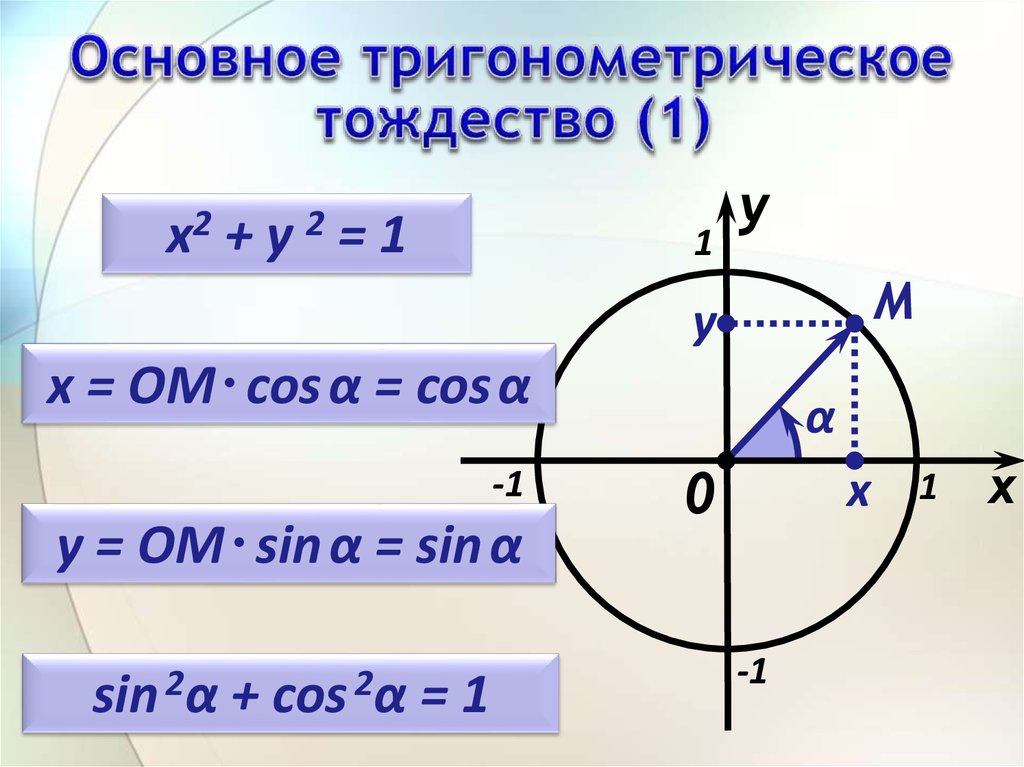
Чаще всего основную формулу применяют для преобразований или упрощений тригонометрических выражений. Имеется возможность заменять сумму квадратов синуса и косинуса на 1 . Подстановка тождества может быть как в прямом, так и обратном порядке: единицу заменяют на выражение суммы квадратов синуса и косинуса.
Тангенс и котангенс через синус и косинус
Из определения косинуса и синуса, тангенса и котангенса видно, что они взаимосвязаны друг с другом, что позволяет отдельно преобразовывать необходимые величины.
t g α = sin α cos α c t g α = cos α sin α
Из определения синус является ординатой у, а косинус – абсциссой x . Тангенс – это и есть отношения ординаты и абсциссы. Таким образом имеем:
t g α = y x = sin α cos α , а выражение котангенса имеет обратное значение, то есть
c t g α = x y = cos α sin α .
Отсюда следует, что полученные тождества t g α = sin α cos α и c t g α = cos α sin α задаются с помощью sin и cos углов. Тангенс считаются отношением синуса к косинусу угла между ними, а котангенс наоборот.
Отметим, что t g α = sin α cos α и c t g α = cos α sin α верны для любого значение угла α , значения которого входят в диапазон. Из формулы t g α = sin α cos α значение угла α отлично от π 2 + π · z , а c t g α = cos α sin α принимает значение угла α , отличные от π · z , z принимает значение любого целого числа.
Связь между тангенсом и котангенсом
Имеется формула, которая показывает связь между углами через тангенс и котангенс. Данное тригонометрическое тождество является важным в тригонометрии и обозначается как t g α · c t g α = 1 . Оно имеет смысл при α с любым значением, кроме π 2 · z , иначе функции будут не определены.
Формула t g α · c t g α = 1 имеет свои особенности в доказательстве. Из определения мы имеем, что t g α = y x и c t g α = x y , отсюда получаем t g α · c t g α = y x · x y = 1 . Преобразовав выражение и подставив t g α = sin α cos α и c t g α = cos α sin α , получим t g α · c t g α = sin α cos α · cos α sin α = 1 .
Тогда выражение тангенса и котангенса имеет смысл того, когда в итоге получаем взаимно обратные числа.
Преобразовав основные тождества, приходим к выводу, что тангенс связан через косинус, а котангенс через синус. Это видно по формулам t g 2 α + 1 = 1 cos 2 α , 1 + c t g 2 α = 1 sin 2 α .
Определение звучит так: сумма квадрата тангенса угла и 1 приравнивается к дроби, где в числителе имеем 1 , а в знаменателе квадрат косинуса данного угла, а сумма квадрата котангенса угла наоборот. Благодаря тригонометрическому тождеству sin 2 α + cos 2 α = 1 , можно разделить соответствующие стороны на cos 2 α и получить t g 2 α + 1 = 1 cos 2 α , где значение cos 2 α не должно равняться нулю. При делении на sin 2 α получим тождество 1 + c t g 2 α = 1 sin 2 α , где значение sin 2 α не должно равняться нулю.
Из приведенных выражений получили, что тождество t g 2 α + 1 = 1 cos 2 α верно при всех значениях угла α , не принадлежащих π 2 + π · z , а 1 + c t g 2 α = 1 sin 2 α при значениях α , не принадлежащих промежутку π · z .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются
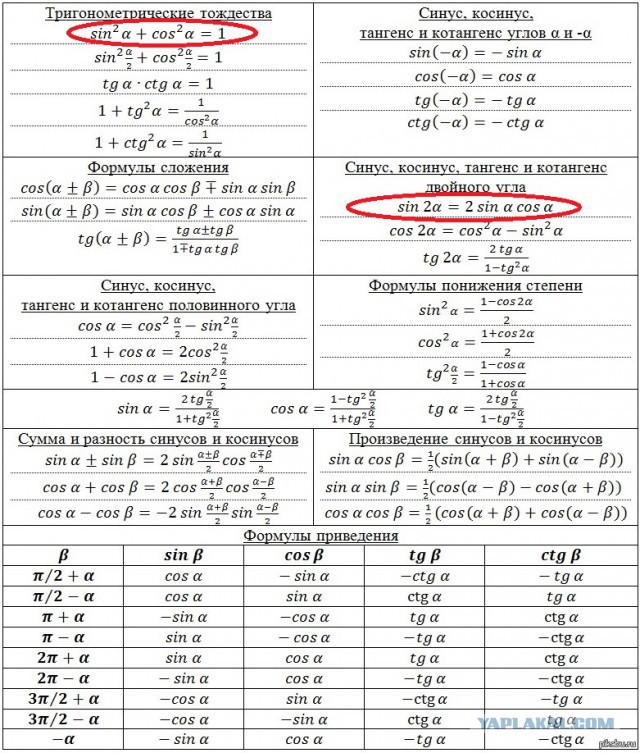 А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т. д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений.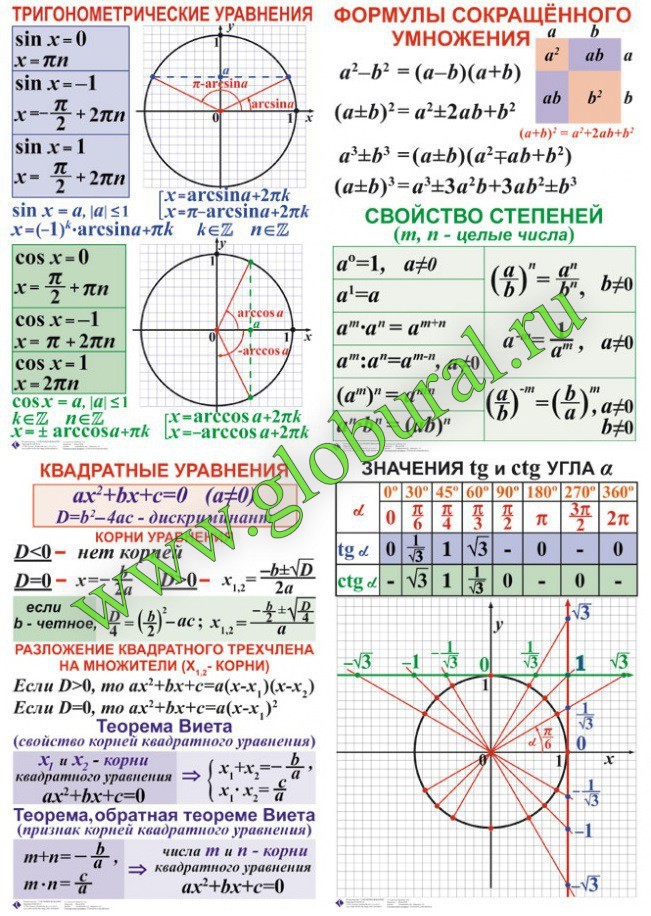
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла »), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см.
 урок «Знаки тригонометрических функций »).
урок «Знаки тригонометрических функций »).Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin 2 α + cos 2 α = 1.
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.

Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2 α (для получения тангенса) или на sin 2 α (для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.

Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α принадлежит промежутку (π 3π /2). Переведем углы из радианной меры в градусную — получим: α ∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α , если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3.
 Знак тангенса определяем по углу α
. Известно, что α
∈ (3π
/2; 2π
). Переведем углы из радианной меры в градусную — получим α
∈ (270°; 360°).
Знак тангенса определяем по углу α
. Известно, что α
∈ (3π
/2; 2π
). Переведем углы из радианной меры в градусную — получим α
∈ (270°; 360°).Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α , если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α ∈ (3π /2; 2π ). Переведем углы из градусной меры в радианную: α ∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α = 0,6.
Задача. Найдите sin α , если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π /2).
 В градусной мере это записывается так: α
∈ (0°; 90°) — I координатная четверть.
В градусной мере это записывается так: α
∈ (0°; 90°) — I координатная четверть.Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Тригонометрические тождества кратко Алгебра
Привет, Вы узнаете про формулы сложения и вычитания аргументов, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое формулы сложения и вычитания аргументов, формулы двойного угла и половинного угла, формулы тройного угла, формулы понижения степени, формулы преобразования произведения функций 7 формулы преобразования суммы функций 8 решение простых тригонометрических уравнений, универсальная тригонометрическая подстановка, вспомогательный аргумент , формулы сложения гармонических колебаний , настоятельно рекомендую прочитать все из категории Алгебра.
Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).

Основные тригонометрические формулы
№ Формула Допустимые значения аргумента 1.1 1.2 1.3 1.4 - Формула (1.1) является следствием теоремы Пифагора.
- Формулы (1.2) и (1.3) получаются из формулы (1.1) делением на и соответственно.
- Формула (1.4) следует из определений тангенса и котангенса.
Замечание
Есть и другие тригонометрические функции.
формулы сложения и вычитания аргументов
№ Формулы сложения и вычитания аргументов 2.  1
12.2 2.3 2.4 Формула (2.3) получается при делении (2.1) на (2.2). А формула (2.4) — при делении (2.2) на (2.1).
формулы двойного угла и половинного угла
Формулы двойного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу α:
№ Формулы двойного угла 3.1 3.2 3.3 3.  4
4Примечания[показать]
Из формулы двойного угла для косинуса (3.2) выводятся формулы половинного угла:
№ Формулы половинного угла 3.5 3.6 3.7 формулы тройного угла
Формулы тройного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу 2α:
№ Формулы тройного угла 4.1 4.2 4.3 4.  4
4формулы понижения степени
Формулы понижения степени выводятся из формул (3.2):
№ Синус № Косинус 5.1 5.5 5.2 5.6 5.3 5.7 5.4 5.8 № Произведение 5.  9
95.10 5.11 5.12 Формулы преобразования произведения функций
№ Формулы преобразования произведений функций 6.1 6.2 6.3 Формулы преобразования суммы функций
№ Формулы преобразования суммы функций 7.1 7.2 7.  3
37.4 7.5 Вывод формул преобразования суммы функций[показать]
Преобразование суммы синусов 3-x разных углов в произведение при : :
(7.6)
Решение простых тригонометрических уравнений
Если — вещественных решений нет.
Если — решением является число вида
Если — вещественных решений нет.
Если — решением является число вида
Решением является число вида
Решением является число вида
универсальная тригонометрическая подстановка
Тождества имеют смысл, только когда существуют обе части (то есть при ).
вспомогательный аргумент ( формулы сложения гармонических колебаний )
Сумма двух гармонических колебаний с одинаковой частотой будет вновь гармоническим колебанием .
 Об этом говорит сайт https://intellect.icu . В частности,
Об этом говорит сайт https://intellect.icu . В частности,где , и не равны нулю одновременно, — это угол, называемый вспомогательным аргументом, который может быть найден из системы уравнений:
Примечание. Из вышеприведенной системы следует, что , однако нельзя всегда считать, что . Нужно учитывать знаки и для определения, к какой четверти принадлежит угол .
Полезные тождества
В приведенных ниже формулах числа и целые.
Следующая формула приводится в двух вариантах для угла заданного в градусах и радианах:
Представление тригонометрических функций в комплексной форме
Формула Эйлера утверждает, что для любого вещественного числа выполнено следующее равенство:
где — основание натурального логарифма,
— мнимая единица.

При помощи формулы Эйлера можно определить функции и следующим образом :
Отсюда следует, что
См. также
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Комплексные числа
- Многочлены Чебышева
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус -верзус
- Сферическая тригонометрия
- Треугольник § Тригонометрические тождества только с углами
- Тригонометрические функции
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырехзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
В общем, мой друг ты одолел чтение этой статьи об формулы сложения и вычитания аргументов.
 Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое формулы сложения и вычитания аргументов, формулы двойного угла и половинного угла, формулы тройного угла, формулы понижения степени, формулы преобразования произведения функций 7 формулы преобразования суммы функций 8 решение простых тригонометрических уравнений, универсальная тригонометрическая подстановка, вспомогательный аргумент , формулы сложения гармонических колебаний
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгебра
Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое формулы сложения и вычитания аргументов, формулы двойного угла и половинного угла, формулы тройного угла, формулы понижения степени, формулы преобразования произведения функций 7 формулы преобразования суммы функций 8 решение простых тригонометрических уравнений, универсальная тригонометрическая подстановка, вспомогательный аргумент , формулы сложения гармонических колебаний
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
АлгебраИз статьи мы узнали кратко, но емко про формулы сложения и вычитания аргументов
Тригонометрические тождества: Таблица тригонометрических тождеств
Учащихся учат тригонометрическим тождествам или тригонометрическим тождествам в школе, и они являются важной частью математики более высокого уровня.
 Итак, чтобы помочь вам понять и выучить все тригонометрические тождества , мы объяснили здесь все концепции тригонометрии. Будучи студентом, вы сочтете trig identity листом , который мы предоставили здесь, полезным. Таким образом, вы можете скачать и распечатать удостоверения личности в формате PDF и использовать его в любое время для решения уравнений.
Итак, чтобы помочь вам понять и выучить все тригонометрические тождества , мы объяснили здесь все концепции тригонометрии. Будучи студентом, вы сочтете trig identity листом , который мы предоставили здесь, полезным. Таким образом, вы можете скачать и распечатать удостоверения личности в формате PDF и использовать его в любое время для решения уравнений.- Формула интегрирования
- Формула тригонометрии
- Тригонометрические соотношения
- Тригонометрические функции с формулами
- Что такое тригонометрические производные
- Высота и расстояние
- Тригонометрическая формула, включающая сумму разностей Идентичность продуктов
- Теорема Пифагора
- Формула дифференциации
- Базовые идентификаторы триггеров
Тригонометрия — важный раздел математики, изучающий отношения между длинами и углами треугольников.
 Это довольно старая концепция, впервые использованная в 3 веке до нашей эры. Этот раздел математики связан с плоскими прямоугольными треугольниками (или прямоугольными треугольниками в двумерной плоскости с одним углом, равным 90 градусам).
Это довольно старая концепция, впервые использованная в 3 веке до нашей эры. Этот раздел математики связан с плоскими прямоугольными треугольниками (или прямоугольными треугольниками в двумерной плоскости с одним углом, равным 90 градусам).Есть и другие отрасли, где тригонометрия внесла огромный вклад в ее рост и развитие. Некоторые из его областей применения;
- В музыке: его можно использовать для разработки музыки в цифровом виде с помощью компьютерной музыки.
- В авиации: очень важно вести самолет в правильном направлении. Например, если известны скорость ветра и угол наклона самолета, их можно использовать для определения направления самолета.
- В криминалистике – тригонометрия также может использоваться в криминалистике, где она используется для вычисления различных важных детерминант места преступления, таких как траектория снаряда, способ падения предмета и т. д.
- Математика: Тригонометрия — один из важнейших разделов математики, без которого не могли бы существовать некоторые другие жизненно важные разделы.
 Например, исчисление основано исключительно на тригонометрии и алгебре.
Например, исчисление основано исключительно на тригонометрии и алгебре.
Что такое идентификаторы триггеров?
Хотя тригонометрия не имеет прямого применения, ее применение в нашей повседневной жизни нельзя игнорировать. Это незаменимый аспект многих областей исследований и отраслей промышленности. Его наиболее распространенным применением является измерение высоты здания, горы или высокого объекта на расстоянии. Единственные две информации, необходимые для определения высоты, — это угол возвышения и расстояние от объекта.
PDF
Тригонометрические тождества — это математические уравнения, составленные из функций. Эти тождества верны для любого значения переменной put.
Существует множество тождеств, которые выводятся из основных функций, т. е. sin, cos, tan и т. д. Самым основным тождеством является пифагорейское тождество, которое выводится из теоремы Пифагора. Он используется для определения уравнений, применяя теорему Пифагора.
 Таким образом, это помогает нам определить соотношение между прямыми и углами в прямоугольном треугольнике.
Таким образом, это помогает нам определить соотношение между прямыми и углами в прямоугольном треугольнике.Другими важными тождествами являются гиперболические тождества, полуугловые тождества, обратные тождества и т. д.
Гиперболические триггерные тождества
PDF
Гиперболическая функция похожа на функцию, но может отличаться от нее в некоторых терминах. Основными гиперболическими функциями являются гиперболический синус и гиперболический косинус, из которых выводятся остальные функции.
Итак, здесь мы представили график гиперболы, что дает вам представление о положениях синуса, косинуса и т. д.
Тождества пифагорейских триггеров
PDF
Тождества Пифагора — это тождества, представляющие теорему Пифагора в форме функций. Таким образом, эти тождества помогают нам в основном определить взаимосвязь между различными функциями синуса и косинуса. Оттуда вы также можете вывести функцию других тождеств.

Фундаментальное пифагорейское тригонометрическое тождество:
sin(x) + cos(x) = 1
Таким образом, из этой формулы мы можем вывести формулы и для других функций:
Идентичности обратных триггеров
Обратные тригонометрические функции также называются аркус-функциями. По сути, они представляют собой тригонометрических взаимных тождества функций sin, cos, tan и других. Эти идентификаторы используются в ситуациях, когда необходимо ограничить область применения функции.
Эти тождества имеют особое значение в технике, навигации, физике и геометрии.
Здесь мы предоставили вам таблицу, показывающую обратные тождества всех тригонометрических функций:
PDF
Основные триггерные тождества
Основные тождества — это уравнения, включающие функции, которые всегда верны для переменных. Таким образом, эти тождества изображают определенные функции одного или нескольких углов.
 Это связано с единичным кругом, где изображены отношения между линиями и углами на декартовой плоскости. Здесь мы предоставили вам таблицу, состоящую из набора тождеств, которые могут быть получены из основных функций
Это связано с единичным кругом, где изображены отношения между линиями и углами на декартовой плоскости. Здесь мы предоставили вам таблицу, состоящую из набора тождеств, которые могут быть получены из основных функцийPDF
Тождества по тригонометрии — Открытый справочник по математике
Тождества по тригонометрии — Открытый справочник по математикеОткрытый математический справочник
Главная Контакт О Тематический указатель
Все эти триггерные тождества могут быть выведены из первых принципов. Но их много и некоторые трудно запомнить. Распечатайте эту страницу в качестве удобного краткого справочного руководства.
Напомним, что эти тождества работают в обе стороны. То есть, если у вас есть выражение, которое соответствует левой или правой части идентификатора, вы можете заменить его тем, что находится на другой стороне.
A. Взаимные тождества
а1 а4 а2 а5 а3 а6 B.
 Соотношение тождеств
Соотношение тождествC. Тождества с противоположными углами
с1 с2 с3 D. Пифагорейские тождества
д1 д2 д3 E. Дополнительные тождества углов
е1 е2 е3 * Примечание: составляет 90° в радианах.
Если A в градусах, используйте 90 вместо
Например:F. Дополнительные тождества углов
Это в основном говорит о том, что если два угла являются дополнительными (добавьте к 180 °), они имеют один и тот же синус.
ф1 или в градусах:
Г. Сумма тождеств
г1 г2 г3 H.
 Отличие тождеств
Отличие тождествh2 h3 h4 Дж. Тождества двойного угла
j1 j2 j3 j4 j5 K. Полуугольные тождества
к1 к2 к3 к4 М. Тождества синусов
Они показывают, как представить синусоидальную функцию в терминах других пяти функций. Некоторые из этих тождеств могут также появляться под другими заголовками.
м1 м2 м3 м4 м5 N. Косинусные тождества
Они показывают, как представить функцию косинуса в терминах других пяти функций.
 Некоторые из этих тождеств могут также появляться под другими заголовками.
Некоторые из этих тождеств могут также появляться под другими заголовками.№1 №2 №3 №4 №5 P. Касательные тождества
Они показывают, как представить функцию тангенса в терминах других пяти функций. Некоторые из этих триггерных тождеств могут появляться и под другими заголовками.
стр.1 стр.2 стр.3 стр.4 стр.5 Q. Косекансные тождества
Они показывают, как представить функцию косеканса в терминах других пяти функций. Некоторые из этих триггерных тождеств могут появляться и под другими заголовками.
Q1 кв2 кв3 четвертый квартал кв5 Р.
 Секущие тождества
Секущие тождестваОни показывают, как представить секущую функцию с точки зрения других пяти функций. Некоторые из этих триггерных тождеств могут появляться и под другими заголовками.
р1 р2 р3 р4 р5 S. Котангенсные тождества
Они показывают, как представить функцию котангенса в терминах других пяти функций. Некоторые из этих тождеств могут также появляться под другими заголовками.
с1 с2 с3 с4 с5 Ссылка на эту страницу
Если вы хотите сделать ссылки на эту страницу, вы можете настроить ссылку так, чтобы она указывала на конкретную личность или группу личностей. Ссылка должна быть URL-адресом страницы, за которым следует #, а затем раздел или идентификатор, который вы хотите.
 Например
Напримерmathopenref.com/trigidentities.htmlБудет ссылка на верхнюю часть этой страницыmathopenref.com/trigidentities.html#cБудет ссылка на эту страницу с прокруткой страницы так, чтобы раздел C был вверхуmathopenref.com/trigidentities.html#h3Будет ссылка на эту страницу со страницей, прокрученной так, чтобы удостоверение личности h3 было вверху и обведено контуром.Например mathopenref.com/trigidentities.html#h3
(C) 2011 Copyright Math Open Reference.
Все права защищеныТригонометрические тождества — Математика средней школы
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- Репетиторство по программе SAT
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Тригонометрия » Тригонометрические тождества
Что такое?
Возможные ответы:
Правильный ответ:
Объяснение:
При работе с основными тригонометрическими тождествами проще всего запомнить мнемонику: .

Когда называют прямоугольный треугольник, противолежащая сторона лежит напротив угла, прилежащая сторона находится рядом с углом, а гипотенуза охватывает два катета прямого угла.
Сообщить об ошибке
Упростить .
Возможные ответы:
Правильный ответ:
Объяснение:
Упрощение трионометрических выражений или тождеств часто связано с небольшими пробами и ошибками, поэтому трудно найти стратегию, которая работает каждый раз. Много раз вам приходится пробовать несколько стратегий и смотреть, какая из них поможет.
Часто, если у вас есть какая-либо форма или в выражении, полезно переписать его в терминах синуса и косинуса. В этой задаче мы можем использовать тождества и .
.
Кажется, это мало помогает. Однако мы должны признать это из-за пифагорейской идентичности.

Мы можем сократить члены в числителе и знаменателе.
.
Сообщить об ошибке
Что такое?
Возможные ответы:
Правильный ответ:
Объяснение:
При работе с основными тригонометрическими тождествами проще всего запомнить мнемонику: .
,
Когда называют прямоугольный треугольник, противолежащая сторона лежит напротив угла, прилежащая сторона находится рядом с углом, а гипотенуза охватывает два катета прямого угла.
Сообщить об ошибке
Что такое?
Возможные ответы:
Правильный ответ:
Объяснение:
При работе с основными тригонометрическими тождествами проще всего запомнить мнемонику: .

,
Когда называют прямоугольный треугольник, противолежащая сторона лежит напротив угла, прилежащая сторона находится рядом с углом, а гипотенуза охватывает два катета прямого угла.
Сообщить об ошибке
Упростить
Возможные ответы:
Правильный ответ:
Объяснение:
. Таким образом:
Сообщить об ошибке
Упростить
Возможные ответы:
Правильный ответ:
Объяснение:
и
.
Сообщить об ошибке
Упростить .
Возможные ответы:
Правильный ответ:
Объяснение:
Помните об этом .
 Мы можем изменить это, чтобы упростить данное уравнение:
Мы можем изменить это, чтобы упростить данное уравнение:Сообщить об ошибке
Упростить:
Возможные ответы:
3 9
Правильный ответ:
Объяснение:
Всякий раз, когда вы видите квадрат тригонометрической функции, начинайте искать тождество Пифагора.
В этой задаче используются два тождества: и .
Подставить и решить.
Сообщить об ошибке
Фактор и упрощение .
Возможные ответы:
Это уже самая сокращенная форма.
Правильный ответ:
Объяснение:
Чтобы уменьшить, умножьте числитель на 9.
 0013
0013Обратите внимание, что мы можем отменить .
Остается .
Сообщить об ошибке
Упростить .
Возможные ответы:
Правильный ответ:
Объяснение:
Для упрощения разбейте их на части SOHCATOA:
.
Обратите внимание, что противоположное значение отменяется, оставляя .
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Просмотр репетиторов
Tia
Сертифицированный репетиторКолледж Джорджии Гвиннетт, бакалавр наук, биология, общие.
Посмотреть репетиторов
Ярослав
Сертифицированный репетиторУниверситет Хериот-Ватт, магистр наук, физика. Университет Хериота Ватта, доктор наук, теоретико-математический факультет…
Просмотреть преподавателей
Мельба
Сертифицированный преподавательУниверситет Эмори, бакалавр наук, сестринское дело (RN).


 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.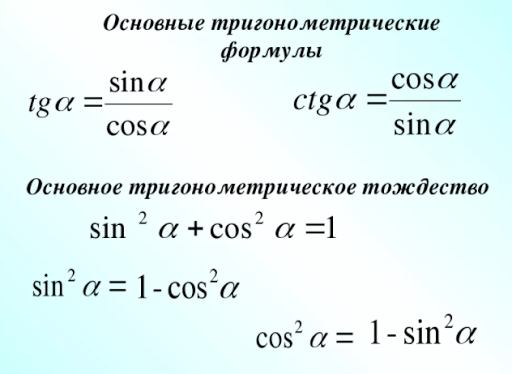 урок «Знаки тригонометрических функций »).
урок «Знаки тригонометрических функций »).

 Знак тангенса определяем по углу α
. Известно, что α
∈ (3π
/2; 2π
). Переведем углы из радианной меры в градусную — получим α
∈ (270°; 360°).
Знак тангенса определяем по углу α
. Известно, что α
∈ (3π
/2; 2π
). Переведем углы из радианной меры в градусную — получим α
∈ (270°; 360°). В градусной мере это записывается так: α
∈ (0°; 90°) — I координатная четверть.
В градусной мере это записывается так: α
∈ (0°; 90°) — I координатная четверть.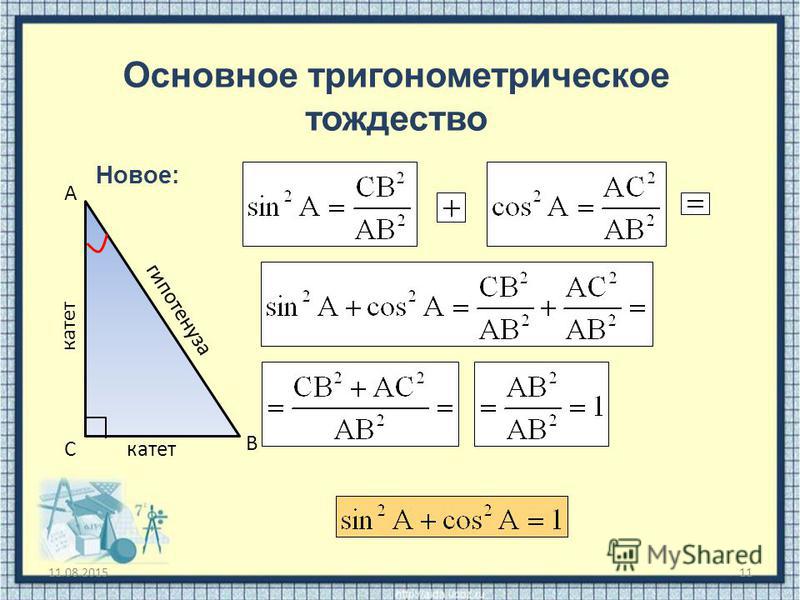
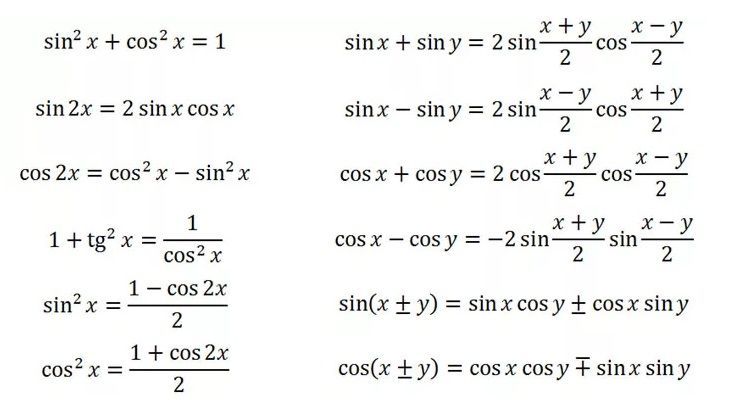 1
1 4
4 4
4 9
9 3
3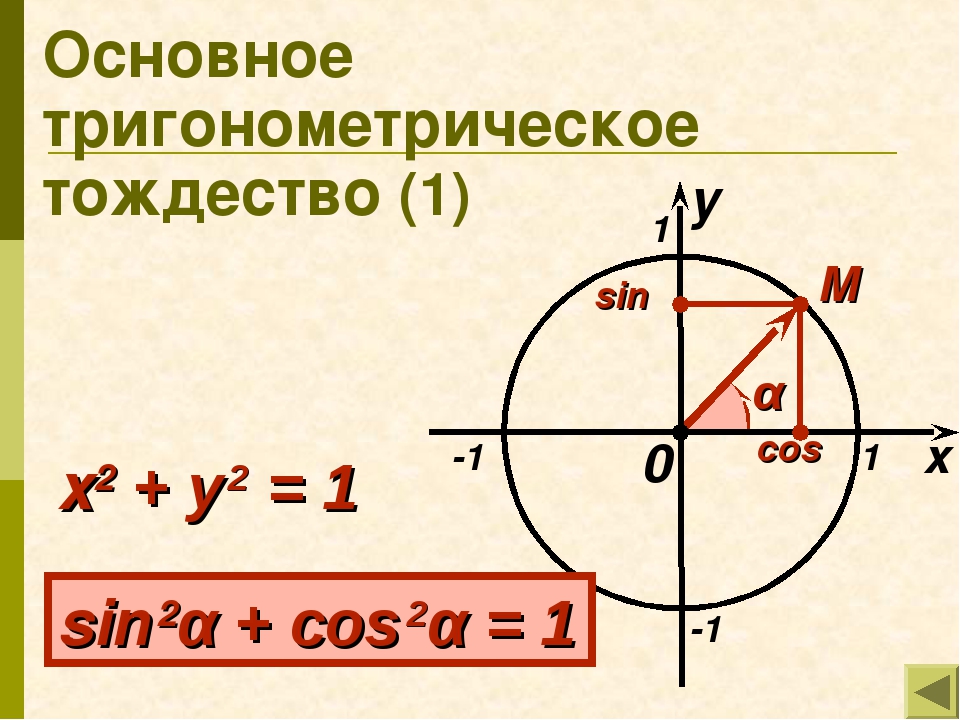 Об этом говорит сайт https://intellect.icu . В частности,
Об этом говорит сайт https://intellect.icu . В частности,
 Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое формулы сложения и вычитания аргументов, формулы двойного угла и половинного угла, формулы тройного угла, формулы понижения степени, формулы преобразования произведения функций 7 формулы преобразования суммы функций 8 решение простых тригонометрических уравнений, универсальная тригонометрическая подстановка, вспомогательный аргумент , формулы сложения гармонических колебаний
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгебра
Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое формулы сложения и вычитания аргументов, формулы двойного угла и половинного угла, формулы тройного угла, формулы понижения степени, формулы преобразования произведения функций 7 формулы преобразования суммы функций 8 решение простых тригонометрических уравнений, универсальная тригонометрическая подстановка, вспомогательный аргумент , формулы сложения гармонических колебаний
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Алгебра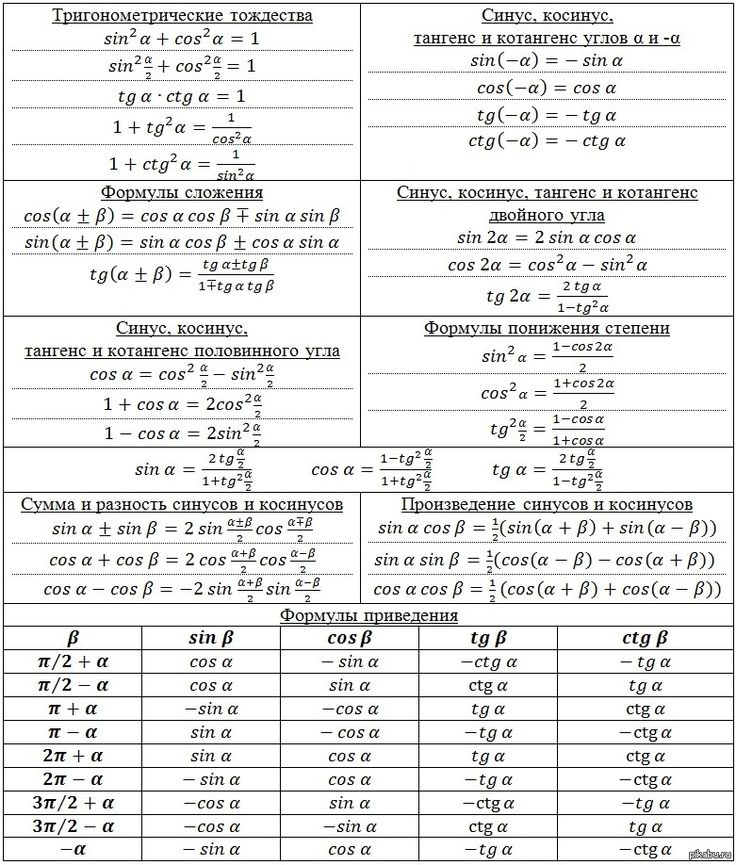 Итак, чтобы помочь вам понять и выучить все тригонометрические тождества , мы объяснили здесь все концепции тригонометрии. Будучи студентом, вы сочтете trig identity листом , который мы предоставили здесь, полезным. Таким образом, вы можете скачать и распечатать удостоверения личности в формате PDF и использовать его в любое время для решения уравнений.
Итак, чтобы помочь вам понять и выучить все тригонометрические тождества , мы объяснили здесь все концепции тригонометрии. Будучи студентом, вы сочтете trig identity листом , который мы предоставили здесь, полезным. Таким образом, вы можете скачать и распечатать удостоверения личности в формате PDF и использовать его в любое время для решения уравнений. Это довольно старая концепция, впервые использованная в 3 веке до нашей эры. Этот раздел математики связан с плоскими прямоугольными треугольниками (или прямоугольными треугольниками в двумерной плоскости с одним углом, равным 90 градусам).
Это довольно старая концепция, впервые использованная в 3 веке до нашей эры. Этот раздел математики связан с плоскими прямоугольными треугольниками (или прямоугольными треугольниками в двумерной плоскости с одним углом, равным 90 градусам).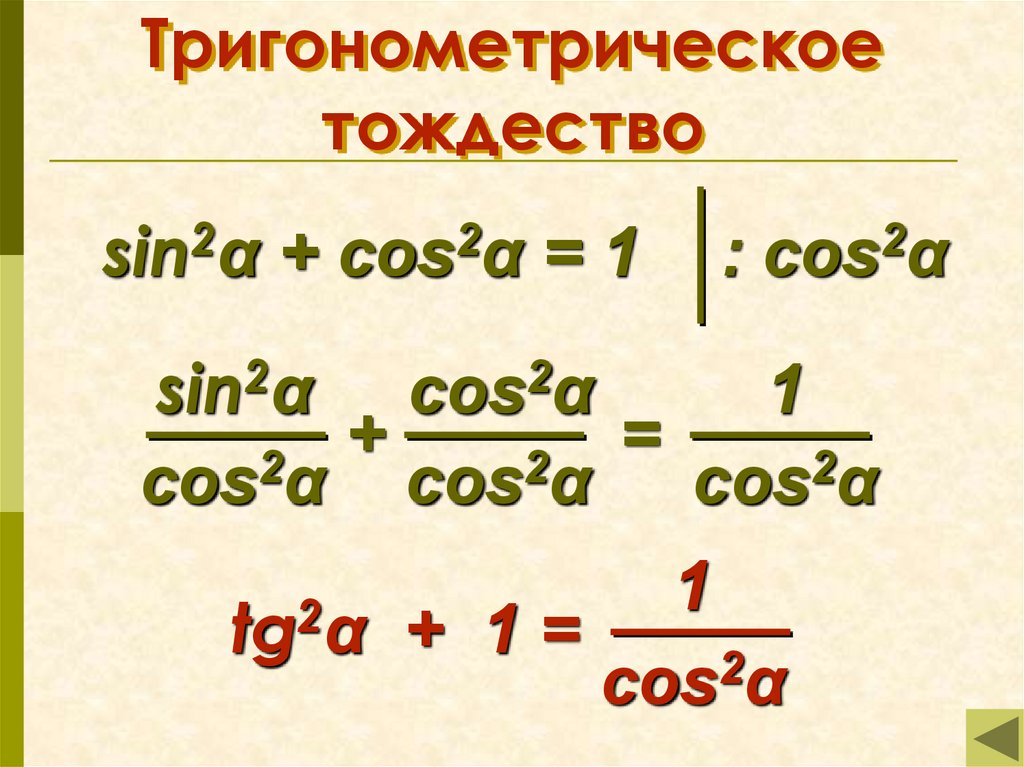 Например, исчисление основано исключительно на тригонометрии и алгебре.
Например, исчисление основано исключительно на тригонометрии и алгебре. Таким образом, это помогает нам определить соотношение между прямыми и углами в прямоугольном треугольнике.
Таким образом, это помогает нам определить соотношение между прямыми и углами в прямоугольном треугольнике.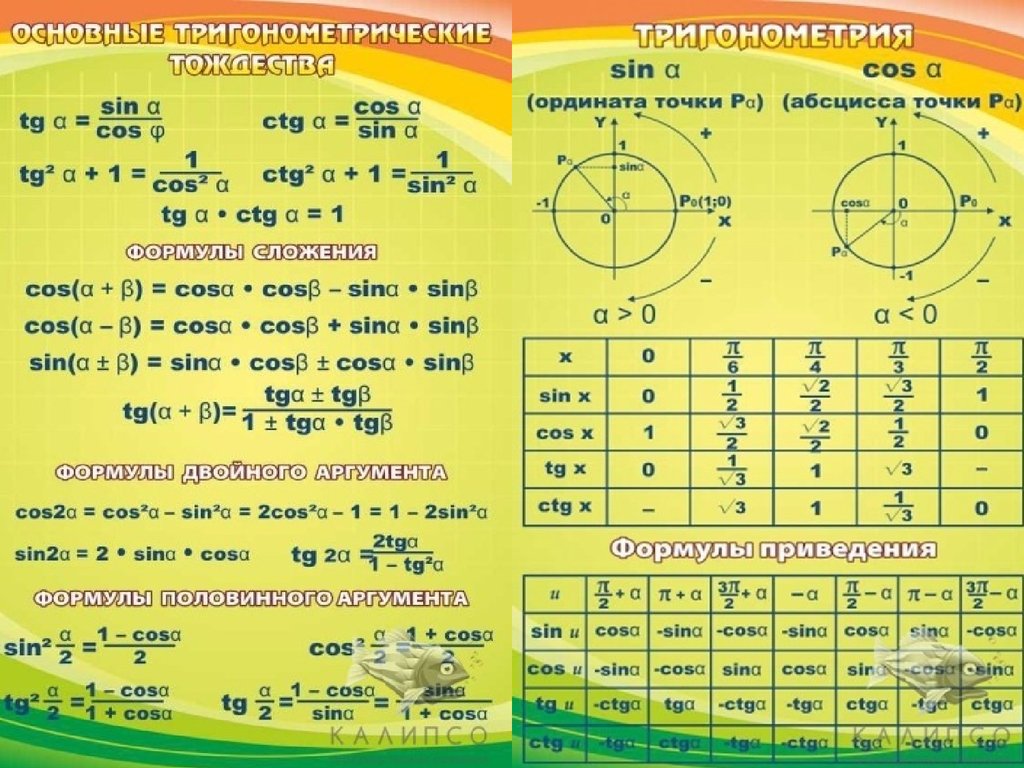
 Это связано с единичным кругом, где изображены отношения между линиями и углами на декартовой плоскости. Здесь мы предоставили вам таблицу, состоящую из набора тождеств, которые могут быть получены из основных функций
Это связано с единичным кругом, где изображены отношения между линиями и углами на декартовой плоскости. Здесь мы предоставили вам таблицу, состоящую из набора тождеств, которые могут быть получены из основных функций Соотношение тождеств
Соотношение тождеств Отличие тождеств
Отличие тождеств Некоторые из этих тождеств могут также появляться под другими заголовками.
Некоторые из этих тождеств могут также появляться под другими заголовками. Секущие тождества
Секущие тождества Например
Например


 Мы можем изменить это, чтобы упростить данное уравнение:
Мы можем изменить это, чтобы упростить данное уравнение: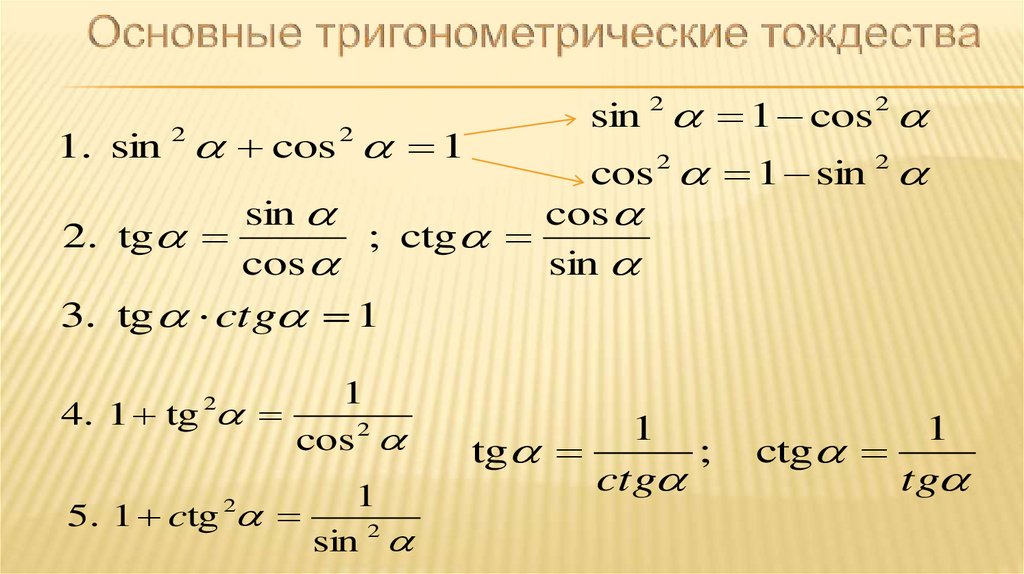 0013
0013