Решение задач по теме «Отношение площадей подобных треугольников»
ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ
Свойство
Если высоты треугольников равны, то площади относятся как основания .
Свойство
Медиана делит треугольник на два равновеликих треугольника.
Три медианы делят треугольник на 6 равновеликих треугольников.
Теорема
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы
Доказать:
Дано:
Дайте ответы на вопросы:
1. Что называют отношением отрезков AB и CD?
2. При каком условии отрезки AB, CD и A 1 B 1 , C 1 D 1 называют пропорциональными?
3.
∠ M=∠Z, ∠K=∠D, ∠L=∠P.
4. Используя свойство биссектрисы треугольника, найдите KN, если OC=4см, CN=3см, OK=2см.
K
M L
Z
P
D
C
O K N
Теорема: «Об отношении площадей подобных треугольников» Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано: ∆ABC ∾ ∆A 1 B 1 C 1
Доказать:
Доказательство:
1. Так как по условию ∆ABC ∾ ∆A 1 B 1 C 1 , то
∠ A=∠A 1 , по теореме об отношении площадей треугольников (п.53), значит
2. Так как
ч.т.д.
C
A B
C 1
A 1 B 1
Реши задачи
- Две сходственные стороны подобных треугольников равны
8 см и 4 см. Периметр второго треугольника равен 12 см.
Периметр второго треугольника равен 12 см.
Чему равен периметр первого треугольника ?
24 см
2. Две сходственные стороны подобных треугольников равны
9 см и 3 см. Площадь второго треугольника равна 9 см 2 .
Чему равна площадь первого треугольника ?
81 см 2
3. Две сходственные стороны подобных треугольников равны
5 см и 10 см. Площадь второго треугольника равна 32 см 2 .
Чему равна площадь первого треугольника ?
8 см 2
4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 .
Одна из сторон первого треугольника равна 4 см. Чему равна
сходственная сторона второго треугольника ?
8 см
Закрепление.
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 ,
Найти : AC
Решение :
1.Так как по условию
то по т . «Об отношении площадей подобных треугольников»:
2. Так как : ∆ABC ∾ ∆A 1 B 1 C 1 , а также
Так как : ∆ABC ∾ ∆A 1 B 1 C 1 , а также
AC и A 1 C 1 – сходственные стороны, k=2, то
Ответ: AC=4,5 (м)
B
A C
B 1
A 1 C 1
Закрепление. № 54 5
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 , AC: A 1 C 1 =6:5
Найти :
Решение :
1.Пусть S A1B1C1 =x см 2 , S ABC =(x+77) см 2
2.Так как AC: A 1 C 1 =6:5 , то
3.По теореме об отношении площадей подобных треугольников:
Значит S A 1 B 1 C 1 = 175 см 2 , S ABC = 252 см 2
Ответ: S A 1 B 1 C 1 = 175 см 2
, S ABC = 252 см 2B
A C
B 1
A 1 C 1
Закрепление. № 537
A
C D B
Дано : ∆ABC, AD – биссектриса ∆ABC, AB=14см, AC=21см, BC=20см
Найти : BD, DC
Решение :
1. Так как по условию BC=20см, BC=CD+DB, то пусть BD=x см , CD=(20-x) см .
Так как по условию BC=20см, BC=CD+DB, то пусть BD=x см , CD=(20-x) см .
2.Так как по условию AD – биссектриса ∆ABC, то по свойству биссектрисы треугольника BD:AB=CD:AC (1).
3.Так как по условию AB=14см, AC=21см, то (1) – примет вид:
Значит BD=8 см , DC=12 см .
Ответ: BD=8 см , DC=12 см .
Домашнее задание:
п.п. 1 — 60 ;
№ 538, №548 (воспользоваться условием № 547)
Самопроверка домашнего задания по образцу № 538
A
C D B
Дано : ∆ABC, AD – биссектриса ∆ABC, CD=4,5 см , BD=13,5 см , P ABC =42 см.
Найти : AB и AC
Решение :
1.Так как CB=CD+DB, CD=4,5 см , BD=13,5 см, то CB=18 см.
2.Пусть AB = х. Так как P ABC =42 см , CB=18 см ,
то AC = 42-(18+х) = 24-х ( см).
3.По свойству биссектрисы треугольника:
т.е.
Значит AB=18 см и AC =6 см .
Ответ: AB=18 см и AC =6 см .
Самопроверка домашнего задания по образцу № 5 47
B
A C
B 1
A 1 C 1
Дано : ∆ABC ∾ ∆A 1 B 1 C 1Доказать :
Доказательство :
1. Так как по условию ∆ABC ∾ ∆A 1 B 1 C 1 , то
2.
ч.т.д.
Итак если ∆ABC ∾ ∆A 1 B 1 C 1 , то
Самопроверка домашнего задания по образцу № 5 48
Дано : ∆ABC ∾ ∆A 1 B 1 C 1 ,
BC и B 1 C 1 – сходственные стороны,
BC = 1,4 м = 140 см , B 1 C 1 = 56 см .
Найти :
Решение :
Ответ:
Площади двух подобных треугольников. «отношение площадей подобных треугольников»
Урок 34. Теорема об отношении площадей подобных треугольников. ТЕОРЕМА. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. где k – коэффициент подобия. Отношение периметров двух подобных треугольников равно коэффициенту подобия. В. А. С. Р. М. К. Решение задач: № 545, 549. Домашнее задание: п. 56-58, № 544, 548.
Теорема об отношении площадей подобных треугольников. ТЕОРЕМА. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. где k – коэффициент подобия. Отношение периметров двух подобных треугольников равно коэффициенту подобия. В. А. С. Р. М. К. Решение задач: № 545, 549. Домашнее задание: п. 56-58, № 544, 548.
Слайд 6 из презентации «Геометрия «Подобные треугольники»» . Размер архива с презентацией 232 КБ.
Геометрия 8 класс
краткое содержание других презентаций
«Определение осевой симметрии» — Симметрия в природе. Подсказка. Оси симметрии. Изобразите точку. Построение точки. Построение треугольника. Построение отрезка. Народы. Симметрия в поэзии. Фигуры, не обладающие осевой симметрией. Фигуры, обладающие двумя осями симметрии. Прямоугольник. Симметрия. Прямая. Постройте точки. Осевая симметрия. Отрезок. Ось симметрии. Начертите две прямые. Точки, лежащие на одном перпендикуляре.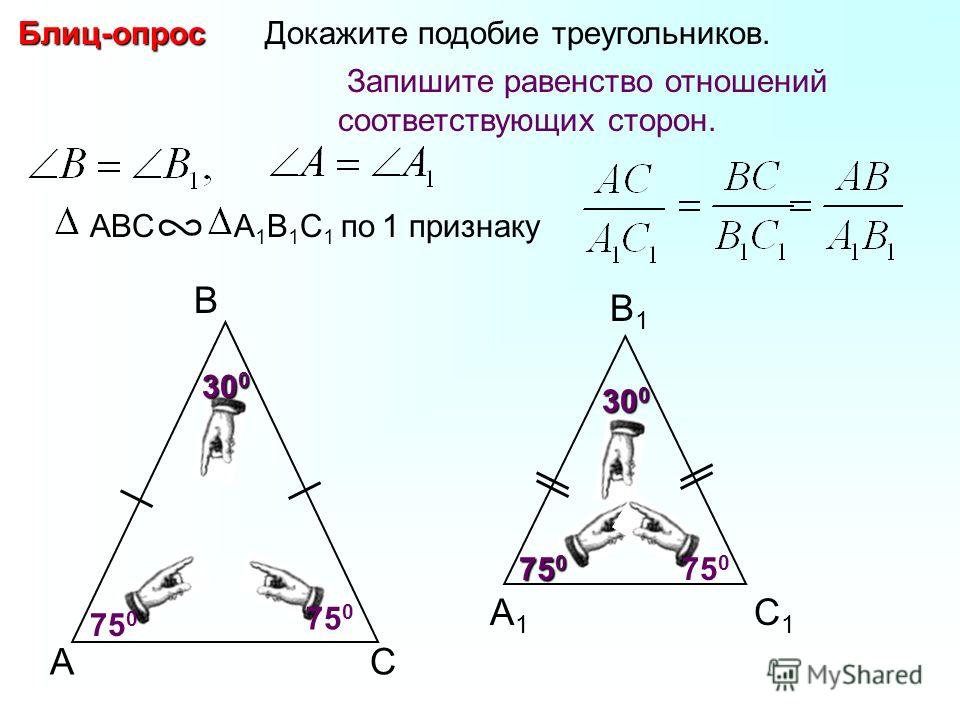 Соразмерность.
Соразмерность.
«Нахождение площади параллелограмма» — Найдите площадь параллелограмма. Площадь параллелограмма. Высота. Найдите площадь квадрата. Площадь квадрата. Высоты параллелограмма. Найдите площадь треугольника. Признаки равенства прямоугольных треугольников. Найдите площадь прямоугольника. Определение высоты параллелограмма. Основание. Площадь треугольника. Найдите периметр квадрата. Свойства площадей. Устные упражнения.
«Задачи на нахождение площади» — Урок -объяснение нового материала, выполнен в виде презентации «Power point». Основная цель. «Площадь параллелограмма». «Площадь трапеции». ПрОВЕРКА УСВОЕННОГО МАТЕРИАЛА. Решить задачу. Рабочая тетрадь №42, повторить все изученные формулы. Вывести формулы площадей прямоугольника, параллелограмма, трапеции, треугольника. Расширить и углубить представления об измерении площадей. Сформировать у учащихся понятие площади.
«Геометрия «Подобные треугольники»» — Два треугольника называются подобными. Пропорциональность сторон угла.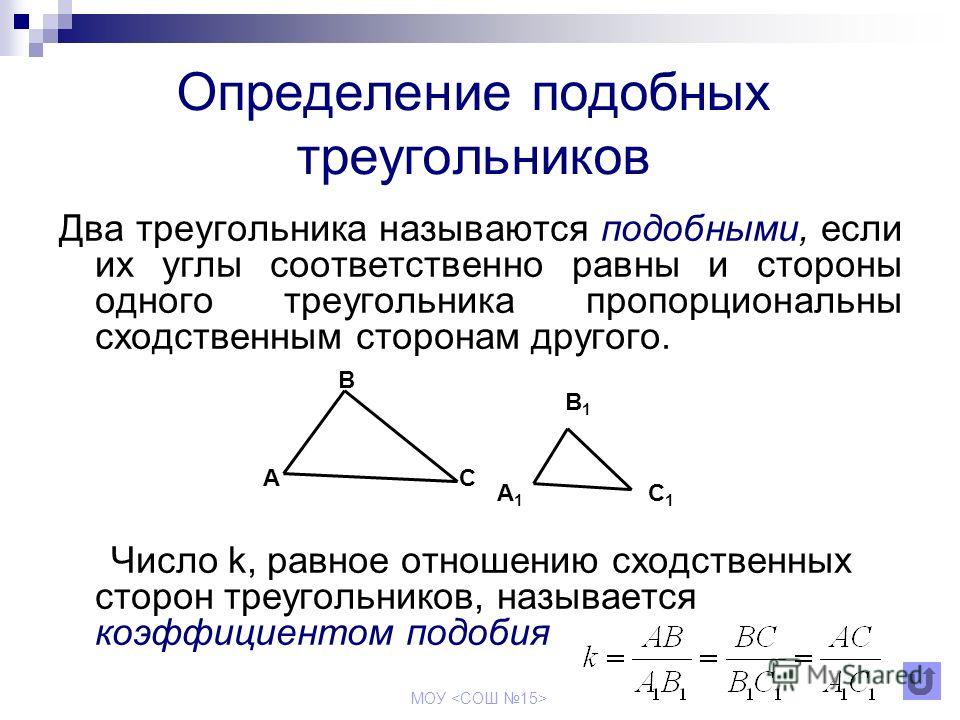 Значения синуса, косинуса и тангенса. Первый признак подобия треугольников. Пропорциональные отрезки в прямоугольном треугольнике. Свойство биссектрисы треугольника. Математический диктант. Найти площадь равнобедренного прямоугольного треугольника. Пропорциональные отрезки. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.
Значения синуса, косинуса и тангенса. Первый признак подобия треугольников. Пропорциональные отрезки в прямоугольном треугольнике. Свойство биссектрисы треугольника. Математический диктант. Найти площадь равнобедренного прямоугольного треугольника. Пропорциональные отрезки. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.
«Прямоугольники» — Человек. Противоположные стороны. Сторона прямоугольника. Сказка о прямоугольнике. Стороны прямоугольника. Прямоугольник в жизни. Периметр прямоугольника. Прямоугольник. Диагонали. Картины. Диагональ. Определение. Площадь прямоугольника.
««Площадь прямоугольника» 8 класс» — Площадь заштрихованного квадрата. Стороны каждого из прямоугольников. АBCD и DСМK – квадраты. На стороне АВ построен параллелограмм. Единицы измерения площадей. Найдите площадь квадрата. Площадь прямоугольника. ABCD – параллелограмм. Свойства площадей. Найдите площадь четырехугольника. Площади квадратов, построенных на сторонах прямоугольника. Пол комнаты, имеющий форму прямоугольника.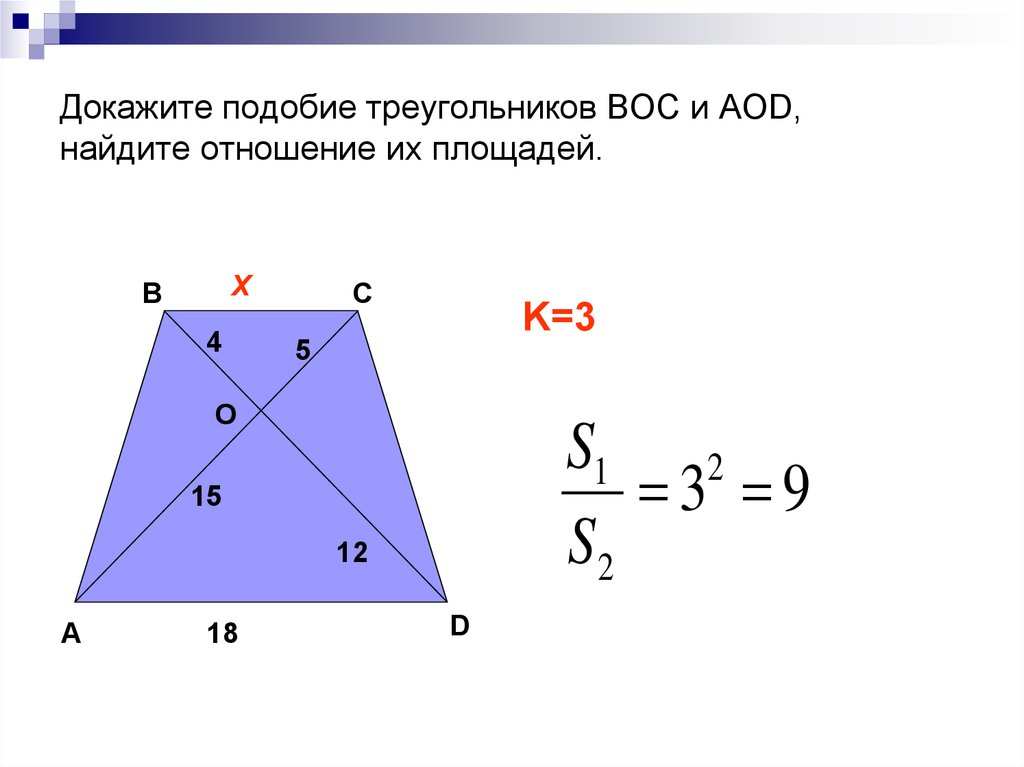
Цель урока: дать определение подобных треугольников, доказать теорему об отношении подобных треугольников.
Задачи урока:
- Образовательные: учащиеся должны знать определение подобных треугольников, теорему об отношении подобных треугольников, уметь применять их при решении задач, реализовывать межпредметные связи с алгеброй и физикой.
- Воспитательные: воспитывать трудолюбие, внимательность, прилежание, воспитывать культуру поведения учащихся.
- Развивающие: развитие у учащихся внимания, развития умения рассуждать, логически мыслить, делать выводы, развития у учащихся грамотной математической речи и мышления, развивать навыки самоанализа и самостоятельности.
- Здоровьесберегающие: соблюдение санитарно-гигиенических норм, смена видов деятельности на уроке.
Оборудование: компьютер, проектор, дидактический материал: самостоятельные и контрольные работы по алгебре и геометрии для 8 класса А.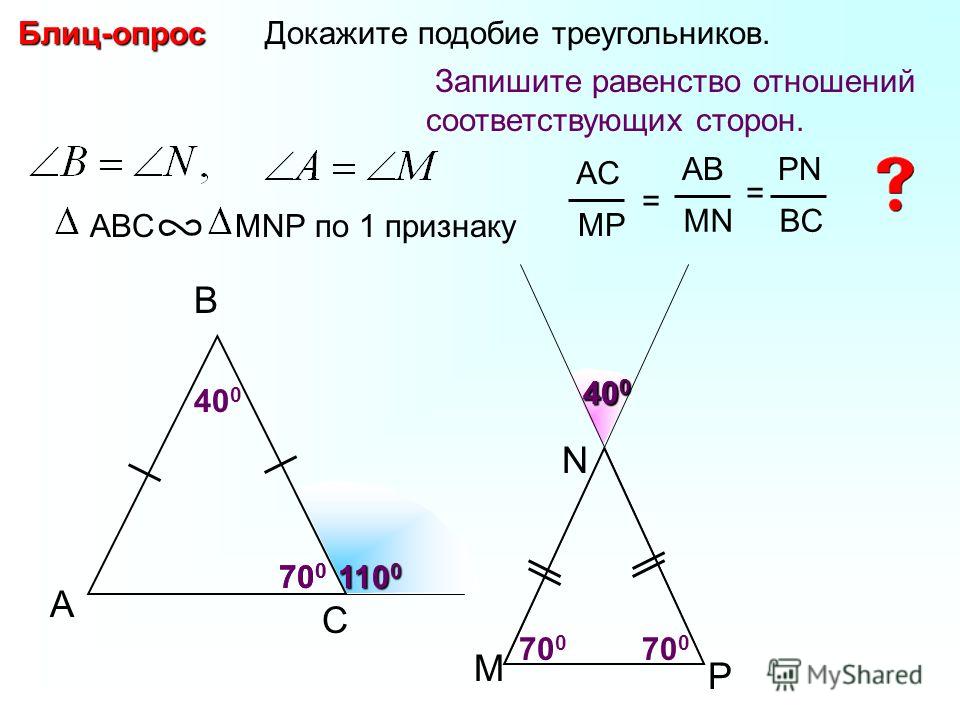
Тип урока: изучение нового материала.
Ход урока
I. Организационный момент (приветствие, проверка готовности к уроку).
II. Сообщение темы урока.
Учитель: В повседневной жизни встречаются предметы одинаковой формы, но разных размеров.
Пример: футбольный и теннисный мячи.
В геометрии фигуры одинаковой формы называют подобными: любые два круга, любые два квадрата.
Введем понятие подобных треугольников.
Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. ΔABC ~ A 1 B 1 C 1
1. Устно: Подобны ли треугольники? Почему? (заготовленный чертеж на экране).
а) Треугольник ABC и треугольник A 1 B 1 C 1 , если AB = 7, BC = 5, AC = 4, ∠A = 46˚, ∠C = 84˚, ∠A 1 = 46˚, ∠B 1 = 50˚, A 1 B 1 = 10,5 , B 1 C 1 = 7,5, A 1 C 1 = 6.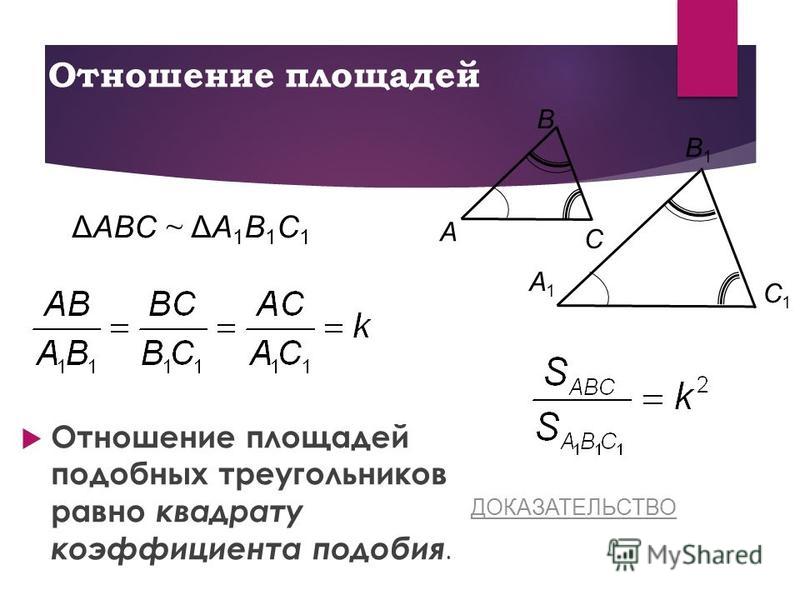
б) В одном равнобедренном треугольнике угол при вершине равен 24˚, а в другом равнобедренном треугольнике угол при основании равен 78˚.
Ребята! Вспомним теорему об отношении площадей треугольников, имеющих по равному углу.
Теорема: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
2. Письменная работа по заготовленным чертежам.
На экране чертеж:
а) Дано: BN: NC = 1:2,
BM = 7 см, AM = 3 см,
S MBN = 7 см 2 .
Найти: S ABC
(Ответ: 30 см 2 .)
б) Дано: AE = 2 см,
S AEK = 8 см 2 .
Найти: S ABC
(Ответ: 56 см 2 .)
3. Докажем теорему об отношении площадей подобных треугольников (доказывает теорему ученик на доске, помогает весь класс ).
Теорема: Отношение двух подобных треугольников равно квадрату коэффициента подобия.
4. Актуализация знаний.
Решение задач:
1. Площади двух подобных треугольников равны 75 см 2 и 300 см 2 . Одна из сторон второго треугольника равна 9см. Найти сходственную ей сторону первого треугольника. (Ответ: 4,5 см.)
2. Сходственные стороны подобных треугольников равны 6см и 4см, а сумма их площадей равна 78 см 2 . Найти площади этих треугольников. (Ответ: 54 см 2 и 24 см 2 .)
При наличии времени самостоятельная работа обучающего характера.
Вариант 1
У подобных треугольников сходственные стороны равны 7 см и 35 см.
Площадь первого треугольника равна 27 см 2 .
Найти площадь второго треугольника. (Ответ: 675 см 2 .)
Вариант 2
Площади подобных треугольников равны 17 см 2 и 68 см 2 . Сторона первого треугольника равна 8см. Найти сходственную сторону второго треугольника. (Ответ: 4 см.)
5. Домашнее задание: учебник геометрии 7-9 Л.С. Атанасян и др., п. 57, 58, № 545, 547.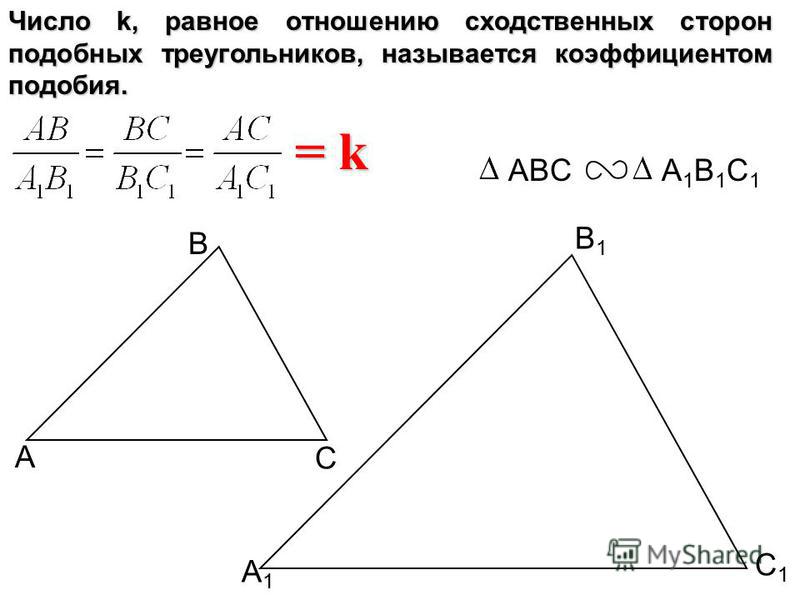
6. Подведение итогов урока.
Тип урока: урок ознакомления с новым материалом.
Цель урока:Доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач.
Задачи урока:
обучающие – доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач;
развивающие – развивать умение анализировать и подбирать аргументацию при решении задачи, способ решения которой неизвестен;
воспитательные – воспитывать интерес к предмету через содержание учебного процесса и создание ситуации успеха, воспитывать умение работать в группе.
Учащийся владеет следующими знаниями:
Единица деятельностного содержания, которое нужно усвоить учащимся:
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
3. Работа с проблемной ситуацией.
4. Подведение итогов урока и запись домашнего задания, рефлексия.
Методы обучения: словесные, наглядные, проблемно-поисковые.
Формы обучения:фронтальная работа, работа в мини-группы, индивидуальная и самостоятельная работа.
Технологии: задачно-целевая, информационные технологии, компетентностный подход.
Оборудование:
компьютер, проектор для демонстрации презентации, интерактивная доска, документ камера;
компьютерная презентация в MicrosoftPowerPoint;
опорный конспект;
Сегодня на уроке мы будем работать не в тетрадях, а в опорных конспектах, которые будете заполнять на продолжение всего урока. Подпишите его. Оценка за урок будет состоять из двух составляющих: за опорный конспект и за активную работу на уроке.
2. Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.
Мы продолжаем с вами изучать тему «подобие треугольников». Поэтому давайте вспомним то, что изучали на прошлом уроке.
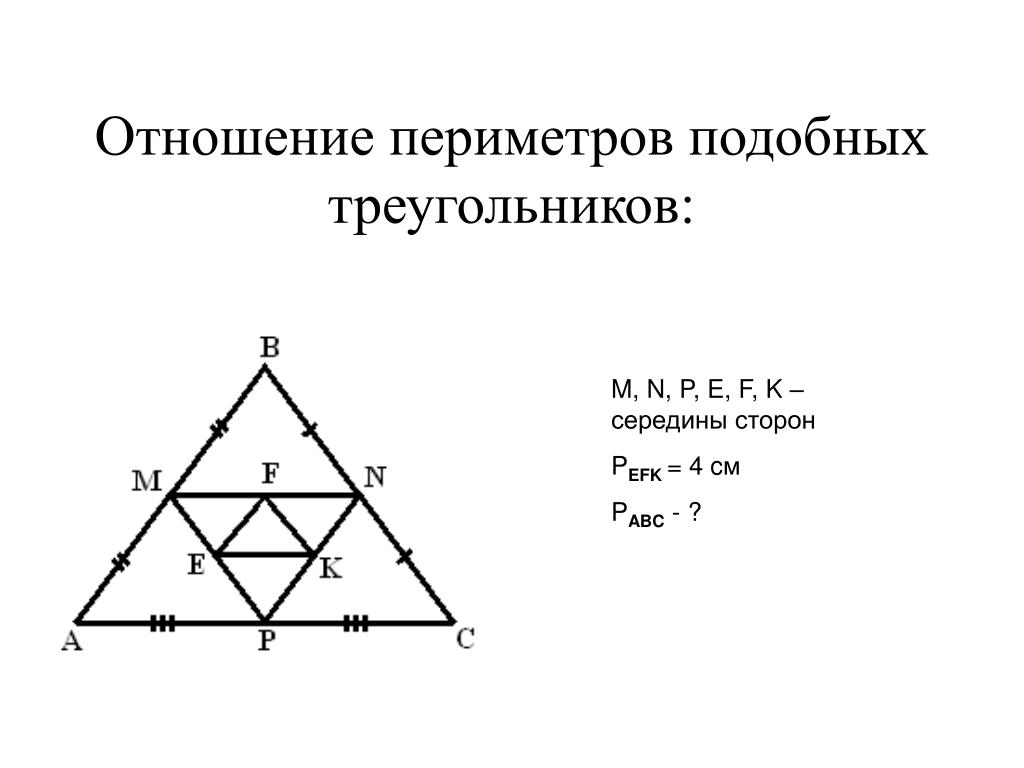 Теоретическая разминка. Тест. В ваших опорных конспектах первое задание имеет тестовый характер. Ответьте на вопросы, выбирая один из предложенных вариантов ответа, где необходимо впишите свой ответ.
Теоретическая разминка. Тест. В ваших опорных конспектах первое задание имеет тестовый характер. Ответьте на вопросы, выбирая один из предложенных вариантов ответа, где необходимо впишите свой ответ.- Учитель: Что называется отношением двух отрезков?
Ответ: Отношением двух отрезков двух отрезков называется отношение их длин.
- Учитель: В каком случае отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1
Ответ: отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 , если
Ваши варианты. Хорошо. Не забудьте исправить у кого не так.
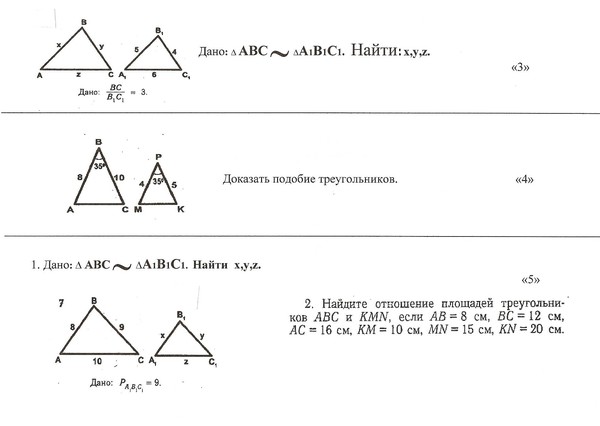
- Учитель: Дайте определение подобных треугольников? Обратитесь к вашему опорному конспекту. У Вас три варианта ответа на этот вопрос. Выберите правильный. Обведите его.
Так, пожалуйста, какой вариант выбрал ты_______
Ответ: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.
Молодцы! Исправьте у кого не так.
- Учитель: Чему равно отношение площадей двух треугольников, имеющих по равному углу?
Ответ: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Решение задач по готовым чертежам. Далее наша разминка будет происходить в ходе решения задач по готовым чертежам. Эти задачи так же вы видите в ваших опорных конспектах.
Рефлексия. Давайте уточним, какие знания и умения позволили нам решить эти задачи. Какими методами решения мы пользовались (фиксация ответов на доске).
Возможные ответы:
Определение подобных треугольников;
Применение определения подобных треугольников при решении задач;
Теорема об отношении площадей треугольников имеющих по равному углу;
А сейчас я предлагаю к решению несколько задач способ решения, которых перекликается с темой урок, но связаны они больше с географией.
Ситуация успеха.
Первая задача перед Вами. Над этой задачей работаем самостоятельно. Первый справившийся покажет свое решение у доски, и кто-то продемонстрирует свое решение через документ камеру, поэтому пишем красиво и аккуратно.
Ответ: стороны бермудского треугольника 2000 км, 1840 км, 2220 км. Длина границы 6060 км.
Рефлексия.
Возможный ответ: у подобных треугольников сходственные стороны пропорциональны.
Ситуация успеха.
С размерами Бермудского треугольника мы разобрались. Ну а теперь выясним измерения цветочной клумбы. Переворачиваем опорные конспекты. Вторая задача. Эту задачу решаем, работая в парах. Проверяем аналогичным способом, но только результат будет представлять уже пара первая справившаяся с заданием.
Ответ: стороны треугольной клумбы 10м и 11м 20 см.
Итак, сверяемся. Все ли согласны? Кто решал другим способом?
Рефлексия.
Каким способом действия вы пользовались при решении этой задачи? Запишите в свой опорный конспект.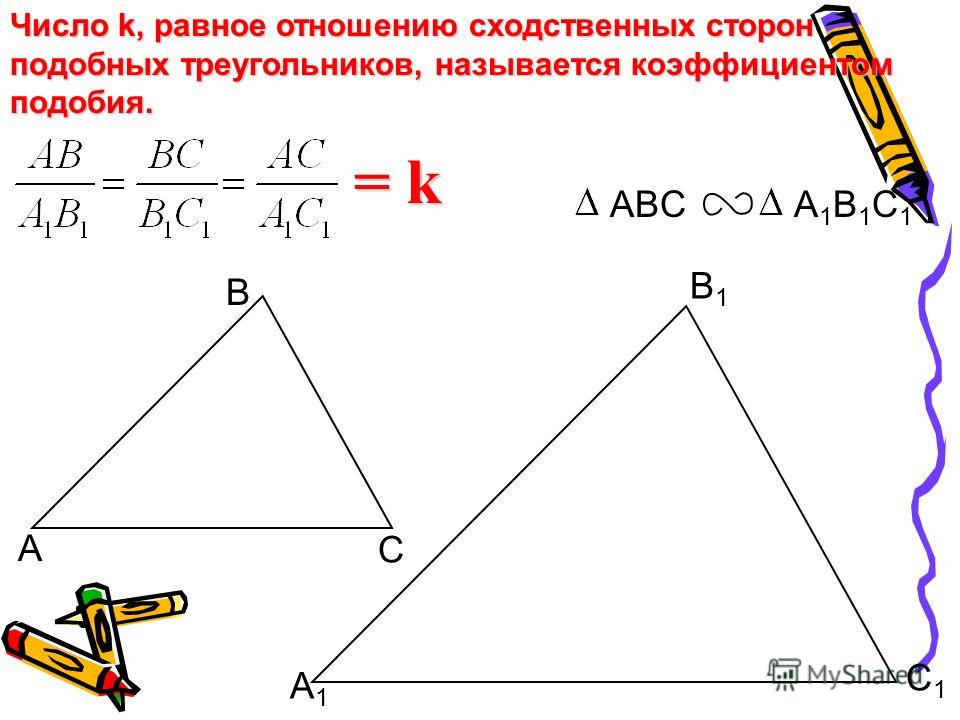
Возможный ответ:
у подобных треугольников соответственные углы равны;
площади треугольников имеющих по равному углу относятся как произведения сторон заключающих равные углы.
Ситуация сбоя.
При решениитретьей задачи учащиеся сталкиваются с проблемой. У них не получается решить задачу, так как по их мнению недостаточно полное условие задачи или получают необоснованный ответ.
С таким типом задач учащиеся не встречались ранее, поэтому произошел сбой при решении задачи.
Рефлексия.
Каким методом пытались решить?
Почему не получилось решить последнее уравнение?
Ученики: Мы не можем найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.
Таким образом, цель нашего урока найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.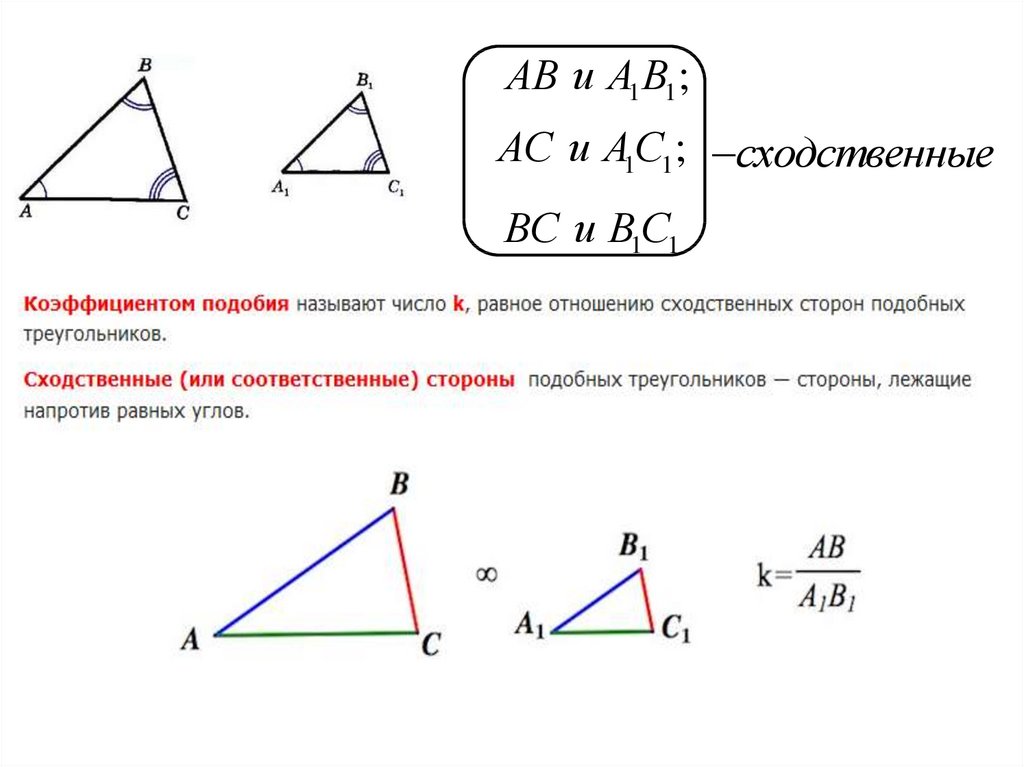
Давайте переформулируем задачу на геометрический язык. Решим ее, а затем вернемся к этой задаче.
Вывод: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Ну а теперь давайте вернемся к задаче №3 и решим ее, опираясь на доказанный факт.
7. Итог урока
Что сегодня вы научились делать нового?
Решать задачи, в которых известны коэффициент подобия и площадь одного из подобных треугольников.
Какое геометрическое свойство нам в этом помогло?
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Домашнее задание.
П. 58 стр.139 №546, 548
Творческое задание.
Найдите чему равно отношение периметров двух подобных треугольников (№547)
До свидания.
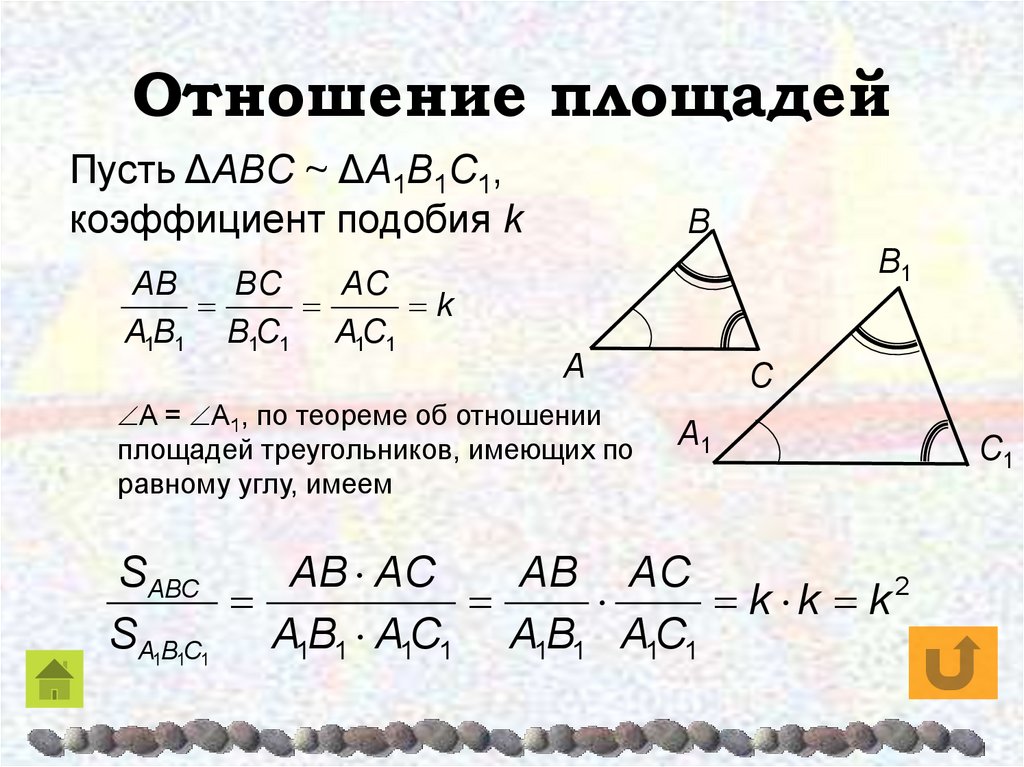
1.3. Отношение площадей подобных треугольников. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Доказательство.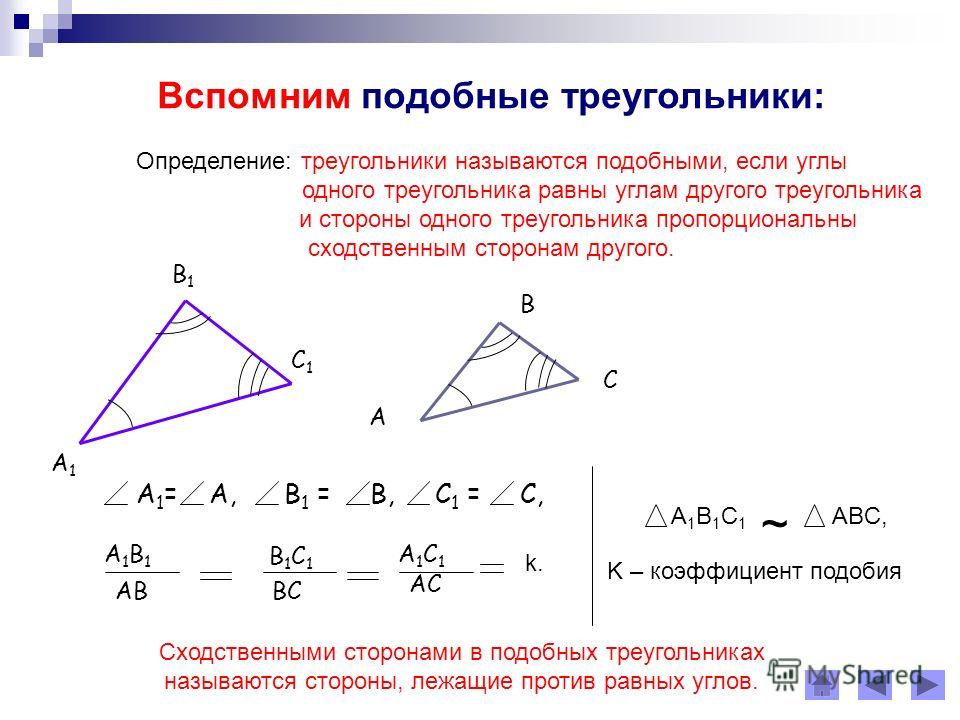 Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то.
Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то.
Слайд 11 из презентации ««Подобные треугольники» 8 класс» . Размер архива с презентацией 1756 КБ.
Геометрия 8 класс
краткое содержание других презентаций
«Прямоугольники» — Диагональ. Картины. Стороны прямоугольника. Периметр прямоугольника. Человек. Площадь прямоугольника. Прямоугольник в жизни. Определение. Сторона прямоугольника. Диагонали. Сказка о прямоугольнике. Прямоугольник. Противоположные стороны.
«Скалярное произведение в координатах» — Вектор. Теорема Наполеона. Следствие. Свойства скалярного произведение векторов. Обменяйтесь карточками. Решим задание. Геометрия. Скалярное произведение в координатах и его свойства. Математический тест. Новый материал. Решение треугольника. Математическая разминка. Имя автора теоремы. Доказательство теоремы Пифагора.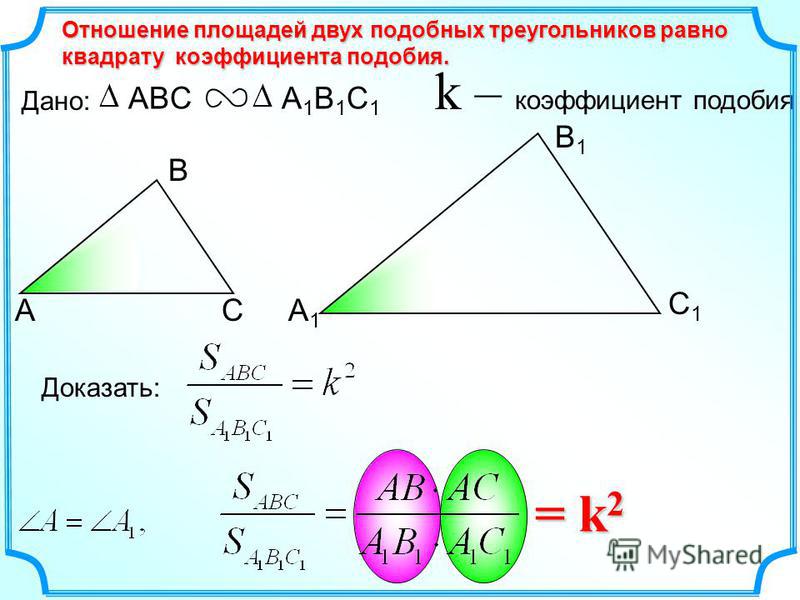
«Нахождение площади параллелограмма» — Площадь параллелограмма. Устные упражнения. Высота. Определение высоты параллелограмма. Высоты параллелограмма. Найдите площадь параллелограмма. Площадь треугольника. Площадь квадрата. Свойства площадей. Найдите площадь треугольника. Найдите периметр квадрата. Основание. Найдите площадь прямоугольника. Найдите площадь квадрата. Признаки равенства прямоугольных треугольников.
«Векторы 8 класс» — Назовите равные и противоположные векторы. Векторы на уроках физики. Абсолютная величина вектора. Абсолютная величина вектора. Прямоугольник, у которого все стороны равны. Понятие вектора. Определите координаты вектора. Найдите и назовите равные векторы на данном рисунке. Равные вектора. Самостоятельная работа в парах. Координаты вектора. Девиз урока. Скалярные физические величины, такие как сила трения, скорость.
«Разные виды симметрии» — Требование. Скользящая симметрия. Равнобедренный треугольник с зеркальной симметрией. Теория групп. Симметрия в биологии.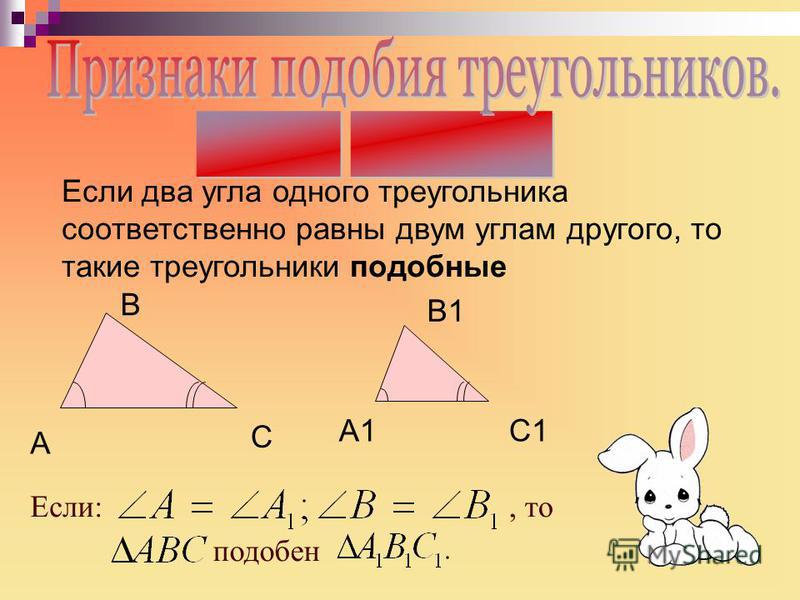 Вращательная симметрия. Двулучевая радиальная симметрия. Что такое симметрия. Суперсимметрия. Симметрия в геометрии. Симметрия в физике. Верхушка колокола. Появление билатеральной симметрии. Билатеральная симметрия. Теорема Нётер. Отсутствие симметрии. Симметрия физике. Центральная симметрия.
Вращательная симметрия. Двулучевая радиальная симметрия. Что такое симметрия. Суперсимметрия. Симметрия в геометрии. Симметрия в физике. Верхушка колокола. Появление билатеральной симметрии. Билатеральная симметрия. Теорема Нётер. Отсутствие симметрии. Симметрия физике. Центральная симметрия.
«Квадрат в жизни» — Квадраты находят нас везде. Индия. Магический квадрат Альбрехта Дюрера. История. Квадраты. Магический квадрат Ло Шу. Черный квадрат. Загадка «Квадрат». Интересные факты о квадрате. Геометрическая фигура квадрат. Квадрат Малевича. Магический квадрат. Прямоугольник. Квадрат. Основное понятие. Интересные факты. Китай.
Подобные треугольники. Как найти отношение площадей
Автор Historian Просмотров 67 Опубликовано
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
Содержание
- Подобные треугольники
- Признаки подобия треугольников
- Свойства подобных треугольников
- Подобие
- Признаки подобия
- Площади подобных треугольников
- Работа по теме урока
- Закрепление изученного материала
- Самостоятельная работа
- I уровень сложности
- II уровень сложности
- III уровень сложности
- Самый главный «секрет» подобия треугольников
- Открыть ответы…
- Второй и третий признаки подобия треугольников
- Отношение площадей подобных треугольников
- Как найти отношение площадей двух треугольников, если стороны одного равны 5 см, 8 см, 12 см, а стороны другого 15 см, 24 см, 36 см?
- Применение площадей
- Метод площадей
- Другие доказательства теоремы Пифагора
Подобные треугольники
Подобные треугольники — это треугольники, углы которых равны между собой, а одна сторона пропорциональна другой.
Коэффициентом подобия является k, который равен отношению сходных сторон подобных треугольников.
Стороны (или сопряженные стороны) подобных треугольников являются противоположными сторонами равных углов.
Признаки подобия треугольников
I Принцип подобия треугольников
Если два угла треугольника равны двум углам другого треугольника, то эти треугольники одинаковы.
II Принцип подобия треугольников
Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные в этих сторонах, равны, то эти треугольники одинаковы.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники одинаковы.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

1. линия, параллельная одной стороне треугольника, пересекает подобный ей треугольник.
2. треугольники, образованные отрезком диагонали и основанием трапеции, подобны. Степень сходства
3. в прямоугольном треугольнике высота, проведенная из вершины прямого угла, делит треугольник на два треугольника, подобных исходному треугольнику.
Здесь вы найдете подборку задач, похожих на «Подобные треугольники».
Работа. Прямая, параллельная AB в BCABC, пересекает BC и AC в точках E и P. Найдем, что EC = 2, BE = 3 и EP = 3,2. Какова длина отрезка AB?
Подобие
Идентичные треугольники — это треугольники, у которых длины всех сторон пропорциональны друг другу, а углы равны. Отношение соответствующих сторон подобных треугольников всегда равно одному и тому же числу, которое называется коэффициентом подобия.
Рисунок 1. Подобные треугольники
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами.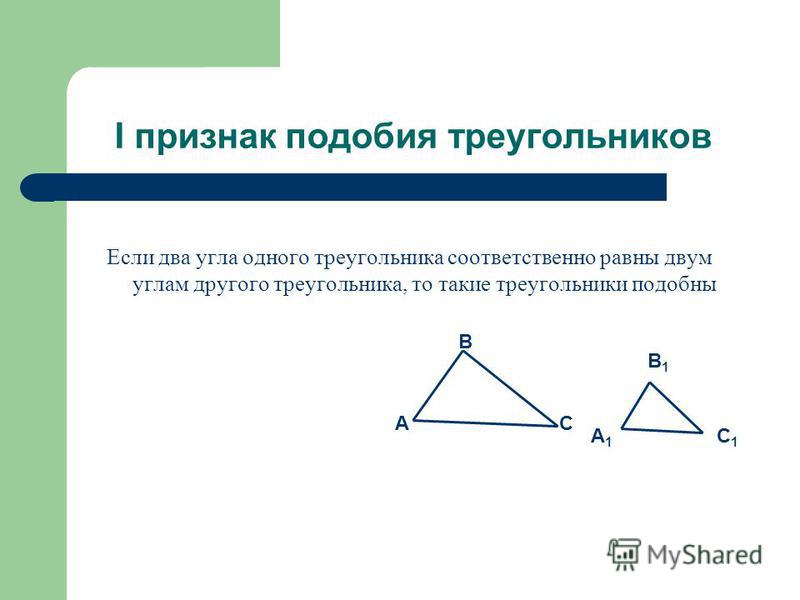 Сходство представлено буквой k.
Сходство представлено буквой k.
Не обязательно концентрироваться на треугольниках. Все фигуры в геометрии имеют сходство, хотя символ сходства появляется только на них. То же самое справедливо и для эквивалентности формы. Все фигуры в геометрии эквивалентны, так как эквивалентность является частным случаем сходства с коэффициентом k=1.
Рисунок 2.Похожие элементы
Признаки подобия
В настоящее время для любого треугольника существует три варианта подобия.
- По двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- По сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
- По трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Чтобы доказать пропорциональность сторон, необходимо вычислить отношение длин каждой стороны.
Работа по теме урока
(Учитель делит класс на группы для решения творческой работы. По завершении задаются и обсуждаются решения).
Работа. Треугольники ABC и A1B1C1 подобны коэффициенту K. Найдите причину в их районе.
Заключение Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Закрепление изученного материала
- Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Вопрос нет. 545
- Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
- Верно ли составлено уравнение исходя из условий задачи?
- Решить задачи № 547, 548 (работа в группах).
 (После завершения работы заслушиваются и обсуждаются варианты решений.)
(После завершения работы заслушиваются и обсуждаются варианты решений.)
Самостоятельная работа
I уровень сложности
II уровень сложности
III уровень сложности
Научитесь правильно писать задачи, делайте записи короткими и не тратьте время на то, чтобы написать все идеи и названия теорий.
Самый главный «секрет» подобия треугольников
Плита научила вас находить подобные треугольники, но как теперь использовать те, которые вы нашли?
А что бы вы хотели с ним сделать? Что же тогда …
Все элементы одного треугольника ровно в ዄ (⌘ displaystyle 2 \) (или во столько раз, во сколько получится) больше элементов других треугольников.
Не только стороны, но и высоты, дихотомии, интерстиции, зарегистрированные, граничные лучи цикла и т.д.
Есть важное исключение: площадь.
Открыть ответы…
Чтобы открыть все выпуски всех учебников, охваченных синим баннером (например, этот), зарегистрируйтесь следующим образом.
Чтобы управлять им, просто разделите длину сторон между ними. Разделите наибольшую сторону одного треугольника на другую и наименьшую сторону на наименьшую. Если результат одинаков для всех трех сторон, то треугольники подобны.
Второй и третий признаки подобия треугольников
Существуют еще два подобия треугольника, которые реже используются при решении задач. Идите прямо от первого участка.
Докажите второе сходство. Пусть DABC и DA1В1Больше.1, мы удовлетворяем соотношению:.
Докажите, что они похожи. Для этого мы построим еще один DABC2которая имеет общие аспекты с DABC.2 Выберите точку C так, чтобы условие было выполнено.
DM1В1Больше.1 Затем слегка постучите.2 Поскольку два угла одинаковы, они подобны. Поэтому необходимо применить следующие уравнения
Но потом ДАБК и ДАБК2 равны, так как углы, образованные двумя сторонами и двумя сторонами, одинаковы.
В результате, DB и DA1В1Больше.1 имеют два одинаковых угла, т.е. похожи друг на друга
Выпуск. На стороне угла отмечены точки a и b, так что ab = 5 см и ag = 16 см. На другой стороне того же угла отмечены точки c и d, такие, что AD = 8 см и AF = 10 см. Похожи ли ΔACD и D AFB?
Рассмотренные треугольники имеют общий угол.
Отношения одинаковы, поэтому треугольники симметричны.
ПРИМЕЧАНИЯ. В этом случае важно понять, какую сторону нужно разделить. У DGD стороны AC и AD равны 16 и 8 см. У DAFB стороны AF и AB равны 10 и 5 см. Наибольшая сторона одного треугольника делится на наибольшую сторону другого треугольника, т.е. 16 x 10, или 8 на 8. Сходство и взятое число — это просто коэффициент сходства.
Рассмотрим третье свойство подобия треугольников.
Давайте докажем это. Пусть DABC и DA1В1Больше.1 Это соизмеримо с их сторонами:.
Мы видим, что DABC2 И да1В1Больше. 1 Они похожи, потому что два угла одинаковы. Тогда пропорции верны:.
1 Они похожи, потому что два угла одинаковы. Тогда пропорции верны:.
Отношение площадей подобных треугольников
Если треугольники подобны, то их стороны зависят от коэффициента K. Здесь K — коэффициент. И как соотносятся между собой их высоты, промежуточные и другие характерные длины? Легко предположить, что они также зависят от коэффициента K.
Докажем это на примере высоты. Предположим, что у нас есть аналогичные DABC и DA1В1Больше.1и их коэффициент сходства равен k.
ch и c, которые построены на этих высотах1н1:.
Аналогично, мы можем доказать, что длины и расщепления промежуточных продуктов отличаются по времени k.
В чем причина одинаковой площади треугольника? Получается, что дважды по k. Докажите это.
Пусть DABC и DA1В1Больше.1 аналогично коэффициенту сходства k. Снова постройте высоты Ch и Ch1:.
Запишите очевидное уравнение: .
В результате площади одного и того же треугольника могут отличаться на коэффициент k 2.
Задание. Площадь DABC равна 10, и мы знаем, что отрезок AB равен 5. Сторона DE, которая подобна AB, равна 15. чтобы вычислить площадь DEF, DEF DB подобна DAB.
Решение. Согласно описанию проблемы, мы находим сходство между DABC и DDEF следующим образом
Задание. Два подобных треугольника имеют площади 75 м 2 и 300 м 2. Одна сторона второго треугольника равна 9 м. Вычислите одинаковую сторону первого треугольника.
Решение. Если известны площади треугольников, то коэффициент подобия легко найти.
Если коэффициент подобия равен 2, то сторона первого треугольника меньше стороны второго.
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами. Сходство представлено буквой k.
Как найти отношение площадей двух треугольников, если стороны одного равны 5 см, 8 см, 12 см, а стороны другого 15 см, 24 см, 36 см?
Как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Треугольники, приведенные в задаче, подобны. Это объясняется тем, что их стороны соизмеримы.
Два треугольника подобны, если три стороны одного треугольника подобны другой стороне.
Площадь подобных треугольников равна квадрату их подобия.
Площадь этих треугольников объясняется следующими причинами.
Найдите отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
Если стороны одного треугольника равны 12 см и 21 см 27 см, а другого треугольника — 4 см 7 см и 9 см, найдите причину возникновения двух треугольников.
На этой странице вы найдете ответ на вопрос, как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см и 12 см, а другая 15 см, 24 см, 36 см и 36 см. Он относится к категории геометрии. Сложность вопроса соответствует базовым знаниям учащихся в классе5-9.Для получения дополнительной информации воспользуйтесь поисковой системой, чтобы найти другие вопросы, связанные с этим. Кроме того, нажмите на кнопку в верхней части страницы и задайте новый вопрос, используя ключевые слова, соответствующие критериям. Поговорите с посетителями вашей страницы и обсудите эту тему. Возможно, их ответы помогут вам найти информацию, которую вы ищете.
Сложность вопроса соответствует базовым знаниям учащихся в классе5-9.Для получения дополнительной информации воспользуйтесь поисковой системой, чтобы найти другие вопросы, связанные с этим. Кроме того, нажмите на кнопку в верхней части страницы и задайте новый вопрос, используя ключевые слова, соответствующие критериям. Поговорите с посетителями вашей страницы и обсудите эту тему. Возможно, их ответы помогут вам найти информацию, которую вы ищете.
ДОКАЗАТЕЛЬСТВО: Предположим, что отрезки AC и BD пересекаются в точке o треугольника. Первое начало согласно треугольнику aob = sod (угол aob, угол SOD перпендикулярны, bo = od, ao = os, где o — середина ac и ua) треугольник abc = треугольник SOD (ac) является общим …
AC = 16 + 2 = 18 (см) BC = 18-8 = 10 (см) P = 16 + 18 + 10 = 44 (см) Ответ: 44 см.
Да, потому что это проекция и поэтому может иметь отображение.
AC = AD + DC = 6 + 8 = 14.Построим график CH, который является высотой ABC. Это также высота треугольника ABD.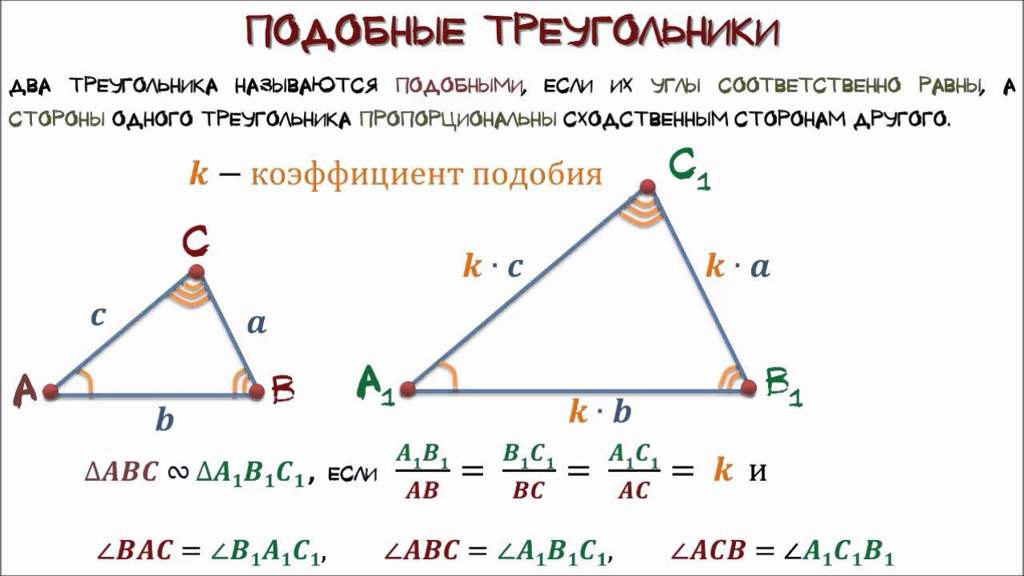 Sabc = 1/2 AC-BHBH = 2Sabc / AC = 2-42/14 = 6Sabd = 1/2 AB-BH = 1/2-6-6 = 18Sq.
Sabc = 1/2 AC-BHBH = 2Sabc / AC = 2-42/14 = 6Sabd = 1/2 AB-BH = 1/2-6-6 = 18Sq.
Решение. Эта диаграмма показывает, что ∠BCA = CESCE и ∠A = ∠E = 90°. Это означает, что BCABC и CESCE похожи, потому что у них два одинаковых угла. Стороны AB и EC похожи, используйте их для нахождения коэффициентов подобия.
Применение площадей
Теорема (Соотношение площадей подобных треугольников).
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Предположим, мы докажем, что с этим коэффициентом.
Проведем в данных треугольниках высоты
Прямоугольные треугольники Это означает, что
Средняя линия отсекает от данного треугольника треугольник с площадью 8
Давайте сделаем сторону, параллельную
Треугольники подобны по двум сторонам и углу между ними, причем Тогда по доказанной теореме откуда Ответ:
Метод площадей
Понятие площади и формула для ее вычисления также могут быть применены к задачам, в которых условия не относятся к площадям. Рассмотрим такой пример.
Рассмотрим такой пример.
Стороны прямоугольника равны 16 см и 12 см. Высота прямоугольника, начерченного по самой длинной стороне, равна 3 см. Найдите высоту меньшего из них.
Предположим, что вам дан прямоугольник со сторонами, высоты которых нарисованы, а длины нужно найти (рис. 163).
Используйте формулу для площади прямоугольника
Итак.
Для решения этой задачи площадь прямоугольника вычислялась двумя разными способами. Поскольку площадь полигона определялась однозначно, независимо от метода расчета, полученное уравнение было уравнено, чтобы соотнести известные значения с требуемыми. Этот метод, использующий площадь в качестве вспомогательного размера, называется методом вспомогательной площади или просто методом площади.
Отметим, что для прямоугольного типа площади следует сделать важный вывод: в прямоугольниках высота, нарисованная на малой стороне, больше, а высота, нарисованная на большой стороне, меньше.
Метод сайта используется как для вычислительных задач, так и для доказательств утверждений.
Сумма расстояний от внутренних точек равностороннего треугольника до его сторон равна высоте треугольника, независимо от выбора точек. Доказательство.
Пусть точка находится на расстоянии одной стороны от этой точки до стороны треугольника (рис. 164).
Точка соединения равна сумме площадей треугольника и возвышения. У нас есть:.
Отсюда т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки
Другие доказательства теоремы Пифагора
Исторически появление и доказательство теоремы Пифагора связано с вычислением площадей. Таким образом, классическая формулировка этой теоремы относится не к квадратам сторон прямоугольного треугольника, а к площади соответствующей фигуры.
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, на котором наглядно представлена эта формулировка, стал отличительным символом геометрии и был назван школьниками прошлого века «пифагорейскими брюками».
т.е.
На рисунках 166, C и D показаны другие способы доказательства теоремы Пифагора с помощью площадей. В работе индийского математика XII века Бхаскари, один из них: «Смотрите!». сопровождается только словом «Смотри!». В целом, в настоящее время существует более 150 различных способов доказательства этой знаменитой теоремы. Однако каждый из вас может изобрести свой собственный метод.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей стороны
Сумма углов многоугольника Сумма углов выпуклости
Сумма внешних углов выпуклой фигуры
Внешние углы выпуклого многоугольника
Если все вершины лежат на окружности, многоугольник регистрируется как окружность.
Полигон описан как зарегистрированный.
Если все стороны принадлежат этому циклу, то многоугольник называется циклом периметра многоугольника.
Аксиомы площади
- Равные многоугольники имеют равные площади.

- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади
Площадь подобных треугольников – формула, теорема, доказательство, примеры
LearnPracticeDownload
Два треугольника называются подобными, если один можно получить из другого равномерным масштабированием. Отношение площадей двух подобных треугольников равно квадрату отношения любой пары соответствующих сторон подобных треугольников. Если два треугольника подобны, это означает, что: Все соответствующие пары углов равны и все соответствующие стороны пропорциональны. Однако, чтобы быть уверенным, что два треугольника подобны, нам не обязательно иметь информацию обо всех сторонах и всех углах.
Для подобных треугольников не только их углы и стороны имеют отношение, но и отношение их периметра, высот, биссектрисы угла, площадей и других аспектов пропорциональны. Давайте изучим и поймем соотношение между площадями подобных треугольников в следующих разделах.
Давайте изучим и поймем соотношение между площадями подобных треугольников в следующих разделах.
| 1. | Площадь подобных треугольников Теорема |
| 2. | Доказательство площади подобных треугольников Теорема |
| 3. | Часто задаваемые вопросы о площади подобных треугольников |
Теорема о площади подобных треугольников
Теорема о площади подобных треугольников помогает установить связь между площадями двух подобных треугольников. В нем говорится, что «отношение площадей двух подобных треугольников равно квадрату отношения любой пары их соответствующих сторон». Рассмотрим следующий рисунок, на котором показаны два подобных треугольника, ΔABC и ΔDEF.
Согласно теореме для площадей подобных треугольников, площадь ΔABC/площадь ΔDEF = (AB) 2 /(DE) 2 = (BC) 2 /(EF) 2 = (AC) 2 /(DF) 2 .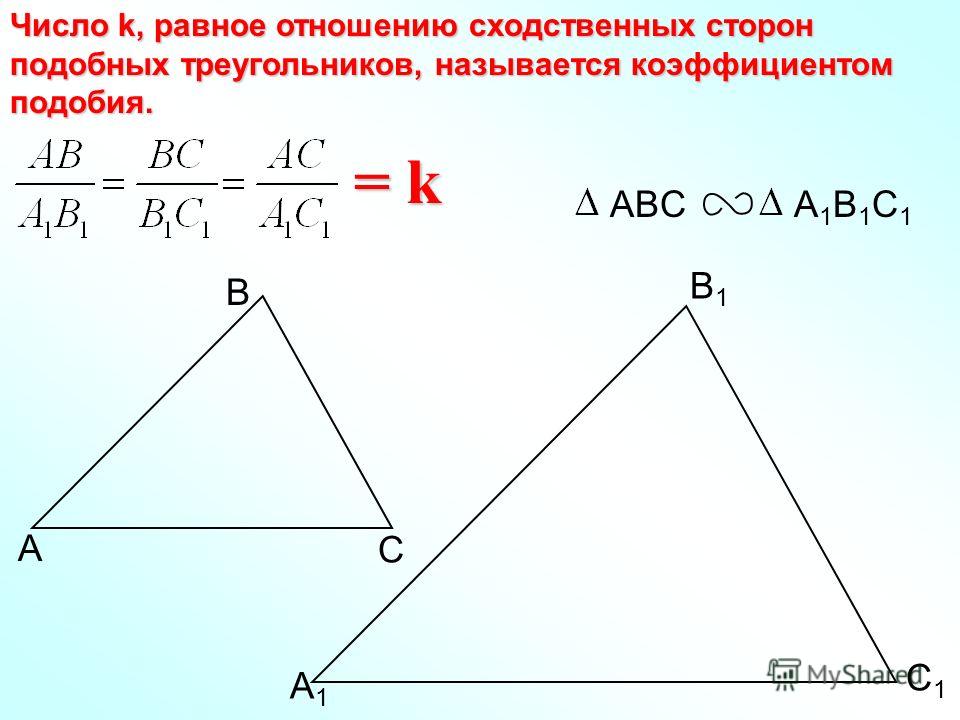 Мы поймем доказательство этой теоремы в следующем разделе.
Мы поймем доказательство этой теоремы в следующем разделе.
Доказательство теоремы о площади подобных треугольников
Утверждение: Отношение площадей двух подобных треугольников равно квадрату отношения любой пары их соответствующих сторон.
Дано: Рассмотрим два треугольника, ΔABC и ΔDEF, такие, что ΔABC~ΔDEF
Чтобы доказать: Площадь ΔABC/площадь ΔDEF = (AB) 2 /(DE) ) 2 /(EF) 2 = (AC) 2 /(DF) 2
Построение: Проведите высоты AP и DQ к сторонам BC и EF соответственно, как показано ниже:
Доказательство: Поскольку ∠B = ∠E, [ ∵ ΔABC ~ ΔDEF ] и,
∠APB = ∠DQE…..[ ∵ AP и DQ перпендикулярны сторонам BC и EF соответственно ⇒ Оба угла равны 90º ]
По, AA свойству подобия треугольников, можно отметить, что ΔABP и ΔDEQ равноугольны.
Следовательно, ΔABP ~ ΔDEQ
Таким образом, AP/DQ = AB/DE
Отсюда далее следует, что
AP/DQ = BC/EF —— (1).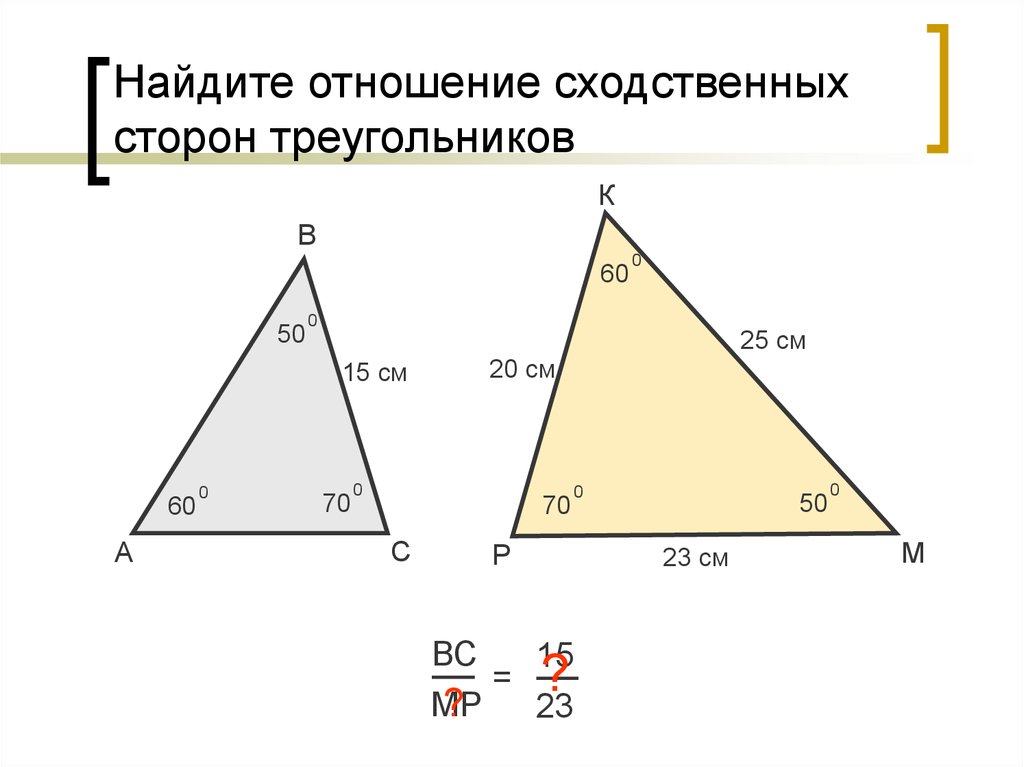 …[ ∵ ΔABC∼ΔDEF ⇒ AB/DE = BC/EF]
…[ ∵ ΔABC∼ΔDEF ⇒ AB/DE = BC/EF]
Таким образом,
Площадь(ΔABC)/площадь(ΔDEF) = [(1/2) × BC × AP]/[(1/2) × EF × DQ ]
= (BC/EF) × (AP/DQ)
= (BC/EF) × (BC/EF) ….[из (1)]
⇒ Площадь(ΔABC)/площадь(ΔDEF) = (BC/EF) 2
Аналогично, мы можем показать, что
Площадь ΔABC/площадь ΔDEF = (AB) 2 /(DE) 2 = (BC) 2 /(EF) 2 = 2 (AC) 2 /(DF) 2
Задающий вопрос:
Дано, что ΔABC ~ ΔXYZ. Площадь ΔABC составляет 45 квадратных единиц, а площадь ΔXYZ — 80 квадратных единиц. YZ = 12 единиц. Найти БК? Подсказка: используйте теорему для площади подобных треугольников.
Важные замечания о площади подобных треугольников
- Отношение площадей двух подобных треугольников равно квадрату отношения любой пары их соответствующих сторон.
- Для подобных треугольников ΔABC и ΔDEF площадь ΔABC/площадь ΔDEF = (AB) 2 /(DE) 2 = (BC) 2 /(EF) 2 = (AC) 2 /(ДФ) 2
- Все соответствующие пары углов равны, и все соответствующие стороны пропорциональны для подобных треугольников.

Темы, связанные с площадью подобных треугольников
- Подобные треугольники
- Формулы подобных треугольников
- Что такое сходство?
Примеры площади подобных треугольников
Пример 1: Рассмотрим два подобных треугольника, ΔABC и ΔDEF, как показано ниже:
AP и DQ — медианы двух треугольников. Покажите, что
ArΔ(ABC)/AP 2 = ArΔ(DEF)/DQ 2 с использованием теоремы о площадях подобных треугольников.
Решение: Поскольку ΔABC ~ ΔDEF,
AB/DE = BC/EF
⇒AB/DE = (1/2)BC/(1/2)EF
⇒AB/DE = BP/EQ →(1)
Кроме того,
∠B = ∠E —— (2) … [ ∵ ΔABC ~ ΔDEF]
Из (1) и (2) и по критерию подобия SAS, мы можем обратите внимание, что
ΔABP ~ ΔDEQ
⇒AB/DE = AP/DQ →(3)
Теперь по теореме для площадей подобных треугольников
ArΔ(ABC)/ArΔ(DEF) = AB 2 /DE 2 = AP 2 /DQ 2 .
 …[из (3)]
…[из (3)]
⇒ ArΔ(ABC)/AP 2 = ArΔ(DEF)/DQ 2Пример 2: Рассмотрим следующую фигуру:
Дано, что XY || г. до н.э. и делит треугольник на две равные по площади части. Найдите отношение AX:XB, используя теорему о площади подобных треугольников.
Решение: С XY || до н.э., ∠X = ∠B и ∠Y = ∠C …[Соответствующие углы]
⇒ ΔAXY должен быть подобен ΔABC… [По критерию подобия AA в треугольниках]Теперь по теореме для площадей подобных треугольников
Ar(ΔABC)/Ar(ΔAXY) = AB 2 /AX 2 → (1)
Также XY делит треугольник на две равные по площади части. Таким образом,
Ar(ΔABC)/Ar(ΔAXY) = 2 → (2)
Из (1) и (2) имеем
AB 2 /AX 2 = 2
⇒AB/AX = √2
⇒(AB/AX) − 1 = √2 − 1
(AB — AX) / (AX) = √2 − 1
⇒XB/AX = √2 − 1
⇒AX/XB = 1/(√2 − 1)
перейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Испытайте Cuemath и приступайте к работе.
Запись на бесплатный пробный урок
Практические вопросы по площади подобных треугольников
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади подобных треугольников
Какова площадь подобных треугольников?
Площадь двух подобных треугольников имеет отношение отношения соответствующих сторон подобных треугольников. Согласно теореме о площади подобных треугольников, мы можем утверждать, что «отношение площадей двух подобных треугольников равно квадрату отношения любой пары их соответствующих сторон».
Каково отношение площадей подобных треугольников?
Отношение площадей двух подобных треугольников равно квадрату отношения любой пары соответствующих сторон подобных треугольников. Например, для любых двух подобных треугольников ΔABC и ΔDEF
Площадь ΔABC/площадь ΔDEF = (AB) 2 /(DE) 2 = (BC) 2 /(EF) 2 = (AC) 2 (DF) 2 .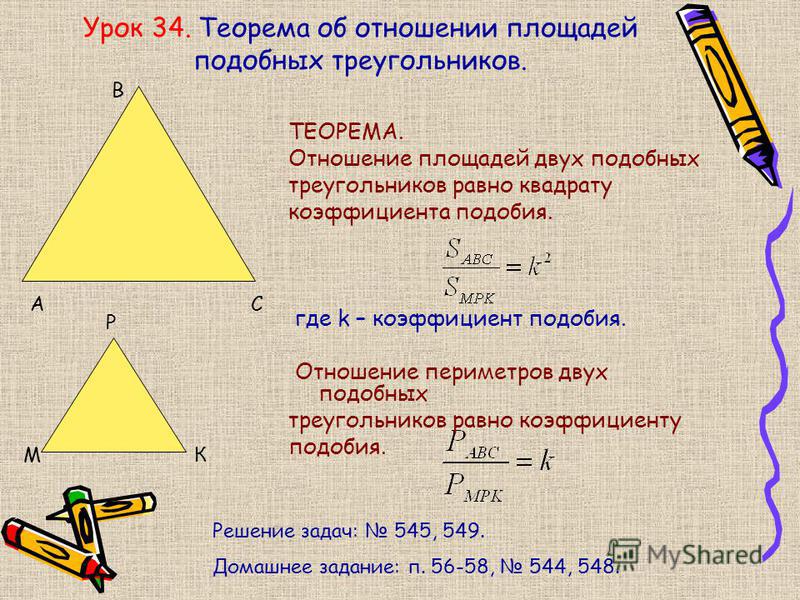
Какая связь между площадью двух подобных треугольников и длиной сторон?
Отношение площадей двух подобных треугольников равно квадрату отношения любой пары соответствующих сторон подобных треугольников.
Имеют ли подобные треугольники равные площади?
Отношение площадей подобных треугольников будет равно квадрату отношения их пар соответствующих сторон. Итак, площади двух треугольников не обязательно могут быть равны. Но учтите, что конгруэнтные треугольники всегда имеют равные площади.
Как найти площади двух подобных треугольников?
Площади подобных треугольников можно найти, связав их отношение с отношением пары соответствующих сторон. Для любых двух подобных треугольников отношение площадей равно квадрату отношения соответствующих сторон.
Что такое теорема о площадях подобных треугольников?
Теорема о площадях подобных треугольников утверждает, что «отношение площадей двух подобных треугольников равно квадрату отношения любой пары их соответствующих сторон»
Как доказать теорему для площадей подобных треугольников?
Теорему о площадях подобных треугольников можно доказать, построив высоты обоих треугольников и сравнив полученную таким образом площадь с отношением соответствующих сторон обоих подобных треугольников.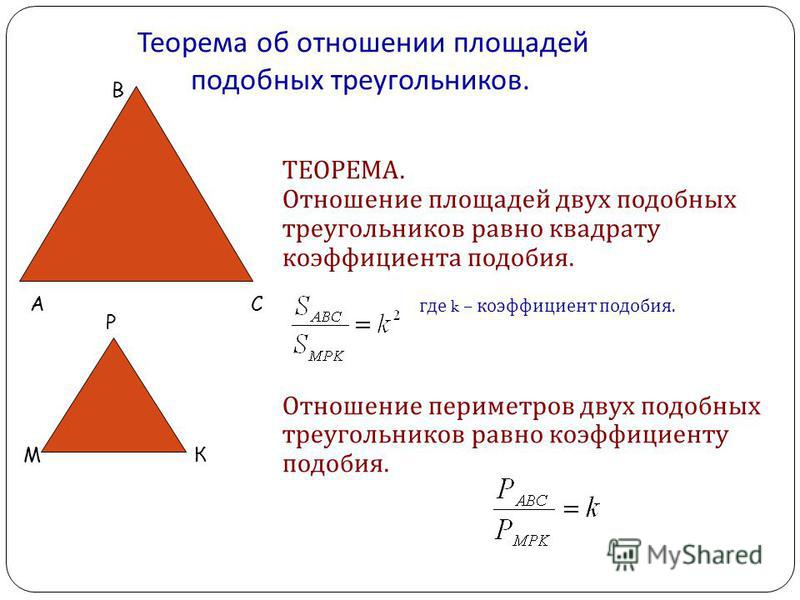 Чтобы понять доказательство в деталях, обратитесь к разделу Доказательство теоремы о площадях подобных треугольников на этой странице.
Чтобы понять доказательство в деталях, обратитесь к разделу Доказательство теоремы о площадях подобных треугольников на этой странице.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по площади
Скачать похожие рабочие листы треугольников
Рабочие листы по математике и
наглядный учебный план
Подобные треугольники – объяснение и примеры
Теперь, когда мы закончили с конгруэнтными треугольниками, мы можем перейти к другому понятию, называемому подобных треугольников.
В этой статье мы узнаем о подобных треугольниках, свойствах подобных треугольников, как использовать постулаты и теоремы для определения подобных треугольников и, наконец, как решать задачи о подобных треугольниках.
Что такое подобные треугольники?
Понятие подобных треугольников и конгруэнтных треугольников — это два разных термина, тесно связанных между собой. Подобные треугольники — это два или более треугольника с одинаковой формой, равными парами соответствующих углов и одинаковым отношением соответствующих сторон.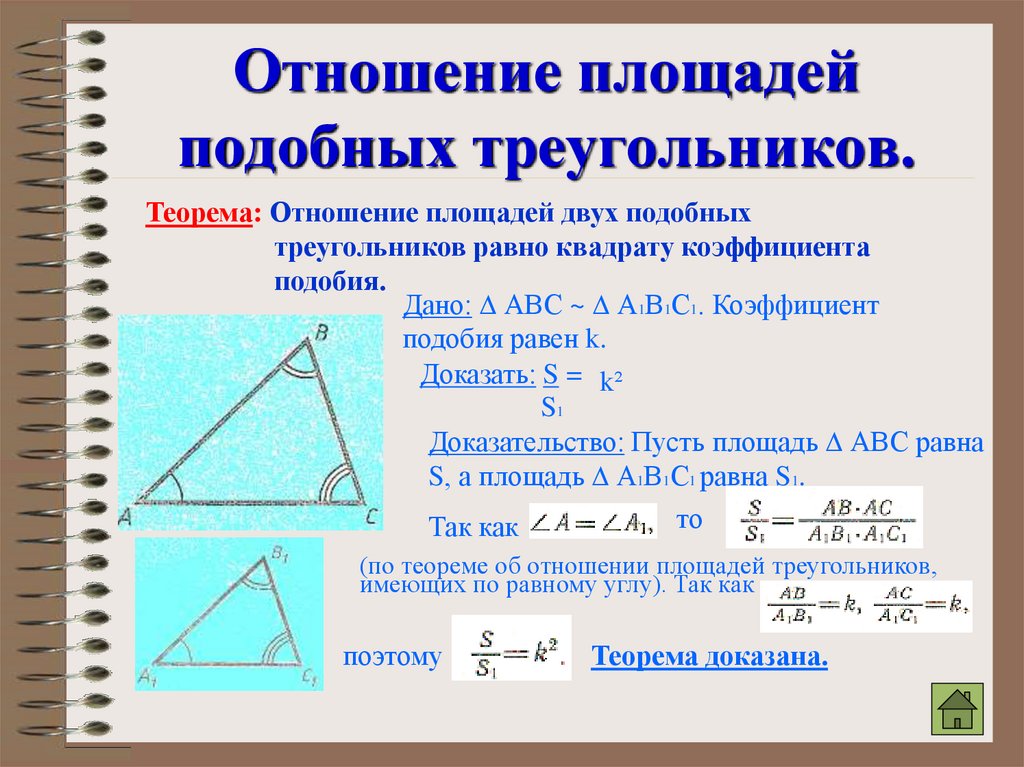
Иллюстрация подобных треугольников:
Рассмотрим три треугольника ниже. Если:
- Отношение их соответствующих сторон равно.
AB/PQ = AC/PR= BC= QR, AB/XY= AC/XZ= BC/YZ
- ∠ A= ∠ P=∠X, ∠B = ∠Q= ∠Y, ∠C= ∠R =∠Z
Следовательно, ΔABC ~ΔPQR~ΔXYZ
Comparison between similar triangles and congruent triangles
| Features | Congruent triangles | Similar Triangles |
| Shape and size | same size and shape | Same shape but different size |
| Символ | ≅ | ~ |
| Длины соответствующих сторон | Отношение соответствующих сторон равно 9 числу равных треугольников.0014 | Отношение всех соответствующих сторон в подобных треугольниках постоянно. |
| Соответствующие углы | Все соответствующие углы равны. | Каждая пара соответствующих углов равна. |
Как определить подобные треугольники?
Сходство треугольников можно доказать, применяя теоремы о подобных треугольниках. Это постулаты или правила, используемые для проверки подобных треугольников.
Существует три правила проверки подобных треугольников: AA 9правило 0006, правило SAS или правило SSS.
Правило угла-угла (AA):
Согласно правилу AA два треугольника называются подобными, если два угла в одном треугольнике равны двум углам другого треугольника.
Правило Side-Angle-Side (SAS):
Правило SAS гласит, что два треугольника подобны, если отношение их соответствующих двух сторон равно, а также угол, образованный двумя сторонами, равен.
Правило Side-Side-Side (SSS):
Два треугольника подобны, если все три соответствующие стороны данных треугольников находятся в одной пропорции.
Как решать подобные треугольники?
Существует два типа подобных задач на треугольник ; это задачи, которые требуют от вас доказать, подобны ли данный набор треугольников, и те, которые требуют от вас вычисления недостающих углов и длин сторон подобных треугольников.
Давайте рассмотрим следующие примеры:
Пример 1
Проверьте, являются ли следующие треугольники с одинаковыми
Решение
Сумма внутренних углов в треугольнике = 180 °
Следовательно, рассмотрев Δ Pqr
° № wmp +or +° эй wмобили. + ∠R = 180°
60° + 70° + ∠R = 180°
130° + ∠R = 180°
Вычтите обе стороны на 130°.
∠ R= 50°
Рассмотрим Δ XYZ
∠X + ∠Y + ∠Z = 180°
∠60° + ∠Y + ∠50°= 180° 0°
1
°
Вычесть обе стороны на 110°
∠ Y = 70°
Отсюда;
- По правилу угла-угла (AA), ΔPQR~ΔXYZ.
- ∠Q = ∠ Y = 70° и ∠Z = ∠ R= 50°
Пример 2
Решение
Учитывая, что два треугольника подобны, тогда;
WY/QR = WX/PR
30/15 = 36/x
Перемножить
30x = 15 * 36
Разделить обе стороны на 30.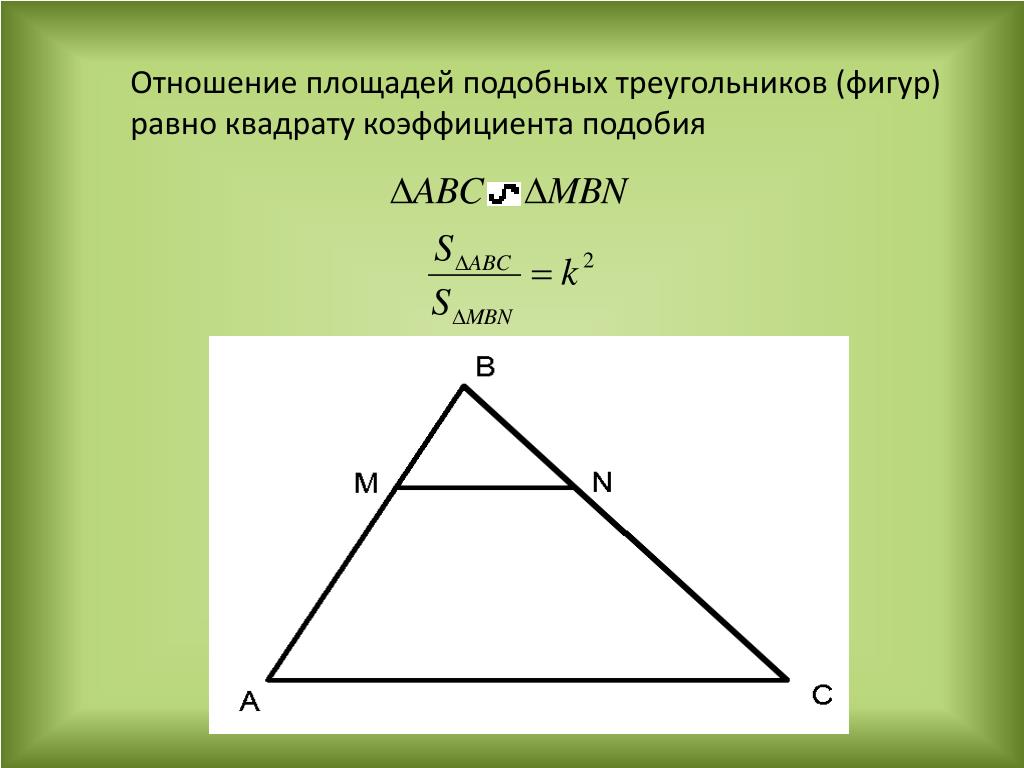 x = 18
x = 18
Следовательно, PR = 18
. Проверим, равны ли пропорции соответствующих двух сторон треугольников.
WY/QR = WX/PR
30/15 = 36/18
2 = 2 (RHS = LHS)
Пример 3
Проверьте, подобны ли два показанных ниже треугольника, и вычислите значение k.
Решение
Согласно правилу SAS, два треугольника подобны.
Доказательство:
8/ 4 = 20/10 (левый = правый)
2 = 2
Теперь вычислите значение k
12/k = 8/4
12/k = 2
900 стороны к.
12 = 2k
Разделить обе части на 2
12/2 = 2k/2
k = 6.
Пример 4
Определите значение x на следующей диаграмме.
Решение
Пусть треугольники ABD и ECD — подобные треугольники.
Применить правило «сторона-угол-сторона» (SAS), где A = 90 градусов.
AE/EC= BD/CD
x/1,8 = (24 + 12)/12
x/1,8 = 36/12
Перемножить
12x = 36 * 1,8
х = (36 * 1,8)/12
= 5,4
Следовательно, значение x равно 5,4 мм.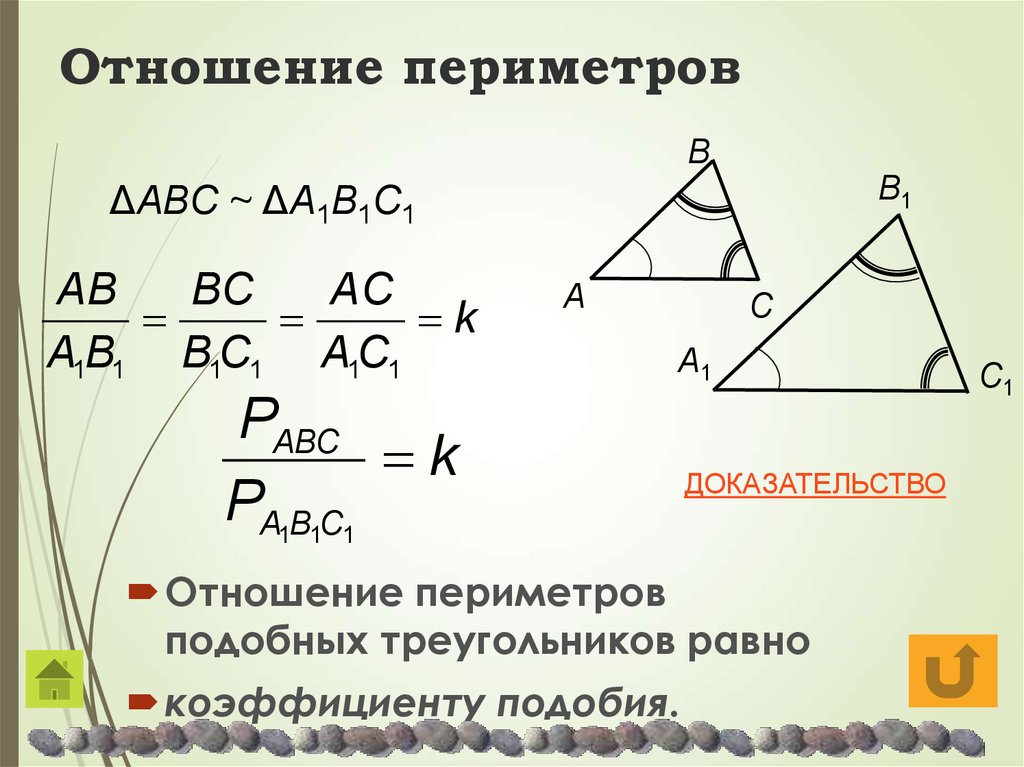
Площадь и подобные треугольники. Как найти отношение площадей из отношения подобия. Все, что вам нужно сделать, это…
Что верно в отношении отношения площадей подобных треугольников?
Ответ: Если 2 треугольника подобны, их площади равны квадрату этого отношения сходства (масштабного коэффициента). 92} = \frac {9}{16} $$
Давайте посмотрим на два похожих треугольника ниже, чтобы увидеть это правило в действии.
Пример 1
Легче всего убедиться в том, что это так, если вы посмотрите на некоторые конкретные примеры реальных подобных треугольников.
Треугольник 1
$$ Площадь = \frac{1}{2}\cdot{12}\cdot{4} \\ Площадь = 24 $$
Треугольник 2
$$ Площадь = \frac{1}{2}\cdot{24}\cdot{8} \\ Площадь = 96 $$
Уведомление: $$ \frac{24}{96} = \frac{1}{4} $$
Следовательно, если вы знаете коэффициент подобия, все, что вам нужно сделать, это возвести его в квадрат, чтобы определить отношение площадей треугольника.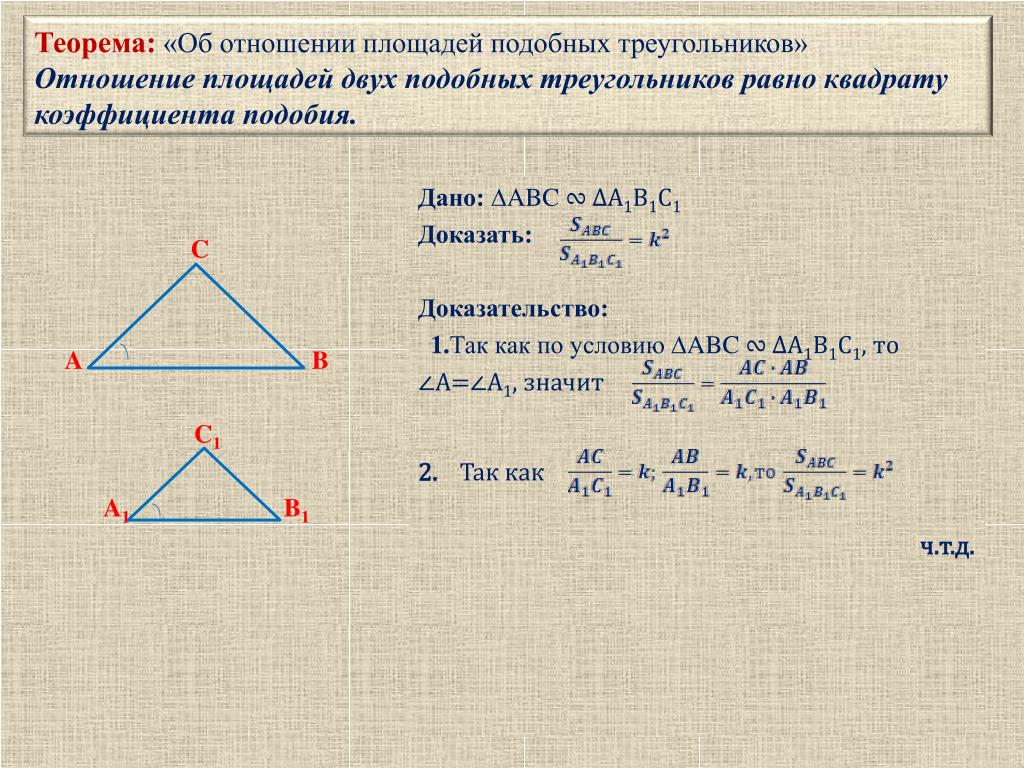
Как насчет периметра подобных треугольников?
Если 2 треугольника подобны, то их периметры имеют одинаковое отношение
Например, если отношение подобия двух треугольников равно $$\frac 3 4 $$ , то отношение их периметров равно $$\frac 3 4 $$
Давайте посмотрим на два похожих треугольника ниже, чтобы увидеть это правило в действии.
Пример 2
Треугольник 1
Периметр треугольника #1
Периметр $$ = 6 + 8 + 10 = 24 $$
Треугольник 2
Периметр треугольника #2
Периметр $$ = 5 + 3 +4 = 12 $$
Соотношение периметров точно такое же, как отношение подобия!
$ \frac{\text{периметр #1}}{\text{периметр #2}} = \frac{24}{12} = \frac{2}{1} $
Практика ПроблемыПроблема 1
$$\triangle ABC$$ ~ $$\triangle XYZ$$ и имеют масштабный коэффициент (или коэффициент подобия) $$ \frac{3}{2} $$. 2 = \text{отношение площадей}
\\
\text{коэффициент подобия} = \sqrt{\text{отношение площадей} }
\\
= \ sqrt {\ большой (\ гидроразрыва {36} {17} \ большой)}
\\
= \ гидроразрыва {\ sqrt {36}} {\ sqrt {17}}
\\
= \ гидроразрыв {6} {\ sqrt {17} }
$
2 = \text{отношение площадей}
\\
\text{коэффициент подобия} = \sqrt{\text{отношение площадей} }
\\
= \ sqrt {\ большой (\ гидроразрыва {36} {17} \ большой)}
\\
= \ гидроразрыва {\ sqrt {36}} {\ sqrt {17}}
\\
= \ гидроразрыв {6} {\ sqrt {17} }
$
Проблема 4
$$\треугольник HIJ$$ ~ $$\треугольник XYZ$$. Отношение их площадей равно $$ \frac{25}{16}$$, если XY имеет длину 40, то какова длина HI?
Каково соотношение их площадей?
Сначала нам нужно найти отношение подобия, так как это отношение дает нам пропорцию между соответствующими сторонами.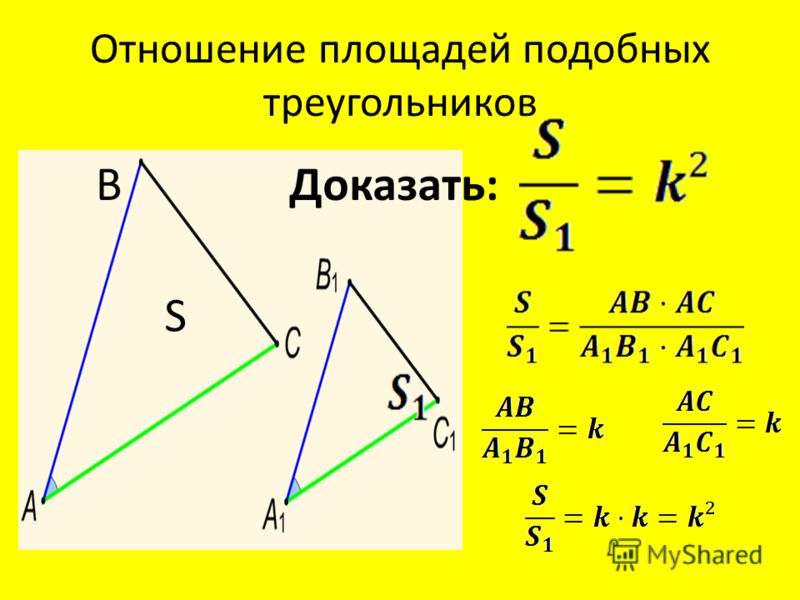



 (После завершения работы заслушиваются и обсуждаются варианты решений.)
(После завершения работы заслушиваются и обсуждаются варианты решений.)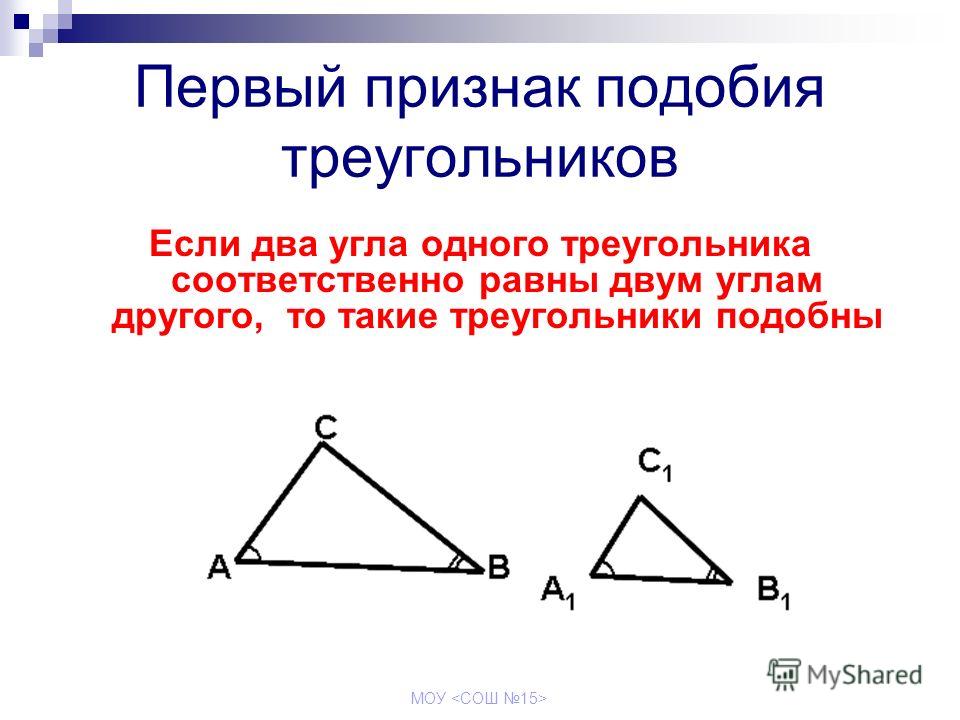

 …[из (3)]
…[из (3)]