Чётность, нечётность, периодичность тригонометрических функций
Урок 2. Алгебра 11 класс ФГОС
В данном видеоуроке мы вспомним формулы, позволяющие перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов, а также формулы приведения. Поговорим о чётности, нечётности тригонометрических функций, а также об их периодичности.
Конспект урока «Чётность, нечётность, периодичность тригонометрических функций»
Сегодня на уроке мы с вами вспомним формулы, позволяющие перейти от вычисления синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов, а также формулы приведения. Напомним, какие функции называются тригонометрическими. Поговорим о чётности, нечётности тригонометрических функций, а также об их периодичности.
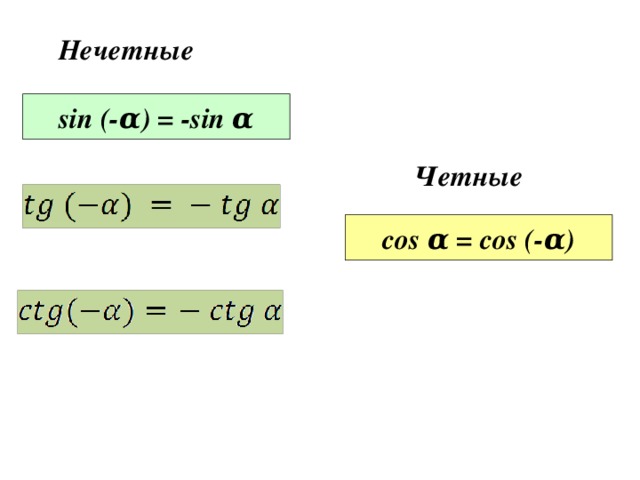
Прежде чем приступить к рассмотрению новой темы, давайте вспомним
формулы, которые позволяют сводить вычисление значений синуса, косинуса,
тангенса и котангенса отрицательных углов к вычислению их значений для
положительных углов.
Напомним:
, ,
, ,
, ,
, .
Вспомним формулы приведения для синуса, косинуса, тангенса и котангенса.
На прошлом занятии мы с вами сказали, что функции , , и называются тригонометрическими функциями.
Также на прошлом занятии мы выяснили, что функция определена на множестве действительных чисел. Для любого значения верно равенство . Следовательно, функция – нечётная функция.
Функция определена на множестве действительных чисел. Для любого значения верно равенство . Следовательно, функция и – чётная функция.
Областью определения функции является множество действительных чисел, кроме , . Для любого из области определения верно равенство . Следовательно, функция – нечётная функция.
Областью определения функции является множество действительных чисел, кроме , . Для любого из области определения верно равенство . Следовательно, функция – нечётная функция.
Отметим, что при исследовании функции на чётность или нечётность
мы будем находить её область определения, чтобы убедиться, что эта область
определения симметрична относительно начала координат.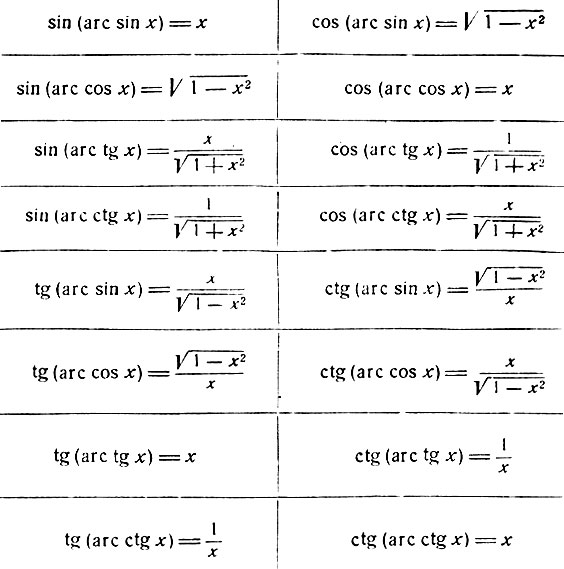
Давайте выполним задание. Установите чётность или нечётность функций:
а) ; б) .
Решение.
Мы знаем, что для любого значения верны равенства: , . Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на . Такие функции называются периодическими с периодом .
Функция называется периодической, если существует такое число , что для любого из области определения этой функции выполняется равенство
.
Число называется периодом функции .
Из этого определения следует, что если принадлежит области определения функции , то числа , и все числа , где , также принадлежат области определения этой периодической функции и , где .
Число является наименьшим положительным периодом для функций и .
Давайте докажем это, например, для функции .
Пусть – период косинуса, то есть равенство выполняется для любого . При получаем , . Отсюда , .
Так как , то может принимать значения при , при , при и так далее.
Поэтому период не может быть меньше . То есть – наименьший положительный период функции .
Задание. Докажите, что – периодическая функция с периодом .
Решение.
Теперь докажем, что функция является периодической с наименьшим положительным периодом .
Итак, пусть принадлежит области определения функции , то есть множеству действительных чисел, кроме , .
, .
Таким образом, мы получили, что . Следовательно, – период функции .
Докажем, что это наименьший положительный период функции . Пусть – период тангенса, тогда .
При получаем , . Откуда , .
При , то есть при наименьшем целом положительном, получаем . Следовательно, – наименьший положительный период функции .
Отметим, что функция также является периодической с наименьшим положительным периодом .
Задание. Докажите, что – периодическая функция с периодом .
Решение.
Задание. Докажите, что – периодическая функция с периодом .
Решение.
Отметим, что периодическими функциями описываются такие физические процессы, как колебания маятника, вращение планет, переменный ток и так далее.
Сейчас на рисунке вы видите графики некоторых периодических функций. Отметим, что график периодической функции имеет один и тот же вид на всех последовательных отрезках числовой прямой, длина которых равна периоду.
Предыдущий урок 1 Область определения и множество значений тригонометрических функций
Следующий урок 3 Функция у = cos x и её график
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 11 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒ Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а. Синус — функция числа x. Ее область определения — множество всех чисел, так как у любого числа можно найти ординату изображающей его точки. Область значений синуса — отрезок от -1 до 1, так как любое число этого отрезка на оси ординат является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период синуса равен . Ведь через каждые положение точки, изображающей число, в точности повторяется. Знак синуса: 1. синус равен нулю при , где n — любое целое число; 2. синус положителен при , где n — любое целое число; 3. синус отрицателен при , где Синус — функция нечетная. Во-первых, область определения этой функции есть множество всех чисел, а значит, симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты — синусы — окажутся также противоположными. То есть для любого x. 1. Синус возрастает на отрезках , где n — любое целое число. 2. Cинус убывает на отрезке , где n — любое целое число. при ; при . Косинус Косинусом числа а называется абсцисса точки, изображающей это число на числовой окружности. Косинус — функция числа. Ее область определения — множество всех чисел, так как у любого числа можно найти ординату изображающей его точки.Область значений косинуса — отрезок от -1 до 1, так как любое число этого отрезка на оси абсцисс является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек. Период косинуса равен . Ведь через каждые положение точки, изображающей число, в точности повторяется. Знак косинуса: 1. косинус равен нулю при , где n — любое целое число; 2. косинус положителен при , где n — любое целое число; 3. косинус отрицателен при , где n — любое целое число. Косинус — функция четная. для любого x. 1. Косинус возрастает на отрезках , где n — любое целое число. 2. Косинус убывает на отрезках , где n — любое целое число. при ; при . Тангенс Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: . Тангенсом угла в а радиан называется тангенс числа а. Тангенс — функция числа. Ее область определения — множество всех чисел, у которых косинус не равен нулю, так как никаких других ограничений в определении тангенса нет. И так как косинус равен нулю при , то , где . Область значений тангенса — множество всех действительных чисел. Период тангенса равен . Ведь если взять любые два допустимые значенияx (не равные ), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию тангенсов в некоторой точке t. Вот и получится, что , то есть число является периодом тангенса. Знак тангенса: тангенс — отношение синуса к косинусу. Значит, он 1. равен нулю, когда синус равен нулю, то есть при , где n — любое целое число. 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при , где а — любое целое число. 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при , где а — любое целое число. Тангенс — функция нечетная. Вот и получилось, что . Значит, тангенс возрастает на каждом участке своей области определения, то есть на всех интервалах вида , где а — любое целое число. Котангенс Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: . Котангенсом угла в а радиан называется котангенс числа а. Котангенс — функция числа. Ее область определения — множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при , то , где Область значений котангенса — множество всех действительных чисел. Период котангенса равен . Ведь если взять любые два допустимые значения x (не равные ), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию котангенсов в некоторой точке t. Вот и получится, что , то есть, что число является периодом котангенса. Знак котангенса: котангенс — отношение косинуса к синусу. Значит, он 1. равен нулю, когда косинус равен нулю, то есть при . 2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при . 3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при . Котангенс — функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна . Вот и получилось, что . Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида . ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 1230; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Измерение угла: градусная, радианная мера. Значения синуса, косинуса. Четность, нечетность функций. Тест
Вопрос 1. На какой окружности изображена точка, которой соответствует угол 1500?
| A. | 3 |
| B. | 4 |
| C. | 1 |
| D. | 2 |
Вопрос 2. На какой окружности изображена точка, которой соответствует угол 2100?
| A. | 2 |
B. |
4 |
| C. | 1 |
| D. | 3 |
Вопрос 3. На какой окружности изображена точка, которой соответствует угол 5400?
| A. | 3 |
| B. | 2 |
| C. | 1 |
| D. | 4 |
Вопрос 4. На какой окружности изображена точка, которой соответствует угол -450?
| A. | 3 |
| B. | 1 |
| C. | 4 |
| D. | 2 |
Вопрос 5.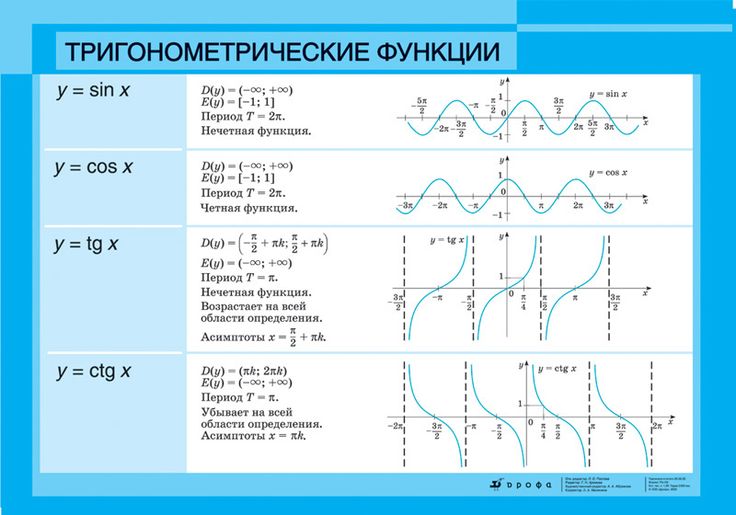 На какой окружности изображена точка, у которой ?
На какой окружности изображена точка, у которой ?
| A. | 3 |
| B. | 2 |
| C. | 4 |
| D. | 1 |
Вопрос 6. На какой окружности изображена точка, у которой ?
| A. | 4 |
| B. | 3 |
| C. | 2 |
| D. | 1 |
Вопрос 7. На какой окружности изображена точка, у которой ?
| A. | 2 |
B.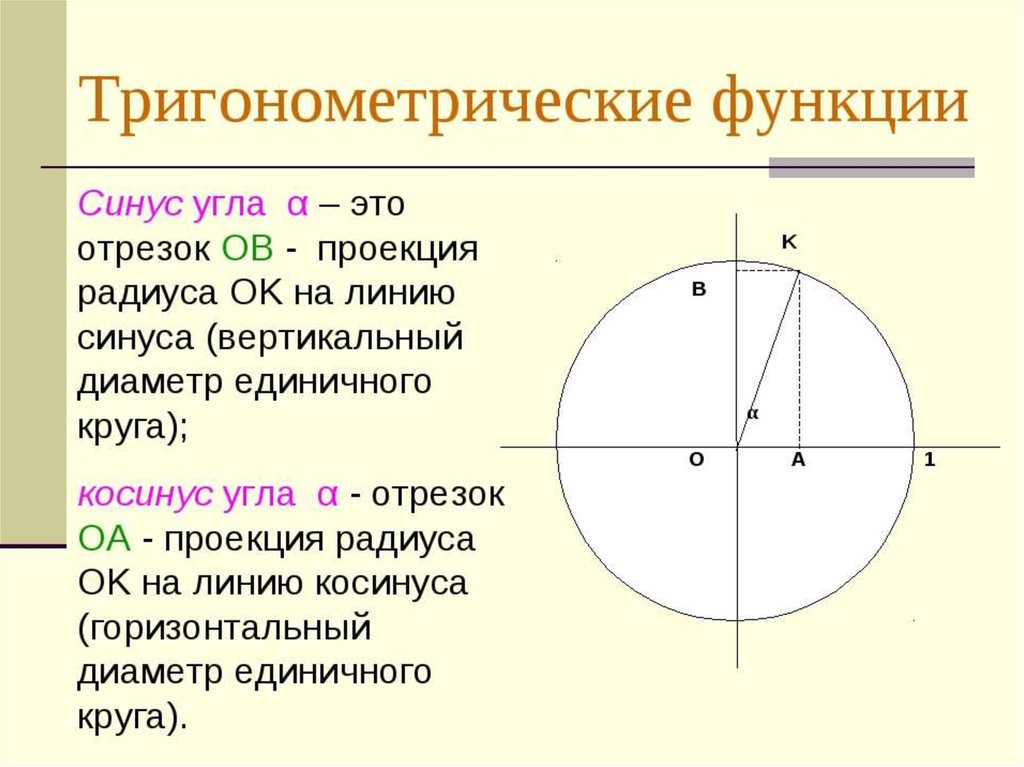 |
1, 3 |
| C. | 1 |
| D. | 3 |
| E. | 4 |
Вопрос 8. На какой окружности изображена точка, у которой ?
| A. | 2 |
| B. | 1 |
| C. | 1, 3 |
| D. | 2, 4 |
Вопрос 9. Укажите несколько значений угла, при которых
| A. | -2700, -900, 900, 2700, -4500, -900, 2700 |
| B. | -4500, -900, 2700 |
C. |
-5400, -1800, 1800, 5400 |
| D. | -1800, 00, 1800, 3600 |
Вопрос 10. Укажите несколько значений угла, при которых
| A. | -1800, -900, 00, 900, 1800 |
| B. | -1350, -450, 450, 1350 |
| C. | -2700, -900, 900, 2700 |
| D. | -3600, -1800, 00, 1800, 3600 |
Вопрос 11. Укажите несколько значений угла, при которых
A. |
-1800, -900, 00, 900, 1800 |
| B. | -2700, 00, 900, 3600 |
| C. | -2700, -900, 900, 2700 |
| D. | -1800, 00, 1800, 3600 |
Вопрос 12. Укажите несколько углов, при которых не имеет смысла выражение
| A. | 00, 1800 |
| B. | 00, 900, 1800, 2700 |
| C. | 900, 2700 |
Вопрос 13. Укажите несколько значений углов, при которых не имеет смысла выражение
A. |
00, 1800 |
| B. | 900, 2700 |
| C. | 00, 900, 1800, 2700 |
Вопрос 14. Какое значение может принимать ?
| A. | |
| B. | |
| C. | |
| D. |
Вопрос 15. Какое значение может принимать ?
| A. | |
| B. | |
| C. | |
| D. |
Четно-временно-симметричные квантовые критические явления | Nature Communications
Четно-временно-симметричные квантовые критические явления
Скачать PDF
Скачать PDF
- Открытый доступ
- Опубликовано:
- Юто Ашида 1 ,
- Сюнсуке Фурукава 1 и
- Масахито Уэда 1,2
Связь с природой том 8 , Номер статьи: 15791 (2017) Процитировать эту статью
9797 Доступ
158 цитирований
3 Альтметрика
Сведения о показателях
Предметы
- Фазовые переходы и критические явления
- Теоретическая физика
- Ультрахолодные газы
Abstract
Синтетические неконсервативные системы с симметричными по времени четности (PT) структурами усиления-потери могут демонстрировать необычное спонтанное нарушение симметрии, которое сопровождает спектральную сингулярность. Недавние исследования PT-симметрии в оптике и слабо взаимодействующих открытых квантовых системах выявили интригующие физические свойства, но корреляции многих тел по-прежнему не играют никакой роли. Здесь, распространяя идею PT-симметрии на сильно коррелированные системы многих тел, мы сообщаем, что комбинация спектральной сингулярности и квантовой критичности дает экзотический класс универсальности, не имеющий аналога в известных критических явлениях. Более того, мы обнаруживаем нетрадиционную низкоразмерную квантовую критичность, где сверхтекучие корреляции аномально усиливаются из-за немонотонных потоков ренормализационной группы в квантовой критической фазе с нарушением PT-симметрии, что резко контрастирует с парадигмой Березинского-Костерлица-Таулесса. Наши выводы могут быть экспериментально проверены в ультрахолодных атомах и предсказывать критические явления за пределами эрмитовой парадигмы квантовой физики многих тел.
Недавние исследования PT-симметрии в оптике и слабо взаимодействующих открытых квантовых системах выявили интригующие физические свойства, но корреляции многих тел по-прежнему не играют никакой роли. Здесь, распространяя идею PT-симметрии на сильно коррелированные системы многих тел, мы сообщаем, что комбинация спектральной сингулярности и квантовой критичности дает экзотический класс универсальности, не имеющий аналога в известных критических явлениях. Более того, мы обнаруживаем нетрадиционную низкоразмерную квантовую критичность, где сверхтекучие корреляции аномально усиливаются из-за немонотонных потоков ренормализационной группы в квантовой критической фазе с нарушением PT-симметрии, что резко контрастирует с парадигмой Березинского-Костерлица-Таулесса. Наши выводы могут быть экспериментально проверены в ультрахолодных атомах и предсказывать критические явления за пределами эрмитовой парадигмы квантовой физики многих тел.
Введение
Исследования фазовых переходов и критического поведения в неэрмитовых системах восходят к открытию краевой сингулярности Ли-Янга 1 , где было показано, что мнимое магнитное поле в высокотемпературной модели Изинга вызывает экзотическую фаза перехода. Совсем недавно спектральный фазовый переход из реального в комплексный был обнаружен в широком классе неэрмитовых гамильтонианов, которые удовлетворяют симметрии времени четности (PT) 2 . Хотя когда-то считалось, что такие системы представляют чисто академический интерес, связанные с ними вопросы теперь находятся в пределах экспериментальной досягаемости 3,4,5,6,7 .
Совсем недавно спектральный фазовый переход из реального в комплексный был обнаружен в широком классе неэрмитовых гамильтонианов, которые удовлетворяют симметрии времени четности (PT) 2 . Хотя когда-то считалось, что такие системы представляют чисто академический интерес, связанные с ними вопросы теперь находятся в пределах экспериментальной досягаемости 3,4,5,6,7 .
Гамильтониан называется PT-симметричным, если он коммутирует с комбинированным оператором , но не обязательно с и по отдельности. Здесь и – операторы четности и обращения времени соответственно. Говорят, что PT-симметрия не нарушена, если каждое собственное состояние PT-симметрично; тогда весь спектр реален, хотя и не является эрмитовым. Говорят, что симметрия PT спонтанно нарушена, если некоторые собственные состояния не являются собственными состояниями оператора PT, хотя ; тогда некоторые пары собственных значений становятся комплексно-сопряженными друг другу. Нарушение PT-симметрии обычно сопровождается слиянием собственных состояний и соответствующих собственных значений в исключительной точке 8 в дискретном спектре или спектральная особенность 9 в непрерывном спектре. В то время как эти особенности также справедливы для определенного класса антилинейных симметрий 10 , симметрия PT позволяет экспериментально реализовывать пространственную инженерию структур усиления-потери, что приводит к богатому взаимодействию между теорией и экспериментом в оптике 4,5,6,7, 11 , сверхпроводники 12 , атомная физика 13 и оптомеханика 14 . В частности, в экспериментах с классическими системами 15 . Однако во всех этих разработках многочастичные корреляции по-прежнему не играют никакой роли.
В то время как эти особенности также справедливы для определенного класса антилинейных симметрий 10 , симметрия PT позволяет экспериментально реализовывать пространственную инженерию структур усиления-потери, что приводит к богатому взаимодействию между теорией и экспериментом в оптике 4,5,6,7, 11 , сверхпроводники 12 , атомная физика 13 и оптомеханика 14 . В частности, в экспериментах с классическими системами 15 . Однако во всех этих разработках многочастичные корреляции по-прежнему не играют никакой роли.
Квантовые критические явления, напротив, возникают в результате коллективного поведения сильно коррелированных систем и демонстрируют универсальные свойства дальнего действия. Ввиду недавних разработок в области проектирования открытых систем многих тел в ультрахолодных атомах 16,17,18,19,20 и экситон-поляритонных конденсатах 21 , кажется, созрело исследовать роль PT-симметрии в квантовых критических явлениях и спросите, нужно ли расширять понятие универсальности в синтетических неконсервативных системах.
Здесь мы сообщаем, что комбинация спектральной сингулярности и квантовой критичности дает экзотическую критическую точку в расширенном пространстве параметров и что в фазе с нарушением PT локальная структура усиления-потери приводит к аномальному усилению сверхтекучей корреляции из-за полукруговые потоки ренормализационной группы (РГ). Это резко контрастирует с подавлением сверхтекучей корреляции из-за гиперболических ренормгрупповых течений в парадигме Березинского-Костерлица-Таулесса (БКТ). Наши результаты показывают, что взаимодействие между корреляциями многих тел и PT-симметрией приводит к возникновению квантовых критических явлений за пределами эрмитовой парадигмы квантовой физики многих тел.
Результаты
Симметричная по четности модель синуса-Гордона
Мы рассматриваем класс одномерных (1D) квантовых систем, описываемых гамильтонианом теории поля
где – скалярное поле, – его сопряженный импульс, удовлетворяющий , и является потенциалом для поля. Без потенциального члена уравнение (1) известно как гамильтониан жидкости Томонага-Латтинджера (TLL), который дает универсальную основу для описания одномерных взаимодействующих бозонов и фермионов 22 . Здесь v — скорость звука, параметр TLL K характеризует силу взаимодействия, а и связаны с плотностью и джозефсоновской фазой соответственно. Введение потенциала косинуса приводит к модели синуса-Гордона, описывающей переход БКТ в фазу с щелью. Для бозонов на решетке это соответствует переходу 23 из сверхтекучей среды в моттовский изолятор (МИ). Здесь мы рассматриваем обобщение на PT-симметричный случай, добавляя мнимый вклад в потенциальный член следующим образом:
Без потенциального члена уравнение (1) известно как гамильтониан жидкости Томонага-Латтинджера (TLL), который дает универсальную основу для описания одномерных взаимодействующих бозонов и фермионов 22 . Здесь v — скорость звука, параметр TLL K характеризует силу взаимодействия, а и связаны с плотностью и джозефсоновской фазой соответственно. Введение потенциала косинуса приводит к модели синуса-Гордона, описывающей переход БКТ в фазу с щелью. Для бозонов на решетке это соответствует переходу 23 из сверхтекучей среды в моттовский изолятор (МИ). Здесь мы рассматриваем обобщение на PT-симметричный случай, добавляя мнимый вклад в потенциальный член следующим образом:
где α r и α i характеризуют силы действительной и мнимой частей потенциала. Когда действительная часть становится значимой, она подавляет флуктуации , стабилизируя некритическую фазу с промежутками. Напротив, если мнимая часть актуальна, она способствует флуктуациям и усиливает корреляцию в сопряженном поле, как мы увидим позже. Теория поля (1) с потенциалом (2) удовлетворяет PT-симметрии, так как поле имеет нечетную четность. PT-симметричный гамильтониан может быть реализован с помощью непрерывно контролируемого одномерного взаимодействия ультрахолодных атомов (см. Дополнительное примечание 1 и Дополнительный рисунок 1).
Теория поля (1) с потенциалом (2) удовлетворяет PT-симметрии, так как поле имеет нечетную четность. PT-симметричный гамильтониан может быть реализован с помощью непрерывно контролируемого одномерного взаимодействия ультрахолодных атомов (см. Дополнительное примечание 1 и Дополнительный рисунок 1).
Заметим, что если α r > α i , имеет реальный спектр и, таким образом, PT-симметрия не нарушена. Это может быть доказано теоремой 24 , которая утверждает, что спектр действителен тогда и только тогда, когда существует оператор, удовлетворяющий , где — эрмитов оператор. Действительно, мы можем явно построить такой оператор для α r > α i выбором , где – постоянная часть и η ≡ arctanh( α i / α r ). Затем потенциальный член в теории эффективного поля преобразуется и сводится к гамильтониану синус-Гордона 25 . Расхождение η при α r = α i свидетельствует о спонтанном нарушении PT-симметрии.
Ренормгрупповой анализ
Чтобы раскрыть универсальное критическое поведение PT-симметричного гамильтониана, мы проведем РГ-анализ 26 , чтобы получить следующую систему уравнений течения, справедливых до третьего порядка по g r,i :
α r,i a 2 /( ħv ) — безразмерные константы связи, где a — отсечка на коротких расстояниях. Скорость v остается постоянной для всех порядков в g r,i из-за лоренц-инвариантности теории. В отличие от двумерной фазовой диаграммы традиционной модели синуса-Гордона, PT-симметричная система имеет трехмерную (3D) фазовую диаграмму (рис. 1а). Когда PT-симметрия не нарушена, то есть g i < g r , спектр эквивалентен спектру закрытой системы, как обсуждалось выше, и воспроизводится обычная блок-схема РГ с гиперболическими потоками (рис. 1б). Здесь граница БКТ между сверхтекучей фазой TLL и фазой MI проходит по искривленной поверхности.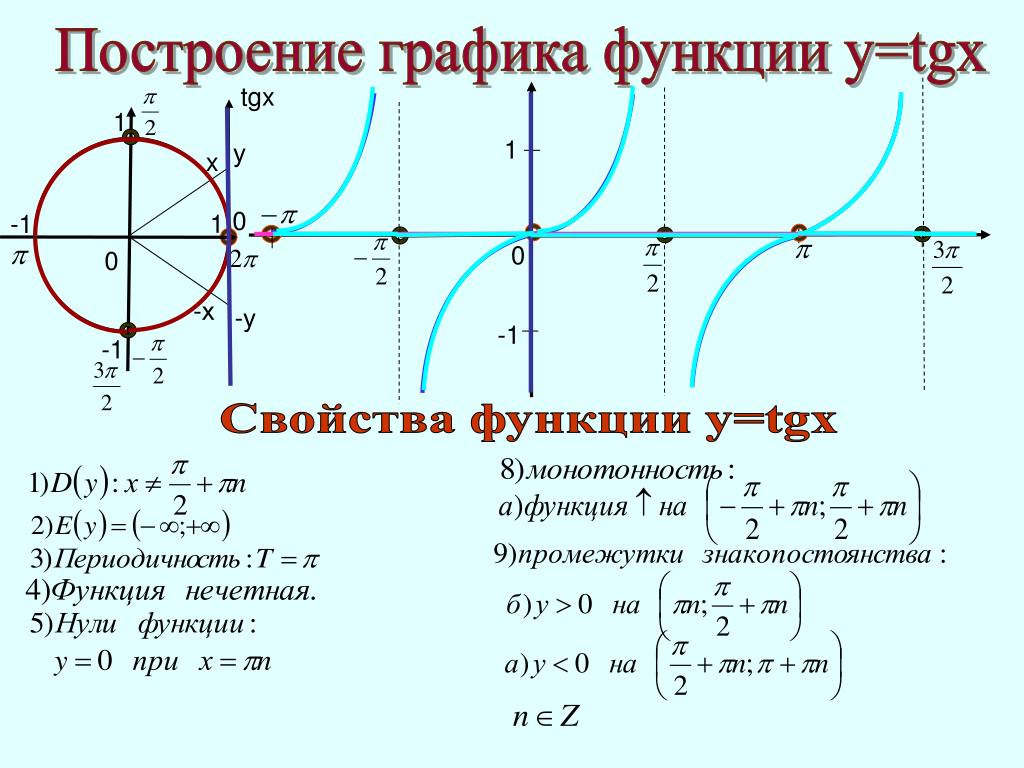 Заметим, что оператор не влияет на критические свойства основного состояния, поскольку он модифицирует только нулевые моды, связанные с полем. Поскольку неэрмитов член может возникать из-за обратного действия измерения, квантовый фазовый переход, вызванный увеличением g i можно рассматривать как индуцированные измерением.
Заметим, что оператор не влияет на критические свойства основного состояния, поскольку он модифицирует только нулевые моды, связанные с полем. Поскольку неэрмитов член может возникать из-за обратного действия измерения, квантовый фазовый переход, вызванный увеличением g i можно рассматривать как индуцированные измерением.
( a ) Трехмерная фазовая диаграмма PT-симметричной системы многих тел в пространстве параметров ( K , g r , g i ). Здесь K и g r ( g i ) характеризуют силу межчастичного взаимодействия и глубину действительной (мнимой) части комплексного потенциала соответственно. Фазы MI и TLL разделены поверхностью перехода БКТ в течение K >2 и PT-перехода для K <2. Пример перехода БКТ (ПТ) показан синей (красной) кривой с точкой перехода, обозначенной закрашенным (открытым) кружком. Фаза MI (TLL) соответствует трехмерной области, содержащей заштрихованную синим (красным) плоскость при g i =0. На критической линии с K =2 лежит SSCP (черный пустой кружок). Штриховыми линиями обозначены фазовые границы на плоскости с фиксированным г r для сравнения с численными результатами на рис. 2а. ( b ) Гиперболические потоки RG в PT-непрерывной области ( g i < g r ), которые воспроизводят обычную блок-схему в модели синуса-Гордона. ( c ) RG течет на двух фазовых границах, разделенных нетрадиционной фиксированной линией (толстая черная линия). ( d ) Нетрадиционные полукруглые РГ-потоки в области PT-нарушения ( g i > g р ). Вдоль каждого течения параметр TLL K монотонно возрастает, что свидетельствует об аномальном усилении сверхтекучей корреляции.
Фаза MI (TLL) соответствует трехмерной области, содержащей заштрихованную синим (красным) плоскость при g i =0. На критической линии с K =2 лежит SSCP (черный пустой кружок). Штриховыми линиями обозначены фазовые границы на плоскости с фиксированным г r для сравнения с численными результатами на рис. 2а. ( b ) Гиперболические потоки RG в PT-непрерывной области ( g i < g r ), которые воспроизводят обычную блок-схему в модели синуса-Гордона. ( c ) RG течет на двух фазовых границах, разделенных нетрадиционной фиксированной линией (толстая черная линия). ( d ) Нетрадиционные полукруглые РГ-потоки в области PT-нарушения ( g i > g р ). Вдоль каждого течения параметр TLL K монотонно возрастает, что свидетельствует об аномальном усилении сверхтекучей корреляции.
Увеличить
В сильнокоррелированном режиме K < 2 на пороговой плоскости ФП появляется новый тип квантового фазового перехода g i = g r .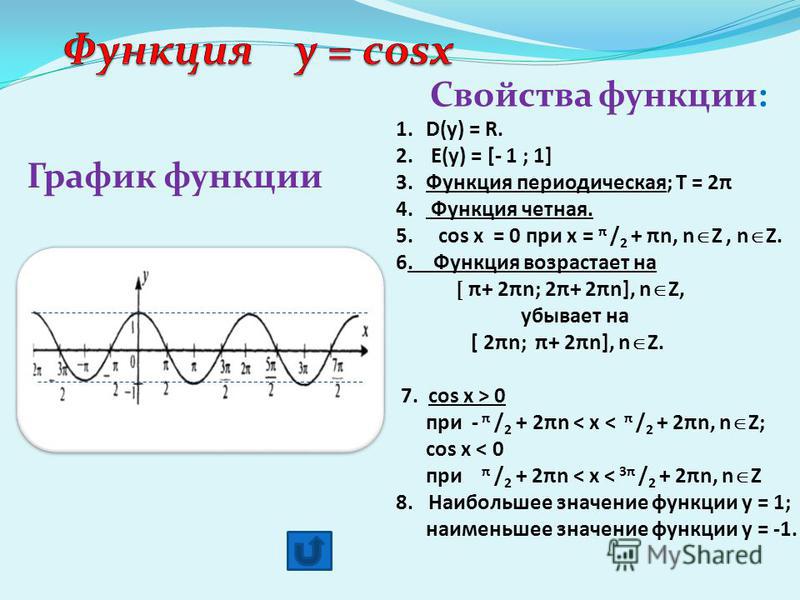 Этот фазовый переход сопровождается спонтанным нарушением симметрии PT в собственных состояниях, в отличие от обычного перехода BKT, не проявляющего нарушения симметрии. Границы фаз БКТ и ПТ сливаются на линии, определяемой K =2 и г i = г r (рис. 1в). В общем, в точке нарушения PT-симметрии спектральная сингулярность 9 возникает там, где два или более собственных значения, а также их собственные состояния сливаются в непрерывном спектре. В оптике спектральная сингулярность приводит к однонаправленным волновым явлениям 5 . Напротив, в системах многих тел сосуществование спектральной сингулярности и квантовой критичности при g i = g r и K =2 приводит к тому, что мы называем спектральной сингулярной критической точкой, которая представляет уникальный класс универсальности в неконсервативных системах.
Этот фазовый переход сопровождается спонтанным нарушением симметрии PT в собственных состояниях, в отличие от обычного перехода BKT, не проявляющего нарушения симметрии. Границы фаз БКТ и ПТ сливаются на линии, определяемой K =2 и г i = г r (рис. 1в). В общем, в точке нарушения PT-симметрии спектральная сингулярность 9 возникает там, где два или более собственных значения, а также их собственные состояния сливаются в непрерывном спектре. В оптике спектральная сингулярность приводит к однонаправленным волновым явлениям 5 . Напротив, в системах многих тел сосуществование спектральной сингулярности и квантовой критичности при g i = g r и K =2 приводит к тому, что мы называем спектральной сингулярной критической точкой, которая представляет уникальный класс универсальности в неконсервативных системах.
При нарушении РТ-симметрии, т.е. K вначале увеличиваются, а после входа в сторону K >2 поток закручивается и сходится к фиксированной линии с г r,i =0 (рис.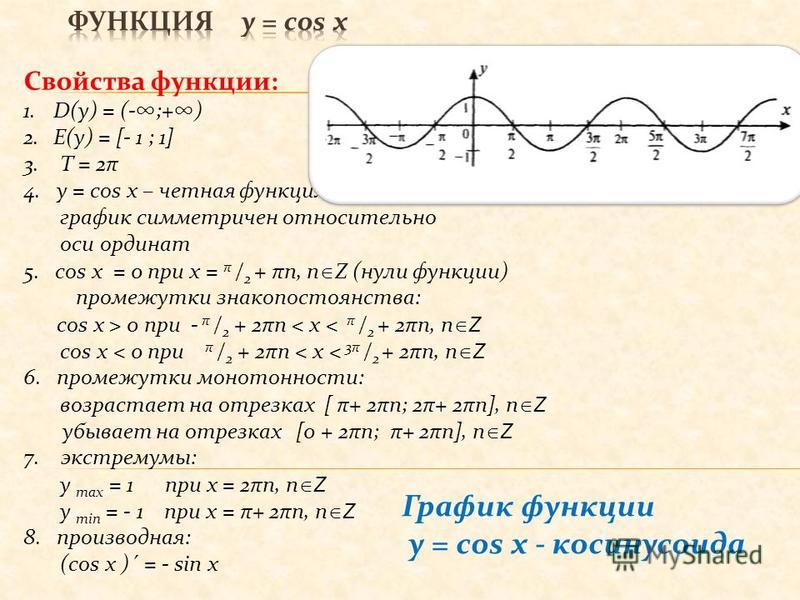 1г). Физически это значительное увеличение параметра TLL K указывает на более медленное затухание сверхтекучей корреляции и, таким образом, усиление неэрмитовости мнимого потенциала. Усиление рассматривается как аномальное, потому что в традиционной парадигме БКТ реальный потенциал подавляет флуктуацию и стабилизирует фазу МИ с промежутком для K <2. Кроме того, благодаря полукруговым течениям РГ мнимый потенциал позволяет существенно увеличить параметр ТЛЛ K даже если его прочность г i изначально очень мала. Фаза с нарушением PT демонстрирует другие наблюдаемые последствия, такие как аномальная генерация и поглощение, наблюдаемые в оптике 27 (см. Дополнительное примечание 2 для экспериментальной реализации в ультрахолодных атомах).
1г). Физически это значительное увеличение параметра TLL K указывает на более медленное затухание сверхтекучей корреляции и, таким образом, усиление неэрмитовости мнимого потенциала. Усиление рассматривается как аномальное, потому что в традиционной парадигме БКТ реальный потенциал подавляет флуктуацию и стабилизирует фазу МИ с промежутком для K <2. Кроме того, благодаря полукруговым течениям РГ мнимый потенциал позволяет существенно увеличить параметр ТЛЛ K даже если его прочность г i изначально очень мала. Фаза с нарушением PT демонстрирует другие наблюдаемые последствия, такие как аномальная генерация и поглощение, наблюдаемые в оптике 27 (см. Дополнительное примечание 2 для экспериментальной реализации в ультрахолодных атомах).
Фазовая диаграмма основного состояния модели решетки
Чтобы численно продемонстрировать эти результаты, мы вводим решеточный гамильтониан
, низкоэнергетическое поведение которого описывается PT-симметричной эффективной теорией поля . Вот операторы спина 1/2 на сайте m , а параметры (−Δ, h s , γ ) связаны с установить Дж =1. Неэрмитов член представляет собой периодическую структуру усиления-потери и эффективно усиливает амплитуду прыжкового члена, что приводит к усилению сверхтекучей корреляции. Определенная фазовая диаграмма и типичный точный спектр конечных размеров показаны на рис. 2. Переход БКТ идентифицируется как точка пересечения соответствующих энергетических уровней 28 , а порог PT определяется как точка слияния на низкоэнергетических уровнях, как подробно описано в разделе «Методы» и «Дополнительные методы». Точка слияния оказывается исключительной точкой из характерного масштабирования квадратного корня 8 энергетической щели (см. вставку на рис. 2b). Отметим, что выше порога ФП некоторые высоковозбужденные состояния оказываются имеющими положительные мнимые части собственных значений и вызывают неустойчивость в долговременном пределе.
Вот операторы спина 1/2 на сайте m , а параметры (−Δ, h s , γ ) связаны с установить Дж =1. Неэрмитов член представляет собой периодическую структуру усиления-потери и эффективно усиливает амплитуду прыжкового члена, что приводит к усилению сверхтекучей корреляции. Определенная фазовая диаграмма и типичный точный спектр конечных размеров показаны на рис. 2. Переход БКТ идентифицируется как точка пересечения соответствующих энергетических уровней 28 , а порог PT определяется как точка слияния на низкоэнергетических уровнях, как подробно описано в разделе «Методы» и «Дополнительные методы». Точка слияния оказывается исключительной точкой из характерного масштабирования квадратного корня 8 энергетической щели (см. вставку на рис. 2b). Отметим, что выше порога ФП некоторые высоковозбужденные состояния оказываются имеющими положительные мнимые части собственных значений и вызывают неустойчивость в долговременном пределе. Наличие таких высокоэнергетических неустойчивых мод напоминает параметрические неустойчивости в экситон-поляритонных системах 29 и может в конечном итоге разрушить одномерную когерентность 30 . В нашей установке, где мнимый член адиабатически увеличивается, амплитуды этих неустойчивых мод могут быть значительно подавлены, и система может оставаться с почти единичной точностью в основном состоянии, в котором поддерживается критическое поведение (см. Дополнительный Примечание 3 и дополнительные рисунки 2 и 3 для подробностей).
Наличие таких высокоэнергетических неустойчивых мод напоминает параметрические неустойчивости в экситон-поляритонных системах 29 и может в конечном итоге разрушить одномерную когерентность 30 . В нашей установке, где мнимый член адиабатически увеличивается, амплитуды этих неустойчивых мод могут быть значительно подавлены, и система может оставаться с почти единичной точностью в основном состоянии, в котором поддерживается критическое поведение (см. Дополнительный Примечание 3 и дополнительные рисунки 2 и 3 для подробностей).
( a ) Фазовая диаграмма основного состояния PT-симметричного решеточного гамильтониана многих тел. Фазы MI и TLL разделены переходом BKT (синяя кривая с закрашенными кружками) и нарушением PT-симметрии (красная линия с закрашенными треугольниками). Точка, в которой сливаются две границы, определяет SSCP (открытый кружок). ( b ) Типичный спектр низкоэнергетических возбуждений в решеточной модели. Три нижних уровня в секторе S z =0 (красная, зеленая и желтая кривые от самого нижнего), а самая низкая энергия возбуждения в секторе S z =±4 (синие кривая). Вот полная намагниченность. Разность энергий δE между двумя сливающимися уровнями (например, красным и зеленым) подчиняется скейлингу квадратного корня (вставка) и замыкается в точке нарушения PT-симметрии. Точка перехода БКТ соответствует пересечению соответствующих уровней (красного и синего). Устанавливаем параметр ч с = 0,1 для обоих ( a , b ). В ( a ) данные на графике получены путем экстраполяции до термодинамического предела, а данные в b получены для N = 16 и — Δ = 0,735. Нанесенные на график переменные безразмерны, так как мы установили J =1.
Три нижних уровня в секторе S z =0 (красная, зеленая и желтая кривые от самого нижнего), а самая низкая энергия возбуждения в секторе S z =±4 (синие кривая). Вот полная намагниченность. Разность энергий δE между двумя сливающимися уровнями (например, красным и зеленым) подчиняется скейлингу квадратного корня (вставка) и замыкается в точке нарушения PT-симметрии. Точка перехода БКТ соответствует пересечению соответствующих уровней (красного и синего). Устанавливаем параметр ч с = 0,1 для обоих ( a , b ). В ( a ) данные на графике получены путем экстраполяции до термодинамического предела, а данные в b получены для N = 16 и — Δ = 0,735. Нанесенные на график переменные безразмерны, так как мы установили J =1.
Изображение в натуральную величину
Численная демонстрация усиленной сверхтекучей корреляции
Чтобы продемонстрировать аномальное усиление сверхтекучей корреляции в режиме PT-нарушения, мы провели численное моделирование с использованием алгоритма децимации блоков с бесконечным временем эволюции (iTEBD) 31 . Корреляционная функция демонстрирует критический спад с изменением критического индекса, и соответствующий параметр TLL значительно увеличивается, превышая K =2, как показано на рис. 3. Физически это усиление сверхтекучей корреляции на больших расстояниях можно интерпретировать следующим образом. Локальная структура усиления-потери, введенная мнимым членом, вызывает локально уравновешенные потоки 15 в основном состоянии. Это приводит к усилению флуктуаций плотности или, что то же самое, к подавлению флуктуаций сопряженной фазы. Именно этот эффект увеличивает сверхтекучую корреляцию. Численные результаты согласуются с аналитическими аргументами, приведенными выше, и демонстрируют, что РГ-анализ играет важную роль в изучении критических свойств неэрмитовой системы многих тел.
Корреляционная функция демонстрирует критический спад с изменением критического индекса, и соответствующий параметр TLL значительно увеличивается, превышая K =2, как показано на рис. 3. Физически это усиление сверхтекучей корреляции на больших расстояниях можно интерпретировать следующим образом. Локальная структура усиления-потери, введенная мнимым членом, вызывает локально уравновешенные потоки 15 в основном состоянии. Это приводит к усилению флуктуаций плотности или, что то же самое, к подавлению флуктуаций сопряженной фазы. Именно этот эффект увеличивает сверхтекучую корреляцию. Численные результаты согласуются с аналитическими аргументами, приведенными выше, и демонстрируют, что РГ-анализ играет важную роль в изучении критических свойств неэрмитовой системы многих тел.
( a ) Критическое затухание корреляционной функции. ( b ) Параметр TLL K как функция расстояния r , дающий критический показатель корреляционной функции, . Показатель степени извлекается путем линейной подгонки корреляционной функции на логарифмическом графике вокруг расстояния r . Параметры установлены равными — Δ = 0,61, h s = 0,1 и γ = 0,08, а χ обозначает размерность состояния матричного произведения, которая контролирует точность моделирования iTEBD.
( b ) Параметр TLL K как функция расстояния r , дающий критический показатель корреляционной функции, . Показатель степени извлекается путем линейной подгонки корреляционной функции на логарифмическом графике вокруг расстояния r . Параметры установлены равными — Δ = 0,61, h s = 0,1 и γ = 0,08, а χ обозначает размерность состояния матричного произведения, которая контролирует точность моделирования iTEBD.
Изображение полного размера
Экспериментальная реализация в одномерном бозе-газе
Рассмотренный выше PT-симметричный многочастичный гамильтониан может быть реализован в одномерном взаимодействующем ультрахолодном бозонном атоме с мелкой PT-симметричной оптической решеткой V ( x ) = V R COS (2 πx / D ) — IV I SIN (2 πx / D 4, где πx / D 4, № . ), V ). V i — глубины действительной и мнимой частей комплексного потенциала, d — постоянная решетки. Воображаемый оптический потенциал можно реализовать, используя слабый почти резонансный свет стоячей волны (раздел «Методы»). Поскольку V ( x ) остается инвариантным при одновременной операции четности ( x → − x ) и обращения времени (т.е. комплексного сопряжения) система удовлетворяет условию PT-симметрии (рис. 4а). В открытых квантовых системах путем постселекции нулевых результатов измерения временная эволюция управляется эффективным неэрмитовым гамильтонианом 32,33,34 . Достигнутая экспериментальная точность уже достаточно высока, чтобы позволить экспериментаторам реализовать различные типы постселекции 35,36,37 . Затем низкоэнергетическое поведение этой системы описывается PT-симметричной эффективной теорией поля. Отметим, что решеточный гамильтониан (4) может быть реализован и в ультрахолодных атомах путем наложения глубокой решетки, не влияющей на универсальное критическое поведение (рис.
V i — глубины действительной и мнимой частей комплексного потенциала, d — постоянная решетки. Воображаемый оптический потенциал можно реализовать, используя слабый почти резонансный свет стоячей волны (раздел «Методы»). Поскольку V ( x ) остается инвариантным при одновременной операции четности ( x → − x ) и обращения времени (т.е. комплексного сопряжения) система удовлетворяет условию PT-симметрии (рис. 4а). В открытых квантовых системах путем постселекции нулевых результатов измерения временная эволюция управляется эффективным неэрмитовым гамильтонианом 32,33,34 . Достигнутая экспериментальная точность уже достаточно высока, чтобы позволить экспериментаторам реализовать различные типы постселекции 35,36,37 . Затем низкоэнергетическое поведение этой системы описывается PT-симметричной эффективной теорией поля. Отметим, что решеточный гамильтониан (4) может быть реализован и в ультрахолодных атомах путем наложения глубокой решетки, не влияющей на универсальное критическое поведение (рис.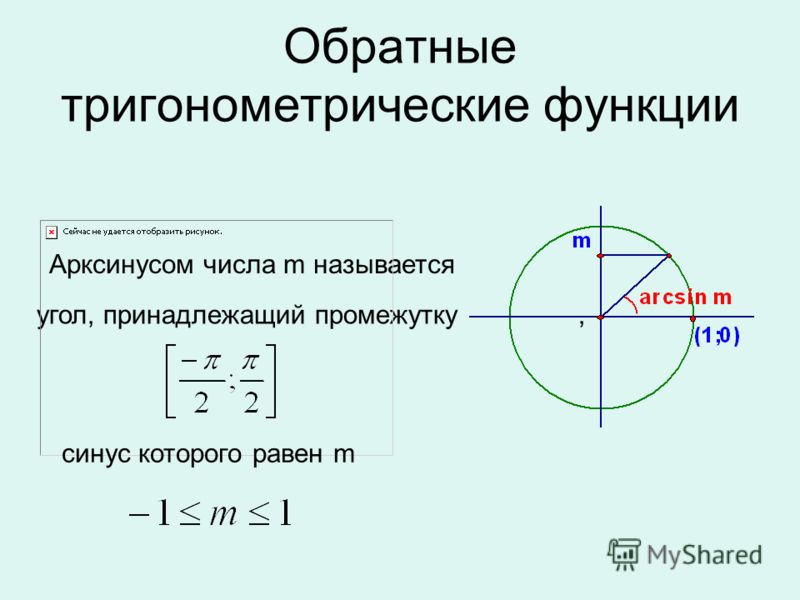 4б).
4б).
( a ) 1D ультрахолодные атомы в PT-симметричной оптической решетке. Действительная (синяя кривая) и мнимая (красная кривая) части сложного потенциала создаются парой далеко расстроенных и слабых почти резонансных стоячих волн. Воображаемый потенциал возникает из-за почти резонансного света (красная стрелка) на атомах, возбужденное состояние которых имеет быстрые моды распада. Два периодических потенциала смещены друг от друга на половину шага решетки, так что система обладает PT-симметрией. ( b ) Преобразование в PT-симметричную модель решетки, которая воспроизводит то же самое критическое поведение, что и континуальная модель. Атомы сильно локализованы глубокой оптической решеткой, которая не влияет на универсальное критическое поведение. Действительная и мнимая части комплексного потенциала вводят внутренние потенциалы ± ч с и мнимые прыжковые члены ± iγ .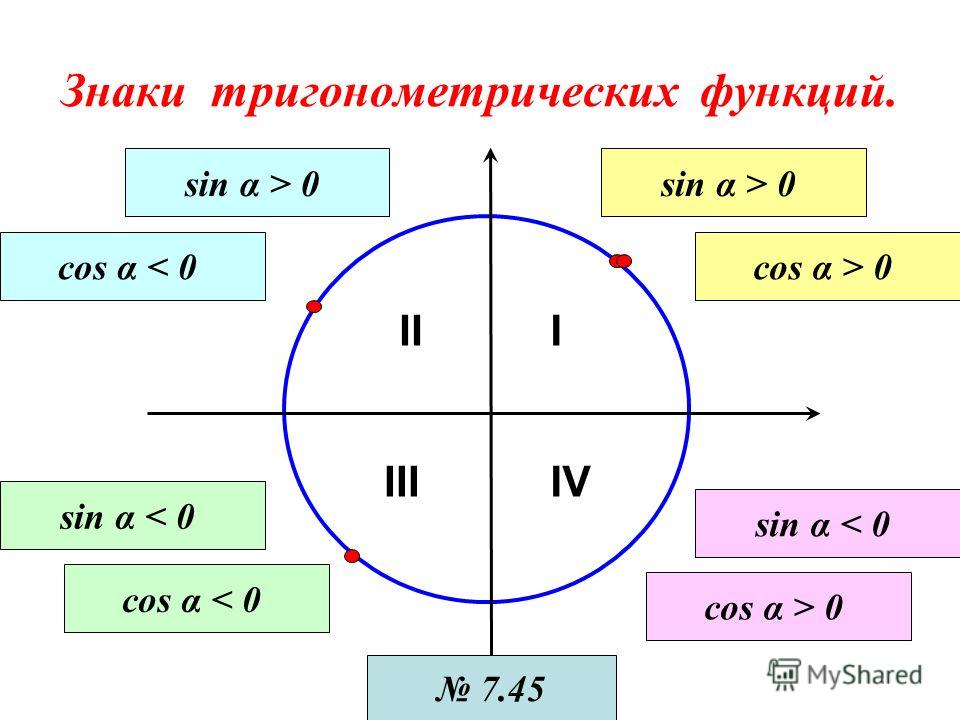 Узел решетки, занятый (не занятый) жестким бозоном, представлен спином вверх (вниз).
Узел решетки, занятый (не занятый) жестким бозоном, представлен спином вверх (вниз).
Изображение полного размера
Подчеркнем, что рассматриваемая здесь динамика отличается от динамики, описываемой основным уравнением, где диссипативные процессы, как правило, стремятся разрушить корреляции, лежащие в основе квантовых критических явлений. Напротив, постселекция позволяет нам изучать систему, свободную от диссипативных скачкообразных процессов, в то время как нетривиальные эффекты из-за обратного воздействия измерения все еще проявляются через неэрмитовы вклады в эффективный гамильтониан.
Обсуждение
Сообщаемые фиксированные точки в расширенном пространстве параметров предполагают, что взаимодействие между спектральной сингулярностью и квантовой критичностью приводит к экзотическому классу универсальности за пределами традиционной парадигмы. Остается открытым вопрос, как универсальность, сопровождающая спектральную сингулярность, обнаруженную в этой работе, связана с неунитарными конформными теориями поля (КТП), изучаемыми в различных областях, от статистической механики 38 до физики высоких энергий 39 . Особо следует отметить, что некоторая критическая точка интегрируемой спиновой цепочки с PT-симметричными граничными полями соответствует исключительной точке и считается описываемой неунитарной КТП 40 . Это предполагает тесную связь между спектральной сингулярной критической точкой и неунитарной КТП. Учитывая недавний успех в измерении энтропии запутанности в ультрахолодных атомах 37 , представляет интерес изучить, как ведет себя квантовая запутанность в присутствии спектральной сингулярности. Мы показали, что в фазе нарушения PT основное состояние демонстрирует повышенную сверхтекучесть корреляции, указывающую на более тесную связь топологических возбуждений, что резко контрастирует с их пролиферацией, обнаруженной в парадигме BKT. В эрмитовых системах соответствующее возмущение вокруг фиксированных точек РГ имеет тенденцию подавлять флуктуации рассматриваемого поля и стабилизировать некритическую фазу с промежутками. Наше открытие показывает, что соответствующее мнимое возмущение может реализовать противоположную ситуацию усиления флуктуаций рассматриваемого поля и облегчения корреляции в сопряженном поле.
Особо следует отметить, что некоторая критическая точка интегрируемой спиновой цепочки с PT-симметричными граничными полями соответствует исключительной точке и считается описываемой неунитарной КТП 40 . Это предполагает тесную связь между спектральной сингулярной критической точкой и неунитарной КТП. Учитывая недавний успех в измерении энтропии запутанности в ультрахолодных атомах 37 , представляет интерес изучить, как ведет себя квантовая запутанность в присутствии спектральной сингулярности. Мы показали, что в фазе нарушения PT основное состояние демонстрирует повышенную сверхтекучесть корреляции, указывающую на более тесную связь топологических возбуждений, что резко контрастирует с их пролиферацией, обнаруженной в парадигме BKT. В эрмитовых системах соответствующее возмущение вокруг фиксированных точек РГ имеет тенденцию подавлять флуктуации рассматриваемого поля и стабилизировать некритическую фазу с промежутками. Наше открытие показывает, что соответствующее мнимое возмущение может реализовать противоположную ситуацию усиления флуктуаций рассматриваемого поля и облегчения корреляции в сопряженном поле. Исследование такой нетрадиционной квантовой критичности в других синтетических, неконсервативных системах многих тел представляет собой интересную задачу. Дальнейшие исследования в этих направлениях вместе с их возможными экспериментальными реализациями могли бы расширить приложения к будущим квантовым метаматериалам.
Исследование такой нетрадиционной квантовой критичности в других синтетических, неконсервативных системах многих тел представляет собой интересную задачу. Дальнейшие исследования в этих направлениях вместе с их возможными экспериментальными реализациями могли бы расширить приложения к будущим квантовым метаматериалам.
Методы
Детали численных расчетов
Фазовая диаграмма на рис. 2а получена из точного диагонализационного анализа решеточного гамильтониана (4). Чтобы идентифицировать точку перехода БКТ, мы вычисляем точный спектр конечного размера и находим пересечение низкоэнергетических уровней, имеющих соответствующие квантовые числа 28 . Точка перехода PT определяется как первая точка слияния в низкоэнергетическом спектре с увеличением γ . Расчеты выполняются для различных размеров системы, а окончательные результаты получают путем экстраполяции данных до термодинамического предела. Дополнительные подробности приведены в дополнительных методах и дополнительном рисунке 4. Корреляционная функция и связанное с ней изменение параметра 9 TLL.0113 K , показанные на рис. 3, рассчитываются с применением алгоритма iTEBD 31 . Подчеркнем, что этот метод может быть применен для изучения свойств основного состояния неэрмитовой системы. Метод может точно рассчитать эволюцию мнимого времени для бесконечного размера системы, где τ — мнимое время, начальное состояние и обозначает норму состояния. В пределе больших τ мы получаем квантовое состояние, действительная часть которого имеет наименьшее собственное значение во всем спектре, т. е. эффективное основное состояние неэрмитовой системы. Заметим, что мнимая часть собственного значения не влияет на расчет, поскольку она только изменяет общую фазу волновой функции в эволюции мнимого времени. Затем определяем параметр TLL K из рассчитанной корреляционной функции по соотношению .
Корреляционная функция и связанное с ней изменение параметра 9 TLL.0113 K , показанные на рис. 3, рассчитываются с применением алгоритма iTEBD 31 . Подчеркнем, что этот метод может быть применен для изучения свойств основного состояния неэрмитовой системы. Метод может точно рассчитать эволюцию мнимого времени для бесконечного размера системы, где τ — мнимое время, начальное состояние и обозначает норму состояния. В пределе больших τ мы получаем квантовое состояние, действительная часть которого имеет наименьшее собственное значение во всем спектре, т. е. эффективное основное состояние неэрмитовой системы. Заметим, что мнимая часть собственного значения не влияет на расчет, поскольку она только изменяет общую фазу волновой функции в эволюции мнимого времени. Затем определяем параметр TLL K из рассчитанной корреляционной функции по соотношению .
Вывод низкоэнергетической теории поля ультрахолодных атомов
Здесь мы объясняем вывод низкоэнергетической эффективной теории поля (1) ультрахолодных атомов. Начнем с гамильтониана, в котором к модели Либа–Линигера 41 добавляется периодический потенциал V r cos(2 πx / d ). Затем мы вводим воображаемый потенциал оптической решетки, используя слабый почти резонансный свет стоячей волны. Эта схема возможна, если возбужденное состояние атома имеет моды распада, отличные от начального основного состояния, и скорость его распада больше, чем скорость спонтанного распада от до и частота Раби 42,43,44 (рис. 4а). Такое условие может быть выполнено, например, с помощью соответствующих атомных уровней 45 или светоиндуцированных переходов 16 . Различие длин волн реального и мнимого периодических потенциалов, вызванное различной расстройкой лазеров, может быть пренебрежимо мало. Используя теорию возмущений второго порядка 8 для связи Раби и адиабатически исключая возбужденное состояние, мы получаем эффективное уравнение эволюции во времени для атомов в основном состоянии.
Начнем с гамильтониана, в котором к модели Либа–Линигера 41 добавляется периодический потенциал V r cos(2 πx / d ). Затем мы вводим воображаемый потенциал оптической решетки, используя слабый почти резонансный свет стоячей волны. Эта схема возможна, если возбужденное состояние атома имеет моды распада, отличные от начального основного состояния, и скорость его распада больше, чем скорость спонтанного распада от до и частота Раби 42,43,44 (рис. 4а). Такое условие может быть выполнено, например, с помощью соответствующих атомных уровней 45 или светоиндуцированных переходов 16 . Различие длин волн реального и мнимого периодических потенциалов, вызванное различной расстройкой лазеров, может быть пренебрежимо мало. Используя теорию возмущений второго порядка 8 для связи Раби и адиабатически исключая возбужденное состояние, мы получаем эффективное уравнение эволюции во времени для атомов в основном состоянии. Затем мы предполагаем, что нулевые результаты измерений выбираются после этого, так что динамика описывается неэрмитовым гамильтонианом 32,33,34 . В этой ситуации общая мнимая константа в спектре собственных значений не влияет на динамику, так как она может быть устранена при нормализации квантового состояния, что приводит к мнимому потенциалу ). Наконец, мы следуем стандартной процедуре 22 принятия низкоэнергетического предела модели и приходим к гамильтониану (1). Детали расчетов и экспериментальная доступность в ультрахолодных атомах описаны в дополнительных примечаниях 1 и 2.
Затем мы предполагаем, что нулевые результаты измерений выбираются после этого, так что динамика описывается неэрмитовым гамильтонианом 32,33,34 . В этой ситуации общая мнимая константа в спектре собственных значений не влияет на динамику, так как она может быть устранена при нормализации квантового состояния, что приводит к мнимому потенциалу ). Наконец, мы следуем стандартной процедуре 22 принятия низкоэнергетического предела модели и приходим к гамильтониану (1). Детали расчетов и экспериментальная доступность в ультрахолодных атомах описаны в дополнительных примечаниях 1 и 2.
Доступность данных
Данные, подтверждающие графики в этой статье и другие результаты этого исследования, можно получить у соответствующего автора по запросу.
Дополнительная информация
Как цитировать эту статью: Ashida, Y. et al . Четно-временно-симметричные квантовые критические явления. Нац. коммун. 8, 15791 doi: 10. 1038/ncomms15791 (2017).
1038/ncomms15791 (2017).
Примечание издателя : Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Литература
Фишер, М. Э. Янг-Ли краевая особенность и φ 3 теория поля. Физ. Преподобный Летт. 40 , 1610–1613 (1978).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Бендер, К.М. и Бётчер, С. Реальные спектры в неэрмитовых гамильтонианах, имеющих симметрию PT . Физ. Преподобный Летт. 80 , 5243–5246 (1998).
Артикул ОБЪЯВЛЕНИЯ MathSciNet КАС Google ученый
Rüter, C. E. et al. Наблюдение симметрии времени четности в оптике. Нац. физ. 6 , 192–195 (2010).

Артикул Google ученый
Регенсбургер, А. и др. Синтетические фотонные решетки с временем четности. Природа 488 , 167–171 (2012).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Фэн, Л. и др. Экспериментальная демонстрация однонаправленного безотражательного метаматериала с временем четности на оптических частотах. Нац. Матер. 12 , 108–113 (2013).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Пэн Б. и др. Симметричные по четности микрорезонаторы шепчущей галереи. Нац. физ. 10 , 394–398 (2014).
Артикул КАС Google ученый
Zhen, B. et al. Нерестовые кольца исключительных точек из конусов Дирака.
 Природа 525 , 354–358 (2015).
Природа 525 , 354–358 (2015).Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Като, Т. Теория возмущений для линейных операторов Springer (1966).
Мостафазаде А. Спектральные особенности комплексных потенциалов рассеяния и бесконечных коэффициентов отражения и прохождения при реальных энергиях. Физ. Преподобный Летт. 102 , 220402 (2009 г.).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Бендер, К.М., Берри, М.В. и Мандилара, А. Обобщенная симметрия PT и реальные спектры. J. Phys. А 35 , L467 (2002).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Макрис К.Г., Эль-Ганайни Р., Христодулидес Д.Н. и Муслимани З.Х. Динамика пучка в PT Решетки симметричные оптические.
 Физ. Преподобный Летт. 100 , 103904 (2009 г.).
Физ. Преподобный Летт. 100 , 103904 (2009 г.).Артикул ОБЪЯВЛЕНИЯ Google ученый
Щелкачев Н.М., Голубов А.А., Батурина Т.И., Винокур В.М. Стимулирование флуктуационной сверхпроводимости PT симметрией. Физ. Преподобный Летт. 109 , 150405 (2012).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Пэн, П. и др. Античетная временная симметрия с летающими атомами. Нац. физ. 12 , 1139–1145 (2016).
Артикул КАС Google ученый
Jing, J. et al. PT -симметричный фононный лазер. Физ. Преподобный Летт. 113 , 053604 (2014).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Бендер С.
 М., Бернтсон Б.К., Паркер Д. и Сэмюэл Э. Наблюдение фазового перехода РТ в простой механической системе. 901:13 утра. Дж. Физ. 81 , 173–179 (2013).
М., Бернтсон Б.К., Паркер Д. и Сэмюэл Э. Наблюдение фазового перехода РТ в простой механической системе. 901:13 утра. Дж. Физ. 81 , 173–179 (2013).Артикул ОБЪЯВЛЕНИЯ Google ученый
Bakr, W. S. et al. Квантовый газовый микроскоп для обнаружения одиночных атомов в оптической решетке режима Хаббарда. Природа 462 , 74–77 (2009).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Barontini, G. et al. Управление динамикой открытой квантовой системы многих тел с локализованной диссипацией. Физ. Преподобный Летт. 110 , 035302 (2013).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Brennecke, F. et al. Наблюдение в режиме реального времени за флуктуациями при фазовом переходе Дикке в управляемую диссипативную фазу.
 Проц. Натл акад. наук США 110 , 11763–11767 (2013).
Проц. Натл акад. наук США 110 , 11763–11767 (2013).Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Патил Ю.С., Чакрам С. и Венгалатторе М. Вызванная измерениями локализация ультрахолодного решеточного газа. Физ. Преподобный Летт. 115 , 140402 (2015).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Ашида Ю. и Уеда М. Дифракционно-неограниченное измерение положения ультрахолодных атомов в оптической решетке. Физ. Преподобный Летт. 115 , 095301 (2015).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Гао, Т. и др. Наблюдение неэрмитовых вырождений в хаотическом экситон-поляритонном бильярде. Природа 526 , 554–558 (2015).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Джамарчи, Т.
 Квантовая физика в одном измерении Издательство Оксфордского университета (2004).
Квантовая физика в одном измерении Издательство Оксфордского университета (2004).Фишер, М. П. А., Вейхман, П. Б., Гринштейн, Г. и Фишер, Д. С. Локализация бозона и переход сверхтекучесть-изолятор. Физ. Rev. B 40 , 546–570 (1989).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Мостафазаде, А. Псевдоэрмитовость против PT-симметрии: необходимое условие реальности спектра неэрмитова гамильтониана. Дж. Матем. физ. 43 , 205–214 (2002).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Бендер, К.М., Джонс, Х.Ф. и Риверс, Р.Дж. Двойные PT-симметричные квантовые теории поля. Физ. лат. B 625 , 333–340 (2005).
Артикул ОБЪЯВЛЕНИЯ MathSciNet КАС Google ученый
Амит, Д.
 Дж., Гольдшмидт, Ю. Ю. и Гринштейн, С. Ренормгрупповой анализ фазового перехода в двумерном кулоновском газе, теория Синус-Гордон и XY-модель. J. Phys. А 13 , 585 (1980).
Дж., Гольдшмидт, Ю. Ю. и Гринштейн, С. Ренормгрупповой анализ фазового перехода в двумерном кулоновском газе, теория Синус-Гордон и XY-модель. J. Phys. А 13 , 585 (1980).Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Пэн, Б. и др. Подавление и возрождение генерации за счет потерь. Наука 346 , 328–332 (2014).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Номура, К. Корреляционные функции двумерной модели синуса-Гордона. J. Phys. А 28 , 5451 (1995).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Сарчи, Д., Карузотто, И., Воутерс, М. и Савона, В. Когерентная динамика и параметрические нестабильности поляритонов микрорезонаторов в двухямных системах. Физ. Ред. B 77 , 125324 (2008 г.
 ).
).Артикул ОБЪЯВЛЕНИЯ Google ученый
Карузотто, И. и Чути, К. Спонтанная когерентность микрорезонатора-поляритона через параметрический порог: квантовые исследования методом Монте-Карло. Физ. Ред. B 72 , 125335 (2005 г.).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Видал Г. Классическое моделирование квантовых решетчатых систем бесконечного размера в одном пространственном измерении. Физ. Преподобный Летт. 98 , 070201 (2007).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Кармайкл, Х. Открытый системный подход к квантовой оптике Springer (1993).
Дейли, А. Дж. Квантовые траектории и открытые квантовые системы многих тел. Доп. Phys 63 , 77–149 (2014).

Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Ашида Ю., Фурукава С. и Уэда М. Квантовое критическое поведение под влиянием обратного воздействия измерения в сверххолодных газах. Физ. Ред. A 94 , 053615 (2016 г.).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Эндрес, М. и др. Наблюдение за коррелированными парами частиц и дырок и струнным порядком в низкоразмерных изоляторах Мотта. Наука 334 , 200–203 (2011).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Fukuhara, T. et al. Обнаружение волны спиновой запутанности в цепочке Боуза-Хаббарда с пространственным разрешением. Физ. Преподобный Летт. 115 , 035302 (2015).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Ислам, Р.
 и др. Измерение энтропии запутанности в квантовой системе многих тел. Природа 528 , 77–83 (2015).
и др. Измерение энтропии запутанности в квантовой системе многих тел. Природа 528 , 77–83 (2015).Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Карди, Дж. Л. Конформная инвариантность и особенность края Янга-Ли в двух измерениях. Физ. Преподобный Летт. 54 , 1354–1356 (1985).
Артикул ОБЪЯВЛЕНИЯ MathSciNet КАС Google ученый
Зайберг, Н. Заметки о квантовой теории Лиувилля и квантовой гравитации. Прогр. Теор. физ. доп. 102 , 319–349 (1990).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Паскье, В. и Салёр, Х. Общие структуры между конечными системами и конформными теориями поля через квантовые группы. Нукл. физ. B 330 , 521–556 (1990).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Либ, Э.
 Х. и Линигер, В. Точный анализ взаимодействующего бозе-газа. I. Общее решение и основное состояние. Физ. Ред. 130 , 1605–1616 (1963).
Х. и Линигер, В. Точный анализ взаимодействующего бозе-газа. I. Общее решение и основное состояние. Физ. Ред. 130 , 1605–1616 (1963).Артикул ОБЪЯВЛЕНИЯ MathSciNet Google ученый
Oberthaler, M.K. et al. Динамическая дифракция волн атомарной материи на кристаллах света. Физ. Ред. A 60 , 456–472 (1999).
Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Турлапов А., Тонюшкин А. и Слеатор Т. Оптическая маска для лазерно-охлаждаемых атомов. Физ. Ред. A 68 , 023408 (2003 г.).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Stützle, R. et al. Наблюдение нерасплывающихся волновых пакетов в мнимом потенциале. Физ. Преподобный Летт. 95 , 110405 (2005 г.).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Johnson, K.
 S. et al. Локализация пучков метастабильных атомов оптическими стоячими волнами: нанолитография в пределе Гейзенберга. Наука 280 , 1583–1586 (1998).
S. et al. Локализация пучков метастабильных атомов оптическими стоячими волнами: нанолитография в пределе Гейзенберга. Наука 280 , 1583–1586 (1998).Артикул ОБЪЯВЛЕНИЯ КАС Google ученый
Ссылки на скачивание
Благодарности
Мы признательны за поддержку KAKENHI Grant No. Материаловедение» (грант KAKENHI № JP15H05855) и сетевой программы Photon Frontier от MEXT Японии, программы ImPACT Совета по науке, технологиям и инновациям (Кабинет министров, правительство Японии). Мы благодарны Юсуке Хориноути, Рюсуке Хамадзаки, Цзунпин Гонгу, Синтаро Такаёси, Юя Накагава, Такеши Фукухара, Такаши Мори и Хошо Кацура за ценные обсуждения. Ю.А. признает поддержку со стороны JSPS (грант № JP16J03613).
Информация об авторе
Авторы и организации
Факультет физики, Токийский университет, 7-3-1 Хонго, Бункё-ку, 113-0033, Токио, Япония
Юто Ашида, Шунсуке Фурукава и Масахито Уэд
Центр Riken по науке о возникновении вещей (CEMS), Wako, 351-0198, Saitama, Japan
Masahito Ueda
Авторы
- Yuto Ashida
ПУБЛИКА в PubMed Google Академия
- Shunsuke Furukawa
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Masahito Ueda
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
Y. A., S.F. и М.У. планировал проект. Ю.А. выполнил аналитические расчеты. Ю.А. и С.Ф. провел численные расчеты. Ю.А., С.Ф. и М.У. проанализировал и интерпретировал результаты и написал рукопись.
A., S.F. и М.У. планировал проект. Ю.А. выполнил аналитические расчеты. Ю.А. и С.Ф. провел численные расчеты. Ю.А., С.Ф. и М.У. проанализировал и интерпретировал результаты и написал рукопись.
Автор, ответственный за переписку
Переписка с Юто Асида.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих финансовых интересов.
Дополнительная информация
Дополнительная информация
Дополнительные примечания, дополнительные цифры, дополнительные методы и дополнительные ссылки (PDF 366 KB)
Права и разрешения
Open Access Эта статья лицензирована по лицензии в соответствии с лицензией. , который разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате, при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения. сделанный. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/
сделанный. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Биортогональная квантовая критичность в неэрмитовых системах многих тел
- Гаойонг Сунь
- Цзя-Чэнь Тан
- Су-Пэн Коу
Границы физики (2022)
Точные края подвижности и топологический фазовый переход в двумерных неэрмитовых квазикристаллах
- Чжи-Хао Сюй
- Сюй Ся
- Шу Чен
Наука Китая Физика, механика и астрономия (2022)
Неразделимость в симметричных по четности микрорезонаторах: спектр мощности
- Кусик Мукерджи
- Пареш Чандра Джана
Оптический журнал (2022)
Невзаимные фазовые переходы
- Мишель Фрюшар
- Ре Ханай
- Винченцо Вителли
Природа (2021)
Исключительные динамические квантовые фазовые переходы в периодически управляемых системах
- Рюсукэ Хамадзаки
Nature Communications (2021)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Скачать PDF
Взаимодействие кинков синус-Гордон и бризеров с симметричным по четности дефектом
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: РезюмеРезюме (текст)АбстрактАбстракт (текст)PubMed
Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
. 2014 ноябрь; 90 (5-1): 052902.
doi: 10.1103/PhysRevE. 90.052902.
Epub 2014 3 ноября.
90.052902.
Epub 2014 3 ноября.
Даниал Саадатманд 1 , Сергей В Дмитриев 2 , Денис I Борисов 3 , Панайотис Г. Кеврекидис 4
Принадлежности
- 1 Факультет физики Мешхедского университета Фирдоуси, 91775-1436 Мешхед, Иран.
- 2 Институт проблем сверхпластичности металлов РАН, Халтурина 39, 450001 Уфа, Россия и Санкт-Петербургский государственный политехнический университет, Политехническая 29, 195251 Санкт-Петербург, Россия.
- 3 Институт математики ВЦ УНЦ РАН, ул.
 Чернышевского, 112, 450008 Уфа, Россия и Башкирский государственный педагогический университет, Октябрьская обр. 3а, 450000 Уфа, Россия.
Чернышевского, 112, 450008 Уфа, Россия и Башкирский государственный педагогический университет, Октябрьская обр. 3а, 450000 Уфа, Россия. - 4 Факультет математики и статистики Массачусетского университета, Амхерст, Массачусетс 01003, США.
- PMID: 25493853
- DOI: 10.1103/PhysRevE.90.052902
Даниал Саадатманд и др. Phys Rev E Stat Nonlin Soft Matter Phys. 2014 ноябрь
. 2014 ноябрь; 90 (5-1): 052902.
doi: 10.1103/PhysRevE.90.052902.
Epub 2014 3 ноября.
Авторы
Даниал Саадатманд 1 , Сергей В Дмитриев 2 , Денис I Борисов 3 , Панайотис Г. Кеврекидис 4
Принадлежности
- 1 Факультет физики Мешхедского университета Фирдоуси, 91775-1436 Мешхед, Иран.
- 2 Институт проблем сверхпластичности металлов РАН, Халтурина 39, 450001 Уфа, Россия и Санкт-Петербургский государственный политехнический университет, Политехническая 29, 195251 Санкт-Петербург, Россия.
- 3 Институт математики ВЦ УНЦ РАН, ул. Чернышевского, 112, 450008 Уфа, Россия и Башкирский государственный педагогический университет, Октябрьская обр.
 3а, 450000 Уфа, Россия.
3а, 450000 Уфа, Россия. - 4 Факультет математики и статистики Массачусетского университета, Амхерст, Массачусетс 01003, США.
- PMID: 25493853
- DOI: 10.1103/PhysRevE.90.052902
Абстрактный
Численно исследовано рассеяние кинков и низкочастотных бризеров нелинейного уравнения синус-Гордон (СГ) на пространственно локализованном четно-временно-симметричном возмущении (дефекте) со сбалансированным усилением и потерями. Показано, что если кинк проходит дефект, он всегда восстанавливает свой первоначальный импульс и энергию, а единственным эффектом взаимодействия с дефектом является фазовый сдвиг излома. Перегиб, приближающийся к дефекту со стороны усиления, всегда проходит, в противном случае он должен иметь достаточно большой начальный импульс, чтобы пройти через дефект, а не застрять в области потерь. Сдвиг фаз кинка и критическая скорость рассчитываются методом коллективных переменных. Кратко рассмотрены также столкновения кинк-кинк (кинк-антикинк) на дефекте, показывающие, как их попарное отталкивающее (соответственно притягивающее) взаимодействие может модифицировать исход столкновения одиночного излома в паре с дефектом. Для бризера результат его взаимодействия с дефектом сильно зависит от параметров бризера (скорости, частоты и начальной фазы) и от параметров дефекта. Бризер может получить часть энергии от дефекта и в результате потенциально даже распасться на пару кинк-антикинк, либо может потерять часть своей энергии. Интересно, что поступательная мода бризера очень слабо подвержена влиянию диссипативного возмущения, так что бризер легче проникает через дефект, когда он приходит со стороны потерь, чем излом.
Перегиб, приближающийся к дефекту со стороны усиления, всегда проходит, в противном случае он должен иметь достаточно большой начальный импульс, чтобы пройти через дефект, а не застрять в области потерь. Сдвиг фаз кинка и критическая скорость рассчитываются методом коллективных переменных. Кратко рассмотрены также столкновения кинк-кинк (кинк-антикинк) на дефекте, показывающие, как их попарное отталкивающее (соответственно притягивающее) взаимодействие может модифицировать исход столкновения одиночного излома в паре с дефектом. Для бризера результат его взаимодействия с дефектом сильно зависит от параметров бризера (скорости, частоты и начальной фазы) и от параметров дефекта. Бризер может получить часть энергии от дефекта и в результате потенциально даже распасться на пару кинк-антикинк, либо может потерять часть своей энергии. Интересно, что поступательная мода бризера очень слабо подвержена влиянию диссипативного возмущения, так что бризер легче проникает через дефект, когда он приходит со стороны потерь, чем излом. Во всех исследованных взаимодействиях солитонов с дефектами потери энергии на излучение протяженных волн малой амплитуды пренебрежимо малы.
Во всех исследованных взаимодействиях солитонов с дефектами потери энергии на излучение протяженных волн малой амплитуды пренебрежимо малы.
Похожие статьи
Взаимодействия бризер-бризер в системах синус-Гордон с использованием коллективного координатного подхода.
Нисида М., Фурукава Ю., Фуджи Т., Хатакенака Н. Нисида М. и др. Phys Rev E Stat Nonlin Soft Matter Phys. 2009 Сентябрь; 80 (3 Часть 2): 036603. doi: 10.1103/PhysRevE.80.036603. Epub 2009, 14 сентября. Phys Rev E Stat Nonlin Soft Matter Phys. 2009. PMID: 194
Взаимодействие кинкового солитона с бризером в цепи Ферми-Паста-Улама.
Хомерики Р. Хомерики Р. Phys Rev E Stat Nonlin Soft Matter Phys. 2002 г., февраль; 65 (2 часть 2): 026605.
 doi: 10.1103/PhysRevE.65.026605. Epub 2002, 18 января.
Phys Rev E Stat Nonlin Soft Matter Phys. 2002.
PMID: 11863676
doi: 10.1103/PhysRevE.65.026605. Epub 2002, 18 января.
Phys Rev E Stat Nonlin Soft Matter Phys. 2002.
PMID: 11863676Рассеяние бризеров синус-Гордон на потенциальной яме.
Пьетт Б., Закшевски В.Дж. Пиетт Б. и соавт. Phys Rev E Stat Nonlin Soft Matter Phys. 2009 апр; 79 (4 часть 2): 046603. doi: 10.1103/PhysRevE.79.046603. Epub 2009 6 апр. Phys Rev E Stat Nonlin Soft Matter Phys. 2009. PMID: 19518367
Решение с кинк-бризером в слабо дискретной модели Френкеля-Конторовой.
Дмитриев С.В., Мияучи Т., Абэ К., Шигенари Т. Дмитриев С.В. и соавт. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 2000 г., май; 61 (5B): 5880-5. doi: 10.1103/physreve.61.5880. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics.
 2000.
PMID: 11031648
2000.
PMID: 11031648Особенности транспорта биоэнергии и влияние неоднородности структуры и температуры систем на транспорт энергии по полипептидным цепям.
Пан XF. Пан XF. Прог Биофиз Мол Биол. 2012 Январь; 108 (1-2): 1-46. doi: 10.1016/j.pbiomolbio.2011.09.005. Epub 2011, 17 сентября. Прог Биофиз Мол Биол. 2012. PMID: 21951575 Обзор.
Посмотреть все похожие статьи
Процитируйте
Формат: ААД АПА МДА НЛМ
Отправить по телефону
Тригонометрические функции — Математическая энциклопедия
Класс элементарных функций синус, косинус, тангенс, котангенс, секанс, косеканс. Они обозначаются соответственно: $\sin x $,
$\cos х $,
$ \mathop{\rm загар} х $(
или $\mathop{\rm tg} x $),
$ \mathop{\rm кроватка} x $(
или $\mathop{\rm cotan} x $),
$ \mathop{\rm сек} х $,
$ \mathop{\rm csc} х $(
или $\cosec x $).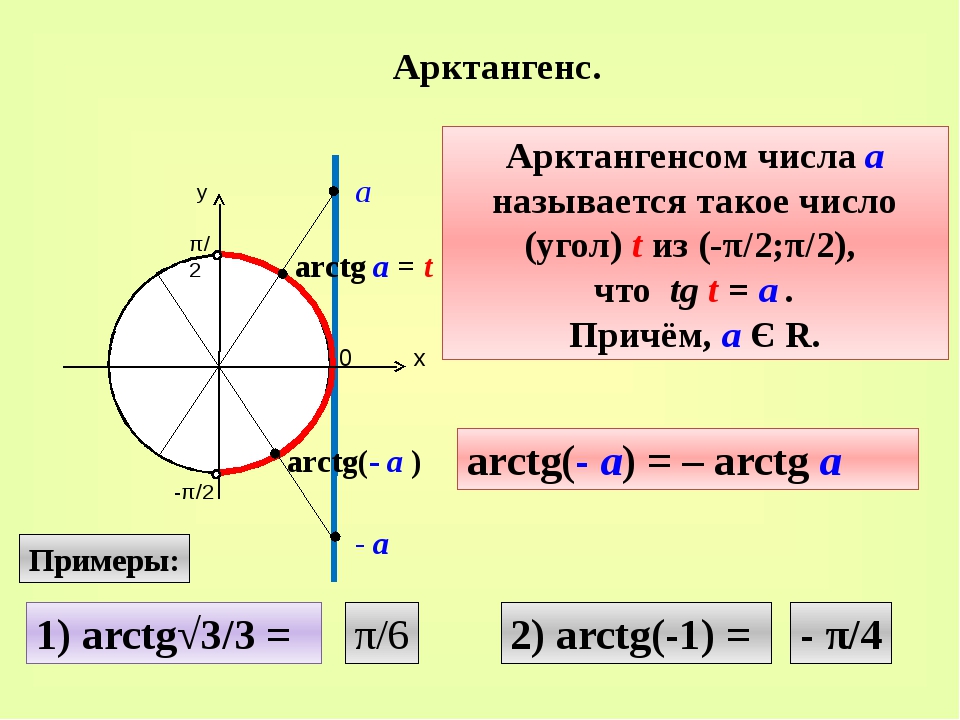 9{2} = 1 $(
см. рис. а) с начальной точкой $ B = ( 1, 0) $
и длина $ | \альфа | $.
Дуга из $B$
до $А$
берется против часовой стрелки, если $\alpha\geq 0 $,
и по часовой стрелке, если $\alpha < 0$.
Если $\альфа = 0$,
тогда $А=В$;
если, например, $ \alpha = (- 7 \pi )/ ( 2) $,
тогда $А = (0, 1)$.
$Б$,
$ | БА | = \ альфа > 0 $
9{2} = 1 $(
см. рис. а) с начальной точкой $ B = ( 1, 0) $
и длина $ | \альфа | $.
Дуга из $B$
до $А$
берется против часовой стрелки, если $\alpha\geq 0 $,
и по часовой стрелке, если $\alpha < 0$.
Если $\альфа = 0$,
тогда $А=В$;
если, например, $ \alpha = (- 7 \pi )/ ( 2) $,
тогда $А = (0, 1)$.
$Б$,
$ | БА | = \ альфа > 0 $
Рисунок: t094210a
Основные тригонометрические функции синуса и косинуса определены в $ \alpha $ по формулам
$$ \ грех \ альфа = \ у _ \альфа,\\ \cos\альфа = \ х _ \ альфа . $$
Остальные тригонометрические функции можно определить по формулам
$$ \ mathop{\ rm tan} \ альфа = \ \ гидроразрыва {\ грех \ альфа} {\ соз \ альфа} ,\\ \mathop{\rm кроватка} \альфа = \ \ гидроразрыва {\ соз \ альфа} {\ грех \ альфа} , $$
$$ \ mathop{\ rm сек} \ альфа = { \ гидроразрыва {1} {\ соз \ альфа} } ,\\ \ mathop{\ rm csc} \ альфа = { \frac{1}{\sin\alpha} } . $$
Все тригонометрические функции являются периодическими. Графики тригонометрических функций приведены на рис. б.
Графики тригонометрических функций приведены на рис. б.
Рисунок: t094210b
Основные свойства тригонометрических функций — область определения, диапазон значений, четность и участки монотонности — приведены в таблице ниже.
| Функция | Домен определения | Секция мон. | $ — \infty < x <+ \infty $ | $ [- 1, + 1] $ | Нечетное | $ \begin{массив}{c} \textrm{ увеличивается на } x \in (( 4n — 1) \pi /2, ( 4n + 1) \pi /2) \\ \textrm{ убывает по } x \in (( 4n + 1) \pi /2, ( 4n + 3) \pi /2) \конец{массив} $ |
| $ \cos x $ | $ — \infty < x <+\infty $ | $ [- 1, + 1] $ | Четный | $ \begin{array}{c} \textrm{ увеличивается на } x \in (( 2n — 1) \pi , 2n \pi) \\ \textrm{ уменьшается на } x \in ( 2n \pi , ( 2n + 1) \pi ) \конец{массив} $ | ||
| $ \mathop{\rm tan} x $ | $ x \neq \pi n + \pi / 2 $ | $ (- \infty, + \infty) $ | Нечетное | Увеличение на $ x \in (( 2n — 1) \pi /2, ( 2n + 1) \pi /2) $ | ||
| $ \mathop{\rm кроватка} x $ | $ x \neq \pi n $ | $ (- \infty, + \infty) $ | Нечетное | убывает при $ x \in ( n \pi , ( n + 1) \pi ) $ | ||
| $ \mathop{\rm sec} x $ | $ x \neq \pi n + \pi / 2 $ | $ (- \infty , — 1 ] \cup [ + 1, + \infty ) $ | Четный | $ \begin{array}{c} \textrm{ увеличивается на } x \in ( 2n \pi , ( 2n + 1) \pi ) \\ \textrm{ уменьшается на } x \in (( 2n — 1) \pi , 2n \pi ) \конец{массив} $ | ||
| $ \mathop{\rm csc} x $ | $ x \neq \pi n $ | $ (- \infty , — 1 ] \cup [ + 1, + \infty ) $ | Нечетное | $ \begin{массив}{c}
\textrm{ увеличивается на } x \in (( 4n + 1) \pi /2, ( 4n + 3) \pi /2) \\
\textrm{ убывает по } x \in (( 4n — 1) \pi /2, ( 4n + 1) \pi /2)
\конец{массив}
$
9{2n — 1} + \точки\справа]
$$ за $0 < | х | < \пи $(
$ B _ {n} $
числа Бернулли). Функция, обратная функции $ x = \sin y $ определяет $y$ как многозначная функция от $x$, это обозначается $ y = \mathop{\rm arc} \sin x $. Аналогично определяются функции, обратные другим тригонометрическим функциям; все они называются обратными тригонометрическими функциями. Тригонометрические функции комплексной переменной.Тригонометрические функции для комплексных значений переменной $ z = x + iy $ определяются как аналитические продолжения (см. Аналитическое продолжение) соответствующих тригонометрических функций действительного переменного в комплексной плоскости. Таким образом, $ \sin z $ и $\cosz$ можно определить с помощью степенного ряда для $ \sin x $ и $\cos х $ приведено выше. Эти ряды сходятся во всей комплексной плоскости, поэтому $ \sin z $ и $\cosz$ являются целыми функциями (ср. Целая функция). Тригонометрические функции тангенс и котангенс определяются по формулам $$
\ mathop{\ rm загар} г = \
\ гидроразрыва {\ грех г } {\ соз г}
,\\
\mathop{\rm кроватка} z = \
\ гидроразрыва {\ соз г } {\ грех г}
. Тригонометрические функции $ \mathop{\rm tan} z $ и $ \mathop{\rm кроватка} z $ являются мероморфными функциями (ср. Мероморфная функция). Полюса $ \mathop{\rm tan} z $ простые (первого порядка) и расположены в точках $ z = \pi / 2 + \pi n $, $ n = 0, \pm 1 ,\dots $. 9{2} — 1 }). $$ Тригонометрические функции $ \mathop{\rm tan} z $ и $ \mathop{\rm кроватка} z $ принимать все комплексные значения, кроме $\pm i $: Уравнения $\mathop{\rm tan} z = a $, $ \mathop{\rm кроватка} z = a $ каждая имеет бесконечно много решений для любого комплексного числа $a\neq\pm i$: $$ z = \ mathop {\ rm arc} \ mathop {\ rm tan} a = \ { \фракция {я} {2} } \ mathop{\ rm ln} \frac{1 — ia} {1 + ia} , $$ $$ z знак равно \ mathop {\ rm arc} \ mathop {\ rm кроватка} a = { \фракция {я} {2} } \ mathop{\ rm ln} \frac{ia + 1} {ia — 1} . $$ 9{-} из } , $$ и гиперболические функции: $$
\sin z = — i \sinh iz,\ \
\cos z = \cos iz,\ \
\mathop{\rm tan} z = — i \mathop{\rm tanh} iz. |

 Знаки значений тригонометрических функций по четвертям.
Знаки значений тригонометрических функций по четвертям. Все правила по сольфеджио
Все правила по сольфеджио
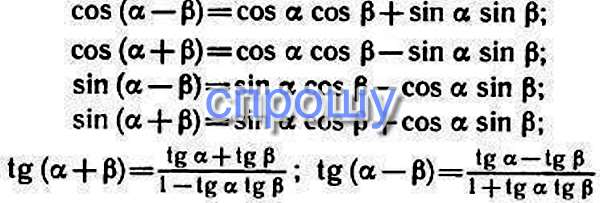
 Косинусом угла в а радиан называется косинус числа а.
Косинусом угла в а радиан называется косинус числа а.

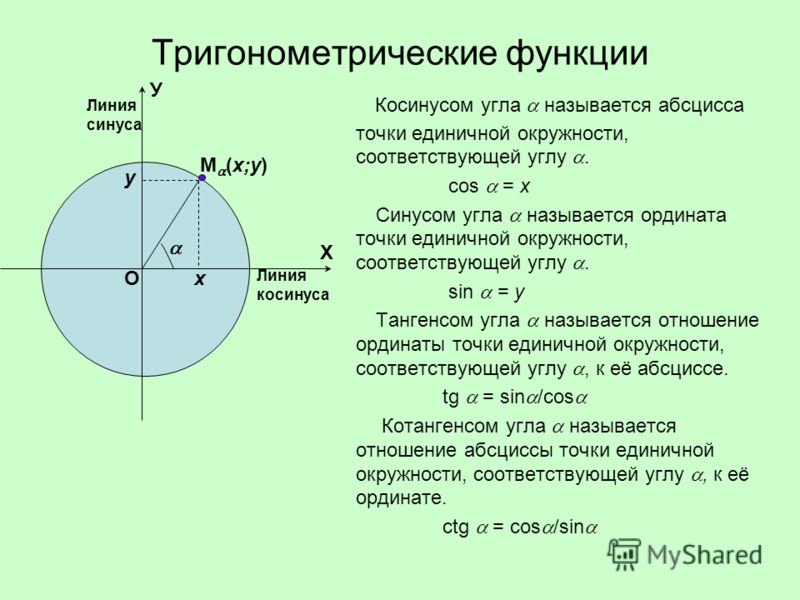 Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .
Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .

 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.009 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.009 с.)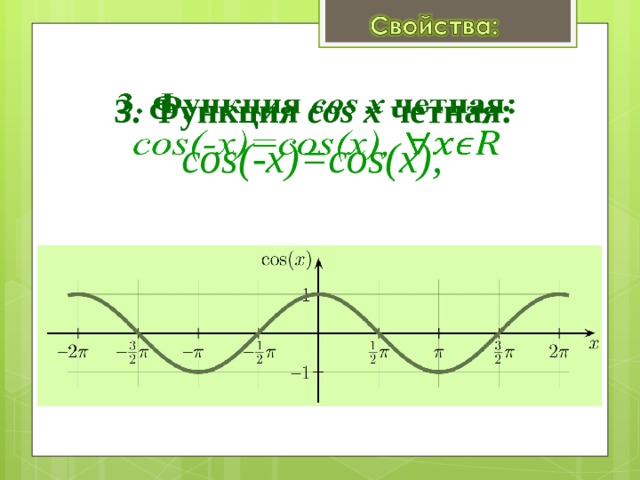
 Природа 525 , 354–358 (2015).
Природа 525 , 354–358 (2015). Физ. Преподобный Летт. 100 , 103904 (2009 г.).
Физ. Преподобный Летт. 100 , 103904 (2009 г.). М., Бернтсон Б.К., Паркер Д. и Сэмюэл Э. Наблюдение фазового перехода РТ в простой механической системе. 901:13 утра. Дж. Физ. 81 , 173–179 (2013).
М., Бернтсон Б.К., Паркер Д. и Сэмюэл Э. Наблюдение фазового перехода РТ в простой механической системе. 901:13 утра. Дж. Физ. 81 , 173–179 (2013). Проц. Натл акад. наук США 110 , 11763–11767 (2013).
Проц. Натл акад. наук США 110 , 11763–11767 (2013). Квантовая физика в одном измерении Издательство Оксфордского университета (2004).
Квантовая физика в одном измерении Издательство Оксфордского университета (2004). Дж., Гольдшмидт, Ю. Ю. и Гринштейн, С. Ренормгрупповой анализ фазового перехода в двумерном кулоновском газе, теория Синус-Гордон и XY-модель. J. Phys. А 13 , 585 (1980).
Дж., Гольдшмидт, Ю. Ю. и Гринштейн, С. Ренормгрупповой анализ фазового перехода в двумерном кулоновском газе, теория Синус-Гордон и XY-модель. J. Phys. А 13 , 585 (1980). ).
).
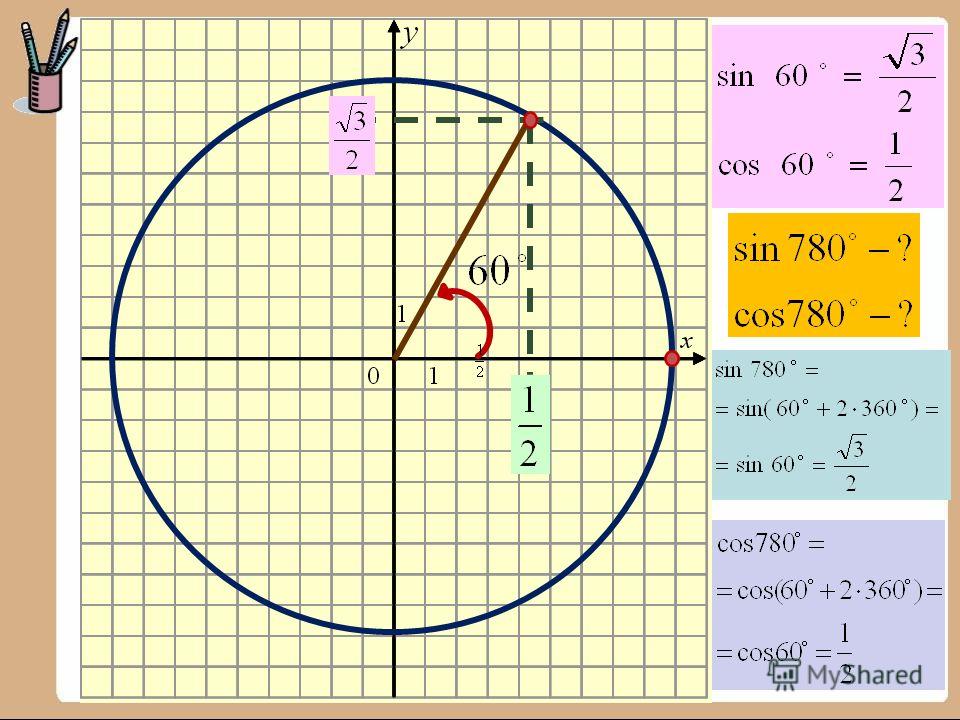 и др. Измерение энтропии запутанности в квантовой системе многих тел. Природа 528 , 77–83 (2015).
и др. Измерение энтропии запутанности в квантовой системе многих тел. Природа 528 , 77–83 (2015). Х. и Линигер, В. Точный анализ взаимодействующего бозе-газа. I. Общее решение и основное состояние. Физ. Ред. 130 , 1605–1616 (1963).
Х. и Линигер, В. Точный анализ взаимодействующего бозе-газа. I. Общее решение и основное состояние. Физ. Ред. 130 , 1605–1616 (1963). S. et al. Локализация пучков метастабильных атомов оптическими стоячими волнами: нанолитография в пределе Гейзенберга. Наука 280 , 1583–1586 (1998).
S. et al. Локализация пучков метастабильных атомов оптическими стоячими волнами: нанолитография в пределе Гейзенберга. Наука 280 , 1583–1586 (1998). Чернышевского, 112, 450008 Уфа, Россия и Башкирский государственный педагогический университет, Октябрьская обр. 3а, 450000 Уфа, Россия.
Чернышевского, 112, 450008 Уфа, Россия и Башкирский государственный педагогический университет, Октябрьская обр. 3а, 450000 Уфа, Россия. 3а, 450000 Уфа, Россия.
3а, 450000 Уфа, Россия. doi: 10.1103/PhysRevE.65.026605. Epub 2002, 18 января.
Phys Rev E Stat Nonlin Soft Matter Phys. 2002.
PMID: 11863676
doi: 10.1103/PhysRevE.65.026605. Epub 2002, 18 января.
Phys Rev E Stat Nonlin Soft Matter Phys. 2002.
PMID: 11863676 2000.
PMID: 11031648
2000.
PMID: 11031648
 $$
$$