Что такое выборочное среднее?
Что такое выборочное среднее?
Выборочной средней`x называется среднее арифметическое значение признака выборочной совокупности. В частном случае, когда выборка содержит по одному значению каждой варианты, выборочная средняя равна: … Аналогично генеральной совокупности можно сделать вывод относительно выборочной средней.
Что такое выборочное?
2. связанный, соотносящийся по значению с существительным выборка; отбирающийся по тому или иному признаку для последующего исследования, обобщения выводов и т.
Как найти выборочное среднее в Excel?
Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки . В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки .
Что характеризует выборочная дисперсия?
Выборочная дисперсия показывает насколько значения выборки отдалены от ее математического ожидания. Чем значение больше, тем данные более разбросаны. … ожидание и возвести разность в квадрат. Просуммировать все полученные выше значения.
Чем значение больше, тем данные более разбросаны. … ожидание и возвести разность в квадрат. Просуммировать все полученные выше значения.
Что такое дисперсия света простыми словами?
Диспе́рсия све́та (разложение света; светорассеяние) — это совокупность явлений, обусловленных зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимостью фазовой скорости света в веществе от частоты (или длины волны).
Что измеряет дисперсия?
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Чем больше дисперсия тем больше?
Величина дисперсии тем больше, чем больше изменчивость в данных. … Теоретическая дисперсия — это изменчивость бесконечного числа значений (значений всей генеральной совокупности).
… Теоретическая дисперсия — это изменчивость бесконечного числа значений (значений всей генеральной совокупности).
Что такое дисперсия в математической статистике?
Дисперсия — (от лат. dispersio — рассеяние), в математической статистике наиболее употребительная мера рассеивания, отклонения случайных значений от среднего. — среднее значение.
Как найти дисперсию если известно математическое ожидание?
Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. Дисперсию находим по формуле d = ∑x2ipi — M[x]2. Дисперсия D[X].
Как считается дисперсия в статистике?
Дисперсия случайной величины Х вычисляется по следующей формуле: D(X)=M(X−M(X))2, которую также часто записывают в более удобном для расчетов виде: D(X)=M(X2)−(M(X))2. Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Как рассчитать среднеквадратичное отклонение?
Среднее квадратичное отклонение, формула Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим. Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ: 1.
Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ: 1.
Как определить отклонение?
Рассчитывается оно следующим образом:
- Необходимо рассчитать среднее значение для проверяемого ряда данных. …
- Найти разницу между каждым показателем и средним значением. …
- Возвести каждое значение разницы в квадрат. …
- Сложить полученные результаты. …
- Полученный результат делиться на количество значений в ряду.
Как найти стандартное отклонение?
Как рассчитать стандартное отклонение вручную
- Находим среднее арифметическое выборки.
- От каждого значения выборки отнимаем среднее арифметическое.
- Каждую полученную разницу возводим в квадрат.
- Суммируем полученные значения квадратов разниц.
- Делим на размер выборки минус 1.
- Находим квадратный корень. Еще по теме
Как найти стандартное отклонение числового ряда?
Пошагово вычисление стандартного отклонения:
- вычисляем среднее арифметическое выборки данных
- отнимаем это среднее от каждого элемента выборки
- все полученные разницы возводим в квадрат
- суммируем все полученные квадраты
- делим полученную сумму на количество элементов в выборке (или на n-1, если n>30)
Какое должно быть стандартное отклонение?
Стандартное отклонение должно равняться нулю, так как единственный способ получить среднее значение 5 — ответить каждому 5. Наоборот, если среднее значение равно 1,0, то стандартная ошибка также должна быть равна 0. Таким образом, стандартное отклонение точно определено с учетом среднего значения.
Наоборот, если среднее значение равно 1,0, то стандартная ошибка также должна быть равна 0. Таким образом, стандартное отклонение точно определено с учетом среднего значения.
Выборочное среднее
Выборочное среднее значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества.
Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.
Выборочное среднее определяется при помощи следующей формулы:
где
хср —выборочная средняя величина или среднее арифметическое значение по выборке;
п — количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина;
 Всего таких
показателей п, поэтому
индекс k данной
переменной принимает значения от 1 до п;
Всего таких
показателей п, поэтому
индекс k данной
переменной принимает значения от 1 до п; ∑ — принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака.
Выражение соответственно означает сумму всех х с индексом k от 1 до n.
Пример. Допустим, что в результате применения психодиагностической методики для оценки некоторого психологического свойства у десяти испытуемых мы получили следующие частные показатели степени развитости данного свойства у отдельных испытуемых: х1= 5, х2 = 4, х3 = 5, х
4 = 6, х5 = 7, х6 = 3, х7 = 6, х8= 2, х9= 8, х10 = 4. Следовательно, п
= 10,
а индекс k меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение1,
вычисленное по этой формуле, будет
равно:
Следовательно, п
= 10,
а индекс k меняет
свои значения от 1 до 10 в приведенной
выше формуле. Для данной выборки
среднее значение1,
вычисленное по этой формуле, будет
равно:1 В дальнейшем, как это и принято в математической статистике, с целью сокращения текста мы будем опускать слова «выборочное» и «арифметическое» и просто говорить о «среднем» или «среднем значении».
В психодиагностике и в экспериментальных психолого-педагогических исследованиях среднее, как правило, не вычисля
В психодиагностических обследованиях большая точность расчетов не требуется и не имеет смысла, если принять во внимание приблизительность тех оценок, которые в них получаются, и достаточность таких оценок для производства сравнительно точных расчетов.
Дисперсия как статистическая, величина характеризует,
насколько
частные значения отклоняются от средней
величины в данной
выборке.
Чем больше дисперсия, тем больше отклонения или разброс данных. Прежде чем представлять формулу для расчетов дисперсии, рассмотрим пример. Воспользуемся теми первичными данными, которые были приведены ранее и на основе которых вычислялась в предыдущем примере средняя величина. Мы видим, что все они разные и отличаются не только друг от друга, но и от средней величины. Меру их общего отличия от средней величины и характеризует дисперсия. Ее определяют для того, чтобы можно было отличать друг от друга величины, имеющие одинаковую среднюю, но разный разброс.
Представим себе другую, отличную от предыдущей выборку первичных значений, например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко убедиться в том, что ее средняя величина также равна 5,0. Но в данной выборке ее отдельные частные значения отличаются от средней гораздо меньше, чем в первой выборке. Выразим степень этого отличия при помощи дисперсии, которая определяется по следующей формуле:
где — выборочная дисперсия, или просто дисперсия;
— выражение, означающее, что для всех xk от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;
п — количество
испытуемых в выборке или первичных
значений,
по которым вычисляется дисперсия.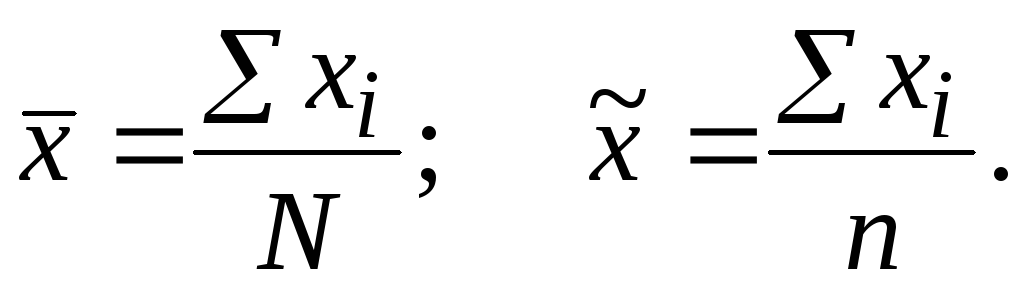
Заметим, что во многих изданиях дисперсию принято обозначать как D(x).
Определим дисперсии для двух приведенных выше выборок частных значений, обозначив эти дисперсии соответственно индексами 1 и 2:
Мы видим, что дисперсия по второй выборке (0,4) значительно меньше дисперсии по первой выборке (3,0). Если бы не было дисперсии, то мы не в состоянии были бы различить данные выборки.
СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТАНДОТКЛОНА в Microsoft Excel.
Описание
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
СТАНДОТКЛОНА(значение1;[значение2];…)
Аргументы функции СТАНДОТКЛОНА описаны ниже.
-
Значение1,значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 значений, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности.
 Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА. -
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
-
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
org/ListItem»>
Аргументы, представляющие собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОН.
-
Функция СТАНДОТКЛОНА вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.

Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
|
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОНА(A3:A12) |
Стандартное отклонение предела прочности для всех инструментов (27,46391572) |
27,46391572 |
[PDF] 17 лекция — Free Download PDF
Лекция 16. Характеристики вариационного ряда Пусть из генеральной совокупности извлечена выборка объёмом n. Случайный выбор элемента рассматривается как независимое наблюдение за величиной ξ, имеющей некоторое распределение вероятностей. Если те значения y1, y2…yn, которые приняла случайная величина ξ в n наблюдениях, записать не в порядке получения, а в порядке возрастания, то получим упорядоченную выборку x1, x2…xn, называемую вариационным рядом. Наблюдаемые значения xi называются вариантами. Разность между максимальным и минимальным элементом выборки xn-x1=w называется размахом выборки. Для каждого полученного значения можно подсчитать, сколько раз оно встретилось в ряде наблюдений. Эти числа называются частотой варианта, или его весом. В дальнейшем частоту варианта xi мы будем обозначать через mi, где i – индекс варианта. Данные наблюдений, среди которых много повторяющихся, удобно изобразить не в виде ряда, а в виде таблицы (табл. 1.2). Таблица 1.2 Значения xi x1 x2 … xk Частоты mi m1 m2 … mk Пример 1.
Характеристики вариационного ряда Пусть из генеральной совокупности извлечена выборка объёмом n. Случайный выбор элемента рассматривается как независимое наблюдение за величиной ξ, имеющей некоторое распределение вероятностей. Если те значения y1, y2…yn, которые приняла случайная величина ξ в n наблюдениях, записать не в порядке получения, а в порядке возрастания, то получим упорядоченную выборку x1, x2…xn, называемую вариационным рядом. Наблюдаемые значения xi называются вариантами. Разность между максимальным и минимальным элементом выборки xn-x1=w называется размахом выборки. Для каждого полученного значения можно подсчитать, сколько раз оно встретилось в ряде наблюдений. Эти числа называются частотой варианта, или его весом. В дальнейшем частоту варианта xi мы будем обозначать через mi, где i – индекс варианта. Данные наблюдений, среди которых много повторяющихся, удобно изобразить не в виде ряда, а в виде таблицы (табл. 1.2). Таблица 1.2 Значения xi x1 x2 … xk Частоты mi m1 m2 … mk Пример 1. На телефонной станции проводились наблюдения над числом X неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; … 1; 1; 5. Расположив эти числа в порядке неубывания, получим следующий ряд: 0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; … 5; 5; 7. Значения 0; 1; 2; …; 7, принятые случайной величиной в процессе наблюдений, являются вариантами. 0 1 2 3 4 5 7 Объём Число в мин xi Частоты mi 8 17 16 10 6 2 1 60 Выборочное среднее x является случайной величиной, значение которой зависит от того, какие значения приняли варианты xi. В таблице 1.3 приведены формулы, по которым в зависимости от описания данных выборки вычисляется среднее значение выборки. Таблица 1.3 Задана таблица Задана таблица Вариационный ряд задан частот относительных частот последовательностью вариационного ряда вариационного ряда n k k Среднее значение mj 1 1 x m x xj ∑ ∑ i j j ∑ выборки x n i =1 n j =1 n j =1 Пример 2. По выборке 4, 6, 7, 7, 10, 15, 18 (n=7) найти x .
На телефонной станции проводились наблюдения над числом X неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1; … 1; 1; 5. Расположив эти числа в порядке неубывания, получим следующий ряд: 0; 0; 0; 0; 0; 0; 0; 0; 1; 1; 1; … 5; 5; 7. Значения 0; 1; 2; …; 7, принятые случайной величиной в процессе наблюдений, являются вариантами. 0 1 2 3 4 5 7 Объём Число в мин xi Частоты mi 8 17 16 10 6 2 1 60 Выборочное среднее x является случайной величиной, значение которой зависит от того, какие значения приняли варианты xi. В таблице 1.3 приведены формулы, по которым в зависимости от описания данных выборки вычисляется среднее значение выборки. Таблица 1.3 Задана таблица Задана таблица Вариационный ряд задан частот относительных частот последовательностью вариационного ряда вариационного ряда n k k Среднее значение mj 1 1 x m x xj ∑ ∑ i j j ∑ выборки x n i =1 n j =1 n j =1 Пример 2. По выборке 4, 6, 7, 7, 10, 15, 18 (n=7) найти x . x =(4+6+7+7+10+15+18)/7=9,57. Группировка состоит в том, что область на оси x, куда попали значения x1,…,xn, разбивают на интервалы I1,…,Ik и подсчитывают частоту попадания значений величины в каждый интервал. Задания для самостоятельной работы 1. Дана выборка 7, 3, 3, 6, 4, 5, 1, 2, 1, 3. Построить вариационный ряд, определить размах выборки. Найти выборочное среднее x . 2. Из генеральной совокупности извлечена выборка объёма n=50: варианта xi 2 5 7 10 частота ni 16 12 8 14 Найти выборочную среднюю.
x =(4+6+7+7+10+15+18)/7=9,57. Группировка состоит в том, что область на оси x, куда попали значения x1,…,xn, разбивают на интервалы I1,…,Ik и подсчитывают частоту попадания значений величины в каждый интервал. Задания для самостоятельной работы 1. Дана выборка 7, 3, 3, 6, 4, 5, 1, 2, 1, 3. Построить вариационный ряд, определить размах выборки. Найти выборочное среднее x . 2. Из генеральной совокупности извлечена выборка объёма n=50: варианта xi 2 5 7 10 частота ni 16 12 8 14 Найти выборочную среднюю.
3. Из генеральной совокупности извлечена выборка объёма n=60: варианта xi 1 3 6 26 частота ni 8 40 10 2 Найти выборочную среднюю. 4. Найти выборочную среднюю по данному распределению выборки объёма n=10: xi 1250 1270 1280 ni 2 5 3 5. Найти выборочную среднюю по данному распределению выборки объёма n=20: xi 2560 2600 2620 2650 2700 ni 2 3 10 4 1 6-7. Решите следующие задания, пользуясь таблицами: 6. Из таблицы 1.4 чисел выборки из равномерного распределения на отрезке [0,100] возьмите подряд 100 чисел, начиная с номера 4N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). По этой таблице сосчитайте эмпирическое среднее ( x ). Таблица 1.4 Последовательность случайных чисел, распределённых равномерно на отрезке [0,100] 10 09 73 25 33 76 52 01 35 86 34 67 35 48 76 80 95 90 91 17 37 54 20 48 05 64 89 47 42 96 24 80 52 40 37 20 63 61 04 02 08 42 26 89 53 19 64 50 93 03 23 20 90 25 60 15 95 33 47 64 99 01 90 25 29 09 37 67 07 15 38 31 13 11 65 88 67 67 43 97 12 80 79 99 70 80 15 73 61 47 64 03 23 66 53 98 95 11 68 77 66 06 57 47 17 34 07 27 68 50 36 69 73 61 70 65 81 33 98 85 31 36 01 08 05 45 57 18 24 06 35 30 34 26 14 86 79 90 74 39 85 26 97 76 02 02 05 16 56 92 68 66 57 48 18 73 05 38 52 47 22 15 67 16 01 76 72 52 73 62 79 88 03 40 47 40 99 58 39 51 05 94 66 77 42 77 53 12 97 87 01 95 47 73 83 68 41 90 12 26 7. Из таблицы 1.5 чисел выборки из нормального распределения N(0,1) возьмите подряд 100 чисел, начиная с номера 4N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). По этой таблице сосчитайте эмпирическое среднее ( x ).
По этой таблице сосчитайте эмпирическое среднее ( x ). Таблица 1.4 Последовательность случайных чисел, распределённых равномерно на отрезке [0,100] 10 09 73 25 33 76 52 01 35 86 34 67 35 48 76 80 95 90 91 17 37 54 20 48 05 64 89 47 42 96 24 80 52 40 37 20 63 61 04 02 08 42 26 89 53 19 64 50 93 03 23 20 90 25 60 15 95 33 47 64 99 01 90 25 29 09 37 67 07 15 38 31 13 11 65 88 67 67 43 97 12 80 79 99 70 80 15 73 61 47 64 03 23 66 53 98 95 11 68 77 66 06 57 47 17 34 07 27 68 50 36 69 73 61 70 65 81 33 98 85 31 36 01 08 05 45 57 18 24 06 35 30 34 26 14 86 79 90 74 39 85 26 97 76 02 02 05 16 56 92 68 66 57 48 18 73 05 38 52 47 22 15 67 16 01 76 72 52 73 62 79 88 03 40 47 40 99 58 39 51 05 94 66 77 42 77 53 12 97 87 01 95 47 73 83 68 41 90 12 26 7. Из таблицы 1.5 чисел выборки из нормального распределения N(0,1) возьмите подряд 100 чисел, начиная с номера 4N, где N – ваш порядковый номер в списке группы (дойдя до конца таблицы, перейдите в её начало). По этой таблице сосчитайте эмпирическое среднее ( x ). Таблица 1.5 Последовательность случайных чисел, имеющих распределение N(0,1) 0,414 0,011 0,666 -1,132 -0,410 -1,077 1,484 -0,340 0,789 -0,494 0,364 -1,237 -0,044 -0,111 -0,210 0,931 0,616 -0,377 -0,433 1,048 -0,037 0,759 0,609 -2,043 -2,290 0,404 -0,543 0,486 0,869 0,347 2,816 -0,464 -0,632 -1,614 0,372 -0,074 -0,916 1,314 -0,038 0,673 0,563 -0,107 0,131 -1,808 0,284 0,458 1,307 -1,625 -0,629 -0,504 -0,0056 -0,131 0,048 1,879 -1,016 0,360 -0,119 2,331 1,672 -1,053 0,840 0,246 -0,237 -1,312 1,603 -0,952 -0,566 1,600 0,465 1,951 0,110 0,251 0,116 -0,957 -0,190 1,479 -0,986 1,249 1,934 0,07 -1,358 -1,246 -0,959 -1,297 -0,722 0,925 0,783 -0,402 0,619 1,826 1,272 -0,945 0,494 0,050 -1,696 1,876 0,063 0,132 0,682 0,544 -0,417 -0,666 -0,104 -0,253 -2,543 -1,133 1,987 0,668 0,360 1,927 1,183 1,211 1,765 0,035 -0,359 0,193 -1,023 -0,222 -0,616 -0,060 -1,319 -0,785 -0,430 -0,298 0,248 -0,088 -1,379 0,295 -0,115 -0,621 -0,618 0,209 0,979 0,906 -0,096 -1,376 1,047 -0,872 -2,200 -1,384 1,425 -0,812 0,748 -1,095 Тренинг умений Пример выполнения упражнений тренинга.
Таблица 1.5 Последовательность случайных чисел, имеющих распределение N(0,1) 0,414 0,011 0,666 -1,132 -0,410 -1,077 1,484 -0,340 0,789 -0,494 0,364 -1,237 -0,044 -0,111 -0,210 0,931 0,616 -0,377 -0,433 1,048 -0,037 0,759 0,609 -2,043 -2,290 0,404 -0,543 0,486 0,869 0,347 2,816 -0,464 -0,632 -1,614 0,372 -0,074 -0,916 1,314 -0,038 0,673 0,563 -0,107 0,131 -1,808 0,284 0,458 1,307 -1,625 -0,629 -0,504 -0,0056 -0,131 0,048 1,879 -1,016 0,360 -0,119 2,331 1,672 -1,053 0,840 0,246 -0,237 -1,312 1,603 -0,952 -0,566 1,600 0,465 1,951 0,110 0,251 0,116 -0,957 -0,190 1,479 -0,986 1,249 1,934 0,07 -1,358 -1,246 -0,959 -1,297 -0,722 0,925 0,783 -0,402 0,619 1,826 1,272 -0,945 0,494 0,050 -1,696 1,876 0,063 0,132 0,682 0,544 -0,417 -0,666 -0,104 -0,253 -2,543 -1,133 1,987 0,668 0,360 1,927 1,183 1,211 1,765 0,035 -0,359 0,193 -1,023 -0,222 -0,616 -0,060 -1,319 -0,785 -0,430 -0,298 0,248 -0,088 -1,379 0,295 -0,115 -0,621 -0,618 0,209 0,979 0,906 -0,096 -1,376 1,047 -0,872 -2,200 -1,384 1,425 -0,812 0,748 -1,095 Тренинг умений Пример выполнения упражнений тренинга. Задание 1. Для случайно отобранных семи рабочих стаж работы оказался равным: 10, 3, 5, 12, 11, 7, 9.
Задание 1. Для случайно отобранных семи рабочих стаж работы оказался равным: 10, 3, 5, 12, 11, 7, 9.
Чему равен для них средний стаж? Решение. Заполните таблицу, подобрав каждому алгоритму конкретное содержание. № Алгоритм Конкретное соответствие данной ситуации п/п предложенному алгоритму 1. Выписать заданные значения, Задана выборка: объём выборки и нужную формулу x1 x2 x3 x4 x5 x6 x7 10, 3, 5, 12, 11, 7, 9. для получения точечной оценки n=7; 1 n x = ∑ xi — формула для среднего. n i =1 2. Сосчитать значение оценки 10 + 3 + 5 + 12 + 11 + 7 + 9 x= = 8,14 года 7 Решите самостоятельно следующую задачу: Построить таблицу дискретного вариационного ряда 60 абитуриентов по числу баллов, полученных ими на приёмных экзаменах. Найти среднее значение: 20 19 22 24 21 18 23 17 20 16 15 23 21 24 21 18 23 21 19 20 24 21 20 18 17 22 20 16 22 18 20 17 21 17 19 20 20 21 18 22 23 21 25 22 20 19 21 24 23 21 19 22 21 19 20 23 22 25 21 21 Примерные тесты 1. Средняя выборочная вариационного ряда 1,2,3,3,4,5 равна: -3 — 2,5 -6 — 3,6 2. Средняя выборочная вариационного ряда 1, 2, 5, 3, 2 равна … -6 -5 — 3,1 — 2,6 3. Средняя выборочная вариационного ряда 2, 2, 4, 6, 6 равна … -4 — 0,2 — 6,7 -5 4. Средняя выборочная вариационного ряда 1, 3, 4, 4, 2 равна … — 3,2 — 2,8 -5 -4 5. Средняя выборочная вариационного ряда 1, 2, 5, 5, 7, 10 равна … — 4,8 -6 -5 — 4,2 6. Средняя выборочная вариационного ряда 1, 5, 5, 6, 2 равна … — 4,2 -4 -5 — 3,8 7. Средняя выборочная вариационного ряда 1, 2, 2, 3, 7 равна … — 1,5 -3
Средняя выборочная вариационного ряда 1, 2, 5, 3, 2 равна … -6 -5 — 3,1 — 2,6 3. Средняя выборочная вариационного ряда 2, 2, 4, 6, 6 равна … -4 — 0,2 — 6,7 -5 4. Средняя выборочная вариационного ряда 1, 3, 4, 4, 2 равна … — 3,2 — 2,8 -5 -4 5. Средняя выборочная вариационного ряда 1, 2, 5, 5, 7, 10 равна … — 4,8 -6 -5 — 4,2 6. Средняя выборочная вариационного ряда 1, 5, 5, 6, 2 равна … — 4,2 -4 -5 — 3,8 7. Средняя выборочная вариационного ряда 1, 2, 2, 3, 7 равна … — 1,5 -3
— 3,75 -5 8. Средняя выборочная вариационного ряда 2, 3, 4, 4, 5 равна … — 4,2 -3 — 3,6 -5 9. Средняя выборочная вариационного ряда 2, 3, 3, 3, 1 равна … -5 — 3,5 — 2,4 -3 10. Средняя выборочная вариационного ряда 2, 3, 4, 3, 2 равна … — 3,2 -5 — 2,8 -3
Python и статистический вывод: часть 2 / Хабр
Предыдущий пост см. здесь.
Выборки и популяции
В статистической науке термины «выборка» и «популяция» имеют особое значение. Популяция, или генеральная совокупность, — это все множество объектов, которые исследователь хочет понять или в отношении которых сделать выводы. Например, во второй половине 19-го века основоположник генетики Грегор Йохан Мендель) записывал наблюдения о растениях гороха. Несмотря на то, что он изучал в лабораторных условиях вполне конкретные сорта растения, его задача состояла в том, чтобы понять базовые механизмы, лежащие в основе наследственности абсолютно всех возможных сортов гороха.
Например, во второй половине 19-го века основоположник генетики Грегор Йохан Мендель) записывал наблюдения о растениях гороха. Несмотря на то, что он изучал в лабораторных условиях вполне конкретные сорта растения, его задача состояла в том, чтобы понять базовые механизмы, лежащие в основе наследственности абсолютно всех возможных сортов гороха.
В статистической науке о группе объектов, из которых извлекается выборка, говорят, как о популяции, независимо от того, являются изучаемые объекты живыми существами или нет.
Поскольку популяция может быть крупной — или бесконечной, как в случае растений гороха Менделя — мы должны изучать репрезентативные выборки, и на их основе делать выводы о всей популяции в целом. В целях проведения четкого различия между поддающимися измерению атрибутами выборок и недоступными атрибутами популяции, мы используем термин статистики, имея при этом в виду атрибуты выборки, и говорим о параметрах, имея в виду атрибуты популяции.
Статистики — это атрибуты, которые мы можем измерить на основе выборок. Параметры — это атрибуты популяции, которые мы пытаемся вывести статистически.
В действительности, статистики и параметры различаются в силу применения разных символов в математических формулах:
Мера | Выборочная статистика | Популяционный параметр |
Объем | n | N |
Среднее значение | x̅ | μx |
Стандартное отклонение | Sx | σx |
Стандартная ошибка | Sx̅ |
|
Если вы вернетесь к уравнению стандартной ошибки, то заметите, что она вычисляется не из выборочного стандартного отклонения Sx, а из популяционного стандартного отклонения σx. Это создает парадоксальную ситуацию — мы не можем вычислить выборочную статистику, используя для этого популяционные параметры, которые мы пытаемся вывести. На практике, однако, предполагается, что выборочное и популяционное стандартные отклонения одинаковы при размере выборки порядка n ≥ 30.
Это создает парадоксальную ситуацию — мы не можем вычислить выборочную статистику, используя для этого популяционные параметры, которые мы пытаемся вывести. На практике, однако, предполагается, что выборочное и популяционное стандартные отклонения одинаковы при размере выборки порядка n ≥ 30.
Теперь вычислим стандартную ошибку средних значений за определенный день. Например, возьмем конкретный день, скажем, 1 мая:
def ex_2_8():
'''Вычислить стандартную ошибку
средних значений за определенный день'''
may_1 = '2015-05-01'
df = with_parsed_date( load_data('dwell-times.tsv') )
filtered = df.set_index( ['date'] )[may_1]
se = standard_error( filtered['dwell-time'] )
print('Стандартная ошибка:', se)Стандартная ошибка: 3.627340273094217
Хотя мы взяли выборку всего из одного дня, вычисляемая нами стандартная ошибка очень близка к стандартному отклонению всех выборочных средних — 3.6 сек. против 3.7 сек. Это, как если бы, подобно клетке, содержащей ДНК, в каждой выборке была закодирована информация обо всей находящейся внутри нее популяции.
Интервалы уверенности
Поскольку стандартная ошибка выборки измеряет степень близости, с которой, по нашим ожиданиям, выборочное среднее соответствует среднему популяционному, то мы можем также рассмотреть обратное — стандартная ошибка измеряет степень близосто, с которой, по нашим ожиданиям, популяционное среднее соответствует измеренному среднему выборочному. Другими словами, на основе стандартной ошибки мы можем вывести, что популяционное среднее находится в пределах некого ожидаемого диапазона выборочного среднего с некоторой степенью уверенности.
Понятия «степень уверенности» и «ожидаемый диапазон», взятые вместе, дают определение термину интервал уверенности.
Примечание. В большинстве языков под термином «confidence» в контексте инференциальной статистики понимается именно уверенность в отличие от отечественной статистики, где принято говорить о доверительном интервале. На самом деле речь идет не о доверии (trust), а об уверенности исследователя в полученных результатах.
Это яркий пример мягкой подмены понятия. Подобного рода ошибки вполне объяснимы — первые переводы появились еще в
доколумбовудоинтернетовскую эпоху, когда источников было мало, и приходилось домысливать в силу своего понимания. Сегодня же, когда существует масса профильных глоссариев, словарей и источников, такого рода искажения не оправданы. ИМХО.
При установлении интервалов уверенности обычной практикой является задание интервала размером 95% — мы на 95% уверены, что популяционный параметр находится внутри интервала. Разумеется, еще остается 5%-я возможность, что он там не находится.
Какой бы ни была стандартная ошибка, 95% популяционного среднего значения будет находиться между -1.96 и 1.96 стандартных отклонений от выборочного среднего. И, следовательно, число 1.96 является критическим значением для 95%-ого интервала уверенности. Это критическое значение носит название z-значения.
Название z-значение вызвано тем, что нормальное распределение называется z-распределением. Впрочем, иногда z-значение так и называют — гауссовым значением.
Впрочем, иногда z-значение так и называют — гауссовым значением.
Число 1.96 используется так широко, что его стоит запомнить. Впрочем, критическое значение мы можем вычислить сами, воспользовавшись функцией scipy stats.norm.ppf. Приведенная ниже функция confidence_interval ожидает значение для p между 0 и 1. Для нашего 95%-ого интервала уверенности оно будет равно 0.95. В целях вычисления положения каждого из двух хвостов нам нужно вычесть это число из единицы и разделить на 2 (2.5% для интервала уверенности шириной 95%):
def confidence_interval(p, xs):
'''Интервал уверенности'''
mu = xs.mean()
se = standard_error(xs)
z_crit = stats.norm.ppf(1 - (1-p) / 2)
return [mu - z_crit * se, mu + z_crit * se]
def ex_2_9():
'''Вычислить интервал уверенности
для данных за определенный день'''
may_1 = '2015-05-01'
df = with_parsed_date( load_data('dwell-times.tsv') )
filtered = df.set_index( ['date'] )[may_1]
ci = confidence_interval(0. 95, filtered['dwell-time'])
print('Интервал уверенности: ', ci)
95, filtered['dwell-time'])
print('Интервал уверенности: ', ci)Интервал уверенности: [83.53415272762004, 97.753065317492741]
Полученный результат говорит о том, что можно на 95% быть уверенным в том, что популяционное среднее находится между 83.53 и 97.75 сек. И действительно, популяционное среднее, которое мы вычислили ранее, вполне укладывается в этот диапазон.
Сравнение выборок
После вирусной маркетинговой кампании веб-команда в AcmeContent извлекает для нас однодневную выборку времени пребывания посетителей на веб-сайте для проведения анализа. Они хотели бы узнать, не привлекла ли их недавняя кампания более активных посетителей веб-сайта. Интервалы уверенности предоставляют нам интуитивно понятный подход к сравнению двух выборок.
Точно так же, как мы делали ранее, мы загружаем значения времени пребывания, полученные в результате маркетинговой кампании, и их резюмируем:
def ex_2_10():
'''Сводные статистики данных, полученных
в результате вирусной кампании'''
ts = load_data('campaign-sample. tsv')['dwell-time']
print('n: ', ts.count())
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение: ', ts.std())
print('Стандартная ошибка: ', standard_error(ts))
ex_2_10()
tsv')['dwell-time']
print('n: ', ts.count())
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение: ', ts.std())
print('Стандартная ошибка: ', standard_error(ts))
ex_2_10()n: 300 Среднее: 130.22 Медиана: 84.0 Стандартное отклонение: 136.13370714388034 Стандартная ошибка: 7.846572839994115
Среднее значение выглядит намного больше, чем то, которое мы видели ранее — 130 сек. по сравнению с 90 сек. Вполне возможно, здесь имеется некое значимое расхождение, хотя стандартная ошибка более чем в 2 раза больше той, которая была в предыдущей однодневной выборке, в силу меньшего размера выборки и большего стандартного отклонения. Основываясь на этих данных, можно вычислить 95%-й интервал уверенности для популяционного среднего, воспользовавшись для этого той же самой функцией confidence_interval, что и прежде:
def ex_2_11():
'''Интервал уверенности для данных,
полученных в результате вирусной кампании'''
ts = load_data('campaign-sample. tsv')['dwell-time']
print('Интервал уверенности:', confidence_interval(0.95, ts))
tsv')['dwell-time']
print('Интервал уверенности:', confidence_interval(0.95, ts))Интервал уверенности: [114.84099983154137, 145.59900016845864]
95%-ый интервал уверенности для популяционного среднего лежит между 114.8 и 145.6 сек. Он вообще не пересекается с вычисленным нами ранее популяционным средним в размере 90 сек. Похоже, имеется какое-то крупное расхождение с опорной популяцией, которое едва бы произошло по причине одной лишь ошибки выборочного обследования. Наша задача теперь состоит в том, чтобы выяснить почему это происходит.
Ошибка выборочного обследования, также систематическая ошибка при взятии выборки, возникает, когда статистические характеристики популяции оцениваются исходя из подмножества этой популяции.
Искаженность
Выборка должна быть репрезентативной, то есть представлять популяцию, из которой она взята. Другими словами, при взятии выборки необходимо избегать искажения, которое происходит в результате того, что отдельно взятые члены популяции систематически из нее исключаются (либо в нее включаются) по сравнению с другими.
Широко известным примером искажения при взятии выборки является опрос населения, проведенный в США еженедельным журналом «Литературный Дайджест» (Literary Digest) по поводу президентских выборов 1936 г. Это был один из самых больших и самых дорогостоящих когда-либо проводившихся опросов: тогда по почте было опрошено 2.4 млн. человек. Результаты были однозначными — губернатор-республиканец от шт. Канзас Альфред Лэндон должен был победить Франклина Д. Рузвельта с 57% голосов. Как известно, в конечном счете на выборах победил Рузвельт с 62% голосов.
Первопричина допущенной журналом огромной ошибки выборочного обследования состояла в искажении при отборе. В своем стремлении собрать как можно больше адресов избирателей журнал «Литературный Дайджест» буквально выскреб все телефонные справочники, подписные перечни журнала и списки членов клубов. В эру, когда телефоны все еще во многом оставались предметом роскоши, такая процедура гарантировано имела избыточный вес в пользу избирателей, принадлежавших к верхнему и среднему классам, и не был представительным для электората в целом. Вторичной причиной искажения стала искаженность в результате неответов — в опросе фактически согласились участвовать всего менее четверти тех, к кому обратились. В этом виде искаженности при отборе предпочтение отдается только тем респондентам, которые действительно желают принять участие в голосовании.
Вторичной причиной искажения стала искаженность в результате неответов — в опросе фактически согласились участвовать всего менее четверти тех, к кому обратились. В этом виде искаженности при отборе предпочтение отдается только тем респондентам, которые действительно желают принять участие в голосовании.
Распространенный способ избежать искаженности при отборе состоит в том, чтобы каким-либо образом рандомизировать выборку. Введение в процедуру случайности делает вряд ли возможным, что экспериментальные факторы окажут неправомерное влияние на качество выборки. Опрос населения еженедельником «Литературный Дайджест» был сосредоточен на получении максимально возможной выборки, однако неискаженная малая выборка была бы намного полезнее, чем плохо отобранная большая выборка.
Если мы откроем файл campaign_sample.tsv, то обнаружим, что наша выборка приходится исключительно на 6 июня 2015 года. Это был выходной день, и этот факт мы можем легко подтвердить при помощи функции pandas:
'''Проверка даты''' d = pd.to_datetime('2015 6 6') d.weekday() in [5,6]
True
Все наши сводные статистики до сих пор основывались на данных, которые мы отфильтровывали для получения только рабочих дней. Искаженность в нашей выборке вызвана именно этим фактом, и, если окажется, что поведение посетителей в выходные отличается от поведения в будние дни — вполне возможный сценарий — тогда мы скажем, что выборки представляют две разные популяции.
Визуализация разных популяций
Теперь снимем фильтр для рабочих дней и построим график среднесуточного времени пребывания для всех дней недели — рабочих и выходных:
def ex_2_12():
'''Построить график времени ожидания
по всем дням, без фильтра'''
df = load_data('dwell-times.tsv')
means = mean_dwell_times_by_date(df)['dwell-time']
means.hist(bins=20)
plt.xlabel('Ежедневное время ожидания неотфильтрованное, сек.')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
Распределение уже не является нормальным. Оно фактически является бимодальным, поскольку у него два пика. Второй меньший пик соответствует вновь добавленным выходным дням, и он ниже потому что количество выходных дней гораздо меньше количества рабочих дней, а также потому что стандартная ошибка распределения больше.
Оно фактически является бимодальным, поскольку у него два пика. Второй меньший пик соответствует вновь добавленным выходным дням, и он ниже потому что количество выходных дней гораздо меньше количества рабочих дней, а также потому что стандартная ошибка распределения больше.
Распределения более чем с одним пиком обычно называются мультимодальными. Они могут указывать на совмещение двух или более нормальных распределений, и, следовательно, возможно, на совмещение двух или более популяций. Классическим примером бимодальности является распределение показателей роста людей, поскольку модальный рост мужчин выше, чем у женщин.
Данные выходных дней имеют другие характеристики в отличие от данных будних дней. Мы должны удостовериться, что мы сравниваем подобное с подобным. Отфильтруем наш первоначальный набор данных только по выходным дням:
def ex_2_13():
'''Сводные статистики данных,
отфильтрованных только по выходным дням'''
df = with_parsed_date( load_data('dwell-times. tsv') )
df.index = df['date']
df = df[df['date'].index.dayofweek > 4] # суббота-воскресенье
weekend_times = df['dwell-time']
print('n: ', weekend_times.count())
print('Среднее: ', weekend_times.mean())
print('Медиана: ', weekend_times.median())
print('Стандартное отклонение: ', weekend_times.std())
print('Стандартная ошибка: ', standard_error(weekend_times))
tsv') )
df.index = df['date']
df = df[df['date'].index.dayofweek > 4] # суббота-воскресенье
weekend_times = df['dwell-time']
print('n: ', weekend_times.count())
print('Среднее: ', weekend_times.mean())
print('Медиана: ', weekend_times.median())
print('Стандартное отклонение: ', weekend_times.std())
print('Стандартная ошибка: ', standard_error(weekend_times)) n: 5860 Среднее: 117.78686006825939 Медиана: 81.0 Стандартное отклонение: 120.65234077179436 Стандартная ошибка: 1.5759770362547678
Итоговое среднее значение в выходные дни (на основе 6-ти месячных данных) составляет 117.8 сек. и попадает в пределы 95%-ого интервала уверенности для маркетинговой выборки. Другими словами, хотя среднее значение времени пребывания в размере 130 сек. является высоким даже для выходных, расхождение не настолько большое, что его нельзя было бы приписать простой случайной изменчивости в выборке.
Мы только что применили подход к установлению подлинного расхождения в популяциях (между посетителями веб-сайта в выходные по сравнению с посетителями в будние дни), который при проведении проверки обычно не используется. Более традиционный подход начинается с выдвижения гипотетического предположения, после чего это предположение сверяется с данными. Для этих целей статистический метод анализа определяет строгий подход, который называется проверкой статистических гипотез.
Это и будет темой следующего поста, поста №3.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Как рассчитать выборочную дисперсию? – Обзоры Вики
Шаги для нахождения выборочной дисперсии следующие:
- Найдите среднее значение данных.
- Вычтите среднее из каждой точки данных.
- Возьмите суммирование квадратов значений, полученных на предыдущем шаге.
- Разделите это значение на n – 1.

Как найти выборочную дисперсию вручную? Чтобы вычислить дисперсию, выполните следующие действия: Определите среднее значение (простое среднее число) Затем для каждого числа: вычесть среднее значение и возвести результат в квадрат (разность в квадрате). Затем вычислите среднее значение этих квадратов разностей.
Дополнительно Что такое выборочная дисперсия в статистике? Выборочная дисперсия (с2) является мера степени разброса чисел в списке. Если все числа в списке близки к ожидаемым значениям, дисперсия будет небольшой. Если они далеко, разница будет большой.
Как быстрее всего найти выборочную дисперсию? Как рассчитать дисперсию
- Найдите среднее значение набора данных. Сложите все значения данных и разделите на размер выборки n. …
- Найдите квадрат разницы от среднего для каждого значения данных.
 Вычтите среднее значение из каждого значения данных и возведите результат в квадрат. …
Вычтите среднее значение из каждого значения данных и возведите результат в квадрат. … - Найдите сумму всех квадратов разностей. …
- Рассчитайте дисперсию.
Как найти выборочную дисперсию в R?
В R выборочная дисперсия равна вычисляется с помощью функции var (). В тех редких случаях, когда вам нужна дисперсия генеральной совокупности, используйте среднее значение генеральной совокупности для расчета выборочной дисперсии и умножьте результат на (n-1)/n; обратите внимание, что по мере того, как размер выборки становится очень большим, дисперсия выборки сходится к дисперсии генеральной совокупности.
Как рассчитать SP в статистике? Чтобы рассчитать SP, вы сначала определить баллы отклонения для каждого X и для каждого Y, затем вы вычисляете произведения каждой пары баллов отклонения, а затем (последний) вы суммируете продукты.
Как выборочная дисперсия измеряет изменчивость? В отличие от предыдущих мер изменчивости, дисперсия включает в расчет все значения путем сравнения каждого значения со средним значением. Чтобы рассчитать эту статистику, вы вычислить набор квадратов разностей между точками данных и средним значением, суммировать их, а затем разделить на количество наблюдений.
Чтобы рассчитать эту статистику, вы вычислить набор квадратов разностей между точками данных и средним значением, суммировать их, а затем разделить на количество наблюдений.
Как найти выборочную дисперсию и стандартное отклонение?
- Шаг 1. Найдите среднее значение.
- Шаг 2: Вычтите среднее значение из каждой оценки.
- Шаг 3: возведите каждое отклонение в квадрат.
- Шаг 4: Добавьте квадраты отклонений.
- Шаг 5: Разделите сумму на количество баллов.
- Шаг 6: извлеките квадратный корень из результата шага 5.
Также Что такое N в формуле выборочной дисперсии? В статистике поправка Бесселя — это использование n — 1 вместо n в формуле для выборочной дисперсии и выборочного стандартного отклонения, где n — количество наблюдений в выборке. Этот метод исправляет систематическую ошибку в оценке дисперсии генеральной совокупности. … Дает объективную оценку дисперсии совокупности.
Как найти выборочную дисперсию в Excel?
Пример формулы дисперсии в Excel
- Найдите среднее значение с помощью функции СРЕДНИЙ: = СРЕДНИЙ (B2: B7)…
- Вычтите среднее значение из каждого числа в выборке:…
- Возведите каждую разницу в квадрат и поместите результаты в столбец D, начиная с D2:…
- Сложите квадраты разностей и разделите результат на количество элементов в выборке минус 1:
Что делает var() в R? Функция var() на языке R вычисляет выборочную дисперсию вектора. Это мера того, насколько значение отличается от среднего значения.
Это мера того, насколько значение отличается от среднего значения.
Как вы находите отклонение от R Squared?
Чтобы вычислить общую дисперсию, вы должны вычесть среднее фактическое значение из каждого фактического значения, возвести результаты в квадрат и просуммировать их. Оттуда, разделить первую сумму ошибок (объясненная дисперсия) на вторую сумму (общая дисперсия), вычтите результат из единицы, и вы получите R-квадрат.
Как рассчитать стандартное отклонение выборки в R studio?
Что такое ИП в статистике? Сумма произведений отклонений это математический термин, используемый для измерения вариации, разделяемой между двумя изучаемыми переменными. … Получить произведения каждой пары отклонений. Наконец, добавьте все значения произведений каждой пары отклонений, которые приводят к сумме произведений отклонений, сокращенно обозначаемых как SP.
Что такое СП и КП? Ответ – CP и SP являются аббревиатурами Себестоимость и цена продажи. Себестоимость — это сумма, которую мы платим за покупку товара, по которой он доступен. Точно так же цена продажи — это скорость, по которой продается товар, которую мы обозначаем сокращенно как SP. … Всегда помните, что вы рассчитываете прибыль или убыток по себестоимости.
Что такое SP и SS в статистике?
Понятия очень похожи. Основное отличие состоит в том, что в SS у нас была только одна переменная (X), а в SP у нас две переменные (X и Y). Сумма квадратов (СС) Сумма произведений (SP)
Как количественно оценить изменчивость? Вариабельность чаще всего измеряется с помощью следующих описательных статистических данных:
- Диапазон: разница между самым высоким и самым низким значениями.
- Межквартильный размах: диапазон средней половины распределения.
- Стандартное отклонение: среднее расстояние от среднего.
- Дисперсия: среднее квадратов расстояний от среднего.

Как лучше всего измерить изменчивость?
Межквартильный размах — лучший показатель изменчивости для искаженных распределений или наборов данных с выбросами. Поскольку он основан на значениях, взятых из средней половины распределения, маловероятно, что на него повлияют выбросы.
Какая мера изменчивости является самой простой? Диапазонеще одна мера распространения — это просто разница между наибольшим и наименьшим значениями данных. Диапазон — это простейшая мера изменчивости для вычисления.
Как найти выборочную дисперсию в R?
В R выборочная дисперсия рассчитывается с помощью функция var(). В тех редких случаях, когда вам нужна дисперсия генеральной совокупности, используйте среднее значение генеральной совокупности для расчета выборочной дисперсии и умножьте результат на (n-1)/n; обратите внимание, что по мере того, как размер выборки становится очень большим, дисперсия выборки сходится к дисперсии генеральной совокупности.
Является ли выборочная дисперсия таким же, как стандартное отклонение? Стандартное отклонение — это разброс группы чисел от среднего. Дисперсия измеряет среднюю степень, в которой каждая точка отличается от среднего значения. … Чай стандартное отклонение выражается в тех же единицах, что и набор данных но дисперсия выражается как большее число, потому что это квадрат результата.
Дисперсия измеряет среднюю степень, в которой каждая точка отличается от среднего значения. … Чай стандартное отклонение выражается в тех же единицах, что и набор данных но дисперсия выражается как большее число, потому что это квадрат результата.
Какова дисперсия первого N натурального числа?
Дисперсия первых n натуральных чисел равна 6n−1.
Как вы рассчитываете статистику выборки? Как рассчитать выборочное среднее
- Сложите образцы элементов.
- Разделите сумму на количество образцов.
- Результат — среднее.
- Используйте среднее значение, чтобы найти дисперсию.
- Используйте дисперсию, чтобы найти стандартное отклонение.
Что означает выборка? (с примерами) – Zippia
- Что означает выборка?
- Почему выборочное среднее значение важно?
- Как рассчитать выборочное среднее
- Что такое дисперсия?
- Как рассчитать дисперсию
- Что такое стандартная ошибка выборки?
- Как рассчитать стандартную ошибку
- Часто задаваемые вопросы о среднем значении выборки
- Заключительные мысли
- Зарегистрируйтесь для получения дополнительных советов и вакансий
Показать больше
Нет ничего более важного для роста и успеха бизнеса, чем их усилия по статистическому анализу. Он предоставляет информацию, необходимую для разработки стратегического планирования и принятия решений. Основа статистики основана на использовании выборок, чтобы предлагать прогнозы, которые можно применить к более крупным группам населения.
Он предоставляет информацию, необходимую для разработки стратегического планирования и принятия решений. Основа статистики основана на использовании выборок, чтобы предлагать прогнозы, которые можно применить к более крупным группам населения.
Обращение к выборочному среднему является ступенькой для формирования более широких выводов и развития.
Что означает образец?
Среднее значение выборки определяется как среднее значение данного набора выборок. Среднее значение выборки представлено математически как x. Это считается отправной точкой для начала дальнейшего анализа.
Обычно выбирают среднее значение выборки, чтобы реализовать это значение в более сложной и подробной формуле, такой как центральная тенденция и стандартное отклонение набора выборки.
Понятие выборочного среднего возникнет на раннем этапе изучения статистики.
Почему выборочное среднее значение важно?
Самым очевидным преимуществом расчета выборочного среднего является то, что он может предоставить информацию, которая точно применима к большей совокупности. Это важно, поскольку позволяет получить статистическую информацию, не прибегая к невыполнимой задаче опроса всех участников.
Это важно, поскольку позволяет получить статистическую информацию, не прибегая к невыполнимой задаче опроса всех участников.
Кроме того, выборочное среднее значение используется в различных отраслях промышленности. Любая область, связанная с научными исследованиями, например, биология и химия, будет использовать среднее значение выборки на ранних этапах своих конкретных исследований.
Ввод данных и ИТ-работы используют выборочные средние значения для достижения ежедневных целей. Даже в бизнесе среднее значение выборки необходимо для выполнения расчетов темпов роста.
Хотя вы можете смутно припоминать среднее значение выборки как далекое воспоминание из школьной математики, оно применяется во многих областях и может быть чрезвычайно полезным по многим причинам.
Как рассчитать выборочное среднее
Математика любого рода поначалу может вызвать стресс у многих людей, но вычисление выборочного среднего — одно из самых простых вычислений, которые вы найдете в статистике.
Как и в любом другом стандартном статистическом уравнении, вам необходимо выполнить определенную формулу и выполнить определенные действия, чтобы получить правильное среднее значение выборки. Прежде чем пытаться найти среднее значение выборки вашей организации, вы должны сначала рассмотреть формулу.
Формула для вычисления среднего значения выборки: x#772;=(Σxi) / n
При первом взгляде на эту формулу вы, возможно, уже готовы сдаться, но кажущийся сложным язык уравнения на самом деле довольно прост, если его разбить.
В уравнении x#772 представляет ответ, который вы ищете, то есть среднее значение выборки.
Символ Σ математически означает «сложите следующие числа».
xi в круглых скобках означает «все значения x», которые будут значениями для каждой части данных, которые вы исследуете.
Наконец, уравнение просит вас разделить на n, что означает общее количество сравниваемых значений.

Сразу нужно понять многое, но давайте рассмотрим это шаг за шагом. Чтобы лучше понять процесс нахождения среднего значения выборки, рассмотрим шаги с точки зрения следующего примера.
Компания-поставщик телефонных услуг заинтересована в получении дополнительной информации о статистических тенденциях своей клиентской базы. Чтобы начать этот процесс, они должны определить среднее значение выборки. Они решают сравнить общее количество клиентов за последние шесть месяцев, чтобы получить среднее количество людей, пользующихся их услугами.
Телефонная компания записывает следующие значения для каждого из шести месяцев:
Январь – 20 000 клиентов
Февраль -18 000 клиентов
Март — 20 400 клиентов
Апрель — 21 050 клиентов
Май – 23 000 клиентов
июнь – 22 300 клиентов
Сложите значения вместе.
 На первом этапе поиска среднего значения выборки нам предлагается сложить вместе все значения в выборке. Чтобы применить это к примеру телефонной компании, они начинают с суммирования количества клиентов, которые у них были каждый месяц.
На первом этапе поиска среднего значения выборки нам предлагается сложить вместе все значения в выборке. Чтобы применить это к примеру телефонной компании, они начинают с суммирования количества клиентов, которые у них были каждый месяц.20 000+18 000+20 400+21 050+23 000+22 300 = 124 750
Число 124 750 представляет собой общее количество клиентов, которые были у поставщика услуг телефонной связи за шесть месяцев выборки.
Определите значение n. Значение n в уравнении для выборочного среднего показывает, сколько элементов сравнивается. Поскольку телефонная компания сравнивает ежемесячное количество клиентов за шесть месяцев, значение n в этом примере будет равно 6,9.0025
Введите значения и разделите. Последний шаг к вычислению среднего значения выборки — ввести значения, которые вы определили, в исходное уравнение и разделить для решения. Для телефонной компании это означало бы, что они должны разделить 124 750 на 6, чтобы получить среднее значение выборки.

124 750 / 6 = 20 792
Среднее значение выборки клиентской базы телефонной компании за шесть месяцев составляет 20 792 человека.
Что такое дисперсия?
Дисперсия означает, насколько разбросаны числа в наборе. Хотя вы получили среднее значение с помощью формулы выборочного среднего, вычисление дисперсии набора покажет вам, насколько далеко каждое значение отличается от других в наборе.
Хотя дисперсия сама по себе является важным значением, основная цель выполнения этого уравнения состоит в том, чтобы иметь возможность завершить процесс определения стандартной ошибки набора позже.
Как рассчитать дисперсию
После того, как вы нашли выборочное среднее для своего набора, вы можете использовать его для определения дисперсии.
Выполните следующие действия, чтобы определить дисперсию выборки.
Вычтите среднее значение выборки из каждого значения. Чтобы начать поиск дисперсии, вам нужно будет вычесть только что найденное вами выборочное среднее из каждого значения в наборе.
 В примере с телефонной компанией это означало бы вычитание 20 792 из стоимости каждого месяца.
В примере с телефонной компанией это означало бы вычитание 20 792 из стоимости каждого месяца.(20 000-20 792) (18 000-20 792) (20 400-20 792) (21 050-20 792) (23 000-29 792) (22 300-20,79)2) = (-792, -2,792, -392, 258, 2,028, 1,328)
Возведите полученные значения в квадрат. После вычитания среднего значения выборки из каждого значения продолжайте возведение в квадрат каждого из оставшихся новых чисел. Для примера с телефонной компанией возведение в квадрат каждого значения приведет к новым значениям:
.(627 264) (7 795 264) (153 664) (66 564) (4 112 784) (1 763 584)
Завершите пример формулы среднего значения. Последний шаг к определению дисперсии в наборе — подставить новые значения, которые вы нашли, вычитая и возводя в квадрат исходную формулу выборочного среднего. Завершите уравнение, как обычно, чтобы получить дисперсию выборки.
(627 264)+(7 795 264)+(153 664)+(66 564)+(4 112 784)+(1 763 584) = 14 519 124
14 519 124 / 6 = 2 419 854
Размер ответа описывает, насколько велика дисперсия в наборе. Результат примера с телефонным провайдером имеет чрезвычайно высокую степень дисперсии, что означает большую разницу между каждым из значений.
Результат примера с телефонным провайдером имеет чрезвычайно высокую степень дисперсии, что означает большую разницу между каждым из значений.
Если мы вернемся к исходным точкам данных о том, сколько клиентов было у компании в месяц, мы увидим, что эта разница очевидна. В период с января по февраль у провайдера наблюдалось резкое падение числа клиентов на 2000 всего за один месяц, за которым последовали более существенные всплески. Разница в этих исходных значениях влияет на результат формулы дисперсии.
Что такое стандартная ошибка выборки?
Стандартная ошибка также является мерой того, как числа распределены по набору, но она оценивает, насколько далеко каждая точка данных находится от среднего значения по сравнению друг с другом. Это также известно как скорость распределения.
Хотя среднее значение выборки дает информацию о среднем значении выборки, а дисперсия измеряет разницу между каждым значением в выборке, стандартная ошибка немного отличается.
В большинстве распределений все значения находятся в пределах двух стандартных отклонений от среднего значения, если только это не выброс.
Как рассчитать стандартную ошибку
Вычисление выборочного среднего и дисперсии требует как минимум нескольких шагов для завершения процесса. Тем не менее, вы уже проделали большую часть работы по поиску стандартной ошибки после того, как запустили эти уравнения. Нахождение стандартной ошибки заданной постдисперсии — это только один шаг.
Найдите квадратный корень из значения дисперсии. Для определения стандартной ошибки по значению дисперсии требуется только найти квадратный корень из этого числа. В примере с телефонной компанией мы найдем квадратный корень из 2 419 854, чтобы определить стандартную ошибку.
#8730;2 419 854 =1 556
Стандартная ошибка для выборки телефонной компании составляет 1556. Это очень большое стандартное отклонение, означающее, что значения, удаленные от среднего значения выборки, разбросаны и более неточны для применения к большей выборке.
 Другими словами, данные, найденные в телефонной компании, демонстрируют противоречивые выборочные значения и не будут отражать средние показатели по всей телефонной отрасли.
Другими словами, данные, найденные в телефонной компании, демонстрируют противоречивые выборочные значения и не будут отражать средние показатели по всей телефонной отрасли.
Дополнительный пример
Профессор колледжа хочет знать статистику оценок последнего теста, который он дал своему классу.
Результаты тестов для класса были следующими: (82, 88, 83, 89, 91, 79, 85, 93, 83)
Он начинает процесс оценки, складывая вместе все тестовые значения в своем классе и разделив результат на 9, количество учеников в классе.
82+88+83+89+91+79+85+93+83 = 773
773 / 9 = 85,89
Среднее выборочное значение тестов в классе профессора составляет 85,89. Он продолжает, находя разницу между тестовыми оценками. Это делается путем вычитания среднего значения выборки 85,89 из каждого значения и возведения в квадрат полученных чисел.
(82-85,89) (88-85,89) (83-85,89) (89-85,89) (91-85,89) (79-85,89) (85-85,89) (93-85,89) (83-85,89) = (-3,89) , 2,11, -2,89, 3,11, 5,11, -6,89, -0,89, 7,11, -2,89)
(-3,89, 2,11, -2,89, 3,11, 5,11, -6,89, -0,89, 7,11, -2,89)² = (15,13, 4,45, 8,35, 9,67, 26,11, 47,47, 0,79, 50,55, 8,35)
Чтобы закончить вычисление дисперсии, профессор подставляет новые значения, которые он нашел, и решает, используя формулу выборочного среднего.
(15,13+4,45+8,35+9,67+26,11+47,47+0,79+50,55+8,35) = 170,87
170,87 / 9 = 18,99
Разница между оценками в этом тесте составляет 18,99, что свидетельствует о значительной вариации между оценками, но ничего необычного.
Теперь, когда профессор собрал все необходимые ему значения, он возводит результат дисперсии в квадрат, чтобы найти стандартную ошибку выборки класса.
радикал;18,99=4,36
Стандартная ошибка оценок за тест составляет 4,36. Это означает, что большинство оценок в классе находятся в пределах 4,36 балла выше или ниже среднего значения 85,89.
Выборочное среднее Часто задаваемые вопросы
Что такое среднее значение выборки и среднее значение генеральной совокупности? Среднее значение выборки совпадает со средним значением распределения генеральной совокупности, однако дисперсия намного больше при меньшем размере выборки и мала при больших размерах выборки.
Чему равно выборочное среднее? Среднее значение выборочного распределения обязательно будет таким же, как и среднее значение исходного распределения.
 Среднее значение выборки равно среднему значению генеральной совокупности.
Среднее значение выборки равно среднему значению генеральной совокупности.Среднее значение выборки и среднее значение одно и то же? Обычно, когда люди говорят о среднем значении, они имеют в виду среднее значение населения. Однако когда вы смотрите только на выборочную группу, вы используете термин выборочное среднее.
Как рассчитывается выборочное среднее? Суммируйте числа в вашем наборе данных и разделите сумму на количество точек данных — это ваше среднее значение.
Что такое центральная предельная теорема? В общих чертах, Центральная предельная теорема утверждает, что по мере того, как среднее значение выборки становится больше, оно приближается к нормальному распределению. Это верно для выборок независимых случайных величин, независимо от распределения совокупности, если стандартное отклонение совокупности не бесконечно.
Это замечательно, потому что дает нам метод превращения ненормальных распределений в нормальные.
 Это, в свою очередь, позволяет нам применять те же правила, которые, как мы знаем, справедливы для нормальных распределений, к ненормальным.
Это, в свою очередь, позволяет нам применять те же правила, которые, как мы знаем, справедливы для нормальных распределений, к ненормальным.
Заключительные мысли
Вам не нужно быть статистиком, чтобы извлечь выгоду из использования выборочных средних. Каждый бизнес заботится о прогнозировании тенденций для большей совокупности на основе меньшего размера выборки. Знание среднего значения определенного набора данных может помочь в оценке ожидаемых результатов.
Выборочное среднее также полезно для расчета выборочной дисперсии, стандартного отклонения и стандартной ошибки. Действительно, основа статистического анализа заключается в возможности делать общие утверждения о больших совокупностях на основе меньших, что делает выборочное среднее одним из самых важных уравнений, которые необходимо знать.
Насколько полезен был этот пост?
Нажмите на звездочку, чтобы оценить!
Средний рейтинг / 5. Количество голосов:
Голосов пока нет! Будьте первым, кто оценит этот пост.
Никогда не упускайте подходящую для вас возможность.
6.1: Среднее значение и стандартное отклонение выборочного среднего
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 569
Цели обучения
- Ознакомиться с концепцией распределения вероятностей выборочного среднего.
- Понимать значение формул для среднего и стандартного отклонения выборочного среднего.
Предположим, мы хотим оценить среднее значение \(µ\) совокупности. На практике мы обычно берем только один образец. Однако представьте, что мы берем выборку за выборкой одинакового размера \(n\) и каждый раз вычисляем среднее значение выборки \(\bar{x}\). Среднее значение выборки \(x\) является случайной величиной: оно меняется от выборки к выборке таким образом, что его нельзя предсказать с уверенностью. Мы будем писать \(\bar{X}\), когда среднее значение выборки рассматривается как случайная величина, и писать \(x\) для значений, которые она принимает. Случайная величина \(\bar{X}\) имеет среднее значение, обозначаемое \(μ_{\bar{X}}\), и стандартное отклонение, обозначаемое \(σ_{\bar{X}}\). Вот пример с таким небольшим населением и небольшим размером выборки, что мы можем записать каждую отдельную выборку.
Среднее значение выборки \(x\) является случайной величиной: оно меняется от выборки к выборке таким образом, что его нельзя предсказать с уверенностью. Мы будем писать \(\bar{X}\), когда среднее значение выборки рассматривается как случайная величина, и писать \(x\) для значений, которые она принимает. Случайная величина \(\bar{X}\) имеет среднее значение, обозначаемое \(μ_{\bar{X}}\), и стандартное отклонение, обозначаемое \(σ_{\bar{X}}\). Вот пример с таким небольшим населением и небольшим размером выборки, что мы можем записать каждую отдельную выборку.
Пример \(\PageIndex{1}\)
Команда гребцов состоит из четырех гребцов весом \(152\), \(156\), \(160\) и \(164\) фунтов. Найдите все возможные случайные выборки с заменой размера два и вычислите среднее значение выборки для каждой из них. Используйте их, чтобы найти распределение вероятностей, среднее значение и стандартное отклонение выборочного среднего \(\bar{X}\).
Решение
В следующей таблице показаны все возможные образцы с заменой размера два вместе со средним значением для каждого:
| Образец | Среднее | Образец | Среднее | Образец | Среднее | Образец | Среднее | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 152, 152 | 152 | 156, 152 | 154 | 160, 152 | 156 | 164, 152 | 158 | |||
| 152, 156 | 154 | 156, 156 | 156 | 160, 156 | 158 | 164, 156 | 160 | |||
| 152, 160 | 156 | 156, 160 | 158 | 160, 160 | 160 | 164, 160 | 162 | |||
| 152, 164 | 158 | 156, 164 | 160 | 160, 164 | 162 | 164, 164 | 164 |
Из таблицы видно, что существует семь возможных значений выборочного среднего \(\bar{X}\). Значение \(\bar{x}=152\) встречается только в одном случае (оба раза должен быть выбран гребец весом \(152\) фунтов), как и значение \(\bar{x}=164\), но другие значения встречаются более чем одним способом, поэтому их можно наблюдать с большей вероятностью, чем \(152\) и \(164\). Поскольку выборки \(16\) равновероятны, мы получаем распределение вероятностей среднего значения выборки, просто подсчитывая:
Значение \(\bar{x}=152\) встречается только в одном случае (оба раза должен быть выбран гребец весом \(152\) фунтов), как и значение \(\bar{x}=164\), но другие значения встречаются более чем одним способом, поэтому их можно наблюдать с большей вероятностью, чем \(152\) и \(164\). Поскольку выборки \(16\) равновероятны, мы получаем распределение вероятностей среднего значения выборки, просто подсчитывая:
\[\begin{array}{c|c c c c c c c} \bar{x} & 152 & 154 & 156 & 158 & 160 & 162 & 164\\ \hline P(\bar{x}) &\frac{1} {16} &\frac{2}{16} &\frac{3}{16} &\frac{4}{16} &\frac{3}{16} &\frac{2}{16} &\ frac{1}{16}\\ \end{массив} \nonumber\]
Теперь применим формулы из раздела 4.2 к \(\bar{X}\). Для \(\mu_{\bar{X}}\) мы получаем.
\[\begin{align*} μ_{\bar{X}} &=\sum \bar{x} P(\bar{x}) \\[4pt] &=152\left ( \dfrac{1} {16}\вправо)+154\влево (\dfrac{2}{16}\вправо)+156\влево (\dfrac{3}{16}\вправо)+158\влево (\dfrac{4}{16) }\right )+160\left ( \dfrac{3}{16}\right )+162\left ( \dfrac{2}{16}\right )+164\left ( \dfrac{1}{16}\ справа ) \\[4pt] &=158 \end{align*} \] 92} \\[4pt] &=\sqrt{10} \end{align*}\]
Среднее значение и стандартное отклонение совокупности \(\{152,156,160,164\}\) в примере равны \(µ = 158\) и \(σ=\sqrt{20}\). Среднее значение выборочного среднего \(\ bar{X}\), которое мы только что вычислили, является в точности средним значением генеральной совокупности. Стандартное отклонение выборочного среднего \(\bar{X}\), которое мы только что вычислили, представляет собой стандартное отклонение генеральной совокупности, деленное на квадратный корень из размера выборки: \(\sqrt{10} = \sqrt{20 }/\sqrt{2}\). Эти отношения не являются совпадениями, а являются иллюстрациями следующих формул.
Среднее значение выборочного среднего \(\ bar{X}\), которое мы только что вычислили, является в точности средним значением генеральной совокупности. Стандартное отклонение выборочного среднего \(\bar{X}\), которое мы только что вычислили, представляет собой стандартное отклонение генеральной совокупности, деленное на квадратный корень из размера выборки: \(\sqrt{10} = \sqrt{20 }/\sqrt{2}\). Эти отношения не являются совпадениями, а являются иллюстрациями следующих формул.
Определение: Среднее значение выборки и стандартное отклонение выборки
Предположим, что случайные выборки размера \(n\) взяты из совокупности со средним значением \(µ\) и стандартным отклонением \(σ\). Среднее \(\mu_{\bar{X}}\) и стандартное отклонение \(σ_{\bar{X}}\) выборочного среднего \(\bar{X}\) удовлетворяют
\[μ_{ \bar{X}} =μ \label{average}\]
и
\[σ_{\bar{X}}=\dfrac{σ}{\sqrt{n}} \label{std}\]
Уравнение \(\ref{average}\) говорит, что если бы мы могли взять каждую возможную выборку из совокупности и вычислить соответствующее среднее значение выборки, то эти числа были бы сосредоточены на числе, которое мы хотим оценить, среднее значение совокупности \(μ\ ). Уравнение \(\ref{std}\) говорит о том, что средние значения, вычисленные по выборкам, различаются меньше, чем отдельные измерения населения, и количественно определяет взаимосвязь.
Уравнение \(\ref{std}\) говорит о том, что средние значения, вычисленные по выборкам, различаются меньше, чем отдельные измерения населения, и количественно определяет взаимосвязь.
Пример \(\PageIndex{2}\)
Среднее значение и стандартное отклонение налоговой стоимости всех транспортных средств, зарегистрированных в определенном штате, составляют \(μ=\$13 525\) и \(σ=\$4 180\). Предположим, что случайные выборки размером \(100\) взяты из совокупности транспортных средств. Каковы среднее \(\mu_{\bar{X}}\) и стандартное отклонение \(σ_{\bar{X}}\) выборочного среднего \(\bar{X}\)?
Решение
Поскольку \(n = 100\), формулы дают
\[\mu _{\bar{X}} =\mu = \$13,525 \nonumber\]
и
\[\sigma _{\bar{x}}=\frac{\sigma}{\sqrt{n}}=\frac{\$4,180}{\sqrt{100}}=\$418 \nonumber \]
- Среднее значение выборки является случайной величиной; как таковой он пишется \(\bar{X}\), а \(\bar{x}\) обозначает отдельные значения, которые он принимает.

- В качестве случайной величины среднее значение выборки имеет распределение вероятностей, среднее значение \(μ_{\bar{X}}\) и стандартное отклонение \(σ_{\bar{X}}\).
- Существуют формулы, связывающие среднее значение и стандартное отклонение среднего значения выборки со средним значением и стандартным отклонением генеральной совокупности, из которой взята выборка.
Эта страница под названием 6.1: Среднее и стандартное отклонение выборочного среднего распространяется по лицензии CC BY-NC-SA 3.0 и была создана, изменена и/или курирована посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Аноним
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать оглавление
- нет
- Теги
- выборочное среднее
- образец Стандартное отклонение
- источник@https://2012books.
 lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics
Калькулятор стандартного отклонения выборочного среднего
Created by Luis Hoyos
Отзыв от Steven Wooding
Последнее обновление: 22 сентября 2022 г.
Содержание:- Каково стандартное отклонение распределения выборочного среднего?
- В чем разница между выборочным распределением и выборочным распределением?
- Как рассчитать стандартное отклонение выборочного среднего?
- Пример определения стандартного отклонения выборочного среднего (с помощью этого калькулятора)
- Часто задаваемые вопросы
Расчет стандартное отклонение выборочного среднего (также известное как стандартное отклонение выборочного распределения среднего) — отличный способ понять, как размер выборки влияет на ошибку наших оценок.
Когда стандартное отклонение среднего умножается на критическое значение, такое как z-показатель или t-статистика, мы получаем погрешность, которая позволяет указать доверительный интервал нашего прогноза. Следовательно, вычисление стандартного отклонения выборочного распределения среднего указывает, где может быть среднее значение генеральной совокупности.
Следовательно, вычисление стандартного отклонения выборочного распределения среднего указывает, где может быть среднее значение генеральной совокупности.
🔎 После расчета стандартного отклонения распределения выборочных средних вы можете сделать еще один шаг вперед и использовать наш калькулятор нормальной вероятности для выборочных распределений.
Каково стандартное отклонение распределения среднего значения выборки?
Прежде всего, важно уточнить, что этот термин известен под разными именами, такими как:
- Стандартное отклонение среднего;
- Стандартное отклонение выборочного среднего;
- Стандартное отклонение распределения выборочных средних; и
- Стандартное отклонение выборочного распределения выборочного среднего.
Также необходимо знать некоторые определения и понятия:
- Статистические данные: точечная оценка или числовая характеристика выборки (т. е. выборочное среднее).
 Он отличается от параметра, такого как среднее значение генеральной совокупности.
Он отличается от параметра, такого как среднее значение генеральной совокупности. - Распределение выборки: распределение вероятностей случайно выбранной статистики. Другими словами, это распределение всех возможных значений, которые может принять статистика при одном и том же размере выборки.
- Выборочное распределение среднего: это расширение предыдущей концепции. Если у вас есть популяция, возьмите бесконечные выборки размером n и нанесите их средние значения на гистограмму, вы получите распределение вероятностей. Это распределение вероятностей — это то, что мы называем выборочным распределением среднего , и, как и любое другое распределение, оно имеет свое собственное среднее значение и стандартное отклонение.
На следующей диаграмме показано, как создать выборочное распределение среднего значения. На самом деле мы используем не шесть сэмплов, а почти бесконечное число (то есть 100 000).
Тем не менее, мы можем определить среднее стандартное отклонение как стандартное отклонение распределения средних (как показано на последней диаграмме). Кроме того, среднее значение этого выборочного распределения равно среднему значению генеральной совокупности.
Теперь, когда вы знакомы с концепцией, давайте посмотрим, как рассчитать стандартное отклонение выборочного среднего.
В чем разница между выборочным распределением и выборочным распределением?
Разница между выборочным и выборочным распределением составляет:
- Выборочное распределение: это термин, который мы обычно слышим. Это относится к распределению вероятностей случайно выбранной статистики. Выборочное распределение среднего является примером.
- Распределение выборки: учитывает распределение наблюдений только в пределах одной выборки.
 Каждое выборочное распределение имеет среднее значение, которое помогает сформировать выборочное распределение .
Каждое выборочное распределение имеет среднее значение, которое помогает сформировать выборочное распределение .
Как рассчитать стандартное отклонение выборочного среднего?
The formula to find the standard deviation of the sample mean is:
σ X̄ = σ /√ n
where:
- σ X̄ – Стандартное отклонение выборочного среднего;
- σ – стандартное отклонение населения; и
- n — Размер выборки.
Ранее мы говорили, что если мы знаем среднее значение выборочного распределения ( μ X̄ ), мы также знаем среднее значение генеральной совокупности ( μ ), поскольку они равны ( μ X̄ = μ ). На практике мы никогда не знаем μ X̄ , но мы можем оценить это, используя среднее значение выборки ( X̄ ).
На практике мы никогда не знаем μ X̄ , но мы можем оценить это, используя среднее значение выборки ( X̄ ).
σ X̄ указывает, как X̄ приближается к μ . Меньшее σ X̄ , ближайшее μ может быть получено из нашей оценки. Поскольку σ постоянно, увеличение размера выборки — единственный способ уменьшить σ X̄ . Следовательно, увеличение n — это способ уменьшить ошибку выборки наших оценок.
Пример того, как найти стандартное отклонение среднего значения выборки (с помощью этого калькулятора)
Мы знаем, что среднее значение и стандартное отклонение роста взрослого женского населения Америки составляет около μ = 161,3 см и σ = 7,1 см . Теперь предположим, что вы случайным образом берете образцы из 100 женщин и каждый раз измеряете их средний рост. Каково среднее стандартное отклонение выборки?
Теперь предположим, что вы случайным образом берете образцы из 100 женщин и каждый раз измеряете их средний рост. Каково среднее стандартное отклонение выборки?
Чтобы узнать ответ, выполните следующие действия:
- Введите 7.1 в поле стандартного отклонения генеральной совокупности.
- Введите 100 в поле размера выборки.
- Вот и все. Ответ должен быть 0,71. Таким образом, стандартное отклонение выборочных распределений средних значений n = 100 равно 0,71 .
Результаты можно проверить по формуле: = 0,71σXˉ=nσ=1007,1=0,71
Часто задаваемые вопросы
Как найти среднее значение и стандартное отклонение выборочного распределения?
- Чтобы найти стандартное отклонение выборочного среднего ( σ X̄ ), разделите стандартное отклонение генеральной совокупности ( σ ) на квадратный корень из размера выборки (n): σ X̄ = σ / √ n .

- В отличие от стандартного отклонения, , чтобы вычислить среднее значение выборочного распределения среднего ( μ X̄ ), вам нужно только среднее значение совокупности ( μ ), так как они оба одинаковы ( μ X̄ = μ ).
Как называется стандартное отклонение среднего значения выборки?
Стандартное отклонение выборочных средних называется по-разному:
- Стандартное отклонение среднего.
- Стандартное отклонение распределения выборочных средних.
- Стандартное отклонение выборочного распределения выборочного среднего.
Математически вы вычисляете стандартное отклонение среднего значения выборки по формуле σ X̄ = σ/√n.
Стандартная ошибка среднего (SE(X̄)) — это другая статистика, в которой вместо σ используется выборочное стандартное отклонение (s). Его формула SE(X̄) = s/√n.
Как создать выборочное распределение среднего значения?
Выполните следующие действия, чтобы создать выборочное распределение среднего:
- Определите размер выборки.

- Возьмите случайную выборку такого размера и рассчитайте ее среднее значение.
- Постройте среднее значение на гистограмме.
- Повторяйте этот процесс почти бесконечное количество раз (т. е. 100 000 раз), пока распределение не сойдется.
Что означает стандартное отклонение, равное 1?
Если мы находимся перед нормальным распределением, стандартное отклонение 1 ( σ = 1) означает, что 68,27% значений распределения лежат в пределах одного стандартного отклонения от среднего. В математической записи: Pr( μ -1 σ ≤ X ≤ μ +1 σ ) ≈ 68,27%.
Луис Ойос
Стандартное отклонение населения (σ)
Размер выборки (n)
Стандартное отклонение среднего значения выборки (σₓ)
Проверить 29 похожих калькуляторов логической статистики 📉
AB testКоэффициент детерминации 2…
4.1 — Выборочное распределение выборочного среднего
В следующем примере мы иллюстрируем выборочное распределение среднего значения выборки для очень небольшой совокупности. Метод выборки осуществляется без замены.
Метод выборки осуществляется без замены.
Выборочные средние значения для небольшой совокупности: веса тыкв
В этом примере совокупность представляет собой вес шести тыкв (в фунтах), отображаемый в карнавальной игровой кабинке «Угадай вес». Вас просят угадать средний вес шести тыкв, взяв случайную выборку без замены из популяции.
Тыква | А | Б | С | Д | Е | Ф |
|---|---|---|---|---|---|---|
Вес (в фунтах) | 19 | 14 | 15 | 9 | 10 | 17 |
Поскольку мы знаем веса населения, мы можем найти среднее значение населения.
\(\mu=\dfrac{19+14+15+9+10+17}{6}=14\) фунтов
Чтобы продемонстрировать распределение выборки, начнем с получения всех возможных выборок размера \ (n=2\) из популяций, выборка без замены. В таблице ниже показаны все возможные выборки, веса выбранных тыкв, среднее значение выборки и вероятность получения каждой выборки. Поскольку мы рисуем случайным образом, у каждого образца будет одинаковая вероятность быть выбранным.
В таблице ниже показаны все возможные выборки, веса выбранных тыкв, среднее значение выборки и вероятность получения каждой выборки. Поскольку мы рисуем случайным образом, у каждого образца будет одинаковая вероятность быть выбранным.
Образец | Масса | \(\boldsymbol{\bar{x}}\) | Вероятность |
|---|---|---|---|
А, Б | 19, 14 | 16,5 | \(\frac{1}{15}\) |
А, С | 19, 15 | 17,0 | \(\frac{1}{15}\) |
А, Д | 19, 9 | 14,0 | \(\frac{1}{15}\) |
А, Е | 19, 10 | 14,5 | \(\frac{1}{15}\) |
А, Ф | 19, 17 | 18,0 | \(\frac{1}{15}\) |
Б, С | 14, 15 | 14,5 | \(\frac{1}{15}\) |
Б, Д | 14, 9 | 11,5 | \(\frac{1}{15}\) |
Б, Е | 14, 10 | 12,0 | \(\frac{1}{15}\) |
Б, Ф | 14, 17 | 15,5 | \(\frac{1}{15}\) |
С, Д | 15, 9 | 12,0 | \(\frac{1}{15}\) |
С, Е | 15, 10 | 12,5 | \(\frac{1}{15}\) |
С, Ф | 15, 17 | 16,0 | \(\frac{1}{15}\) |
Д, Е | 9, 10 | 9,5 | \(\frac{1}{15}\) |
Д, Ф | 9, 17 | 13,0 | \(\frac{1}{15}\) |
Э, Ф | 10, 17 | 13,5 | \(\frac{1}{15}\) |
Мы можем объединить все значения и создать таблицу возможных значений и их соответствующих вероятностей.
\(\boldsymbol{\bar{x}}\) | 9,5 | 11,5 | 12,0 | 12,5 | 13,0 | 13,5 | 14,0 | 14,5 | 15,5 | 16,0 | 16,5 | 17,0 | 18,0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Вероятность | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{2}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{2}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) | \(\frac{1}{15}\) |
Таблица представляет собой таблицу вероятностей для среднего значения выборки и представляет собой выборочное распределение выборочного среднего веса тыкв при размере выборки 2. Также стоит отметить, что сумма всех вероятностей равна 1. Может быть полезно изобразить эти значения в виде графика.
Также стоит отметить, что сумма всех вероятностей равна 1. Может быть полезно изобразить эти значения в виде графика.
Теперь, когда у нас есть выборочное распределение среднего значения выборки, мы можем вычислить среднее значение всех средних значений выборки. Другими словами, мы можем найти среднее (или ожидаемое значение) всех возможных \(\bar{x}\).
Среднее значение выборки равно
\(\mu_\bar{x}=\sum \bar{x}_{i}f(\bar{x}_i)=9,5\left(\frac{1) {15}\вправо)+11,5\влево(\frac{1}{15}\вправо)+12\влево(\frac{2}{15}\вправо)\\+12,5\влево(\frac{1 {15}\вправо)+13\влево(\frac{1}{15}\вправо)+13,5\влево(\frac{1}{15}\вправо)+14\влево(\frac{1}{) 15}\вправо)\\+14,5\влево(\frac{2}{15}\вправо)+15,5\влево(\frac{1}{15}\вправо)+16\влево(\frac{1}{) 15}\вправо)+16,5\влево(\frac{1}{15}\вправо)\\+17\влево(\frac{1}{15}\вправо)+18\влево(\frac{1}{) 15}\right)=14\)
Несмотря на то, что каждая выборка может дать вам ответ с некоторой ошибкой, ожидаемое значение точно соответствует цели: точно среднее значение генеральной совокупности. Другими словами, если проводить эксперимент снова и снова, общее среднее значение выборки будет в точности средним значением генеральной совокупности.
Другими словами, если проводить эксперимент снова и снова, общее среднее значение выборки будет в точности средним значением генеральной совокупности.
Теперь давайте проделаем то же самое, что и выше, но с размером выборки \(n=5\)
Образец | Гири | \(\boldsymbol{\bar{x}}\) | Вероятность |
|---|---|---|---|
А, Б, С, Г, Е | 19, 14, 15, 9, 10 | 13,4 | 1/6 |
А, Б, В, Г, Ф | 19, 14, 15, 9, 17 | 14,8 | 1/6 |
А, Б, С, Д, Ф | 19, 14, 15, 10, 17 | 15,0 | 1/6 |
А, Б, Г, Д, Ф | 19, 14, 9, 10, 17 | 13,8 | 1/6 |
А, С, Г, Д, Ф | 19, 15, 9, 10, 17 | 14,0 | 1/6 |
Б, С, Г, Д, Ф | 14, 15, 9, 10, 17 | 13,0 | 1/6 |
Распределение выборки:
\(\boldsymbol{\bar{x}}\) | 13,0 | 13,4 | 13,8 | 14,0 | 14,8 | 15,0 |
|---|---|---|---|---|---|---|
Вероятность | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Среднее значение выборки равно. ..
..
\(\mu=(\dfrac{1}{6})(13+13,4+13,8+14,0+14,8+15,0)=14\) фунтов
На следующих точечных диаграммах показано распределение выборочных средних, соответствующих размеру выборки \(n=2\) и \(n=5\).
Среднее значение совокупности9 10 11 12 13 14 15 16 17 18 2 5 Размер выборкиОпять же, мы видим, что использование среднего значения выборки для оценки среднего значения совокупности связано с ошибкой выборки. Однако ошибка при размере выборки \(n=5\) в среднем меньше, чем при размере выборки \(n= 2\).
Ошибка выборки и размер
- Ошибка выборки
- Ошибка, возникшая в результате использования характеристики выборки для оценки характеристики генеральной совокупности.
Размер выборки и ошибка выборки: Как показано на точечных графиках выше, возможные выборочные средние группируются ближе к среднему генеральной совокупности по мере увеличения размера выборки. Таким образом, возможная ошибка выборки уменьшается по мере увеличения размера выборки.
Таким образом, возможная ошибка выборки уменьшается по мере увеличения размера выборки.
Что происходит, когда популяция не маленькая, как в примере с тыквой?
Выборочные средние для больших выборок: пример экзамена
Преподаватель курса «Введение в статистику» обучает 200 студентов. На гистограмме показаны результаты из 100 баллов.
Среднее значение генеральной совокупности равно \(μ=71,18\), а стандартное отклонение генеральной совокупности равно \(σ=10,73\)
Давайте продемонстрируем выборочное распределение средних значений выборки с помощью веб-сайта StatKey. Первое видео продемонстрирует выборочное распределение среднего значения выборки при n = 10 для данных экзаменационных баллов. Во втором видео будут показаны те же данные, но с выборками n = 30.
- n=10
- n=30
Вы должны начать видеть некоторые закономерности. Среднее значение выборочного распределения очень близко к среднему по совокупности. Стандартное отклонение выборочного распределения меньше, чем стандартное отклонение генеральной совокупности.
В примерах до сих пор нам давали совокупность и производили выборку из этой совокупности.
Что происходит, когда у нас нет населения для выборки? Что происходит, когда все, что нам дано, — это образец? К счастью, мы можем использовать некоторую теорию, чтобы помочь нам. Математические детали теории выходят за рамки этого курса, но результаты представлены на этом уроке.
В следующих двух разделах мы обсудим выборочное распределение выборочного среднего, когда население распределено нормально, а когда нет.
Среднее значение выборки — значение, формула, расчет, пример
Что такое среднее значение выборки?
Выборочное среднее относится к среднему значению выборки данных, рассчитанному из большой совокупности данных.
Это хороший инструмент для оценки среднего значения генеральной совокупности, если размер выборки велик, а статистические исследователи случайным образом берут фрагменты из генеральной совокупности.
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Выборочное среднее (wallstreetmojo.com)
Статистики и исследователи используют это Среднее значение для расчета дисперсии распределения населения, центральной тенденции и стандартного отклонения. Он очень эффективен для измерения средней численности населения страны. Статистики также используют его для прогнозирования стандарта нормальности конкретной изучаемой группы населения. Наконец, они используют его для тех популяций, среднее значение которых неизвестно. Инвесторы используют его для понимания динамики акций.
Содержание
- Что означает выборка?
- Среднее значение выборки, объясненное
- Формула
- Пример распределения
- Распределение выборки.
 Среднее значение выборки
Среднее значение выборки - Среднее значение выборки в отношении популяции среднее значение
- Часто задаваемые вопросы (FAQS)
- Рекомендуемые статьи
- Среднее всего из выборки. Образец
- . значения данных называется выборочным средним. Это полезно для оценки среднего значения и поведения населения. Например, исследователи широко используют простое среднее значение для расчета средней численности населения стран.
- Можно найти методом среднего арифметического и среднего геометрического. Последнее сложнее первого. Арифметический метод делит общее значение данных в выборке на общее количество наборов данных.
- Если размер выборки очень велик, Среднее нормальное, а стандартное отклонение известно для генеральной совокупности. Обычно распределяют простое среднее выборочного распределения.
- Среднее значение для населения трудно рассчитать по сравнению со средним значением выборки.

Среднее значение выборки Объяснение
Среднее значение выборки — это среднее математическое значение значений выборки. Это статистический показатель, используемый для анализа различных переменных во времени. Статистики и исследователи получают его, разделив общую сумму значений всех фрагментов данных, а затем разделив ее на общее количество наборов данных. Исследователи-статистики математически представляют это следующим образом:
Где X̄ = простое среднее или среднее
X = переменная с разными значениями и
N= общее количество переменных наблюдений.
На практике центром любого количества наборов данных является среднее значение. Тем не менее, опрос каждого человека или набора данных для точного определения средних значений населения невозможен. Это отнимает много времени, требует огромных капиталовложений и делает работу громоздкой. Кроме того, прогнозирование поведения населения и оценка населения очень важны для принятия важных политических решений. Поэтому в таких случаях нам на помощь приходит простое среднее. Кроме того, статистики и исследователи дополнительно используют простое среднее значение для расчета выборочной средней дисперсии и выборочного среднего стандартного отклонения совокупности.
Поэтому в таких случаях нам на помощь приходит простое среднее. Кроме того, статистики и исследователи дополнительно используют простое среднее значение для расчета выборочной средней дисперсии и выборочного среднего стандартного отклонения совокупности.
Для вычисления Среднего необходимо несколько раз выбирать случайные образцы данных и записывать информацию в виде таблицы. Образец — это уменьшенная версия большой группы. Как только исследователи записывают данные, они используют каждую группу выборок, чтобы найти их уважаемое среднее значение случайной выборки. Эти средства очень важно знать о поведении населения.
Формула
Исследователи-статистики используют формулу среднего для расчета среднего значения, относящегося к представленным выборочным наборам данных. Таким образом, они могут найти формулу среднего арифметического, разделив все значения наборов данных на общее количество наборов данных.
Математически формула среднего арифметического представлена следующим образом:
Простое среднее или Среднее = Сумма всех значений наборов данных / Общее количество наборов данных.
= (A 1 +A 2 +A 3 +A 4 +A 5 +A 6 +…. i /N, где Sigma a i = сумма всех значений наборов данных, а
N = общее количество наборов данных
Метод среднего геометрического дает примерно такой же результат, но является более сложным и сложным. Извлекает корень n-й степени после умножения. Формула среднего геометрического:
Где Π = Среднее геометрическое
n = Количество значений
x i = Среднее значение
Пример расчета
Ниже приведен пример расчета, помогающий лучше понять концепцию среднего или простого среднего.
Предположим, группа студентов-финансистов изучает инвестиционно-банковское дело в известном колледже. Группа состоит из 6 студентов A, B, C, D, E и F , которые занимаются 5 часов, 4,5 часа, 3 часа, 1 час, 2 часа и 2,5 часа 9.0333 с соответственно. Теперь давайте найдем простое среднее значение учебного времени, затраченного этой группой студентов.
Вот таблица для представления значений.
| Students | Study hours requirement |
| A | 5 |
| B | 4.5 |
| C | 3 |
| D | 1 |
| Е | 2 |
| F | 2,5 |
Следовательно, для нахождения простого среднего времени обучения для группы соберем соответствующие данные следующим образом:
Общее время обучения по классам A, B, C, D, E , & F, T = 5 часов + 4,5 часа + 3 часа + 1 час + 2 часа + 2,5 часа.
Или, T = 5+4,5+3+1+2+2,5 = 18 часов.
Здесь общее количество студентов = 6.
Среднее арифметическим методом для учебного времени, S среднее = общее количество учебного времени/количество студентов
= 18/6 = 3 часа
или , S Среднее = 3 часа
Простой средний по геометрическому методу для времени обучения, S Среднее = время изучения продукта (часы). Найдите n-й корень произведений.
= 5*4,5*3*1*2*2,5 = 337,5 часа
Общее количество студентов = n = 6
Найдите 6 -й корень 337,5 Один GET = 2,6386
т. е. 3
Следовательно, простое среднее значение времени обучения составляет 3 часа.
Выборочное распределение среднего значения выборки
Это можно объяснить как ситуацию, когда заданный случайный размер выборки n многократно берется из определенной совокупности с определенными значениями, связанными с числовой переменной, имеющей mu (μ) в качестве среднего значения совокупности. Например, если сигма (σ) является стандартным отклонением совокупности, то Среднее значение для всех средних значений (x-bars или X̅) будет точно представлять среднее значение совокупности mu (μ).
Например, если сигма (σ) является стандартным отклонением совокупности, то Среднее значение для всех средних значений (x-bars или X̅) будет точно представлять среднее значение совокупности mu (μ).
Другими словами, можно взять выборочное распределение как выборочное среднее распределение вероятностей, которое может присоединить выборочную статистику, относящуюся к образцу. Более того, если предположить, что:
- X обозначает совокупность, имеющую среднее μ для своего распределения вместе со стандартным отклонением σ
- Исследователи распределяют X нормально, а
- Выборка очень большая.
Тогда простое среднее значение X̅ будет распределено нормально, имея среднее значение μ плюс стандартную ошибку как σ/ √n
Важно отметить, что:
- X почти нормальное значение или размер выборки очень большой.
- Для генеральной совокупности известно стандартное отклонение.
Тогда справедливо только выборочное распределение среднего значения, показанное ранее; иначе нет.
Среднее значение по выборке и среднее по совокупности
Ниже приведен список основных различий между средним значением по выборке и по совокупности.
- Первое представляет собой среднее значение всех значений выборки, собранной из большей совокупности для оценки совокупности.
- С другой стороны, среднее значение генеральной совокупности представляет собой среднее полных значений, содержащихся в генеральной совокупности.
- Первое вычислить легко, а второе — нет.
- Среднее значение генеральной совокупности является более точным, чем среднее значение выборки.
Часто задаваемые вопросы (FAQ)
Как найти среднее значение генеральной совокупности по среднему значению выборки?
Среднее значение выборки представляет собой среднее значение всех собранных значений выборки, тогда как среднее значение генеральной совокупности принимается как среднее значение среднего значения генеральной совокупности. Простое среднее можно использовать как точное приближение к среднему для генеральной совокупности, если выборка неоднородна и размер выборки достаточно велик.
Простое среднее можно использовать как точное приближение к среднему для генеральной совокупности, если выборка неоднородна и размер выборки достаточно велик.
Как найти среднее значение выборки в Excel?
Его можно найти, выполнив следующие действия:
● Перейдите к последней пустой ячейке столбца данных образца.
● Введите знак равенства и синтаксическое среднее значение или = Среднее значение
● Выберите все ячейки от первой ячейки данных (A1) до последней ячейки данных (A30), которые будут использоваться для расчета среднего значения, и нажмите клавишу ввода.
● Окончательный результат будет средним значением выборки.
Как найти среднее значение выборки из доверительного интервала?
Да, статистики и исследователи могут рассчитать выборочное среднее из доверительного интервала, вычитая наименьшее значение из самого верхнего значения в интервале, а затем разделив полученное значение на 2.
Зачем использовать случайную выборку для выборочного среднего?
Среднее значение выборки основано на многократном использовании нескольких случайных выборок. В таком случае результат является беспристрастным, более точным и всесторонне представляет среднее значение генеральной совокупности.
Рекомендуемые статьи
Эта статья представляет собой руководство по выборочному среднему и его значению. Здесь мы обсудим его формулу на примере, его выборочное распределение, а также сравним его со средним значением генеральной совокупности. Вы можете узнать больше из следующих статей –
- Размер эффекта
- Дисперсионный анализ
- Дисперсионный анализ против MANOVA
Выборочное распределение выборочного среднего
Центральная предельная теорема
«Пример 6.1» в разделе 6.1. «Среднее значение и стандартное отклонение среднего значения выборки» мы построили распределение вероятностей среднего значения выборки для выборок размера два, взятых из популяции четырех гребцов. Распределение вероятностей:
Распределение вероятностей:x-152154156158160162164P(x-)116216316416316216116
На рис. 6.1 «Распределение совокупности и выборочное среднее» показано параллельное сравнение гистограммы для исходной совокупности и гистограммы для этого распределения. В то время как распределение населения является однородным, выборочное распределение среднего имеет форму, приближающуюся к форме знакомой колоколообразной кривой. Это явление выборочного распределения среднего значения, принимающего форму колокола, даже если распределение совокупности не является колоколообразным, происходит в целом. Вот несколько более реалистичный пример.
Рис. 6.1 Распределение совокупности и выборочное среднее что среднее значение населения равно 0,5. Распределения выборки:
n = 1:
x-01P(x-)0.50.5
n = 5:
x-00.20.40.60.81P(x-)0.601. 310.160.03
n = 10:
х-00. 10.20.30.40.50.60.70.80.91P(x-)0.000.010.040.120.210.250.210.120.040.010.00
10.20.30.40.50.60.70.80.91P(x-)0.000.010.040.120.210.250.210.120.040.010.00
n = 20:
x-00.050.100.150.200.250.300.350.400.450.50P(x-)0.000.000.000.000.000.010.040 .070.120.160.18x-0.550.600.650.700.750.800.850.900.951P(x-)0.160.120.070.040.010.000.000.000.000.00
Гистограммы, иллюстрирующие эти распределения. Рис. 6.2 Распределение выборочного среднего . Если бы мы продолжали увеличивать n , то форма выборочного распределения стала бы более гладкой и более колоколообразной.
То, что мы видим в этих примерах, не зависит от конкретного распределения населения. В общем, можно начать с любого распределения, и выборочное распределение выборочного среднего будет все больше напоминать колоколообразную нормальную кривую по мере увеличения размера выборки. Это содержание центральной предельной теоремы.
Центральная предельная теорема
Для выборок размером 30 и более среднее значение выборки приблизительно нормально распределено со средним значением μX-=μ и стандартным отклонением σX-=σ/n, где n — размер выборки. Чем больше размер выборки, тем лучше аппроксимация.
Чем больше размер выборки, тем лучше аппроксимация.
Центральная предельная теорема проиллюстрирована для нескольких распространенных распределений совокупности на рисунке 6.3 «Распределение совокупностей и выборочные средние».
Рисунок 6.3 Распределение совокупностей и выборочные средние
Вертикальные пунктирные линии на рисунках показывают среднее значение совокупности. Независимо от распределения населения, по мере увеличения размера выборки форма выборочного распределения выборочного среднего становится все более колоколообразной с центром в среднем по совокупности. Обычно к тому времени, когда размер выборки достигает 30, распределение выборочного среднего практически совпадает с нормальным распределением.
Важность центральной предельной теоремы заключается в том, что она позволяет нам делать утверждения о вероятности выборочного среднего, особенно в отношении его значения по сравнению со средним значением генеральной совокупности, как мы увидим в примерах. Но чтобы правильно использовать результат, мы должны сначала понять, что в игре участвуют две отдельные случайные величины (и, следовательно, два распределения вероятностей):
Но чтобы правильно использовать результат, мы должны сначала понять, что в игре участвуют две отдельные случайные величины (и, следовательно, два распределения вероятностей):
- X , измерение одного элемента, выбранного случайным образом из совокупности; распределение X — распределение генеральной совокупности, где среднее значение генеральной совокупности составляет μ , а стандартное отклонение — стандартное отклонение генеральной совокупности σ ;
- X-, среднее значение измерений в выборке размером n ; распределение X- является его выборочным распределением со средним значением µX-=µ и стандартным отклонением σX-=σ/n.
Пример 3
Пусть X- будет средним значением случайной выборки размером 50, взятой из совокупности со средним значением 112 и стандартным отклонением 40.
- Найдите среднее значение и стандартное отклонение X-.

- Найдите вероятность того, что X- примет значение от 110 до 114.
- Найдите вероятность того, что X- примет значение больше 113.
Раствор
По формулам предыдущего раздела
μX-=μ=112 и σX-=σn=4050=5,65685Поскольку размер выборки составляет не менее 30, применима центральная предельная теорема: X- приблизительно нормально распределено. Мы вычисляем вероятности, используя рис. 12.2 «Суммарная нормальная вероятность» обычным способом, стараясь использовать только σX-, а не 9.0705 σ при стандартизации:
P(110Аналогично
P(X->113)=P(Z>113−μX-σX-)=P(Z>113−1125,65685)=P(Z>0,18)=1−P(Z<0,18)=1−0,5714=0,4286
Обратите внимание, что если бы в примечании 6. 11 «Пример 3» нас попросили вычислить вероятность того, что значение одного случайно выбранного элемента совокупности превышает 113, то есть вычислить число P ( X > 113), мы не смогли бы этого сделать, так как мы не знаем распределения X , а только то, что его среднее значение равно 112, а стандартное отклонение равно 40. Напротив, мы мог вычислить P(X->113) даже без полного знания распределения X , потому что центральная предельная теорема гарантирует, что X- приблизительно нормально.
11 «Пример 3» нас попросили вычислить вероятность того, что значение одного случайно выбранного элемента совокупности превышает 113, то есть вычислить число P ( X > 113), мы не смогли бы этого сделать, так как мы не знаем распределения X , а только то, что его среднее значение равно 112, а стандартное отклонение равно 40. Напротив, мы мог вычислить P(X->113) даже без полного знания распределения X , потому что центральная предельная теорема гарантирует, что X- приблизительно нормально.
Пример 4
Численная совокупность средних баллов в колледже имеет среднее значение 2,61 и стандартное отклонение 0,5. Если из генеральной совокупности будет взята случайная выборка размером 100, какова вероятность того, что среднее значение выборки будет находиться в пределах от 2,51 до 2,71?
Решение
Среднее значение выборки X- имеет среднее значение µX-=µ=2,61 и стандартное отклонение σX-=σ/n=0,5/10=0,05, поэтому
P(2,51 Центральная предельная теорема утверждает, что независимо от того, каково распределение популяции, до тех пор, пока выборка «большая», что означает размер 30 или более, выборочное среднее приблизительно нормально распределено. Для выборок любого размера , взятых из нормально распределенной совокупности, среднее значение выборки имеет нормальное распределение со средним значением μX-=μ и стандартным отклонением σX-=σ/n, где n — размер выборки. Эффект увеличения размера выборки показан на рисунке 6.4 «Распределение выборочных средних для нормальной совокупности». Рисунок 6.4 Распределение выборочных средних для нормальной совокупности Расчетный срок службы прототипа автомобильной шины составляет 38 500 миль при стандартном отклонении 2 500 миль. Изготовлено и испытано пять таких шин. При допущении, что фактическое среднее значение населения составляет 38 500 миль, а фактическое стандартное отклонение населения составляет 2 500 миль, найдите вероятность того, что среднее значение выборки будет меньше 36 000 миль. Решение Для простоты мы используем тысячи миль. Тогда выборочное среднее значение X- имеет среднее значение µX-=µ=38,5 и стандартное отклонение σX-=σ/n=2,5/5=1,11803. Поскольку население распределено нормально, то и X-, следовательно, P(X-<36)=P(Z<36−μX-σX-)=P(Z<36−38,51,11803)=P(Z< −2,24)=0,0125 То есть, если шины работают так, как было задумано, вероятность того, что среднее значение выборки такого размера будет таким низким, составляет всего около 1,25%. Производитель автомобильных аккумуляторов утверждает, что средний срок службы их аккумуляторов среднего класса составляет 50 месяцев при стандартном отклонении 6 месяцев. Допустим, распределение времени автономной работы именно этой марки примерно нормальное. Раствор Поскольку известно, что популяция имеет нормальное распределение Среднее значение выборки имеет среднее значение μX-=μ=50 и стандартное отклонение σX-=σ/n=6/36=1. Таким образом, Совокупность имеет среднее значение 128 и стандартное отклонение 22. Совокупность имеет среднее значение 1542 и стандартное отклонение 246. Популяция имеет среднее значение 73,5 и стандартное отклонение 2,5. Популяция имеет среднее значение 48,4 и стандартное отклонение 6,3. Нормально распределенная популяция имеет среднее значение 25,6 и стандартное отклонение 3,3. Нормально распределенная популяция имеет среднее значение 57,7 и стандартное отклонение 12,1. Совокупность имеет среднее значение 557 и стандартное отклонение 35. Популяция имеет среднее значение 16 и стандартное отклонение 1,7. Нормально распределенная совокупность имеет среднее значение 1214 и стандартное отклонение 122. Нормально распределенная совокупность имеет среднее значение 57 800 и стандартное отклонение 750. Совокупность имеет среднее значение 72 и стандартное отклонение 6. Популяция имеет среднее значение 12 и стандартное отклонение 1,5. Предположим, что среднее число дней до прорастания различных семян равно 22, при стандартном отклонении 2,3 дня. Предположим, что среднее время, в течение которого вызывающий абонент находится на удержании при звонке в центр обслуживания клиентов, составляет 23,8 секунды со стандартным отклонением 4,6 секунды. Найдите вероятность того, что средняя продолжительность ожидания в выборке из 1200 вызовов будет в пределах 0,5 секунды от среднего значения генеральной совокупности. Предположим, что среднее количество холестерина в яйцах с пометкой «большие» составляет 186 миллиграммов со стандартным отклонением 7 миллиграммов. Найдите вероятность того, что среднее количество холестерина в образце из 144 яиц будет в пределах 2 миллиграммов от среднего по популяции. Предположим, что в одном регионе страны средняя сумма долга по кредитной карте на домохозяйство в домохозяйствах, имеющих долг по кредитной карте, составляет 15 250 долларов США при стандартном отклонении 7 125 долларов США. Предположим, что скорости транспортных средств на определенном участке дороги нормально распределены со средним значением 36,6 миль в час и стандартным отклонением 1,7 миль в час. Многие акулы в перевернутом состоянии входят в состояние тонической неподвижности. Предположим, что у определенного вида акул время, в течение которого акула остается в состоянии тонической неподвижности в перевернутом положении, нормально распределено со средним значением 11,2 минуты и стандартным отклонением 1,1 минуты. Предположим, что средняя стоимость 30-дневного запаса непатентованного лекарственного средства по стране составляет 46,58 долл. США при стандартном отклонении 4,84 долл. США. Найдите вероятность того, что среднее значение выборки из 100 цен на 30-дневный запас этого лекарства будет находиться в пределах от 45 до 50 долларов. Предположим, что средний промежуток времени между подачей налоговой декларации штата с запросом на возмещение и выдачей возмещения составляет 47 дней со стандартным отклонением 6 дней. Баллы на общем выпускном экзамене в большом наборе, многосекционный курс для первокурсников обычно распределяются со средним значением 72,7 и стандартным отклонением 13,1. Предположим, что средний вес школьных сумок для книг составляет 17,4 фунта со стандартным отклонением 2,2 фунта. Найти вероятность того, что средний вес выборки из 30 сумок с книгами превысит 17 фунтов. Предположим, что в некотором регионе страны средняя продолжительность первых браков, заканчивающихся разводом, составляет 7,8 года, стандартное отклонение 1,2 года. Борачио каждый день ест в одном и том же ресторане быстрого питания. Предположим время X 907:08 между моментом, когда Борачио входит в ресторан, и моментом, когда ему подают еду, нормально распределяется со средним значением 4,2 минуты и стандартным отклонением 1,3 минуты. Высокоскоростная упаковочная машина может быть настроена на подачу от 11 до 13 унций жидкости. Производитель шин заявляет, что средний срок службы шин определенного типа составляет 60 000 миль. Предположим, что время жизни нормально распределено со стандартным отклонением σ= 3500 миль. 0,9940 0,9994 Нормально распределенные популяции
 Если население изначально нормальное, то среднее значение выборки также имеет нормальное распределение, независимо от размера выборки.
Если население изначально нормальное, то среднее значение выборки также имеет нормальное распределение, независимо от размера выборки. Пример 5
 Предположим, что распределение сроков службы таких шин нормальное.
Предположим, что распределение сроков службы таких шин нормальное. Пример 6

Ключевые выводы
Упражнения
Базовый






Приложения
 Найти вероятность того, что среднее время прорастания выборки из 160 семян будет в пределах 0,5 дня от среднего по совокупности.
Найти вероятность того, что среднее время прорастания выборки из 160 семян будет в пределах 0,5 дня от среднего по совокупности. Найдите вероятность того, что средняя сумма долга по кредитной карте в выборке из 1600 таких домохозяйств будет в пределах 300 долларов от среднего значения для населения.
Найдите вероятность того, что средняя сумма долга по кредитной карте в выборке из 1600 таких домохозяйств будет в пределах 300 долларов от среднего значения для населения.
 Найти вероятность того, что в выборке из 50 обращений с запросом на возврат средств средний такой срок будет более 50 дней.
Найти вероятность того, что в выборке из 50 обращений с запросом на возврат средств средний такой срок будет более 50 дней. Найти вероятность того, что в выборке из 75 разводов средний возраст заключенных не более 8 лет.
Найти вероятность того, что в выборке из 75 разводов средний возраст заключенных не более 8 лет. Дополнительные упражнения
 Для любой настройки доставки в этом диапазоне доставленное количество нормально распределяется со средним некоторым количеством μ и со стандартным отклонением 0,08 унции. Для калибровки машины она настроена на подачу определенного количества, наполняется множество контейнеров, случайным образом выбираются 25 контейнеров и измеряется количество, которое они содержат. Найдите вероятность того, что среднее значение пробы будет в пределах 0,05 унции от фактического среднего количества, доставленного во все контейнеры.
Для любой настройки доставки в этом диапазоне доставленное количество нормально распределяется со средним некоторым количеством μ и со стандартным отклонением 0,08 унции. Для калибровки машины она настроена на подачу определенного количества, наполняется множество контейнеров, случайным образом выбираются 25 контейнеров и измеряется количество, которое они содержат. Найдите вероятность того, что среднее значение пробы будет в пределах 0,05 унции от фактического среднего количества, доставленного во все контейнеры. Найдите вероятность того, что средний срок службы пяти шин составит 57 000 миль или менее. Если среднее значение такое низкое, является ли это убедительным доказательством того, что шина не так хороша, как заявлено?
Найдите вероятность того, что средний срок службы пяти шин составит 57 000 миль или менее. Если среднее значение такое низкое, является ли это убедительным доказательством того, что шина не так хороша, как заявлено? Ответы


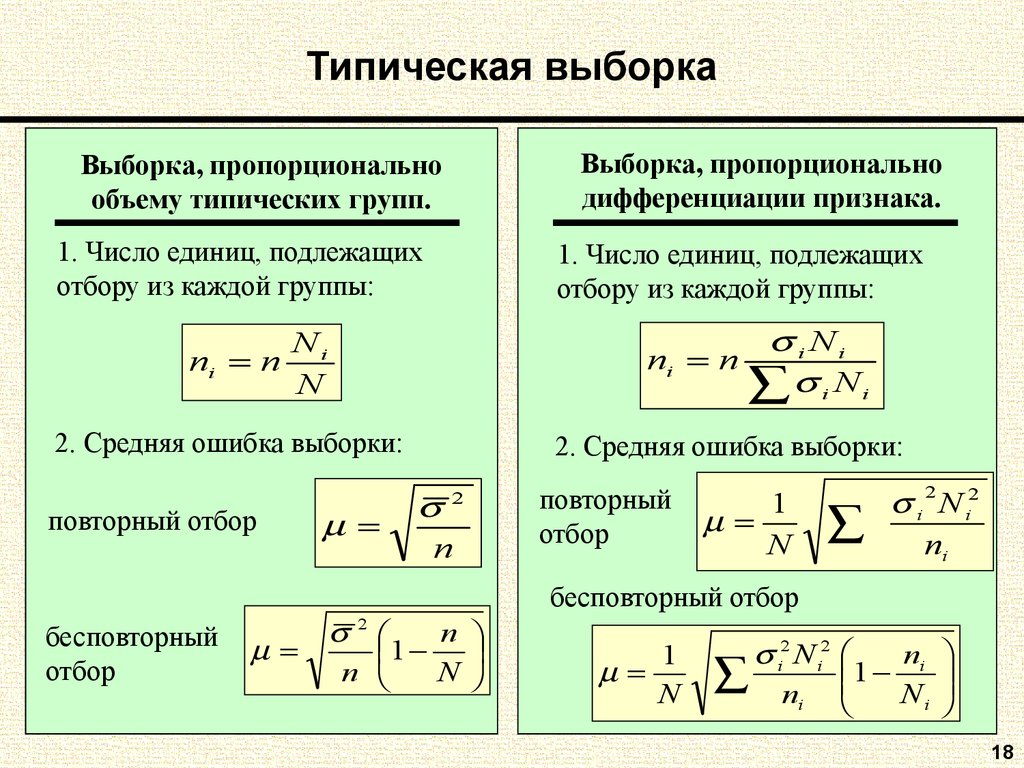 Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
 Это яркий пример мягкой подмены понятия. Подобного рода ошибки вполне объяснимы — первые переводы появились еще в
Это яркий пример мягкой подмены понятия. Подобного рода ошибки вполне объяснимы — первые переводы появились еще в  95, filtered['dwell-time'])
print('Интервал уверенности: ', ci)
95, filtered['dwell-time'])
print('Интервал уверенности: ', ci) tsv')['dwell-time']
print('n: ', ts.count())
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение: ', ts.std())
print('Стандартная ошибка: ', standard_error(ts))
ex_2_10()
tsv')['dwell-time']
print('n: ', ts.count())
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение: ', ts.std())
print('Стандартная ошибка: ', standard_error(ts))
ex_2_10() tsv')['dwell-time']
print('Интервал уверенности:', confidence_interval(0.95, ts))
tsv')['dwell-time']
print('Интервал уверенности:', confidence_interval(0.95, ts)) to_datetime('2015 6 6')
d.weekday() in [5,6]
to_datetime('2015 6 6')
d.weekday() in [5,6] tsv') )
df.index = df['date']
df = df[df['date'].index.dayofweek > 4] # суббота-воскресенье
weekend_times = df['dwell-time']
print('n: ', weekend_times.count())
print('Среднее: ', weekend_times.mean())
print('Медиана: ', weekend_times.median())
print('Стандартное отклонение: ', weekend_times.std())
print('Стандартная ошибка: ', standard_error(weekend_times))
tsv') )
df.index = df['date']
df = df[df['date'].index.dayofweek > 4] # суббота-воскресенье
weekend_times = df['dwell-time']
print('n: ', weekend_times.count())
print('Среднее: ', weekend_times.mean())
print('Медиана: ', weekend_times.median())
print('Стандартное отклонение: ', weekend_times.std())
print('Стандартная ошибка: ', standard_error(weekend_times)) 
 Вычтите среднее значение из каждого значения данных и возведите результат в квадрат. …
Вычтите среднее значение из каждого значения данных и возведите результат в квадрат. …

 На первом этапе поиска среднего значения выборки нам предлагается сложить вместе все значения в выборке. Чтобы применить это к примеру телефонной компании, они начинают с суммирования количества клиентов, которые у них были каждый месяц.
На первом этапе поиска среднего значения выборки нам предлагается сложить вместе все значения в выборке. Чтобы применить это к примеру телефонной компании, они начинают с суммирования количества клиентов, которые у них были каждый месяц.
 В примере с телефонной компанией это означало бы вычитание 20 792 из стоимости каждого месяца.
В примере с телефонной компанией это означало бы вычитание 20 792 из стоимости каждого месяца. Другими словами, данные, найденные в телефонной компании, демонстрируют противоречивые выборочные значения и не будут отражать средние показатели по всей телефонной отрасли.
Другими словами, данные, найденные в телефонной компании, демонстрируют противоречивые выборочные значения и не будут отражать средние показатели по всей телефонной отрасли.
 Среднее значение выборки равно среднему значению генеральной совокупности.
Среднее значение выборки равно среднему значению генеральной совокупности. Это, в свою очередь, позволяет нам применять те же правила, которые, как мы знаем, справедливы для нормальных распределений, к ненормальным.
Это, в свою очередь, позволяет нам применять те же правила, которые, как мы знаем, справедливы для нормальных распределений, к ненормальным.
 lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics Он отличается от параметра, такого как среднее значение генеральной совокупности.
Он отличается от параметра, такого как среднее значение генеральной совокупности. Каждое выборочное распределение имеет среднее значение, которое помогает сформировать выборочное распределение .
Каждое выборочное распределение имеет среднее значение, которое помогает сформировать выборочное распределение .

 Это хороший инструмент для оценки среднего значения генеральной совокупности, если размер выборки велик, а статистические исследователи случайным образом берут фрагменты из генеральной совокупности.
Это хороший инструмент для оценки среднего значения генеральной совокупности, если размер выборки велик, а статистические исследователи случайным образом берут фрагменты из генеральной совокупности. Среднее значение выборки
Среднее значение выборки
