Решить уравнение пошагово онлайн: Решение систем уравнений · Калькулятор Онлайн

Содержание

Лови Ответ для решения примеров и уравнений

Бесплатная программа ЛовиОтвет — функциональный калькулятор для решения примеров и уравнений. В программе Лови Ответ происходит автоматическое решение математических примеров и уравнений с выводом действий и этапов их решения.

Для чего нужна такая программа? Программа Лови Ответ — это своего рода математический решебник, который выводит ответ, с пошаговым решением выполненного задания.

Содержание:

Установка программы Лови Ответ
Обзор программы Лови Ответ
Лови Ответ онлайн
Выводы статьи
ЛовиОтвет — программа для решения примеров и уравнений (видео)

Программа Лови Ответ будет интересна школьникам и их родителям. С помощью этой программы родители могут проверять домашние задания, которые выполнил учащийся. Также школьники и студенты могут решать примеры и уравнения при помощи этого математического калькулятора.

Взрослые, которые уже не помнят многого из школьного курса, а также учащиеся смогут при помощи данной программы, быстро решить математический пример любой степени сложности.

В программе ЛовиОтвет можно будет выполнять такие математические действия:

Совершать действия с натуральными числами.
Производить действия с дробями (десятичными, обыкновенными, смешанными).
В программе можно будет упрощать выражения, производить действия с многочленами.
Решать линейные и квадратные уравнения.

Примеры и уравнения будут решены в программе Лови Ответ пошагово, с последовательными действиями. Визуально, в окне программы, вы увидите решение примера или уравнения. Ответ и пошаговые действия для его решения, будут записаны на своеобразном тетрадном листе. Все этапы решения можно будет записывать в программе в столбик.

Скачать программу ЛовиОтвет можно с официального сайта производителя. Программа доступна для работы на компьютерах с операционной системой Windows. Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone/iPod), для мобильных телефонов (java, java-mini).

Лови Ответ скачать

После загрузки, вам можно будет установить программу на свой компьютер.

Установка программы Лови Ответ

Запустите процесс установки программы LoviOtvet на своем компьютере.

При установке программы будьте внимательны! Снимите флажки в тех пунктах, где вам предложат установить дополнительные программы, для того, чтобы не устанавливать на свой компьютер постороннее программное обеспечение.

По завершению установки программы на компьютер, будет открыто главное окно программы ЛовиОтвет.

Обзор программы Лови Ответ

В верхней части окна программы расположены кнопки меню для управления программой.

С помощью кнопки меню «Правка» вы можете скопировать решение на свой компьютер, выбрав необходимый вариант копирования из контекстного меню. Из меню «Настройки» вы можете выбрать размер листа, клеток, очистить историю. Здесь вы можете изменить цвет отображения окна программы, передвинув в нужное место ползунок, по шкале цвета.

Под панелью меню расположено поле, в которое вводится задание.

В левой части окна расположены кнопки и переключатели для ввода данных. Здесь находится основная и дополнительная панель.

Дополнительную панель можно будет скрыть с помощью кнопки «Скрыть дополнительную панель». Отсюда, в случае необходимости, вы можете изменить размер листа и размер клеток в рабочей области.

Остальную часть окна программы занимает рабочая область, в которой будет отображено решение задания.

Для решения примера, с помощью соответствующих кнопок введите выражение, а затем нажмите на кнопку «Ответ». Решение можно будет выводить в нескольких вариантах: стандартное решение, обыкновенные дроби, решение «в столбик».

После клика по треугольнику в крайней правой части поля, в котором вводится пример или уравнение, откроется дополнительное поле, в котором будут отображена история расчетов. В этом поле можно будет очистить историю расчетов.

Подробнее о том, как пользоваться математическим калькулятором, можно будет прочитать на официальном сайте производителя программы ЛовиОтвет, на странице сайта «Как пользоваться».

Лови Ответ онлайн

Производитель запустил онлайн версию программы ЛовиОтвет, которая доступна по такому адресу: https://calc.loviotvet.ru/.

По заявлению производителя, версия Лови Ответ онлайн менее функциональна, чем программа, которая устанавливается на компьютер или мобильное устройство. Но, все равно, онлайн калькулятор может быть полезен в некоторых случаях, для выполнения решения поставленных задач.

Выводы статьи

Бесплатная программа Лови Ответ — математический решебник и калькулятор, который помогает школьникам, студентам и родителям выполнять или проверять решение примеров и уравнений любой степени сложности.

ЛовиОтвет — программа для решения примеров и уравнений (видео)

Нажимая на кнопку, я даю согласие на обработку персональных данных и принимаю политику конфиденциальности

Решение примеров по фото онлайн

Фото калькулятор Photomath

Когда-то калькулятор был незаменимым помощником в решении различных задач. Времена меняются и на смену ему приходят смартфоны с универсальными приложениями. Программа Photomath даёт возможность решать большинство примеров по математике автоматически.

Скачайте её для своего смартфона с Android или для Айфона.
Всё что для этого нужно — сфотографировать пример или уравнение по математике или физике.
И предоставить фото приложению.
Сколько будет на изображении примеров, столько и решит программа.

Кнопка для создания снимка находится в середине основного меню. Работает по принципу создания изображения на телефоне через камеру мобильного. На экране можно выделять пример с помощью небольшого окна фокусировки.

Увеличьте его, если пример большой. Или сделайте меньше, если требует решить лишь часть уравнения, с которой у вас возникают проблемы. Приложение Photomath умеет решать задачи и без Интернета. В нём более 250 различных математических функций.

Решение уравнения через камеру

Программа может быть использована как обычный калькулятор. Поддерживаются: вычитание, сложение, деление, умножение, дроби.

Можно решать примеры по тригонометрии, алгебре, вычислять квадратные корни, упрощения, базовые алгоритмы. Пока что нет возможности решать через фото системы уравнений, исчисления, полиномы и прочее. Первое использование программы заставит пользователя немного подождать. Приложение будет копировать базу данных. Когда процесс завершится, на экране появится решение.

Яндекс Переводчик для решения домашнего задания по английскому языку

Программа в Интернете и одноименное мобильное приложение Яндекс.Переводчик поможет переводить на 100 различных языков мира. Программа умеет переводить не только введенную текстовую информацию, но и способна определять языки по картинке или изображению. Требуется после установки приложения выбрать этот режим в меню и навести камеру смартфона на иностранный текст. На экране в реальном времени появится текст перевода на язык, который вы выберите в настройках.

Переводчиком можно воспользоваться онлайн по ссылке Яндекс Переводчик. Или скачать его для мобильных платформ на Android и IOS.

Чтобы сделать ГДЗ по английскому языку, необходимо выполнить некоторые настройки приложения и сделать фото задания:

При первом запуске на экране появится интерфейс Яндекс Переводчика со всеми кнопками для управления;
Выберите язык для ввода текста. Он расположена слева. Затем укажите язык, на который будет переводиться фраза — английский;
Справа на панели выберите иконку фотоаппарата — это кнопка для перевода по фото;
Нажмите на фотоаппарат и наведите камеру на текст домашнего задания по английскому языку;
На экране вы увидите точный перевод текста. Его можно сохранить.

Переводчик позволяет загружать готовые фотографии иностранного текста и переводить его. Легко справляется с переводом, который пользователь диктует голосом. Для этого нужно нажать на иконку с микрофоном и проговорить речь на иностранном языке. Или сказать на русском, чтобы переводчик отобразил текст на английском.

Mathway — решит примеры по вашей фотографии

На очереди для обзора ещё одна умная и полезное приложение — Mathway. Оно доступно для телефонов Андроид в Google Play и устройств на базе IOS.

Это приложение решает задачи любой сложности. Его разработкой занимались опытные программисты. В нём есть возможность решить примеры по картинке, задачи и уравнения любой сложности: от простейшей алгебры, до полноценных, комплексных расчётов. Поэтому программу могут использовать не только дети, но и учёные и преподаватели.

Пояснение решения

Для того, чтобы воспользоваться программой, нужно ввести в ней условия задания или создать средствами камеры фотографию примера. Среди возможностей программы в меню можно найти:

Начальная математика;
Алгебра;
Тригонометрия; Решение уравнений по фото
Конечная математика;
Построение графиков;
Начало анализа;
Математический анализ;
Химия;
Статистика.

Это приложение уже было отмечено и одобрено многими популярными западными изданиями, такими как «Новости Yahoo!», «CNET», «Lifehack» и другими.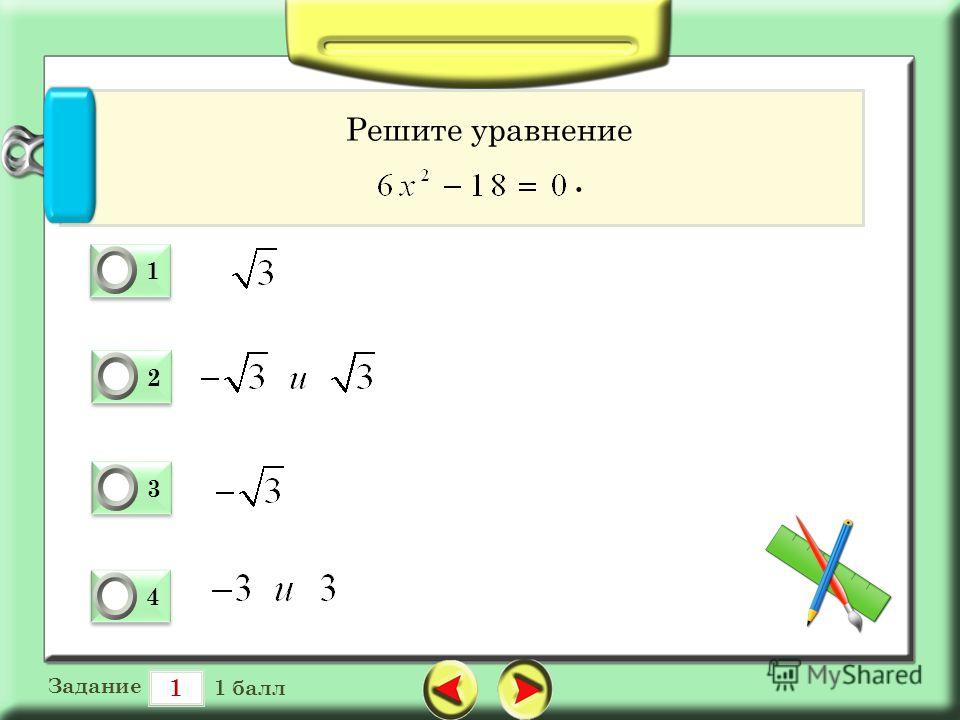 Программа очень проста для пользователей. И в то же время бесконечна сложна со стороны технической реализации.

Меню приложения

В одном продукте разместилось большое количество полезных инструментов, которые работают автоматически. Стоит отметить что в ней также встроен отличный алгоритм распознавания объектов на фотографии.

Это интересно: как определить национальность по фото онлайн.

Сервисы для перевода с французского на русский по картинке

Кроме перечисленных нами приложений, рекомендуем обратить внимание на следующие сетевые сервисы:

Ссылки:	Описание:
translate.yandex.ru	Ресурс Яндекса, выполняющий распознавание текста и его перевод по фото. Имеет хорошее качество распознавания.
i2ocr.com	OCR-сервис, выполняющий распознавание более сотни языков и имеющий бесплатный характер. Распознанный текст можно перевести на нужный язык. Качество работы среднее.
newocr. com	Ещё один OCR-сервис, поддерживающий распознавание 122 языков на фото. Распознанный текст можно перевести на любой язык с помощью функционала Google Translate.

Математический сканер и решебник по фото

Мобильное приложение на Андроид «Математический сканер» может без остановки решать примеры по фотографии онлайн. Оно не только само решит задачу или уравнение, но и расскажет пользователю, как это сделать.

Полезный инструмент, который вполне может заменить учителя во время выполнения задания. Любую задачу он решает через камеру мобильного устройства.

Решение примеров по фото

Даже тем учащимся, которые хотят любую задачу решить своими силами, чтобы получить драгоценный опыт. Не обязательно решать задачи через сканер. Он может выступать в роли проверяющего преподавателя. Попробуйте сделать задание и решить задачу в приложении.

Если ответы совпадут — значит вы всё сделали правильно. Математический сканер работает онлайн и оффлайн. При первом запуске необходимо подключение, так как оно скачивает необходимые данные с серверов разработчика.

Сразу же после первого использование приложение можно применять offline. В программе масса примеров и готовых решений, статей и графиков с таблицами. Если какое-нибудь уравнение ему не под силу, попробуйте разбить его на несколько простых. И решить по частям, фотографируя примеры. В приложении есть платная подписка. В бесплатной версии пользователь вынужден смотреть рекламу в отдельном блоке. Но это не мешает процессу работы с программой.

Google Переводчик — приложение для перевода по картинке

Сложно сомневаться в качестве авторитетного Google Переводчик, который вырывает самых разных людей из пучины непонимания незнакомого языка. Лидер мирового рынка предлагает множество полезных, прогрессивных функций, в том числе и фотоперевод. Как и с любым языком, подвластным Google Переводчик, не приходится погружаться в сомнения насчёт качества перевода с китайского языка: он гарантирует правильное толкование и точное распознание материалов с изображения. Не верите? Убедитесь сами.

Скачайте бесплатное приложение Google Переводчик, источником может стать Play Market или AppStore.
Войдите в свой Google-аккаунт.
Выберете перевод с китайского языка на русский.
Загрузите изображение, или же снимите его сразу.
Получите мгновенный перевод текста с изображения, которому если и нужна корректировка, то лишь минимальная. Как и при работе с любым искусственным интеллектом.

Google — интернациональная компания, и их переводчик — отличный выбор при работе с китайским языком!

Онлайн-калькулятор дробей по изображению

Нередко знакомство с дробями в школе у подростков вызывает шок. Во всех начальных школах по программе они следуют сразу же за обычной и более понятной все математикой. Детям бывает не легко понять, как можно целое число разделить на 20 частей.

Уравнения с дробями

Материал усваивается со временем. А для решения более трудных примеров можно применять «Калькулятор дробей». С его помощью можно решать проценты со скобками, десятичные дроби. Каждый пример приводится пошагово. Поэтому он поможет понять, как такие задачи могут быть выполнены.

Калькулятор дробей

Калькулятором дробей можно решать как простые, так и сложные примеры с преобразованием дробей в десятичные числа по фотографии. Показывая варианты выполнения примеров, приложение делает это в простой и понятной форме.

В примерах поддерживаются скобки и задания с процентами. В программе можно работать с большими числами. Не дробные (в периоде) результаты показывает по аналогии с калькулятором.

Кроме этого интерфейс приложения может быть настроен пользователем. Выбирайте темы для калькулятора и изменяйте расположение кнопок управления. Калькулятор может быть установлен на устройства Android 4.1 или выше.

Яндекс.Переводчик — поможет перевести по фото

Кроме уже привычного нам всем текстового перевода, замечательные веб-переводчики поддерживают и распознавание текста с изображений. Это очень удобно: будь то учебная работа или необходимость в работе. Напимер, программы всегда выручат и приблизят к пониманию загадочного языка прекрасного Китая.

Российский «Яндекс», знакомый нам всем, способен разобрать великое многообразие иероглифов даже с неровно отснятой или отсканированной картинки. От других переводчиков его отличает максимальная художественная точность и адекватность при переводе на русский язык. Конечно погрешность в работе с китайским — минимальна, а простота в использовании приложения — абсолютна. Разберёмся, как получить перевод от продукта наших соотечественников пошагово.

Первый шаг — установка бесплатного приложения Яндекс.Переводчика. Вы можете скачать его из Play Маркет или AppStore, в зависимости от операционной системы Вашего устройства.
Авторизуйтесь в приложении, используя учётную запись Яндекс Переводчика. Ваш телефон может войти в аккаунт сам, если он подключён к другим вспомогательным службам от Яндекс.
Выберите язык.
Следуя подсказкам интерфейса, загрузите изображение или сделайте мгновенный снимок. Не переживайте за качество.
Готово — Вам не нужно переживать из-за того, что Вы не поняли важные для Вас материалы, ведь Яндекс с лёгкостью адаптировал их под Ваш родной язык.

«Яндекс» рушит все стереотипы и уверенно идёт в темпе со временем, а значит в будущем нас ждут новые любопытные «плюшки» от разработчиков!

Камера калькулятор — решение задач по математике

Очередной калькулятор с камерой может быть полезен для решения математических задач и не только. В нём сосредоточено большое количество функций, которые будут полезны в разных сферах деятельности. В дополнение в нём можно найти научный калькулятор, который может быть использован инженерами и студентами. Калькулятор уравнений может решать уравнения и неравенства разной сложности. В результатах отображает графики.

Ссылка: https://play.google.com/store/apps/details?id=math.scientific.calculator. camera.plus

Приложение «Калькулятор с камерой» работает через внешнюю камеру смартфона. Загрузив и запустив его, необходимо навести объектив на пример и нажать на кнопку для создания фото. На окне результатов можно переключаться при помощи вкладок, чтобы посмотреть графики и варианты решения примеров и уравнений.

ГДЗ по фото задания через Google Translate

Поможет решить задания по английскому также переводчик от Гугл. Его можно найти по веб-адресу: https://translate.google.com/.

Скачайте его для IOS или Android в мобильных маркетах. Переводчик отлично справляется с 103 языками онлайн и 100 в мобильных приложениях. Умеет переводить по изображению, написанный текст от руки, текст введённый голосом. Распознаёт даже плохо проявляемый на бумаге текст и переводит его на выбранный язык.

Управлять им сможет даже ребёнок. В интерфейсе программы необходимо выбрать кнопку «Камера» и навести объектив на задание по английскому.

Управлять переводом можно при помощи кнопок, которые появляются поверх текста у краёв экрана. Чтобы включить освещение текста для лучшего распознавания, нажмите на иконку с молнией.

Если нужен снимок перевода выберите на панели кнопку с картинкой. Изображение с переводом можно поворачивать по и против часовой стрелки.

После включения кнопки для определения написанного, на экране можно уменьшить или увеличить размер рамки, в которую входит текст. Бывает нужно выделить лишь часть текста, чтобы не переводить весь при выполнении домашнего задания по английскому языку. На экране это можно сделать при помощи пальца, выделив нужный текст.

В таком случае переводчик будет работать только с помеченной областью. А остальной текста останется без перевода. Это удобно, когда нужно быстро понять, о чём говорится в одном предложении из всего текста.

Это интересно: решение дробей по фото.

Решение примеров в Google Lens по картинке

Несколько месяцев назад в Интернет попала новость, что популярное приложение от Гугл — Google Lens научилось также выполнять математические задания и решать примеры. Для пользователей IOS доступно приложение Гугл в магазине, в котором реализован алгоритм программы. Принцип его работы остаётся прежним: запустите камеру и наведите её на пример. Посередине экрана в нижней его части нажмите на большую круглую кнопку.

Google Lens

Спустя некоторое время Гугл Лэнс найдёт решение в своей поисковой системе. В результатах можно выбрать сайт или изображение с уже решённым примером.

Уравнения онлайн

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.

Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы.

Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой.

Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ.

Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий.

Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции.

Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета.

Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории.

В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность.

Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их.

Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи.

Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы.

Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители.

Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение.

В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.

Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы.

Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.

Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов.

Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц.

Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.

Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа , и как правильно раскрывать выражения, содержащие знак модуля , то наличие в уравнении выражения, стоящего под знаком модуля , перестает быть препятствием для его решения.

Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.

Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.

Число -5 имеет знак «-» и абсолютное значение 5.

Абсолютные значения чисел 5 и -5 равны 5.

Абсолютное значение числа х называется модулем числа и обозначается |x|.

Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.

Это же касается любых выражений, которые стоят под знаком модуля.

Правило раскрытия модуля выглядит так:

|f(x)|= f(x), если f(x) ≥ 0, и

|f(x)|= — f(x), если f(x)

Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3

Чтобы решить уравнение, содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля .

Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.

Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.

А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.

Рассмотрим простой пример.

Решим уравнение:

|x-3|=-x 2 +4x-3

1. Раскроем модуль.

|x-3|=x-3, если x-3≥0, т.е. если х≥3

|x-3|=-(x-3)=3-x, если x-3

2. Мы получили два числовых промежутка: х≥3 и х

Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:

А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:

Внимание! Это уравнение существует только на промежутке х≥3!

Раскроем скобки, приведем подобные члены:

и решим это уравнение.

Это уравнение имеет корни:

х 1 =0, х 2 =3

Внимание! поскольку уравнение x-3=-x 2 +4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 2 =3.

Б) При x

Внимание! Это уравнение существует только на промежутке х

Раскроем скобки, приведем подобные члены. Получим уравнение:

х 1 =2, х 2 =3

Внимание! поскольку уравнение 3-х=-x 2 +4x-3 существует только на промежутке x

Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.

Инструкция

Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.

Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!

Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.

Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т.е.
х=4

Видео по теме

Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.

Вам понадобится

— линейное уравнение с двумя переменными;
— второе уравнение или дополнительные условия.

Инструкция

Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую. Найдите у и подставьте в любое из первоначальных уравнений, найдите х.

Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.

Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.

Источники:

как решить уравнение с одной переменной

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

— система из трех уравнений с тремя неизвестными.

Инструкция

Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.

Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.

Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.

Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.

Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.

Источники:

решений уравнений с тремя неизвестными

Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.

Инструкция

Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.

Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.

Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.

В первом выражении все члены 2, можно вынести 2 за скобку распределительному свойству умножения:2*(2х-у-3)=0. Теперь обе части выражения можно сократить на это число, а затем выразить у, так как коэффициент по модулю при нем равен единице:-у=3-2х или у=2х-3.

Так же, как и в первом случае, подставляем данное выражение во второе уравнение и получаем:3х+2*(2х-3)-8=0;3х+4х-6-8=0;7х-14=0;7х=14;х=2.Подставляем полученное значение в выражение: у=2х-3;у=4-3=1.

Мы видим, что коэффициент при у одинаков по значению, но различен по знаку, следовательно, если мы сложим данные уравнения, то вовсе избавимся от у:4х+3х-2у+2у-6-8=0;7х-14=0;х=2.Подставляем значение х в любое из двух уравнений системы и получаем у=1. 2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.

Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.

Видео по теме

Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.

Инструкция

Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. Мысленно определите коэффициенты, стоящие перед каждой неизвестной, а также коэффициенты в правой части каждого уравнения.

Решение показательных уравнений. Примеры.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Что такое показательное уравнение ? Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся в показателях каких-то степеней. И только там! Это важно.

Вот вам примеры показательных уравнений :

3 х ·2 х = 8 х+3

Обратите внимание! В основаниях степеней (внизу) — только числа . В показателях степеней (вверху) — самые разнообразные выражения с иксом. Если, вдруг, в уравнении вылезет икс где-нибудь, кроме показателя, например:

это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Здесь мы будем разбираться с решением показательных уравнений в чистом виде.

Вообще-то, даже чистые показательные уравнения чётко решаются далеко не всегда. Но существуют определённые типы показательных уравнений, которые решать можно и нужно. Вот эти типы мы и рассмотрим.

Решение простейших показательных уравнений.

Для начала решим что-нибудь совсем элементарное. Например:

Даже безо всяких теорий, по простому подбору ясно, что х=2. Больше-то никак, верно!? Никакое другое значение икса не катит. А теперь глянем на запись решения этого хитрого показательного уравнения:

Что мы сделали? Мы, фактически, просто выкинули одинаковые основания (тройки). Совсем выкинули. И, что радует, попали в точку!

Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, эти числа можно убрать и приравнять показатели степеней. Математика позволяет. Остаётся дорешать куда более простое уравнение. Здорово, правда?)

Однако, запомним железно: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов. Скажем, в уравнениях:

2 х +2 х+1 = 2 3 , или

двойки убирать нельзя!

Ну вот, самое главное мы и освоили. Как переходить от злых показательных выражений к более простым уравнениям.

«Вот те раз!» — скажете вы. «Кто ж даст такой примитив на контрольных и экзаменах!?»

Вынужден согласиться. Никто не даст. Но теперь вы знаете, куда надо стремиться при решении замороченных примеров. Надо приводить его к виду, когда слева — справа стоит одно и то же число-основание. Дальше всё будет легче. Собственно, это и есть классика математики. Берём исходный пример и преобразовываем его к нужному нам виду. По правилам математики, разумеется.

Рассмотрим примеры, которые требуют некоторых дополнительных усилий для приведения их к простейшим. Назовём их простыми показательными уравнениями.

Решение простых показательных уравнений. Примеры.

При решении показательных уравнений, главные правила — действия со степенями. Без знаний этих действий ничего не получится.

К действиям со степенями надо добавить личную наблюдательность и смекалку. Нам требуются одинаковые числа-основания? Вот и ищем их в примере в явном или зашифрованном виде.

Посмотрим, как это делается на практике?

Пусть нам дан пример:

2 2х — 8 х+1 = 0

Первый зоркий взгляд — на основания. Они… Они разные! Два и восемь. Но впадать в уныние — рано. Самое время вспомнить, что

Двойка и восьмёрка — родственнички по степени.) Вполне можно записать:

8 х+1 = (2 3) х+1

Если вспомнить формулку из действий со степенями:

(а n) m = a nm ,

то вообще отлично получается:

8 х+1 = (2 3) х+1 = 2 3(х+1)

Исходный пример стал выглядеть вот так:

2 2х — 2 3(х+1) = 0

Переносим 2 3 (х+1) вправо (элементарных действий математики никто не отменял!), получаем:

2 2х = 2 3(х+1)

Вот, практически, и всё. Убираем основания:

Решаем этого монстра и получаем

Это правильный ответ.

В этом примере нас выручило знание степеней двойки. Мы опознали в восьмёрке зашифрованную двойку. Этот приём (шифровка общих оснований под разными числами) — очень популярный приём в показательных уравнениях! Да и в логарифмах тоже. Надо уметь узнавать в числах степени других чисел. Это крайне важно для решения показательных уравнений.

Дело в том, что возвести любое число в любую степень — не проблема. Перемножить, хоть на бумажке, да и всё. Например, возвести 3 в пятую степень сможет каждый. 243 получится, если таблицу умножения знаете.) Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот… Узнавать, какое число в какой степени скрывается за числом 243, или, скажем, 343… Здесь вам никакой калькулятор не поможет.

Степени некоторых чисел надо знать в лицо, да… Потренируемся?

Определить, какими степенями и каких чисел являются числа:

2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.

Ответы (в беспорядке, естественно!):

5 4 ; 2 10 ; 7 3 ; 3 5 ; 2 7 ; 10 2 ; 2 6 ; 3 3 ; 2 3 ; 2 1 ; 3 6 ; 2 9 ; 2 8 ; 6 3 ; 5 3 ; 3 4 ; 2 5 ; 4 4 ; 4 2 ; 2 3 ; 9 3 ; 4 5 ; 8 2 ; 4 3 ; 8 3 .

Если приглядеться, можно увидеть странный факт. Ответов существенно больше, чем заданий! Что ж, так бывает… Например, 2 6 , 4 3 , 8 2 — это всё 64.

Предположим, что вы приняли к сведению информацию о знакомстве с числами.) Напомню ещё, что для решения показательных уравнений применим весь запас математических знаний. В том числе и из младших-средних классов. Вы же не сразу в старшие классы пошли, верно?)

Например, при решении показательных уравнений очень часто помогает вынесение общего множителя за скобки (привет 7 классу!). Смотрим примерчик:

3 2х+4 -11·9 х = 210

И вновь, первый взгляд — на основания! Основания у степеней разные… Тройка и девятка. А нам хочется, чтобы были — одинаковые. Что ж, в этом случае желание вполне исполнимое!) Потому, что:

9 х = (3 2) х = 3 2х

По тем же правилам действий со степенями:

3 2х+4 = 3 2х ·3 4

Вот и отлично, можно записать:

3 2х ·3 4 — 11·3 2х = 210

Мы привели пример к одинаковым основаниям. И что дальше!? Тройки-то нельзя выкидывать… Тупик?

Вовсе нет. Запоминаем самое универсальное и мощное правило решения всех математических заданий:

Не знаешь, что нужно — делай, что можно!

Глядишь, всё и образуется).

Что в этом показательном уравнении можно сделать? Да в левой части прямо просится вынесение за скобки! Общий множитель 3 2х явно намекает на это. Попробуем, а дальше видно будет:

3 2х (3 4 — 11) = 210

3 4 — 11 = 81 — 11 = 70

Пример становится всё лучше и лучше!

Вспоминаем, что для ликвидации оснований нам необходима чистая степень, безо всяких коэффициентов. Нам число 70 мешает. Вот и делим обе части уравнения на 70, получаем:

Оп-па! Всё и наладилось!

Это окончательный ответ.

Случается, однако, что выруливание на одинаковые основания получается, а вот их ликвидация — никак. Такое бывает в показательных уравнениях другого типа. Освоим этот тип.

Замена переменной в решении показательных уравнений.

Примеры.

Решим уравнение:

4 х — 3·2 х +2 = 0

Сначала — как обычно. Переходим к одному основанию. К двойке.

4 х = (2 2) х = 2 2х

Получаем уравнение:

2 2х — 3·2 х +2 = 0

А вот тут и зависнем. Предыдущие приёмы не сработают, как ни крутись. Придётся доставать из арсенала ещё один могучий и универсальный способ. Называется он замена переменной.

Суть способа проста до удивления. Вместо одного сложного значка (в нашем случае — 2 х) пишем другой, попроще (например — t). Такая, казалось бы, бессмысленная замена приводит к потрясным результатам!) Просто всё становится ясным и понятным!

Итак, пусть

Тогда 2 2х = 2 х2 = (2 х) 2 = t 2

Заменяем в нашем уравнении все степени с иксами на t:

Ну что, осеняет?) Квадратные уравнения не забыли ещё? Решаем через дискриминант, получаем:

Тут, главное, не останавливаться, как бывает… Это ещё не ответ, нам икс нужен, а не t. Возвращаемся к иксам, т.е. делаем обратную замену. Сначала для t 1:

Стало быть,

Один корень нашли. Ищем второй, из t 2:

Гм… Слева 2 х, справа 1… Неувязочка? Да вовсе нет! Достаточно вспомнить (из действий со степенями, да…), что единичка — это любое число в нулевой степени. Любое. Какое надо, такое и поставим. Нам нужна двойка. Значит:

Вот теперь всё. Получили 2 корня:

Это ответ.

При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:

Из семёрки двойка через простую степень не получается. Не родственники они… Как тут быть? Кто-то, может и растеряется… А вот человек, который прочитал на этом сайте тему «Что такое логарифм?» , только скупо улыбнётся и запишет твёрдой рукой совершенно верный ответ:

Такого ответа в заданиях «В» на ЕГЭ быть не может. Там конкретное число требуется. А вот в заданиях «С» — запросто.

В этом уроке приведены примеры решения самых распространённых показательных уравнений. Выделим основное.

Практические советы:

1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!

2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах — считаем.

3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего — квадратное. Или дробное, которое тоже сводится к квадратному.

4. Для успешного решения показательных уравнений надо степени некоторых чисел знать «в лицо».

Как обычно, в конце урока вам предлагается немного порешать.) Самостоятельно. От простого — к сложному.

Решить показательные уравнения:

Посложнее:

2 х+3 — 2 х+2 — 2 х = 48

9 х — 8·3 х = 9

2 х — 2 0,5х+1 — 8 = 0

Найти произведение корней:

2 3-х + 2 х = 9

Получилось?

Ну, тогда сложнейший пример (решается, правда, в уме. ..):

7 0.13х + 13 0,7х+1 + 2 0,5х+1 = -3

Что, уже интереснее? Тогда вот вам злой пример. Вполне тянет на повышенную трудность. Намекну, что в этом примере спасает смекалка и самое универсальное правило решения всех математических заданий.)

2 5х-1 · 3 3х-1 · 5 2х-1 = 720 х

Пример попроще, для отдыха):

9·2 х — 4·3 х = 0

И на десерт. Найти сумму корней уравнения:

х·3 х — 9х + 7·3 х — 63 = 0

Да-да! Это уравнение смешанного типа! Которые мы в этом уроке не рассматривали. А что их рассматривать, их решать надо!) Этого урока вполне достаточно для решения уравнения. Ну и, смекалка нужна… И да поможет вам седьмой класс (это подсказка!).

Ответы (в беспорядке, через точку с запятой):

1; 2; 3; 4; решений нет; 2; -2; -5; 4; 0.

Всё удачно? Отлично.

Есть проблемы? Не вопрос! В Особом разделе 555 все эти показательные уравнения решаются с подробными объяснениями. Что, зачем, и почему. Ну и, конечно, там имеется дополнительная ценная информация по работе со всякими показательными уравнениями. Не только с этими.)

Последний забавный вопрос на соображение. В этом уроке мы работали с показательными уравнениями. Почему я здесь ни слова не сказал про ОДЗ? В уравнениях — это очень важная штука, между прочим…

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Как легко решать уравнения вида x + 3 = 4

Умножить/РазделитьМногошаговые СкобкиНоль/Нет/Все Sol’n

Purplemath

Что такое линейное уравнение?

«Линейные» уравнения — это уравнения, содержащие просто старую переменную, такую как « x », а не что-то более сложное, например, x ² , или ^x / _y , или квадратные корни, или другие более сложные выражения. Линейные уравнения — это простейшие уравнения, с которыми вам придется иметь дело.

Возможно, вы уже решали линейные уравнения; ты просто этого не знал.

Содержание продолжается ниже

MathHelp.com

Решение одношаговых уравнений

Еще в ранние годы, когда вы изучали сложение, ваш учитель, вероятно, давал вам рабочие листы, которые содержали такие упражнения, как следующие:

Заполнить поле: &квадрат; + 3 = 5

Заполните поле: &квадрат; + 3 = 5

Как только вы достаточно хорошо изучили факты сложения, вы поняли, что вам нужно поставить «2» в квадратик.

Решение уравнений работает почти так же, но теперь нам нужно выяснить, что входит в x , а не в коробку. Однако, поскольку мы стали старше, чем раньше, когда заполняли поля, уравнения также могут быть намного сложнее, и поэтому методы, которые мы будем использовать для решения уравнений, будут немного более продвинутыми.

Что значит решить уравнение?

Решение уравнения означает нахождение значения переменной, которая делает уравнение верным. В общем, чтобы решить уравнение для данной переменной, нам нужно «отменить» все, что было сделано с переменной. Мы делаем это для того, чтобы получить переменную саму по себе; с технической точки зрения, мы «изолируем» переменную. Это приводит к тому, что уравнение перестраивается следующим образом: «(переменная) равна (какому-то числу)», где (некоторое число) — это ответ, который они ищут.

Как решить сложением или вычитанием?

Чтобы решить линейное уравнение путем сложения или вычитания, вы берете число, связанное с переменной (в x + 3 = 5 это будет число 3). Обратите внимание, как это число связано с переменной (в в этом случае оно добавляется), и вы должны сделать противоположное с обеими частями уравнения (в данном случае, вычитая 3 из обеих частей уравнения).

Переменная представляет собой букву x . Чтобы решить это уравнение, мне нужно получить x само по себе; то есть мне нужно получить х с одной стороны от знака «равно», а с другой стороны какое-то число.

Так как я хочу только x с одной стороны, это означает, что мне не нравится «плюс шесть», который в настоящее время находится на той же стороне, что и x . Поскольку 6 — это , добавленное к x , мне нужно вычесть из этого 6, чтобы избавиться от него. То есть мне нужно будет вычесть 6 из x , чтобы «отменить» их, добавив к нему 6.

Это приводит к наиболее важному соображению, связанному с уравнениями:

Независимо от того, с каким уравнением мы имеем дело — линейным или нет — что бы мы ни делали с одной частью уравнения, мы должны делать то же самое в другую часть уравнения. Уравнения в этом отношении подобны малышам:

Мы должны быть тотально, тотально справедливыми по отношению к обеим сторонам, иначе последует несчастье!

Что бы вы ни делали с уравнением, делайте ТОЧНО ОДИНАКОВОЕ действие с ОБЕИМИ сторонами этого уравнения!

Вероятно, лучший способ отслеживать вычитание 6 с обеих сторон — это отформатировать вашу работу таким образом:

Изображение выше анимировано на «живой» странице.

Здесь вы видите, что я вычел 6 из обеих сторон, начертил горизонтальную черту «равно» под всем уравнением, а затем прибавил. В левой части (LHS) уравнения это дает мне:

x плюс ничего равно x , а 6 минус 6 равно нулю последняя строчка моей работы; а именно:

x = −9

Та же процедура «отмены» работает для уравнений, в которых переменная была соединена с вычитанием.

Решить
х — 3 = -5

Переменная находится в левой части уравнения (слева) и связана с «вычесть три». Поскольку я хочу получить x само по себе, мне не нравится «3», которое в настоящее время вычитается из него. Противоположностью вычитания является сложение, поэтому я отменю «вычитание 3», добавив 3 к обеим частям уравнения, а затем прибавив, чтобы упростить, чтобы получить мой ответ:

Тогда мой ответ:

x = −2

Вас могут попросить «проверить свои решения», по крайней мере, на ранних этапах обучения решению уравнений.

Как проверить свое решение?

Чтобы проверить свое решение заданного уравнения, вы просто подставляете значение ответа в исходное уравнение (вместо переменной) и убедитесь, что в итоге вы получите верное утверждение. В конце концов, это определение решения уравнения; а именно, решением является любое значение или набор значений (для более сложных уравнений позже), что делает исходное уравнение верным утверждением.

Итак, чтобы проверить мое решение приведенного выше уравнения, вы должны подставить «-2» вместо x в левой части (LHS) исходного уравнения, и убедитесь, что это упрощает получение исходного значения для правой части (RHS) уравнения:

Проверка:

LHS: (−2 ) − 3 = −5

Справа: −5

Поскольку теперь каждая часть исходного уравнения дает одно и то же значение, это подтверждает, что решение действительно правильное.

На этот раз переменная находится в правой части уравнения. Это нормально; не имеет значения, где находится переменная, пока я изолирую ее (то есть, пока я могу получить ее саму по одну сторону от знака «равно»).

В этом уравнении у меня есть тройка, которая вычитается из переменной. Чтобы отменить вычитание, я добавлю три к каждой стороне уравнения.

4 = х — 3
+3 + 3
————
7 = x

(правую часть после прибавления можно было бы записать как « x + 0″, но «плюс ноль» обычно игнорируется. Поэтому я записал только x на справа.)

Теперь, как часть моей ручной работы, мне нужно показать, что я проверил это решение, подключив его обратно к правой части исходного уравнения и подтвердив, что в итоге я получил LHS исходного уравнения; то есть что у меня получается 4:

Проверка:

RHS: (7) − 3 = 4 = LHS

Часть «проверки» — это то, что я только что сделал выше. Я позаботился о том, чтобы маркировать вещи четко, чтобы оценщик мог найти мою «галочку» (так что я получу полную оценку за упражнение). Мой окончательный ответ:

x = 7

Когда я решил последнее упражнение выше, переменная оказалась справа от знака «равно». Но в своем решении я написал ответ с переменной слева от знака «равно». Это довольно стандартно. Когда вы решаете, переменная окажется там, где она заканчивается. Когда вы записываете решение, переменная идет слева. Почему? Потому что.

Решите 2 = − x

Это уравнение почти решено. Но не совсем. У меня нет старого доброго x справа; вместо этого у меня — x . Что делать?

Я могу представить, что − x равно 0 − x . Итак, что произойдет, если я добавлю x к каждой части уравнения?

2 = –х
+х +х
———-
х + 2 = 0

Хорошо; это вроде помогло. Взяв переменную и «добавив ее на другую сторону», я получил переменную в том формате, который мне нравится (другими словами, без знака «минус»). И это также преобразовало исходное уравнение в простое одношаговое уравнение. Я избавлюсь от 2 с левой стороны, «вычитая его» с правой стороны:

х + 2 = 0
-2 = -2
———-
x = -2

Этот ответ имеет смысл. Если отрицательное значение переменной равно положительной двойке, то положительное значение переменной должно равняться отрицательной двойке. Итак, мой ответ:

x = −2

Технически последний пример представлял собой уравнение, состоящее из двух шагов, потому что для его решения требовалось прибавлять одно значение к обеим частям уравнения, а затем вычитать еще одно из обеих частей. Важно отметить, что вы можете добавлять и вычитать переменные с другой стороны уравнения, точно так же, как вы можете складывать и вычитать числа с другой стороны. Одни и те же методы работают как с переменными, так и с числами.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении линейного уравнения путем сложения или вычитания. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

Страница 2Страница 3Страница 4Страница 5

▷Step by Step Приложения для TI-Nspire CX & CX CAS Бесплатная загрузка. Пройдите курсы по математике, естественным наукам и бизнесу

Для подготовки к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—


95% купили больше ПРИЛОЖЕНИЙ.	97% сообщили об улучшении результатов.	Рейтинг: 4,89 из 5 звезд.	Доступно 46 ПРИЛОЖЕНИЙ.

КОВИД СПЕЦИАЛЬНЫЙ

Купите 3 приложения Made Easy по цене 2 приложений.

Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamics Made EasyThermodynamik Leicht GemachtTrigonometry Made EasyTrigonometria de Manera FacilTr igonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtТригонометрия Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.

Находится в разделе 5:Настройки → 4:Статус → О программе

ID может выглядеть так: 1008000007206E210B0 BD92F455 . ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.

или на международном уровне:

В конце оплаты через PayPal вам будет отправлено электронное письмо с вашим ключом и программным обеспечением.

Хотите купить TI-калькулятор?

Получите самые низкие цены на TI-калькуляторы
(со сравнением цен)

СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.

Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Настройте оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, восстановленные, подержанные калькуляторы.
Смотрите обучающие видео и читайте руководства по калькуляторам.
Читайте последние новости о калькуляторах в Интернете.

БЕСПЛАТНАЯ загрузка:
Решение квадратных уравнений (шаг за шагом)

Загрузите пошаговый решатель квадратных уравнений

. Этот решатель является частью приложения Algebra Made Easy.

— Загрузите бесплатные пробные версии здесь.

— Срок действия пробных и платных приложений неограничен.

— Будущие обновления бесплатны — навсегда!

Онлайн-репетиторство по математике

Получите онлайн-репетиторство.

Репетиторы с отличными оценками по математике будут рады помочь вам.

Получите индивидуальную помощь по математике.

Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, AP исчисление AB и BC, AP статистику, тригонометрию, дискретную математику.

Репетиторы более 10 лет работали в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).

Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.

Наши преподаватели имеют более 20 лет опыта преподавания.

1. урок стоит 50$, после этого 100$ в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.

Забронируйте сеанс репетиторства по электронной почте: [email protected]

Для вопросов, заказов и т. д.: НАПИШИТЕ С НАМИ.

Первый урок (50 долларов США)	Один урок (100 долларов США)	Несколько уроков

Как превратить текстовые задачи в уравнения

Хотите прочитать это позже? Скачать в формате PDF!

54 акции

Фейсбук
Твиттер

Задачи со словами могут стать настоящей проблемой для учащихся, но с помощью калькулятора задач со словами в уравнения их можно решить намного проще. Эти удобные инструменты берут текстовые задачи и превращают их в уравнения, которые легче решать. Всего несколькими щелчками мыши учащиеся могут получить помощь, необходимую им для понимания и решения текстовых задач с помощью калькулятора решения текстовых задач. Это отличный инструмент для учащихся, у которых проблемы с математикой, или для тех, кто хочет улучшить свои навыки решения задач.

Отказ от ответственности: этот пост содержит партнерские ссылки для вашего удобства. Ознакомьтесь с нашей политикой раскрытия информации здесь.

Быстрая навигация

Как преобразовать текстовую задачу в уравнение?

На этот вопрос нет универсального ответа, так как процесс преобразования словесной задачи в уравнение зависит от задачи. Однако есть несколько общих советов, которые могут помочь вам начать работу:

Внимательно прочитайте задачу и определите всю предоставленную информацию.
Укажите тип задачи (например, задачи со словами на сложение, умножение и т. д.).
Переведите полученную информацию в математические символы и уравнения.
Решите уравнение, чтобы найти правильный ответ на задачу со словами.

Немного потренировавшись, вы сможете легко превращать текстовые задачи в уравнения! И если вы когда-нибудь застрянете, вы всегда можете использовать калькулятор для решения математических задач за помощью.

Использование калькулятора решения текстовых задач для решения текстовых задач

Словесная задача — это математическая головоломка, которую может быть трудно решить. Вам может понадобиться помощь в калькуляторе уравнений, если у вас возникли проблемы с решением текстовых задач самостоятельно.

Он возьмет любую текстовую задачу и превратит ее в уравнение, которое будет легче решать и находить ответ. Вы также можете использовать этот тип инструмента в качестве средства проверки, если вы хотите убедиться, что ваш ответ правильный во время практики.

Вот как можно использовать калькулятор решения математических задач

Чтобы использовать калькулятор для решения задач , сначала необходимо ввести информацию в инструмент. Вы можете сделать это, введя математическую задачу в предоставленную область.

Например, вы можете ввести: Поезд отправляется со станции в полдень и движется на север с определенной скоростью. Через час с той же станции отправляется второй поезд, идущий на юг с той же скоростью. Когда встречаются два поезда?

Затем нажмите кнопку «Решить» или кнопку «Отправить», чтобы решить уравнение. Калькулятор словесных задач в уравнения решит уравнение и даст нам ответ. Мы также можем использовать этот инструмент для проверки наших ответов, если мы хотим убедиться, что они верны.

Калькулятор текстовых задач — отличный инструмент для учащихся, у которых проблемы с математикой, или для всех, кто хочет улучшить свои навыки решения задач. Всего несколькими щелчками мыши они могут получить помощь, необходимую им для понимания и решения текстовых задач.

Калькулятор решения текстовых задач: как работает процесс вычисления

Калькулятор возьмет математическую задачу и превратит ее в уравнение. В этом случае уравнение будет таким: t+60 минут = 0. Затем калькулятор словесных задач в уравнения решит уравнение и даст нам ответ.

Вы также можете использовать этот инструмент для проверки своих ответов, если мы хотим убедиться, что они верны. Для этого просто введите задачу в текстовое поле и нажмите где-нибудь кнопку «Решить» — в большинстве калькуляторов есть эта кнопка.

Калькулятор решения математических задач решит уравнение и даст вам ответ. Если ответ правильный, калькулятор сообщит вам об этом. Если ответ неверный, он также сообщит вам об этом.

Этот калькулятор — отличный инструмент для учащихся, у которых проблемы с математикой, или для тех, кто хочет улучшить свои навыки решения задач. Всего несколькими щелчками мыши они могут получить помощь, необходимую им для понимания и решения текстовых задач.

Калькулятор текстовых задач в уравнения преобразует любую текстовую задачу в уравнение, которое легче решать и находить ответ. И, опять же, вы также можете использовать этот тип инструмента в качестве средства проверки, если вы хотите убедиться, что ваш ответ правильный во время практики.

Есть ли приложение или веб-сайт для решения математических задач?

Да! На самом деле, существует несколько приложений и онлайн-калькуляторов, которые могут решать математические задачи. Некоторые из них предназначены для решения задач со словами, в то время как другие являются более общими математическими калькуляторами.

Если вы ищете приложение, которое поможет вам решать задачи со словами, обязательно ознакомьтесь с нашим списком лучших приложений для решения математических задач. Лучший опыт, который вы можете получить с онлайн-калькулятором, — это взять систему уравнений и узнать цель, которую вы хотите получить от калькулятора.

Под целью я подразумеваю математические задачи каждого типа, которые вы пытаетесь решить с помощью системы уравнений с помощью калькулятора текстовых задач. Например, некоторые калькуляторы идеально подходят для практики решения задач, а другие могут быть генераторами текстовых задач. Некоторые помогут вам с пошаговым объяснением, как будто показывая вашу собственную работу, а другие покажут вам простые расчеты.

Вы обнаружите, что многие калькуляторы имеют широкий набор типов математических уравнений, таких как задачи на соотношение слов, целые числа, помощь в поиске неизвестной переменной конкретной задачи, линейные уравнения, квадратный корень, процентное изменение, сумма деньги, общая сумма денег и просто различные математические навыки, чтобы подготовить своих детей к реальному миру!

Список из 9 математических онлайн-калькуляторов

Вы найдете почти мгновенные пошаговые решения с помощью калькулятора решения математических задач, и в большинстве из них используются системы уравнений и ключевые слова, поэтому обратите особое внимание на алгебраические выражения с помощью онлайн-инструмента, который вы используете.

Вы готовы попробовать свои задачи в калькуляторе уравнений? Вот несколько разных ссылок для начала, просто обратите внимание на важную информацию о каждой из них, касающуюся условий использования или того, что именно решит калькулятор:

Бесплатное решение математических задач — Базовая математика. Это бесплатное решение математических задач поможет вам мгновенно решить любые математические задачи.

Калькулятор словесных задач — Symbolab — Этот калькулятор поможет вам шаг за шагом решать словесные задачки по словосочетаниям и находить неизвестное число, среди других понятий, которые может предоставить этот онлайн-калькулятор алгебры!

Калькулятор словесных задач – MathCelebrity – Множество математических калькуляторов, которые помогают решать различные типы математических задач, например, на произведение, процент, площадь, задачи на монеты, задачи на разницу в возрасте и многое другое!

Word Tasks — Calculator Soup — Уравнение создано и решено в деталях, чтобы вы могли проверить свою работу.

Калькуляторы словесных задач — AtoZmath — помогают решать различные математические задачи онлайн.

Решатель текстовых задач по алгебре — шляпа-сова — помогает решать алгебраические уравнения и текстовые задачи.

Solve — Бесплатное решение математических задач — Алгебратор — Берите задачи по алгебре, квадратные уравнения и задачи по предварительной алгебре и решайте их с помощью калькулятора.

Мэтуэй | Решатель задач по алгебре. Бесплатная программа для решения математических задач может ответить на ваши вопросы по алгебре с пошаговыми объяснениями.

Математика — это весело — вы увидите, что он предоставляет около 20 или 30 различных калькуляторов, которые вы можете использовать для различных математических концепций, таких как калькулятор наименьшего общего кратного, калькулятор площади, калькулятор взаимопростых чисел, калькулятор сложных процентов и многие другие.

Эти калькуляторы предназначены для того, чтобы показать наилучшие способы решения математических задач для повседневной жизни с помощью понятий от алгебраических выражений до различных основных математических понятий. А некоторые могут выдать новые словесные задачи для решения вашего ребенка, предоставляя бесплатную практику! Некоторые из них имеют премиум-версию, но я не думаю, что это необходимо.

Теперь, когда вы знаете об этих замечательных инструментах-калькуляторах, не забудьте добавить в закладки те из них или все из них, которые помогут вам в математической практике. Или добавьте его на рабочий стол, чтобы он всегда был под рукой, когда вам это нужно! Даже если они вам сейчас не нужны, сохраните их на потом.

С помощью калькулятора для решения математических задач вы можете быстро и легко превратить любую математическую задачу в уравнение, которое будет легче решить. Попробуйте сегодня и посмотрите, как это работает! На самом деле это довольно весело! Так что, возможно, вы и ваши дети будете с нетерпением ждать математики каждый день и не бояться ее!

Решайте задачи по алгебре с помощью калькулятора

Возьмите эти математические задачи и подключите их к одному из калькуляторов из списка, который я дал вам выше. Это будет веселое знакомство!

1. Сантехник берет 25 долларов за вызов службы поддержки плюс 50 долларов за час работы. Напишите уравнение для стоимости C после h часов работы.

2. Лодка может двигаться со скоростью 12 миль в час в стоячей воде. Напишите уравнение зависимости скорости лодки S от времени t в часах.

3. Стоимость автомобиля уменьшается на 5% каждый год. Напишите уравнение для определения стоимости V автомобиля через n лет.

Все они должны были бы решить уравнение в форме точки пересечения наклона… которое представляет собой уравнение, которое выглядит как y=mx+b, где m — наклон, а b — точка пересечения с осью y.

Чтобы найти решения, используя уравнения этого типа, нам нужно найти наклоны и точки пересечения по оси Y для каждой задачи. Получив эти значения, мы можем подставить их в уравнение и найти искомую переменную.

Для первой задачи ищем стоимость услуг сантехника после h часов работы. Y-пересечение в этом случае равно 25, так как это стоимость служебного вызова. Наклон равен 50, так как это сумма, взимаемая за час обслуживания. Затем мы можем записать уравнение как y=50x+25.

Во второй задаче мы ищем скорость лодки как функцию времени. Точка пересечения с осью Y в этом случае равна 12, так как это максимальная скорость лодки в стоячей воде. Наклон равен -12, так как это изменение скорости каждый час. Тогда мы можем записать уравнение как S=-12t+12.

Для третьей задачи мы ищем стоимость автомобиля через n лет. Y-отрезок равен 0, так как это стоимость автомобиля при его первой покупке. Наклон равен -0,05, так как это процент, на который стоимость автомобиля уменьшается каждый год. Тогда мы можем записать уравнение как V=-0,05n+0.

Это всего лишь несколько примеров математических задач, которые можно преобразовать в уравнения с помощью калькулятора решения текстовых задач.

Вы также можете использовать калькуляторы для простых математических фактов, не для школьников, а для школьников!

Попробуйте сами решить некоторые математические задачи и посмотрите, как работает калькулятор!

Калькулятор преобразования задач Word в уравнения для помощи по математике

Калькулятор решения математических задач — отличный инструмент для учащихся, испытывающих трудности с математикой, или для всех, кто хочет улучшить свои навыки решения задач. Всего несколькими щелчками мыши они могут получить помощь, необходимую им для понимания и решения текстовых задач.

Калькуляторы такого типа возьмут любое математическое выражение и превратят его в уравнение, с которым легче работать и находить ответ. Вы также можете использовать этот тип инструмента в качестве средства проверки, если вы хотите убедиться, что ваш ответ правильный во время практики.

Проблемы со словами могут быть неприятными, но калькулятор для решения математических задач со словами является превосходным инструментом, чтобы помочь с ними. Эти калькуляторы предлагают отличный способ для студентов, которые борются с математикой, или для тех, кто хочет улучшить свои навыки решения, давая им возможность практиковать математические задачи в свободное время! Попробуйте — возможно, вы только что нашли свое совершенное секретное оружие для проверки словесных задач и решения уравнений!

Решите мое уравнение онлайн

Выражение
Уравнение
Неравенство
Свяжитесь с нами

Simplify
Factor
Expand
GCF
LCM

Solve
Graph
System

Solve
Graph
System

Math solver on your site

Наших пользователей:

Я использую, чтобы почесать голову, решая сложные арифметические задачи. Я могу вспомнить то ужасное время, когда я смотрел на уравнения и чувствовал, что никогда не смогу их решить, но как только я начал работать с Алгебратором, все стало совершенно иначе
Марк Хансен, Иллинойс

Хорошо, вот что мне нравится: гораздо более дружественный интерфейс, охват функций, триггер. лучшая графика, волшебники. Однако до сих пор нет текстовых задач, предварительно вычислить, вычислить. (Пожалуйста, скажите мне, что вы работаете над этим — кто будет делать мою домашнюю работу, когда я закончу алгебру колледжа?!?
J.R. Turnston, NY

Мой сын использовал вашу программу по алгебре в этом учебном году. Он чувствовал, что это обеспечило ему дополнительную поддержку, которая не всегда была доступна в школе, и помогло получить пятерки за оба семестра. Кроме того, он считал, что программное обеспечение является отличным обзором для выпускного экзамена. Сегодня я рад сообщить, что приобрел для него программное обеспечение «Алгебра».
Соня Гойко, MS

Я мать троих детей, и я купила программное обеспечение Algebrator для своего старшего сына, чтобы помочь ему с домашним заданием по алгебре, но мои младшие сыновья увидели, как легко им пользоваться, и теперь у них есть фора. Спасибо за такой отличный и доступный продукт.
Энни Хайнс, Кентукки

Мне никогда не было легко понять математику, но эта программа облегчает ее понимание. Спасибо!
Энни Хайнс, Кентукки

Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?

Поисковые фразы, использованные 15 февраля 2010 г.:

экзамены по квадратному уравнению
онлайн-версия книги по промежуточной алгебре
Листы с упражнениями по алгебре для 8 класса
задачи по алгебре с ключом ответа
онлайн-тесты для повышения квалификации по математике с ключом ответа
свободный рабочий лист логарифма
бесплатная рабочая тетрадь по решению математических задач
График 6-го класса
бревенчатая база ти-86
рабочие листы с подписанными номерами
бесплатных рабочих листа по совместимым номерам
mcdougal littell курс математики 3 глава 2 ресурс ответы
ответы на учебник по алгебре 2 Макдугал Литтел
ti-30xa учения
Бесплатная помощь по алгебре среднего уровня
рабочие листы по алгебре «словные задачи»
бесплатные преобразования графа рабочего листа
как решить уравнение третьей степени на ti 84
экспоненты расширительных скобок
Алгебра Холта i рабочие листы
Помощник по предварительной алгебре по математике
лист вычитания умножить добавить разделить дроби
рабочих листа по умножению и делению одночленов
как построить маршрут в кубе в excel
Алгебра мелочи
формула факторинга чисел
кнопка процентов на ti 83
как складывать и вычитать положительные и отрицательные дроби
вопросы по булевой алгебре
вычитание целых чисел бумага
паспорт к учебнику математики 2 глава 4 листа
«ответы» на учебники по математике «предварительная алгебра по математике для учеников» «Вирджиния» «7 класс»
как сделать интерполяцию на TI 83
решение задачи на наибольший общий делитель
наименьшее общее кратное чисел 18 и 21
символьный метод решения линейных уравнений
Процентная доля
набор трюков алгебра
Алгебра 2 примера уравнений и графиков
м файл для нелинейных уравнений
вопросы и ответы на тестах способностей
Упрощение многочленов с использованием распределительного свойства
способ узнать GCF с помощью калькулятора
как решать многочлены скидки словесные задачи алгебра
Рабочие листы для интерпретации графиков
g. e.d задачи по алгебре
лист правил логарифмических переменных
квадратный корень квадратный
Решатель полиномиальных задач
как кодировать факториалы в java
решение уравнений, содержащих подкоренные выражения
Умножение и деление выражений квадратного корня
квадратные уравнения и уравнения на уравнения
напишите программу, используя цикл for для вычисления суммы в java
ti 89 свертка
умножение и упрощение квадратных корней рациональных выражений
график простых неравенств рабочий лист
стихи по алгебраической математике
Рабочий лист по алгебре и функциям для четвертого класса
бесплатная таблица правил алгебры
алгебра 1a сложение/вычитание одношаговых уравнений
Вычислитель тройных интегралов
определение корней многочленов 3-го порядка
кубический корень в ti83
рабочих листа с целыми числами
Калькулятор квадратичного факторинга
стихотворения об алгебре
«математика 6 класс»
экзаменационные работы за 4 класс: математика
математические формулы проценты
порядок дробей наименьший наибольший калькулятор
Алгебра 2 Обзор главы 2 с листом ответов
Макдугал Литтел Алгебра 2 лист ответов
техасская алгебра 1 книга прентис холл
как строить графики целых и целых чисел
добавление суммы рабочего листа целых чисел
задачи по алгебре 8 лет
помощь в задаче по математике до алгебры
копия для учителя Прентис холл математика алгебра 1
понятие параболы, гиперболы и эллипса с решением примера
как расширить квадратные скобки
+Помогите написать статью о том, как G. E.D. изменить мою жизнь
Упростить подкоренное выражение
Рабочий лист наклона и точки пересечения по оси Y
как решить линейное дифференциальное уравнение первого порядка
бесплатные рабочие листы для координатной плоскости для детей
программы системы уравнений для т.и. 83
балансировка линейной алгебры
математические мелочи с ответами алгебра
алгебраические формулы
логарифмические выражения как функция двух переменных
ответы на уроки для второго издания предварительной алгебры
Рабочие листы дерева факторов
glencoe вопрос по физике с ответом
онлайн-шкала по математике
учебник по математике, глава 2, тестовая шпаргалка
11+ экзаменационных работ проходят онлайн-тест
бесплатные рабочие листы с квадратным корнем

Expression
Equation
Inequality
Contact us

Simplify
Factor
Expand
GCF
LCM

Решить
График
Система

Решить
График
Система

9005 9053 9053 ваш сайт
Наши пользователи:
Я начал с такого рода программ, так как учусь в онлайн-классе, и бывают моменты, когда «я понятия не имею». Я нахожу вашу программу легче следовать. СПАСИБО!
Роландо Контрерас, Аризона
Этот продукт является величайшей вещью. Я всегда ходил к своим друзьям, чтобы использовать ее, пока мне не удавалось убедить родителей купить ее для меня. Ненавижу это говорить, но мне действительно нужна была помощь с алгеброй, и теперь я ее получил!
GO, Канзас
Какой отличный инструмент! Я бы порекомендовал это программное обеспечение всем, кому нужна помощь с алгеброй. Все процедуры были такими простыми и понятными.
Дания Дж. Гут, Канзас
Я просто хотел сначала сказать, что ваша программа по алгебре потрясающая! Это действительно помогло мне в моем классе! Я очень беспокоился о своем классе по алгебре, и этап решения действительно расширил мое понимание алгебры и позволил мне перепроверить свою работу и указать, где я ошибся во время своих решений. Спасибо!
Мария Питер, Нью-Йорк
Мой профессор математики предложил мне использовать ваш продукт Algebrator, чтобы помочь мне выучить квадратные уравнения и нелинейные неравенства, так как я просто не мог следовать тому, чему он учил. Сначала я был настроен очень скептически, но когда я начал понимать, как вводить уравнения, я был поражен процессом решения, который обеспечивает ваше программное обеспечение. Я говорю всем в моем классе, у которых есть проблемы, чтобы купить ваш продукт.
Дэниел Томпсон, Калифорния
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?

Поисковые фразы, использованные 26.12.2014:
преобразователь дробей в номер смеси
решение задач на сложение и вычитание десятичных дробей
бесплатный научный онлайн калькулятор кубический корень
упрощение сложных рациональных выражений
бесплатные документы модели экономики ca cpt для скачивания
выучить предварительную алгебру бесплатно
найти наклон точки на ti 84
десятичная дробь Matlab
Второй экзамен по алгебре
комбинированные задачи по математике
Ответы по алгебре 1 Книга
калькулятор упрощения дробей с переменными с показателями степени
ответы по тригонометрии бесплатно
учебный центр умножения и деления целых чисел
Элементарная алгебра седьмое издание bittinger online
Презентация конических сечений в Powerpoint
преобразование формул алгебры
разделение дробей вручную
Предварительная алгебра Рабочий лист квадратного корня
сложные задачи с графами+рабочий лист+скачать
калькулятор неявного дифференцирования
графический вычислитель
поиск слов в девятом классе для печати
упростить подкоренные выражения
логарифмическая программа ti-83
онлайн факторинг трехчленный
Тесты по алгебре для печати
описывают разницу между оценкой и упрощением выражения.
No related posts.

Лови Ответ для решения примеров и уравнений

Установка программы Лови Ответ

Обзор программы Лови Ответ

Лови Ответ онлайн

Выводы статьи

Решение примеров по фото онлайн

Фото калькулятор Photomath

Яндекс Переводчик для решения домашнего задания по английскому языку

Mathway — решит примеры по вашей фотографии

Сервисы для перевода с французского на русский по картинке

Математический сканер и решебник по фото

Google Переводчик — приложение для перевода по картинке

Онлайн-калькулятор дробей по изображению

Яндекс.Переводчик — поможет перевести по фото

Камера калькулятор — решение задач по математике

ГДЗ по фото задания через Google Translate

Решение примеров в Google Lens по картинке

Уравнения онлайн

Приложение

Решение показательных уравнений. Примеры.

Решение простейших показательных уравнений.

Решение простых показательных уравнений. Примеры.

Замена переменной в решении показательных уравнений.

Как легко решать уравнения вида x + 3 = 4

Purplemath

Что такое линейное уравнение?

MathHelp.com

Что значит решить уравнение?

Как решить сложением или вычитанием?

Решить

Как проверить свое решение?

▷Step by Step Приложения для TI-Nspire CX & CX CAS Бесплатная загрузка. Пройдите курсы по математике, естественным наукам и бизнесу

Для подготовки к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—

Как превратить текстовые задачи в уравнения

Как преобразовать текстовую задачу в уравнение?

Использование калькулятора решения текстовых задач для решения текстовых задач

Вот как можно использовать калькулятор решения математических задач

Калькулятор решения текстовых задач: как работает процесс вычисления

Есть ли приложение или веб-сайт для решения математических задач?

Список из 9 математических онлайн-калькуляторов

Решайте задачи по алгебре с помощью калькулятора

Калькулятор преобразования задач Word в уравнения для помощи по математике

Похожие посты, которые вам также могут понравиться:

Решите мое уравнение онлайн

Наших пользователей:

Поисковые фразы, использованные 15 февраля 2010 г.:

Algebra equation solving calculator

Наши пользователи:

Поисковые фразы, использованные 26.12.2014:

Добавить комментарий Отменить ответ