Выборочное среднее найти онлайн: Math.by — Выборочное среднее.

Онлайн калькулятор: Показатели вариации

Пользователь Мария попросила написать такой калькулятор: Показатели вариации и анализ частотных распределений.

Расчеты не очень сложные, поэтому вот и он. Теория, по уже сложившейся традиции, под калькулятором.

Показатели вариации

addimport_exportmode_editdelete

Исследуемая совокупность

Размер страницы: chevron_leftchevron_right

Исследуемая совокупность

Сохранить Отменить

Импортировать данныеОшибка импорта

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;50

Загрузить данные из csv файла

Импортировать Назад Отменить Точность вычисления

Знаков после запятой: 2

Среднее арифметическое

 

Размах вариации

 

Среднее линейное отклонение

 

Среднее квадратическое отклонение

 

Коэффициент осцилляции (проценты)

 

Относительное линейное отклонение (проценты)

 

Коэффициент вариации (проценты)

 

save Сохранить extension Виджет

Вариация — это различие индивидуальных значений какого-либо признака внутри изучаемой совокупности.

Ну, например, есть класс учеников — изучаемая совокупность, у них есть, скажем, годовая оценка по русскому языку. У кого-то она «5», у кого-то «4» ну и так далее. Набор этих оценок по всему классу, вместе с их частотой (т. е. встречаемостью, скажем, у 10 человек – «5», у 7 человек – «4», у 5 человек – «3») и есть вариация, по которой можно рассчитать массу показателей.

Этим мы сейчас и займемся.

Абсолютные показатели

1. Размах вариации — разность между максимальным и минимальным значениями признака
   

2. Среднее линейное отклонение — среднее арифметическое отклонение индивидуальных значений от средней.
   ,
   где — частота появления значения.

Если индивидуальных значений слишком много, для упрощения расчетов данные могут группировать, т. е. объединять в интервалы. Тогда имеет смысл середины i-го интервала, или среднего значения признака на i-том интервале

3. Дисперсия — средняя из квадратов отклонений значений признаков от средней.
   

Дисперсию также можно рассчитать и таким способом:
, где

4. Среднее квадратическое отклонение — , корень из дисперсии.

Относительные показатели

Абсолютные показатели измеряются в тех же величинах, что и сам признак, и показывают абсолютный размер отклонений, поэтому их неудобно применять для сравнения изменчивости разных признаков совокупности. Поэтому дополнительно рассчитывают относительные показатели вариации, которые обычно выражают в в процентах.

1. Коэффициент осцилляции — характеризует колеблемость крайних значений признака вокруг средней арифметической.
   

2. Относительное линейное отклонение или линейный коэффициент вариации — характеризует долю усредненного значения абсолютных отклонений от средней арифметической.
   

3. Коэффициент вариации — характеризует степень однородности совокупности, наиболее часто применяемый показатель.
   

Совокупность считается однородной при значениях меньше 40%. При значениях больше 40% говорят о большой колеблемости признаков и совокупность считается неоднородной.

Среднее значение, дисперсия и стандартное отклонение дискретной случайной величины

Этот калькулятор поможет вычислить основные характеристики дискретной случайной величины: математическое ожидание (матожидание, среднее или ожидаемое), дисперсию, и стандартное отклонение.

Среднее или ожидаемое значение дискретной случайной величины определяется как:

Дисперсия рандомной величины определяется как:

Альтернативный способ вычислить дисперсию:

Положительный квадратный корень дисперсии называется стандартным отклонением .

Как вы можете видеть, эти величины находятся с помощью простых формул. Иногда вам нужно вычислить их для решения задач по теории вероятностей. Для дискретной случайной величины, трюк в том, чтобы найти верные пары значение — вероятность, тогда это простое математическое сложение и умножение. Так, этот калькулятор выполняет простые вычислениядля вас, используя единожды введенные пары значение-вероятность в таблице вероятности. Вы можете найти примеры использования ниже под калькулятором.

Среднее значение, дисперсия и стандартное отклонение дискретной случайной величины

addimport_exportmode_editdelete

Таблица вероятности

Размер страницы: chevron_leftchevron_right

Таблица вероятности

Сохранить Отменить

Импортировать данныеОшибка импорта

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;? -50.5 ?

Загрузить данные из csv файла

Импортировать Назад Отменить Точность вычисления

Знаков после запятой: 4

Среднее значение

 

Стандартное отклонение

 

save Сохранить

extension Виджет

Примеры

Задача: В наборе из 10 микроволновых печей попались 3 бракованных. Если пять микроволновых печей выбрали случайно для поставки в отель, сколько бракованных печей может попасться?

Как использовать калькулятор:

1. Выберите текущие данные в таблице вероятности, нажимая на флажок сверху и удалите их, нажимая по иконке «корзина» в загаловке таблицы.
2. Добавьте пары значение-вероятность (вам нужно определить их, но в этом вся сущность проблемы). записать их — быстрый способ «импортировать» данные. Нажмите на иконку «импортировать» в заголовке таблицы и введите следующие значения
   0;0.0833
1;0.4167
2;0.4167
3;0.0833

После этого вы получите среднее значение равное 1.5. Конечно, 1.5 бракованные печи не имеют никакого физического смысла. Вместо этого, это следует интерпретировать как среднюю стоимость, если повторные поставки будут осуществляться на этих условиях.

Show me

Формулы числовых характеристик статистического распределения

Сейчас Вы научитесь находить числовые характеристики статистического распределения выборки. Примеры подобраны на основании индивидуальных заданий по теории вероятностей, которые задавали студентам ЛНУ им. И. Франка. Ответы послужат для студентов математических дисциплин хорошей инструкцией на экзаменах и тестах. Подобные решения точно используют в обучении экономисты , поскольку именно им задавали все что приведено ниже. ВУЗы Киева, Одессы, Харькова и других городов Украины имеют подобную систему обучения поэтому много полезного для себя должен взять каждый студент. Задачи различной тематики связаны между собой линками в конце статьи, поэтому можете найти то, что Вам нужно.

Индивидуальное задание 1
Вариант 11

Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

1. выборочное среднее;
2. выборочную дисперсию;;
3. подправленную дисперсию;
4. выборочное среднее квадратичное отклонение;
5. подправленное среднее квадратичное отклонение;
6. размах выборки;
7. медиану;
8. моду;
9. квантильное отклонение;
10. коэффициент вариации;
11. коэффициент асимметрии;
12. эксцесс для выборки:

Выборка задана рядом 11, 9, 8, 7, 8, 11, 10, 9, 12, 7, 6, 11, 8, 7, 10, 9, 11, 8, 13, 8.

Решение:
Запишем выборку в виде вариационного ряда (в порядке возрастания):
6; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 10; 10; 11; 11; 11; 11; 12; 13.
Далее записываем статистическое распределение выборки в виде дискретного статистического распределения частот:

Эмпирическую функцию распределения определим по формуле

Здесь n_x – количество элементов выборки которые меньше х. Используя таблицу и учитывая что объем выборки равен n = 20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.
Выборочное среднее вычисляем по формуле

Выборочную дисперсию находим по формуле


Выборочное среднее, что фигурирует в формуле дисперсии в квадрате найдено выше. Остается все подставить в формулу

Подправленную дисперсию вычисляем согласно формулы

Выборочное среднее квадратичное отклонение вычисляем по формуле

Подправленное среднее квадратичное отклонение вычисляем как корень из подправленной дисперсии

Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

Медиану находим по 2 формулам:
если число n — четное;
если число n — нечетное.
Здесь берем индексы в x_i согласно нумерации варианта в вариационном ряду.
В нашем случае n = 20, поэтому

Мода – это варианта которая в вариационном ряду случается чаще всего, то есть

Квантильное отклонение находят по формуле

где – первый квантиль,

Дисперсия: генеральная, выборочная, исправленная

Генеральная дисперсия

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Готовые работы на аналогичную тему

Определение 3

Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

\[{\sigma }_г=\sqrt{D_г}\]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.

Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

\[{\sigma }_в=\sqrt{D_в}\]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $\frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Решение:

Для решения этой задачи для начала сделаем расчетную таблицу:

Рисунок 2.

Величина $\overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]

То есть

\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{305}{20}=15,25\]

Найдем выборочную дисперсию по формуле:

\[D_в=\frac{\sum\limits^k_{i=1}{{{(x}_i-\overline{x_в})}^2n_i}}{n}=\frac{523,75}{20}=26,1875\]

Выборочное среднее квадратическое отклонение:

\[{\sigma }_в=\sqrt{D_в}\approx 5,12\]

Исправленная дисперсия:

\[{S^2=\frac{n}{n-1}D}_в=\frac{20}{19}\cdot 26,1875\approx 27,57\]

Исправленное среднее квадратическое отклонение:

\[S=\sqrt{S^2}\approx 5,25\]

Найти моду, медиану, дисперсию может каждый!

Найти моду, медиану, дисперсию и другие характеристики учат в курсе теории вероятностей для анализа статистического распределения выборки. Если Вы имеете заготовленные формулы или методичку, то само по себе вычисления числовых характеристик статистических выборок не является сложным. Однако на контрольных, индивидуальных заданиях, а еще для заочников все всегда выглядит сложнее, чем есть на самом деле. Ниже приведены решения которые многие вещи из вероятности сделают для Вас простыми и понятными. Главное не спешите и в подобных примерах поступайте по аналогии.

Индивидуальное задание 1
Вариант 8

Задача 1. Составить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:

1. выборочное среднее;
2. выборочную дисперсию;
3. подправленную дисперсию;
4. выборочное среднее квадратичное отклонение;
5. подправленное среднее квадратичное отклонение;
6. размах выборки;
7. медиану;
8. моде;
9. квантильное отклонения;
10. коэффициент вариации;
11. коэффициент асимметрии;
12. эксцесс для выборки:

Выборка задана следующими значениями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Решение: Записываем выборку в виде вариационного ряда (в порядке возрастания):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:

Значение эмпирической функции распределения определяем по формуле

где n_x количество элементов выборки меньше х. Используя таблицу, а также учитывая, что объем выборки n=1+3+5+3+2+4+1+1=20, запишем эмпирическую функцию распределения:

Далее вычислим числовые характеристики статистического распределения выборки.

1. Выборочное среднее вычисляем по формуле

2. Выборочную дисперсию вычисляем по формуле



3. Подправленную дисперсию находим по формуле

4. Выборочное среднее квадратичное отклонение вычисляем по формуле

5. Подправленное среднее квадратичное отклонение находим по формуле

6. Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:

7. Медиану вычисляют по формулам:
если число n — четное;
если число n — нечетное.
Здесь берем индексы в x[i] согласно нумерации вариант в вариационном ряду.
В нашем случае п=20, поэтому

8. Мода — это варианта которая в вариационном ряду случается чаще всего, то есть

9. Квантильное отклонение найдем по формуле

половины разницы – третьего и – первого квантилей.
Сами же квантили получаем искусственной разбивкой вариационного ряда на 4 равные части. В нашем случае

10. Коэффициент вариации вычисляем по формуле

11. Коэффициент асимметрии находим по формуле

Здесь m³ центральный эмпирический момент 3-го порядка,

Отсюда коэффициент асимметрии равен 0,3

12. Эксцессом статистического распределения выборки называется число которое находят по формуле:

В числителе имеем центральный эмпирический момент 4-го порядка

Момент и среднее квадратичное отклонение подставляем в формулу и определяем эксцесс

По тому как все доступно и понятно на практике выглядит делаем вывод, что найти моду, медиану и дисперсию должен уметь каждый студент, который изучает теорию вероятностей.

Готовые решения по теории вероятностей

Среднее значение, медиана, режим Калькулятор

Использование калькулятора

Вычислить среднее значение, медианное значение, режим, а также минимум, максимум, диапазон, количество и сумму для набора данных.

Введите значения через запятую или пробел. Вы также можете копировать и вставлять строки данных из электронных таблиц или текстовых документов. См. Все допустимые форматы в таблице ниже.

Что такое средняя медиана и мода?

Среднее значение, медиана и мода — все это меры центральной тенденции в статистике. Каждый из них по-разному сообщает нам, какое значение в наборе данных является типичным или репрезентативным для набора данных.

Среднее значение совпадает со средним значением набора данных и находится с помощью вычислений. Сложите все числа и разделите их на количество чисел в наборе данных.

Медиана — это центральное число набора данных.Расположите точки данных от наименьшего к наибольшему и найдите центральное число. Это медиана. Если в середине два числа, то медиана — это среднее значение этих двух чисел.

Режим — это номер в наборе данных, который встречается наиболее часто. Подсчитайте, сколько раз каждое число встречается в наборе данных. Режим — это номер с наибольшим подсчетом. Ничего страшного, если есть более одного режима. И если все числа встречаются одинаковое количество раз, режима нет.

Как найти среднее значение

1. Сложите все значения данных, чтобы получить сумму
2. Подсчитайте количество значений в вашем наборе данных
3. Разделите сумму на количество

Среднее значение совпадает со средним значением в наборе данных.{n} x_i} {n} \]

Как найти медиану

Медиана \ (\ widetilde {x} \) — это значение данных, отделяющее верхнюю половину набора данных от нижней половины.

• Упорядочить значения данных от наименьшего к наибольшему значению
• Медиана — это значение данных в середине набора
• Если в середине есть 2 значения данных, медиана — это среднее значение этих 2 значений.

Пример медианы

Для набора данных 1, 1, 2, 5 , 6, 6, 9 медиана равна 5.

Для набора данных 1, 1, 2 , 6 , 6, 9 медиана равна 4. Возьмите среднее значение 2 и 6 или (2 + 6) / 2 = 4.

Медианная формула

Заказ набора данных x ₁ ≤ x ₂ ≤ x ₃ ≤… ≤ x _n от наименьшего к наибольшему значению, медиана \ (\ widetilde {x} \) — это точка данных, отделяющая верхнюю половину значений данных от нижней половины.

Если размер набора данных n нечетный, медиана — это значение в позиции p , где

\ [p = \ dfrac {n + 1} {2} \] \ [\ widetilde {x} = x_p \]

Если n даже, медиана — это среднее значение в позициях p и п + 1 где

\ [p = \ dfrac {n} {2} \] \ [\ widetilde {x} = \ dfrac {x_ {p} + x_ {p + 1}} {2} \]

Как найти режим

Mode — это значение или значения в наборе данных, которые встречаются наиболее часто.

Для набора данных 1 , 1 , 2, 5, 6 , 6 , 9 режим 1, а также 6.

Межквартильный размах

IQR = Q ₃ — Q ₁

Выбросы

Потенциальные выбросы — это значения, которые лежат выше верхней границы или ниже нижней границы набора выборки.
Верхний забор = Q ₃ & plus; 1.5 × Межквартильный размах
Нижняя граница = Q ₁ — 1,5 × Межквартильный размах

Калькуляторы связанной статистики и анализа данных

Допустимые форматы данных

Колонна (новые строки)

42
54
65
47
59
40
53

42, 54, 65, 47, 59, 40, 53

через запятую

42,
54,
65,
47,
59,
40,
53,

или

42, 54, 65, 47, 59, 40, 53

42, 54, 65, 47, 59, 40, 53

Помещения

42 54
65 47
59 40
53

или

42 54 65 47 59 40 53

42, 54, 65, 47, 59, 40, 53

Смешанные разделители

42
54 65« 47« 59,
40 53

42, 54, 65, 47, 59, 40, 53

,

Среднее значение, Медиана, Режим, Расчет диапазона

Для расчета укажите числа, разделенные запятыми.

Калькулятор связанной статистики | Калькулятор стандартного отклонения | Калькулятор размера выборки

Среднее

Слово mean, являющееся омонимом множества других слов в английском языке, также неоднозначно даже в области математики. В зависимости от контекста, математического или статистического, то, что подразумевается под «средним», меняется. В простейшем математическом определении наборов данных используемое среднее — это среднее арифметическое, также называемое математическим ожиданием или средним.В этой форме среднее значение относится к промежуточному значению между дискретным набором чисел, а именно к сумме всех значений в наборе данных, деленной на общее количество значений. Уравнение для расчета среднего арифметического практически идентично уравнению для расчета статистических концепций генеральной совокупности и выборочного среднего, с небольшими вариациями в используемых переменных:

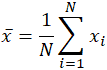
Среднее значение часто обозначается как x ̄ , произносится как «x bar», и даже в других случаях, когда переменная не равна x , обозначение столбца является обычным индикатором некоторой формы среднего.В конкретном случае среднего значения генеральной совокупности вместо использования переменной x ̄ используется греческий символ mu, или μ . Точно так же, или, скорее, сбивает с толку, выборочное среднее в статистике часто обозначается с большой буквы X . Учитывая набор данных 10, 2, 38, 23, 38, 23, 21, применение суммирования выше дает:

10 + 2 + 38 + 23 + 38 + 23 + 21 7

=

= 22.143

Как упоминалось ранее, это одно из простейших определений среднего, а некоторые другие включают взвешенное среднее арифметическое (которое отличается только тем, что одни значения в наборе данных вносят больший вклад, чем другие) и среднее геометрическое. Правильное понимание данных ситуаций и контекстов часто может дать человеку инструменты, необходимые для определения того, какой статистически значимый метод использовать. В целом, среднее значение, медиана, мода и диапазон в идеале должны быть вычислены и проанализированы для данной выборки или набора данных, поскольку они проливают свет на различные аспекты данных и, если их рассматривать отдельно, могут привести к искажению данных, что будет продемонстрировано в следующих разделах.

Медиана

Статистическая концепция медианы — это значение, которое делит выборку данных, совокупность или распределение вероятностей на две половины. Поиск медианы по существу включает в себя нахождение значения в выборке данных, физическое расположение которой находится между остальными числами. Обратите внимание, что при вычислении медианы конечного списка чисел важен порядок выборок данных. Обычно значения перечисляются в порядке возрастания, но нет реальной причины, по которой перечисление значений в порядке убывания дало бы разные результаты.В случае, когда общее количество значений в выборке данных нечетное, медиана — это просто число в середине списка всех значений. Когда выборка данных содержит четное количество значений, медиана является средним из двух средних значений. Хотя это может сбивать с толку, просто помните, что даже несмотря на то, что медиана иногда включает вычисление среднего, когда возникает этот случай, он будет включать только два средних значения, в то время как среднее значение включает все значения в выборке данных. В нечетных случаях, когда есть только две выборки данных или есть четное количество выборок, где все значения одинаковы, среднее и медиана будут одинаковыми.Учитывая тот же набор данных, что и раньше, медиана будет получена следующим образом:

2,10,21, 23 , 23,38,38

После перечисления данных в порядке возрастания и определения нечетного числа значений становится ясно, что 23 — это медиана для данного случая. Если в набор данных было добавлено другое значение:

2,10,21, 23 , 23 , 38,38,1027892

Поскольку существует четное число значений, медиана будет средним из двух средних чисел, в данном случае 23 и 23, среднее из которых равно 23.Обратите внимание, что в этом конкретном наборе данных добавление выброса (значение, выходящее далеко за пределы ожидаемого диапазона значений), значение 1 027 892, не оказывает реального влияния на набор данных. Если, однако, вычислить среднее значение для этого набора данных, результатом будет 128 505,875. Это значение явно не является хорошим представлением семи других значений в наборе данных, которые намного меньше и ближе по значению, чем среднее значение и выброс. Это главное преимущество использования медианы при описании статистических данных по сравнению со средним значением.Хотя оба, а также другие статистические значения должны вычисляться при описании данных, если можно использовать только одно, медиана может обеспечить лучшую оценку типичного значения в данном наборе данных, когда между значениями очень большие различия.

Режим

В статистике режим — это значение в наборе данных, которое имеет наибольшее количество повторов. Набор данных может быть мультимодальным, то есть иметь более одного режима. Например:

2,10,21,23,23,38,38

И 23, и 38 появляются дважды каждый, что делает их режимом для указанного выше набора данных.

Подобно среднему значению и медиане, этот режим используется как способ выражения информации о случайных величинах и совокупностях. Однако, в отличие от среднего и медианного, этот режим представляет собой концепцию, которая может применяться к нечисловым значениям, таким как марка чипсов из тортильи, которые чаще всего покупаются в продуктовом магазине. Например, при сравнении брендов Tostitos, Mission и XOCHiTL, если будет обнаружено, что в продаже чипсов из тортильи XOCHiTL является модным и продается в соотношении 3: 2: 1 по сравнению с чипами из тортильи Tostitos и Mission соответственно, это соотношение можно использовать для определения количества мешков каждой марки на складе.В случае, если в течение определенного периода будет продано 24 пакета чипсов тортильи, в магазине будет храниться 12 пакетов чипсов XOCHiTL, 8 пакетов Tostitos и 4 пакета Mission при использовании режима. Если, однако, магазин просто использовал среднее значение и продавал по 8 пакетов каждого, он потенциально мог потерять 4 продажи, если бы покупатель хотел только чипы XOCHiTL, а не какой-либо другой бренд. Как видно из этого примера, важно принимать во внимание все виды статистических значений при попытке сделать выводы о любой выборке данных.

Диапазон

Диапазон набора данных в статистике — это разница между наибольшим и наименьшим значениями. Хотя диапазон действительно имеет разные значения в разных областях статистики и математики, это его самое основное определение, и именно оно используется предоставленным калькулятором. На том же примере:

2,10,21,23,23,38,38
38 — 2 = 36

Диапазон в этом примере равен 36. Подобно среднему значению, на диапазон могут существенно влиять очень большие или маленькие значения.Используя тот же пример, что и ранее:

2,10,21, 23 , 23 , 38,38,1027892

Диапазон в этом случае будет 1 027 890 по сравнению с 36 в предыдущем случае. Таким образом, важно тщательно анализировать наборы данных, чтобы обеспечить учет выбросов.

,

Среднее значение, режим и калькулятор медианы

калькулятор измерения центральной тенденции — онлайн-инструмент для анализа вероятностных и статистических данных, позволяющий найти среднее, медианное значение и режим для данной выборки или набора данных по населению. Мода, медиана и среднее — все вместе называются Мерами центральной тенденции. Меры центральной тенденции — это меры положения в распределении. Они суммируют в одном значении ту оценку, которая лучше всего описывает центральность данных

среднее набора данных иллюстрирует среднее значение.Чтобы найти среднее значение, сложите все числа в наборе данных, а затем разделите на общее количество экземпляров в данном наборе данных. На среднее значение будет значительно влиять, если одно из чисел в наборе данных является выбросом. Среднее значение является хорошей мерой центральной тенденции к использованию, когда в наборе данных нет выбросов, на которое часто ссылаются с оценкой стандартного отклонения .

Медиана набора данных иллюстрирует среднее значение, когда набор упорядочен по возрастанию или убыванию.Медиана — это среднее значение двух средних значений, если набор данных содержит четное количество значений. Медиана является хорошей мерой центральной тенденции к использованию, когда набор данных имеет выброс.

Режим набора данных показывает, какое значение встречается очень часто. Другими словами, максимальное повторение одного и того же числа в наборе данных считается режимом для набора данных. В наборе данных нет режима, при котором каждое число в наборе данных встречается в одно и то же время

В сборе инструментов используется изучение методов и процедур, используемых для сбора, систематизации и анализа данных для понимания теории вероятностей и статистика.Набор идей, которые призваны предложить способ научного вывода из таких итоговых обобщенных данных. В статистическом анализе данных для многих приложений необходимо вычислить меру центральной тенденции для набора данных. С помощью этого онлайн-калькулятора среднего, медианного и модового значений вы можете легко рассчитать любой набор наблюдений.

,

Все о выборочном распределении выборочного среднего — Криста Кинг Математика

Точно так же, как мы нашли параметров для генеральной совокупности, мы можем найти статистики для выборки. Затем, основываясь на статистике для выборки, мы можем сделать вывод, что соответствующий параметр для генеральной совокупности может быть аналогичен соответствующей статистике для выборки.

Выборочное распределение среднего значения выборки

Учтите, однако, что выборка одной выборки из генеральной совокупности может дать статистику, которая не является хорошей оценкой соответствующего параметра генеральной совокупности.

Например, может быть средний рост девочек в вашем классе ??? 65 ??? дюймов. Допустим, есть ??? 30 ??? девочки из вашего класса, а вы берете пробу ??? 3 ??? из них. Если вам довелось выбрать трех самых высоких девушек, то среднее значение вашей выборки не будет хорошей оценкой среднего значения для всей совокупности, потому что средний рост из вашей выборки будет значительно выше, чем средний рост населения. Точно так же, если вместо этого вы просто выбрали трех самых низких девушек для своей выборки, ваше среднее значение по выборке будет намного ниже, чем фактическое среднее значение по совокупности.

Итак, как это исправить? Что ж, вместо того, чтобы брать только одну выборку из совокупности, мы будем брать много-много выборок. Фактически, если мы хотим, чтобы размер нашей выборки был ??? n = 3 ??? девочки, мы действительно могли бы взять образец каждой комбинации ??? 3 ??? девочки в классе. Мы можем найти общее количество образцов, вычислив комбинацию

??? _ nC_k = \ frac {n!} {K! (N-k)!} ???

??? _ {30} C_ {3} = \ frac {30!} {3! (30-3)!} = \ Frac {30!} {3! 27!} = \ Frac {30 \ cdot29 \ cdot28 \ cdot27 \ cdot26 \ CDOT…} {3! (27 \ cdot26 \ cdot25 \ cdot24 \ CDOT …)} = \ гидроразрыва {30 \ cdot29 \ cdot28} {3!} ???

??? _ {30} C_ {3} = \ frac {30 \ cdot29 \ cdot28} {3 \ cdot2 \ cdot1} = \ frac {10 \ cdot29 \ cdot28} {2 \ cdot1} = \ frac {10 \ cdot29 \ cdot14} {1} = 4060 ???

В этом примере, если мы использовали каждую возможную выборку (каждую возможную комбинацию ??? 3 ??? девочек), количество выборок (сколько групп мы используем) будет ??? 4 060 ??? и размер выборки (насколько велика каждая группа) ??? 3 ??? девушки.

Будет выборка с заменой , что означает, что мы выберем случайную выборку из трех девочек, а затем «вернем их обратно» в генеральную совокупность и выберем еще одну случайную выборку из трех девочек.Мы будем делать это снова и снова, пока не попробуем все возможные комбинации трех девочек в нашем классе.

Каждая из этих выборок имеет среднее значение, и если мы соберем все эти средние значения вместе, мы сможем создать распределение вероятностей, которое описывает распределение этих средних значений. Это распределение всегда является нормальным (пока у нас достаточно выборок, подробнее об этом позже), и это нормальное распределение называется распределением выборки для выборочного среднего .

Поскольку выборочное распределение выборочного среднего является нормальным, мы, конечно, можем найти среднее и стандартное отклонение для распределения и ответить на вопросы вероятности по этому поводу.

Центральная предельная теорема

Мы только что сказали, что выборочное распределение выборочного среднего всегда нормальное . Другими словами, независимо от того, является ли распределение населения нормальным, выборочное распределение выборочного среднего всегда будет нормальным, что является глубоким! Центральная предельная теорема является нашим обоснованием того, почему это верно.

Итак, на самом деле большинство распределений не являются нормальными, что означает, что они не аппроксимируют колоколообразную кривую нормального распределения.Реальные распределения встречаются повсюду, потому что реальные явления не всегда следуют совершенно нормальному распределению.

Центральная предельная теорема (CLT) — это теорема, которая дает нам способ превратить ненормальное распределение в нормальное. Это говорит нам о том, что, даже если распределение населения не является нормальным, его выборочное распределение выборочного среднего будет нормальным для большого количества выборок (по крайней мере, 30 ???).

Центральная предельная теорема полезна, потому что она позволяет нам применять то, что мы знаем о нормальных распределениях, например свойства среднего, дисперсии и стандартного отклонения, к ненормальным распределениям.

Среднее значение, дисперсия и стандартное отклонение

Среднее значение выборочного распределения выборочного среднего всегда будет таким же, как среднее значение исходного ненормального распределения. Другими словами, среднее значение выборки равно среднему значению генеральной совокупности.

??? \ mu _ {\ bar x} = \ mu ???

Если совокупность бесконечна, а выборка является случайной, или если совокупность конечна, но мы осуществляем выборку с заменой, то дисперсия выборки равна дисперсии совокупности, деленной на количество выборок, поэтому дисперсия распределения выборки дается как

??? \ sigma _ {\ bar x} ^ 2 = \ frac {\ sigma ^ 2} {n} ???

где ??? \ sigma ^ 2 ??? дисперсия населения и ??? n ??? размер выборки.Стандартное отклонение выборочного распределения, также называемое стандартным отклонением выборки или стандартной ошибкой или стандартной ошибкой среднего, , следовательно, определяется как

??? \ sigma _ {\ bar x} = \ frac {\ сигма} {\ SQRT {п}} ???

где ??? \ сигма ??? стандартное отклонение населения и ??? n ??? размер выборки.

Поправочный коэффициент конечной численности

Если размер популяции ??? N ??? конечно, а если пробовать без замены более ??? 5 \% ??? популяции, то вам нужно использовать так называемый поправочный коэффициент конечной совокупности (FPC) .2} {N} \ влево (\ гидроразрыва {N-п} {N-1} \ справа) ???

И тогда стандартное отклонение выборки будет

??? \ sigma _ {\ bar x} = \ frac {\ sigma} {\ sqrt {n}} \ sqrt {\ frac {Nn} {N-1}}? ??

Условия для вывода

Всегда есть три условия, на которые мы хотим обратить внимание, когда пытаемся использовать выборку, чтобы сделать вывод о генеральной совокупности.

Случайная выборка

Любая выборка, которую мы берем, должна быть простой случайной выборкой. Часто в задаче нам говорят, что выборка была случайной.

Нормальное состояние, большое количество

В общем, нам всегда нужно быть уверенным, что мы отбираем достаточно образцов, и / или что размер нашей выборки достаточно велик. В случае выборочного распределения выборочного среднего ??? 30 ??? — это магическое число для количества выборок, которые мы используем для создания выборочного распределения. Другими словами, нам нужно взять минимум ??? 30 ??? образцы для того, чтобы CLT был действительным.

Если мы берем большое количество выборок (по крайней мере, 30 ???), то обычно считаем, что этого достаточно, чтобы получить нормально распределенное распределение выборки среднего значения выборки.

Но когда мы используем меньше ??? 30 ??? samples, у нас недостаточно выборок, чтобы сместить распределение с ненормального на нормальное, поэтому распределение выборки будет повторять форму исходного распределения. Таким образом, если исходное распределение смещено вправо, распределение выборки будет смещено вправо; и если исходное распределение смещено влево, то распределение выборки также будет смещено влево.

Если исходное распределение нормальное, то это правило не применяется, потому что распределение выборки также будет нормальным, независимо от того, сколько выборок мы используем, даже если оно меньше ??? 30 ??? образцы.

Условие независимости, ??? 10 \% ??? правило

Если отбирать с заменой, то ??? 10 \% ??? Правило говорит нам, что мы можем предположить независимость наших выборок. Но если мы отбираем образцы без замены (мы не «возвращаем наших субъектов» в совокупность каждый раз, когда мы берем новую выборку), то нам нужно держать количество субъектов в наших выборках ниже ??? 10 \%? ?? от общей популяции (или оставьте количество выборок ниже «10%» от общей популяции).

Например, если исходное население составляет ??? 2,000 ??? субъектов, мы должны убедиться, что каждая выборка, которую мы берем для создания выборочного распределения выборочного среднего, меньше ??? 200 ??? предметы. Мы все еще можем взять столько образцов, сколько захотим (чем больше, тем лучше), но каждый образец должен включать ??? 200 ??? субъектов или меньше, чтобы мы оставались ниже ??? 200 / 2,000 = 1/10 = 10 \% ??? порог.

Другими словами, пока мы держим каждый образец на уровне менее ??? 10 \% ??? от общей численности населения, мы можем «избежать наказания» с выборкой, которая не является действительно независимой (без замены), потому что это ??? 10 \% ??? порог фактически приближается к независимости.

.