Название углов – острый, прямой, развёрнутый, смежные и вертикальные

Углы при параллельных прямых и их свойства

Пусть прямая с пересекает параллельные прямые  и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

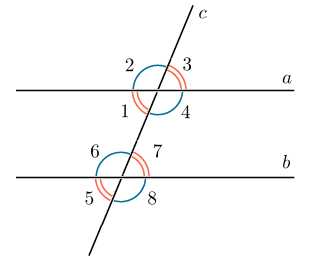
Углы  и  — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы  и ,  и  — тоже вертикальные.

Углы  и  — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы  и  (а также  и ,  и ,  и ) — накрест лежащие. Накрест лежащие углы равны.

,

,

,

.

Углы  и  — односторонние. Они лежат по одну сторону от всей «конструкции». Углы  и  — тоже односторонние. Сумма односторонних углов равна , то есть

,

.

Углы  и  (а также  и ,  и ,  и ) называются

соответственными.

Соответственные углы равны, то есть

,

.

Углы  и  (а также  и ,  и ,  и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

,

,

,

.

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть  — биссектриса тупого угла . По условию, отрезки и  равны  и  соответственно.

Рассмотрим углы и . Поскольку и  параллельны,  — секущая, углы и  являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник  — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

.

Отсюда , .

Ответ: .

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы  и  — односторонние при параллельных прямых и секущей, следовательно,

°.

Итак,

, тогда .

Ответ: .

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Угол. Виды углов — СПИШИ У АНТОШКИ

Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.

 Вершина угла — это точка, в которой два луча берут начало.Точка О — вершина угла AOD

Стороны угла — это лучи, которые образуют угол.

OA и  OD — это лучи  угла AOD

Для обозначения угла в тексте используется символ: знак угла ∠ AOB

Способы обозначения углов

Способ 1. Одной заглавной латинской буквой, указывающей его вершину. ∠ C = 90° или ∠ О
Способ 2. Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки , расположенные на сторонах угла.  Называть угол можно с любого края, но НЕ с вершины.

                             

                                Угол в таком случае имеет два названия — ∠ AOD или ∠ DOA. Но вершина всегда должна быть 

                                 в     середине названия

Способ 3. Иногда углы обозначают цифрами. ∠ 1 или ∠ 2

Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла, а другую – внешней областью угла.

Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.

Для обозначения градусов в тексте используется символ: °  градус.

Один градус – это угол, равный одной сто восьмидесятой части развернутого угла. 90 градусов обозначаются так: 90°. 

Минута – это одна шестидесятая часть градуса.

Секунда – это одна шестидесятая часть минуты.

spishy-u-antoshki.ru

Свойства углов, с примерами

ОПРЕДЕЛЕНИЕ

Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

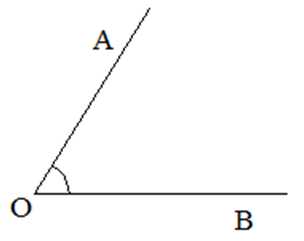
Обозначают угол тремя буквами: , где – вершина угла, – стороны угла.

Величиной измерения угла является градус.

ОПРЕДЕЛЕНИЕ Углы бывают острые (если их градусная мера меньше ),

прямые (если их градусная мера равна ) и тупые (если их градусная мера больше ).

Развернутый угол – это угол .

ОПРЕДЕЛЕНИЕ

Смежные углы – это углы, у которых одна сторона общая, а другие стороны лежат на одной прямой.

ОПРЕДЕЛЕНИЕ

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

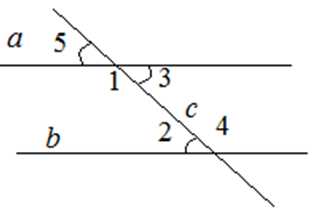
При пересечении двух параллельных прямых секущей образуются

– накрест лежащие углы: ;

– соответственные углы: ;

– односторонние углы: .

ОПРЕДЕЛЕНИЕ

Вписанный углом в окружность называется угол, вершина которого лежит на окружности, а стороны пересекают ее.

Сумма углов любого треугольника равна . Сумма углов любого n-угольника равна .

ОПРЕДЕЛЕНИЕ

Биссектрисой угла называется луч, который исходит из вершины угла и делит данный угол пополам.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Угол. Виды углов. Видеоурок. Математика 4 Класс

Ранее мы были ознакомлены с понятием «луч». Луч – это часть прямой, ограниченная с одной стороны точкой. На рисунке можно увидеть луч с началом в точке  и луч с началом в точке  (рис. 1).

Рис. 1. Лучи

Фигура, образованная двумя лучами с одним и тем же началом, называется

углом. Лучи, образующие угол, называются сторонами угла, а их общее начало – вершиной угла (рис. 2).

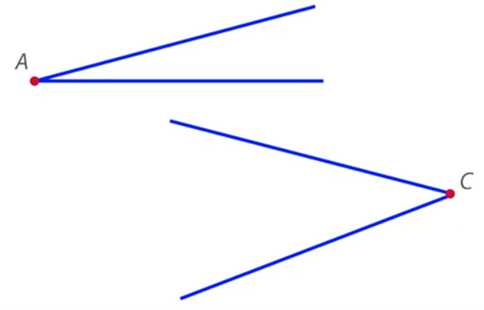
Рис. 2. Углы

Угол может быть назван одной заглавной латинской буквой по его вершине. На рис. 2 можно увидеть угол  и угол . Но углы можно обозначить и другим способом.

Угол многоугольника обозначают тремя заглавными буквами. Называть угол начинают с буквы, стоящей у одной стороны, затем называют букву у вершины, а заканчивают буквой у другой стороны. Например, в треугольнике , угол с вершиной  является угол  (рис. 3) или в обратном порядке – .

В треугольнике  угол с вершиной  – это угол  или .

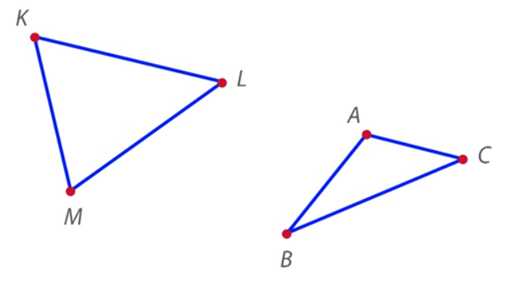
Рис. 3. Углы в треугольнике

Необходимо помнить, что в середине названия угла должна стоять та буква, которой обозначена вершина угла.

Иногда угол обозначают малой буквой или цифрой, ставя их внутри угла (рис. 4). Между сторонами угла проводят для ясности дужку.

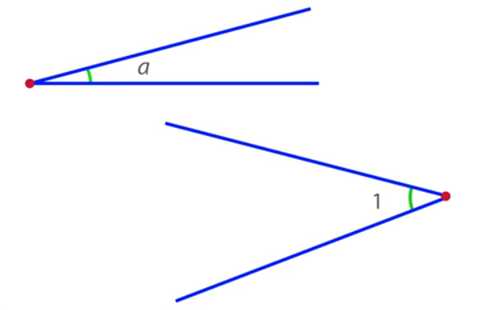
Рис. 4. Обозначение угла буквой или цифрой

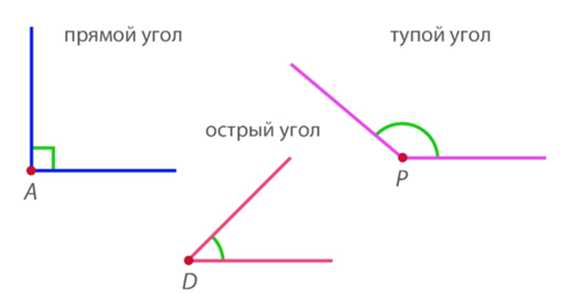
Рис. 5. Виды углов

Существуют различные виды углов.

1. Если стороны угла лежат на одной прямой, то такой угол называют развернутым. На рис. 6 угол М – развернутый (уместно сравнение с развернутым веером).

Рис. 6. Развернутый угол

2. Прямым углом называют тот угол, который составляет половину развернутого угла (рис. 7). Например, прямой угол можно получить путем складывания бумаги (если лист сложить дважды).

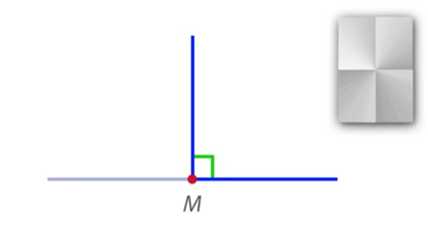
Рис. 7. Прямой угол

Для удобства определения, прямой угол или нет, есть особый инструмент – прямоугольный треугольник, у которого один из углов – прямой (рис. 8).

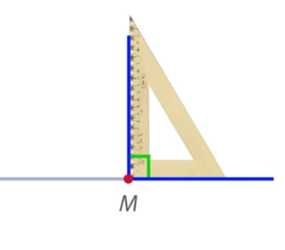
Рис. 8. Прямоугольный треугольник и его применение

3. Непрямые углы делятся на тупые и острые.

Угол, который меньше прямого, – это острый угол (рис. 9).

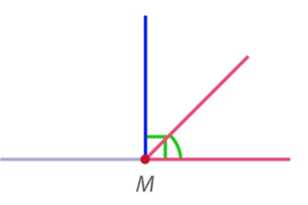
Рис. 9. Острый угол
Угол, который больше прямого, но меньше развернутого угла, – это тупой угол (рис. 10).

Рис. 10. Тупой угол

Найдите на чертеже прямые, тупые и острые углы (рис. 11).

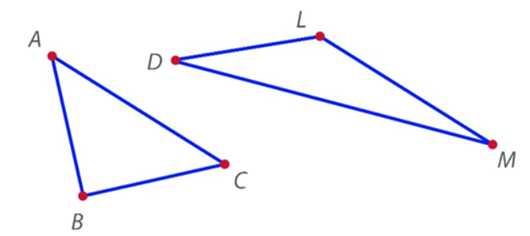
Рис. 11. Иллюстрация к заданию

В нахождении решения нам поможет инструмент – прямоугольный треугольник, который будет приложен к каждой из вершин треугольника путем совмещения одной из сторон. Если он будет совпадать с углом, то этот угол прямой. Если угол будет меньше прямого угла инструмента, то этот угол острый. А если же угол больше прямого угла инструмента – то это тупой угол.

Прямые углы:  

Тупые углы:

Острые углы: , , ,

В построении 4 прямых углов с общей вершиной на нелинованной бумаге нам помогут циркуль и линейка.

Сначала необходимо провести прямую. Отложим на прямой произвольный отрезок . Проведем две окружности с центрами в точке  и  с радиусами, равными длине отрезка .

Обозначим точки пересечения окружностей  и . Проведем через точки  и  прямую. Точку пересечения прямых обозначим буквой .

Рис. 12. Построение 4 прямых углов с общей вершиной на нелинованной бумаге

С помощью прямоугольного треугольника можно проверить, что все 4 угла с вершиной в точке  – прямые. При построении прямых углов на нелинованной бумаге вместо окружностей можно проводить дуги, то есть части окружности. Причем дуги могут быть любого радиуса, но больше, чем половина длины отрезка .

На этом уроке мы познакомились с понятием угла и видами углов: развернутым углом, прямым углом, тупым углом и острым углом. Научились строить прямые углы на нелинованной бумаге с помощью циркуля и линейки.

 

Список литературы

1. Петерсон Л.Г. Математика 4 класс. Учебник в 3 частях, М.: 2013. Часть 1 96с., часть 2 128с., часть 3 96с.
2. Моро М.И., Бантова М.А., Бельтюкова Г.В., Волкова С.И., Степанова С.В.
   Учебник. – 8-е изд. – М.: Просвещение, 2011. – 112 с.: ил. – (Школа России). – ISBN 978–5–09–023769–7.
3. Математика. 4 класс. Учебник в 3 ч. Демидова Т.Е., Козлова С.А., Тонких А.П. 2-е изд., испр. – М.: 2013.; Ч.1 – 96 с., Ч.2 – 96 с., Ч.3 – 96 с.

 

Домашнее задание

1. Определите количество углов в квадрате. Ромбе.
2. Может ли быть в прямоугольном треугольнике тупой угол?

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Shkolo.ru (Источник).
2. Интернет-портал Festival.1september.ru (Источник).
3. Интернет-портал Math-prosto.ru (Источник).

interneturok.ru

определение угла, измерение углов, обозначения и примеры, угол 270 градусов рисунок

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Yandex.RTB R-A-339285-1

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O.

Угол в математике обозначается знаком «∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h, то угол обозначается как ∠kh или ∠hk .

Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия OA и OB. В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠AOB и ∠BOA . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.

zaochnik.com

Как называются углы треугольника | Треугольники

Как называются углы треугольника? Ответ может зависеть от того, сколько углов имеется при вершине треугольника.

Если при вершине треугольника есть только один угол, то его можно назвать одной буквой, по названию вершины.

Например, в треугольнике MKF (рисунок 1) при каждой вершине есть только один угол. Следовательно, каждый из углов   можно назвать одной буквой, по названию вершины, из которой исходят образующие этот угол лучи:

рисунок 1

Угол M, угол K и угол F.

  Для обозначения угла существует специальный знак: ∠

Запись ∠M читают как «угол M».

Каждый из углов треугольника MKF можно назвать также тремя буквами. При этом вершина в названии угла должна стоять посередине.

Угол M также можно назвать углом KMF или углом FMK,

∠K — ∠MKF или ∠FKM,

∠F — ∠MFK или ∠KFM.

рисунок 2

 

В треугольниках, изображенных на рисунке 2, одной буквой могут быть названы только углы при вершинах A и D: ∠A и ∠D.

При вершине B есть три угла, поэтому каждый из этих углов нужно назвать тремя буквами: ∠ABC, ∠CBD и ∠ABD.

Аналогично, углы при вершине C могут быть названы только тремя буквами: ∠ACB, ∠BCD и ∠ACD. Назвать какой-либо из этих углов ∠C нельзя.

рисунок 3

Каждый из углов треугольников, изображенных на рисунке 3, может быть назван только тремя буквами.

Углы треугольника ABO: ∠ABO, ∠BAO, ∠AOB.

Углы треугольника BOC: ∠BOC,  ∠OBC,  ∠BCO.

Углы треугольника OCD: ∠OCD, ∠COD,  ∠CDO.

Углы треугольника AOD: ∠AOD, ∠ADO,∠OAD.

Углы треугольника ABC: ∠ABC, ∠BAC, ∠BCA.

Углы треугольника BCD: ∠BCD, ∠CBD, ∠BDC.

Углы треугольника ACD: ∠ACD, ∠CAD, ∠ADC.

Углы треугольника ABD: ∠ABD, ∠BAD, ∠ADB.

 

www.treugolniki.ru

Угол. Виды углов / Основы геометрии / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Основы геометрии
5. Угол. Виды углов

Мы узнаем, что углы бывают, острыми, прямыми и тупыми.

Вспомни, чтобы начертить угол, нужно поставить точку и из неё провести два луча в разные стороны.

Луч — это сторона угла.

Вершина — это точка, из которой выходят лучи.

---

Прямой угол

Прямой угол — это угол в 90^о (90 градусов). Его легко определять по треугольнику, например, такому:

---

Острый угол

Острый угол — это угол, который МЕНЬШЕ прямого угла, меньше 90^о.

м

---

Тупой угол

Острый угол — это угол, который БОЛЬШЕ прямого угла, больше 90^о.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Круг. Шар. Овал

Треугольники

Многоугольники

Обозначение геометрических фигур буквами

Периметр многоугольника

Площадь фигуры

Окружность

Основы геометрии

Правило встречается в следующих упражнениях:

2 класс

Страница 44. Вариант 1. № 2, Моро, Волкова, Проверочные работы

Страница 72. Вариант 1. Тест 3, Моро, Волкова, Проверочные работы

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 9, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 45, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 70, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 79, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 12, Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 36, Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 16, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 43, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 35, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

---

© 2019 — budu5.com, Буду отличником!

budu5.com

No related posts.