Модуль числа и свойства модуля
Определение модуля
Определение: Модулем положительного числа называется само это число, модулем отрицательного числа называется число, ему противоположное, модуль нуля равняется нулю.
Примеры нахождения модуля


Геометрический смысл модуля
Задан отрезок  .
.

Определение: На координатной прямой модуль — это расстояние от начала координат до точки, изображающей данное число.
Определение: Модуль разности двух чисел 
 — это расстояние между точками
— это расстояние между точками  и
и  на координатной прямой.
на координатной прямой.
Свойства модуля
 (Модуль любого числа — неотрицательное число)
(Модуль любого числа — неотрицательное число) (Модули противоположных чисел равны)
(Модули противоположных чисел равны) (Величина числа не превышает величина его модуля)
(Величина числа не превышает величина его модуля) (Модуль произведения дорівнєю произведению модулей сомножителей)
(Модуль произведения дорівнєю произведению модулей сомножителей) (Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))
(Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))


 (Модуль суммы не превышает суммы модулей слагаемых)
(Модуль суммы не превышает суммы модулей слагаемых)
Модуль числа
Модулем неотрицательного действительного числа a называют само это число:
|а| = а
Модулем отрицательного действительного числа х называют противоположное число:
|а| = — а
Короче это записывают так:
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).
Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5
Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:
|-а| = |а|
Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:
|0| = 0
На практике используют различные свойства модулей:
|а| ? 0
|а·b| = |а| · |b|
|а|n = аn , n є Z, a ? 0, n > 0
|а| = | — а|
|а + b| ? |а| + |b|
|а·q| = q·|а| , где q — положительное число
|а|2 = а2
Значение |a — b| равно расстоянию на числовой прямой между точками, изображающими числа a и b.
Пример 1.
, т.к.
, т.к.
Пример 2.
Упростить выражение , если a
Решение.
Так как по условию а
Ответ:
Пример 3.
Вычислить
Решение.
Имеем
Теперь раскроем знаки модулей.
Воспользуемся тем, что 1 0.
Но тогда |?3 — 2| = -(?3 — 2) = 2- ?3 ,
а |?3 — 1| = ?3 — 1
В итоге получаем
Ответ: 1
Здесь Вы нашли ответ на вопрос : что такое модуль числа , и какие его свойства.
Модуль числа – что это такое: что значит абсолютная величина — объяснение и решение для 6 класса
В школе на уроке математики каждый год ученики разбирают новые темы. 6 класс обычно изучает модуль числа – это важное понятие в математике, работа с которым встречается далее в алгебре и высшей математики. Очень важно изначально правильно понять объяснение термина и разобраться в этой теме, чтобы успешно проходить прочие темы.
Величины в математике
Для начала следует понимать, что абсолютная величина – это параметр в статистике (измеряется количественно), который характеризует изучаемое явление по его объему. При этом явление должно осуществляться в определенных временных рамках и с определенным месторасположением. Различают значения:
- суммарные – подходят для группы единиц или полностью всей совокупности,
- индивидуальные – подходят только для работы с единицей некой совокупности.
Это интересно! Основы геометрии: что это такое биссектриса треугольника
Понятия широко используются в статистических измерениях, результатом которых являются показатели, характеризующие абсолютные размеры у каждой единицы некоего явления. Измеряются они в двух показателях: натуральном, т.е. физические единицы (шт., люди) и условно-натуральном. Модуль в математике является отображением данных показателей.
 Модуль числа
Модуль числа
Что такое модуль числа?
Важно! Данное определение «module» с латыни переводиться как «мера» и означает абсолютную величину любого натурального числа.
 Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.
Но у данного понятия есть и геометрическое объяснение, поскольку модулю в геометрии равняется расстояние от начала системы координат до точки X, которое измеряется в привычных единицах измерения.
Для того, чтобы определить данный показатель у числа, следует не учитывать его знак (минус, плюс), но при этом следует помнить то, что он никогда не может быть отрицательным. Данное значение на бумаге выделяется графически в виде квадратных скобок |a|. При этом, математическое определение такое:
|х| = х, если х больше или равен нулю и -х, если меньше нуля.
Английский ученый Р. Котес был тем человеком, кто впервые применил данное понятие в математических расчетах. А вот К. Вейерштрасс, математик из Германии, придумал и ввел в использование графический символ.
Это интересно! Как разложить на множители квадратный трехчлен: формула
В геометрии module можно рассмотреть на примере координатной прямой, на которое нанесены 2 произвольные точки. Предположим, одна А имеет значение 5, а вторая В — 6. При подробном изучении чертежа станет ясно, что расстояние от А до В – 5 единиц от нуля, т.е. начала координат, а точка В размещена от начала координат на 6 единиц. Можно сделать вывод, что module точки, А = 5, а точки В = 6. Графически это можно обозначить так: | 5 | = 5. Т. е. расстояние от точки до начала координат является модулем данной точки.
Полезное видео: что такое модуль действительного числа?
Свойства
Как у любого математического понятия, у module есть свои математические свойства:
- Он всегда положительный, поэтому модулем положительного значения будет оно само, например, модуль числа 6 и -6 равен 6. Математически это свойство можно записать как |a| = a, при a>, 0,
- Показатели противоположных чисел равны между собой. Это свойство понятнее в геометрическом изложении, поскольку на прямой данные числа располагаются в разных местах, но при этом от начала отсчета их отделяет равное количество единиц. Математически это записывается так: |а| = |-а|,
- Модуль нуля равен нулю, при условии, что действительное число – это ноль. Это свойство подтверждается тем фактом, что ноль является началом координат. Графически это записывают так: |0| = 0,
- Если требуется найти модуль двух умножающихся цифр, стоит понимать, что он будет равен полученному произведению. Другими словами, произведение величин А и В = АВ, при условии, что они положительные или же отрицательные, и тогда произведение равняется -АВ. Графически это можно записать как |А*В| = |А| * |В|.
Это интересно! Считаем правильно: как находить процент от суммы и числа
Успешное решение уравнений с модулем зависит от знания данных свойств, которое поможет любому правильно вычислять и работать с данным показателем.
 Свойства модуля
Свойства модуля
Важно! Показатель не может быть отрицательным, поскольку он определяет расстояние, которое всегда положительное.
В уравнениях
В случае работы и решения математических неравенств, в которых присутствует module, всегда необходимо помнить, что для получения итогового правильного результата следует раскрыть скобки, т.е. открыть знак module. Зачастую, в этом и есть смысл уравнения.
При этом стоит помнить, что:
- если в квадратных скобках записано выражение, его необходимо решить: |А + 5| = А + 5, при А больше или равным нулю и 5-А, в случае А меньше нуля,
- квадратные скобки чаще всего должны раскрываться независимо от значений переменной, например, если в скобках заключено выражение в квадрате, поскольку при раскрытии в любом случае будет положительное число.
Это интересно! Уроки математики: умножение на ноль главное правило
Очень легко решаются уравнения с module путем занесения значений в систему координат, поскольку тогда легко увидеть визуально значения и их показатели.
Полезное видео: модуль действительного числа и его свойства
Вывод
Принцип понимания такого математического понятия, как module, крайне важен, поскольку оно используется в высшей математике и прочих науках, поэтому необходимо уметь работать с ним.
Модуль числа. Абсолютная величина | Математика
Модуль числа обозначается двумя вертикальными чертами, между которыми заключается число:
|-7| — модуль числа -7.
Модуль числа — это абсолютная величина числа. Абсолютная величина — это неотрицательное число, удовлетворяющее условиям:
|x| = x, если x ⩾ 0;
|x| = —x, если x < 0.
Следовательно, модуль числа – это положительное число или нуль.
Модуль на координатной прямой
Модуль числа — это расстояние от начальной точки до соответствующей точки на координатной прямой. Рассмотрим координатную прямую с точками A и B:

Точка A соответствует числу -5
, которое находится в пяти единичных отрезках от начальной точки, то есть длина отрезка AO равна 5. Так как модуль равен расстоянию от начала координат до точки, то модуль числа -5 равен 5, это можно записать так:
|-5| = 5.
Точка B соответствует числу 4,5
, значит длина отрезка OB равна 4,5. Следовательно, модуль числа 4,5 равен 4,5:
|4,5| = 4,5.
Точка O соответствует числу 0
и является начальной точкой, следовательно, модулем нуля будет нуль:
|0| = 0.
Следует иметь ввиду, что чем дальше от нуля точка, изображающая данное число, тем больше модуль этого числа.
Свойства абсолютной величины
Абсолютной величиной нуля является число нуль.
Пример:
Модулем положительного числа называется само это число.
Пример:
|+2| = 2; |+35| = 35 и т. д.
Модулем отрицательного числа называется противоположное ему числу.
Пример:
|-10| = 10,
потому что -(-10) = 10.
Модули противоположных чисел равны.
Пример:
|+7| = |-7| = 7, |-5| = |+5| = 5.
Модуль числа в математике — что это такое, как раскрыть абсолютную величину, решение уравнений
 Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a|.
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Это интересно: умножение на 0 правило для любого числа.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
 Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.- Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
- В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
- Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.
Графически это можно выразить следующим образом: |a| = OA.
Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
 Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.- Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
- Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
- Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
- Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
- Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
- Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
- Такое же правило распространяется и на показатель степени выражения.
Это интересно: что такое разность в математике?
Особенности решения уравнений с модулем
 Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5, если, А больше или равняется нулю.
5-А, если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Онлайн урок: Модуль числа по предмету Математика 6 класс
Рассмотрим некоторые свойства модуля числа.
1. Модуль нуля равен нулю
Так как от нуля до начала отсчета нет никакого расстояния (0 единичных отрезков), модуль нуля и есть нуль.
|0| = 0
2. Модуль числа всегда число неотрицательное (т.е. положительное или нуль)
Модуль положителен, так как по определению модуль — это расстояние, а расстояние всегда является положительным числом.
Приведем пример:
Мяч катнули вдоль прямой на расстояние, равное 3 м вправо, мяч ударился о стену и покатился вдоль прямой в обратном направлении на 3 м и остановился.
Изобразим на координатной прямой координаты точек в момент каждой остановки мяча.
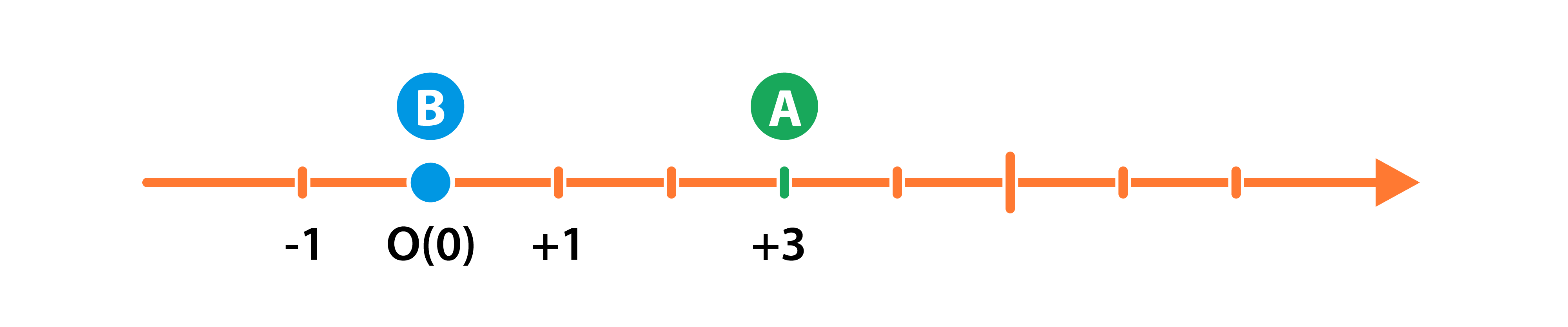
Точка О на координатной прямой- это точка откуда катнули мяч- точка начала отсчета.
Единичный отрезок координатной прямой равен 1 деление- 1метр.
Точка А с координатой А (+3) — момент удара мяча о стенку.
Точка В с координатой В (0) — совпадает с точкой отсчета.
Можно ли утверждать, что мяч не преодолевал никакого расстояния, оставаясь в исходной точке в состоянии покоя, ведь в конечном счете мяч оказался в точке 0 м (от точки ноль до начала отсчета О не помещается ни одного единичного отрезка)? Конечно же, нет!
Путь мяча был бы равен нулю, если бы его вообще никуда не пинали, и он оставался в состоянии покоя в точке О.
Но мы должны понимать, что путь (расстояние), которое преодолел мяч, состоит из 3 единичных отрезков в правую сторону и 3 единичных отрезков в левую сторону; сложив все единичные отрезки, получим:
3 единичных отрезка + 3 единичных отрезка = 6 единичных отрезков
6 единичных отрезков = 6 м
Для определения пути мы складывали только числовое значение без учета направления. Это числовое значение и есть модуль числа.
Таким образом, можно сказать, что любое число состоит из знака и абсолютного значения (модуля).
Поэтому, чтобы найти модуль числа, нужно записать это число без учета знака.
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьВ математике для лучшего восприятия темы «Модуль числа» придумали шуточную ассоциацию.
Представляют, что модуль- это баня, а знак «минус» — это грязь.
Заходя в баню (оказываясь под знаком модуль), отрицательное число моется, освобождается от знака. Из бани (из под знака модуль) число выходит «чистым»- без знака «минус».
В такой бане могут «мыться» положительные, отрицательные числа и ноль.
3. Модули противоположных чисел равны
Рассмотрим на примере данное утверждение:
Пусть модуль х равен 4, получим равенство |x| = 4
Отметим на координатной прямой точки, которые удовлетворяют этому равенству:
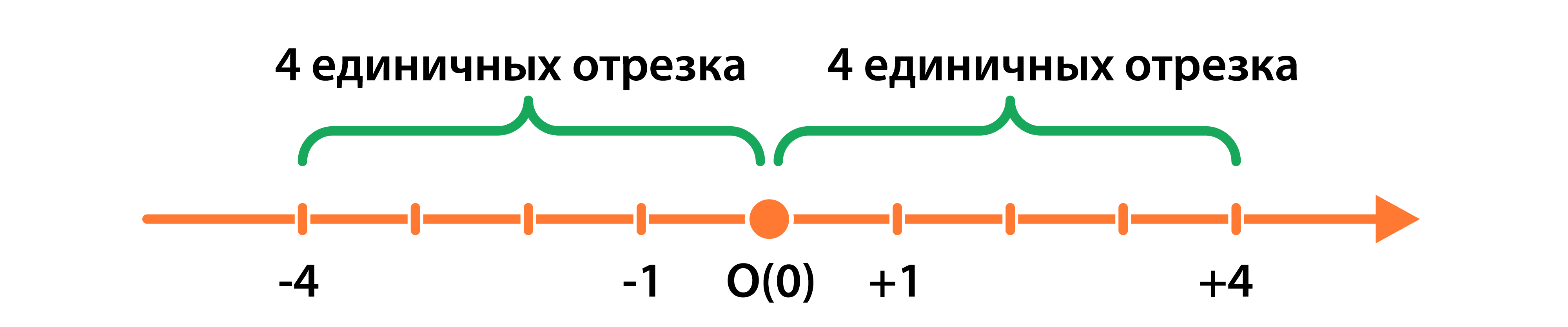
Точка О — начало отсчета координатной прямой х.
Модул ь- это расстояние от начала отсчета до точки в единичных отрезках, равное в данном случае четырем.
Откладываем 4 единичных отрезка вправо, получаем точку с координатой 4
Но такое же количество единичных отрезков можно отложить влево, тогда получим точку с координатой (-4)
Получим на координатной прямой две точки, которые удовлетворяют условию |x| = 4
В данном примере значение х может быть равным:
х = 4
х = —4
Числа 4 и —4 отличаются только знаками, поэтому смело можем сказать, что это противоположные числа.
На координатной прямой противоположные числа, хоть и по разные стороны от точки начала отсчета, но находятся на равных расстояниях от этой точки, т.е. по модулю равны.
4. Модуль произведения двух чисел равен произведению модулей этих чисел
В буквенном выражении это можно записать так:
\(\mathbf{|a \cdot b| = |a| \cdot |b|}\)
Пример: \(\mathbf{|5 \cdot 6| = |5| \cdot |6| = 5 \cdot 6 = 30}\)
5. Квадрат модуля числа равен квадрату этого числа
\(\mathbf{|a|^2 = a^2 }\)
Пример:
\(\mathbf{|10|^2 = 10^2 = 100 }\)
\(\mathbf{|-2|^2 = 2^2 = 4}\)
6. Модуль частного двух чисел равен частному их модулей
\(\mathbf{\Bigl| \frac{x}{y}\Bigr| = \frac{|x|}{|y|} , y \neq 0}\)(так как на нуль делить нельзя).
Пример:
\(\mathbf{\Bigl| \frac{8}{2}\Bigr| = \frac{|8|}{|2|}= \frac{8}{2} = 4 }\)
\(\mathbf{\Bigl| -\frac{8}{2}\Bigr| = \frac{|-8|}{|2|}= \frac{8}{2} = 4 }\)
Тема урока: «Модуль числа» (6 класс)
1. Модуль числа. Иллюстрирующий пример. Определение. Примеры
Рассмотрим чертеж. Координата точки М –  . Знак минус указывает, что точка М лежит левее начала отсчета. Число шесть говорит о том, что расстояние от точки О до точки М равно шесть единичных отрезков.
. Знак минус указывает, что точка М лежит левее начала отсчета. Число шесть говорит о том, что расстояние от точки О до точки М равно шесть единичных отрезков.
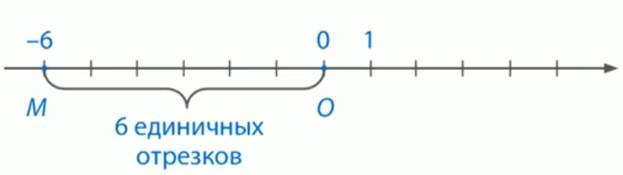
Число 6 называют модулем числа  . Записывают это так:
. Записывают это так:
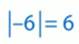
Определение.
Модулем числа a называют расстояние от начала координат до точки с координатой a.
Мы помним, что расстояние на координатной прямой измеряется в единичных отрезках.
Примеры.

Модуль числа 5 равен 5, так как точка с координатой пять удалена от точки начала отсчета на пять единичных отрезков.
Модуль 0 равен 0, так как точка с координатой ноль – это и есть начало отсчета.
2. Модуль противоположных чисел
Модуль числа – это расстояние. Поэтому он не может быть отрицательным. Для положительного числа его модуль равен самому числу, а для отрицательного – противоположному.
Примеры:
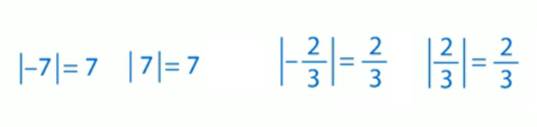
Заметим, что противоположные числа имеют равные модули. В общем виде это можно записать так:
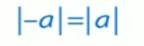
3. Задание 1
Найдите значение выражения 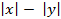 , если
, если 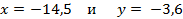 .
.
Решение.
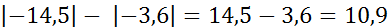
Сначала подставим значения переменных.
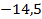 – число отрицательное. Его модуль равен противоположному числу
– число отрицательное. Его модуль равен противоположному числу 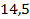 .
.
Модуль числа 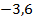 равен 3,6.
равен 3,6.
Выполним вычитание. Получим: 10,9.
4. Задание 2
Отметьте на координатной прямой числа, модуль которых равен 2.
Решение.
Начертим координатную прямую. Для этого на прямой выберем начало отсчета, единичный отрезок и направление.
Поставим точки на расстоянии 2 единичных отрезка от начала отсчета.
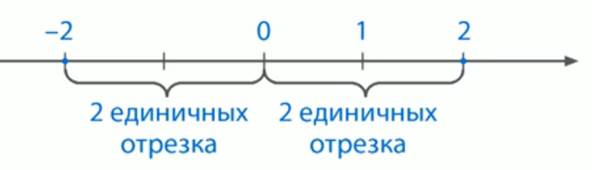
Таких точки две. Одной соответствует число 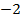 , а другой число 2.
, а другой число 2.
5. Задание 3
Найдите значение выражений:

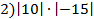 ;
; 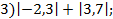 4
4 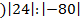
Решение.
1) 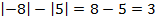
Модуль числа 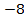 равен 8. Модуль числа 5 равен 5.
равен 8. Модуль числа 5 равен 5.
2) 
Модуль числа 10 равен 10. Модуль числа 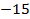 равен 15.
равен 15.
3) 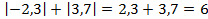 .
.
Раскрыв модули, получим сумму чисел 2,3 и 3,7
4) 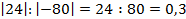
Модули данных чисел равны соответственно 24 и 80.
6.
чисел — Числовые абстрактные базовые классы — документация Python 3.8.5
Исходный код: Lib / numbers.py
Модуль номеров ( PEP 3141 ) определяет иерархию числовых
абстрактные базовые классы, которые постепенно определяют
больше операций. Ни один из типов, определенных в этом модуле, не может быть создан.
- класс
номеров.Номер Корень числовой иерархии.Если вы просто хотите проверить, является ли аргумент x — это число, неважно какого вида, используйте
isinstance (x, Number).
Числовая башня
- класс
номеров.Комплекс Подклассы этого типа описывают комплексные числа и включают операции которые работают на встраиваемом комплексе
типа. Это: преобразования вкомплексныеиbool,реальные,imag,+,-,*,/,абс (),конъюгат (),==и! =.Все кроме-и! =являются абстрактными.-
реал Аннотация. Извлекает реальную составляющую этого числа.
-
имидж Аннотация. Извлекает мнимую составляющую этого числа.
- абстрактный метод
конъюгат() Аннотация. Возвращает комплексное сопряжение. Например,
(1 + 3j).конъюгат () == (1-3j).
-
- класс
номеров.Реальный К
Комплекс,Реальныйдобавляет операции, которые работают на реальном номера.Вкратце это: преобразование в
с плавающей запятой,math.trunc (),раунд (),math.floor (),math.ceil (),divmod (),//,%,<,<=,>и> =.Real также предоставляет значения по умолчанию для
complex (),real,imagисопряженный ().
- класс
номеров.Рациональный Подтипы
Реальныйи добавляетчислительи знаменательс плавающей точкой ().-
числитель Аннотация.
- Знаменатель
Аннотация.
-
- класс
номеров.Интегральный Подтип
Rationalи добавляет преобразование вint. Обеспечивает значения по умолчанию дляfloat (),числительи Знаменатель**и битовые операции:<<,>>,и,^,|,~.
Примечания для разработчиков типов
Разработчики должны быть осторожны, чтобы равные числа были равны и хэш
их к одинаковым значениям. Это может быть незаметно, если есть два разных
расширения действительных чисел. Например, дроби .
реализует hash () следующим образом:
def __hash __ (сам):
если self.denominator == 1:
# Получите правильные числа.
вернуть хеш (self.numerator)
# Дорогой чек, но определенно правильный.если self == float (self):
вернуть хеш (float (self))
еще:
# Используйте хеш кортежа, чтобы избежать высокой частоты конфликтов на
# простые дроби.
вернуть хеш ((self.numerator, self.denominator))
Добавление дополнительных цифровых ABC
Конечно, есть и другие возможные буквы ABC для чисел, и это
быть плохой иерархией, если она исключает возможность добавления
те. Вы можете добавить MyFoo между Complex и
Python чисел, преобразование типов и математика
Числовой тип данных в Python
Python поддерживает целые числа, числа с плавающей запятой и комплексные числа. В Python они определены как int , float и сложный .
Целые числа и числа с плавающей запятой разделяются наличием или отсутствием десятичной запятой. Например, 5 - целое число, а 5.0 - число с плавающей запятой.
Комплексные числа записываются в виде x + yj , где x - действительная часть, а y - мнимая часть.
Мы можем использовать функцию type () , чтобы узнать, к какому классу принадлежит переменная или значение, и функцию isinstance () , чтобы проверить, принадлежит ли она определенному классу.
Давайте посмотрим на пример:
а = 5
печать (тип (а))
печати (тип (5,0))
с = 5 + 3j
печать (c + 3)
print (isinstance (c, комплекс)) Когда мы запускаем указанную выше программу, мы получаем следующий результат:
<класс 'int'> <класс 'float'> (8 + 3j) Правда
Хотя целые числа могут иметь любую длину, число с плавающей запятой является точным только до 15 десятичных знаков (16-е место неточно).
Числа, с которыми мы имеем дело каждый день, имеют десятичную (основание 10) систему счисления. Но компьютерные программисты (обычно встроенные программисты) должны работать с двоичной (основание 2), шестнадцатеричной (основание 16) и восьмеричной (основание 8) системами счисления.
В Python мы можем представить эти числа, поместив соответствующий префикс перед этим числом. В следующей таблице перечислены эти префиксы.
| Система счисления | Префикс |
|---|---|
| двоичный | '0b' или '0B' |
| восьмеричное | '0o' или '0O' |
| Шестнадцатеричный | '0x' или '0X' |
Вот несколько примеров
# Вывод: 107
печать (0b1101011)
# Вывод: 253 (251 + 2)
печать (0xFB + 0b10)
# Вывод: 13
печать (0o15) Когда вы запустите программу, на выходе будет:
107 253 13
Преобразование типа
Мы можем преобразовать один тип чисел в другой.Это также известно как принуждение.
Такие операции, как сложение и вычитание, неявно (автоматически) заставляют целое число плавать, если один из операндов является плавающим.
>>> 1 + 2,0
3,0 Мы видим выше, что 1 (целое число) приводится к 1.0 (с плавающей запятой) для сложения, и результат также является числом с плавающей запятой.
Мы также можем использовать встроенные функции, такие как int () , float () и complex () , для явного преобразования между типами.Эти функции могут даже преобразовывать из строк.
>>> число (2.3)
2
>>> интервал (-2,8)
-2
>>> float (5)
5.0
>>> комплекс ('3 + 5j')
(3 + 5j) При преобразовании из числа с плавающей точкой в целое число обрезается (десятичные части удаляются).
Десятичный Python
Встроенный в Python класс float выполняет некоторые вычисления, которые могут нас удивить. Все мы знаем, что сумма 1,1 и 2,2 составляет 3,3, но Python, похоже, с этим не согласен.
>>> (1,1 + 2,2) == 3,3
Ложь Что происходит?
Оказывается, числа с плавающей запятой реализованы в компьютерном оборудовании как двоичные дроби, поскольку компьютер понимает только двоичные (0 и 1). По этой причине большинство известных нам десятичных дробей невозможно точно сохранить на нашем компьютере.
Рассмотрим пример. Мы не можем представить дробь 1/3 в виде десятичного числа. Это даст 0,33333333 ... что бесконечно долго, и мы можем только приблизить его.
Оказывается, десятичная дробь 0,1 приведет к бесконечно длинной двоичной дроби 0,000110011001100110011 ... и наш компьютер хранит только ее конечное число.
Это будет приблизительно 0,1, но никогда не будет равным. Следовательно, это ограничение нашего компьютерного оборудования, а не ошибка Python.
>>> 1,1 + 2,2
3,3000000000000003 Чтобы решить эту проблему, мы можем использовать модуль decimal, который поставляется с Python.В то время как числа с плавающей запятой имеют точность до 15 десятичных разрядов, десятичный модуль имеет точность, устанавливаемую пользователем.
Давайте посмотрим на разницу:
импорт десятичный
печать (0.1)
печать (десятичное. десятичное (0,1)) Выход
0,1 0,1000000000000000055511151231257827021181583404541015625
Этот модуль используется, когда мы хотим выполнять десятичные вычисления, как мы учились в школе.
Это также сохраняет значение.Мы знаем, что 25,50 кг более точное значение, чем 25,5 кг, поскольку в нем два значащих знака после запятой по сравнению с одним.
из десятичного импортировать десятичный как D
print (D ('1.1') + D ('2.2'))
print (D ('1,2') * D ('2,50')) Выход
3,3 3.000
Обратите внимание на нули в конце в приведенном выше примере.
Мы можем спросить, почему бы не реализовать каждый раз Decimal вместо float? Основная причина - оперативность. Операции с плавающей запятой должны выполняться быстрее, чем десятичных операций.
Когда использовать десятичное число вместо числа с плавающей запятой?
Обычно мы используем Decimal в следующих случаях.
- Когда мы создаем финансовые приложения, требующие точного десятичного представления.
- Когда мы хотим контролировать необходимый уровень точности.
- Когда мы хотим реализовать понятие значащих десятичных знаков.
Python Фракции
Python предоставляет операции с дробными числами через модуль fractions .
У дроби есть числитель и знаменатель, оба целые числа. Этот модуль поддерживает арифметику рациональных чисел.
Мы можем создавать объекты Fraction различными способами. Посмотрим на них.
импортных фракций
печати (fractions.Fraction (1.5))
печати (fractions.Fraction (5))
печать (дроби. дробь (1,3)) Выход
3/2 5 1/3
Создавая Fraction из с плавающей запятой , мы можем получить некоторые необычные результаты.Это происходит из-за несовершенного представления двоичного числа с плавающей запятой, как обсуждалось в предыдущем разделе.
К счастью, Fraction позволяет нам также создавать экземпляры со строкой. Это предпочтительный вариант при использовании десятичных чисел.
импортных фракций
# Как float
# Выход: 2476979795053773/2251799813685248
печати (fractions.Fraction (1.1))
# Как строка
# Вывод: 11/10
печать (дроби. дробь ('1,1')) Выход
2476979795053773/2251799813685248 11/10
Этот тип данных поддерживает все основные операции.Вот несколько примеров.
из фракций импорт фракций как F
печать (F (1, 3) + F (1, 3))
печать (1 / F (5, 6))
печать (F (-3, 10)> 0)
печать (F (-3, 10) <0) Выход
2/3 6/5 Ложь Правда
Python Математика
Python предлагает такие модули, как math и random , для выполнения различных математических задач, таких как тригонометрия, логарифмы, вероятность и статистика и т. Д.
импорт математики
печать (математика.число Пи)
печать (Math.cos (math.pi))
печати (Math.exp (10))
печать (math.log10 (1000))
печати (math.sinh (1))
печать (math.factorial (6)) Выход
3,141592653589793 -1,0 +22026,465794806718 3.0 1,1752011936438014 720
Вот полный список функций и атрибутов, доступных в математическом модуле Python.
случайный импорт
печать (random.randrange (10, 20))
x = ['a', 'b', 'c', 'd', 'e']
# Получить случайный выбор
печать (случайный.выбор (х))
# Перемешать x
random.shuffle (х)
# Вывести перетасованный x
печать (х)
# Печатать случайный элемент
печать (random.random ()) Когда мы запускаем указанную выше программу, мы получаем следующий результат (значения могут отличаться из-за случайного поведения).
18 е ['c', 'e', 'd', 'b', 'a'] 0,5682821194654443
Вот полный список функций и атрибутов, доступных в модуле Python random.
,math - Математические функции - документация Python 3.8.5
Этот модуль обеспечивает доступ к математическим функциям, определенным C стандарт.
Эти функции нельзя использовать с комплексными числами; использовать функции
то же имя из модуля cmath , если вам требуется поддержка сложных
номера. Различие между функциями, поддерживающими комплексные числа, и
те, которых не делают, поскольку большинство пользователей не хотят учиться так много
математика, необходимая для понимания комплексных чисел.Получение исключения
вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс
число, используемое в качестве параметра, чтобы программист мог определить, как и почему он
был создан в первую очередь.
Этот модуль предоставляет следующие функции. За исключением случаев, когда явно в противном случае все возвращаемые значения являются плавающими.
Теоретико-числовые функции и функции представлений
-
математика.потолок( x ) Вернуть потолок x , наименьшее целое число, большее или равное x .Если x не является float, делегирует
x .__ ceil __ (), который должен вернутьИнтегральное значение.
-
математика.гребень( n , k ) Вернуть количество способов выбора k элементов из n элементов без повторения и без заказа.
Оценивается как
n! / (k! * (n - k)!), когдаk <= nи вычисляет к нулю, когдаk> n.Также называется биномиальным коэффициентом, потому что он эквивалентен к коэффициенту k-го члена в полиномиальном разложении выражение
(1 + x) ** n.Вызывает
TypeError, если какой-либо из аргументов не является целым числом. ВызываетValueError, если любой из аргументов отрицательный.
-
математика.копия( x , y ) Вернуть число с плавающей запятой с величиной (абсолютным значением) x , но со знаком л .На платформах, поддерживающих нули со знаком,
copysign (1.0, -0.0)возвращает -1,0 .
-
математика.фабрик( x ) Вернуть абсолютное значение x .
-
математика.факториал( x ) Вернуть факториал x как целое число. Вызывает
ValueError, если x не является целым или отрицательный.
-
математика.этаж( x ) Вернуть нижний предел x , наибольшее целое число, меньшее или равное x . Если x не является плавающим, делегирует
x .__ floor __ (), который должен вернутьИнтегральное значение.
-
математика.fmod( x , y ) Вернуть
fmod (x, y), как определено библиотекой платформы C.Обратите внимание, что Выражение Pythonx% yможет не возвращать тот же результат. Намерение C стандартным является то, чтоfmod (x, y)будет точно (математически; до бесконечности точности) равнымx - n * yдля некоторого целого числа n , так что результат имеет тот же знак, что и x , и величина меньшеабс (y). Pythonx% yвместо этого возвращает результат со знаком y и может быть неточно вычислимым для аргументов с плавающей запятой.Например,fmod (-1e-100, 1e100)равно-1e-100, но результат Python-1e-100% 1e100будет1e100-1e-100, что не может быть представлен в точности как поплавок и округляется до удивительного1e100. Для по этой причине функцияfmod ()обычно предпочтительнее при работе с float, тогда как Pythonx% yпредпочтительнее при работе с целыми числами.
-
математика.frexp( x ) Вернуть мантиссу и показатель степени x как пару
(m, e). м - поплавок и e - целое число, такое чтоx == m * 2 ** eточно. Если x равно нулю, возвращает(0,0, 0), иначе0,5 <= abs (m) <1. Это используется, чтобы «выбрать отдельно »внутреннее представление поплавка портативным способом.
-
математика.fsum( итерация ) Вернуть точную сумму значений с плавающей запятой в итерируемом объекте. Избегает потеря точности из-за отслеживания нескольких промежуточных частичных сумм:
>>> сумма ([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 0,9999999999999999 >>> fsum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 1,0
Точность алгоритма зависит от арифметических гарантий IEEE-754 и типичный случай, когда режим округления половинный. На некоторых не-Windows сборки, базовая библиотека C использует сложение с расширенной точностью и может иногда двойное округление промежуточной суммы, в результате чего она младший значащий бит.
Для дальнейшего обсуждения и двух альтернативных подходов см. Поваренную книгу ASPN. рецепты точного суммирования с плавающей запятой.
-
математика.gcd( a , b ) Вернуть наибольший общий делитель целых чисел a и b . Если либо a или b не равно нулю, тогда значение
gcd (a, b)является наибольшим положительное целое число, которое делит на и на .gcd (0, 0)возвращает0.
-
математика.isclose( a , b , * , rel_tol = 1e-09 , abs_tol = 0,0 ) Вернуть
Истина, если значения a и b близки друг к другу иНеверноиначе.Вт · ч
9,1. числа - Числовые абстрактные базовые классы - документация Python 2.7.18
Модуль номеров ( PEP 3141 ) определяет иерархию числовых
абстрактные базовые классы, которые постепенно определяют
больше операций. Ни один из типов, определенных в этом модуле, не может быть создан.
- класс
номера.Номер Корень числовой иерархии. Если вы просто хотите проверить, является ли аргумент x - это число, неважно какого вида, используйте
isinstance (x, Number).
9.1.1. Цифровая башня
- класс
номера.Комплекс Подклассы этого типа описывают комплексные числа и включают операции которые работают на встраиваемом комплексе
типа. Это: преобразования вкомплексныеиbool,реальные,imag,+,-,*,/,абс (),конъюгат (),==и! =.Все кроме-и! =являются абстрактными.-
реал Аннотация. Извлекает реальную составляющую этого числа.
-
имидж Аннотация. Извлекает мнимую составляющую этого числа.
-
конъюгат() Аннотация. Возвращает комплексное сопряжение. Например,
(1 + 3j) .conjugate () == (1-3j).
-
- класс
номера.Реальный К
Комплекс,Реальныйдобавляет операции, которые работают на реальном номера.Короче говоря, это преобразование в
с плавающей запятой,math.trunc (),раунд (),math.floor (),math.ceil (),divmod (),//,%,<,<=,>и> =.Real также предоставляет значения по умолчанию для
complex (),real,imagисопряженный ().
- класс
номера.Рациональный Подтипы
Реальныйи добавляетчислительи знаменательс плавающей точкой ().-
числитель Аннотация.
- Знаменатель
Аннотация.
-
- класс
номера.Интегральный Подтип
Rationalи добавляет преобразование вint. Обеспечивает значения по умолчанию дляfloat (),числительи Знаменатель**и битовые операции:<<,>>,и,^,|,~.
9.1.2. Примечания для разработчиков типов
Разработчики должны быть осторожны, чтобы равные числа были равны и хэш
их к одинаковым значениям. Это может быть незаметно, если есть два разных
расширения действительных чисел. Например, дробь .
реализует hash () следующим образом:
def __hash __ (сам):
если self.denominator == 1:
# Получите правильные числа.
вернуть хеш (self.numerator)
# Дорогой чек, но определенно правильный.если self == float (self):
вернуть хеш (float (self))
еще:
# Используйте хеш кортежа, чтобы избежать высокой частоты конфликтов на
# простые дроби.
вернуть хеш ((self.numerator, self.denominator))
9.1.2.1. Добавление дополнительных цифр ABC
Конечно, есть и другие возможные буквы ABC для чисел, и это
быть плохой иерархией, если она исключает возможность добавления
те. Вы можете добавить MyFoo между Complex и Real с:

 (Модуль любого числа — неотрицательное число)
(Модуль любого числа — неотрицательное число) (Модули противоположных чисел равны)
(Модули противоположных чисел равны) (Величина числа не превышает величина его модуля)
(Величина числа не превышает величина его модуля) (Модуль произведения дорівнєю произведению модулей сомножителей)
(Модуль произведения дорівнєю произведению модулей сомножителей) (Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))
(Модуль дроби равен модулю числителя, деленному на модуль знаменателя (если знаменатель не равен нулю))


 (Модуль суммы не превышает суммы модулей слагаемых)
(Модуль суммы не превышает суммы модулей слагаемых)
 Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6. Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.
Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a>, 0.