Выборочный коэффициент корреляции: Выборочный коэффициент корреляции

Линейный коэффициент корреляции Пирсона — statanaliz.info

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

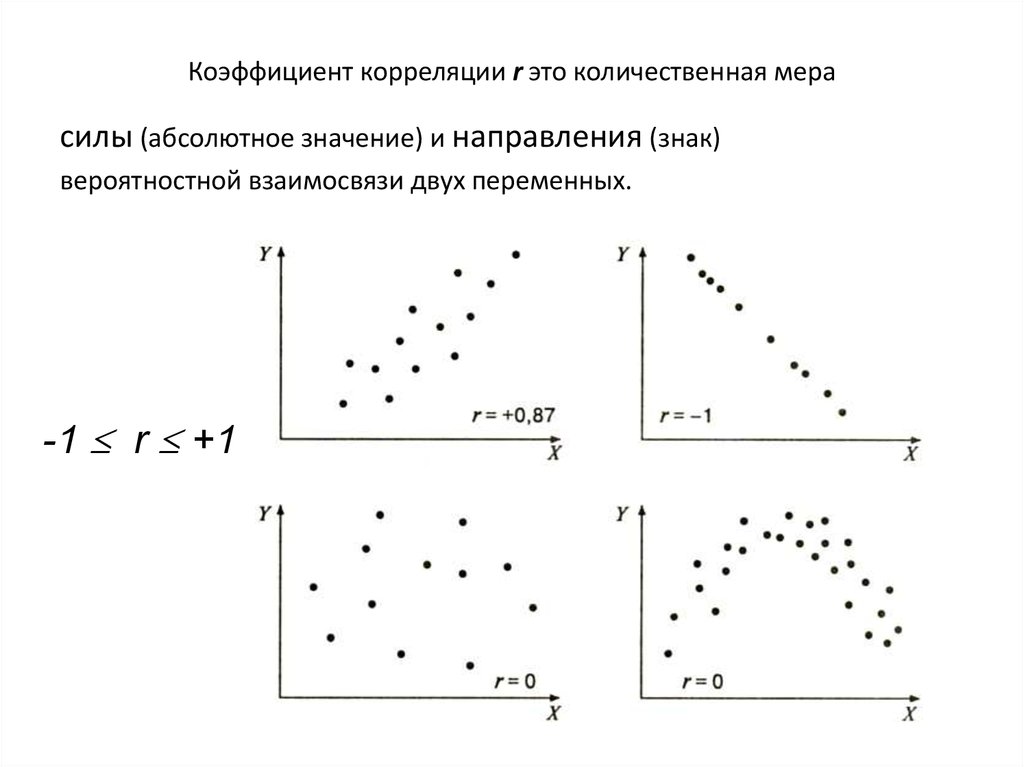
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т. к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

Корреляционный анализ в Excel лучше начинать с визуализации.

На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ. СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Python, корреляция и регрессия: часть 1 / Хабр

Чем больше я узнаю людей, тем больше мне нравится моя собака.

 —Марк Твен

В предыдущих сериях постов для начинающих из ремикса книги Генри Гарнера «Clojure для исследования данных» (Clojure for Data Science) на языке Python мы рассмотрели методы описания выборок с точки зрения сводных статистик и методов статистического вывода из них параметров популяции. Такой анализ сообщает нам нечто о популяции в целом и о выборке в частности, но он не позволяет нам делать очень точные утверждения об их отдельных элементах. Это связано с тем, что в результате сведения данных всего к двум статистикам — среднему значению и стандартному отклонению — теряется огромный объем информации.

Нам часто требуется пойти дальше и установить связь между двумя или несколькими переменными либо предсказать одну переменную при наличии другой. И это подводит нас к теме данной серии из 5 постов — исследованию корреляции и регрессии. Корреляция имеет дело с силой и направленностью связи между двумя или более переменными. Регрессия определяет природу этой связи и позволяет делать предсказания на ее основе.

В этой серии постов будет рассмотрена линейная регрессия. При наличии выборки данных наша модель усвоит линейное уравнение, позволяющее ей делать предсказания о новых, не встречавшихся ранее данных. Для этого мы снова обратимся к библиотеке pandas и изучим связь между ростом и весом спортсменов-олимпийцев. Мы введем понятие матриц и покажем способы управления ими с использованием библиотеки pandas.

О данных

В этой серии постов используются данные, любезно предоставленные компанией Guardian News and Media Ltd., о спортсменах, принимавших участие в Олимпийских Играх 2012 г. в Лондоне. Эти данные изначально были взяты из блога газеты Гардиан.

Обследование данных

Когда вы сталкиваетесь с новым набором данных, первая задача состоит в том, чтобы его обследовать с целью понять, что именно он содержит.

Файл all-london-2012-athletes.tsv достаточно небольшой. Мы можем обследовать данные при помощи pandas, как мы делали в первой серии постов «Python, исследование данных и выборы», воспользовавшись функцией read_csv:

def load_data():
    return pd.read_csv('data/ch03/all-london-2012-athletes-ru.tsv', '\t')
                                            
def ex_3_1():
    '''Загрузка данных об участниках 
       олимпийских игр в Лондоне 2012 г.'''
    return load_data()

Если выполнить этот пример в консоли интерпретатора Python либо в блокноте Jupyter, то вы должны увидеть следующий ниже результат:

Столбцы данных (нам повезло, что они ясно озаглавлены) содержат следующую информацию:

• ФИО атлета

• страна, за которую он выступает

• возраст, лет

• рост, см.

• вес, кг.

• пол «М» или «Ж»

• дата рождения в виде строки

• место рождения в виде строки (со страной)

• число выигранных золотых медалей

• число выигранных серебряных медалей

• число выигранных бронзовых медалей

• всего выигранных золотых, серебряных и бронзовых медалей

• вид спорта, в котором он соревновался

• состязание в виде списка, разделенного запятыми

Даже с учетом того, что данные четко озаглавлены, очевидно присутствие пустых мест в столбцах с ростом, весом и местом рождения. При наличии таких данных следует проявлять осторожность, чтобы они не сбили с толку.

Визуализация данных

В первую очередь мы рассмотрим разброс роста спортсменов на Олимпийских играх 2012 г. в Лондоне. Изобразим эти значения роста в виде гистограммы, чтобы увидеть характер распределения данных, не забыв сначала отфильтровать пропущенные значения:

def ex_3_2():
    '''Визуализация разброса значений 
       роста спортсменов на гистограмме'''
    df = load_data()
    df['Рост, см']. hist(bins=20)
    plt.xlabel('Рост, см.')
    plt.ylabel('Частота')
    plt.show()

Этот пример сгенерирует следующую ниже гистограмму:

Как мы и ожидали, данные приближенно нормально распределены. Средний рост спортсменов составляет примерно 177 см. Теперь посмотрим на распределение веса олимпийских спортсменов:

def ex_3_3():
    '''Визуализация разброса значений веса спортсменов'''
    df = load_data()
    df['Вес'].hist(bins=20)
    plt.xlabel('Вес')
    plt.ylabel('Частота')
    plt.show()

Приведенный выше пример сгенерирует следующую ниже гистограмму:

Данные показывают четко выраженную асимметрию. Хвост с правой стороны намного длиннее, чем с левой, и поэтому мы говорим, что асимметрия — положительная. Мы можем оценить асимметрию данных количественно при помощи функции библиотеки pandas

skew:

def ex_3_4():
    '''Вычисление асимметрии веса спортсменов'''
    df = load_data()
    swimmers = df[ df['Вид спорта'] == 'Swimming']
    return swimmers['Вес']. skew()

0.23441459903001483

К счастью, эта асимметрия может быть эффективным образом смягчена путем взятия логарифма веса при помощи функции библиотеки numpy np.log:

def ex_3_5():
    '''Визуализация разброса значений веса спортсменов на
       полулогарифмической гистограмме с целью удаления 
       асимметрии'''
    df = load_data()
    df['Вес'].apply(np.log).hist(bins=20)
    plt.xlabel('Логарифмический вес')
    plt.ylabel('Частота')
    plt.show()

Этот пример сгенерирует следующую ниже гистограмму:

Теперь данные намного ближе к нормальному распределению. Из этого следует, что вес распределяется согласно логнормальному распределению.

Логнормальное распределение

Логнормальное распределение — это распределение набора значений, чей логарифм нормально распределен. Основание логарифма может быть любым положительным числом за исключением единицы. Как и нормальное распределение, логнормальное распределение играет важную роль для описания многих естественных явлений.

Логарифм показывает степень, в которую должно быть возведено фиксированное число (основание) для получения данного числа. Изобразив логарифмы на графике в виде гистограммы, мы показали, что эти степени приближенно нормально распределены. Логарифмы обычно берутся по основанию 10 или основанию e, трансцендентному числу, приближенно равному 2.718. В функции библиотеки numpy np.log и ее инверсии np.exp используется основание e. Выражение log_e также называется натуральным логарифмом, или ln, из-за свойств, делающих его особенно удобным в исчислении.

Логнормальное распределение обычно имеет место в процессах роста, где темп роста не зависит от размера. Этот феномен известен как закон Джибрэта, который был cформулирован в 1931 г. Робертом Джибрэтом, заметившим, что он применим к росту фирм. Поскольку темп роста пропорционален размеру, более крупные фирмы демонстрируют тенденцию расти быстрее, чем фирмы меньшего размера.

^{Нормальное распределение случается в ситуациях, где много мелких колебаний, или вариаций, носит суммирующий эффект, тогда как логнормальное распределение происходит там, где много мелких вариаций имеет мультипликативный эффект.}

С тех пор выяснилось, что закон Джибрэта применим к большому числу ситуаций, включая размеры городов и, согласно обширному математическому ресурсу Wolfram MathWorld, к количеству слов в предложениях шотландского писателя Джорджа Бернарда Шоу.

В остальной части этой серии постов мы будем использовать натуральный логарифм веса спортсменов, чтобы наши данные были приближенно нормально распределены. Мы выберем популяцию спортсменов примерно с одинаковыми типами телосложения, к примеру, олимпийских пловцов.

Визуализация корреляции

Один из самых быстрых и самых простых способов определить наличие корреляции между двумя переменными состоит в том, чтобы рассмотреть их на графике рассеяния. Мы отфильтруем данные, выбрав только пловцов, и затем построим график роста относительно веса спортсменов:

def swimmer_data():
    '''Загрузка данных роста и веса только олимпийских пловцов'''
    df = load_data()
    return df[df['Вид спорта'] == 'Swimming']. dropna()
def ex_3_6():
    '''Визуализация корреляции между ростом и весом'''
    df = swimmer_data()
    xs = df['Рост, см']
    ys = df['Вес'].apply( np.log )
    pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
    plt.xlabel('Рост, см.')
    plt.ylabel('Логарифмический вес')
    plt.show()

Этот пример сгенерирует следующий ниже график:

Результат ясно показывает, что между этими двумя переменными имеется связь. График имеет характерно смещенную эллиптическую форму двух коррелируемых, нормально распределенных переменных с центром вокруг среднего значения. Следующая ниже диаграмма сравнивает график рассеяния с распределениями вероятностей роста и логарифма веса:

Точки, близко расположенные к хвосту одного распределения, также демонстрируют тенденцию близко располагаться к тому же хвосту другого распределения, и наоборот. Таким образом, между двумя распределениями существует связь, которую в ближайших нескольких разделах мы покажем, как определять количественно. Впрочем, если мы внимательно посмотрим на предыдущий график рассеяния, то увидим, что из-за округления измерений точки уложены в столбцы и строки (в см. и кг. соответственно для роста и веса). Там, где это происходит, иногда желательно внести в данные искажения, которые также называются сдвигом или джиттером с тем, чтобы яснее показать силу связи. Без генерирования джиттера (в виде случайных отклонений) может оказаться, что, то, что по внешнему виду составляет одну точку, фактически представляет много точек, которые обозначены одинаковой парой значений. Внесение нескольких случайных помех делает эту ситуацию вряд ли возможной.

Генерирование джиттера

Поскольку каждое значение округлено до ближайшего сантиметра или килограмма, то значение, записанное как 180 см, на самом деле может быть каким угодно между 179.5 и 180.5 см, тогда как значение 80 кг на самом деле может быть каким угодно между 79.5 и 80.5 кг. Для создания случайных искажений, мы можем добавить случайные помехи в каждую точку данных роста в диапазоне между -0.

5 и 0.5 и в том же самом диапазоне проделать с точками данных веса (разумеется, это нужно cделать до того, как мы возьмем логарифм значений веса):

def jitter(limit):
    '''Генератор джиттера (произвольного сдвига точек данных)'''
    return lambda x: random.uniform(-limit, limit) + x
def ex_3_7():
    '''Визуализация корреляции между ростом и весом с джиттером'''
    df = swimmer_data()
    xs = df['Рост, см'].apply(jitter(0.5))
    ys = df['Вес'].apply(jitter(0.5)).apply(np.log)
    pd.DataFrame(np.array([xs,ys]).T).plot.scatter(0, 1, s=12, grid=True)
    plt.xlabel('Рост, см.')
    plt.ylabel('Логарифмический вес')
    plt.show()

График с джиттером выглядит следующим образом:

Как и в случае с внесением прозрачности в график рассеяния в первой серии постов об описательной статистике, генерирование джиттера — это механизм, который обеспечивает исключение несущественных факторов, таких как объем данных или артефакты округления, которые могут заслонить от нас возможность увидеть закономерности в данных.

Ковариация

Одним из способов количественного определения силы связи между двумя переменными является их ковариация. Она измеряет тенденцию двух переменных изменяться вместе.

Если у нас имеется два ряда чисел, X и Y, то их отклонения от среднего значения составляют:

Здесь x_i — это значение X с индексом i, y_i — значение Y с индексом i, x̅ — среднее значение X, и y̅ — среднее значение Y. Если X и Y проявляют тенденцию изменяться вместе, то их отклонения от среднего будет иметь одинаковый знак: отрицательный, если они — меньше среднего, положительный, если они больше среднего. Если мы их перемножим, то произведение будет положительным, когда у них одинаковый знак, и отрицательным, когда у них разные знаки. Сложение произведений дает меру тенденции этих двух переменных отклоняться от среднего значения в одинаковом направлении для каждой заданной выборки.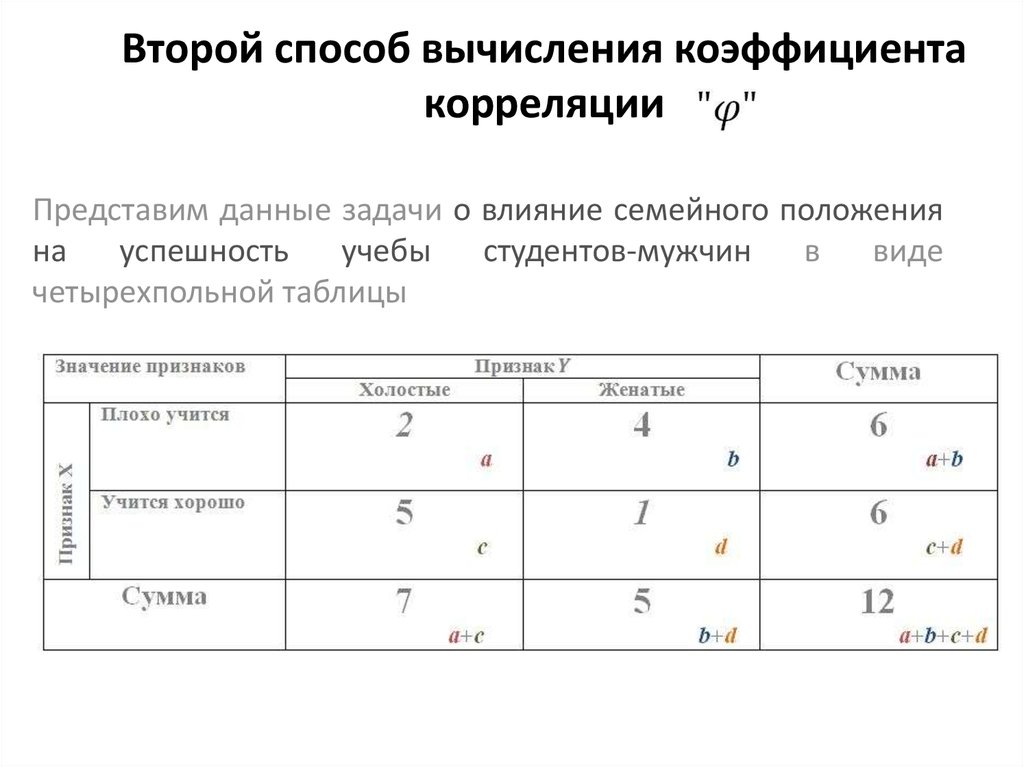

Ковариация определяется как среднее этих произведений:

На чистом Python ковариация вычисляется следующим образом:

def covariance(xs, ys):
    '''Вычисление ковариации (несмещенная, т.е. n-1)'''
    dx = xs - xs.mean() 
    dy = ys - ys.mean()
    return (dx * dy).sum() / (dx.count() - 1)

В качестве альтернативы, мы можем воспользоваться функцией pandas cov:

df['Рост, см'].cov(df['Вес'])

1.3559273321696459

Ковариация роста и логарифма веса для наших олимпийских пловцов равна 1.356, однако это число сложно интерпретировать. Единицы измерения здесь представлены произведением единиц на входе.

По этой причине о ковариации редко сообщают как об отдельной сводной статистике. Сделать число более понятным можно, разделив отклонения на произведение стандартных отклонений. Это позволяет трансформировать единицы измерения в

стандартные оценки и ограничить выход числом в диапазоне между -1 и +1. Этот результат называется корреляцией Пирсона.

^{Стандартная оценка, англ. standard score, также z-оценка — это относительное число стандартных отклонений, на которые значение переменной отстоит от среднего значения. Положительная оценка показывает, что переменная находится выше среднего, отрицательная — ниже среднего. Это безразмерная величина, получаемая при вычитании популяционного среднего из индивидуальных значений и деления разности на популяционное стандартное отклонение.}

Корреляция Пирсона

Корреляция Пирсона часто обозначается переменной r и вычисляется следующим образом, где отклонения от среднего

dx_i и dy_i вычисляются как и прежде:

Поскольку для переменных X и Y стандартные отклонения являются константными, уравнение может быть упрощено до следующего, где σ_x и σ_y — это стандартные отклонения соответственно X и Y:

В таком виде формула иногда упоминается как коэффициент корреляции смешанных моментов Пирсона или попросту коэффициент корреляции и, как правило, обозначается буквой r.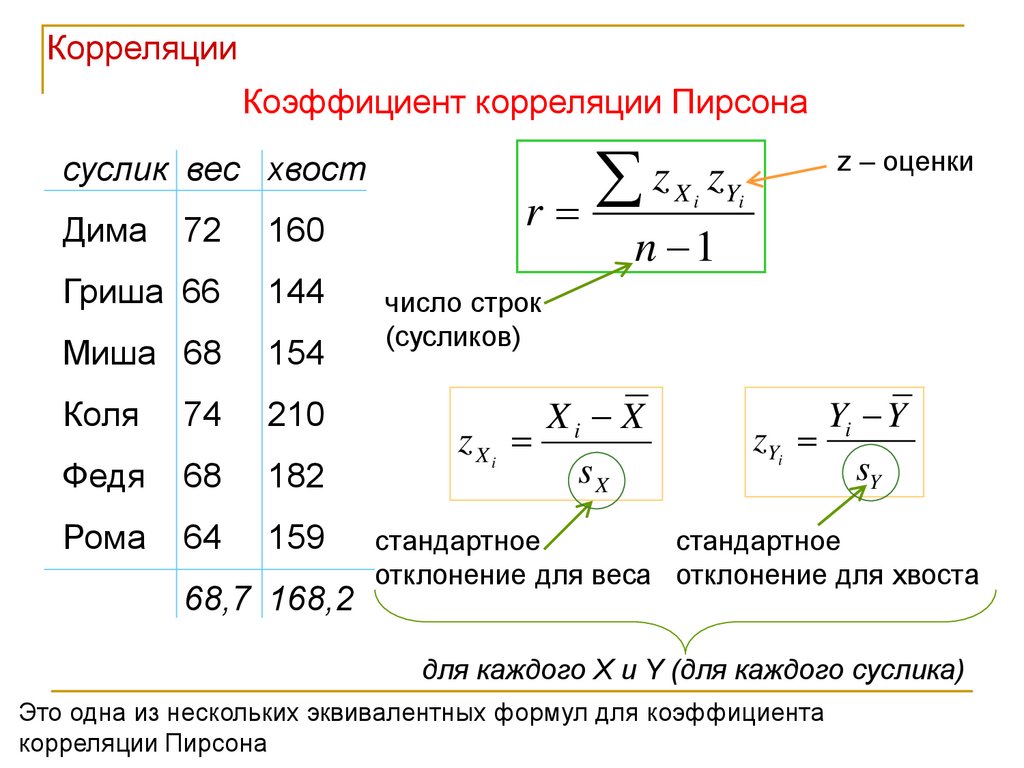

Ранее мы уже написали функции для вычисления стандартного отклонения. В сочетании с нашей функцией с вычислением ковариации получится следующая ниже имплементация корреляции Пирсона:

def variance(xs):
    '''Вычисление корреляции,
       несмещенная дисперсия при n <= 30'''
    x_hat = xs.mean()
    n = xs.count()
    n = n - 1 if n in range( 1, 30 ) else n  
    return sum((xs - x_hat) ** 2) / n
def standard_deviation(xs):
    '''Вычисление стандартного отклонения'''
    return np.sqrt(variance(xs))
def correlation(xs, ys): 
    '''Вычисление корреляции'''
    return covariance(xs, ys) / (standard_deviation(xs) * 
                                 standard_deviation(ys))

В качестве альтернативы мы можем воспользоваться функцией pandas corr:

df['Рост, см'].corr(df['Вес'])

Поскольку стандартные оценки безразмерны, то и коэффициент корреляции r тоже безразмерен. Если r равен -1.0 либо 1.0, то переменные идеально антикоррелируют либо идеально коррелируют.

Правда, если r = 0, то с необходимостью вовсе не следует, что переменные не коррелируют. Корреляция Пирсона измеряет лишь линейные связи. Как продемонстрировано на следующих графиках, между переменными может существовать еще некая нелинейная связь, которую r не объясняет:

Отметим, что корреляция центрального примера не определена, потому что стандартное отклонение y = 0. Поскольку наше уравнение для r содержало бы деление ковариации на 0, то результат получается бессмысленным. В этом случае между переменными не может быть никакой корреляции; y всегда будет иметь среднее значение. Простое обследование стандартных отклонений это подтвердит.

Мы можем вычислить коэффициент корреляции для данных роста и логарифма веса наших пловцов следующим образом:

def ex_3_8():
    '''Вычисление корреляции средствами pandas
       на примере данных роста и веса'''
    df = swimmer_data()
    return df['Рост, см'].corr( df['Вес'].apply(np. log))

0.86748249283924894

В результате получим ответ 0.867, который количественно выражает сильную, положительную корреляцию, уже наблюдавшуюся нами на точечном графике.

Выборочный r и популяционный ρ

Аналогично среднему значению и стандартному отклонению, коэффициент корреляции является сводной статистикой. Он описывает выборку; в данном случае, выборку спаренных значений: роста и веса. Коэффициент корреляции известной выборки обозначается буквой r, тогда как коэффициент корреляции неизвестной популяции обозначается греческой буквой ρ (рхо).

Как мы убедились в предыдущей серии постов о тестировании гипотез, мы не должны исходить из того, что результаты, полученные в ходе измерения нашей выборки, применимы к популяции в целом. К примеру, наша популяция может состоять из всех пловцов всех недавних Олимпийских игр. И будет совершенно недопустимо обобщать, например, на другие олимпийские виды спорта, такие как тяжелая атлетика или фитнес-плавание.

Даже в допустимой популяции — такой как пловцы, выступавшие на недавних Олимпийских играх, — наша выборка коэффициента корреляции является всего лишь одной из многих потенциально возможных. То, насколько мы можем доверять нашему r, как оценке параметра ρ, зависит от двух факторов:

• Размера выборки

• Величины r

Безусловно, чем больше выборка, тем больше мы ей доверяем в том, что она представляет всю совокупность в целом. Возможно, не совсем интуитивно очевидно, но величина  тоже оказывает влияние на степень нашей уверенности в том, что выборка представляет параметр . Это вызвано тем, что большие коэффициенты вряд ли возникли случайным образом или вследствие случайной ошибки при отборе.

Проверка статистических гипотез

В предыдущей серии постов мы познакомились с проверкой статистических гипотез, как средством количественной оценки вероятности, что конкретная гипотеза (как, например, что две выборки взяты из одной и той же популяции) истинная. Чтобы количественно оценить вероятность, что корреляция существует в более широкой популяции, мы воспользуемся той же самой процедурой.

В первую очередь, мы должны сформулировать две гипотезы, нулевую гипотезу и альтернативную:

H₀ — это гипотеза, что корреляция в популяции нулевая. Другими словами, наше консервативное представление состоит в том, что измеренная корреляция целиком вызвана случайной ошибкой при отборе.

H₁ — это альтернативная возможность, что корреляция в популяции не нулевая. Отметим, что мы не определяем направление корреляции, а только что она существует. Это означает, что мы выполняем двустороннюю проверку.

Стандартная ошибка коэффициента корреляции r по выборке задается следующей формулой:

Эта формула точна, только когда r находится близко к нулю (напомним, что величина ρ влияет на нашу уверенность), но к счастью, это именно то, что мы допускаем согласно нашей нулевой гипотезы.

Мы можем снова воспользоваться t-распределением и вычислить t-статистику:

В приведенной формуле df — это степень свободы наших данных. Для проверки корреляции степень свободы равна n — 2, где n — это размер выборки. Подставив это значение в формулу, получим:

В итоге получим t-значение 102.21. В целях его преобразования в p-значение мы должны обратиться к t-распределению. Библиотека scipy предоставляет интегральную функцию распределения (ИФР) для t-распределения в виде функции stats.t.cdf, и комплементарной ей (1-cdf) функции выживания stats.t.sf. Значение функции выживания соответствует p-значению для односторонней проверки. Мы умножаем его на 2, потому что выполняем двустороннюю проверку:

def t_statistic(xs, ys):
    '''Вычисление t-статистики'''
    r = xs.corr(ys)  # как вариант, correlation(xs, ys)
    df = xs.count() - 2
    return r * np. sqrt(df / 1 - r ** 2)
def ex_3_9():
    '''Выполнение двухстороннего t-теста'''
    df = swimmer_data()
    xs = df['Рост, см']
    ys = df['Вес'].apply(np.log)
    t_value = t_statistic(xs, ys)
    df = xs.count() - 2 
    p = 2 * stats.t.sf(t_value, df)  # функция выживания 
    return {'t-значение':t_value, 'p-значение':p}

{'p-значение': 1.8980236317815443e-106, 't-значение': 25.384018200627057}

P-значение настолько мало, что в сущности равно 0, означая, что шанс, что нулевая гипотеза является истинной, фактически не существует. Мы вынуждены принять альтернативную гипотезу о существовании корреляции.

Интервалы уверенности

Установив, что в более широкой популяции, безусловно, существует корреляция, мы, возможно, захотим количественно выразить диапазон значений, внутри которого, как мы ожидаем, будет лежать параметр ρ, вычислив для этого интервал уверенности. Как и в случае со средним значением в предыдущей серии постов, интервал уверенности для r выражает вероятность (выраженную в %), что параметр ρ популяции находится между двумя конкретными значениями.

Однако при попытке вычислить стандартную ошибку коэффициента корреляции возникает сложность, которой не было в случае со средним значением. Поскольку абсолютное значение коэффициента корреляции r не может превышать 1, распределение возможных выборок коэффициентов корреляции r смещается по мере приближения r к пределу своего диапазона.

Приведенный выше график показывает отрицательно скошенное распределение r-выборок для параметра ρ, равного 0.6.

К счастью, трансформация под названием z-преобразование Фишера стабилизирует дисперсию r  по своему диапазону. Она аналогична тому, как наши данные о весе спортсменов стали нормально распределенными, когда мы взяли их логарифм.

Уравнение для z-преобразования следующее:

Стандартная ошибка z равна:

Таким образом, процедура вычисления интервалов уверенности состоит в преобразовании r в z с использованием z-преобразования, вычислении интервала уверенности в терминах стандартной ошибки SE_z и затем преобразовании интервала уверенности в r.

В целях вычисления интервала уверенности в терминах SE_z, мы можем взять число стандартных отклонений от среднего, которое дает нам требуемый уровень доверия. Обычно используют число 1.96, так как оно является числом стандартных отклонений от среднего, которое содержит 95% площади под кривой. Другими словами, 1.96 стандартных ошибок от среднего значения выборочного r содержит истинную популяционную корреляцию ρ с 95%-ой определенностью.

Мы можем убедиться в этом, воспользовавшись функцией scipy stats.norm.ppf. Она вернет стандартную оценку, связанную с заданной интегральной вероятностью в условиях односторонней проверки.

Однако, как показано на приведенном выше графике, мы хотели бы вычесть ту же самую величину, т.е. 2.5%, из каждого хвоста с тем, чтобы 95%-й интервал уверенности был центрирован на нуле. Для этого при выполнении двусторонней проверки нужно просто уменьшить разность наполовину и вычесть результат из 100%. Так что, требуемый уровень доверия в 95% означает, что мы обращаемся к критическому значению 97.5%:

def critical_value(confidence, ntails): # ДИ и число хвостов
    '''Расчет критического значения путем
       вычисления квантиля и получения 
       для него нормального значения'''
    lookup = 1 - ((1 - confidence) / ntails) 
    return stats.norm.ppf(lookup, 0, 1)  # mu=0, sigma=1
critical_value(0.95, 2)

1.959963984540054

Поэтому наш 95%-й интервал уверенности в z-пространстве для ρ задается следующей формулой:

Подставив в нашу формулу z_rи SE_z, получим:

Для r=0.867 и n=859 она даст нижнюю и верхнюю границу соответственно 1.137 и 1.722. В целях их преобразования из z-оценок в r-значения, мы используем следующее обратное уравнение z-преобразования:

Преобразования и интервал уверенности можно вычислить при помощи следующего исходного кода:

def z_to_r(z):
    '''Преобразование z-оценки обратно в r-значение'''
    return (np. exp(z*2) - 1) / (np.exp(z*2) + 1)
def r_confidence_interval(crit, xs, ys): 
    '''Расчет интервала уверенности
       для критического значения и данных'''
    r   = xs.corr(ys)
    n   = xs.count()
    zr  = 0.5 * np.log((1 + r) / (1 - r)) 
    sez = 1 / np.sqrt(n - 3)
    return (z_to_r(zr - (crit * sez))), (z_to_r(zr + (crit * sez)))
def ex_3_10():
    '''Расчет интервала уверенности
       на примере данных роста и веса'''
    df = swimmer_data()
    X = df['Рост, см']
    y = df['Вес'].apply(np.log)
    interval = r_confidence_interval(1.96, X, y) 
    print('Интервал уверенности (95%):', interval)

Интервал уверенности (95%): (0.8499088588880347, 0.8831284878884087)

В результате получаем 95%-й интервал уверенности для ρ, расположенный между 0.850 и 0.883. Мы можем быть абсолютно уверены в том, что в более широкой популяции олимпийских пловцов существует сильная положительная корреляция между ростом и весом.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

В следующем посте, посте №2, будет рассмотрена сама тема серии — регрессия и приемы оценивания ее качества.

Парная корреляция

Для измерения тесноты статистической связи между случайными величинами  и  введён коэффициент корреляции , который можно вычислить, если известна функция распределения системы из двух случайных величин (совместная функция распределения).

Поскольку на практике истинная совместная функция корреляции неизвестна, задача состоит не в вычислении, а в получении оценки коэффициента корреляции по результатам эксперимента, по выборке.

Получив оценку,  следует ответить на вопрос «значимо ли оцененный коэффициент корреляции отличен от нуля», и если это отличие значимо, то для формулировки содержательного и точного утверждения о присутствии или отсутствии статистической связи между случайными величинами, следует построить доверительный интервал для коэффициента корреляции.

Итак, для исследования тесноты стохастической связи случайных величин  и  в нашем распоряжении выборка значений случайных величин, полученная в серии из  одинаковых экспериментов:

Номер эксперимента	Значения	Значения
1
2
…	…	…

 

Выборочный коэффициент корреляции (точечная оценка коэффициента корреляции) вычисляется по формуле

,

где, как обычно, ,  – выборочные средние, ,  – стандартные отклонения, квадратные корни из выборочных дисперсий.

Когда оценка  получена, проверяем значимость коэффициента корреляции.

Формулируем нулевую гипотезу  против альтернативы .

Если известно, что двумерный вектор , система случайных величин  и , распределён по двумерному нормальному закону, то критерием для проверки гипотезы служит «агрегат»

.

Этот «агрегат», эта случайная величина,  в предположении о справедливости нулевой гипотезы, имеет распределение Стьюдента с -мя степенями свободы.

Зададимся уровнем значимости   и вычислим критическую точку , решение уравнения .

Если , то событие   представляется вполне возможным, с уровнем значимости  не отвергаем гипотезу  о нулевом значении коэффициента корреляции. Коэффициент корреляции полагаем незначимым. Полагаем, что никакой статистической связи между случайными величинами  и  нет.

Если же , то событие   маловероятно, отвергаем с уровнем значимости  гипотезу  о нулевом значении коэффициента корреляции, принимаем альтернативу, .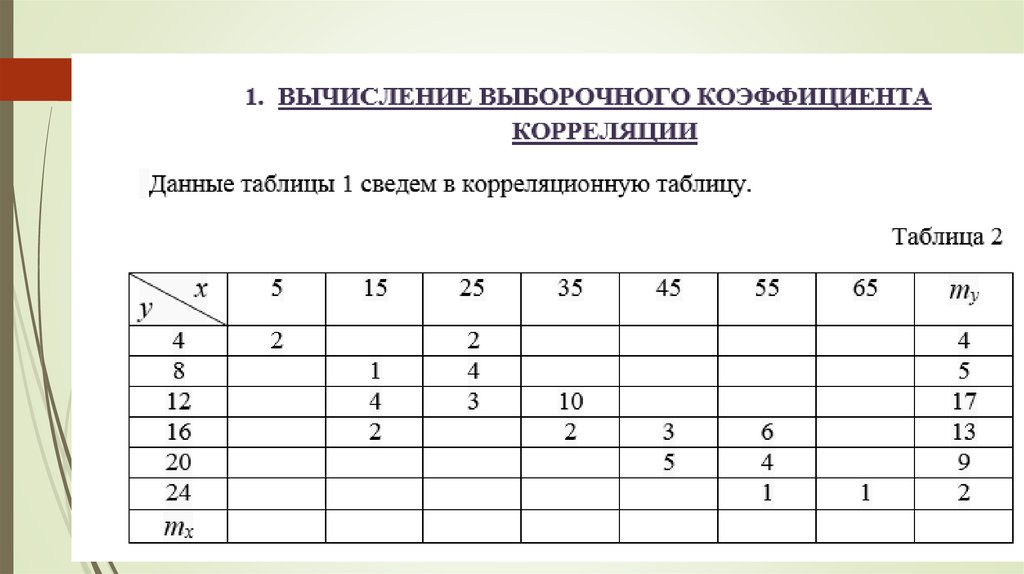 Коэффициент корреляции полагаем значимым. Допускаем существование статистической связи между случайными величинами  и . Переходим к построению доверительного интервала для коэффициента корреляции.

Воспользуемся методикой Фишера. Он показал, что при  величина

распределена практически нормально с математическим ожиданием  и дисперсией .

Тогда, если , доверительная вероятность, а точки  – границы критической двусторонней области для стандартного нормального распределения, то доверительный интервал для случайной величины  записывается в виде , обозначим его .

Отсюда, выполнив несложные алгебраические вычисления (решив систему неравенств), получим доверительный интервал для коэффициента корреляции :

,

где  решения уравнений , ,   – тангенс гиперболический.

И тогда можно утверждать, что с доверительной вероятностью  интервал  накрывает истинное значение коэффициента корреляции .

По величине значений границ этого интервала мы сможем формулировать утверждения относительно тесноты статистической связи между случайными величинами  и .  О том, что эта связь существует, мы утверждаем на основании проверенной нами значимости коэффициента корреляции.

Замечание. Исторически так сложилось, что гиперболические функции были не «в почете» у представителей гуманитарных наук и Фишер дал своё имя функции , которая есть не что иное, как обычный  гиперболический арктангенс (ареатангенс). Компьютеров тогда не было и для практической работы были составлены таблицы функции Фишера и обратной. Разработчики Excel, следуя традиции, включили в число функций пакета одинаковые функции под разными именами, т.е. есть одинаковые функции ATANH и ФИШЕР, а также одинаковые функции TANH и ФИШЕРОБР

Пример 1

Пример 1.Исследовать тесноту статистической связи между случайными величинами  и , представленными выборочными значениями

37	39
33	40
15	35
36	48
26	53
24	42
15	54
33	54
44	50
34	53
63	46
8	50
44	43
43	55
31	51

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

Пример 2

Пример 2.Исследовать тесноту статистической связи между случайными величинами  и , представленными выборочными значениями

39	26
40	33
35	24
48	29
53	42
42	24
54	52
54	56
50	26
53	45
46	27
50	54
43	34
55	48
51	45

На приведенном ниже рисунке изображён фрагмент листа Excel с вычислениями.

 

Простое определение, формула, простые шаги расчета

Коэффициенты корреляции используются для измерения того, насколько сильна взаимосвязь между двумя переменными. Существует несколько типов коэффициента корреляции, но наиболее популярным является коэффициент Пирсона. Корреляция Пирсона (также называемая R Пирсона) — это коэффициент корреляции , обычно используемый в линейной регрессии. Если вы начинаете заниматься статистикой, вы, вероятно, узнаете о 9 Пирсоновских0007 R первый. На самом деле, когда кто-то ссылается на коэффициент корреляции , он обычно имеет в виду коэффициент Пирсона.

Посмотрите видео с обзором коэффициента корреляции или прочитайте ниже:

Знакомство с коэффициентом корреляции

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Содержание:

1. Что такое коэффициент корреляции?
2. Что такое корреляция Пирсона? Как рассчитать:

• Вручную
• ТИ 83
• Эксель
• СПСС
• Минитаб
• Что означают результаты?

V-корреляция Крамера

Откуда взялся коэффициент корреляции?

Проверка гипотезы коэффициента корреляции.

Отношение к косинусу

Дополнительные статьи / Коэффициенты корреляции

Формулы коэффициента корреляции используются для определения того, насколько сильна связь между данными. Формулы возвращают значение от -1 до 1, где:

• 1 указывает на сильную положительную связь.
• -1 указывает на сильную отрицательную связь.
• Нулевой результат означает полное отсутствие связи.

Графики, демонстрирующие корреляцию -1, 0 и +1

Значение

• Коэффициент корреляции, равный 1, означает, что при каждом положительном увеличении одной переменной происходит положительное увеличение фиксированной пропорции другой. Например, размеры обуви увеличиваются в (почти) идеальной зависимости от длины стопы.
• Коэффициент корреляции, равный -1, означает, что при каждом положительном увеличении одной переменной происходит отрицательное уменьшение другой в фиксированной пропорции. Например, количество бензина в баке уменьшается в (почти) полной корреляции со скоростью.
• Ноль означает, что для каждого увеличения нет положительного или отрицательного увеличения. Эти два просто не связаны.

Абсолютное значение коэффициента корреляции дает нам силу связи. Чем больше число, тем сильнее связь. Например, |-.75| = 0,75, что имеет более сильную связь, чем 0,65.

Нравится объяснение? Прочтите «Руководство по статистике практического мошенничества», в котором есть сотни пошаговых решений задач!

Типы формул коэффициентов корреляции.

Существует несколько типов формул коэффициента корреляции.

Одной из наиболее часто используемых формул является формула коэффициента корреляции Пирсона. Если вы посещаете базовый курс статистики, вы, вероятно, будете использовать это:

Коэффициент корреляции Пирсона

Обычно используются две другие формулы: коэффициент корреляции выборки и коэффициент корреляции генеральной совокупности.

Коэффициент корреляции выборки

S _x и s _y — стандартные отклонения выборки, а s _xy — ковариация выборки.

Коэффициент корреляции населения

Коэффициент корреляции населения использует σ _x и σ _y в качестве стандартных отклонений населения, и σ _xy как ковариация генеральной совокупности.

Посетите мой канал Youtube, чтобы получить дополнительные советы и помощь со статистикой!

В начало

Корреляция между наборами данных является мерой того, насколько хорошо они связаны. Наиболее распространенной мерой корреляции в статистике является корреляция Пирсона. Полное название: Pearson Product Moment Correlation (PPMC) . Он показывает линейную зависимость между двумя наборами данных. Проще говоря, он отвечает на вопрос: Могу ли я нарисовать линейный график для представления данных? Для обозначения корреляции Пирсона используются две буквы: греческая буква rho (ρ) для генеральной совокупности и буква «r» для выборки.

Возможные проблемы с корреляцией Пирсона.

PPMC не может определить разницу между зависимыми переменными и независимыми переменными. Например, если вы пытаетесь найти корреляцию между высококалорийной диетой и диабетом, вы можете найти высокую корреляцию 0,8. Однако вы также можете получить тот же результат с переключением переменных. Другими словами, можно сказать, что диабет вызывает высококалорийную диету. Это явно не имеет смысла. Следовательно, как исследователь, вы должны знать, какие данные вы подключаете. Кроме того, PPMC не предоставит вам никакой информации о наклоне линии; это только говорит вам, есть ли отношения.

Пример из реальной жизни

Корреляция Пирсона используется в тысячах реальных жизненных ситуаций. Например, ученые в Китае хотели узнать, существует ли связь между генетическими различиями популяций сорного риса. Цель состояла в том, чтобы выяснить эволюционный потенциал риса. Была проанализирована корреляция Пирсона между двумя группами. Он показал положительную корреляцию момента продукта Пирсона между 0,783 и 0,895 для сорных популяций риса. Эта цифра достаточно высока, что свидетельствует о достаточно прочной связи.

Если вам интересно увидеть больше примеров PPMC, вы можете найти несколько исследований на веб-сайте Openi Национального института здравоохранения, которые показывают результаты различных исследований, от визуализации кисты молочной железы до роли, которую углеводы играют в потере веса.
Вернуться к началу

Посмотрите видео, чтобы узнать, как найти PPMC вручную.

Как найти коэффициент корреляции Пирсона (вручную)

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Пример вопроса : Найдите значение коэффициента корреляции из следующей таблицы:

Субъект	Возраст х	Уровень глюкозы y
1	43	99
2	21	65
3	25	79
4	42	75
5	57	87
6	59	81

Шаг 1: Создайте диаграмму. Используйте полученные данные и добавьте еще три столбца: xy, x ² и y ² .

Тема	Возраст х	Уровень глюкозы y	ху	х 2	г 2
1	43	99
2	21	65
3	25	79
4	42	75
5	57	87
6	59	81

Шаг 2: Умножьте x и y, чтобы заполнить столбец xy. Например, строка 1 будет 43 × 9.9 = 4 257 .

Тема	Возраст х	Уровень глюкозы y	ху	х 2	г 2
1	43	99	4257
2	21	65	1365
3	25	79	1975
4	42	75	3150
5	57	87	4959
6	59	81	4779

Шаг 3: Возьмем квадрат чисел в столбце x и поместим результат в столбец x ² .

Тема	Возраст х	Уровень глюкозы y	ху	х 2	г 2
1	43	99	4257	1849
2	21	65	1365	441
3	25	79	1975	625
4	42	75	3150	1764
5	57	87	4959	3249
6	59	81	4779	3481

Шаг 4: Возьмем квадрат чисел в столбце у и поместим результат в столбец у ² .

Тема	Возраст х	Уровень глюкозы y	ху	х 2	г 2
1	43	99	4257	1849	9801
2	21	65	1365	441	4225
3	25	79	1975	625	6241
4	42	75	3150	1764	5625
5	57	87	4959	3249	7569
6	59	81	4779	3481	6561

Шаг 5: Сложите все числа в столбцах и поместите результат в конец столбца. Греческая буква сигма (Σ) — это короткий способ сказать «сумма» или суммирование.

Тема	Возраст х	Уровень глюкозы y	ху	х 2	г 2
1	43	99	4257	1849	9801
2	21	65	1365	441	4225
3	25	79	1975	625	6241
4	42	75	3150	1764	5625
5	57	87	4959	3249	7569
6	59	81	4779	3481	6561
Σ	247	486	20485	11409	40022

Шаг 6: Используйте следующую формулу коэффициента корреляции.

Ответ: 2868 / 5413,27 = 0,529809

Щелкните здесь, если вам нужны простые пошаговые инструкции по решению этой формулы.

Из нашей таблицы:

• Σx = 247
• Σy = 486
• Σху = 20 485
• Σx ² = 11 409
• Σy ² = 40 022
• n — объем выборки, в нашем случае = 6

Коэффициент корреляции =

• 6(20 485) – (247 × 486) / [√[[6(11 409) – (247 ² )] × [6(40,022) – 486 ² ]]]

= 0,5298

Диапазон коэффициента корреляции от -1 до 1. Наш результат 0,5298 или 52,98%, что означает, что переменные имеют умеренную положительную корреляцию.
Наверх.

Нравится объяснение? Прочтите «Руководство по статистике практического мошенничества», в котором есть еще сотни пошаговых объяснений, таких как это!

Если вы принимаете статистику AP, вам фактически не придется работать с формулой корреляции вручную. Вы будете использовать свой графический калькулятор. Вот как найти r на TI83.

Шаг 1: Введите данные в список и постройте точечный график, чтобы убедиться, что ваши переменные приблизительно коррелированы. Другими словами, ищите прямую линию. Не знаете, как это сделать? См.: TI 83 Диаграмма рассеяния.

Шаг 2: Нажмите кнопку STAT.

Шаг 3: Прокрутите вправо до меню CALC.

Шаг 4: Прокрутите вниз до 4:LinReg(ax+b), затем нажмите ENTER. Вывод покажет «r» в самом низу списка.

Совет : Если вы не видите r, включите диагностику, а затем повторите шаги.

Посмотрите видео:

Найдите коэффициент корреляции в Excel

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Шаг 1: Введите данные в два столбца в Excel. Например, введите данные «x» в столбец A и данные «y» в столбец B.

Шаг 2: Выберите любую пустую ячейку.

Шаг 3: Нажмите функциональную кнопку на ленте.

Шаг 4: Введите «корреляция» в поле «Поиск функции».

Шаг 5: Нажмите «Перейти». КОРРЕЛ будет выделен.

Шаг 6: Нажмите «ОК».

Шаг 7: Введите местоположение ваших данных в поля «Массив 1» и «Массив 2» . В этом примере введите «A2:A10» в поле «Массив 1», а затем введите «B2:B10» в поле «Массив 2».

Шаг 8: Нажмите «ОК». Результат появится в ячейке, выбранной на шаге 2. Для этого конкретного набора данных коэффициент корреляции (r) равен -0,1316.

Предупреждение. Результаты этого теста могут ввести в заблуждение, если только вы не построили точечный график, чтобы убедиться, что ваши данные примерно соответствуют прямой линии. Коэффициент корреляции в Excel 2007 будет , всегда будет возвращать значение, даже если ваши данные отличаются от линейных (т. е. данные соответствуют экспоненциальной модели).

Вот и все!

Подпишитесь на наш канал Youtube, чтобы получать дополнительные советы и статистику по Excel.
Наверх.

Посмотрите видео для шагов:

Коэффициент корреляции Пирсона в SPSS

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Шаг 1: Нажмите «Анализ», затем нажмите «Корреляция», затем нажмите «Двумерный анализ». Появится окно двумерных корреляций.

Шаг 2: Щелкните одну из переменных в левом всплывающем окне Двумерные корреляции. Затем щелкните центральную стрелку, чтобы переместить переменную в окно «Переменные:». Повторите это для второй переменной.

Шаг 3: Установите флажок «Pearson» , если он еще не установлен. Затем щелкните переключатель «односторонний» или «двусторонний» тест. Если вы не уверены, является ли ваш тест односторонним или двусторонним, см. раздел: Это односторонний или двусторонний тест?

Шаг 4: Нажмите «ОК» и прочтите результаты. Каждое поле в выходных данных показывает корреляцию между двумя переменными. Например, PPMC для числа старших братьев и сестер и среднего балла составляет -0,098, что означает практически отсутствие корреляции. Вы можете найти эту информацию в двух местах в выходных данных. Почему? Эти перекрестные ссылки на столбцы и строки очень полезны, когда вы сравниваете PPMC для десятков переменных.

Совет № 1: Всегда полезно сделать диаграмму рассеяния SPSS для набора данных до выполнения этого теста. Это потому, что SPSS будет всегда давать вам какой-то ответ и будет предполагать, что данные линейно связаны. Если у вас есть данные, которые могут лучше подходить для другой корреляции (например, экспоненциально связанные данные), SPSS по-прежнему будет запускать для вас Pearson, и вы можете получить вводящие в заблуждение результаты.
Совет № 2 : Нажмите кнопку «Параметры» в окне «Двумерные корреляции», если вы хотите включить описательную статистику, такую ​​как среднее значение и стандартное отклонение.
Наверх.

Посмотрите это видео о том, как рассчитать коэффициент корреляции в Minitab :

Как найти коэффициент корреляции Пирсона в Minitab

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Коэффициент корреляции Minitab вернет значение r от -1 до 1.

Пример вопроса : Найдите коэффициент корреляции Minitab на основе возраста и уровня глюкозы из следующей таблицы из преддиабетического исследования 6 участников. :

Тема	Возраст х	Уровень глюкозы y
1	43	99
2	21	65
3	25	79
4	42	75
5	57	87
6	59	81

Шаг 1: Введите данные в рабочий лист Minitab . Я ввел этот образец данных в три столбца.
Данные введены в три столбца рабочего листа Minitab.

Шаг 2: Нажмите «Статистика», затем нажмите «Основная статистика», а затем нажмите «Корреляция».
«Корреляция» выбирается в меню «Статистика > Базовая статистика».

Шаг 3: Щелкните имя переменной в левом окне, а затем нажмите кнопку «Выбрать» , чтобы переместить имя переменной в поле «Переменная». Для этого примера вопроса нажмите «Возраст», затем нажмите «Выбрать», затем нажмите «Уровень глюкозы», затем нажмите «Выбрать», чтобы перенести обе переменные в окно «Переменная».

Шаг 4: (Необязательно) Установите флажок «P-значение» , если вы хотите отобразить P-значение для r.

Шаг 5: Нажмите «ОК». Коэффициент корреляции Minitab будет отображаться в окне сеанса. Если вы не видите результатов, нажмите «Окно», а затем нажмите «Плитка». Должно появиться окно сеанса.
Результаты корреляции Minitab.
Для этого набора данных:

• Значение r: 0,530
• P-значение: 0,280

Вот оно!

Совет: Дайте своим столбцам понятные имена (в первой строке столбца, прямо под C1, C2 и т. д.). Таким образом, когда дело доходит до выбора имен переменных на шаге 3, вы легко увидите, что вы пытаетесь выбрать. Это становится особенно важным, когда в таблице данных десятки столбцов переменных!

Коэффициент корреляции Пирсона — это коэффициент линейной корреляции, который возвращает значение от -1 до +1. -1 означает, что существует сильная отрицательная корреляция, а +1 означает, что существует сильная положительная корреляция. 0 означает отсутствие корреляции (это также называется 9).0003 нулевая корреляция ).

Поначалу это может быть немного сложно понять (кто любит иметь дело с отрицательными числами?). Департамент политологии Университета Куиннипиак опубликовал этот полезный список значений коэффициентов корреляции Пирсона. Они отмечают, что это « грубых оценок » для интерпретации сил корреляции с использованием корреляции Пирсона:

r значение =
+0,70 или выше	Очень сильная положительная связь
+,40 до +,69	Сильные позитивные отношения
+,30 до +,39	Умеренно положительные отношения
+,20 до +,29	слабая положительная связь
+,01 до +,19	Связь отсутствует или незначительна
0	Нет связи [нулевая корреляция]
от -.01 до -.19	Связь отсутствует или незначительна
от -.20 до -.29	слабая отрицательная связь
от -.30 до -.39	Умеренное негативное отношение
от -.40 до -.69	Сильные отрицательные отношения
-0,70 или выше	Очень сильная отрицательная связь

Может быть полезно увидеть графически, как выглядят эти корреляции:
Графики, показывающие корреляцию -1 (отрицательная корреляция), 0 и +1 (положительная корреляция)

Изображения показывают, что сильная отрицательная корреляция означает, что график имеет нисходящий наклон слева направо: по мере увеличения значений x значения y уменьшаются. Сильная положительная корреляция означает, что график имеет восходящий наклон слева направо: по мере увеличения значений x значения y становятся больше.
Наверх.

V-корреляция Крамера аналогична коэффициенту корреляции Пирсона. В то время как корреляция Пирсона используется для проверки прочности линейных отношений, V Крамера используется для расчета корреляции в таблицах с более чем 2 x 2 столбцами и строками. V-корреляция Крамера варьируется от 0 до 1. Значение, близкое к 0, означает, что связь между переменными очень мала. V Крамера, близкий к 1, указывает на очень сильную связь.

Крамер V
.25 или выше	Очень крепкие отношения
от 0,15 до 0,25	Крепкие отношения
от 0,11 до 0,15	Умеренные отношения
от 0,06 до 0,10	слабые отношения
от 0,01 до 0,05	Связь отсутствует или незначительна

Наверх.

Коэффициент корреляции дает представление о том, насколько хорошо данные соответствуют линии или кривой. Пирсон не был изобретателем термина «корреляция», но его использование стало одним из самых популярных способов измерения корреляции.

Фрэнсис Гальтон (который также принимал участие в разработке межквартильного диапазона) был первым, кто измерил корреляцию, первоначально названную «корреляцией», что на самом деле имеет смысл, учитывая, что вы изучаете взаимосвязь между парой различных переменных. . В «Соотношениях и их измерении» он сказал

: «Статус родственников — взаимосвязанные переменные; таким образом, рост отца соответствует росту взрослого сына и т. д.; но показатель корреляции… в разных случаях различен».

Стоит отметить, однако, что Гальтон упомянул в своей статье, что он заимствовал термин из биологии, где использовалось «Корреляция и корреляция структуры», но до времени его статьи он не был должным образом определен.

В 1892 году британский статистик Фрэнсис Исидро Эджворт опубликовал статью под названием «Коррелированные средние значения», Philosophical Magazine, 5th Series, 34, 190-204, где он использовал термин «коэффициент корреляции». Только в 1896 году британский математик Карл Пирсон использовал «коэффициент корреляции» в двух статьях: «Вклад в математическую теорию эволюции» и «Математический вклад в теорию эволюции». III. Регрессия, наследственность и панмиксия. Это была вторая статья, в которой была представлена ​​формула корреляции Пирсона «произведение-момент» для оценки корреляции.
Уравнение корреляции продукта и момента Пирсона.
Наверх.

Если вы умеете читать таблицу — вы можете проверить коэффициент корреляции. Обратите внимание, что корреляции следует рассчитывать только для всего диапазона данных. Если ограничить диапазон, r будут ослаблены.

Пример задачи : проверить значимость коэффициента корреляции r = 0,565, используя критические значения для таблицы PPMC. Тест при α = 0,01 для размера выборки 9.

Шаг 1: Вычтите два из размера выборки, чтобы получить df, степени свободы .
9 – 7 = 2

Шаг 2: Найдите значения в таблице PPMC. При df = 7 и α = 0,01 табличное значение = 0,798

Шаг 3: Нарисуйте график, чтобы вам было легче увидеть взаимосвязь.

r = 0,565 не попадает в область отклонения (выше 0,798), поэтому недостаточно доказательств, чтобы утверждать, что в данных существует сильная линейная зависимость.

Тригонометрия редко используется в статистике (например, вам никогда не понадобится находить производную тангенса (х)!), но связь между корреляцией и косинусом является исключением. Корреляцию можно выразить через углы:

• Положительная корреляция = острый угол <45°,
• Отрицательная корреляция = тупой угол >45°,
• Некоррелированный = ортогональный (прямой угол).

Более конкретно, корреляция — это косинус угла между двумя векторами, определяемый следующим образом (Knill, 2011):

Если X, Y — две случайные величины с нулевым средним значением, то ковариация Cov[XY] = E[X · Y] — это скалярное произведение X и Y. Стандартное отклонение X — это длина X.

Ссылки

Эктон, Ф. С. Анализ прямолинейных данных. Нью-Йорк: Довер, 1966.
Эдвардс, А. Л. «Коэффициент корреляции». Ч. 4 в Введение в линейную регрессию и корреляцию. Сан-Франциско, Калифорния: WH Freeman, стр. 33–46, 1976.
Гоник, Л. и Смит, В. «Регрессия». Ч. 11 в The Cartoon Guide to Statistics. Нью-Йорк: Harper Perennial, стр. 187–210, 19.93.
Книл, О. (2011). Лекция 12: Корреляция. Получено 16 апреля 2021 г. с: http://people.math.harvard.edu/~knill/teaching/math29b_2011/handouts/lecture12.pdf

Другие подобные формулы, которые могут вам встретиться, включают корреляцию ( клик для статьи ) :

• Конкордантность Коэффициент корреляции.
• Внутриклассовая корреляция.
• Тау Кендалла.
• Коэффициент корреляции Мэтьюза
• Моран I.
• Частичная корреляция.
• Коэффициент Фи.
• Бисериальная корреляция точек.
• Полихорическая корреляция.
• Корреляция ранга копейщика.
• Тетрахорная корреляция.
• Корреляция нулевого порядка.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Коэффициент корреляции: простое определение, формула, простые шаги» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/correlation-coefficient-formula/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Коэффициент корреляции (r)

Коэффициент корреляции выборки (r) является мерой близости точек на диаграмме рассеяния к линии линейной регрессии, основанной на этих точках, как в приведенном выше примере для накопленных сбережений со временем. Возможные значения коэффициента корреляции находятся в диапазоне от -1 до +1, где -1 указывает на совершенно линейную отрицательную, т. е. обратную корреляцию (наклон вниз), а +1 указывает на совершенно линейную положительную корреляцию (наклон вверх).

Коэффициент корреляции, близкий к 0, предполагает небольшую корреляцию, если она вообще есть. Диаграмма рассеяния предполагает, что измерения IQ не меняются с возрастом, т. е. нет никаких доказательств того, что IQ связан с возрастом.

Расчет коэффициента корреляции

Приведенные ниже уравнения показывают расчеты для вычисления «r». Однако вам не нужно запоминать эти уравнения. Мы будем использовать R для выполнения этих вычислений за нас. Тем не менее, уравнения дают представление о том, как вычисляется «r».

где Cov(X,Y) — ковариация, т. е. насколько далеко каждая наблюдаемая пара (X,Y) от среднего значения X и среднего значения Y одновременно, и и s _x ² и s _y ² — выборочные дисперсии для X и Y.

. Cov (X,Y) вычисляется как:

Вам не нужно запоминать или использовать эти уравнения для ручных вычислений. Вместо этого мы будем использовать R для расчета коэффициентов корреляции. Например, мы могли бы использовать следующую команду для вычисления коэффициента корреляции для AGE и TOTCHOL в подмножестве Framingham Heart Study следующим образом:

> cor(ВОЗРАСТ,ТОЧОЛ)
[1] 0,23

Описание коэффициентов корреляции

В таблице ниже приведены некоторые рекомендации по описанию силы коэффициентов корреляции, но это всего лишь рекомендации для описания. Кроме того, имейте в виду, что даже слабые корреляции могут быть статистически значимыми, как вы скоро узнаете.

Коэффициент корреляции (r)	Описание (Приблизительные указания)
+1,0	Совершенно положительный + ассоциация
+0,8 до 1,0	Очень сильная + ассоциация
+0,6 до 0,8	Сильный + ассоциация
+0,4 до 0,6	Умеренный + ассоциация
+0,2 до 0,4	Слабый + ассоциация
от 0,0 до +0,2	Очень слабая + или нет ассоциации
от 0,0 до -0,2	Очень слабый — или нет ассоциации
от -0,2 до – 0,4	Слабый — ассоциация
от -0,4 до -0,6	Умеренный — ассоциация
от -0,6 до -0,8	Сильный — ассоциация
от -0,8 до -1,0	Очень сильная — ассоциация
-1,0	Идеальная отрицательная ассоциация

 Четыре изображения ниже дают представление о том, как некоторые коэффициенты корреляции могут выглядеть на точечной диаграмме.

Диаграмма рассеяния ниже иллюстрирует взаимосвязь между систолическим артериальным давлением и возрастом у большого числа субъектов. Это свидетельствует о слабой (r=0,36), но статистически значимой (p<0,0001) положительной связи между возрастом и систолическим артериальным давлением. Разброса довольно много, но наблюдений много, и есть четкий линейный тренд.

Как корреляция может быть слабой, но все же статистически значимой? Учтите, что большинство исходов имеют несколько детерминант. Например, индекс массы тела (ИМТ) определяется несколькими факторами («воздействием»), такими как возраст, рост, пол, потребление калорий, физические упражнения, генетические факторы и т. д. Таким образом, рост является лишь одним из определяющих факторов и является сопутствующим фактором. , но не единственный детерминант ИМТ. В результате рост может быть важным определяющим фактором, т. е. он может быть в значительной степени связан с ИМТ, но быть лишь частичным фактором. Если это так, то даже слабая корреляция может быть статистически значимой, если размер выборки достаточно велик. По сути, обнаружение слабой корреляции, которая является статистически значимой, предполагает, что это конкретное воздействие оказывает влияние на переменную результата, но есть и другие важные детерминанты.

Остерегайтесь нелинейных взаимосвязей

Многие взаимосвязи между измеряемыми переменными достаточно линейны, но другие нет. Например, на изображении ниже показано, что риск смерти не имеет линейной корреляции с индексом массы тела. Вместо этого этот тип отношений часто описывается как «U-образный» или «J-образный», поскольку значение Y-переменной сначала уменьшается с увеличением X, но при дальнейшем увеличении X Y-переменная существенно увеличивается. . Связь между потреблением алкоголя и смертностью также имеет «J-образную форму».

Источник: Calle EE, et al.: N Engl J Med 1999; 341:1097-1105

Простой способ оценить, является ли зависимость достаточно линейной, — это изучить график рассеяния. Чтобы проиллюстрировать это, посмотрите на приведенный ниже график рассеяния роста (в дюймах) и массы тела (в фунтах) с использованием данных Weymouth Health Survey в 2004 году. Для создания графика рассеяния и вычисления коэффициента корреляции использовался R.

wey<-na.omit(Weymouth_Adult_Part)
прикрепить(вей)
участок (hgt_inch, вес)
cor(hgt_inch,вес)
[1] 0,5653241

Существует довольно большой разброс, и большое количество точек данных затрудняет полную оценку корреляции, но тенденция достаточно линейна. Коэффициент корреляции +0,56.

Остерегайтесь аномалий

Обратите внимание, что на графике выше есть два человека с видимым ростом 88 и 99 дюймов. Рост 88 дюймов (7 футов 3 дюйма) правдоподобен, но маловероятен, а рост 99 дюймов — это, безусловно, ошибка кодирования. Очевидные ошибки кодирования следует исключить из анализа, поскольку они могут оказать чрезмерное влияние на результаты. Всегда полезно просмотреть необработанные данные, чтобы выявить любые грубые ошибки в кодировании.

После исключения двух выбросов график выглядит следующим образом:

вернуться наверх | предыдущая страница | следующая страница

Коэффициент корреляции | Типы, формулы и примеры

A коэффициент корреляции — это число от -1 до 1, которое говорит вам о силе и направлении связи между переменными.

Другими словами, он отражает, насколько похожи измерения двух или более переменных в наборе данных.

Значение коэффициента корреляции	Тип корреляции	Значение
1	Идеальная положительная корреляция	При изменении одной переменной другие переменные изменяются в том же направлении.
0	Нулевая корреляция	Между переменными нет связи.
-1	Идеальная отрицательная корреляция	При изменении одной переменной другие переменные изменяются в противоположном направлении.

Содержание

1. О чем говорит коэффициент корреляции?
2. Использование коэффициента корреляции
3. Интерпретация коэффициента корреляции
4. Визуализация линейных корреляций
5. Типы коэффициентов корреляции
6. Rho Пирсона
7. Rho Спирмена
8. Другие коэффициенты
9. Часто задаваемые вопросы о коэффициентах корреляции

О чем говорит коэффициент корреляции?

Коэффициенты корреляции суммируют данные и помогают сравнивать результаты между исследованиями.

Обобщение данных

Коэффициент корреляции является описательной статистикой . Это означает, что он суммирует выборочные данные, не позволяя вам делать какие-либо выводы о населении. Коэффициент корреляции является двумерной статистикой, когда он суммирует отношения между двумя переменными, и многомерной статистикой, когда у вас более двух переменных.

Если ваш коэффициент корреляции основан на выборочных данных, вам понадобится выводная статистика, если вы хотите обобщить свои результаты на генеральную совокупность. Вы можете использовать тест F или тест t , чтобы вычислить статистику теста, которая говорит вам о статистической значимости вашего вывода.

Сравнение исследований

Коэффициент корреляции также является мерой размера эффекта , которая говорит вам о практической значимости результата.

Коэффициенты корреляции не содержат единиц измерения, что позволяет напрямую сравнивать коэффициенты между исследованиями.

Использование коэффициента корреляции

В корреляционном исследовании вы изучаете, связаны ли изменения одной переменной с изменениями других переменных.

Пример корреляционного исследования. Вы изучаете, связаны ли стандартизированные баллы в средней школе с академическими оценками в колледже. Вы предсказываете, что существует положительная корреляция: более высокие баллы SAT связаны с более высокими средними баллами колледжа, а более низкие баллы SAT связаны с более низкими средними баллами колледжей.

После сбора данных вы можете визуализировать свои данные с помощью диаграммы рассеяния, отложив одну переменную по оси x, а другую по оси y. Неважно, какую переменную вы поместите на любую из осей.

Визуально осмотрите график на наличие шаблона и решите, есть ли линейный или нелинейный шаблон между переменными. Линейный шаблон означает, что вы можете разместить прямую линию наилучшего соответствия между точками данных, в то время как нелинейный или криволинейный шаблон может принимать всевозможные формы, такие как U-образная форма или линия с кривой.

Пример визуального осмотраВы собираете выборку из 5000 выпускников колледжей и опрашиваете их на предмет их результатов SAT в средней школе и среднего балла колледжа. Вы визуализируете данные на диаграмме рассеяния, чтобы проверить наличие линейного шаблона:

Существует множество различных коэффициентов корреляции, которые можно рассчитать. После удаления любых выбросов выберите подходящий коэффициент корреляции, основанный на общей форме диаграммы рассеяния. Затем вы можете выполнить корреляционный анализ, чтобы найти коэффициент корреляции для ваших данных.

Вы вычисляете коэффициент корреляции, чтобы обобщить взаимосвязь между переменными, не делая никаких выводов о причинно-следственной связи.

Пример корреляционного анализа. Вы проверяете, соответствуют ли данные всем предположениям теста корреляции Пирсона.

Обе переменные являются количественными и нормально распределены без выбросов, поэтому вы рассчитываете коэффициент корреляции Пирсона r .

Коэффициент корреляции сильный, равный 0,58.

Предотвратите плагиат, запустите бесплатную проверку.

Попробуй бесплатно

Интерпретация коэффициента корреляции

Значение коэффициента корреляции всегда находится в диапазоне от 1 до -1, и вы рассматриваете его как общий показатель силы связи между переменными.

Знак коэффициента отражает, изменяются ли переменные в одном или противоположном направлении: положительное значение означает, что переменные изменяются вместе в одном и том же направлении, а отрицательное значение означает, что они изменяются вместе в противоположном направлении.

Абсолютное значение числа равно числу без знака. Абсолютное значение коэффициента корреляции говорит вам о величине корреляции: чем больше абсолютное значение, тем сильнее корреляция.

Существует множество различных рекомендаций по интерпретации коэффициента корреляции, поскольку результаты могут сильно различаться в разных областях исследования. Вы можете использовать приведенную ниже таблицу в качестве общего руководства для интерпретации силы корреляции по значению коэффициента корреляции.

Хотя это руководство в крайнем случае полезно, гораздо важнее учитывать контекст и цель вашего исследования при формировании выводов. Например, если в большинстве исследований в вашей области коэффициент корреляции приближается к 0,9, коэффициент корреляции 0,58 может быть низким в этом контексте.

Коэффициент корреляции	Сила корреляции	Тип корреляции
от -. 7 до -1	Очень сильный	Отрицательный
от -.5 до -.7	Сильный	Отрицательный
от -.3 до -.5	Умеренный	Отрицательный
от 0 до -.3	Слабый	Отрицательный
0	Нет	Ноль
от 0 до 0,3	Слабый	Положительный
от 0,3 до 0,5	Умеренный	Положительный
от 0,5 до 0,7	Сильный	Положительный
от 0,7 до 1	Очень сильный	Положительный

Визуализация линейных корреляций

Коэффициент корреляции показывает, насколько точно ваши данные укладываются в линию. Если у вас есть линейная зависимость, вы нарисуете прямую линию наилучшего соответствия, которая учитывает все ваши точки данных на точечной диаграмме.

Чем ближе ваши точки к этой линии, тем выше абсолютное значение коэффициента корреляции и тем сильнее ваша линейная корреляция.

Если все точки точно лежат на этой линии, у вас есть идеальная корреляция.

Если все точки близки к этой линии, абсолютное значение вашего коэффициента корреляции будет максимум .

Если эти точки разбросаны далеко от этой линии, абсолютное значение вашего коэффициента корреляции будет низким .

Обратите внимание, что крутизна или наклон линии не связаны со значением коэффициента корреляции. Коэффициент корреляции не поможет вам предсказать, насколько изменится одна переменная в зависимости от заданного изменения другой, потому что два набора данных с одинаковым значением коэффициента корреляции могут иметь линии с очень разными наклонами.

Типы коэффициентов корреляции

Вы можете выбрать один из множества различных коэффициентов корреляции на основе линейности отношения, уровня измерения ваших переменных и распределения ваших данных.

Для обеспечения высокой статистической мощности и точности лучше всего использовать коэффициент корреляции, наиболее подходящий для ваших данных.

Наиболее часто используемым коэффициентом корреляции является коэффициент Пирсона r, поскольку он позволяет делать надежные выводы. Он параметрический и измеряет линейные отношения. Но если ваши данные не соответствуют всем предположениям для этого теста, вам нужно вместо этого использовать непараметрический тест.

Непараметрические тесты коэффициентов ранговой корреляции суммируют нелинейные отношения между переменными. Ро Спирмена и тау Кендалла имеют одинаковые условия для использования, но тау Кендалла обычно предпочтительнее для небольших выборок, тогда как ро Спирмена используется более широко.

В таблице ниже представлены часто используемые коэффициенты корреляции, и в этой статье мы подробно рассмотрим два наиболее широко используемых коэффициента.

Коэффициент корреляции	Тип отношения	Уровни измерения	Распространение данных
Пирсонс р	Линейный	Две количественные переменные (интервал или отношение)	Нормальное распределение
Копьеносец	Нелинейный	Две порядковые, интервальные или относительные переменные	Любой дистрибутив
Двухрядная точка	Линейный	Одна дихотомическая (бинарная) переменная и одна количественная (интервальная или отношение) переменная	Нормальное распределение
V Крамера (φ Крамера)	Нелинейный	Две номинальные переменные	Любой дистрибутив
Тау Кендалла	Нелинейный	Две порядковые, интервальные или относительные переменные	Любой дистрибутив

Pearson’s r

Коэффициент корреляции продукта и момента Пирсона, также известный как r Пирсона, описывает линейную зависимость между двумя количественными переменными.

Это предположения, которым должны соответствовать ваши данные, если вы хотите использовать Pearson r:

• Обе переменные находятся на уровне измерения интервала или отношения
• Данные обеих переменных подчиняются нормальному распределению
• В ваших данных нет выбросов
• Ваши данные взяты из случайной или репрезентативной выборки
• Вы ожидаете линейную зависимость между двумя переменными

Критерий Пирсона r является параметрическим, поэтому он имеет большую мощность. Но это не очень хорошая мера корреляции, если ваши переменные имеют нелинейную связь или если ваши данные имеют выбросы, асимметричные распределения или получены из категориальных переменных. Если какое-либо из этих предположений нарушается, следует рассмотреть меру ранговой корреляции.

Формула для r Пирсона сложна, но большинство компьютерных программ могут быстро вычислить коэффициент корреляции из ваших данных. В более простой форме формула делит ковариацию между переменными на произведение их стандартных отклонений.

Формула	Пояснение
	= сила корреляции между переменными x и y = размер выборки = сумма следующего… = каждое значение x-переменной = каждое значение переменной y = произведение каждого показателя x-переменной и соответствующего показателя y-переменной

Выборка Пирсона против формулы коэффициента корреляции генеральной совокупности

При использовании формулы коэффициента корреляции Пирсона необходимо учитывать, имеете ли вы дело с данными из выборки или всего населения.

Формулы выборки и генеральной совокупности отличаются символами и входными данными. Коэффициент корреляции выборки называется r , а коэффициент корреляции генеральной совокупности называется ро (греческая буква ρ).

Коэффициент выборочной корреляции использует выборочную ковариацию между переменными и их выборочными стандартными отклонениями.

Пример формулы коэффициента корреляции	Пояснение
	r xy = сила корреляции между переменными x и y cov ( x , y ) = ковариация x и y с x = стандартное отклонение выборки x s y = выборочное стандартное отклонение y

Коэффициент корреляции совокупности использует ковариацию совокупности между переменными и их стандартными отклонениями совокупности.

Формула коэффициента корреляции населения	Пояснение
	ρ XY = сила корреляции между переменными X и Y cov ( X , Y ) = ковариация X и Y σ X = стандартное отклонение совокупности X σ Y = стандартное отклонение совокупности Y

Ро Спирмена

Ро Спирмена, или ранговый коэффициент корреляции Спирмена, является наиболее распространенной альтернативой Пирсоновскому r . Это коэффициент ранговой корреляции, поскольку он использует ранжирование данных каждой переменной (например, от низшего к высшему), а не сами необработанные данные.

Вы должны использовать ро Спирмена, когда ваши данные не соответствуют предположениям Пирсона r . Это происходит, когда хотя бы одна из ваших переменных находится на порядковом уровне измерения или когда данные одной или обеих переменных не подчиняются нормальному распределению.

В то время как коэффициент корреляции Пирсона измеряет линейность отношений, коэффициент корреляции Спирмена измеряет монотонность отношений.

При линейной зависимости каждая переменная изменяется в одном направлении с одинаковой скоростью во всем диапазоне данных. В монотонной зависимости каждая переменная также всегда изменяется только в одном направлении, но не обязательно с одинаковой скоростью.

• Положительная монотонность: при увеличении одной переменной увеличивается и другая.
• Отрицательная монотонность: когда одна переменная увеличивается, другая уменьшается.

Монотонные отношения имеют меньше ограничений, чем линейные отношения.

 

 

Формула коэффициента ранговой корреляции Спирмена

Символы для ро Спирмена: ρ для коэффициента генеральной совокупности и r _s для коэффициента выборки. Формула вычисляет коэффициент корреляции Пирсона r между ранжированием переменных данных.

Чтобы использовать эту формулу, вы сначала ранжируете данные каждой переменной отдельно от низкого к высокому: каждая точка данных получает ранг от первого, второго или третьего и т. д.

Затем вы найдете различия (d _i ) между рангами ваших переменных для каждой пары данных и возьмете их в качестве основных входных данных для формулы.

Формула коэффициента ранговой корреляции Спирмена	Пояснение
	r s = сила ранговой корреляции между переменными d i = разница между рангом переменной x и рангом переменной y для каждой пары данных ∑ d 2 i = сумма квадратов разностей между рангами переменных x и y n = объем выборки

Если коэффициент корреляции равен 1, все рейтинги каждой переменной совпадают для каждой пары данных. Если у вас есть коэффициент корреляции -1, ранжирование одной переменной прямо противоположно ранжированию другой переменной. Коэффициент корреляции, близкий к нулю, означает, что нет монотонной связи между рейтингами переменных.

Прочие коэффициенты

Коэффициент корреляции связан с двумя другими коэффициентами, и они дают вам больше информации о взаимосвязи между переменными.

Коэффициент детерминации

Когда вы возводите коэффициент корреляции в квадрат, вы получаете корреляцию детерминации ( r ² ). Это доля общей дисперсии между переменными. Коэффициент детерминации всегда находится в диапазоне от 0 до 1 и часто выражается в процентах.

Коэффициент детерминации	Пояснение
р 2	Коэффициент корреляции, умноженный сам на себя

Коэффициент детерминации используется в регрессионных моделях для измерения того, какая часть дисперсии одной переменной объясняется дисперсией другой переменной.

Регрессионный анализ помогает найти уравнение для линии наилучшего соответствия, и его можно использовать для прогнозирования значения одной переменной при заданном значении другой переменной.

Высокая r ² означает, что большое количество изменчивости одной переменной определяется ее отношением к другой переменной. Низкое значение r ² означает, что лишь небольшая часть изменчивости одной переменной объясняется ее связью с другой переменной; отношения с другими переменными с большей вероятностью объясняют дисперсию переменной.

Коэффициент корреляции часто может завышать взаимосвязь между переменными, особенно в небольших выборках, поэтому коэффициент детерминации часто является лучшим индикатором взаимосвязи.

Коэффициент отчуждения

Если из единицы (единицы) отнять коэффициент детерминации, то получится коэффициент отчуждения. Это доля общей дисперсии, не разделенной между переменными, необъяснимой дисперсии между переменными.

Коэффициент отчуждения	Пояснение
1 – р 2	Один минус коэффициент детерминации

Высокий коэффициент отчуждения указывает на то, что две переменные имеют очень мало общего. Низкий коэффициент отчуждения означает, что большое количество дисперсии объясняется взаимосвязью между переменными.

Часто задаваемые вопросы о коэффициентах корреляции

Что такое корреляция?

Корреляция отражает силу и/или направление связи между двумя или более переменными.

• Положительная корреляция означает, что обе переменные изменяются в одном направлении.
• Отрицательная корреляция означает, что переменные изменяются в противоположных направлениях.
• нулевая корреляция означает отсутствие связи между переменными.

О чем говорят знак и значение коэффициента корреляции?

Коэффициенты корреляции всегда находятся в диапазоне от -1 до 1.

Знак коэффициента говорит вам о направлении зависимости: положительное значение означает, что переменные изменяются вместе в одном и том же направлении, а отрицательное значение означает, что они изменяются вместе в противоположных направлениях. .

Абсолютное значение числа равно числу без знака. Абсолютное значение коэффициента корреляции говорит вам о величине корреляции: чем больше абсолютное значение, тем сильнее корреляция.

No related posts.