Площадь и периметр прямоугольника 4 класс формула: Как найти периметр прямоугольника, формула ⬅️

Прямоугольник. Площадь и периметр прямоугольника

Урок по  теме: «Прямоугольник. Площадь и периметр прямоугольника»

 

Цели урока:
-закрепить понятие прямоугольник , квадрат и их  элементов
-учиться  находить периметр и площадь прямоугольника и квадрата
-учиться применять математические формулы периметра и площади  в повседневной жизни

Критерии успеха:
-Я знаю формулы периметра и площади фигур.
-Я умею  находить  периметр и площадь прямоугольника и квадрата;
-Я могу  различать формулы для нахождения периметра и площади прямоугольника;
-Я умею  синтезировать полученные знания  для создания новых формул

.      

                                                      Ход урока

 

 

1 Организационный момент

Игра “Танграм”.

Каждому из вас пришли письма, в которых разные фигурки. Используя эти фигурки, вы должны собрать кошечку.

А у вас дома есть кошки? Как их зовут? Расскажите  интересную историю про свою кошку.

 

 

2. Актуализация знаний.

 

На доске записаны формулы:1) s = ab

                                                  2) p = 4a

                                                  3) s = vt

                                                  4) p = (a + b)?2

                                                  5) s = a2

                                                  6) с=аn

 

учитель: «Ребята, что записано на доске?»

учащиеся: «Формулы»

учитель: «Что мы будем изучать сегодня на уроке?»

учащиеся: «Формулы»

учитель: «Запишем тему урока: «Формулы»

Задание классу (устно): найдите дружную пару: «Название формулы – Формула»

                                                                                        

1) площадь прямоугольника

                                                                                         2) площадь квадрата

                                                                                         3) формула пути

                                                                                         4) периметр квадрата

                                                                                          5) периметр прямоугольника

                                                                                         6) стоимости

Ребята давайте дадим название каждой формуле. Учащиеся подписывают  соответствующее название рядом с формулой.

 

2. Объяснение нового материала.

 

Учитель показывает фигуру. ( прямоугольник и квадрат)

1. Какая это фигура. Что вы о ней знаете.
2. Какие величины можно найти у данной фигуры.
3. По каким формулам.
4. Где и как можно использовать площадь и периметр прямоугольника и квадрата в жизни.

 

3. Закрепление нового материала.

1) работа в парах: решение задач по учебнику при помощи карточек   инструкции

Вычислите по формуле площадь и периметр квадрата со стороной а см, если:

1) а = 7 см;

 2) а = 13 см;

 

Вычислите по формуле площадь и периметр пря­моугольника со сторонами, равными х см и у см, если:

1)           х = 5,3 см; у = 3,4 см;

2)           х = 11,6 см; у = 14,1 см.

 

Тренинг  « Землетрясение»

 

2)работа в группах:  решение задач по карточкам

1.

Площадь поля прямоугольной формы 116 га, а ширина – 800м. Найдите длину   этого поля.

   2.Найдите площадь земельного участка, если его ширина 800 м, а длина 900 м. Результат выразите в га.

1. Площадь садового участка прямоугольной формы равна 6а. Длина участка 30 м. Чему равна ширина участка?

    2.  Найдите площадь земельного участка, если его ширина 800 м, а длина 900 м. Результат выразите в га.

4 .Мини- тест .

1)Выбрать формулу для нахождения площади прямоугольника

А) а+в     Б) (а+в)*2    В) а*в         С) а(а+в)

2) Выбрать формулу для нахождения периметра квадрата

           А) а              Б) 4а            В) а+в        С)а*в

3)Чему равна площадь прямоугольники с измерениями 5,1 и 3,5

  А) 8,6 см             Б) 17,85 см2            В) 8,6 см2        С)17,85 см

4)Чему равен периметр прямоугольника с измерениями 10,4 и 1,8

  А) 24,4см2             Б) 18,72 см2            В) 24,4 см        С)18,72 см

5)  Чему равен периметр квадрата с измерениями   0,5

  А) 0,25 см             Б) 2 см2            В) 0,25 см2        С)2 см

Учащиеся проводят взаимопроверку своих ответов  и оценивают выполненную работу.

 

5. Рефлексия

— Закончите предложения:

Чему я научился на уроке………………..

Что мне этот урок дал для жизни……………

Привлек меня тем………..

Показался интересным………..

Заставил задуматься…………

 

 6. Дом.задание: Разноуровневое  домашнее задание:

1.  Найти  площадь пола  своей  комнаты, выразить ее в м?, дм?, см?;

2.Дома вам необходимо произвести расчёт расходных материалов для покрытия пола линолеумом и потолка потолочной плиткой.

 

 

Просмотр содержимого документа
«Прямоугольник. Площадь и периметр прямоугольника »

Урок по теме: «Прямоугольник. Площадь и периметр прямоугольника»

Цели урока:
-закрепить понятие прямоугольник , квадрат и их элементов
-учиться находить периметр и площадь прямоугольника и квадрата
-учиться применять математические формулы периметра и площади в повседневной жизни

Критерии успеха:
-Я знаю формулы периметра и площади фигур.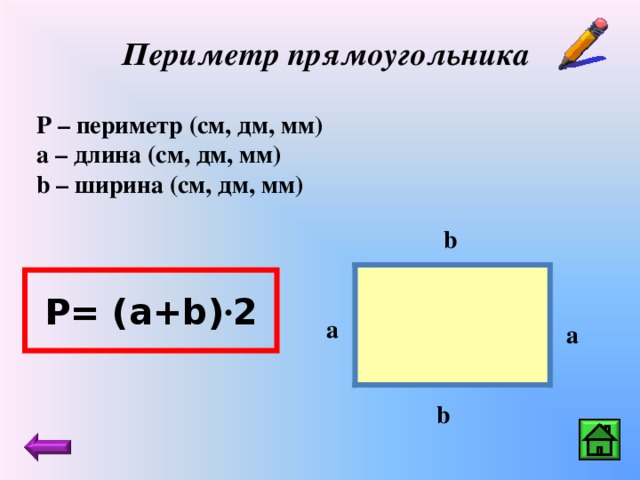
-Я умею находить периметр и площадь прямоугольника и квадрата;
-Я могу различать формулы для нахождения периметра и площади прямоугольника;
-Я умею синтезировать полученные знания для создания новых формул

.

Ход урока

1 Организационный момент Игра “Танграм”. Каждому из вас пришли письма, в которых разные фигурки. Используя эти фигурки, вы должны собрать кошечку. А у вас дома есть кошки? Как их зовут? Расскажите интересную историю про свою кошку.

2. Актуализация знаний.

На доске записаны формулы:1) s = ab

2) p = 4a

3) s = vt

4) p = (a + b)∙2

5) s = a²

6) с=аn

учитель: «Ребята, что записано на доске?»

учащиеся: «Формулы»

учитель: «Что мы будем изучать сегодня на уроке?»

учащиеся: «Формулы»

учитель: «Запишем тему урока: «Формулы»

Задание классу (устно): найдите дружную пару: «Название формулы – Формула»

1) площадь прямоугольника

2) площадь квадрата

3) формула пути

4) периметр квадрата

5) периметр прямоугольника

6) стоимости

Ребята давайте дадим название каждой формуле. Учащиеся подписывают соответствующее название рядом с формулой.

2. Объяснение нового материала.

Учитель показывает фигуру. ( прямоугольник и квадрат)

1. Какая это фигура. Что вы о ней знаете.

2. Какие величины можно найти у данной фигуры.

3. По каким формулам.

4. Где и как можно использовать площадь и периметр прямоугольника и квадрата в жизни.

3. Закрепление нового материала.

1) работа в парах: решение задач по учебнику при помощи карточек инструкции

Вычислите по формуле площадь и периметр квадрата со стороной а см, если:

1) а = 7 см;

2) а = 13 см;

Вычислите по формуле площадь и периметр пря­моугольника со сторонами, равными х см и у см, если:

1) х = 5,3 см; у = 3,4 см;

2) х = 11,6 см; у = 14,1 см.

Тренинг « Землетрясение»

2)работа в группах: решение задач по карточкам

1.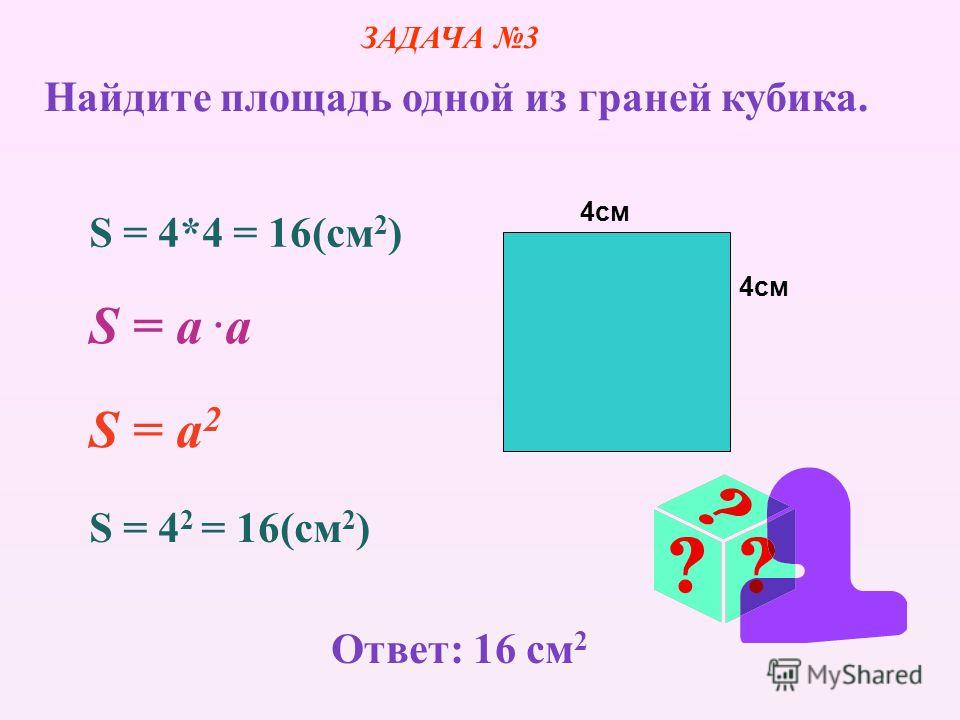 Площадь поля прямоугольной формы 116 га, а ширина – 800м. Найдите длину этого поля.

2.Найдите площадь земельного участка, если его ширина 800 м, а длина 900 м. Результат выразите в га.

1. Площадь садового участка прямоугольной формы равна 6а. Длина участка 30 м. Чему равна ширина участка?

2. Найдите площадь земельного участка, если его ширина 800 м, а длина 900 м. Результат выразите в га.

4 .Мини- тест .

1)Выбрать формулу для нахождения площади прямоугольника

А) а+в Б) (а+в)*2 В) а*в С) а(а+в)

2) Выбрать формулу для нахождения периметра квадрата

А) а Б) 4а В) а+в С)а*в

3)Чему равна площадь прямоугольники с измерениями 5,1 и 3,5

А) 8,6 см Б) 17,85 см² В) 8,6 см² С)17,85 см

4)Чему равен периметр прямоугольника с измерениями 10,4 и 1,8

А) 24,4см² Б) 18,72 см² В) 24,4 см С)18,72 см

5) Чему равен периметр квадрата с измерениями 0,5

А) 0,25 см Б) 2 см² В) 0,25 см² С)2 см

Учащиеся проводят взаимопроверку своих ответов и оценивают выполненную работу.

5. Рефлексия

— Закончите предложения:

Чему я научился на уроке………………..

Что мне этот урок дал для жизни……………

Привлек меня тем………..

Показался интересным………..

Заставил задуматься…………

6. Дом.задание: Разноуровневое домашнее задание:

1. Найти площадь пола своей  комнаты, выразить ее в м?, дм?, см?;

2.Дома вам необходимо произвести расчёт расходных материалов для покрытия пола линолеумом и потолка потолочной плиткой.

Как найти площадь квадрата если известен периметр

Калькулятор вычислит площадь квадрата по периметру! 1. Заполните значение периметра квадрата. 2. Мы вычислим площадь и сторону квадрата. 3. Представим подробное решение письменно и с комментариями и объяснениями!

Вычисли площадь квадрата периметр которого равен 24!

Некоторых такой вопрос ставит в тупик, но достаточно вспомнить, что квадрат равносторонняя фигура и у него 4 ре стороны. И сразу всё становится очень просто!

1. Вы не поняли? Тогда разберём этот пример как узнать площадь квадрата зная периметр.

Пример: вычислить площадь квадрата периметр которого равен 24. Для начала разделим на 4-ре значение периметра 24 и получим 6 см или дм, единицы вычисления используются те, которые были в задаче.

После это го умножим полученное значение стороны квадрата на саму себя, или возведём во вторую степень. 6 х 6 = 36 см2.

Это и будет искомое значение площадь квадрата с периметром 24, сначала мы вычислили сторону равную 6 и затем нашли площадь равную 36.

Как найти площадь квадрата по периметру?

Просто используй наш онлайн калькулятор квадрата и вычисли площадь квадрата периметр которого равен абсолютно любому числу, 12, 16, 360 хоть 81 см или дм . Любое решение будет расписано с комментариями и двумя вариантами написания, тебе останется только переписать и использовать полученное значение.

Периметр квадрата, да и любой геометрической фигуры, равен сумме длин всех сторон.

Квадрат — правильный четырехугольник, то есть четыре его стороны имеют равную длину и образуют

четыре прямых угла.

Квадрат является боковой гранью куба.

Найти периметр квадрата крайне просто. Для этого просто следуйте этим шагам.

Метод 1 из 3: Найдите периметр квадрата, если известна длина одной стороны

Умножьте длину стороны на 4. Квадрат имеет четыре стороны одинаковой длины, значит для нахождения

периметра квадрата нужно просто умножить длину любой из сторон на 4.

Следуйте простой формуле:

где P = периметр и S = длина стороны.

Пример: Если одна из сторон квадрата 5, то P = 4 * 5 или 20.

Метод 2 из 3: Найдите периметр квадрата, если известна его площадь

Для этого нужно понимать формулу нахождения площади квадрата

или длина умноженная на ширину.

Так как все стороны квадрата равны, то формулу можно упростить до:

или квадрат длины стороны.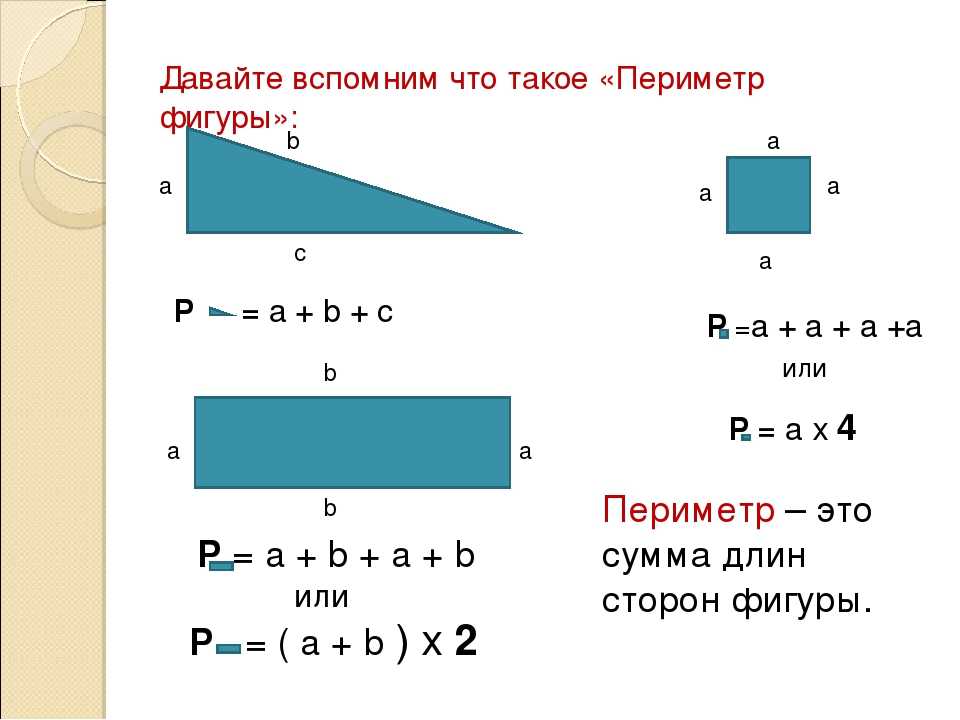

Например, если одна из сторон – 4, то площадь — 4 2 или 4 * 4, что дает нам 16.

Метод 3 из 3: Найдите периметр квадрата, если известна его диагональ

Периметр квадрата равен произведению длины его диагонали на два корня из двух.

Квадрат представляет собой положительный четырехугольник (либо ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у всякого другого верного многоугольника, у квадрата дозволено высчитать периметр и площадь. Если площадь квадрата теснее знаменита, то обнаружить его стороны, а после этого и периметр не составит труда.

Инструкция

1. Площадь квадрата находится по формуле:S = a?Это обозначает, что для того, дабы вычислить площадь квадрата , надобно умножить длины 2-х его сторон друг на друга. Как следствие, если знать площадь квадрата , то при извлечении корня из данного значения дозволено узнать длину стороны квадрата . Пример: площадь квадрата 36 см?, дабы узнать сторону данного квадрата , нужно извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см

2. Для нахождения периметр а квадрата нужно сложить длины всех его сторон. С подмогой формулы это дозволено выразить так:P = a+a+a+a.Если извлечь корень из значения площади квадрата , а после этого сложить получившуюся величину 4 раза, то дозволено обнаружить периметр квадрата .

3. Пример: Дан квадрат с площадью 49 см?. Требуется обнаружить его периметр .Решение:Вначале нужно извлечь корень площади квадрата : ?49 = 7 смЗатем, вычислив длину стороны квадрата , дозволено вычислить и периметр : 7+7+7+7 = 28 смОтвет: периметр квадрата площадью 49 см? составляет 28 см

Зачастую в геометрических задачах требуется обнаружить длину стороны квадрата, если вестимы другие его параметры – такие, как площадь, диагональ либо периметр.

Вам понадобится

Инструкция

1. Если вестима площадь квадрата, то для того, дабы обнаружить сторону квадрата, нужно извлечь квадратный корень из числового значения площади (потому что площадь квадрата равняется квадрату его стороны):a=?S, гдеa – длина стороны квадрата;S – площадь квадрата.Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Скажем, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны получится примитивно в сантиметрах.Пример:Площадь квадрата составляет 9 квадратных метров.Обнаружить длину стороны квадрата.Решение:a=?9=3Ответ:Сторона квадрата равняется 3 метрам.

2. В том случае, когда знаменит периметр квадрата, для определения длины стороны необходимо числовое значение периметра поделить на четыре (потому что квадрат имеет четыре стороны идентичной длины):a=P/4, где:a – длина стороны квадрата;P – периметр квадрата. 2), где:a – длина стороны квадрата;d – длина диагонали квадрата.Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Скажем, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.Пример:Диагональ квадрата равняется 10 метров.Обнаружить длину стороны квадрата.Решение:a=10/?2, либо примерно: 7,071Ответ:Длина стороны квадрата равняется 10/?2, либо приблизительно 1,071 метра.

Квадрат – прекрасная и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же обнаружить периметр квадрата , если знаменита длина его стороны?

Инструкция

1. Раньше каждого, стоит припомнить, что периметр есть ни что иное как сумма длин сторон геометрической фигуры. Рассматриваемый нами квадрат имеет четыре стороны. Больше того, по определению квадрата , все эти стороны равны между собой.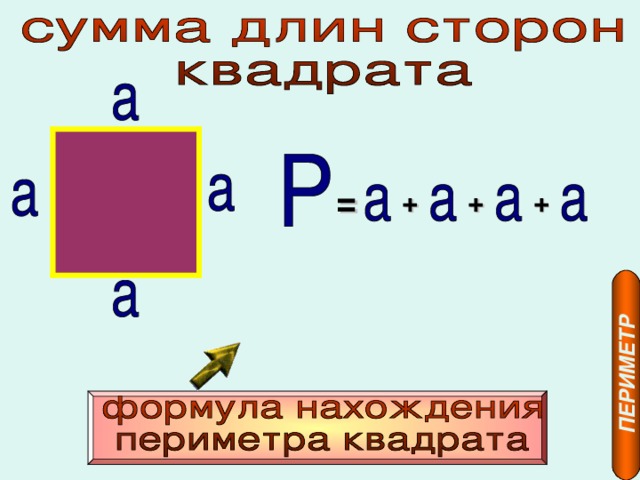 Из этих предпосылок вытекает простая формула для нахождения периметр а квадрата – периметр квадрата равен длине стороны квадрата , умноженной на четыре:Р = 4а, где а – длина стороны квадрата .

Видео по теме

Периметром называют всеобщую длину границы фигуры почаще каждого на плоскости. Квадрат — положительный четырехугольник либо ромб, у которого все углы прямые, либо параллелограмм, у которого все стороны и углы равны.

Вам понадобится

Инструкция

1. Периметр квадрата равен сумме длин его сторон. Потому что квадрат, по своей сути, есть четырехугольник, то и сторон у него четыре, а значит периметр равен сумме длин четырех сторон либо P = a+b+c+d.

2. Квадрат, как видно из определения, верная геометрическая фигура, а это значит, что все его стороны равны. Значит a=b=c=d. Следственно P = a+a+a+a либо P = 4*a.

3. Пускай сторона квадрата равна 4, то есть a=3. Тогда периметр либо длина квадрата , по полученной формуле, будет равен P = 4*3 либо P=12. Число 12 и будет являться длиной либо, что одно и тоже, периметром квадрата .

Видео по теме

Обратите внимание!
Периметр квадрата величина неизменно правильная, как и любая иная длина.

Полезный совет
Аналогичным образом дозволено обнаружить и периметр ромба, потому что квадрат является частным случаем ромба с прямыми углами.

Периметр характеризует длину замкнутого силуэта. Как и площадь, он может быть обнаружен по иным величинам, приведенным в условии задачи. Задачи на нахождении периметра крайне зачастую встречаются в школьном курсе математики.

Инструкция

1. Зная периметр и сторону фигуры, дозволено обнаружить иную ее сторону, а также площадь. Сам же периметр, в свою очередь, может быть обнаружен по нескольким заданным сторонам либо по углу и сторонам, в зависимости от условий задачи. Также в ряде случаев его выражают через площадь. Особенно примитивно находится периметр прямоугольника. Начертите прямоугольник с одной из сторон, равной а, и диагональю, равной d. Зная эти две величины, обнаружьте по теореме Пифагора иную его сторону, которая является шириной прямоугольника. Обнаружив ширину прямоугольника, вычислите его периметр дальнейшим образом: p=2(a+b). Эта формула объективна для всех прямоугольников, от того что у всякого из них четыре стороны.

2. Обратите внимание на тот факт, что периметр треугольника в большинстве задач находят при наличии информации правда бы об одном его угле. Впрочем, имеются и задачи, в которых все стороны треугольник знамениты, и тогда периметр может быть вычислен простым суммированием, без применения тригонометрических вычислений: p=a+b+c, где a, b и c – стороны. Но такие задачи встречаются в учебниках редко, от того что метод их решения явствен.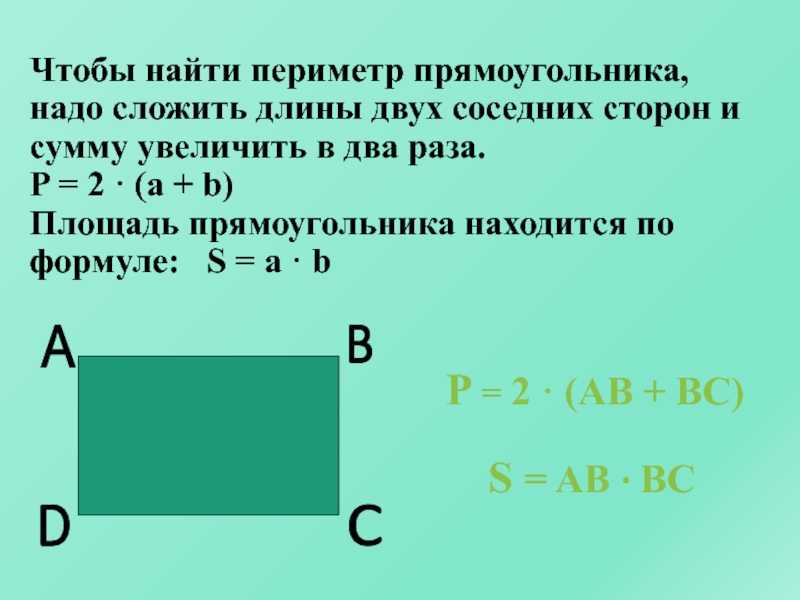 Больше трудные задачи по нахождению периметра треугольника решайте поэтапно. Скажем, начертите равнобедренный треугольник, у которого знамениты основание и угол при нем. Для того дабы обнаружить его периметр, сначала обнаружьте стороны a и b дальнейшим образом: b=c/2cos?. От того что a=b (треугольник равнобедренный), сделайте дальнейший итог: a=b=c/2cos?.

3. Периметр многоугольника вычисляйте аналогичным образом, складывая длины всех его сторон: p=a+b+c+d+e+f и так дальше. Если многоугольник положительный и вписан в окружность либо описан около нее, вычислите длину одной из его сторон, а после этого умножьте на их число. Скажем, дабы обнаружить стороны шестиугольника, вписанного в окружность, действуйте дальнейшим образом: a=R, где a – сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник верный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r?3/3. Соответственно, периметр такой фигуры обнаружьте дальнейшим образом: p=12r?3/3.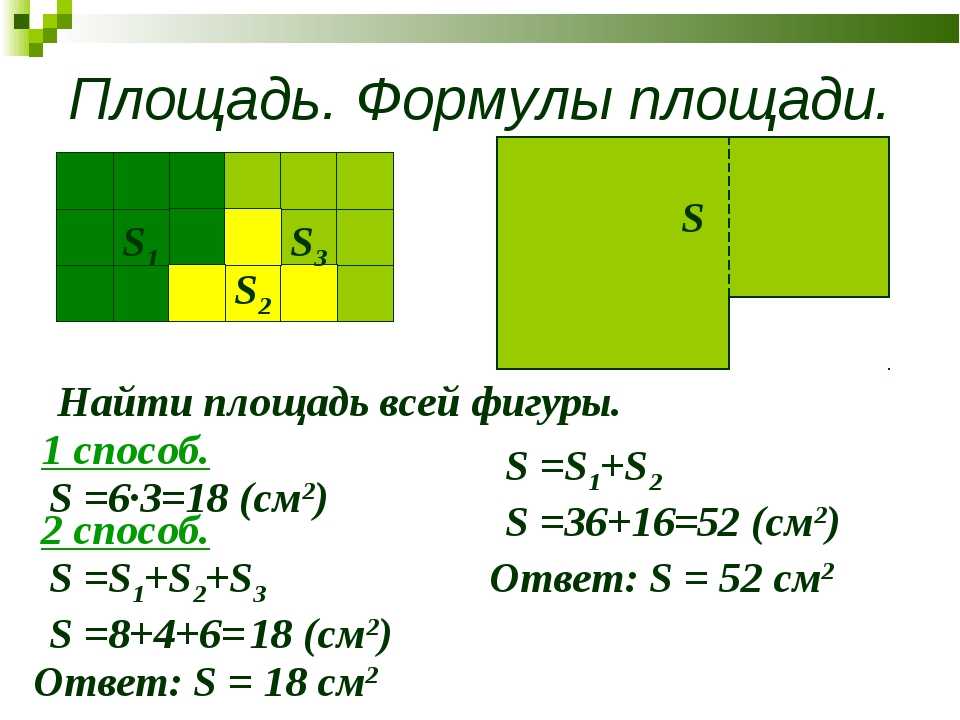

Хоть слово «периметр» и случилось от греческого обозначения окружности, им принято называть суммарную длину границ всякий плоской геометрической фигуры, включая квадрат. Вычисление этого параметра, как водится, трудности не представляет и может быть осуществлено несколькими методами, в зависимости от знаменитых начальных данных.

Инструкция

1. Если вестима длина стороны квадрата (t), то для нахождения его периметра (p) примитивно увеличьте эту величину в четыре раза: p=4*t.

2. Если длина стороны незнакома, но в условиях задачи дана длина диагонали (c), то этого довольно для вычисления длины сторон, а следственно и периметра (p) многоугольника. Используйте теорему Пифагора, которая заявляет, что квадрат длины длинной стороны прямоугольного треугольника (гипотенузы) равен сумме квадратов длин коротких сторон (катетов). В прямоугольном треугольнике, составленном из 2-х смежных сторон квадрата и соединяющего их крайние точки отрезка, гипотенуза совпадает с диагональю четырехугольника.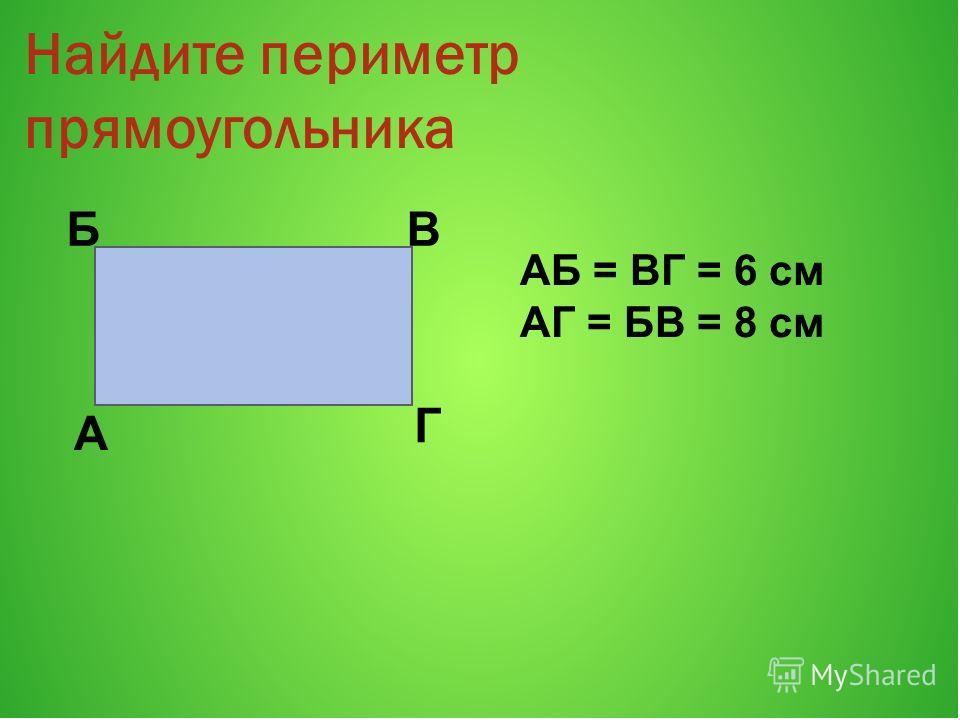 Из этого вытекает, что длина стороны квадрата равна отношению длины диагонали к квадратному корню из двойки. Используйте это выражение в формуле для вычисления периметра из предыдущего шага: p=4*c/?2.

3. Если дана лишь площадь (S) ограниченного периметром квадрата участка плоскости, то и этого будет довольно, дабы определить длину одной стороны. Потому что площадь всякого прямоугольника равна произведению длин его смежных сторон, то для нахождения периметра (p) извлеките квадратный корень из площади, а итог увеличьте в четыре раза: p=4*?S.

4. Если знаменит радиус описанной вблизи квадрата окружности (R), то для нахождения периметра многоугольника (p) умножьте его на восемь и поделите полученный итог на квадратный корень из двойки: p=8*R/?2.

5. Если окружность, радиус которой вестим, вписана в квадрат, то вычисляйте его периметр (p) простым умножением радиуса (r) на восьмерку: P=8*r.

6. Если рассматриваемый квадрат в условиях задачи описан координатами своих вершин, то для вычисления периметра вам потребуются данные лишь о 2-х вершинах, принадлежащих к одной из сторон фигуры. Определите длину этой стороны, исходя из все той-же теоремы Пифагора для треугольника, составленного из нее самой и ее проекций на оси координат, а полученный итог увеличьте в четыре раза. Потому что длины проекций на координатные оси равны модулю разностей соответствующих координат 2-х точек (X?;Y? и X?;Y?), то формулу дозволено записать так: p=4*?((X?-X?)?+(Y?-Y?)?).

Периметром в всеобщем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину дозволено измерить, а для многих фигур и легко рассчитать, если вестимы длины соответствующих элементов.

Вам понадобится

• – линейка либо рулетка;
• – крепкая нить;
• – роликовый дальномер.

Инструкция

1. Дабы измерить периметр произвольного многоугольника, измерьте при помощи линейки либо иным измерительным прибором все его стороны, а после этого обнаружьте их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, обнаружьте периметр, сложив их совместно Р=5+3+7+4=19 см.

2. Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр традиционной веревкой либо ниткой. Для этого расположите ее так, дабы она верно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если дозволено, примитивно обрежьте ее дабы избежать путаницы. После этого при помощи рулетки либо линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Непременно следите за тем, дабы нить максимально верно повторяла линию для большей точности итога.

3. Периметр трудной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в начальную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.

4. Периметр некоторых геометрических фигур вычисляйте. Скажем, дабы обнаружить периметр всякого положительного многоугольника (выпуклого многоугольника, стороны которого равны), длину стороны умножьте на число углов либо сторон (они равны). Дабы обнаружить периметр верного треугольника со стороной 4 см умножьте это число на 3 (Р=4?3=12 см).

5. Дабы обнаружить периметр произвольного треугольника, сложите длины всех его сторон. Если не даны все стороны, а есть углы между ними, обнаружьте их по теореме синуса либо косинуса. Если знамениты две стороны прямоугольного треугольника, третью обнаружьте по теореме Пифагора и обнаружьте их сумму. Скажем, если знаменито, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна ?(3?+4?)=5 см. Тогда периметр Р=3+4+5=12 см.

6. Дабы обнаружить периметр круга, обнаружьте длину окружности, которая его ограничивает. Для этого ее радиус r умножьте на число ??3,14 и число 2 (P=L=2.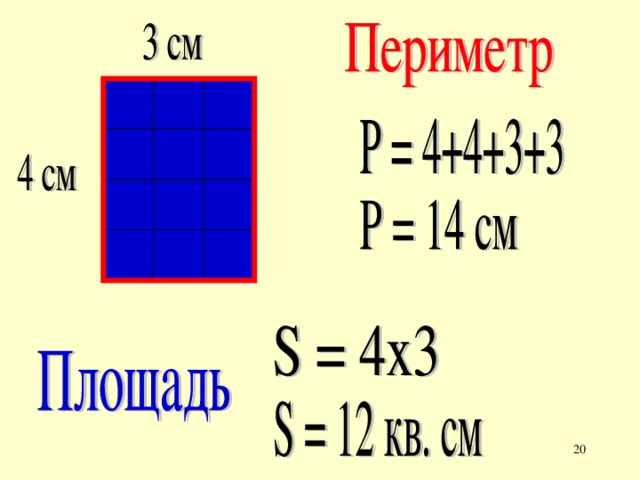 r). Если знаменит диаметр, рассматривайте, что он равен двум радиусам.

Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется верным. В этом случае вычисление периметра гораздо упрощается.

Инструкция

1. В самом простом случае, когда вестимы длина стороны (а) верного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) примитивно перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.

2. Вычислить периметр такого многоугольника по вестимому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.

3. Схожим методом дозволено посчитать периметр, не зная длины стороны положительного многоугольника , если он описан около окружности с знаменитым радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.

Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.

Инструкция

1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры. Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.

2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.

3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.

4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.

Видео по теме

Обратите внимание!
Для квадрата объективны следующие определения:Квадрат – это прямоугольник, тот, что владеет равными между собой сторонами.Квадрат – это специальная разновидность ромба, у которого весь из углов равен 90 градусам.Являясь положительным четырехугольником, вокруг квадрата дозволено описать либо вписать окружность. Радиус вписанной в квадрат окружность дозволено обнаружить по формуле:R = t/2, где t – сторона квадрата.Если же окружность описана вокруг него, то ее радиус находится так:R = (?2*t)/2Исходя из данных формул, дозволено вывести новые для нахождения периметра квадрата:P = 8*R, где R – радиус вписанной окружности;P = 4*?2*R, где R – радиус описанной окружности. Квадрат является уникальной геометрической фигурой, от того что он безусловно симметричен, самостоятельно от того, как и где провести ось симметрии.

Математика площадь периметр — Стоматология в Химках

Математика площадь периметр

1. Длина стороны квадрата равна см. Чему равны его периметр и площадь, если = 8?

Периметр квадрата равен сумме длин всех его сторон.

P = + + + или P = · 4

Площадь квадрата равна произведению длин двух его сторон.

S = ·

Периметр фигуры обозначают большой латинской буквой P, площадь — большой латинской буквой S, а стороны фигур — маленькими латинскими буквами, b и др.

Формулы — это равенства, которые устанавливают взаимосвязь между величинами.

2. Составь формулу для вычисления периметра каждой фигуры. Между какими величинами они устанавливают взаимосвязь?

3. Между какими величинами устанавливают взаимосвязь формулы:

S = c · c, P = c · 4?

4. Составь формулы периметра и площади прямоугольника.

1) Длина прямоугольника равна см, ширина — b см. Чему равна его площадь, если = 11, b = 6?

2) Длина прямоугольника равна см, ширина — b см. Чему равен периметр, если = 12, b = 4?

Площадь прямоугольника равна произведению его длины и ширины.

S = · b, где S — площадь, — длина, b — ширина прямоугольника.

Периметр прямоугольника равен удвоенной сумме его длины и ширины.

P = ( + b ) · 2, где P — периметр, — длина, b — ширина прямоугольника.

5. Найди площадь и периметр прямоугольника со сторонами:

6. Маша хочет обшить кружевом салфетку прямоугольной формы. Размеры салфетки 20 см и 25 см. Сколько сантиметров кружев ей потребуется? Укажи правильный ответ.

7. 1) Площадь прямоугольника 56 см 2 , ширина — 4 см. Чему равна длина прямоугольника?

2) Площадь прямоугольника ABCD равна 49 см 2 , а сторона AB равна 7 см. Найди длину стороны BC. Как называется прямоугольник ABCD?

Чтобы найти длину прямоугольника, надо его площадь разделить на ширину.

= S : b

8. 1) Запиши формулы периметра и площади квадрата со стороной b см.

2) Найди периметр и площадь квадрата, сторона которого равна 10 см.

3) Найди периметр квадрата, площадь которого 81 см 2 .

9. Между какими величинами устанавливают связь формулы?

10. Запиши формулы площади и периметра каждой фигуры, изображённой на рисунке.

11. Площадь прямоугольника равна 32 см 2 , а ширина — 4 см. Найди площадь квадрата, периметр которого равен периметру данного прямоугольника.

12. 1) Периметр квадрата 20 см. Из двух таких квадратов составили прямоугольник. Запиши выражение, с помощью которого можно узнать периметр получившегося прямоугольника.

2) Периметр изображённого квадрата равен см. Запиши формулу для нахождения периметра прямоугольника.

13. Начерти такие четырёхугольники. Дорисуй каждый из них до прямоугольника. Найди периметры и площади полученных прямоугольников.

14. Каждую изображённую фигуру сложили из двух треугольников со сторонами 3 см, 4 см, 5 см. Чему равны площади и периметры составленных фигур?

15. Ширина прямоугольника см, а длина — b см. Известно, что длина на 8 см больше, чем ширина. Какие числа пропущены в таблице?

Укажи формулы, устанавливающие взаимосвязь между длиной и шириной прямоугольника.

1) b = + 8;

2) b = – 8;

3) = b + 8;

4) = b – 8.

16. Для каждой таблицы подбери формулу, устанавливающую связь между величинами.

17. 1) Проверь формулу Р = Г + В – 2 взаимосвязи количества граней (Г), вершин (В) и рёбер (Р) пирамиды.

2) Проверь, будет ли верна эта формула для граней, вершин и рёбер призмы.

В Древнем Египте были установлены налоги на владение земельными участками. При этом необходимо было вычислять площади участков. Река Нил после дождей разливалась и часто меняла своё русло, смывая границы участков. Приходилось восстанавливать их и заново измерять. К этому времени относится зарождение науки геометрии.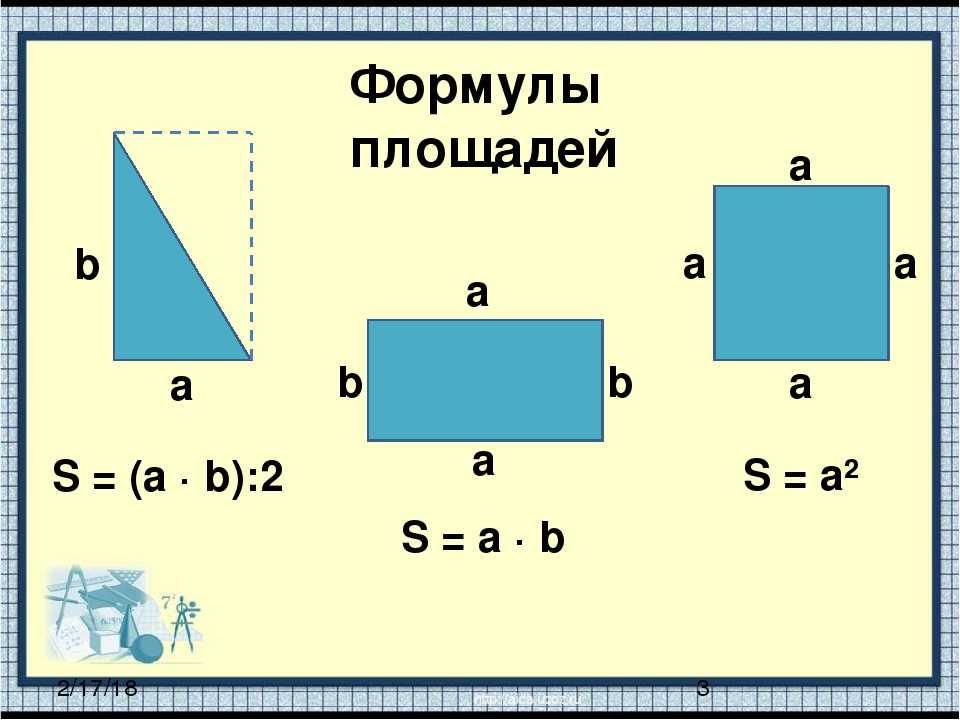 В переводе с греческого языка слово геометрия означает землемерие.

18. Какие единицы измерения площади ты знаешь? Какая связь между этими единицами измерения?

19. Единицы измерения площади.

Выполни проект по плану.

1) История развития единиц измерения на Руси (или в других странах).

2) Современные единицы измерения площади и соотношения между ними.

3) Способы измерения площадей фигур.

1. Запиши формулу: площади квадрата, периметра квадрата, площади прямоугольника; периметра равностороннего треугольника, периметра прямоугольника, периметра равностороннего шестиугольника, периметра разностороннего треугольника.

2. Вычисли площадь и периметр прямоугольника со сторонами: 12 см и 4 см, 6 см и 7 см, 3 см и 18 см.

Периметр фигуры обозначают большой латинской буквой P, площадь — большой латинской буквой S, а стороны фигур — маленькими латинскими буквами, b и др.

2) Периметр изображённого квадрата равен см. Запиши формулу для нахождения периметра прямоугольника.

2 Длина прямоугольника равна см, ширина b см.

Reader. lecta. rosuchebnik. ru

02.06.2020 8:45:17

2020-06-02 08:45:17

Источники:

Https://reader. lecta. rosuchebnik. ru/demo/7909-62/data/chapters/Chapter07/index. xhtml

Периметр и площадь прямоугольника: как найти периметр квадрата по его стороне или чему он равен и какие формулы для нахождения этого » /> » /> .keyword { color: red; }

Математика площадь периметр

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Математика – 3 класс. Прямоугольники

Что такое прямоугольник и квадрат

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2. Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.

PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см. Решение:

Нарисуем прямоугольник ABCD с исходными данными.

PABCD = 2 * (AB + BС)

Подставим в формулу наши данные:

PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: PABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

PABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

PABCD= 4 * AB

Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата. Решение:

Нарисуем квадрат ABCD с исходными данными.

PABCD = 4 * AB

Подставим в формулу наши данные:

PABCD = 4 * 6 см = 24 см

Ответ: PABCD = 24 см.

Задачи на нахождение периметра прямоугольника

Измерь ширину и длину прямоугольников. Определи их периметр.

Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника. 3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора. 2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.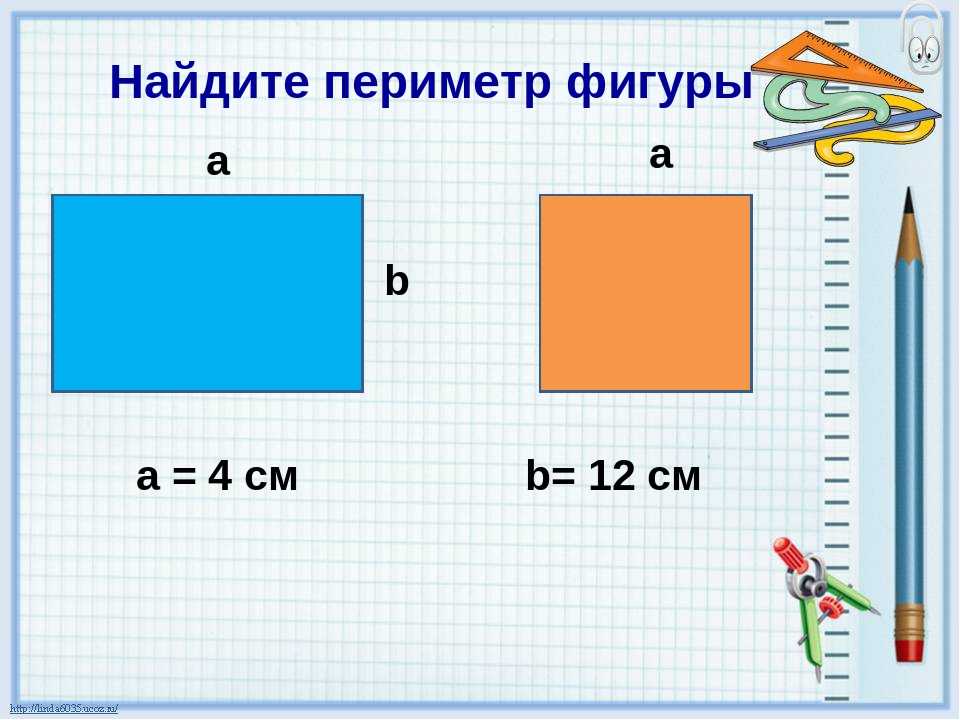 Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т. д.). В вычислениях обозначается латинской буквой S.

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.

S AKMO = AK * KM S AKMO= AK * KM = 7 см * 2 см = 14 см2.

Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя. Пример:

В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB S AKMО = AK * KM = 8 см * 8 см = 64 см2

Определи площадь квадрата AKMO со стороной 8 см.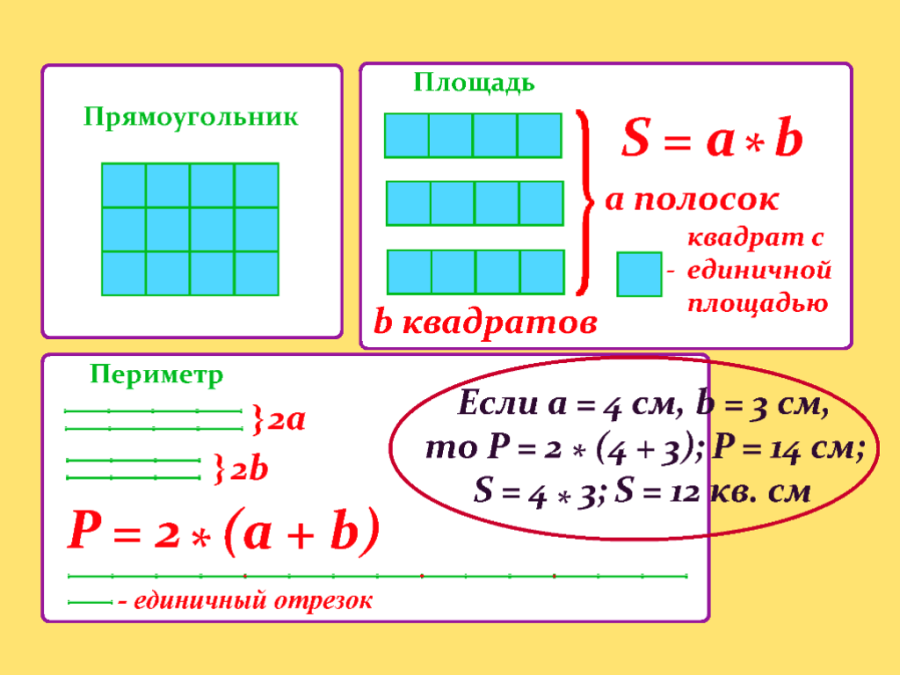

Задачи на нахождение площади прямоугольника и квадрата:

Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др. ).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

Например, перед нами квадрат со стороной 10 см:

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности.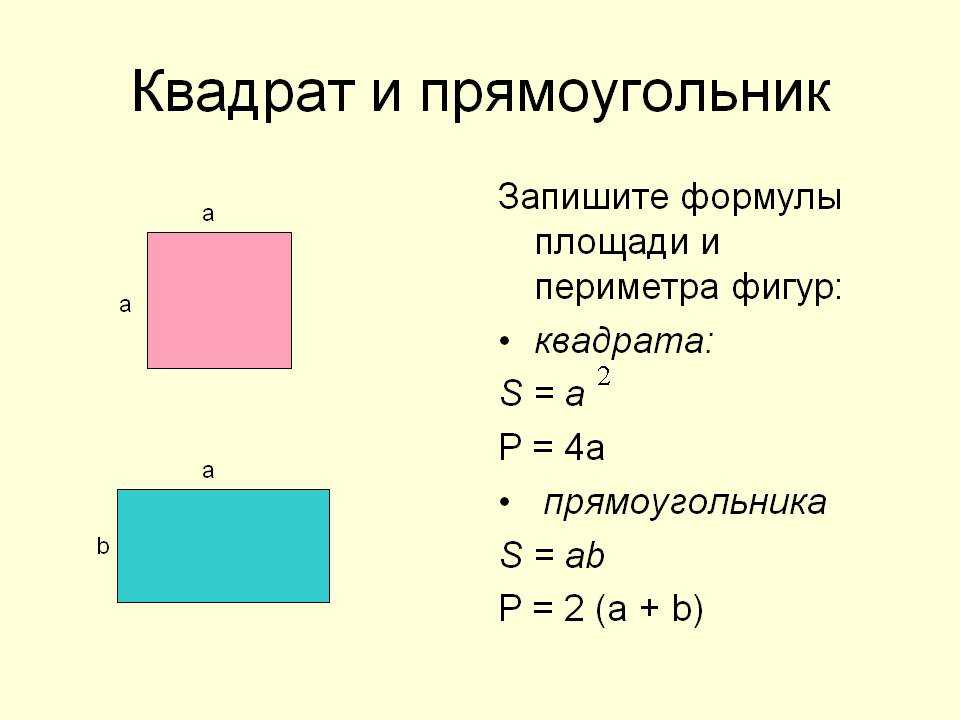 Существует формула для нахождения длины окружности:

L – длина окружности

Π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

Π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр:

L= 2*3,14*3 L=6π L=6*3.14 L = 18.84 см Pк= 18,84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Площадь прямоугольника

Площадь прямоугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.

Площадь прямоугольника через две стороны

A — сторона

B — сторона

A (или b) — сторона

P — периметр

A (или b) — сторона

D — диагональ

D — диагональ

Α° — угол между диагоналями

A (или b) — сторона

R — радиус описанной окружности

A (или b) — сторона

D — диаметр описанной окружности

Прямоугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т. д.

Нарисуем квадрат ABCD с исходными данными.

Нарисуем прямоугольник ABCD с исходными данными.

Площадь это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Rgiufa. ru

01.09.2017 12:39:50

2017-09-01 12:39:50

Источники:

Https://rgiufa. ru/matematika-fizika-himiya/kak-najti-perimetr-i-ploshhad-pryamougolnika. html

Площадь прямоугольника – формула нахождения через диагональ и периметр (5 класс, математика) » /> » /> .keyword { color: red; }

Математика площадь периметр

Начиная с 5 класса, ученики начинают знакомиться с понятием площадей разных фигур. Особая роль отводится площади прямоугольника, так как эта фигура одна из наиболее простых в изучении.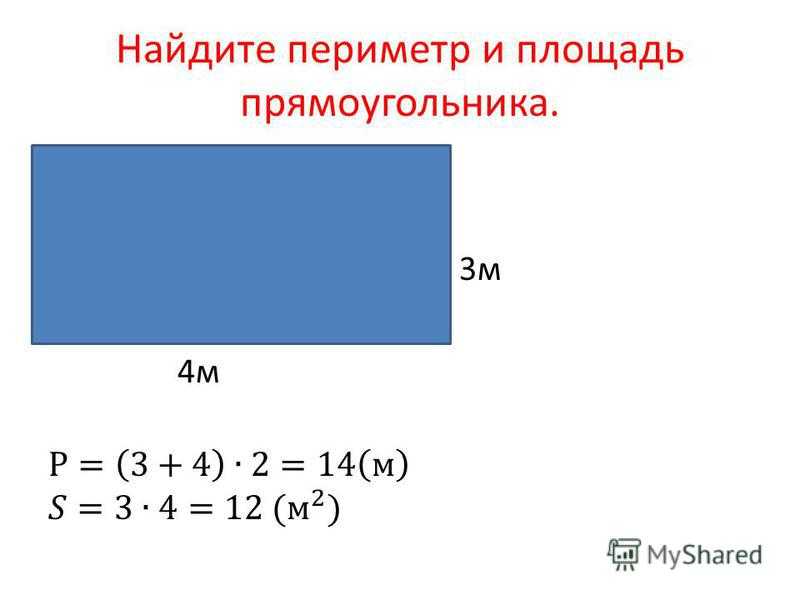 2$.

Формула площади прямоугольника

Для того, чтобы найти площадь прямоугольника без формулы необходимо посчитать количество единичных квадратов, на которые разбита фигура.

Рис. 1. Прямоугольник, разбитый на единичные квадраты

Прямоугольник разбит на 15 квадратов, то есть его площадь равна 15 см 2 . Стоит обратить внимание, что в ширину фигура занимает 3 квадрата, а в длину 5, поэтому чтобы вычислить количество единичных квадратов, необходимо умножить длину на ширину. Меньшая сторона четырехугольника – ширина, большая длина. Таким образом, можно вывести формулу площади прямоугольника:

S = a · b, где a, b – ширина и длина фигуры.

К примеру, если длина прямоугольника 5 см, а ширина 4 см, то площадь будет равна 4*5=20 см 2 .

Расчет площади прямоугольника, с использованием его диагонали

Для того, чтобы рассчитать площадь прямоугольника через диагональ необходимо применить формулу:

Если в задании дано значения угла между диагоналями, а также значение самой диагонали, то можно вычислить площадь прямоугольника по общей формуле произвольных выпуклых четырехугольников.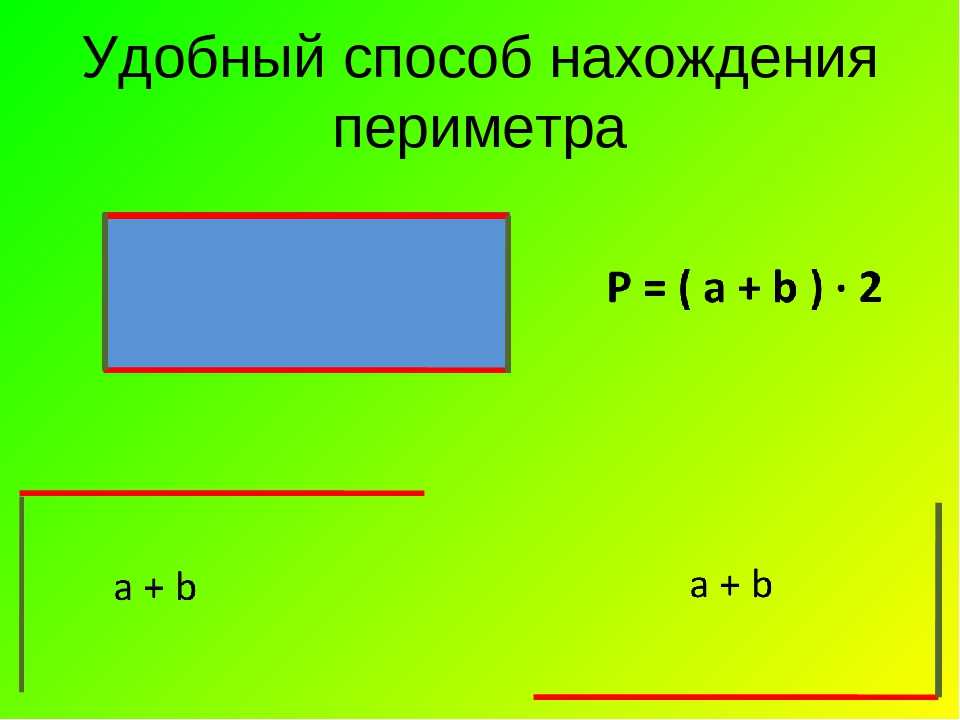 2$.

Диагонали разделяют прямоугольник на 4 фигуры – 4 треугольника. При этом треугольники попарно равны. Если провести одну диагональ в прямоугольнике, то она разделяет фигуру на два равных прямоугольных треугольника.

Диагонали не являются биссектрисами углов прямоугольника. А также если провести биссектрисы каждого угла, то при их пересечении получится прямоугольник.

Рис. 4. Рисунок к утверждению

Что мы узнали?

Мы научились находить площадь прямоугольника. Ту или иную формулы нахождения площади используют в зависимости от исходных данных. Также не стоит забывать, что если в задании разные единицы измерения сторон, то необходимо перевести их одну.

Рис. 4. Рисунок к утверждению

Рис. 2. Прямоугольник с начерченными диагоналями

Площадь прямоугольника.

Obrazovaka. ru

09.02.2017 3:46:45

2017-02-09 03:46:45

Источники:

Https://obrazovaka. ru/matematika/ploschad-pryamougolnika-formula-5-klass. html

открытых учебников | Siyavula

Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.

Математика

• • Читать онлайн

  • Учебники

    • Английский

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)

    • Африкаанс

      • • 7A PDF (CC-BY-ND)
        • 7B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)

    • Африкаанс

      • • 8A PDF (CC-BY-ND)
        • 8B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)

    • Африкаанс

      • • 9A PDF (CC-BY-ND)
        • 9B PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

    • Английский

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

    • Африкаанс

      • • PDF (CC-BY-ND)
        • ePUB (CC-BY-ND)
        • ePUB (CC-BY)

  • Пособия для учителей

    • Английский

      • • PDF (CC-BY-ND)

    • Африкаанс

      • • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 7А

        • PDF (CC-BY-ND)

      • Класс 7Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 7А

        • PDF (CC-BY-ND)

      • Граад 7Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 8А

        • PDF (CC-BY-ND)

      • Класс 8Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 8А

        • PDF (CC-BY-ND)

      • Граад 8Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 9А

        • PDF (CC-BY-ND)

      • Класс 9Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 9А

        • PDF (CC-BY-ND)

      • Граад 9Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 4А

        • PDF (CC-BY-ND)

      • Класс 4Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 4А

        • PDF (CC-BY-ND)

      • Граад 4Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 5А

        • PDF (CC-BY-ND)

      • Класс 5Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 5А

        • PDF (CC-BY-ND)

      • Граад 5Б

        • PDF (CC-BY-ND)
• • Читать онлайн

  • Учебники

  • Пособия для учителей

    • Английский

      • Класс 6А

        • PDF (CC-BY-ND)

      • Класс 6Б

        • PDF (CC-BY-ND)

    • Африкаанс

      • Граад 6А

        • PDF (CC-BY-ND)

      • Граад 6Б

        • PDF (CC-BY-ND)

Лицензирование наших книг

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.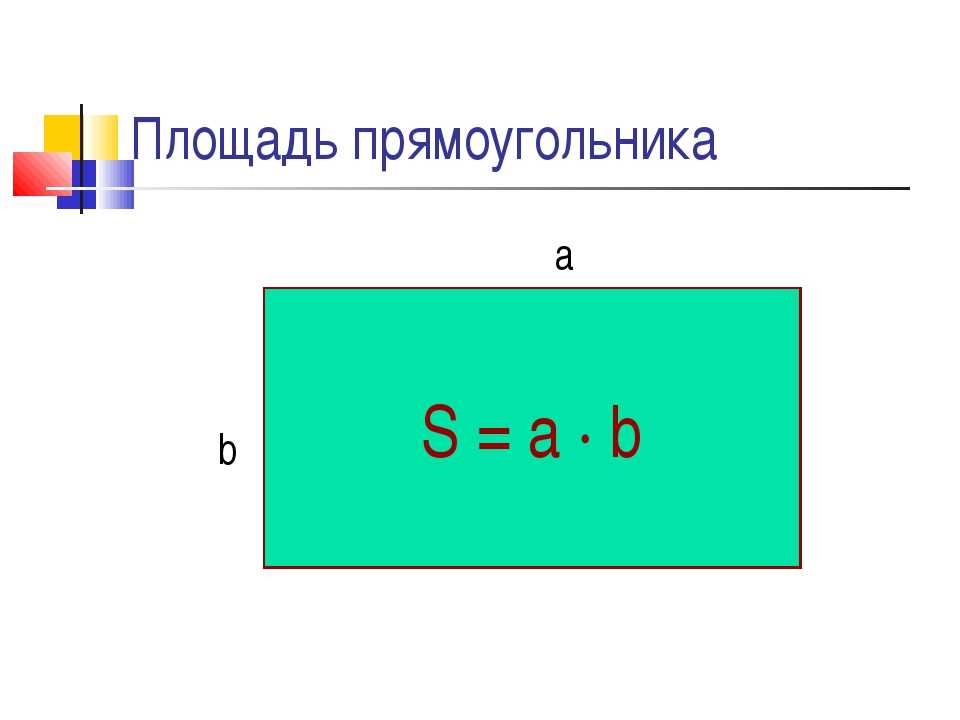 Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.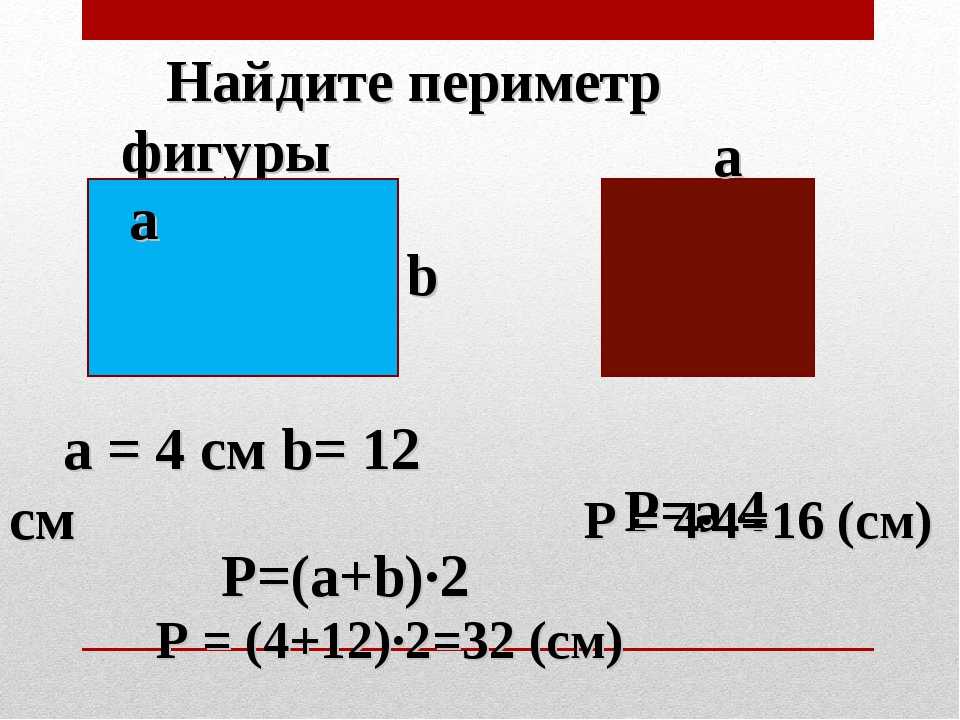 Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

площадь и периметр прямоугольника

Единицы измерения

Пожалуйста, включите JavaScript

Единицы измерения

Мы в ask-math считаем, что образовательные материалы должны быть бесплатными для всех. Пожалуйста, используйте содержимое этого веб-сайта для более глубокого понимания концепций. Кроме того, мы создали и разместили видеоролики на нашем YouTube.

Мы также предлагаем индивидуальные / групповые занятия / помощь в выполнении домашних заданий по математике с 4 по 12 классы по алгебре, геометрии, тригонометрии, предварительному исчислению и исчислению для учащихся из США, Великобритании, Европы, Юго-Восточной Азии и ОАЭ.

Также приветствуются связи со школами и учебными заведениями.

Пожалуйста, свяжитесь с нами по [email protected] / Whatsapp +919998367796 / Skype ID: anitagovilkar.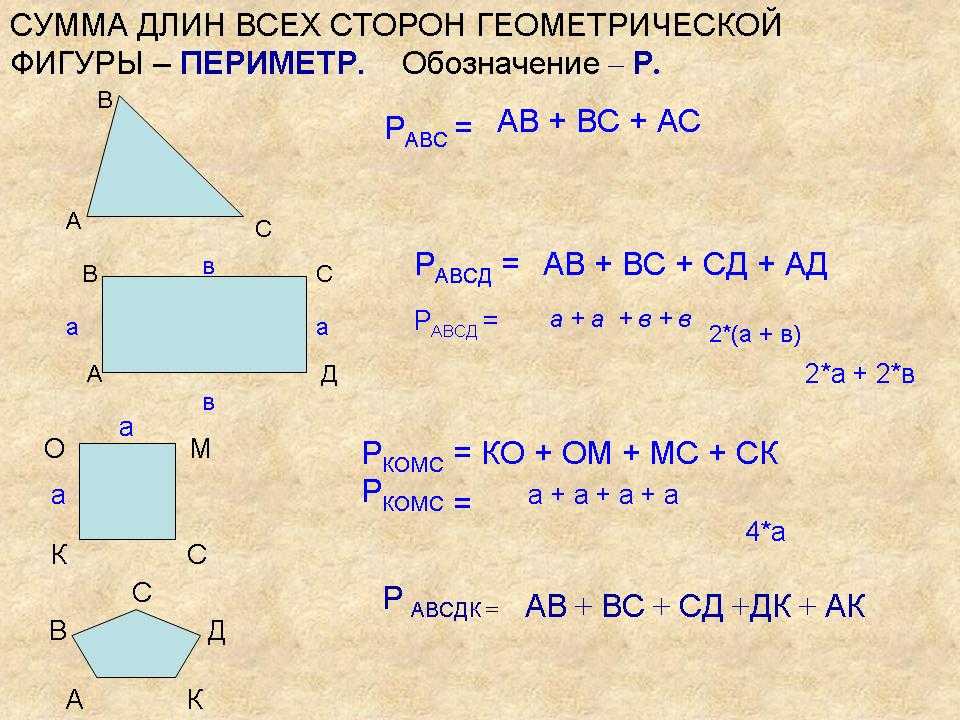 abhijit

Мы также будем рады разместить видео в соответствии с вашими требованиями. Напишите нам.

Площадь и периметр прямоугольника поясняются ниже:

Длина обозначается буквой l, ширина (ширина) обозначается буквой w(b), а диагональ обозначается буквой d. Две длины, две ширины и две диагонали.

Площадь и периметр прямоугольника

Формулы для площади и периметра прямоугольника приведены ниже:

• Периметр прямоугольника = 2(l + w) единиц
• Длина прямоугольника = p/2 — w единиц
• Ширина (w) прямоугольника = p/2 — l единиц
• Диагональ прямоугольника = √(l ² + w ² ) единиц
• Площадь прямоугольника = l x w кв. /w единиц
• Ширина прямоугольника = A/l единиц

Некоторые решенные примеры площади и периметра прямоугольника

1) Найдите периметр прямоугольника, длина и ширина которого равны 25 м и 15 м соответственно.
Решение:
Длина = l = 25 м и ширина = w = 15 м
∴ P = 2 (l + w)
⇒ = 2 (25 + 15)
⇒ = 2 x 40
⇒ = 80 м
Периметр = 80 м
_________________________________________________________________________
2)Сколько прямоугольников можно нарисовать с периметром 36 см, если стороны являются целыми положительными числами в см?
Решение:
Периметр = 36
⇒ 2 ( l + w ) = 36
⇒ l + w = ​​18
Так как длина и ширина — положительные целые числа в сантиметрах. Следовательно, возможные размеры:
(1, 17) см, (2, 16) см, (3, 15) см, (4, 14) см, (5,13) см, (6, 12) см, ( 7, 11) см, (8, 10) см, (9, 9) см.
Значит, прямоугольников 9.
_________________________________________________________________
4) Длина прямоугольного поля в два раза больше его ширины. Человек обежал вокруг него 5 раз и преодолел расстояние в 3 км. Какова длина поля?
Решение:
При прохождении одного раунда поля пройденное расстояние равно периметру поля.
∴ Расстояние, пройденное за 5 раундов = 5 x периметр
= 5 x 2 (l + w)
= 10 x (l + w)
= 10 x (2w + w) [длина = l = 2w]
= 10 x 3w
= 30 w
Но общее пройденное расстояние дано = 3 км = 3000 м.
∴ 30 x w = 3000
⇒ w = 3000 / 30
⇒ w = 100 м
⇒ Длина = 2 w = 2 x 100 = 200 м.
_________________________________________________________________
Некоторые решенные примеры на площадь прямоугольника

1) Найдите площадь в гектарах поля, длина которого 240 м, а ширина 110 м.
Решение:
Длина = L = 240 м и ширина = W = 110 м
∴ Площадь поля = L x W
⇒ = 240 x 110
= 26 400 м ²
= 26 400 /10 000 2 = 1 га ]
Площадь поля = 2,64 га
________________________________________________________________
2) Дверная коробка размерами 4 м х 5 м крепится к стене размером 11 м 11 м. Найдите общие затраты труда на покраску стены, если затраты труда на покраску 1 м ² стены стоит 2,50$.
Решение:
Покраска стены должна быть выполнена без учета площади двери
Площадь двери = Д х Ш
= 4 х 5
= 20 м ²
Площадь стены, включая дверь = сторона х сторона
= 11 x 11
= 121 м ²
Площадь стены без двери = (121 — 20) м ²
= 101 м ²
Общие затраты на покраску стены
= 2,59 x 103 $ 252,50
________________________________________________________________
3) Найдите ширину прямоугольного участка земли, если его площадь 440 м ² , а длина 22 м. Также найдите его периметр.
Решение:
Площадь прямоугольного листа = 440 м ²
Длина (l) = 22 м
Площадь прямоугольника = l x w (где w = ширина прямоугольного участка
Следовательно, ширина (w) = площадь /l = 440/22 = 20 м
Периметр листа = 2(l + w)
= 2(22 + 20)м
= 84 м
Итак, ширина прямоугольного участка 20 м, а его периметр 84 м.
_________________________________________________________________
3) Прямоугольный сад имеет длину 90 м и ширину 75 м. Вокруг него должна быть проложена дорожка шириной 5 м. Найдите площадь пути.

Решение:

Тогда ясно,
Площадь пути = Площадь прямоугольника EFGH – Площадь прямоугольника ABCD
Из рисунка имеем
EF = 90 + 5 + 5
= 100 м
и FG = 75 + 5 + 5 = 85 м
Теперь площадь прямоугольника EFGH = 100 x 85 = 8500 м ²
А площадь прямоугольника ABCD = 90 x 75 = 6750 м ²
Следовательно,
Площадь пути = Площадь прямоугольника EFGH – Площадь прямоугольника ABCD
= 8500 – 6750
= 1750 м ² 0________________ 0001 Измерение: площадь и периметр прямоугольника

• Периметр и площадь неправильной формы
• Площадь и периметр прямоугольника
• Площадь квадрата (периметр квадрата)
• Периметр параллелограмма (площадь параллелограмма)
• Площадь ромба (периметр ромба)
• Площадь трапеции (трапеции)
• Площадь треугольника (периметр треугольника)
• Формула Герона

Измерение

Математика 7-го класса

3

3

3 Главная

Российско-украинский кризис: 3 марта 2022 г.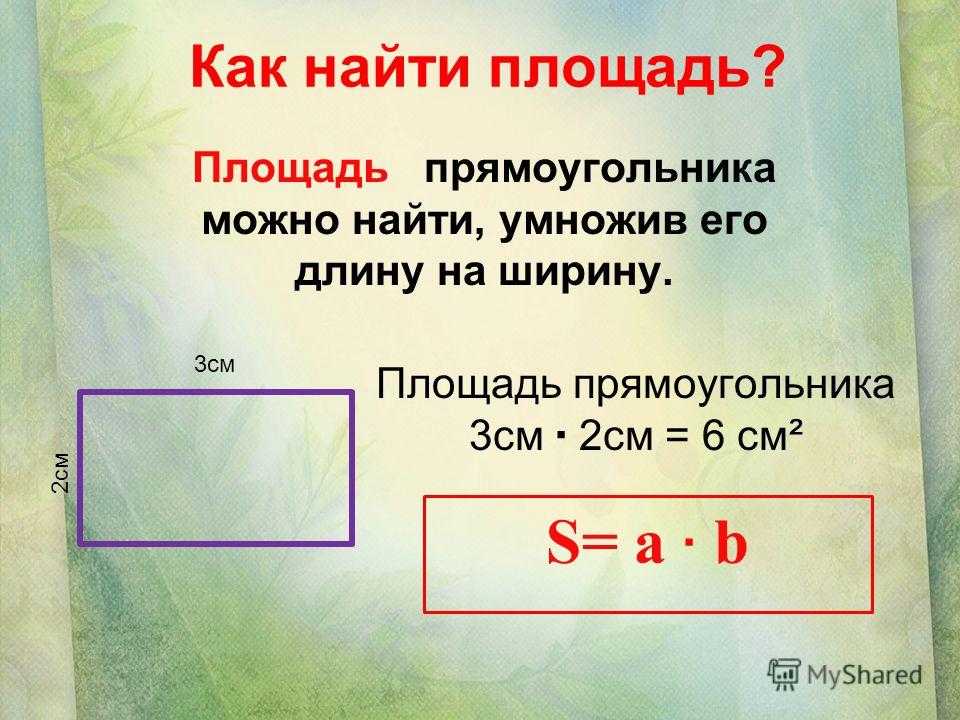

Генеральная ассамблея ООН на экстренном заседании проголосовала за требование немедленного прекращения нападения Москвы на Украину и вывода российских войск.

Что такое площадь и периметр?

Площадь и периметр — важная и основная тема Измерения двумерных или плоских фигур. Площадь используется для измерения пространства, занимаемого плоскими фигурами. Периметр используется для измерения границ замкнутых фигур. В математике это две основные формулы для решения задач в двумерных фигурах.

Каждая фигура имеет два свойства: Площадь и Периметр. Студенты могут найти площадь и периметр различных фигур, таких как круг, прямоугольник, квадрат, параллелограмм, ромб, трапеция, четырехугольник, пятиугольник, шестиугольник и восьмиугольник. Свойства фигур будут различаться в зависимости от их структуры, углов и размера. Прокрутите эту страницу вниз, чтобы узнать больше о площади и периметре всех двумерных фигур.

Площадь: Площадь определяется как мера пространства, ограниченного плоской фигурой или формой. Единицы измерения площади замкнутой фигуры — квадратные сантиметры или метры.

Периметр: Периметр определяется как мера длины границы двумерной плоской фигуры. Единицы измерения периметра замкнутых фигур — сантиметры или метры.

Формулы площади и периметра двумерных фигур

1. Площадь и периметр прямоугольника:

• Площадь = l × b
• Периметр = 2 (l + b)
• Диагностика = √l² + b²

Где l = длина
b = ширина

2. Площадь и периметр квадрата:

• Площадь = s × s
• Периметр = 4 с

Где s = сторона квадрата

3. Площадь и периметр параллелограмма:

• Площадь = bh
• Периметр = 2(b + h)

Где b = основание
h = высота

4. Площадь и периметр трапеции:

• Площадь = 1/2 × h (a + b)
• Периметр = а + b + с + d

Где, a, b, c, d — стороны трапеции
h — высота трапеции

5. Площадь и периметр треугольника:

• Площадь = 1/2 × b × h
• Периметр = а + b + с

Где, b = основание
h = высота
a, b, c — стороны треугольника

6. Площадь и периметр Пентагона:

• Площадь = (5/2) с × a
• Периметр = 5 с

Где s — сторона пятиугольника
a — длина

7. Площадь и периметр шестиугольника:

• Площадь = 1/2 × P × a
• Периметр = s + s + s + s + s + s = 6s

Где s — сторона шестиугольника.

8. Площадь и периметр ромба:

• Площадь = 1/2 (d1 + d2)
• Периметр = 4a

Где d1 и d2 — диагонали ромба
а — сторона ромба

9. Площадь и периметр круга:

• Площадь = Πr²
• Длина окружности = 2Πr

Где r — радиус окружности
Π = 3,14 или 22/7

10. Площадь и периметр восьмиугольника:

• Площадь = 2(1 + √2) с²
• Периметр = 8 с

Где s — сторона восьмиугольника.

Решенные примеры площади и периметра

Вот несколько примеров площади и периметра геометрических фигур. Студенты могут легко понять понятие площади и периметра с помощью этих задач.

1. Найдите площадь и периметр прямоугольника, длина которого 8м, а ширина 4м?

Решение:

Дано,
l = 8м
b = 4м
Площадь прямоугольника = l × b
A = 8м × 4м
A = 32 кв. метра
Периметр прямоугольника = 2(l + b)
P = 2(8м + 4м)
P = 2(12м)
P = 24 метра
Следовательно, площадь и периметр прямоугольника равны 32 кв.м и 24 метров.

2. Вычислите площадь ромба, диагонали которого равны 6 см и 5 см?

Решение:

Дано,
d1 = 6 см
d2 = 5 см
Площадь = 1/2 (d1 + d2)
A = 1/2 (6 см + 5 см)
A = 1/2 × 11 см
A = 5,5 кв. см
Таким образом, площадь ромба равна 5,5 кв. см

3. Найдите площадь треугольника, основание и высота которого равны 11 см и 7 см?

Решение:

Дано,
Основание = 11 см
Высота = 7 см
Мы знаем, что
Площадь треугольника = 1/2 × b × h
A = 1/2 × 11 см × 7 см
A = 1/2 × 77 кв. см
A = 38,5 кв. см
Таким образом, площадь треугольника равна 38,5 кв. см.

4. Найдите площадь круга, радиус которого равен 7 см?

Решение:

Дано,
Радиус = 7 см
Мы знаем, что
Площадь круга = Πr²
Π = 3,14
A = 3,14 × 7 см × 7 см
A = 3,14 × 49 кв. см
A = 153,86 кв. см
Следовательно, площадь круга равна 153,86 кв. см.

5. Найдите площадь трапеции, если длина, ширина и высота равны 8 см, 4 см и 5 см?

Решение:

Дано,
a = 8 см
b = 4 см
h = 5 см
Мы знаем, что
Площадь трапеции = 1/2 × h(a + b)
A = 1/ 2 × (8 + 4)5
A = 1/2 × 12 × 5
A = 6 см × 5 см
A = 30 кв. см
Следовательно, площадь трапеции равна 30 кв. см.

6. Найдите периметр пятиугольника, сторона которого равна 5 метрам?

Решение:

Учитывая, что
Сторона = 5 м
Периметр пятиугольника = 5s
P = 5 × 5 м
P = 25 метров
Следовательно, периметр пятиугольника равен 25 метрам.