Исследовательская работа «Решение логических задач с помощью кругов Эйлера» • Наука и образование ONLINE
Главная Работы на конкурс Предметное образование Физико-математические дисциплины Исследовательская работа «Решение логических задач с помощью кругов Эйлера»
Автор: Борисевич Александра Алексеевна
Место работы/учебы (аффилиация): Кордонская средняя школа Шумилинского района Витебской области Республики Беларусь, 8 класс
Научный руководитель: Борисевич Алеся Александровна
Цель исследования: показать широту применения решений логических задач с помощью кругов Эйлера для привития интереса учащихся к математике.
Задачи исследования:
- Познакомиться с историей возникновения науки комбинаторики.
- Уметь составлять и решать задачи с помощью кругов Эйлера.
- Применять полученные знания в дальнейшем обучении.
- Расширить и углубить представление о практическом значении математики в жизни.

- Уметь работать с научно-познавательной литературой, анализировать, делать выводы.
Гипотеза исследования: Показать, что решение логических задач с помощью кругов Эйлера имеет практическое применение.
Предмет исследования: понятие «Круги Эйлера» и задачи, решаемые с помощью кругов Эйлера.
В результате работы над данной темой я изучила теоретический материал по теме «Круги Эйлера» и пришла к следующим выводам:
- Логические задачи заставляют думать, рассуждать, составлять цепочку действий, последовательность, учат алгоритмизации, что немаловажно в современной жизни. А исследовательские работы учат искать информацию из различных источников (включая и интернет) и обрабатывать её, учат находить из большого материала лишь тот, который необходим.
- Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет показать, что решение логических задач с помощью кругов Эйлера имеет практическое применение.
 Таким образом, моя гипотеза подтвердилась.
Таким образом, моя гипотеза подтвердилась. - Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными. Автор метода — ученый Леонард Эйлер, говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Я согласна с его словами. Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Физико-математические дисциплины
Исследовательская работа «Школьный прогноз погоды»
Гипотеза: возможно создать собственную метеорологическую станцию из подручных средств, которая будет описывать и прогнозировать погоду на данной местности. Цели: создать метеорологическую станцию, используя подручные средства; описывать и прогнозиров…
Посмотреть работу
Физико-математические дисциплины
4″>Исследовательская работа «Создание домашнего термоса»Доступна к просмотру полнотекстовая версия работы
Я люблю смотреть познавательную программу «Галилео». В ней рассказывают о различных явлениях, окружающих человека, научных фактах, технике. В одной из передач говорили про такой предмет, как термос. И здесь я узнал, что его можно применять не только…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа по математике «Финансовая математика. Вклады»
Доступна к просмотру полнотекстовая версия работы
В современном мире люди проводят миллионы банковских операций. С развитием технологий можно управлять своими средствами через гаджеты, стали возможны переводы средств другому человеку/организации и т.д., Online инвестиции, вклады, расчеты пенсии. Воз…
Посмотреть работу
Физико-математические дисциплины
4″>Исследовательская работа «Компьютерные вирусы и борьба с ними»В настоящее время компьютер прочно вошел в повседневную жизнь. Его возможности используются в школе, на работе, при проведении досуга, в быту и других сферах жизни человека. Несмотря на принятые во многих странах законы о борьбе с компьютерными прест…
Посмотреть работу
Технические дисциплины, Физико-математические дисциплины
Исследовательская работа «Три телефона, созданные в домашних условиях»
Летние каникулы я провела у бабушки и дедушки. Мое внимание привлек их домашний телефон. Он был с необычной трубкой и диском. Такого я еще никогда не видела. У нас дома тоже есть домашний телефон. Он немного похож на мобильный, с ним можно легко пере…
Посмотреть работу
Физико-математические дисциплины
Исследовательская работа «Влияют ли числа на судьбу человека»
Доступна к просмотру полнотекстовая версия работы
Мир нас восхищает многообразием, как мы с вами постоянно говорим, различных загадок. Мало кто знает, что пароль к загадкам вселенной — это числа. Разумеется, ученые в глубочайшей древности увидели связь личности и числа. Конечно же, все мы знаем, что…
Мало кто знает, что пароль к загадкам вселенной — это числа. Разумеется, ученые в глубочайшей древности увидели связь личности и числа. Конечно же, все мы знаем, что…
Посмотреть работу
Мероприятие завершено
Круги Эйлера. Идеальный математик XVIII века (1707 – 1783гг.)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Круги Эйлера
2. Леонард Эйлер-известный швейцарский ученый
Идеальный математикXVIII ВЕКА
(1707 – 1783гг.
 )
)(к 300-летию со дня
рождения)
Нет ученого, имя которого
упоминалось бы в учебной
литературе по математике
столь же часто, как имя
Эйлера. В Энциклопедии
можно найти сведения о
шестнадцати формулах,
уравнениях, теоремах и т. д.,
носящих имя Эйлера.
«Письма о разных
физических и
философических
материях,
написанные к
некоторой
немецкой
принцессе…», где
появились впервые
«круги Эйлера»
Эйлер писал тогда, что «круги
очень подходят для того, чтобы
облегчить наши размышления».
При решении целого ряда задач
Леонард Эйлер использовал идею
изображения множеств с помощью
кругов и они получили название
«круги Эйлера».
6. Типы кругов Эйлера
Диаграмма Эйлера-Венна — наглядное средстводля работы со множествами. На этих диаграммах
изображаются все возможные варианты
пересечения множеств. Количество пересечений
(областей) n определяется по формуле:
n
N=2 ,
где n — количество множеств.
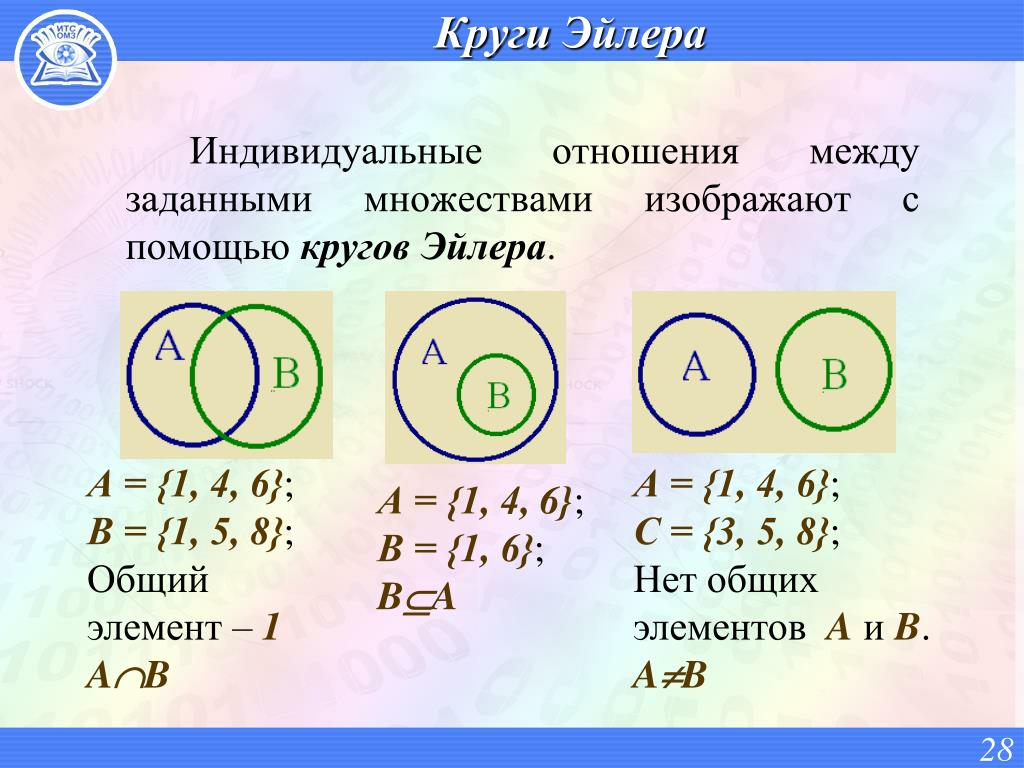
Таким образом, если в задаче используется два
множества, то N=22=4, если три множества, то
N=23=8, если четыре множества, то N=24=16.
Диаграммы Эйлера-Венна используются в
основном для N<=4.
Для диаграмм Эйлера-Венна
справедливы два основных
понятия:
Универсальное множество
(универсум) U (в контексте
задачи) — множество, содержащее
все элементы рассматриваемой
задачи: элементы всех множеств
задачи и элементы, не входящие
в них.
Пустое множество Ø (в контексте
задачи) — множество, не
содержащее ни одного элемента
рассматриваемой задачи. На
диаграмме строят
пересекающиеся множества,
заключают их в универсум.
9. Множество чисел
Множество всехдействительных чисел
Эйлер изобразил с
помощью этих кругов:
N-множество
натуральных чисел,
Z – множество целых
чисел,
Q – множество
рациональных чисел,
R – множество вех
действительных
чисел.
10.
 Решение задач с помощью кругов Эйлера.Часть жителей
Решение задач с помощью кругов Эйлера.Часть жителейнашего города умеет
говорить только порусски, часть –
только по-башкирски
и часть умеет
говорить на обоих
языках. Побашкирски говорят
85%, по-русски 75%.
Сколько процентов
жителей говорят на
обоих языках?
11. Решение:
(жителейговорят только по-русски)
75%-15%=60% (жителей
говорят на обоих языках)
100%-85%=15%
12. Задача 2. О подругах
Все мои подругивыращивают в своих
квартирах какиенибудь растения.
Шестеро из них
разводят кактусы, а
пятеро — фиалки. И
только у двоих есть
и кактусы и фиалки.
Угадайте, сколько у
меня подруг?
13. Спортивная задача
В футбольной команде«Баймак» 30 игроков:
18 нападающих.
11 полузащитников,
17 защитников
Вратари
3 могут быть
нападающими и
защитниками,
10 защитниками и
полузащитниками,
6 нападающими и
защитниками
1 и нападающим, и
защитником, и
полузащитником.
Вратари не заменимы.
Сколько в команде
«Баймак» вратарей?
14. Решение
18+11+17-3-106+1=28 (игроков)на этой
диаграмме. Но в
команде всего 30
футболистов.
Значит вратарей
будет 30-28=2.
Ответ: 2 вратаря.
15. «Озеро Графское»
«Озеро Графское»
Из 100 отдыхающих
на турбазе
«Графское»,
30 детей — отличники
учебы,
28 — участники
олимпиад,
42 — спортсмены.
8 учащихся
одновременно
участники олимпиад и
спортсмены,
10 – участники
олимпиад и отличники,
5 – спортсмены и
отличники учебы,
3 – и отличники, и
участники олимпиад, и
спортсмены.
Сколько отдыхающих
не относятся ни к
одной из групп?
16. Решение
•20+13+30+3+5+7+2=80 (детей)
•100-80=20 (детей не
входят ни в одну из
групп)
•Ответ: 20 детей.
17. Выводы
КругиЭйлера – инструмент
визуализации работы со
множествами,
Применение кругов Эйлера
(диаграмм Эйлера-Венна)
позволяет легко решить задачи,
которые обычным путем
разрешимы лишь при
составлении системы трех
уравнений с тремя неизвестными.

18. Инструмент формализации – формула включений и исключений
Введем следующее понятие: числоэлементов конечного множества A
называется мощностью этого
множества и обозначается |A|.
Формула включений и исключений
даёт возможность находить
мощность объединения любого
конечного набора множеств.
Формула включений и исключений для
двух множеств. Для любых конечных
множеств A и B справедливо равенство:
|A ∪ B| = |A| + |B| − |A ∩ B|.
Формула включений и исключений для
трёх множеств. Для любых конечных
множеств A, B и C справедливо равенство:
|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| −
|B ∩ C| − |A ∩ C| + |A ∩ B ∩ C|.
20. Выводы
Формулавключений и
исключений – инструмент
формализации работы со
множествами,
Применение формулы включений
и исключений основывается на
формальном языке математики,
то есть на составлении уравнения
или системы уравнений.
English Русский Правила
🍒 Что Это и Зачем Она Нужна, Как Построить?
13 сентября, 2022 г.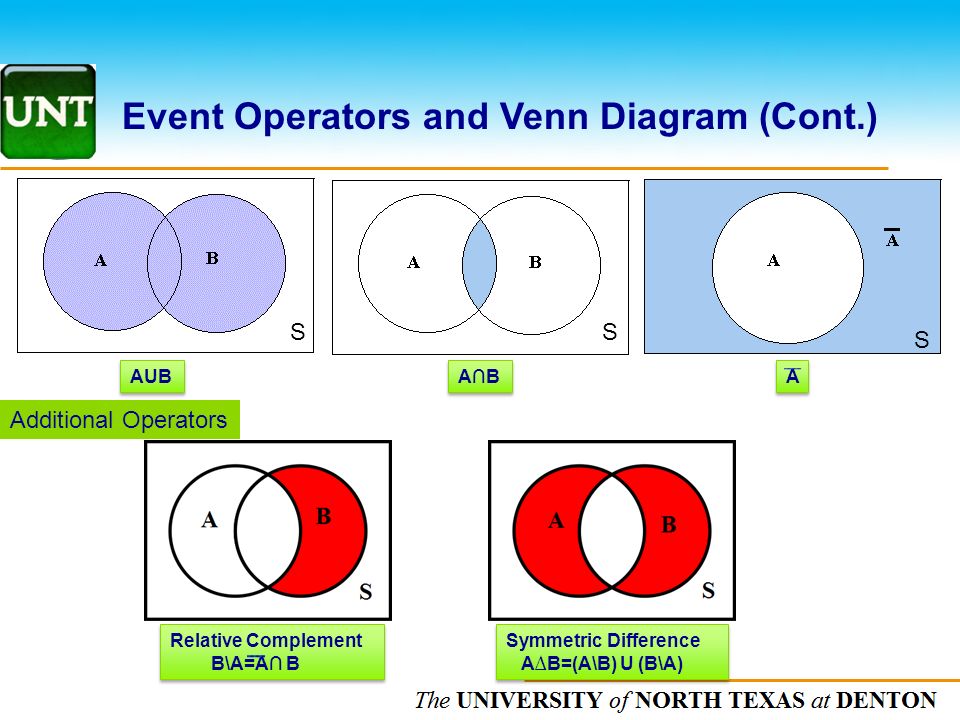
1 отзыв, в среднем 5 из 5
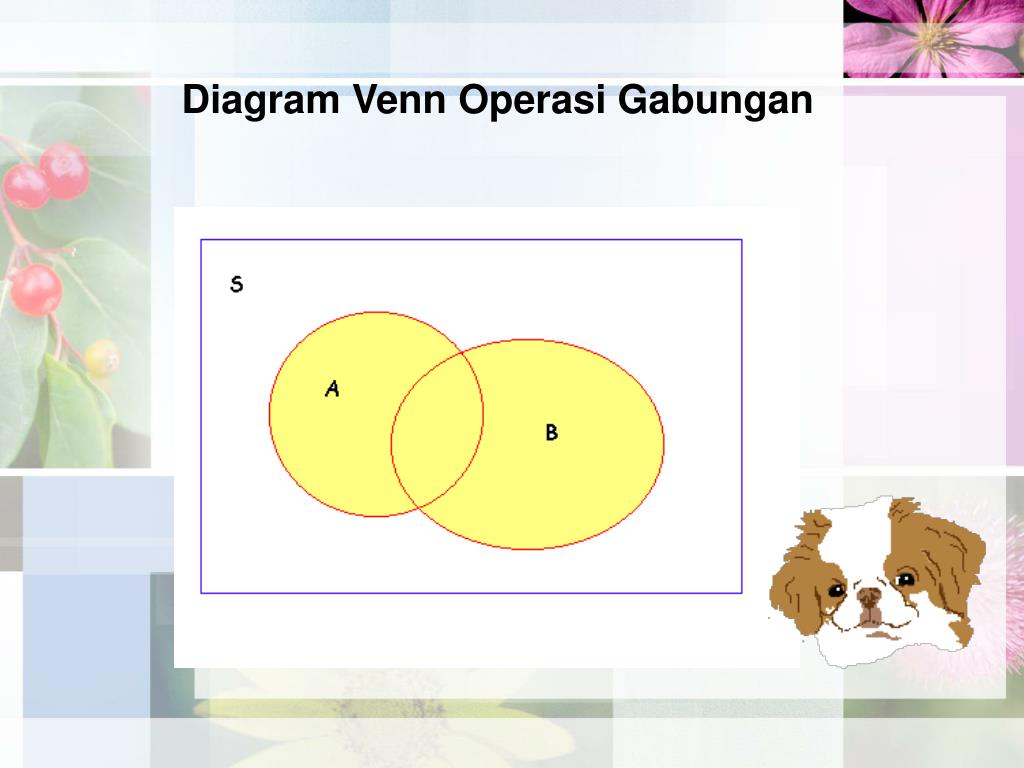
Диаграмма Венна — это графический способ выражения связи между разными элементами, событиями или тем, что надо между собой сравнить.
1. | Что такое Venn diagram? |
2. | Когда нужны диаграммы Венна? |
3. | Как создать venn diagram? |
4. | Venn Diagram |
Когда нужны диаграммы Венна | |
6. | Как создать venn diagram |
7. | Из чего состоит диаграмма Венна |
8. | История создания venn diagram |
9. | В чем разница между venn diagram и кругами Эйлера? |
10. | Пример использования venn diagram |
11. | Диаграмма Венна в дизайн–мышлении |
12. | Инструменты для построения venn diagram |
3 профессия
21 курсов
24 тренингов
431 модулей
2 765 уроков
128 часов видео
Длительность обучения — 6 месяцев
2 занятия в неделю
+ 2 765 уроков на платформе
Освойте IT–профессию «Продакт–менеджер»
С нуля, без опыта в IT. Цель обучения — трудоустроить вас в Enterprise IT–компании: Сбер, ВТБ, Ozon и Yandex.
Цель обучения — трудоустроить вас в Enterprise IT–компании: Сбер, ВТБ, Ozon и Yandex.
- Вы получите железную уверенность в ваших компетенциях — для новой работы или развития карьеры в вашей текущей компании
- Вы получите реальный коммерческий опыт до конца обучения
- Работаем до этапа закрытия собеседования и трудоустройства
- Начнете участвовать в карьерных активностях с первого занятия
- Дополнительные карьерные активности по поиску работы за рубежом и релокации — по желанию, без дополнительной платы
- Индивидуальный подход — проводим Welcome–интервью, оцениваем уровень и составляем индивидуальный Roadmap
- Обучение продуктовой аналитике и работе с продуктовыми метриками, с обязательной реальной «Data Science» практикой
- Доступ к материалам профессии «Скрам–мастер & Agile–коуч»
- Единый доступ к образовательной платформе со всеми курсами, тренингами, воркшопами и профессиями — включая обновления
- Поможем в создании правильного экспертного имиджа и сделаем вам крутое интро в профессиональное продуктовое комьюнити
- Погрузим вас в продуктовый контекст и научим разговаривать с разработчиками, аналитиками и руководством на одном языке
- Научим отстаивать свою позицию, защищать бэклог и иметь вес при принятии продуктовых решений на всех уровнях компании
Шаблон диаграммы Венна | Примеры диаграмм Венна для решения проблем.
 Информатика. Иерархия Хомского | Диаграммы Венна
Информатика. Иерархия Хомского | Диаграммы ВеннаНевозможно переоценить полезность и удобство использования готовых шаблонов при создании собственных диаграмм и графиков. И диаграммы Венна не исключение. Программное обеспечение ConceptDraw PRO для построения диаграмм и векторного рисования представляет решение Venn Diagrams из раздела «Что такое диаграмма», которое предлагает набор шаблонов и образцов диаграмм Венна. Используйте подходящий шаблон диаграммы Венна, чтобы создать собственную диаграмму Венна любой сложности.
Диаграмма Венна, иногда называемая диаграммой множеств, представляет собой стиль построения диаграмм, используемый для отображения всех возможных логических отношений между конечным числом множеств. С математической точки зрения набор — это набор отдельных объектов, собранных вместе в группу, которую затем можно назвать единым объектом.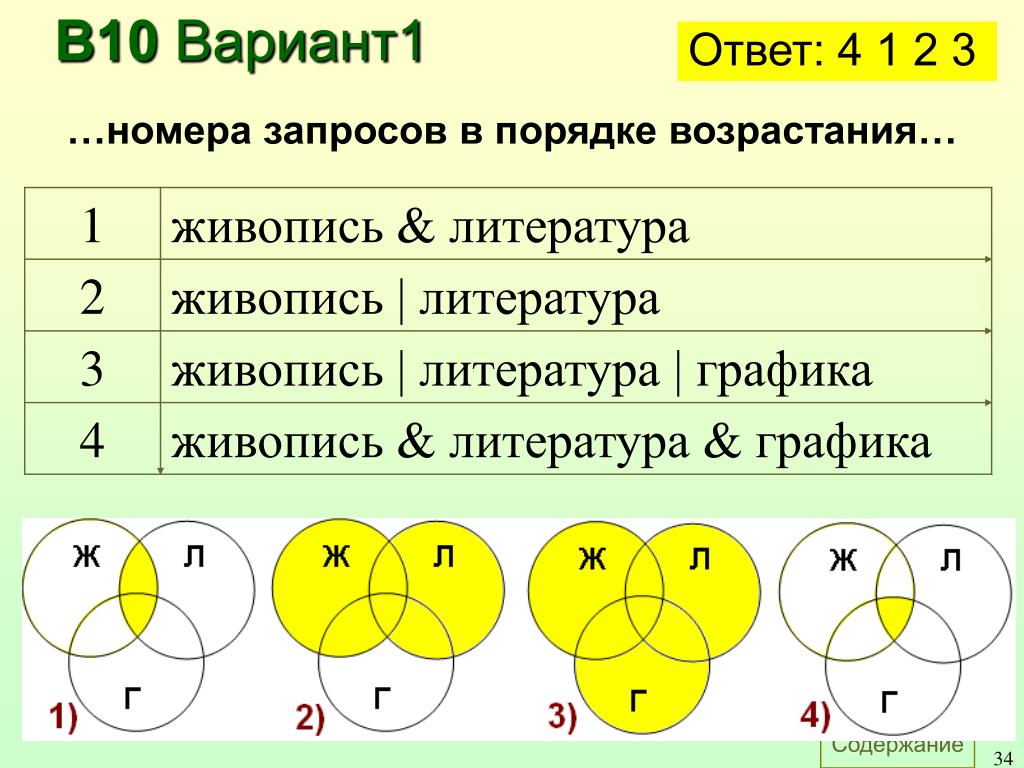 Диаграммы Венна представляют эти объекты на странице в виде кругов или эллипсов, а их размещение по отношению друг к другу описывает отношения между ними.
Диаграммы Венна представляют эти объекты на странице в виде кругов или эллипсов, а их размещение по отношению друг к другу описывает отношения между ними.
Приведенный ниже пример диаграммы Венна визуализирует класс языковых включений, описываемых иерархией Хомского.
Диаграммы Венна активно используются для иллюстрации простых отношений множеств в теории множеств и теории вероятностей, логике и статистике, математике и информатике, лингвистике, социологии и маркетинге. Диаграммы Венна также часто используются для визуального обобщения статуса и будущей жизнеспособности проекта.
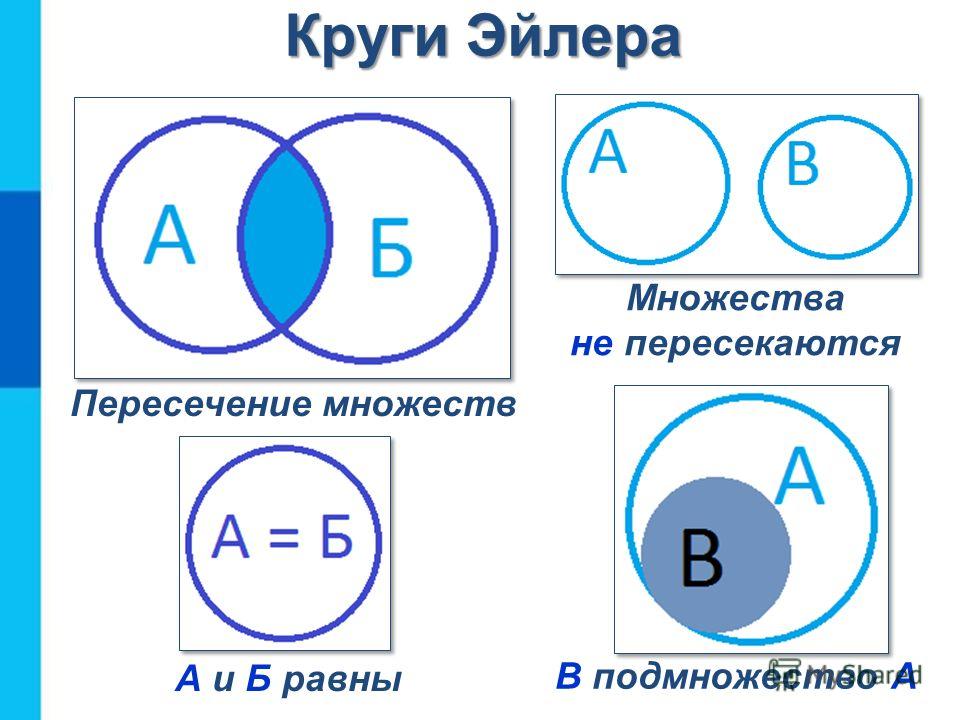
Диаграммы Венна — это интуитивно понятный способ работы с множествами, который позволяет визуализировать все возможные логические отношения между несколькими множествами. Они широко используются в математике, маркетинге, логике, статистике, социологии и др.
Программное обеспечение ConceptDraw PRO для построения диаграмм и векторного рисования, дополненное решением Venn Diagrams из области «Что такое диаграмма», предлагает набор полезных инструментов для рисования, упрощающих создание диаграмм Венна для любого количества наборов.
Чтобы визуализировать отношения между подмножествами универсального множества, вы можете использовать диаграммы Венна. Чтобы его построить, нужно разбить плоскость на несколько клеток с помощью n фигур. Каждая цифра на диаграмме представляет один набор, а n — количество представленных наборов. Разбиение производится таким образом, чтобы для любого набора этих фигур была одна и только одна ячейка, точки которой принадлежат всем фигурам из набора и не принадлежат другим. Плоскость, на которой изображены фигуры, есть универсальное множество U. Таким образом, точка, не принадлежащая ни одной из фигур, принадлежит только U.
Используйте этот шаблон для создания пяти наборов диаграмм Венна.
«Диаграмма Венна из пяти наборов с использованием конгруэнтных эллипсов в радиально-симметричном расположении, разработанная Бранко Грюнбаумом. Метки были упрощены для большей удобочитаемости». [Диаграмма Венна. Википедия]
Шаблон «Диаграмма Венна из 5 наборов» для программного обеспечения ConceptDraw PRO для построения диаграмм и векторного рисования включен в решение «Диаграммы Венна» из области «Что такое диаграмма» в парке решений ConceptDraw.
Шаблон
Вам нужен дизайн Cylinder Venn Diagram? Нет ничего проще с программным обеспечением для построения диаграмм и векторной графики ConceptDraw PRO, дополненным решением Venn Diagrams Solution из области «Что такое диаграмма». ConceptDraw PRO позволяет создавать различные диаграммы Венна, включая цилиндрические диаграммы Венна.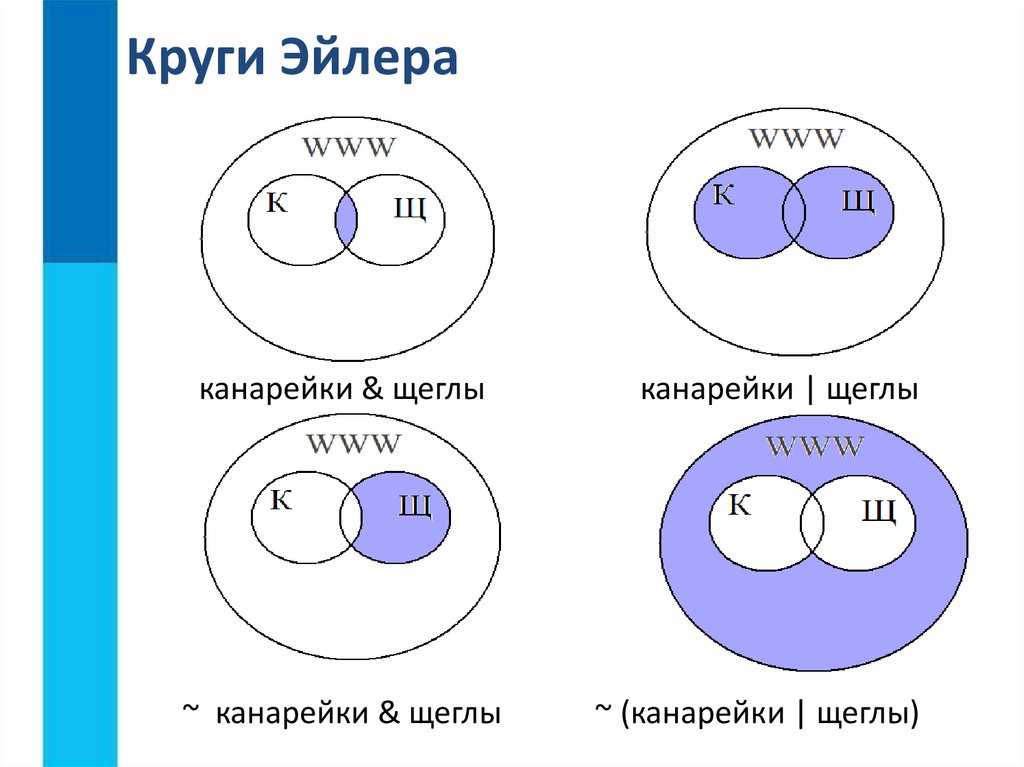
Библиотека векторных шаблонов «Диаграммы Венна» содержит 12 шаблонов диаграмм Венна и Эйлера.
Используйте эти фигуры для рисования диаграмм Венна и Эйлера в программном обеспечении для построения диаграмм и векторной графики ConceptDraw PRO, дополненном решением Venn Diagrams из раздела «Что такое диаграмма» в ConceptDraw Solution Park.
2-компонентная диаграмма Венна
3-компонентная диаграмма Венна
4-компонентная диаграмма Венна
5-компонентная диаграмма Венна
2-компонентная диаграмма Венна
3-компонентная диаграмма Венна
5-компонентная диаграмма Венна
2-компонентная диаграмма Венна
3 набора диаграмм Венна
4 набора диаграмм Венна
5 наборов диаграмм Венна
Используемые растворы
Что такое диаграмма >
Диаграммы Венна
Программное обеспечение ConceptDraw PRO для построения диаграмм и векторного рисования, дополненное решением Venn Diagrams из области «Что такое диаграмма», предлагает широкий набор профессионально разработанных примеров диаграмм Венна, которые могут стать хорошим началом и прекрасным источником вдохновения для ваших собственных диаграмм Венна.
Venn Diagrams Solution предлагает вам библиотеку Venn Diagrams, состоящую из готовых к использованию векторных объектов, а также большую коллекцию шаблонов и образцов, позволяющих создавать собственные интерактивные диаграммы Венна за считанные минуты.
Диаграммы Венна, разработанные в ConceptDraw PRO, наглядны, ярки, красочны, поэтому их можно с успехом использовать в различных докладах, выступлениях на конференциях, совещаниях.
Программное обеспечение ConceptDraw PRO для построения диаграмм и векторного рисования, дополненное решением Venn Diagrams из раздела «Что такое диаграмма» в ConceptDraw Solution Park, является мощным средством создания диаграмм Венна. Создавайте быстро и легко свои собственные диаграммы Венна для визуализации: всех возможных логических отношений между наборами, простых отношений наборов в логике, статистике, математике, социологии, маркетинге, суммируйте статус и будущую жизнеспособность проекта.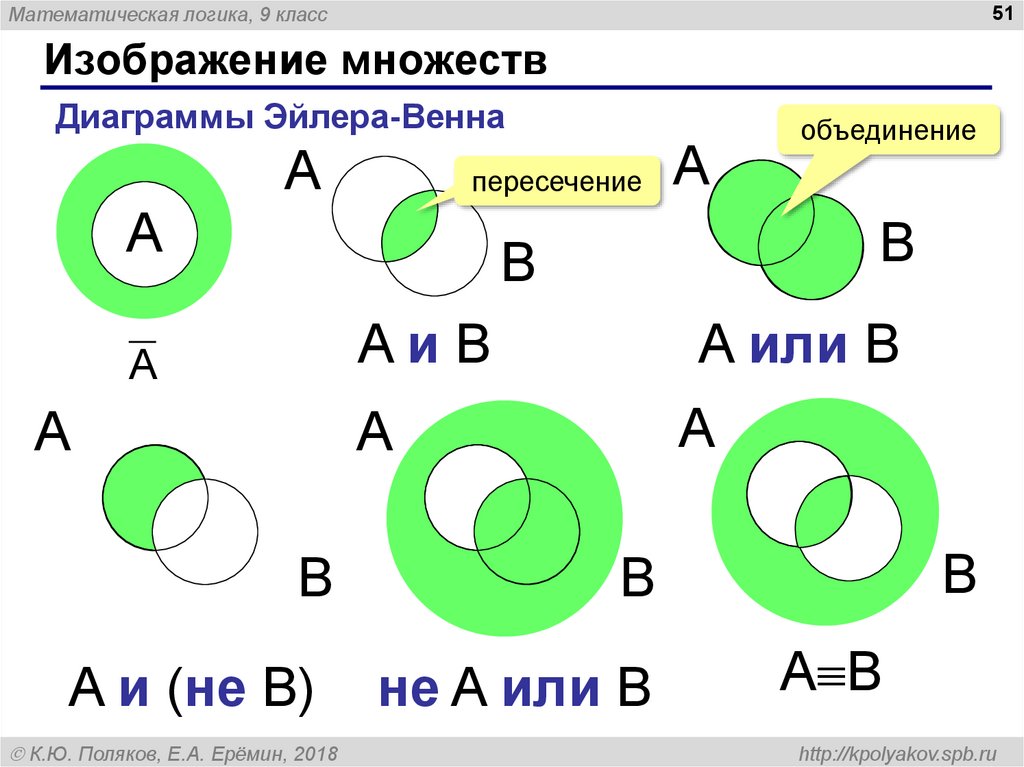
Что такое круговая диаграмма? Это диаграмма, в которой центральный элемент окружен другими элементами по кругу. Диаграммы круговых спиц часто используются для демонстрации функций или компонентов центрального элемента в маркетинговых и управленческих документах и презентациях. ConceptDraw PRO, дополненный решением для диаграмм с круговыми спицами из области «Что такое диаграмма», является лучшим программным обеспечением для создания диаграмм с круговыми спицами.
Target Diagram — удобный и наглядный способ представления информации, популярный и широко используемый в маркетинге, бизнесе и экономике. Программное обеспечение ConceptDraw PRO для построения диаграмм и векторного рисования, дополненное решением Target and Circular Diagrams из области маркетинга ConceptDraw Solution Park, идеально подходит для быстрого и простого рисования целевых диаграмм.
Это решение расширяет возможности ConceptDraw PRO версии 10 (или более поздней) образцами, шаблонами и библиотеками векторных трафаретов для рисования диаграмм Венна.
Диаграммы Венна — это иллюстрации, используемые в разделе математики, известном как теория множеств. Они показывают математическую или логическую связь между различными группами вещей (наборами). Диаграмма Венна показывает все возможные логические отношения между множествами.
Бесплатная программа для создания диаграмм Венна | Lucidchart
Lucidchart — это визуальное рабочее пространство, которое сочетает в себе создание диаграмм, визуализацию данных и совместную работу для ускорения понимания и внедрения инноваций.
Создайте диаграмму Венна
Посмотрите видеоОсновной генератор диаграмм Венна для всех
Начните с шаблонов диаграмм Венна
Диаграммы Венна могут быть простыми для визуализации сравнений и контрастов.
 Если вы не хотите создавать диаграмму Венна с нуля, наша галерея шаблонов в Lucidchart поможет вам начать работу. Всего несколькими щелчками мыши вы можете превратить свой пустой холст в настраиваемую диаграмму Венна. В нашей галерее создателей диаграмм Венна представлено множество примеров на выбор, чтобы вы могли быстро и легко создать диаграмму Венна онлайн. Если вы хотите быстро сравнить продукты и услуги или найти корреляции между несколькими наборами данных для принятия обоснованных решений, у нас есть шаблоны, которые помогут вам начать работу.
Если вы не хотите создавать диаграмму Венна с нуля, наша галерея шаблонов в Lucidchart поможет вам начать работу. Всего несколькими щелчками мыши вы можете превратить свой пустой холст в настраиваемую диаграмму Венна. В нашей галерее создателей диаграмм Венна представлено множество примеров на выбор, чтобы вы могли быстро и легко создать диаграмму Венна онлайн. Если вы хотите быстро сравнить продукты и услуги или найти корреляции между несколькими наборами данных для принятия обоснованных решений, у нас есть шаблоны, которые помогут вам начать работу.С легкостью настраивайте и оформляйте
Функция перетаскивания в Lucidchart проста и интуитивно понятна. Все, что вам нужно сделать, это выбрать прозрачный круг из библиотеки форм диаграммы Венна, что дает вам возможность перекрывать ваши фигуры. Поделитесь своими идеями и выводами с талантом – вы можете редактировать и форматировать фигуры и текст, настраивать цвета, уровни градиента, шрифты, размеры, границы и многое другое.
 Lucidchart — это генератор диаграмм Венна, упрощающий построение диаграмм.
Lucidchart — это генератор диаграмм Венна, упрощающий построение диаграмм.Использование диаграмм Венна в классе
Не зря диаграммы Венна являются одним из основных предметов в каждом классе и учебнике. Визуальные подсказки помогают учащимся лучше запоминать и извлекать информацию. Эти мощные графические ссылки дают учащимся возможность быстро сортировать информацию по группам и определять сходства и различия. Это делает Lucidchart выбранным генератором диаграмм Венна для классных комнат, позволяя учащимся и учителям легко комбинировать текст и формы, чтобы облегчить визуальное обучение и способствовать глубокому пониманию в любой учебной среде.
Публикуйте с помощью популярных интеграций
Публикуйте и делитесь своими диаграммами Венна в Интернете с кем угодно, откуда угодно и когда угодно.
 Lucidchart работает на всех основных операционных системах, включая Windows, Mac и Linux. Используйте наш инструмент для создания диаграмм Венна, чтобы делиться своими идеями с другими — даже с теми, у кого нет учетных записей Lucidchart — с помощью любой из наших мощных интеграций с ведущими приложениями, которые вы уже используете, такими как G Suite, Microsoft Office, Confluence, Jira и Slack. Просто экспортируйте свою диаграмму Венна или создайте общий URL-адрес, чтобы начать совместную работу и распространять идеи, которыми стоит поделиться.
Lucidchart работает на всех основных операционных системах, включая Windows, Mac и Linux. Используйте наш инструмент для создания диаграмм Венна, чтобы делиться своими идеями с другими — даже с теми, у кого нет учетных записей Lucidchart — с помощью любой из наших мощных интеграций с ведущими приложениями, которые вы уже используете, такими как G Suite, Microsoft Office, Confluence, Jira и Slack. Просто экспортируйте свою диаграмму Венна или создайте общий URL-адрес, чтобы начать совместную работу и распространять идеи, которыми стоит поделиться.
Используйте наш конструктор диаграмм Венна в Lucidchart
Определите основные идеи для сравнения
Начните с шаблона для настройки или начните с выбора библиотеки форм диаграммы Венна, а затем перетащите круглые формы или наборы на холст.
 Вы можете дублировать или изменять размер этих фигур, чтобы они были больше, меньше или даже овалами.
Вы можете дублировать или изменять размер этих фигур, чтобы они были больше, меньше или даже овалами.Создайте перекрывающиеся круги и пометьте
Пометьте оба отдельных набора на диаграмме Венна. Чтобы добавить текст, просто перетащите текстовое поле поверх фигур и выделите метку полужирным шрифтом или подчеркните ее, чтобы отличить ее от заметок.
Введите различия, уникальные для каждого набора
Сравните и сопоставьте каждую из основных идей, отметив как можно больше соответствующих различий.
Введите сходства, общие для каждого перекрестка.
Отформатируйте информацию в виде маркеров и списков, щелкнув значок «Параметры текста».

Публикация и совместное использование
Поделитесь своей диаграммой Венна в Интернете с помощью общей ссылки, по электронной почте, в Slack или социальных сетях или вставьте свою диаграмму в вики.
Создание диаграммы Венна
Часто задаваемые вопросы о шаблонах диаграмм Венна в Lucidchart
Как мне создать диаграммы Венна из нескольких наборов?
Как изменить цвета диаграммы Венна?
Как создать диаграмму Венна в Excel?
Как создать диаграмму Венна в PowerPoint?
Узнайте, почему Lucidchart — идеальное средство для создания диаграмм Венна
Используется миллионами людей по всему миру
«Этот продукт легко превосходит Visio, Xmind или любое другое приложение в своем роде. Даже с бесплатной версией вы получаете лучший и простой пользовательский опыт, и поскольку вы используете продукт чаще, вы получаете больше возможностей в бесплатной версии».
Даже с бесплатной версией вы получаете лучший и простой пользовательский опыт, и поскольку вы используете продукт чаще, вы получаете больше возможностей в бесплатной версии».
4.5/5 stars 650+ reviews
Browse Venn diagram templates
Venn Diagram Template
Multi-Set Venn Diagram Template
Triple Venn Diagram Template
Scaled Venn Diagram Template
Шаблон диаграммы Венна треугольник Рело
Диаграмма Венна с 4 кругами
Шаблон диаграммы Венна с квадратом
Шаблон диаграммы Венна с 5 кругами
Шаблон диаграммы Венна Эйлера
Узнайте, почему 99% компаний из списка Fortune 500 надежно масштабируют свои предприятия с помощью Lucidchart
Узнайте больше
Диаграммы типов Венна и Эйлера для векторных пространств и абелевых групп
Популярный способ визуализации взаимосвязей между некоторым конечным числом множеств — это диаграммы Венна или, в более общем случае, диаграммы Эйлера.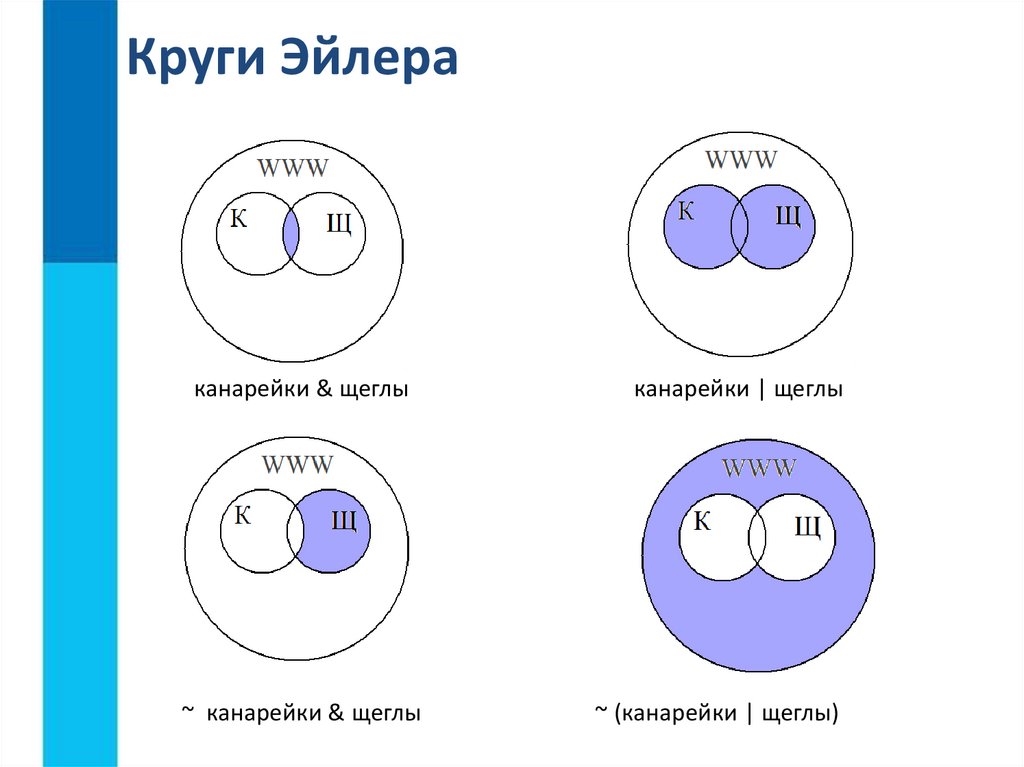 На этих диаграммах множество изображается в виде двумерной формы, такой как диск или прямоугольник, и различные логические отношения между этими множествами (например, то, что одно множество содержится в другом, или что пересечение двух множеств равен трети) представлен булевой алгеброй этих форм; Диаграммы Венна соответствуют случаю, когда множества находятся в «общем положении» в том смысле, что все нетривиальные булевы комбинации множеств непусты. Например, чтобы изобразить общую ситуацию двух множеств вместе с их пересечением, можно использовать диаграмму Венна, такую как
На этих диаграммах множество изображается в виде двумерной формы, такой как диск или прямоугольник, и различные логические отношения между этими множествами (например, то, что одно множество содержится в другом, или что пересечение двух множеств равен трети) представлен булевой алгеброй этих форм; Диаграммы Венна соответствуют случаю, когда множества находятся в «общем положении» в том смысле, что все нетривиальные булевы комбинации множеств непусты. Например, чтобы изобразить общую ситуацию двух множеств вместе с их пересечением, можно использовать диаграмму Венна, такую как
(где мы обозначили каждую область разным цветом и немного отодвинули края каждой области друг от друга, чтобы сделать их видимыми по отдельности), но если бы кто-то хотел вместо этого изобразить ситуацию, в которой пересечение было пустым , можно было бы использовать диаграмму Эйлера, такую как
Можно использовать площадь различных областей на диаграмме Венна или Эйлера в качестве эвристического заместителя мощности (или меры) множества, соответствующего такой области.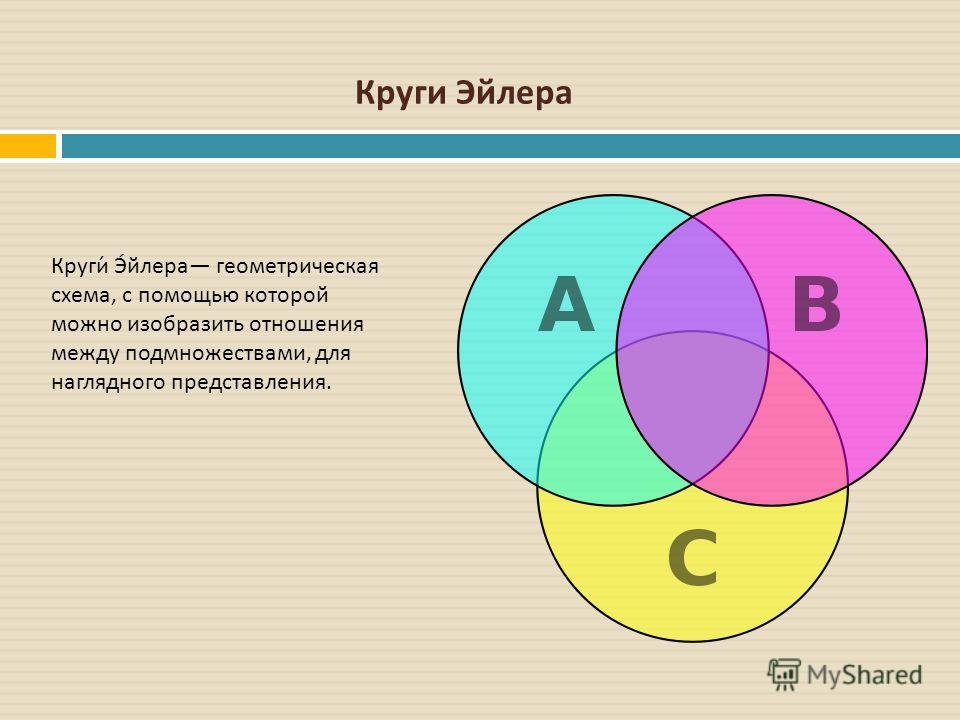 Например, приведенную выше диаграмму Венна можно использовать для интуитивного обоснования формулы включения-исключения 9.0003
Например, приведенную выше диаграмму Венна можно использовать для интуитивного обоснования формулы включения-исключения 9.0003
для конечных множеств, в то время как приведенная выше диаграмма Эйлера аналогичным образом оправдывает частный случай
для конечных непересекающихся множеств.
Хотя диаграммы Венна и Эйлера традиционно двумерны по своей природе, ничто не мешает использовать одномерные диаграммы, такие как
или даже трехмерные диаграммы, такие как эта из Википедии:
Конечно, в таких случаях можно было бы использовать длину или объем в качестве эвристического показателя мощности или меры, а не площади.
С добавлением стрелок диаграммы Венна и Эйлера также могут вмещать (в некоторой степени) функции между наборами. Вот, например, изображение функции, изображение этой функции и изображение некоторого подмножества:
Здесь можно проиллюстрировать сюръективность, заполнив все ; аналогичным образом можно проиллюстрировать инъективность, задав точно такую же форму (или, по крайней мере, ту же площадь), что и .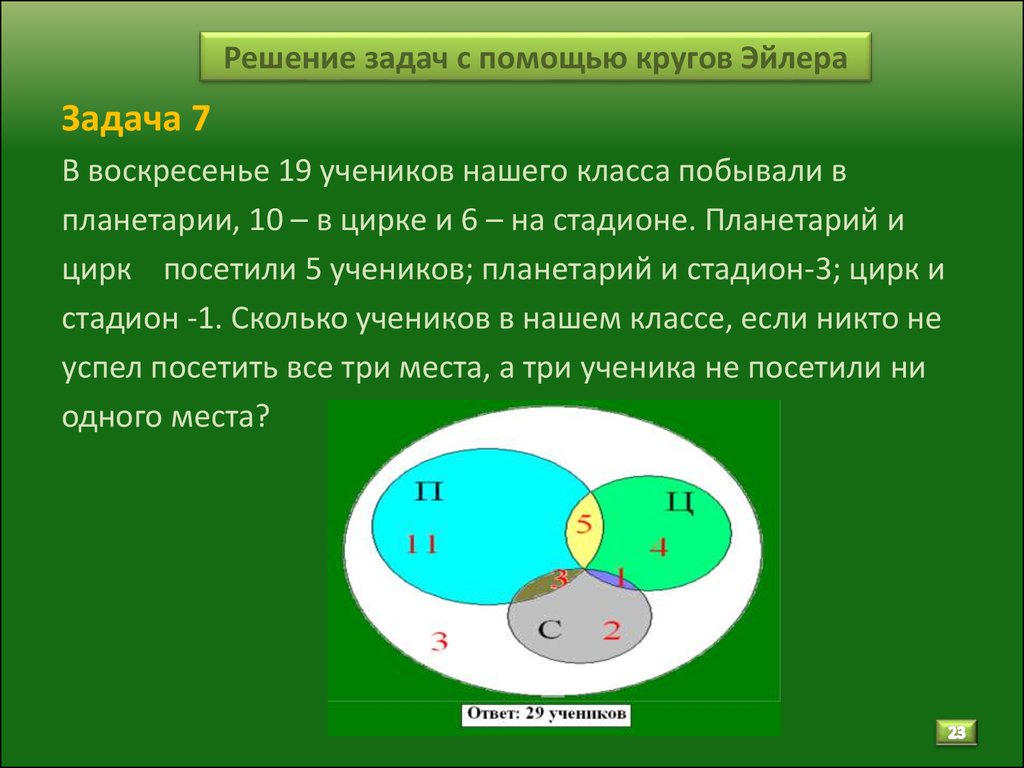 Вот, например, как можно проиллюстрировать инъективную функцию:
Вот, например, как можно проиллюстрировать инъективную функцию:
Декартовы операции произведения могут быть включены в эти диаграммы с помощью соответствующих комбинаций одномерных и двумерных диаграмм. Вот, например, диаграмма, иллюстрирующая тождество:
В этом сообщении блога я хотел бы предложить аналогичное семейство диаграмм для иллюстрации отношений между 90 219 векторными пространствами 90 220 (над фиксированным базовым полем, таким как вещественные числа) или 90 219 абелевыми группами 90 220, а не множествами. Категории (-)векторных пространств и абелевых групп во многом очень похожи; первая состоит из модулей над базовым полем, а вторая состоит из модулей над целыми числами; кроме того, обе категории являются основными примерами абелевых категорий. Понятие размерности векторного пространства во многом аналогично понятию мощности множества; см. этот предыдущий пост для примера этой аналогии (в контексте энтропии Шеннона). (ОБНОВЛЕНИЕ: я узнал, что по существу идентичная запись была также предложена в неопубликованной рукописи Рави Вакиля.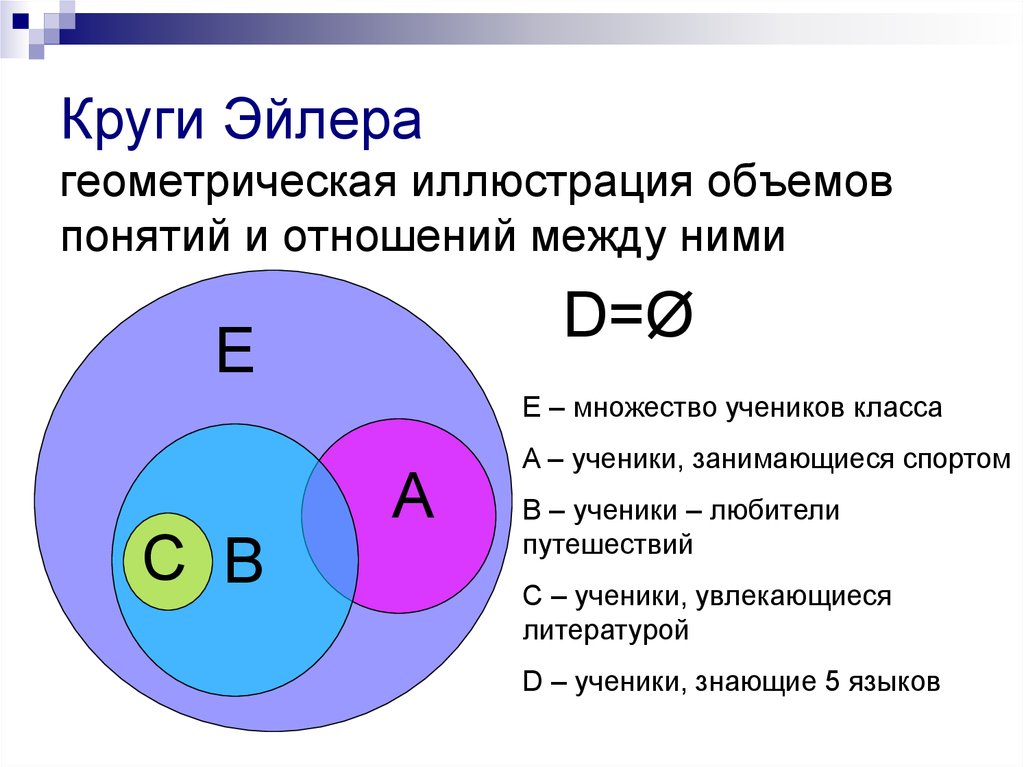 )
)
Как и в случае с диаграммами Венна и Эйлера, диаграммы, которые я предлагаю для векторных пространств (или абелевых групп), могут быть построены в любом измерении. Для простоты начнем с одного измерения и ограничимся векторными пространствами (ситуация для абелевых групп в основном идентична). В этой одномерной модели мы сможем изобразить следующие отношения и операции между векторными пространствами:
- Включение одного векторного пространства в другое (здесь я предпочитаю использовать для включения групповое обозначение, а не множество).
- Фактор векторного пространства по подпространству .
- Линейное преобразование между векторными пространствами, а также ядром, образом, коядром и кообразом.
- Одна короткая или длинная точная последовательность между векторными пространствами.
- (эвристический аналог) размерности векторного пространства.
- Прямая сумма двух пробелов.
Идея состоит в том, чтобы использовать полуоткрытые интервалы в реальной прямой для любого моделирования векторных пространств. Фактически мы можем сделать явное соответствие: отождествим каждый полуинтервал с (бесконечномерным) векторным пространством
Фактически мы можем сделать явное соответствие: отождествим каждый полуинтервал с (бесконечномерным) векторным пространством
то есть отождествляется с пространством непрерывных на отрезке функций, обращающихся в нуль на правом конце. Такие функции непрерывно продолжаются нулем до полупрямой.
Обратите внимание, что если тогда векторное пространство является подпространством , если мы продолжим функции в обоих пространствах нулем до полупрямой ; кроме того, частное естественно отождествляется с . Таким образом, включение , как и факторпространство , здесь можно смоделировать следующим образом:
Напротив, если , значительно менее «естественно» рассматривать его как подпространство ; это можно было бы сделать, расширив функции справа нулем и слева константами, но в этом соглашении об обозначениях следует рассматривать такое отождествление как «искусственное», и его следует избегать.
Все пространства бесконечномерны, но с моральной точки зрения размерность векторного пространства «пропорциональна» длине соответствующего интервала. Интуитивно, если мы попытаемся дискретизировать это векторное пространство путем выборки в некоторой сетке интервалов , можно получить конечномерное векторное пространство размерностью примерно . Уже на приведенной выше диаграмме теперь изображена основная идентичность
Интуитивно, если мы попытаемся дискретизировать это векторное пространство путем выборки в некоторой сетке интервалов , можно получить конечномерное векторное пространство размерностью примерно . Уже на приведенной выше диаграмме теперь изображена основная идентичность
между конечномерным векторным пространством, подпространством этого пространства и фактором этого пространства.
Обратите внимание, что если , то существует линейное преобразование из векторного пространства в векторное пространство, которое берет функцию в , ограничивает ее до , а затем расширяет ее нулем до . Ядро этого преобразования есть , образ (изоморфен) , коядро (изоморфно) , а кообраз (изоморфен) . Имея это в виду, теперь мы можем изобразить общее линейное преобразование и связанные с ним пространства с помощью следующей диаграммы:
Обратите внимание, как первая теорема об изоморфизме и теорема об отсутствии ранга эвристически иллюстрируются этой диаграммой.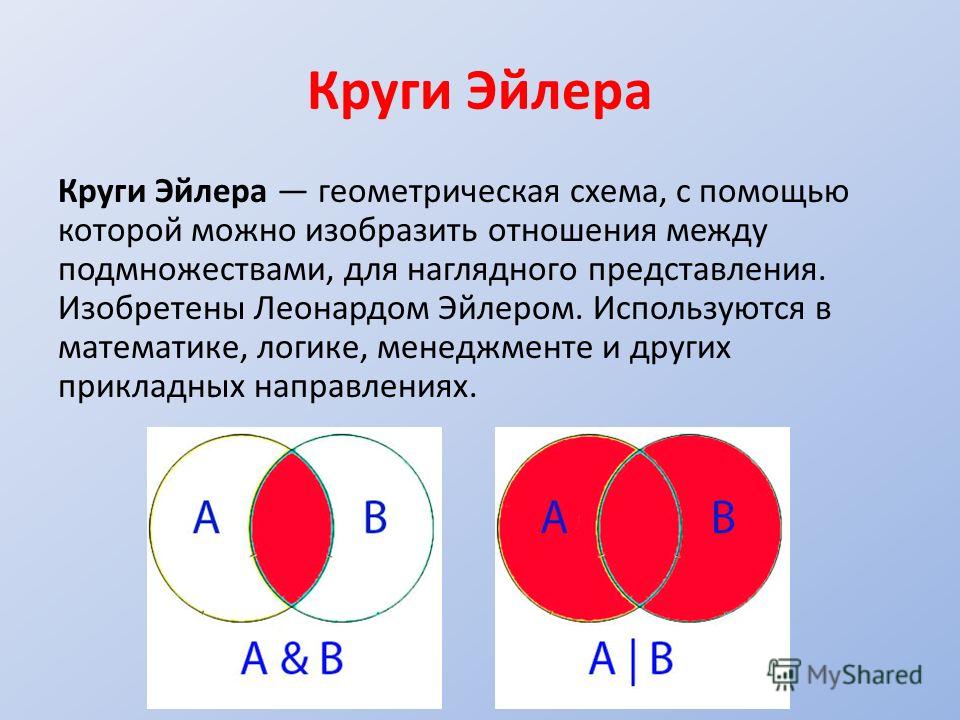 Можно специализироваться на случае инъективных, сюръективных или биективных преобразований, вырождая один или несколько полуоткрытых интервалов на приведенной выше диаграмме в пустой интервал. Сдвиг влево порождает нильпотентное линейное преобразование от самого себя:
Можно специализироваться на случае инъективных, сюръективных или биективных преобразований, вырождая один или несколько полуоткрытых интервалов на приведенной выше диаграмме в пустой интервал. Сдвиг влево порождает нильпотентное линейное преобразование от самого себя:
В том же духе короткая точная последовательность векторных пространств (или абелевых групп) теперь может быть изображена диаграммой
и длинную точную последовательность можно аналогичным образом изобразить диаграммой
ОБНОВЛЕНИЕ: как я узнал из неопубликованной рукописи Рави Вакиля, это обозначение также может легко изображать группы когомологий коцепного комплекса с помощью диаграммы
и аналогичным образом изобразить группы гомологии цепного комплекса диаграммой
Можно связать несвязное объединение полуоткрытых интервалов с прямой суммой связанных векторных пространств, что дает возможность изображать прямые суммы с помощью этого обозначения:
Чтобы увеличить выразительность этой записи, мы теперь перейдем к двум измерениям, где мы также можем изобразить следующие дополнительные отношения и операции:
- Пересечение и сумма двух подпространств объемлющего пространства ;
- Несколько коротких или длинных точных последовательностей;
- Тензорное произведение двух векторных пространств.

Здесь мы заменяем полуоткрытые интервалы полуоткрытыми множествами: геометрическими фигурами, такими как многоугольники или диски, которые содержат часть границы (нарисованы сплошными линиями), но пропускают часть границы (нарисованы пунктирными линиями). . Каждая такая форма может быть связана с векторным пространством, а именно с непрерывными функциями, обращающимися в нуль на пропущенной части границы. Все отношения, которые раньше изображались с помощью одномерных диаграмм, теперь можно аналогичным образом изобразить с помощью двумерных диаграмм. Например, вот двумерное изображение векторного пространства, подпространства и его частного:
(В этом посте я попытаюсь последовательно сделать нижнюю и левую границы этих областей закрытыми, а верхнюю и правую — открытыми, хотя это не обязательно для применимости этого обозначения.)
Но теперь мы можем изобразить некоторые дополнительные отношения. Вот, например, один из способов изобразить пересечение и сумму двух подпространств:
Обратите внимание, как это иллюстрирует тождество
. между конечномерными векторными пространствами , а также некоторыми стандартными изоморфизмами, такими как .
между конечномерными векторными пространствами , а также некоторыми стандартными изоморфизмами, такими как .
Две конечные подгруппы абелевой группы называются соизмеримыми , если есть подгруппа с конечным индексом группы . Это можно изобразить, сделав область между и маленькой и/или окрашенной в определенный цвет:
Здесь соизмеримость эквивалентна конечности групп и , которые соответствуют серым треугольникам на приведенной выше диаграмме. Теперь, например, становится интуитивно понятно, почему соизмеримость должна быть отношением эквивалентности.
Чтобы проиллюстрировать, как эта нотация может поддерживать несколько коротких точных последовательностей, я дал себе задание использовать эту нотацию для изображения леммы о змее, как показано на этой следующей диаграмме, взятой из только что связанной страницы Википедии:
Это оказалось чрезвычайно сложно выполнить без введения вырождений (например, исчезновение одного из ядер или коядер). Вот одно решение, которое я придумал; возможно, есть более элегантные. В частности, должно быть изображение, которое более явно отражает двойственную симметрию диаграммы змеи.
Вот одно решение, которое я придумал; возможно, есть более элегантные. В частности, должно быть изображение, которое более явно отражает двойственную симметрию диаграммы змеи.
Здесь карты между шестью пространствами являются очевидными картами ограничения (и можно визуально убедиться, что два квадрата на диаграмме змеи действительно коммутируют). Затем каждое из пространств ядра и коядра трех вертикальных карт ограничения связывается с объединением двух подобластей, как показано на диаграмме. Обратите внимание, как перекрытия между этими ядрами и коядрами создают длинную точную «змейку».
ОБНОВЛЕНИЕ: изменив аналогичную диаграмму в неопубликованной рукописи Рави Вакила, я теперь могу создать более симметричную версию приведенной выше диаграммы, опять же с очень заметной «змеей»:
В наших обозначениях (алгебраическое) тензорное произведение интервала и другого интервала не совсем , но это становится верным, если использовать -алгебраическую версию тензорного произведения благодаря теореме Стоуна-Вейерштрасса. Таким образом, можно правдоподобно использовать декартовы произведения в качестве прокси для произведения тензора векторного пространства. Например, вот описание отношения когда является подпространством:
Таким образом, можно правдоподобно использовать декартовы произведения в качестве прокси для произведения тензора векторного пространства. Например, вот описание отношения когда является подпространством:
К сожалению, у этой записи есть некоторые ограничения: например, независимо от того, сколько измерений вы используете для своих диаграмм, эти диаграммы будут предлагать неверную идентичность.
(который, кстати, на данный момент является ответом, набравшим наибольшее количество голосов на вопрос MathOverflow «Примеры распространенных ложных убеждений в математике»). (См. также эту предыдущую запись в блоге о подобном явлении при использовании наборов или векторных пространств для моделирования энтропии информационных переменных.) Тем не менее, оно кажется достаточно точным, чтобы его можно было использовать для иллюстрации многих общих отношений между векторными пространствами и абелевыми группами. С соответствующей долей скептицизма ее можно было бы использовать и для других категорий помимо этих двух, хотя для неабелевых категорий следует действовать с осторожностью, поскольку диаграмма может указывать на отношения, которые на самом деле неверны в этой категории.


 Таким образом, моя гипотеза подтвердилась.
Таким образом, моя гипотеза подтвердилась.

 Lucidchart — это генератор диаграмм Венна, упрощающий построение диаграмм.
Lucidchart — это генератор диаграмм Венна, упрощающий построение диаграмм.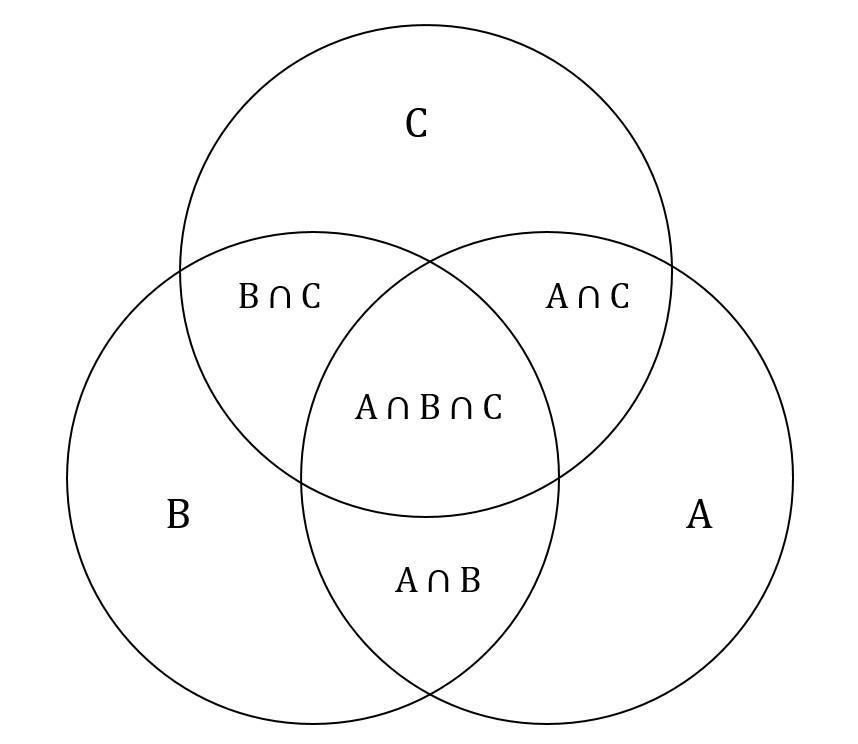 Lucidchart работает на всех основных операционных системах, включая Windows, Mac и Linux. Используйте наш инструмент для создания диаграмм Венна, чтобы делиться своими идеями с другими — даже с теми, у кого нет учетных записей Lucidchart — с помощью любой из наших мощных интеграций с ведущими приложениями, которые вы уже используете, такими как G Suite, Microsoft Office, Confluence, Jira и Slack. Просто экспортируйте свою диаграмму Венна или создайте общий URL-адрес, чтобы начать совместную работу и распространять идеи, которыми стоит поделиться.
Lucidchart работает на всех основных операционных системах, включая Windows, Mac и Linux. Используйте наш инструмент для создания диаграмм Венна, чтобы делиться своими идеями с другими — даже с теми, у кого нет учетных записей Lucidchart — с помощью любой из наших мощных интеграций с ведущими приложениями, которые вы уже используете, такими как G Suite, Microsoft Office, Confluence, Jira и Slack. Просто экспортируйте свою диаграмму Венна или создайте общий URL-адрес, чтобы начать совместную работу и распространять идеи, которыми стоит поделиться.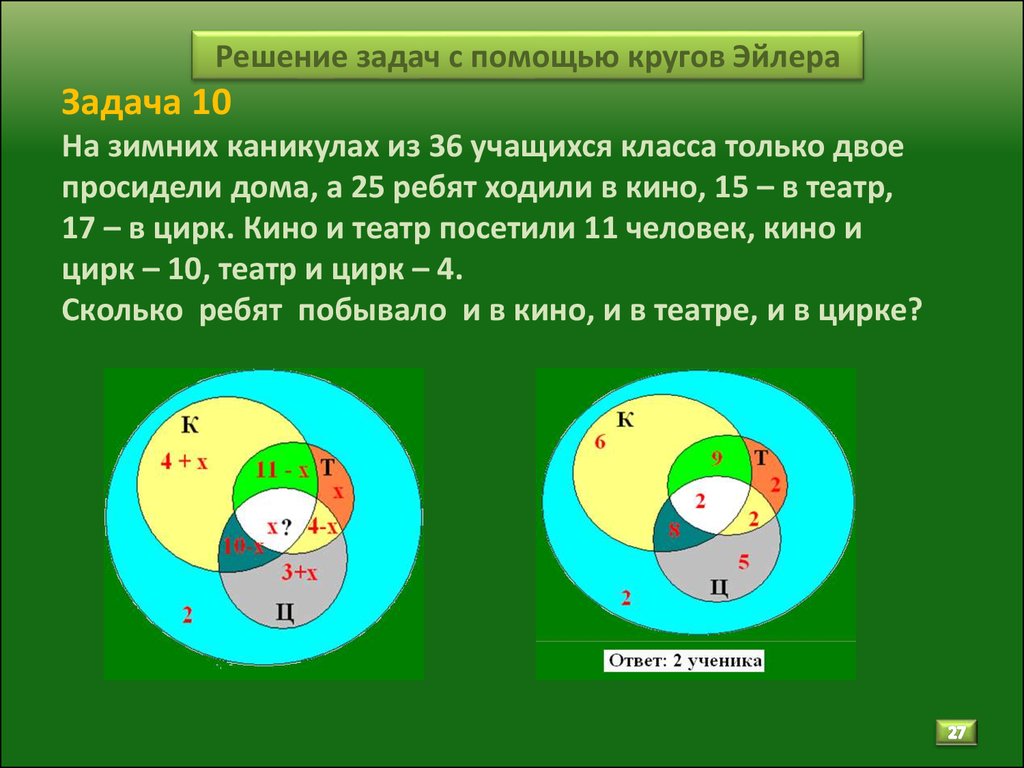 Вы можете дублировать или изменять размер этих фигур, чтобы они были больше, меньше или даже овалами.
Вы можете дублировать или изменять размер этих фигур, чтобы они были больше, меньше или даже овалами.