Раздел 14 (ответы)
Раздел 14. Комплексные числа.
Записать в алгебраической форме число:
Ответ:
Записать в алгебраической форме число:
Запишем число в тригонометрической форме:
Тогда искомое число равно:
Ответ:
Для числа найти и
Ответ:
Записать в алгебраической форме число;
Для упрощения вычислений запишем числитель и знаменатель в показательной форме:
Ответ;
Нарисовать на комплексной плоскости область, заданную неравенствами:
Первое неравенство задает внутреннюю часть окружности с границей с радиусом и центром в точке .
Второе
неравенство задает первую четверть
комплексной плоскости (включая
положительные полуоси).
Таким образом, система задает внутреннюю часть с границей расположенной в первой четверти половины окружности с центром в точке .
Нарисовать на комплексной плоскости область, заданную неравенством:
Представим число в алгебраической форме и решим неравенство:
Решить уравнение. Ответ записать в алгебраической форме
Ответ:
Решить уравнение. Ответ записать в алгебраической форме
Запишем комплексное число в алгебраической форме и решим уравнение:
Ответ:
Найти все решения уравнения , лежащие в области
Определим все корни уравнения:
Проверим принадлежность полученных корней заданной области:
Все решения
уравнения лежат вне заданной области.
Ответ: в заданной области нет решений уравнения.
Найти все решения уравнения , лежащие в области
Определим все корни уравнения:
Проверим принадлежность полученных корней заданной области:
Ответ:
Соседние файлы в папке Вступительный экзамен 2018
- #
26.08.2018152.84 Кб138Раздел 1(ответы).docx
- #
26.08.2018348.96 Кб133Раздел 10 (ответы).docx
- #
26.08.201882.04 Кб123Раздел 11 (ответы).docx
26.08.201881.58 Кб134Раздел 12 (ответы).docx
- #
26.08.201893.51 Кб131Раздел 13 (ответы).docx
- #
26.08.2018240.59 Кб140Раздел 14 (ответы).docx
- #
26.
 08.201874.19 Кб142Раздел 15 (ответы).docx
08.201874.19 Кб142Раздел 15 (ответы).docx - #
26.08.201898.74 Кб134Раздел 17 (ответы).docx
- #
26.08.201894.69 Кб131Раздел 18 (ответы).docx
- #
26.08.201882.36 Кб129Раздел 19 (ответы).docx
- #
26.08.2018444.78 Кб129Раздел 2(ответы).docx
Контрольная работа 3 страница
⇐ Предыдущая123
Из условия задачи получаем:
1) ; ; ;
2) ; ; ;
Из (1) и (2):3) ; ; .
Интегралы от по промежутку от до равны нулю, поэтому при вычислении эти части сразу отбрасываем. Тогда получится = = = = = = .
Ответ: .
Задача 12. Найти все значения корня.
Решение:
Корни для комплексных чисел вычисляются по формуле = , где k целое число больше или равно 0 и меньше n. Т.е. всегда имеется n корней; — главное значение аргумента z; r – модуль числа z.
Т.е. всегда имеется n корней; — главное значение аргумента z; r – модуль числа z.
Для z = 1 будет, и r = 1, тогда получим, при n = 3, три корня: , где ; ; .
Ответ: ; ; .
Задача 13. Представить в алгебраической форме комплексные числа.
$p = Arch(-2).$
Решение:
= = = .
Ответ: 1) , 2) .
Задача 14.
1) , 2) .
Решение:
Пусть . Первое неравенство задает замкнутую область в виде круг радиуса 2, с центром в точке . Второе неравенство задает открытую область в виде полуплоскости лежащей праве прямой . Оба неравенства задают пересечение этих областей .
Задача 15. Восстановить аналитическую в окрестности точки функцию по известной действительной или мнимой части и значению .
, .
Решение:
Для комплексных аналитических функций выполняются следующие условия: , Откуда получаем:
1) , где — функция зависящая только от y.
2) .
= ; = =
= . Вычисляем действительную часть по формуле (1) подставляя полученные занчения:
= .
Из условия найдем С: = = .Ответ: = .
Задача 17. Данную функцию разложить в ряд Лорана в окрестности точки .
= .
Решение:
= = .
Разложим в ряд Тейлора по степеням : = = .
= = =
= = =
= . = = = .
Ответ: .
Задача 18. Вычислить интеграл.
.
Решение:
Подынтегральная функция имеет один полюс в точке . Поэтому =
= Вычислим вычет как коэффициент ряда Лорана:
= = = = . = = .
= = .
Ответ: .
Задача 20. Вычислить интеграл с помощью комплексных чисел.
.
Решение:
Выполним подстановку , , тогда = =
= = , где — полюса подынтегральной функции лежащие внутри круга . Такими полюсами будут корни уравнения лежащие внутри круга . Корни равны: , . — внутри круга, — вне круга = = = = .
Ответ: .
Задача 21. Вычислить интеграл с помощью вычетов.
.
Решение:
= ,где -полюса подынтегральной функции лежащие в верхней полуплоскости. Корни Уравнения равны:
= , = , = , = .
Все корни имеют кратность два, следовательно, полюсы будут второго порядка. В верхней полуплоскости лежат и .
= .
Вычеты вычисляем по формуле .
= , = =
= = .
Ответ: .
⇐ Предыдущая123 |
Дата добавления: 2015-06-04; Просмотров: 866; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Объяснение урока: Области на комплексной плоскости
В этом объяснении мы узнаем, как использовать локусы для идентификации областей на комплексной плоскости.
Прежде чем мы будем работать с областями на комплексной плоскости, мы кратко повторим некоторые уравнения мы используем для определения кругов, линий и полупрямых на комплексной плоскости.
Типы регионов, которые мы будем рассматривать в этом объяснении, определяются в терминах неравенства, такие как |𝑧−𝑧|𝑟 и составные области, определенные в терминах множественных неравенств. Например, рассмотрим регион определяется |𝑧+1+𝑖|2. Чтобы представить это на Argand диаграмме мы сначала рассмотрим круг, определяемый |𝑧+1+𝑖|=2. Мы обратите внимание, что это круг радиуса 2 с центром в (-1,-1). Поскольку неравенство является строгим неравенством, мы должны нарисовать этот круг, используя пунктирную линию, чтобы обозначить тот факт, что заштрихованная область не включает свою границу.
После того, как мы нарисовали граничные линии, нам нужно заштриховать область. Чтобы сделать это правильно, мы
нужно рассмотреть, должны ли мы затенить внутреннюю или внешнюю сторону круга. Это будет
диктуется направлением неравенства. Если мы рассматриваем неравенство в
форме |𝑧−𝑧|𝑟, нас будет интересовать
внутреннюю часть круга, тогда как, если мы рассматриваем |𝑧−𝑧|>𝑟, нас будет интересовать внешность круга. Фигура
показывает области комплексной плоскости, представленные |𝑧+1+𝑖|2 и |𝑧+1+𝑖|>2.
Это будет
диктуется направлением неравенства. Если мы рассматриваем неравенство в
форме |𝑧−𝑧|𝑟, нас будет интересовать
внутреннюю часть круга, тогда как, если мы рассматриваем |𝑧−𝑧|>𝑟, нас будет интересовать внешность круга. Фигура
показывает области комплексной плоскости, представленные |𝑧+1+𝑖|2 и |𝑧+1+𝑖|>2.
Теперь мы покажем, как мы можем распознать область комплексной плоскости, данную нам в условия неравенства.
Пример 1: Представление областей на комплексной плоскости
Что из следующего представляет область комплексной плоскости, определяемую −𝜋2≤(𝑧+3−2𝑖)𝜋4?argОтвет
Начнем с рассмотрения границ области. Есть два, которые мы должны рассмотреть:
arg(𝑧+3−2𝑖)=𝜋4 и arg(𝑧+3−2𝑖)=−𝜋2. Начиная с первого из них, мы замечаем, что это половина
линия, исходящая из −3+2𝑖, которая образует положительный угол
𝜋4 с положительной горизонталью. Аналогично, второй
граница области определяется как arg(𝑧+3−2𝑖)=−𝜋2,
которая представляет собой половину линии, исходящей из −3 + 2𝑖, что составляет отрицательный угол
из 𝜋2 с положительной горизонталью. Все фигуры включают
обе эти пограничные линии.
Все фигуры включают
обе эти пограничные линии.
Область определяется как −𝜋2≤(𝑧+3−2𝑖)𝜋4arg; следовательно, это будет область между этими двумя полупрямыми. Это исключает оба возможных ответа (а) и (е).
Теперь рассмотрим, входят ли граничные точки в регион или нет. С arg(𝑧+3−2𝑖)𝜋4 — строгое неравенство, это границу области следует изобразить пунктирной линией. Это исключает (c) как вариант ответа.
У нас остается либо (b), либо (d) в качестве возможных ответов. Разница между этими двумя цифры зависит от того, использовали ли мы сплошной круг • или полый круг ∘ для обозначения конечной точки −3+2𝑖. Напомним, что мы используем сплошной круг, чтобы указать, что линия включает в себя конечную точку, тогда как пустой кружок означает, что конечная точка не включена. Кроме того, напомнить что аргумент комплексного числа не определен для нуля.
Следовательно, область, определяемая −𝜋2≤(𝑧+3−2𝑖)𝜋4arg, не будет включать конечную точку и, следовательно, правильный
представительство региона (б).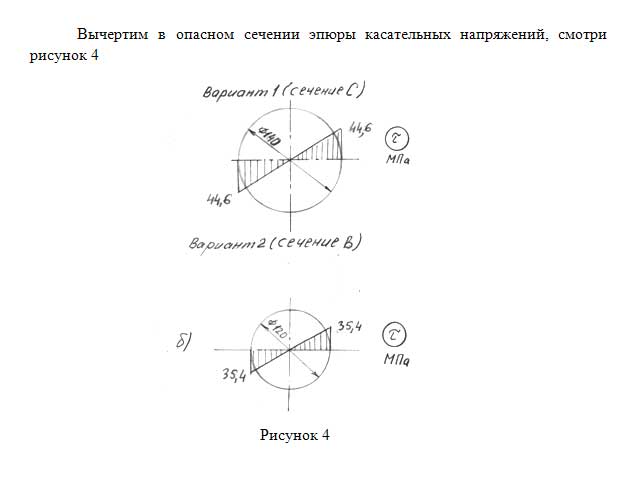
Пример 2: Описание областей на комплексной плоскости
На рисунке показана область на комплексной плоскости.
Напишите алгебраическое описание заштрихованной области.
Ответ
Существует несколько способов описать окружность на комплексной плоскости. Например, мы можно попробовать использовать форму |𝑧−𝑧|=𝑘|𝑧−𝑧|. Однако в большинстве случаев это значительно больше сложный процесс, чтобы попытаться найти две точки, расстояние которых до данной окружности находится в постоянное соотношение. Поэтому мы склонны выражать области, включающие круги, используя форму |𝑧−𝑧|=𝑟. это вообще намного проще сделать, так как все, что нам нужно сделать, это определить центр и радиус.
На рисунке нам дан центр. Поэтому мы можем просто констатировать, что
𝑧=4+𝑖. Однако нам нужно вычислить радиус. Во-первых, мы
обратите внимание, что окружность пересекает мнимую ось в точке 7𝑖. Поэтому,
чтобы найти радиус, мы можем либо использовать теорему Пифагора, либо просто вычислить
модуль разности этого комплексного числа с 𝑧.
Следовательно, 𝑟=|7𝑖−(4+𝑖)|=|−4+6𝑖|.
Используя определение модуля, мы имеем 𝑟=√(−4)+6=√52=2√13.
Обратите внимание, что мы рассматриваем область вне этого круга. Поэтому мы учитывая точки, которые находятся дальше от центра, чем радиус. Кроме того, на рисунке использована сплошная линия, которая показывает, что граничные точки включены. Следовательно, область описывается следующим неравенством: |𝑧−4−𝑖|≥2√13.
Чтобы описать более интересные области на комплексной плоскости, мы часто хотим говорить о области, которые подвержены множественным ограничениям на значение 𝑧. Один из распространенные способы сделать это — использовать нотацию множества и операции над множествами.
Напомним, что запись {𝑧∈ℂ∶(𝑧)0}Re означает, что мы говорим о множестве всех комплексных чисел, которые имеют
положительная действительная часть. Эта нотация называется нотацией построителя наборов. Кроме того, когда
Говоря о множествах, мы выполняем ряд общих операций.
Объединения, пересечения и дополнения
Для двух множеств 𝐴,𝐵⊂𝑈, где 𝑈 — универсальная множество, которое содержит как 𝐴, так и 𝐵, мы определяем объединение 𝐴 и 𝐵 быть набором всех элементов, которые находятся в 𝐴 или в 𝐵. Обратите внимание, что когда мы говорим «или» мы используем включающее или; то есть мы имеем в виду, что элемент находится в 𝐴 или 𝐵 или как в 𝐴, так и в 𝐵. Мы используем обозначение 𝐴∪𝐵 для представления союза. Используя нотацию построителя наборов, мы можно написать 𝐴∪𝐵={𝑥∈𝑈∶𝑥∈𝐴𝑥∈𝐵}.или
Пересечение 𝐴 и 𝐵 определяется как множество все элементы, которые есть как в 𝐴, так и в 𝐵. Мы пишем это как 𝐴∩𝐵. Используя нотацию построителя наборов, мы можем написать 𝐴∩𝐵={𝑥∈𝑈∶𝑥∈𝐴𝑥∈𝐵}.and
Наконец, мы определяем дополнение множества 𝐴 как все элементы
которые есть в универсальном множестве, но не в 𝐴. Мы используем обозначение
𝐴 для представления этого. Используя нотацию построителя наборов, мы
можно записать как 𝐴={𝑥∈𝑈∶𝑥∉𝐴}.
Используя нотацию построителя наборов, мы
можно записать как 𝐴={𝑥∈𝑈∶𝑥∉𝐴}.
Мы можем представить каждое из них с помощью диаграммы Венна следующим образом.
Пример 3: Представление составных областей на комплексной плоскости
Мы определяем области 𝐴, 𝐵 и 𝐶 в комплексной плоскости как 𝐴={𝑧∈ℂ∶(𝑧)4},𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−8−12𝑖|},𝐶={𝑧∈ℂ∶|𝑧−6 −5𝑖|5}.Re
Какая из следующих фигур может представлять область комплексной плоскости, определяемую (𝐴∩𝐵)∪𝐶?
Ответ
Наилучший подход к решению этой задачи состоит в том, чтобы сначала рассмотреть регионы, представленные
𝐴, 𝐵 и 𝐶
в отдельности. Начиная с 𝐴, мы сначала
рассмотрим область, представленную 𝐴={𝑧∈ℂ∶(𝑧)4}Re, а затем ее дополнение. Заметить, что
𝐴 представляет все комплексные числа с действительными частями меньше 4. Следовательно, это будет область слева от строки 𝑥=4. Уведомление
что, поскольку неравенство строгое, мы обозначим границу штриховой линией. На рисунке ниже показан регион 𝐴.
На рисунке ниже показан регион 𝐴.
Нам, однако, не нужно рассматривать область 𝐴; нам нужно рассмотреть 𝐴. Это будет область всех точек, не в 𝐴. Мы можем думать об этом визуально, инвертируя области, которые у нас есть. заштрихованы в плоскости. Обратите внимание, что при этом нам нужно изменить границу с пунктирную линию в сплошную. В качестве альтернативы, мы можем думать об этом более абстрактно, как следует. Поскольку 𝐴 представляет все комплексные числа с действительной частью меньше чем 4, 𝐴 будет представлять все комплексные числа с действительная часть больше или равна 4. Какой бы подход мы ни использовали, мы можем представить 𝐴 как следующий регион.
Теперь рассмотрим 𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−8−12𝑖|}. Начнем с рассмотрения границы области, где |𝑧|≤|𝑧−8−12𝑖|. Обратите внимание, что это представляет собой
серединный перпендикуляр к отрезку прямой между началом координат и точкой, представленной
𝑧=8+12𝑖. Мы можем изобразить это на диаграмме Аргана со сплошной линией.
прямой, так как область содержит граничные точки. Тогда заметим, что неравенство
представляет все точки, находящиеся ближе к началу координат, чем 8+12𝑖. Следовательно,
мы можем представить область 𝐵 следующим образом.
Мы можем изобразить это на диаграмме Аргана со сплошной линией.
прямой, так как область содержит граничные точки. Тогда заметим, что неравенство
представляет все точки, находящиеся ближе к началу координат, чем 8+12𝑖. Следовательно,
мы можем представить область 𝐵 следующим образом.
Теперь мы можем рассмотреть пересечение 𝐴∩𝐵 эти два региона. Это будут все точки, находящиеся в обоих регионах. Мы можем представить это следующим образом.
Теперь мы можем рассмотреть 𝐶={𝑧∈ℂ∶|𝑧−6−5𝑖|5}. Это представляет собой круг радиуса 5 с центром в точке 6+5𝑖. Обратите внимание, что поскольку неравенство строгое, область не содержит границы. Следовательно, мы можем представить эту область следующим образом.
Наконец, мы рассматриваем объединение 𝐴∩𝐵 и 𝐶. Напомним, что это область, которую мы получаем, складывая все точки в оба региона вместе. Мы можем представить это следующим образом.
Следовательно, правильный ответ (г).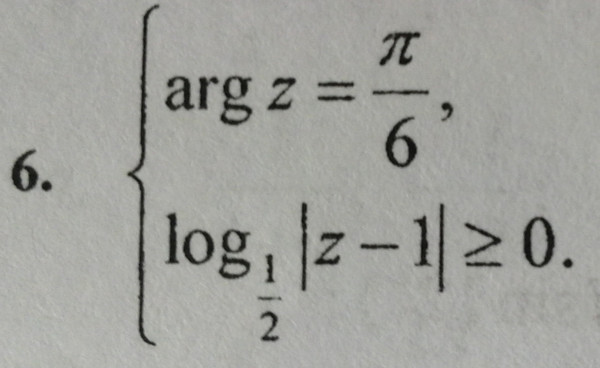
Пример 4. Описание составных областей на комплексной плоскости
Заштрихованная область на следующем рисунке может быть алгебраически описана как 𝐴∩𝐵∩𝐶, где 𝐴={𝑧∈ℂ∶(𝑧)𝑎},𝐵={𝑧 ∈ℂ∶|𝑧|≤|𝑧−𝑧|},𝐶={𝑧∈ℂ∶|𝑧|≤|𝑧−𝑧|}.Im
Найдите значения 𝑎, 𝑧, и 𝑧, где 𝑎∈ℝ и 𝑧,𝑧∈ℂ.
Ответ
Область ограничена тремя линиями: 𝐿, 𝐿, и 𝐿, как показано ниже.
Первый из них, 𝐿, представлен
Im(𝑧)=2. Регион не содержит
граничные точки вдоль этой линии. Следовательно, 𝐴={𝑧∈ℂ∶(𝑧)2}Im. Теперь обратим внимание на
𝐿. Нам нужно описать эту прямую как серединный перпендикуляр к
отрезок линии между началом координат и другой точкой, которую мы обозначили
𝑃. Иногда, как в этом примере, это можно сделать с помощью
осмотр. Мы видим, что прямая проходит через две диагонально противоположные стороны.
вершины квадрата, определяемые точками (0,0), (3,0), (3,−3) и
(0,−3). Следовательно, это серединный перпендикуляр к отрезку.
между двумя другими диагонально противоположными вершинами. Следовательно, 𝐿 является
серединный перпендикуляр к отрезку между (0,0) и
𝑃(3,−3).
Следовательно, это серединный перпендикуляр к отрезку.
между двумя другими диагонально противоположными вершинами. Следовательно, 𝐿 является
серединный перпендикуляр к отрезку между (0,0) и
𝑃(3,−3).
Следовательно, 𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−(3−3𝑖)|}. Наконец, обращаем внимание на третью строку, 𝐿. Еще раз, нам нужно описать эту линию как перпендикуляр биссектриса отрезка между началом координат и другой точкой, которую мы обозначили 𝑃. В этом случае сделать это путем осмотра сложнее. Поэтому мы продемонстрируем технику, которая легче обобщается.
Начнем с нахождения наклона 𝑚 линии 𝐿. Мы можно вычислить по формуле 𝑚=𝑦−𝑦𝑥−𝑥.
Поскольку прямая проходит через точки (0,−3) и (−2,0), имеем 𝑚=−3−00−(−2)=−32.
Таким образом, мы можем записать уравнение прямой как 𝑦=−32𝑥−3.
Теперь найдем уравнение прямой, перпендикулярной этой, которая проходит через
источник. Напомним, что произведение наклонов двух перпендикулярных прямых равно
−1. Следовательно, наклон прямой, перпендикулярной
𝐿 равно 23. Следовательно, уравнение
перпендикулярная линия, проходящая через начало координат, определяется как 𝑦=23𝑥.
Напомним, что произведение наклонов двух перпендикулярных прямых равно
−1. Следовательно, наклон прямой, перпендикулярной
𝐿 равно 23. Следовательно, уравнение
перпендикулярная линия, проходящая через начало координат, определяется как 𝑦=23𝑥.
Теперь нам нужно найти точку на этой прямой, расстояние которой до 𝐿 равно равно расстоянию между 𝐿 и началом координат. Для этого мы сначала найти точку пересечения этих двух прямых. Приравняв два уравнения строк, мы можем найти 𝑥 следующим образом: 23𝑥=−32𝑥−3.
Собирая наши 𝑥 члены в левой части, мы имеем 136𝑥=−3.
Следовательно, 𝑥=−1813.
Подставляя это обратно в одно из двух уравнений, мы находим соответствующее значение
из 𝑦 будет 𝑦=−1213. Мы можем представить это
как комплексное число 𝑤=−1813−1213𝑖. Мы хотели бы
эта точка должна лежать в середине 𝑃 и начала координат. Напомним, что
мы можем найти среднюю точку двух комплексных чисел, просто взяв их среднее значение. Следовательно,
так как 𝑤 является серединой отрезка между началом координат и
точка 𝑃, которую мы будем обозначать комплексным числом
𝑧, мы можем написать 𝑤=12(𝑧+0).
Следовательно,
так как 𝑤 является серединой отрезка между началом координат и
точка 𝑃, которую мы будем обозначать комплексным числом
𝑧, мы можем написать 𝑤=12(𝑧+0).
Следовательно, 𝑧=2𝑤=2−1813−1213𝑖=−3613−2413𝑖.
Следовательно, |. Следовательно, мы можем представить область как 𝐴∩𝐵∩𝐶, где 𝐴={𝑧∈ℂ∶(𝑧)2},𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−(3−3𝑖)|},𝐶=𝑧∈ℂ∶|𝑧|≤|||𝑧 −−3613−2413𝑖|||.Im
Пример 5. Рисование составных областей на комплексной плоскости
Комплексное число 𝑧 удовлетворяет следующим условиям: |𝑧|≥2|𝑧+12−9𝑖|,|𝑧−2𝑖|≥|𝑧+6+4𝑖|,(𝑧)12.Im
- Какая из следующих заштрихованных областей представляет геометрическое место 𝑧?
- Найдите площадь геометрического места 𝑧.
Ответ
Часть 1
Мы рассматриваем области, представленные каждым условием, по порядку. Начиная с первого
условие, |𝑧|≥2|𝑧+12−9𝑖|, его граница
окружность на комплексной плоскости. Чтобы найти его центр и начало, мы можем найти его декартово
уравнение путем подстановки 𝑧=𝑥+𝑦𝑖 в уравнение |𝑧|=2|𝑧+12−9𝑖| и преобразовать его в стандартный вид
круга. Следовательно, |𝑥+𝑦𝑖|=2|𝑥+𝑦𝑖+12−9𝑖|=2|(𝑥+12)+(𝑦−9)𝑖|.
Чтобы найти его центр и начало, мы можем найти его декартово
уравнение путем подстановки 𝑧=𝑥+𝑦𝑖 в уравнение |𝑧|=2|𝑧+12−9𝑖| и преобразовать его в стандартный вид
круга. Следовательно, |𝑥+𝑦𝑖|=2|𝑥+𝑦𝑖+12−9𝑖|=2|(𝑥+12)+(𝑦−9)𝑖|.
Возводя в квадрат обе части уравнения, мы имеем |𝑥+𝑦𝑖|=4|(𝑥+12)+(𝑦−9)𝑖|.
Используя определение модуля, мы можем переписать это как 𝑥 +𝑦=4(𝑥+12)+(𝑦−9).
Раскрытие скобок дает 𝑥+𝑦=4𝑥+24𝑥+144+𝑦−18𝑦+81=4𝑥+96𝑥 +4𝑦−72𝑦+900.
Собирая все члены в правой части уравнения, мы имеем 0=3𝑥+96𝑥+3𝑦−72𝑦+900.
Обратите внимание, что во всех терминах есть общий делитель 3. Следовательно, мы можем отменить это как следующим образом: 0=𝑥+32𝑥+𝑦−24+300.
Теперь заполним квадрат в 𝑥 и 𝑦 следующим образом: 0=(𝑥+16)−256+(𝑦−12)−144+300=(𝑥+16)+(𝑦−12)−100.
Мы можем переписать это как (𝑥+16) +(𝑦−12)=10, которое представляет собой уравнение окружности радиуса 10 с центром в
(−16,12). Следовательно, мы можем представить область комплексной плоскости
𝐴 представляется неравенством |𝑧|≥2|𝑧+12−9𝑖| следующее.
Следовательно, мы можем представить область комплексной плоскости
𝐴 представляется неравенством |𝑧|≥2|𝑧+12−9𝑖| следующее.
Теперь рассмотрим второе условие |𝑧−2𝑖|≥|𝑧+6+4𝑖|. Границей этой области является серединный перпендикуляр к прямой отрезок между (0,2) и (−6,−4). Таким образом, регион 𝐵 представлено неравенством |𝑧−2𝑖|≥|𝑧+6+4𝑖| будет полуплоскостью над этой линией.
Сечение плоскости, удовлетворяющее обоим этим условиям, |𝑧|≥2|𝑧+12−9𝑖| и |𝑧−2𝑖|≥|𝑧+6+4𝑖|, будет дано пересечением этих двух областей как показано ниже.
Наконец, рассмотрим область, представленную точками, удовлетворяющими третьему условию:
Я(𝑧)12. Это представляет весь комплекс
числа с мнимой частью меньше 12. Следовательно, область 𝐶
представленное неравенством Im(𝑧)12 есть
полуплоскости ниже линии 𝑦=12. Обратите внимание, что равенство является строгим, поэтому мы
Обозначьте границу этой области пунктирной линией.
Наконец, рассмотрим область, которая удовлетворяет всем условиям |𝑧|≥2|𝑧+12−9𝑖|, |𝑧−2𝑖|≥|𝑧+6+4𝑖| и Im(𝑧)12, заданным пересечением этих областей, как показано ниже.
Часть 2
Чтобы найти площадь этой области, заметим, что это сектор круга. Следовательно, его площадь будет равна 12𝑟𝜃, где 𝑟 — радиус окружности, а 𝜃 — угол опирается на дугу в центре окружности.
Угол 𝜃 при 𝐶 и ∠𝐶𝐷𝐴 альтернативные углы и, следовательно, равны. Кроме того, учитывая треугольник 𝐴𝐸𝐷, мы можем видеть 𝜃=𝜋2−𝜙.
Мы можем найти меру 𝜙, используя координаты точек 𝐴 и 𝐵 следующим образом: 𝜙=62−(−4)=𝜋4.arctan
Следовательно, 𝜃=𝜋4 и площадь региона определяется выражением 12𝑟𝜃=1210𝜋4=25𝜋2.
Пример 6. Составные области на комплексной плоскости
Рассмотрим следующие области на комплексной плоскости: ,𝐵={𝑧∈ℂ∶(𝑧)(𝑧)0}.ReIm
Область 𝑅 определяется как 𝑅=𝐴∩𝐵.
- Какая из следующих заштрихованных областей представляет 𝑅 на диаграмме Аргана?
- Найдите площадь области 𝑅.
Ответ
Часть 1
Начнем с рассмотрения области 𝐴. Он определяется как область между два круга |𝑧|=2 и |𝑧|=4. Обратите внимание, что область содержит внутреннюю границу, но не внешнюю. Следовательно, мы можем представить эту область следующим образом.
Теперь рассмотрим область 𝐵. Это область на комплексной плоскости где произведение действительной и мнимой частей отрицательно. Чтобы это условие было удовлетворены, нам нужно, чтобы либо действительная, либо мнимая часть были отрицательными, но не оба. Следовательно, эта область является вторым и четвертым квадрантами плоскости. Снова, обратите внимание, что это не содержит границы; следовательно, мы можем представить это в виде Диаграмма Аргана выглядит следующим образом.
Прежде чем рассматривать область 𝑅, сначала рассмотрим дополнение
𝐵. Это будут первый и третий квадранты комплексной плоскости. Однако, поскольку 𝐵 не включает свои граничные точки,
𝐵 будет. Следовательно, мы можем представить
𝐵 на диаграмме Аргана следующим образом.
Это будут первый и третий квадранты комплексной плоскости. Однако, поскольку 𝐵 не включает свои граничные точки,
𝐵 будет. Следовательно, мы можем представить
𝐵 на диаграмме Аргана следующим образом.
Наконец, мы хотели бы пересечь 𝐴 с 𝐵. Это область точек в обоих 𝐴 и 𝐵. Следовательно, мы можем представить это следующим образом.
Часть 2
Чтобы найти площадь этой области, заметим, что она будет равна половине площади большего круга минус половина площади меньшего круга: 12𝜋𝑟−12𝜋𝑟=12𝜋𝑟−𝑟.
имеем, что площадь сечения 𝑅 определяется выражением комплексной плоскости, мы можем представить области в комплексная плоскость на диаграмме Аргана.

: Определение квадранта, содержащего заданное комплексное число в алгебраической форме
Стенограмма видео
В каком квадранте диаграммы Аргана находится комплексное число три минус два 𝑖?
В этом вопросе нам дано комплексное число три минус два 𝑖, и нам нужно определить, в каком квадранте нашей диаграммы Аргана находится это комплексное число. Для этого начнем с того, что вспомним, что мы понимаем под диаграммой Аргана. На диаграмме Аргана мы рисуем пару осей, горизонтальную ось и вертикальную ось. И мы обозначаем горизонтальную ось как действительную часть нашего числа, а вертикальную ось — как мнимую часть нашего числа. Таким образом, каждая точка на нашей диаграмме Аргана будет иметь реальное значение и мнимое значение, полностью основанное на ее координатах на нашей диаграмме. И в этом вопросе мы собираемся нанести точку три минус два 𝑖 на нашу диаграмму Аргана.
И в этом вопросе мы собираемся нанести точку три минус два 𝑖 на нашу диаграмму Аргана.
Итак, для этого нам нужно определить действительную и мнимую части этого числа. Мы можем сделать это прямо с номера. Тем не менее, есть некоторые полезные обозначения, чтобы записать это. Во-первых, мы можем представить действительную часть комплексного числа, используя следующие обозначения. И действительная часть комплексного числа три минус два 𝑖 будет равна трем. На самом деле, для любого комплексного числа, заданного в алгебраической форме, то есть в виде 𝑎 плюс 𝑏𝑖, где 𝑎 и 𝑏 — действительные числа, действительная часть этого числа всегда будет равна 𝑎. Так что же это говорит нам о нашей диаграмме Аргана? Ну а если реальная точка нашего комплексного числа равна трем, то на нашей диаграмме Аргана горизонтальная координата этой точки должна быть равна трем.
Далее нам нужно найти мнимую часть этого числа. Представим это в следующих обозначениях. И на этот раз мнимая часть комплексного числа, заданного в алгебраической форме 𝑎 плюс 𝑏𝑖, просто равна 𝑏.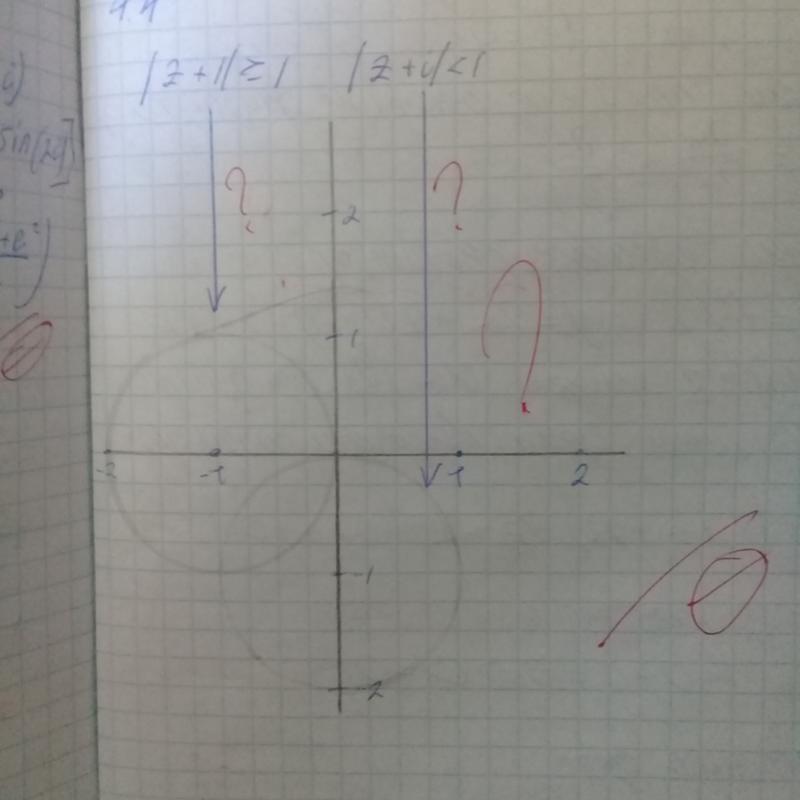

 08.201874.19 Кб142Раздел 15 (ответы).docx
08.201874.19 Кб142Раздел 15 (ответы).docx