Криволинейный интеграл 1-го рода (криволинейный интеграл по длине дуги). Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Пусть функция непрерывна в каждой точке гладкой кривой . Разобьем кривую произвольным образом на частей длиной . Обозначим . В каждой части возьмем произвольную точку , тогда предел последовательности интегральных сумм
при и называется криволинейным интегралом I рода:
Основные свойства криволинейных интегралов I рода
1. Криволинейный интеграл не зависит от направления пути интегрирования:
2. Если кривая разбита на части и , то
3. Если и – непрерывные функции на и – постоянные числа, то
Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода зависит от того, каким
образом задана кривая интегрирования.
1. Если пространственная кривая задана параметрическими уравнениями
то
2. В частности для плоской кривой :
Получаем:
3. Если плоская кривая определена уравнением , , то
4. Если кривая задана полярным уравнением , то
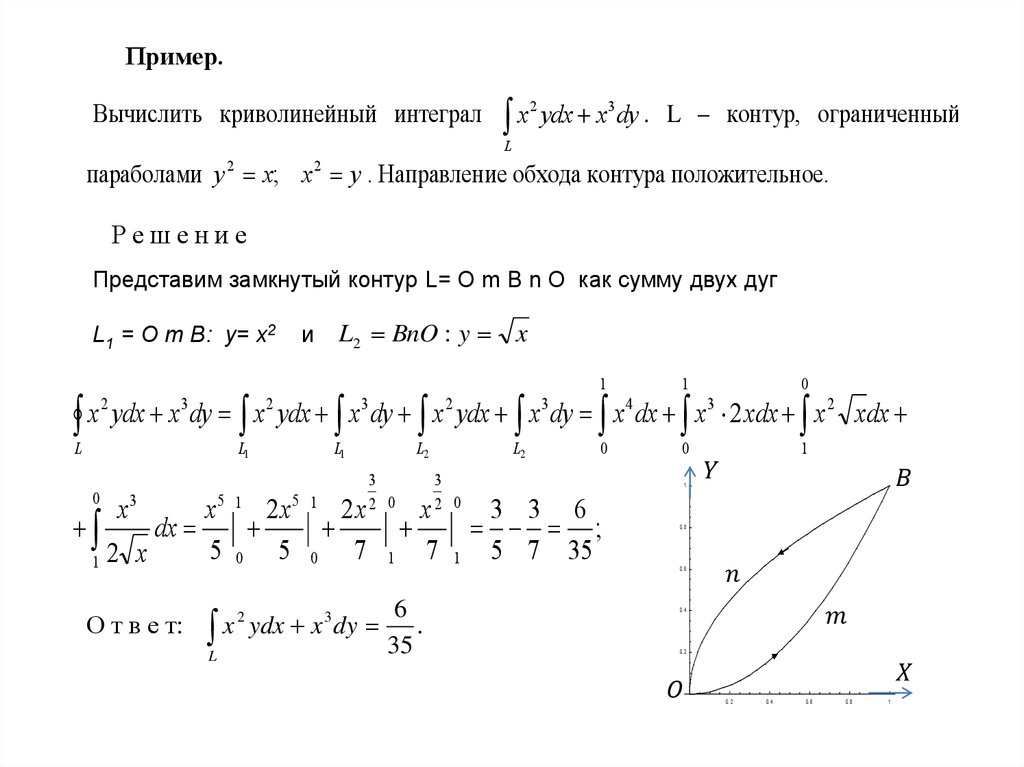
Примеры решения задач
Задача 1
Вычислить криволинейный интеграл 1-го рода
По замкнутому контуру , образованному сторонами треугольника с вершинами .
Решение
Искомый криволинейный интеграл будет равен:
Для отрезка :
Для отрезка ВС:
Найдем уравнение прямой BC:
Для отрезка СА:
Найдем уравнение прямой СА:
Искомый интеграл:
Ответ:
Задача 2
Вычислить
криволинейный интеграл по указанной кривой.
– дуга кривой от до
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Криволинейный интеграл 1-го рода можно вычислить по формуле:
Производная:
Получаем:
Ответ:
Задача 3
В задаче вычислить криволинейные интегралы по кривой :
Решение
Криволинейный интеграл 1-го рода можно вычислить по формуле:
Ответ:
21.1. Криволинейные интегралы первого рода
Рассмотрим пространственную кусочно-гладкую кривую, ограниченную точкамиИ(рис. 21.1), и определенную на ней непрерывную функцию Где- точка кривой. ДугуРазобьем точками
21.1), и определенную на ней непрерывную функцию Где- точка кривой. ДугуРазобьем точками
НаЭлементарных дуг
Длины которых обозначим соответственно черезА
Наибольшую из этих длин-через.На каждой из элементарных дугВыберем произвольно
Одну точкуИ составим сумму
(21.1)
Называемую интегральной суммой для функции По длине дуги кривой Криволинейным интегралом первого родаили криволинейным интегралом по дуге кривойОт функцииНазывается предел интеграль — Рис — 21.1
Ной суммы (21.1) при
На кривойЦеликом лежащей на плоскостиФункцияОт координаты не зависит, поэтому по определению имеем
Если подынтегральную функциюРассматривать как линейную
Плотность кривойТо криволинейный интеграл первого рода представляет собой массу этой кривой.
Основные свойства криволинейного интеграла первого рода следующие.
1. Криволинейный интеграл первого рода не зависит от направления пути интегрирования:
4. Если йуть интегрированияРазбит на части, то
Вычисление 1фиволинейного интеграла первого рода сводится к вычислению определенного интеграла.
Если пространственная криваяЗадана параметрическими уравнениями
, то
(21.2)
Если криваяЛежит в плоскости, то
(21.3)
В частности, для плоской кривой, заданной уравнениемИмеем
(21.4)
Если плоская кривая задана уравнениемВ полярных
Координатах, то
(21.5)
Если кривая задана уравнением, то криволинейный интеграл
Вычисляется по формуле
(21.6)
Пример 21.1. Вычислить криволинейный интеграл, где
— дуга кривойМежду точками, для которых
Поскольку,И на дуге кривойФункция
, то по формуле (21.4) находим
Пример 21.2. ВычислитьГде- дуга кривой
Между точками, для которых
Применяем формулу (2J.6). В данном случае
Пр имер 21.3. Вычислить криволинейный интегралГде-
Контур треугольника(рис. 21.2) с вершинами
В соответствии со свойством 4) криволинейного интегра первого рода имеем
На отрезкеПоэтому
На отрезкеНа отрезке
Принимая во внимание свойство 1) криволинейного интеграла, используя формулы (21.
Пример 21.4. ВычислитьГде- лепесток лемнискаты
Расположенный в первом координатном углу.
ЛинияЗадана уравнением в полярных координатах, поэтому здесь целесообразно воспользоватьсяформулой (21.S).
Так какТо
Заметив еще, чтоТ. е.По формуле (21.5) получим
Пример 21.5. ВычислитьГде- отрезок прямой
Между точками
Составим сначала уравнения прямой, проходящей через точкиИ
Или
Таким образом, получаем параметрические уравнения прямой:
ТочкаПробегает отрезок, когдаИзменяется отДо 1, т. е.
Так какТо
По формуле (21.2) находим
Пример 21.6. ВычислитьГде-дуга винтовой линии
Отраниченной точками, для которых Применяем формулу (21.2). Поскольку
И
| < Предыдущая | Следующая > |
|---|
Линейные интегралы векторных полей
Определение
 Кривая. Тогда производная вектор-функции
Кривая. Тогда производная вектор-функции\[\frac{{d\mathbf{r}}}{{dt}} = \boldsymbol{\tau} = \left({\cos\alpha,\cos\beta,\cos\gamma}\right) \]
— единичный вектор касательной к этой кривой (рис. 1).
Рис. 1.Здесь \(\alpha, \beta\) и \(\gamma\) — углы между касательной и положительной осью \(Ox, Oy\) и \(Oz,\) соответственно.
Введем вектор-функцию \(\mathbf{F}\left( {P,Q,R} \right)\), определенную над кривой \(C\), так что для скалярной функции
\[\mathbf{F} \cdot \boldsymbol{\tau} = P\cos\alpha + Q\cos\beta + R\cos\gamma,\]
9S {\ left ({P \ cos \ alpha + Q \ cos \ beta} \ right) ds} .\]Свойства линейных интегралов векторных полей
Линейный интеграл векторной функции обладает следующими свойствами:- Обозначим через \(C\) кривую \(AB\), которую проводят из \(A\) в \(B,\), а через \(-C\) обозначим кривую \(BA\) с противоположная ориентация — от \ (B \) до \ (A. \) Тогда
\[\int\limits_{ — C} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} = — \int\limits_C {\left({\mathbf{F}} \cdot d\mathbf{r}} \right)} ;\]
- Если \(C\) является объединением кривых \({C_1}\) и \({C_2}\) (рис.
 \(2\)), то
\(2\)), то\[\int\limits_C {\left({\mathbf{F} \cdot d\mathbf{r}} \right)} = \int\limits_{{C_1} \cup {C_2}} {\left({\mathbf{F} \cdot d\mathbf{r}} \right)} знак равно \int\limits_{{C_1}} {\left( {\mathbf{F} \cdot d\mathbf{r}} \right)} + \int\limits_{{C_2}} {\left({\mathbf {F} \cdot d\mathbf{r}} \right)} ;\]
Рис. 2. - Если кривая \(C\) параметризована выражением \(\mathbf{r}\left( t \right) = \left( {x\left( t \right),y\left( t \right ),z\left( t \right)} \right),\) \(\alpha \le t \le \beta ,\) тогда
9\ бета {\ влево [ {P \ влево ( {x \ влево ( т \ вправо), y \ влево ( т \ вправо), z \ влево ( т \ вправо)} \ вправо) \ frac {{dx}} { {dt}} + Q\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dy}}{{dt }} + R\left( {x\left( t \right),y\left( t \right),z\left( t \right)} \right)\frac{{dz}}{{dt}} } \right]dt} .\]
- Если \(C\) лежит в \(xy\)-плоскости и задается уравнением \(y = f\left( x \right)\) (в этом случае \(R = 0\) и \ (t = x\)), то последнюю формулу можно записать в виде
9б {\ Big [ {P \ влево ( {х, е \ влево ( х \ вправо)} \ вправо) + Q \ влево ( {х, е \ влево ( х \ вправо)} \ вправо) \ гидроразрыва {{df }}{{dx}}} \Big]dx} .
 3}\) от начала координат \(\left( {0,0} \right)\) до \ (\слева({2,8}\справа).\) 98} \справа] = 8.\]
3}\) от начала координат \(\left( {0,0} \right)\) до \ (\слева({2,8}\справа).\) 98} \справа] = 8.\] Дополнительные проблемы см. на стр. 2.
Исчисление III — Линейные интегралы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 16.2: Линейные интегралы – Часть I
В этом разделе мы познакомим вас с новым видом интеграла. Однако, прежде чем мы это сделаем, важно отметить, что вам нужно будет помнить, как параметризовать уравнения, или, другими словами, вам нужно будет уметь записывать набор параметрических уравнений для данной кривой. Вы должны были видеть некоторые из них в своем курсе исчисления II. Если вам нужен обзор, вы должны вернуться и просмотреть некоторые основы параметрических уравнений и кривых.
Вот некоторые из наиболее простых кривых, которые нам нужно знать, как сделать, а также ограничения на параметры, если они потребуются.
В последнем мы дали как векторную форму уравнения, так и параметрическую форму, и если нам нужна двумерная версия, мы просто опускаем компоненты \(z\). На самом деле, в этом разделе мы будем использовать двумерную версию.
Для эллипса и окружности мы дали две параметризации, одна из которых описывает кривую по часовой стрелке, а другая против часовой стрелки.
 Как мы в конечном итоге увидим, направление, в котором прослеживается кривая, может иногда изменить ответ. Кроме того, оба они «начинаются» на положительной оси \(x\) в точке \(t = 0\).
Как мы в конечном итоге увидим, направление, в котором прослеживается кривая, может иногда изменить ответ. Кроме того, оба они «начинаются» на положительной оси \(x\) в точке \(t = 0\).Теперь перейдем к линейным интегралам. В исчислении I мы интегрировали \(f\left(x\right)\), функцию одной переменной, по интервалу \(\left[{a,b} \right]\). В этом случае мы думали, что \(x\) принимает все значения в этом интервале, начиная с \(a\) и заканчивая \(b\). С линейными интегралами мы начнем с интегрирования функции \(f\left({x,y} \right)\), функции двух переменных и значений \(x\) и \(y\), которые мы будем использовать точки \(\left( {x,y} \right)\), которые лежат на кривой \(C\). Обратите внимание, что это отличается от двойных интегралов, с которыми мы работали в предыдущей главе, где точки выходят из некоторой двумерной области.
Начнем с кривой \(C\), от которой исходят точки. Будем считать, что кривая гладкая (определена кратко) и задана параметрическими уравнениями
\[x = h\left( t \right)\hspace{0.
 25in}y = g\left( t \right)\hspace{0.25in}\,\,\,\,a \le t \le b\ ]
25in}y = g\left( t \right)\hspace{0.25in}\,\,\,\,a \le t \le b\ ]Нам часто нужно записать параметризацию кривой в виде векторной функции. В этом случае кривая задается как
\[\vec r\left( t \right) = h\left( t \right)\,\vec i + g\left( t \right)\vec j\hspace{0.25in}\hspace{0.25in} а \ле т \ле б\]
Кривая называется гладкой , если \(\vec r’\left( t \right)\) непрерывна и \(\vec r’\left( t \right) \ne 0\) для всех \( т\).
Линейный интеграл от \(f\left({x,y} \right)\) вдоль \(C\) обозначается как,
\[\int\limits_{C}{{f\left( {x,y} \right)\,ds}}\]
Мы используем \(ds\) здесь, чтобы подтвердить тот факт, что мы движемся вдоль кривой \(C\), а не по оси \(x\) (обозначаемой \(dx\)) или \(y\)-ось (обозначается \(dy\)). Из-за \(ds\) это иногда называют 92} = 16\), прочерченных против часовой стрелки.

Показать решение
Сначала нам нужна параметризация круга. Это дано,
\[x = 4\cos t\hspace{0,25 дюйма}y = 4\sin t\]
Теперь нам нужен диапазон \(t\), который даст правую половину круга. Следующий диапазон \(t\) сделает это.
\[ — \frac{\pi }{2} \le t \le \frac{\pi }{2}\] 9{\ frac {\ pi} {2}} \\ & = \ frac {{8192}} {5} \ end {align *} \]
Далее нам нужно поговорить о линейных интегралах по кусочно-гладким кривым . Кусочно-гладкая кривая — это любая кривая, которую можно записать как объединение конечного числа гладких кривых, \({C_1}\),…,\({C_n}\), где конечная точка \({C_i}\ ) является отправной точкой \({C_{i + 1}}\). Ниже приведена иллюстрация кусочно-гладкой кривой.
Вычисление линейных интегралов по кусочно-гладким кривым относительно просто.
 Все, что мы делаем, это оцениваем линейный интеграл по каждой из частей, а затем складываем их. Линейный интеграл для некоторой функции по приведенной выше кусочной кривой будет равен 93}\,ds}}\\ & = — 16 + 2,268 + 8\\ & = — 5,732\end{align*}\]
Все, что мы делаем, это оцениваем линейный интеграл по каждой из частей, а затем складываем их. Линейный интеграл для некоторой функции по приведенной выше кусочной кривой будет равен 93}\,ds}}\\ & = — 16 + 2,268 + 8\\ & = — 5,732\end{align*}\]Обратите внимание, что в приведенном выше примере мы поместили стрелки направления на кривую. Направление движения по кривой может изменить значение линейного интеграла, как мы увидим в следующем разделе. Также обратите внимание, что кривую можно рассматривать как кривую, которая ведет нас от точки \(\left( {- 2, — 1} \right)\) к точке \(\left( {1,2} \right) \). Давайте сначала посмотрим, что произойдет с линейным интегралом, если мы изменим путь между этими двумя точками. 93}\,ds}}\) где \(C\) — отрезок от \(\left( { — 2, — 1} \right)\) до \(\left( {1,2} \right )\).
Показать решение
Из формул параметризации в начале этого раздела мы знаем, что отрезок, начинающийся в \(\left( { — 2, — 1} \right)\) и заканчивающийся в \(\left( {1,2} \справа)\) определяется как,
\[\begin{align*}\vec r\left( t \right) & = \left( {1 — t} \right)\left\langle { — 2, — 1} \right\rangle + t\left \langle {1,2} \right\rangle \\ & = \left\langle { — 2 + 3t, - 1 + 3t} \right\rangle \end{align*}\] 91\\ & = 12\sqrt 2 \left( { — \frac{5}{4}} \right)\\ & = — 15\sqrt 2 = — 21.
 213\end{align*}\]
213\end{align*}\]При выполнении этих интегралов не забывайте о простых подстановках Calc I, чтобы избежать таких действий, как вычисление члена в кубе. Выделить его не так сложно, но это больше работы, чем простая замена.
Таким образом, предыдущие два примера предполагают, что если мы изменим путь между двумя точками, то значение линейного интеграла (относительно длины дуги) изменится. Хотя это будет происходить довольно регулярно, мы не можем предполагать, что это будет происходить всегда. В следующем разделе мы рассмотрим эту идею более подробно. 93}\,ds}}\) где \(C\) — отрезок от \(\left( {1,2} \right)\) до \(\left( { — 2, — 1} \right )\).
Показать решение
С точки зрения работы этот не сильно отличается от предыдущего примера. Вот параметризация кривой.
\[\begin{align*}\vec r\left( t \right) & = \left( {1 — t} \right)\left\langle {1,2} \right\rangle + t\left\langle { — 2, — 1} \right\rangle \\ & = \left\langle {1 — 3t,2 — 3t} \right\rangle \end{align*}\] 91\\ & = 12\sqrt 2 \left( { — \frac{5}{4}} \right)\\ & = — 15\sqrt 2 = — 21.
 213\end{align*}\]
213\end{align*}\]Получается, что при изменении направления кривой линейный интеграл (относительно длины дуги) не изменится. Это всегда будет верно для таких линейных интегралов. Однако есть и другие виды линейных интегралов, в которых это не так. Мы увидим больше примеров этого в следующих нескольких разделах, так что не вбивайте себе в голову, что изменение направления никогда не изменит значение линейного интеграла.
Прежде чем работать с другим примером, давайте несколько формализуем эту идею. Предположим, что кривая \(C\) имеет параметризацию \(x = h\left( t \right)\), \(y = g\left( t \right)\). Предположим также, что начальная точка кривой — \(A\), а конечная точка кривой — \(B\). Параметризация \(x = h\left( t \right)\), \(y = g\left( t \right)\) затем определит ориентацию для кривой, где положительное направление является направлением, которое прослеживается по мере увеличения \(t\). Окончательно, пусть \(-C\) будет кривой с теми же точками, что и \(C\), однако в этом случае кривая имеет \(B\) в качестве начальной точки и \(A\) в качестве конечной точки, снова \ (t\) увеличивается по мере того, как мы пересекаем эту кривую.
 Другими словами, если задана кривая \(C\), кривая \(-C\) является той же кривой, что и \(C\), за исключением того, что направление было изменено на противоположное.
Другими словами, если задана кривая \(C\), кривая \(-C\) является той же кривой, что и \(C\), за исключением того, что направление было изменено на противоположное.Тогда мы имеем следующий факт о линейных интегралах по длине дуги.
Факт
\[\int\limits_{C}{{f\left( {x,y} \right)\,ds}} = \int\limits_{{ — C}}{{f\left( {x,y} \справа)\,дс}}\]
Итак, для линейного интеграла по длине дуги мы можем изменить направление кривой, но не изменить значение интеграла. Это полезно помнить, так как некоторые линейные интегралы будут проще в одном направлении, чем в другом.
92},\,\,\, — 1 \le x \le 1\) - \({C_2}\): сегмент линии от \(\left( { — 1,1} \right)\) до \(\left( {1,1} \right)\).
- \({C_3}\): сегмент линии от \(\left( {1,1} \right)\) до \(\left( { — 1,1} \right)\).
Показать все решения Скрыть все решения
Показать обсуждение
Прежде чем работать с любым из этих линейных интегралов, заметим, что все эти кривые являются путями, соединяющими точки \(\left( { — 1,1} \right)\) и \(\left( {1,1} \ верно)\). Также обратите внимание, что \({C_3} = — {C_2}\) и, следовательно, по факту выше эти два должны давать один и тот же ответ. 91 = 0\]
Также обратите внимание, что \({C_3} = — {C_2}\) и, следовательно, по факту выше эти два должны давать один и тот же ответ. 91 = 0\]
b \({C_2}\): сегмент линии от \(\left( { — 1,1} \right)\) до \(\left( {1,1} \right)\). Показать решение
Здесь для этой кривой можно использовать две параметризации. Первый — использовать формулу, которую мы использовали в предыдущих примерах. Эта параметризация
\[\begin{align*}{C_2}:\vec r\left( t \right) & = \left( {1 — t} \right)\left\langle { — 1,1} \right\rangle + t\left\langle {1,1} \right\rangle \\ & \hspace{0.25in}\,\,{\kern 1pt} = \left\langle {2t — 1,1} \right\rangle \end {выровнять*}\]
для \(0 \le t \le 1\).
Иногда у нас нет другого выбора, кроме как использовать эту параметризацию. Однако в этом случае есть вторая (вероятно) более легкая параметризация. Второй использует тот факт, что мы на самом деле просто рисуем часть линии \(y = 1\). Используя это параметрирование,
Используя это параметрирование,
\[{C_2}:x = t,\,\,y = 1,\,\,\, — 1 \le t \le 1\]
Это будет гораздо более простая параметризация, поэтому мы будем использовать ее. Вот линейный интеграл для этой кривой. 91 = 0\]
Обратите внимание, что на этот раз, в отличие от линейного интеграла, с которым мы работали в примерах 2, 3 и 4, мы получили одно и то же значение интеграла, несмотря на то, что пути разные. Это будет происходить при случае. Мы также не должны ожидать, что этот интеграл будет одинаковым для всех путей между этими двумя точками. На данный момент все, что мы знаем, это то, что для этих двух путей линейный интеграл будет иметь одинаковое значение. Вполне возможно, что между этими двумя точками есть другой путь, который даст другое значение линейного интеграла.
c \({C_3}\): сегмент линии от \(\left( {1,1} \right)\) до \(\left( { — 1,1} \right)\). Показать решение
Показать решение
Теперь, согласно нашему факту выше, нам действительно не нужно ничего здесь делать, поскольку мы знаем, что \({C_3} = — {C_2}\). Факт говорит нам о том, что этот линейный интеграл должен быть таким же, как и вторая часть (, т.е. нулей). Тем не менее, давайте проверим это, плюс здесь нужно сделать замечание о параметризации.
Вот параметризация этой кривой.
\[\begin{align*}{C_3}:\vec r\left( t \right) & = \left( {1 — t} \right)\left\langle {1,1} \right\rangle + t \left\langle { — 1,1} \right\rangle \\ & \hspace {0.25in}\,\,{\kern 1pt} = \left\langle {1 — 2t,1} \right\rangle \end {выровнять*}\]
для \(0 \le t \le 1\).
Обратите внимание, что на этот раз мы не можем использовать вторую параметризацию, которую мы использовали в части (b), так как нам нужно двигаться справа налево по мере увеличения параметра, а вторая параметризация, использованная в предыдущей части, будет двигаться в противоположном направлении. . 91 = 0\]
. 91 = 0\]
Конечно, мы получили тот же ответ, что и во второй части.
До сих пор в этом разделе мы рассматривали только линейные интегралы по двумерной кривой. Однако нет причин так себя ограничивать. Мы также можем выполнять линейные интегралы по трехмерным кривым.
Предположим, что трехмерная кривая \(C\) задана параметризацией,
\[x = x\left( t \right),\,\hspace{0.25in}y = y\left(t\right)\hspace{0.25in}z = z\left(t\right)\hspace{ 0,25 дюйма}a \le t \le b\] 92}} \,дт}}\]
Обратите внимание, что часто при работе с трехмерным пространством параметризация задается векторной функцией.
\[\vec r\left( t \right) = \left\langle {x\left( t \right),y\left( t \right),z\left( t \right)} \right\rangle \ ]
Обратите внимание, что мы немного изменили обозначение параметризации. Поскольку мы редко используем имена функций, мы просто сохранили \(x\), \(y\) и \(z\) и добавили к части \(\left( t \right)\), чтобы обозначить, что они могут быть функциями параметра.

 \(2\)), то
\(2\)), то 3}\) от начала координат \(\left( {0,0} \right)\) до \ (\слева({2,8}\справа).\) 98} \справа] = 8.\]
3}\) от начала координат \(\left( {0,0} \right)\) до \ (\слева({2,8}\справа).\) 98} \справа] = 8.\] 
 Как мы в конечном итоге увидим, направление, в котором прослеживается кривая, может иногда изменить ответ. Кроме того, оба они «начинаются» на положительной оси \(x\) в точке \(t = 0\).
Как мы в конечном итоге увидим, направление, в котором прослеживается кривая, может иногда изменить ответ. Кроме того, оба они «начинаются» на положительной оси \(x\) в точке \(t = 0\). 25in}y = g\left( t \right)\hspace{0.25in}\,\,\,\,a \le t \le b\ ]
25in}y = g\left( t \right)\hspace{0.25in}\,\,\,\,a \le t \le b\ ]
 Все, что мы делаем, это оцениваем линейный интеграл по каждой из частей, а затем складываем их. Линейный интеграл для некоторой функции по приведенной выше кусочной кривой будет равен 93}\,ds}}\\ & = — 16 + 2,268 + 8\\ & = — 5,732\end{align*}\]
Все, что мы делаем, это оцениваем линейный интеграл по каждой из частей, а затем складываем их. Линейный интеграл для некоторой функции по приведенной выше кусочной кривой будет равен 93}\,ds}}\\ & = — 16 + 2,268 + 8\\ & = — 5,732\end{align*}\] 213\end{align*}\]
213\end{align*}\] 213\end{align*}\]
213\end{align*}\] Другими словами, если задана кривая \(C\), кривая \(-C\) является той же кривой, что и \(C\), за исключением того, что направление было изменено на противоположное.
Другими словами, если задана кривая \(C\), кривая \(-C\) является той же кривой, что и \(C\), за исключением того, что направление было изменено на противоположное.