Обратная матрица есть только у квадратной матрицы, у неквадратных и вырожденных (det = 0) матриц не существует обратной матрицы.
Квадратная матрица, определитель которой отличен от нуля, имеет обратную матрицу и притом только одну.
Свойства:
Нахождение обратной матрицы возможно с помощью метода алгебраических дополнений
http://www.mathprofi.ru/kak_naiti_obratnuyu_matricu.html
Либо методом Гаусса:
Для нахождения обратной матрицы методом Гаусса необходимо:
1) построить вспомогательную матрицу приписав к столбцам матрицы справа столбцы единичной матрицы того же порядка, что и матрица
2) элементарными преобразованиями строк привести матрицу к матрице, в левой части которой стоит единичная матрица:
3) матрица, стоящая в правой части полученной матрицы и будет обратной матрицей
20. Ранг матрицы
Ранг
матрицы — это число равное наивысшему
порядку миноров этой матрицы, отличной
от 0.
Ранг матрицы не меняется, если к нему применить любое из элементарных преобразований, хотя сама матрица изменится.
Элементарные преобразования:
1. Перестановка двух параллельных рядов
2. Умножение всех элементов любого ряда на число отличное от нуля
3. Транспонирование матрицы
4. Удаление из матрицы или приписывание к ней ряда, состоящего из нулей
5. Замена оного ряда матрицы его суммой с другим параллельным рядом, умноженным на некоторое число
Пример:
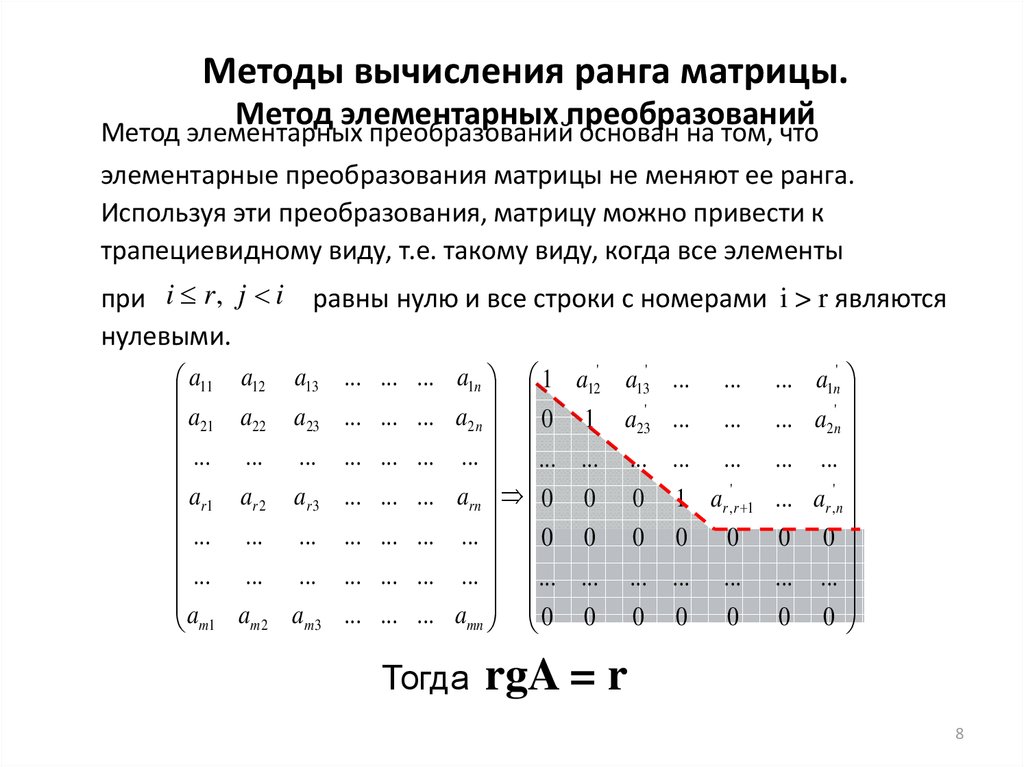
Ранг матрицы равен числу ненулевых строк
Для нахождения ранга существует метод элементарных преобразований – складывать строки, прибавлять к строке строку; умножать на число, переставлять строки и столбцы местами, превратив матрицу в трапецеидальную, а после посчитать количество ненулевых строк.
ЕСЛИ 2 СТРОКИ ПРОПОРЦИОНАЛЬНЫ, ТО М=0, ЕСЛИ ВСЕ МИНОРЫ = 0, ТО РАНГ=1
ЕСЛИ ЕСТЬ НЕНУЛЕВЫЕ ЭЛЕМЕНТЫ, ТО РАНГ НЕ МЕНЕЕ 1
22.
Теорема Кронекера-Капелли.Общий вид СЛАУ
Xj – неизвестные числа, которые при подстановке в уравнение превращают его в тождество
О бозначим
Для того, чтобы система линейных уравнений с n неизвестными была совместна, необходимо и достаточно, чтобы ранг основной матрица (матрица А) был равен рангу расширенной (матрица В).
В случае совместности, если общий ранг этих матриц равен числу неизвестных, то система имеет единственное решение, если меньше их числа, то множество решений.
Запишем следующим образом:
Если rang A = rang B, то система совместна.
Если rang A не = rang B, то система несовместна.
Если rang A = rang B = n, то система имеет единственное решение.
Если rang A = rang B < n, то система имеет бесконечное множество решений.
Таким образом, можно, не решая Систему линейных алгебраических уравнений (СЛАУ), исследовать ее совместность.
23. Метод Гаусса-Жордана
СЛАУ
Xj – неизвестные числа, которые при подстановке в уравнение превращают его в тождество
Обозначим расширенную матрицу
Две
СЛАУ называются эквивалентными, если
все решения одной системы являются
решениями другой системы и наоборот.
Метод Гаусса-Жордана основан на элементарных преобразованиях расширенной матрицы-системы:
1.перестановка 2-х строк
2.умножение i-строки на некоторое число неравное 0
3.прибавление одной строки, умноженной на некоторое число к другой строке
4.исключение нулевых строк: 0*X1 + 0*X2 + … + 0*Xn = 0
Элементарные преобразования СЛАУ переводят одну систему в эквивалентную ей, то есть не меняют решения.
Алгоритм метода Гаусса-Жордана состоит из отдельных шагов: на каждом шаге с помощью элементарных преобразований в одном из уравнений системы выделяется базисное неизвестное с коэффициентом равным 1, которое исключается из всех остальных уравнений.
Шаги повторяются до тех пор, пока в каждом уравнении будет выделена базисная неизвестная или встретится противоречивое уравнение.
Например,
Каждый шаг исключения состоит из 2-х преобразований:
1.деление выбранного уравнения на выбранный элемент
2.прибавление данного уравнения, умноженного на подобранное определенным образом число, ко всем уравнениям
Перепишем
СЛАУ в виде расширенной матрицы.
СЛАУ
Расширенная матрица
Тогда применим метод Гаусса-Жордана на матрице.
-am1
В итоге получим
Выбираем следующее уравнение и повторяем шаги.
Процесс исключения продолжается до тех пор, пока в каждом уравнении не будет выделена базисная переменная.
Пример
Частным решением системы называется всякое решение, полученное из общего при определенных значениях свободных неизвестных. Придавая какие угодно значения свободным неизвестным, можно из общего решения получить сколько угодно много частных решений.
Частное решение, в котором все свободные неизвестные равны 0, называется базисным решением системы.
X4=1 X3=1 (3/5 ; — 19/5 ; 1 ; 1) ЧАСТНОЕ РЕШЕНИЕ
Проверка: подставляем в условие.
лекции_1_курс_2_поток_осень_2019 | Кафедра высшей алгебры
1-я лекция 07.09. Решение систем линейных уравнений методом Гаусса. Теоретические следствия метода Гаусса.
2-я лекция 11.
09.
Операции над матрицами, их свойства. Правило умножения матриц в терминах линейных комбинаций строк (столобцов) второй (первой) матрицы. Умножение на диагональную матрицу. Единичная матрица. Элементарные преобразования строк (столбцов) матрицы как умножения слева (справа) на «элементарные» матрицы.
Обратная матрица, ее единственность. Обратимость элементарных матриц и произведения обратимых матриц.
3-я лекция 14.09. Критерий обратимрсти квадратной матрицы в терминах ее ступенчатого вида. Практический способ нахождения обратной матрицы.
Абелевы группы, кольца и поля. Подгруппы и подкольца.
4-я лекция 21.09. Понятие изоморфизма алгебраических структур. Аксиоматическое определение и построение поля комплексных чисел.
5-я лекция 25.09. Алгебраическая форма комплексного числа. Комплексное сопряжение.
Геометрическое изображение комплексного числа. Геометрический смысл сложения и вычитания комплексных чисел.
Тригонометрическая форма комплексного числа.
Умножение, деление, возведение в степень и извлечение корня в тригонометрической форме.
Векторные пространства. Подпространства. Линейная зависимость. Порождающие системы векторов и базисы.
6-я лекция 02.10. Конечномерные векторные пространства, базис и размерность. Описание всех базисов конечномерного векторного пространства. Формула преобразования координат.
Линейная оболочка и ранг системы векторов. Ранг матрицы как ранг системы ее строк, его сохранение при элементарных преобразованиях строк. Ранг ступенчатой матрицы.
7-я лекция 05.10. Теорема о том, что линейные зависимости между столбцами матрицы не меняются при элементарных преобразованиях строк. Совпадение рангов систем строк и столбцов матрицы.
Критерии совместности и определенности системы линейных уравнений в терминах рангов матриц. Размерность пространства решений системы однородных линейных уравнений. Связь между множествами решений совместной системы линейных уравнений и соответствующей системы однородных линейных уравнений.
Ранг произведения матриц. Критерий обратимости квадратной матрицы в терминах ее ранга.
8-я лекция 09.10. Перестановки. Четность и знак перестановки, их изменение при транспозиции.
Определение определителя квадратной матрицы (явной формулой). Теорема о том, что определитель является кососимметрической полилинейной функцией строк матрицы. Поведение определителя при элементарных преобразованиях строк матрицы. Определитель треугольной матрицы. Критерий обратимости матрицы в терминах ее определителя.
9-я лекция 12.10. Определитель транспонированной матрицы. Определитель матрицы с углом нулей. Разложение определителя по строке (столбцу). Определитель Вандермонда. Определитель произведения матриц.
10-я лекция 19.10. Формулы Крамера. Явный вид обратной матрицы. Теорема о ранге матрицы. Вычисление ранга матрицы методом окаймления миноров.
Объем параллелепипеда (площадь параллелограмма) как определитель матрицы координат его ребер.
11-я лекция 23.
12-я лекция 26.10. Алгебры. Таблица умножения алгебры.
Формальное построение алгебры многочленов K[x} над произвольным полем K. Совпадение формального и функционального равенства многочленов над бесконечным полем.
Степень многочлена. Степень суммы и произведения многочленов. Отсутствие делителей нуля в алгебре K[x].
13-я лекция 30.10. Деление многочленов с остатком. Деление на x-c. Теорема Безу. Схема Горнера. Разложение многочлена по степеням x-c. Формула Тейлора (для многочленов над полем нулевой характеристики).
Кратность корня многочлена. Число корней многочлена с учетом их кратностей. Определение кратности корня по значениям производных (над полем нулевой характеристики).
14-я лекция 06.11. Основная теорема алгебры комплексных чисел. Число корней (с учетом кратностей) многочлена над полем комплексных чисел.
15-я лекция 09.11.
Многочлены с вещественными коэффициентами: свойство мнимых корней и разложение на линейные множители и квадратичные множители с отрицательным дискриминантом.
Теорема Декарта.
16-я лекция 16.11. Евклидовы кольца: наибольший общий делитель и разложение на простые множители.
17-я лекция 20.11. Многочлены с рациональными коэффициентами: рациональные корни, лемма Гаусса. Неприводимость многочлена деления круга на простое число частей.
Алгебра многочленов от нескольких переменных. Совпадение формального и функционального равенства многочленов в случае бесконечного поля. Отсутствие делителей нуля в алгебре многочленов. Степень многочлена по совокупности переменных. Однородные многочлены. Степень суммы и произведения многочленов.
18-я лекция 23.11. Лексикографическое упорядочение одночленов. Симметрические многочлены, их выражение через элементарные симметрические многочлены.
19-я декция 30.11. Дискриминант (неполного) кубического многочлена. Определение числа вещественных корней кубического многочлена с вещественными коэффициентами.
Поле отношений целостного кольца.
20-я лекция 04.12. Поле рациональных дробей.
Представление рациональной дроби в виде суммы многочлена и правильной дроби. Представление правильной рациональной дроби в виде суммы простейших дробей (без доказательства единственности). Явная формула для случая, когда знаменатель данной дроби разложен в произведение различных линейных множителей, ее связь с интерполяционной формулой Лагранжа.
Понятия группы и подгруппы. Простейшие следствия из аксиом группы. Группы преобразований.
21-я лекция 07.12. Разбиение группы на смежные классы по подгруппе. Теорема Лагранжа.
Гомоморфизмы и изоморфизмы групп. Ядро и образ гомоморфизма. Полный прообраз элемента при гомоморфизме.
Знак подстановки. Группа четных подстановок.
Гомоморфизм группы S_4 нв группу S_3, его ядро.
22-я лекция 14.12. Порядок элемента группы. Циклическая подгруппа, порожденнная элементом группы, ее строение. Порядок элемента конечной группы. Группы простого порядка.
Малая теорема Ферма и теорема Эйлера, их групповой смысл.
Подгруппы циклических групп.
23-я лекция 18.12. Квадратичные расширения полей.
Обратная матрица элементарными операциями — Матрицы | Класс 12 Математика
Метод исключения Гаусса также известен как метод сокращения строк и представляет собой алгоритм, который используется для решения системы линейных уравнений. Под ним обычно понимают последовательность операций, выполняемых над соответствующей матрицей коэффициентов. Этот алгоритм используется для нахождения:
- Ранг матрицы.
- Определитель матрицы.
- Обратная матрица.
Операции, которые мы можем выполнять с матрицей для изменения:
- Перестановка/перестановка двух строк.
- Умножение или деление строки на положительное целое число.
- Добавление или вычитание кратного одной строки другой.
Теперь, используя эти операции, мы можем изменить матрицу и найти ее обратную. Используемые шаги:
- Шаг 1: Создайте единичную матрицу размера n x n.
- Шаг 2: Выполните операции со строками или столбцами над исходной матрицей (A), чтобы сделать ее эквивалентной единичной матрице.
- Шаг 3: Выполните аналогичные операции и с единичной матрицей.
Теперь результирующая единичная матрица после всех операций является обратной матрицей .
Строка 90Примечание:
Здесь, R1: Строка 1, R2: Строка 2, R3: Строка 3
Решение:
Давайте выполним операции со строками или столбцами над исходной матрицей (A), чтобы сделать ее эквивалентной единичной матрице.
Шаг 1: Поменять местами Ряды R2 и R3 (чтобы получить A[2][2] = 1)
Шаг 2: R1 = R1 + R3 (чтобы получить A[1][1 ] = 1)
Шаг 3: R2 = R2 – 3R3 (чтобы получить A[2][1] = 0)
Шаг 4: R3 = R3 + R1 (чтобы получить A[ 3][1] = 0)
Шаг 5: R2 = R2/-8 (чтобы A[2][2] = 1)
Шаг 6: R1 = R1 – R2 (чтобы A[1][3] = 0)
Шаг 7: R3 – 6R2 (чтобы A[3][2] = 0)
Шаг 8: R2 = R2 + R3 (чтобы A[2][3] ] = 0)
Шаг 9: R1 = R1 – 2R2 (чтобы A[1][2] = 0)
Теперь выполните ту же операцию, что и выше, над единичной матрицей.
Результат после каждой аналогичной вышеописанной операции над единичной матрицей получаем:
Шаг 1: Обмен R2 и R3 Rows
Шаг 2: R1 = R1 + R3
Шаг 3: R2 = R2 — 3R3
Шаг 5: R2 = R2/-8
Шаг 6: R1 = R1-R2
Шаг 7: R3-6R2
. Шаг 8: R2 = R2 + R3 Шаг 9: R1 = R1 – 2R2 Итак, обратная матрица A: Решение: Шаг 1: R1 = R1 + R2 Шаг 2: R2 = R2 x -1 Аналогичные операции на идентификационной матрик Решение: Шаг 1: SWAP R2 и R3 Шаг 2: R2 = R2 — R3 Аналогичные операции на личности Матрикс. Последняя обновленная дата: 27 декабря 2022 г. • Общее представление: 280,8K • Просмотры сегодня: 28,00K Ответ Проверено 280,8K+ виды HINT найти обратную заданной матрице с помощью элементарных преобразований. Элементарные преобразования означают, что мы начинаем со строки или столбца и, применяя различные преобразования к выбранному объекту, будь то строки или столбцы, мы пытаемся сделать как можно больше нулей. Используйте эту концепцию вместе с A=IA, где I — единичная матрица, чтобы получить обратную. Полный пошаговый ответ: 
С помощью элементарного преобразования найти обратную матрицу $\\left[ {\\begin{array}{*{20}{c}}3{10} \\\\ 27 \\end{array}} \\право]$.
Данная матрица равна
$\left[ {\begin{array}{*{20}{c}}
3&{10} \\
2&7
\end{array}} \right]$
Теперь нам нужно найти обратную эту матрицу с помощью элементарных преобразований,
Пусть,
$A = \left[ {\begin{array}{*{20}{c}}
3&{10} \\
2&7
\end{array}} \right]$
Как мы знаем, A также записывается как $A = IA$, где I — единичная матрица.
$I = \left[ {\begin{массив}{*{20}{c}}
1&0 \\
0&1
\end{массив}} \right]$
$
\Стрелка вправо IA = \left[ {\begin{array}{*{20}{c}}
3&{10} \\
2&7
\end{array}} \right] \\
\Стрелка вправо \left[ {\begin{array}{*{20}{c}}
3&{10} \\
2&7
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
1&0 \\
0&1
\end{array}} \right]A \\
$
Теперь примените преобразования строк, чтобы что матрица LHS становится единичной матрицей, поэтому мы применяем,
${R_1} \to {R_1} — {R_2}$
$ \Rightarrow \left[ {\begin{array}{*{20}{c}}
{3 — 2}&{10 — 7} \ \
2&7
\end{массив}} \right] = \left[ {\begin{array}{*{20}{c}}
{1 — 0}&{0 — 1} \\
0&1
\ end{array}} \right]A$
$ \Rightarrow \left[ {\begin{array}{*{20}{c}}
1&3 \\
2&7
\end{array}} \right] = \ left[ {\begin{array}{*{20}{c}}
1&{ — 1} \\
0&1
\end{array}} \right]A$
Теперь примените ${R_2} \ к {R_2 } — 2{R_1}$
$ \Rightarrow \left[ {\begin{array}{*{20}{c}}
1&3 \\
{2 — 2}&{7 — 6}
\end{массив}} \right] = \ left[ {\begin{array}{*{20}{c}}
1&{ — 1} \\
{0 — 2}&{1 + 2}
\end{array}} \right]
австралийских долларов $ \Rightarrow \left[ {\begin{array}{*{20}{c}}
1&3 \\
00&1
\end{array}} \right] = \left[ {\begin{array}{*{ 20}{c}}
1&{ — 1} \\
{ — 2}&3
\end{array}} \right]A$
Теперь примените ${R_1} \to {R_1} — 3{R_2}$
$ \Rightarrow \left[ {\begin{array}{*{20}{c}}
{1 — 0}&{3 – 3} \\
0&1
\end{массив}} \right] = \ left[ {\begin{array}{*{20}{c}}
{1 + 6}&{ — 1 — 9} \\
{ — 2}&3
\end{array}} \right]A$
$ \Rightarrow \left[ {\begin{array}{*{20}{c}}
1&0 \\
0&1
\end{array}} \right] = \left[ {\begin{array}{* {20}{c}}
7&{ — 10} \\
{ — 2}&3
\end{array}} \right]A$
Теперь сдвиньте A на L.