§ 11. Четные и нечетные функции. Периодические функции
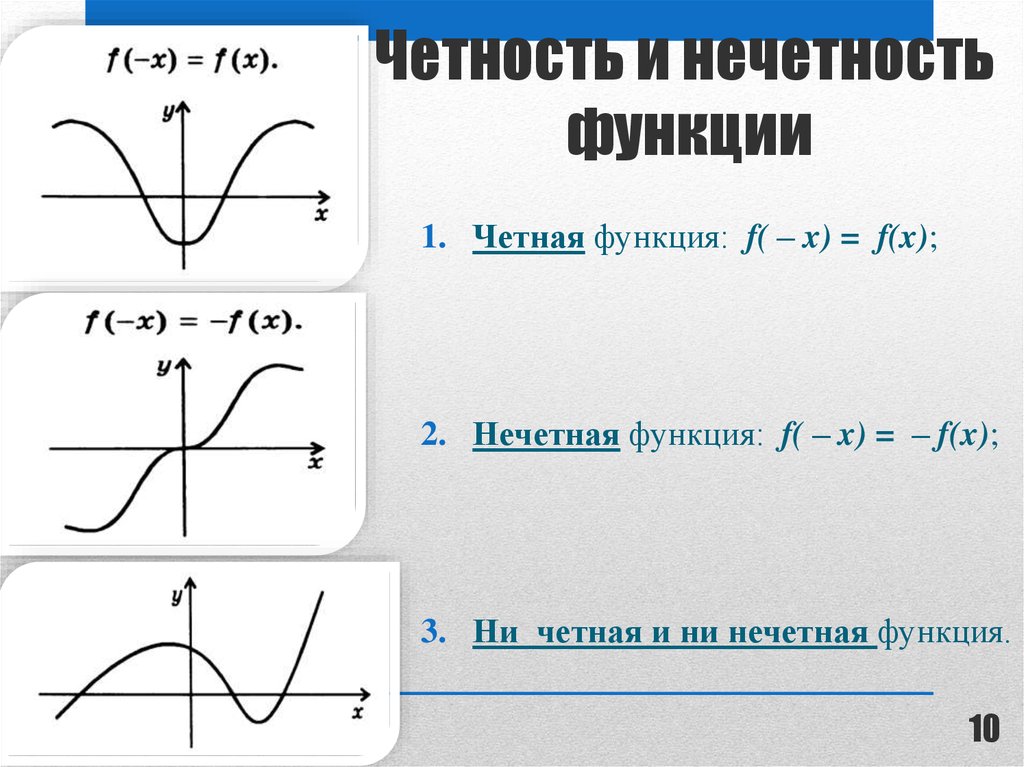
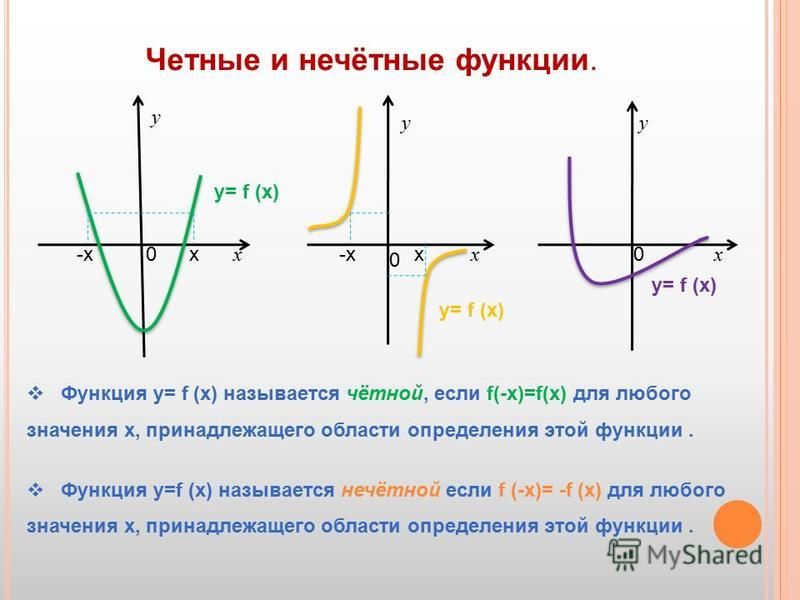
Определение 1. Функцияназываетсячетной (нечетной), если вместе с каждым значением переменнойзначение –хтакже принадлежити выполняется равенство
(11.1)
Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на числовой прямой (числа х и –ходновременно принадлежат). Например, функцияне является четной и нечетной, так как ее область определенияне симметрична относительно начала координат.
Функция четная, так каксимметрична относительно начала координат и.
Функция нечетная, так каки.
Функция
не является четной и нечетной, так как
хотяи симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
Например,.
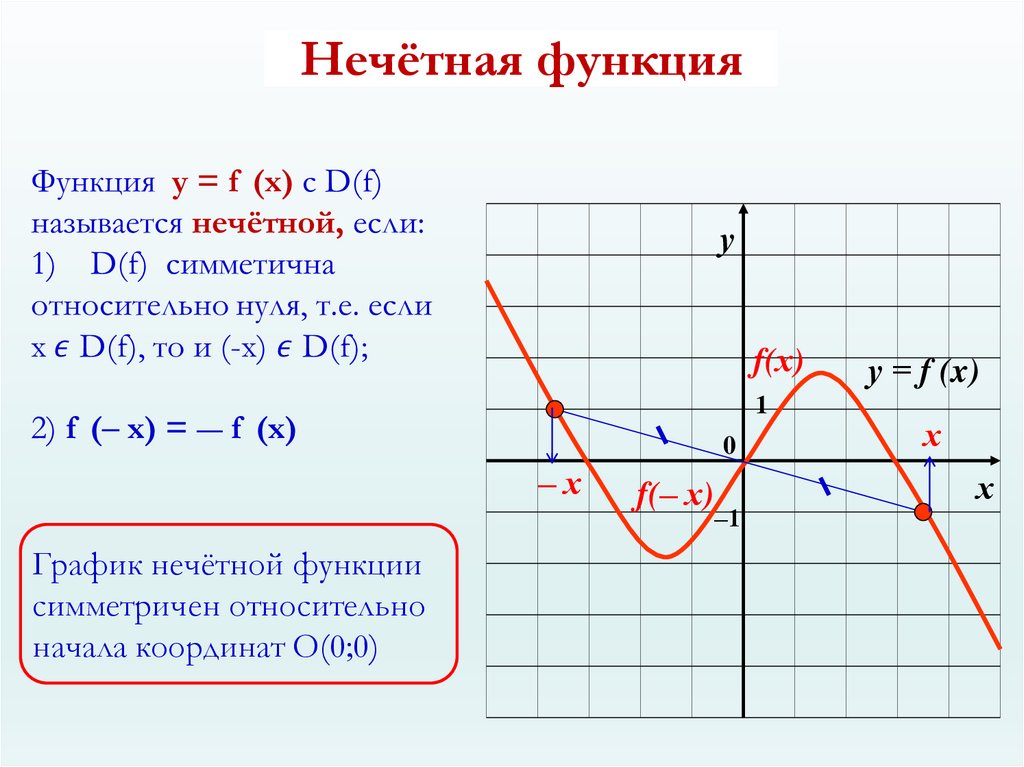
График четной функции симметричен относительно оси Оу, так как если точкапринадлежит графику, то и точкатоже принадлежит графику. График нечетной функции симметричен относительно начала координат, так как еслипринадлежит графику, то и точкатоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f– четная функция на множествеХ, а функцияg определена на множестве, то функция– четная.
д) Если f– нечетная
функция на множествеХ, а функцияg определена на
множествеи четная (нечетная), то функция–
четная (нечетная).
Доказательство. Докажем, например, б) и г).
б) Пусть и– четные функции. Тогда, поэтому. Аналогично рассматривается случай нечетных функцийи.
г) Пусть f – четная функция. Тогда.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию, заданную на множествеХ, симметричном относительно начала координат, можно представить в виде суммы четной и нечетной функций.
Доказательство. Функциюможно записать в виде
.
Функция – четная, так как, а функция– нечетная, поскольку. Таким образом,, где– четная, а– нечетная функции. Теорема доказана.
Определение 2. Функцияназывается
.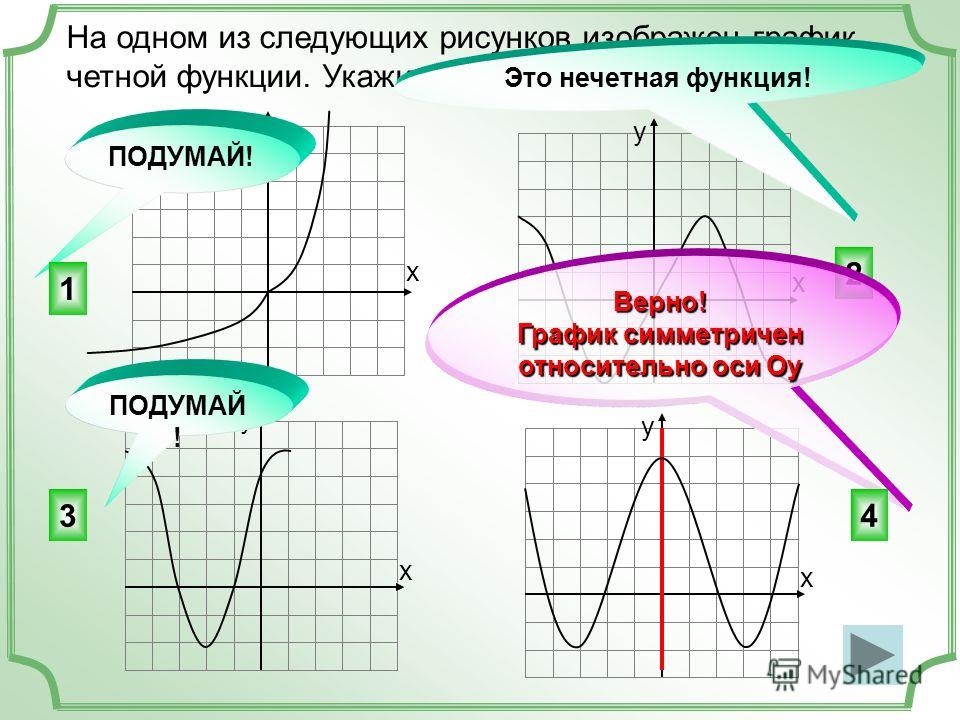
Такое число Tназываетсяпериодом функции.
Из определения 1 следует, что если Т – период функции, то и число –Т тоже является периодом функции (так как при заменеТ на –Т равенство сохраняется). С помощью метода математической индукции можно показать, что еслиТ– период функцииf, то и, тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ– основной период функцииf, то остальные периоды кратны ему.
Доказательство. Предположим противное, то есть что существует периодфункцииf (>0), не кратныйТ. Тогда, разделивнаТ с остатком, получим, где. Поэтому
,
то есть
– период функцииf,
причем,
а это противоречит тому, чтоТ–
основной период функцииf. Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические функции являются периодическими. Основной период иравен,и. Найдем период функции. Пусть- период этой функции. Тогда
(так как.
Отсюда
илиилиили.
Значение T, определяемое из первого равенства, не может быть периодом, так как зависит отх, т.е. является функцией отх
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T– рациональное число, тоиявляются рациональными числами при рациональномхи иррациональными при иррациональномх. Поэтому
при любом рациональном числе T.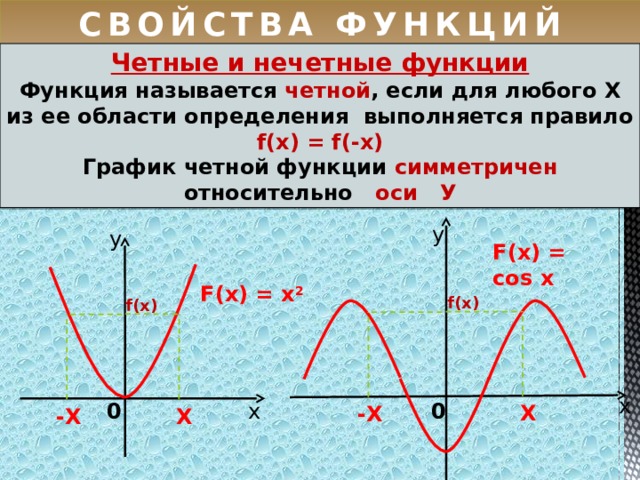 Следовательно, любое рациональное числоTявляется периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомnсколь угодно близким к нулю).
Следовательно, любое рациональное числоTявляется периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомnсколь угодно близким к нулю).
Теорема 4. Если функция f задана на множествеХи имеет периодТ, а функцияg задана на множестве, то сложная функциятоже имеет периодТ.
Доказательство. Имеем, поэтому
,
то есть утверждение теоремы доказано.
Например, так как cos x имеет период, то и функцииимеют период.
Определение 4. Функции, не являющиеся периодическими, называютсянепериодическими.
Четные и нечетные функции. 9 класс А.Г.Мордкович
Название предмета Алгебра
Класс 9
УМК (название учебника, автор, год издания) Алгебра 9класс, в 2-х частях, А.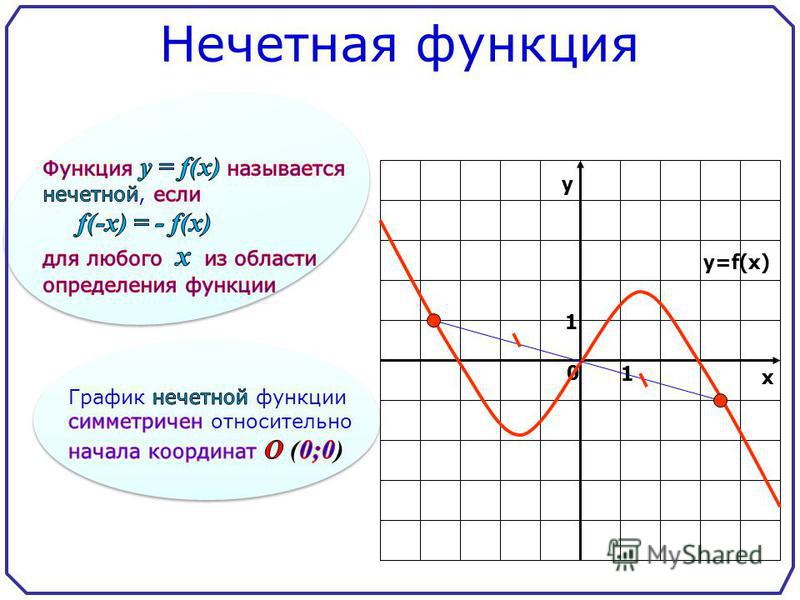 Г.Мордкович, 2010
Г.Мордкович, 2010
Уровень обучения (базовый, углубленный, профильный) базовый
Тема урока Четные и нечетные функции
Общее количество часов, отведенное на изучение темы 2 часа
Место урока в системе уроков по теме Числовые функции (26 часов), 10 урок в разделе
Цель урока
Образовательные:
знакомство с определениями четной и нечетной функции; использование алгоритма исследования функции на четность; исследование симметричности графиков четной/нечетной функции и их построение.
Развивающие:
развитие навыков построения графиков четной и нечетной функции; развитие логического мышления; развитие умений анализировать и делать выводы; развитие коммуникативных навыков.
Воспитательные:
воспитывать аккуратность, графическую культуру, культуру речи; воспитывать умение работать в парах, прислушиваться к мнению одноклассника.
Задачи урока
Ввести понятие симметричного множества.
Сформулировать определения четной/нечетной функции.
Вывести алгоритм исследования функции на четность.
Научиться исследовать функцию на четность с использованием алгоритма.
Научиться определять графики четных/нечетных функций.
Планируемые результаты
осознанное усвоение учащимися материала по теме учебного занятия;
научатся различать четные и нечетные функции; формулировать выводы.
Техническое обеспечение урока
учебник А.Г.Мордкович «Алгебра 9 класс», М.: Мнемозина, 2006;
задачник А.Г.Мордкович «Алгебра 9 класс», М.: Мнемозина, 2006;
карты с индивидуальными заданиями;
мультипроектор;
компьютер.
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)
Содержание урока
1. Приветствие. Мобилизация на работу.
Приветствие. Мобилизация на работу.
2. Актуализация.
1) что мы называем числовой функцией?(Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число y, зависящее от х.)
2) что такое область определения функции?( Все допустимые значения х)
3) что такое область значения функции?( Все допустимые значения у)
4) Найдите область определения функции:
а)
б)
в)
г)
Сравнить значение каждой функции для каждой пары значения аргумента:
1 и -1, 2 и -2.
Для каких из данных функций в области определения выполняются равенства
f(– х) = f(х), f(– х) = – f(х)?
(полученные данные занести в таблицу)
Функция | D (f) | f(2) и f(– 2) | f(1) и f(– 1) |
0,5 и -0,5 | 1 и -1 | ||
0 и 0 | |||
32 и -32 | 1 и -1 | ||
2 и 2 | 1 и 1 |
3. Новый материал
Новый материал
– Выполняя, данную работу мы выявили ещё одно свойство функции, незнакомое вам, но не менее важное, чем остальные – это чётность и нечетность функции. Запишите тему урока: «Чётные и нечётные функции», сегодня мы постараемся научиться определять чётность и нечётность функции, выяснять значимость этого свойства в исследовании функций и построении графиков.
Итак, дадим определения четной и нечетной функции
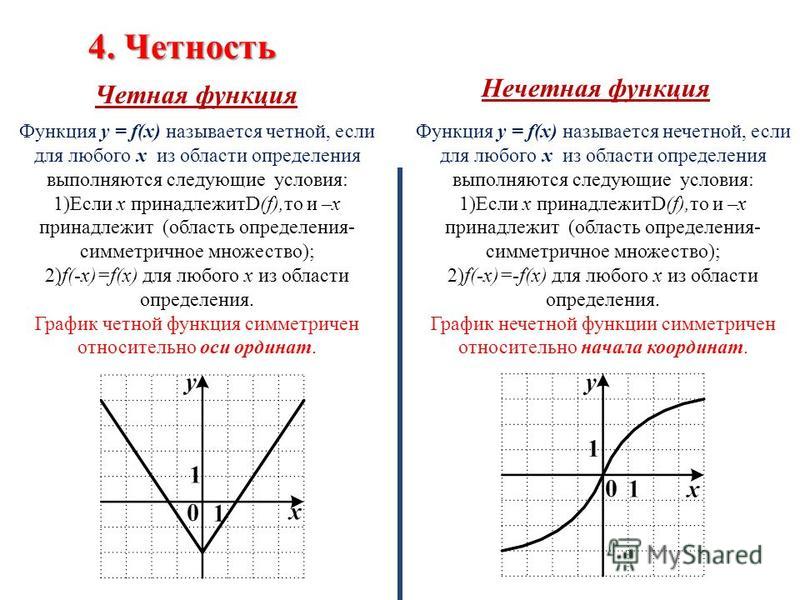
Опр. 1 Функция у = f (х), заданная на множестве Х называется чётной, если для любого значения х Є Х выполняется равенство f(–х)= f(х).
Приведите примеры.
Опр. 2 Функция у = f (х), заданная на множестве Х называется нечётной, если для любого значения х Є Х выполняется равенство f(–х)= –f(х).
Приведите примеры.
Где мы встречались с терминами «четные» и «нечётные»?
Какие из данных функций будут чётными, как вы думаете? Почему? Какие нечётными? Почему?
Для любой функции вида у = хn, где n – целое число можно утверждать, что функция нечётна при n – нечётном и функция чётна при n – чётном.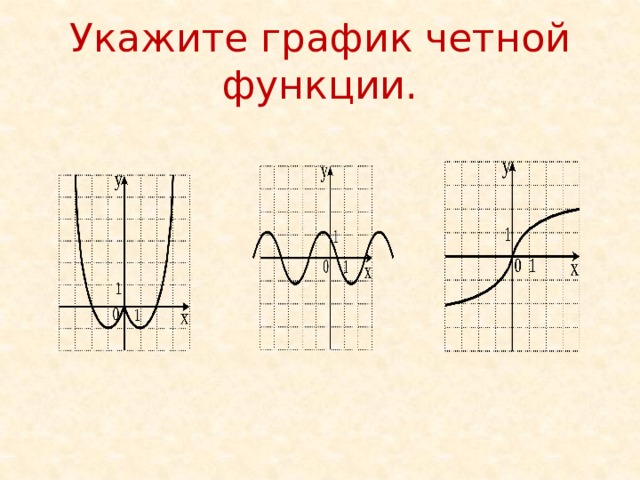
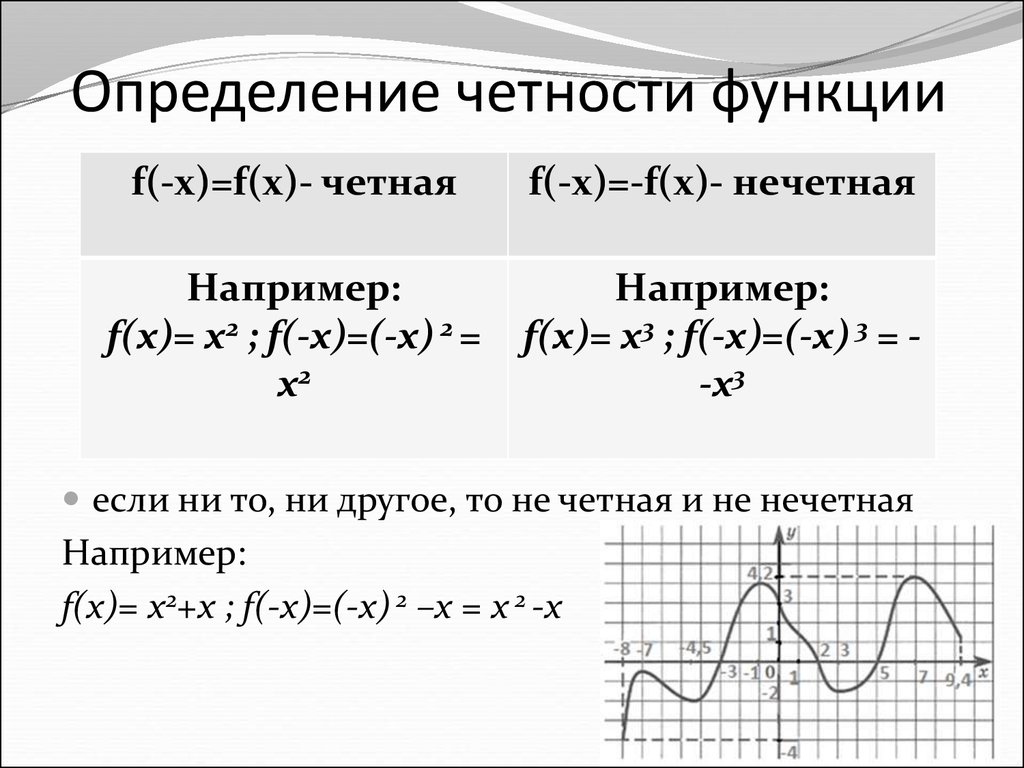
Вопрос: может ли быть, что для функции не выполняется ни одно из условий:
f(-x)=f(x) или f(-x)=-f(x)? Приведите пример.
Функции такого вида не являются ни чётным, ни нечётными.
Функции вида и не являются ни чётным, ни нечётными, т.к. не выполняются равенства f(– х) = – f(х), f(– х) = f(х)
Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность.
В определениях 1 и 2 шла речь о значениях функции при х и – х, тем самым предполагается, что функция определена и при значении х, и при – х.
Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.
Привести примеры симметричных множеств, не симметричных множеств.
У чётных функций область определения – симметричное множество?
У нечётных?
Если же D(f) – несимметричное множество, то функция какая?
Таким образом, если функция у = f(х) – чётная или нечётная, то её область определения D(f) – симметричное множество.
А верно ли обратное утверждение, если область определения функции симметричное множество, то она чётна, либо нечётна?
Таким образом наличие симметричного множества области определения – это необходимое условие, но недостаточное.
Так как же исследовать функцию на четность? Давайте попробуем составить алгоритм.
Алгоритм исследования функции на чётность
1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.
2. Составить выражение для f(– х).
3. Сравнить f(– х) и f(х):
если f(– х)= f(х), то функция чётная;
если f(– х)= – f(х), то функция нечётная;
если f(– х) ≠ f(х) и f(– х) ≠ –f(х), то функция не является ни чётной, ни нечётной.

Примеры:
Исследовать на чётность функцию и схематически изобразить график
Карта 1. y = -2x2 — 1
1.D(f)=R
2. f(-x)=-2(-x)2-1=-2x2-1=f(x)
3. Функция четная
Карта 2. y = -1/2 x3
1.D(f)=R
2. f(-x)= -1/2 (-x)3 =1/2 x3 =- f(x)
3. Функция нечетная
Карта 3. y = -x2 +3x
1.D(f)=R
2. f(-x)= -(-x)2 +3(-x) =-x2 -3x
f(– х) ≠ f(х) и f(– х) ≠ –f(х)
3. Функция ни нечетная, ни четная
Функция ни нечетная, ни четная
Карта 4. y =
1.D(f)=не симметричное множество
2. Функция ни нечетная, ни четная
В результате работы учащихся получаются следующие схематические построения.
Карта 1 Карта 2
Карта 3 Карта 4
Ребята, сделайте вывод о графике функции и четностью функции
Вывод:
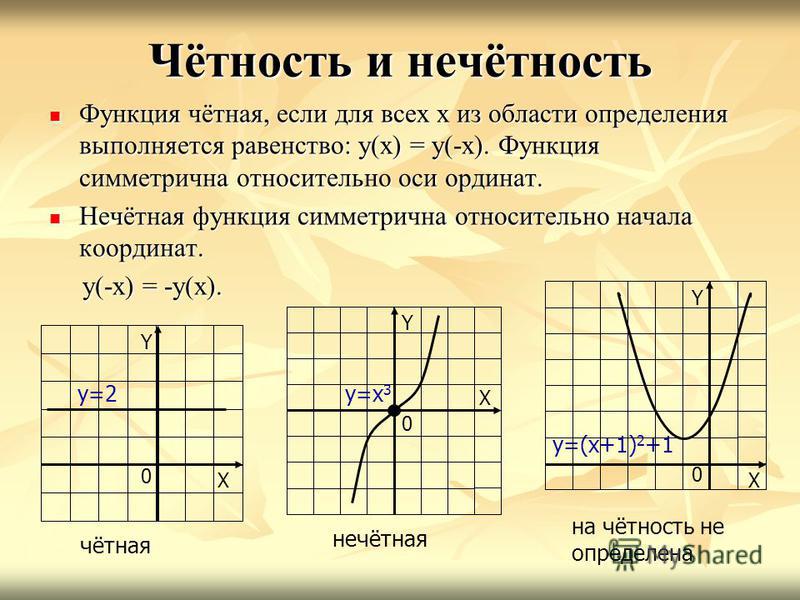
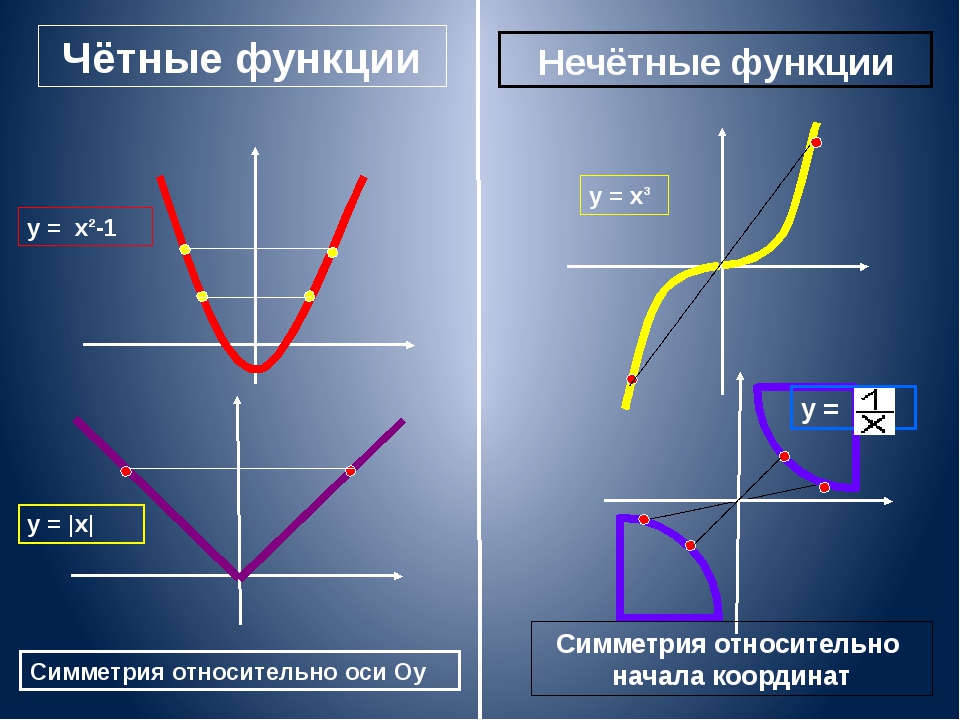
График чётной функции симметричен относительно оси у.
График нечётной функции симметричен относительно начала координат.
Верны ли обратные утверждения?
Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) – чётная функция.
Если график функции у = f(х) симметричен относительно начала координат, то у = f(х) – нечётная функция.
4. Закрепление
№ 11.1, 11.2 (устно)
№11. 3(а.б), 11.4(а,б)
3(а.б), 11.4(а,б)
№ 11.8 (а,б).
№ 11.11 (а,б)
5. Итог занятия
С чем мы с вами познакомились на уроке?
Какая функция называется четной/нечетной?
Алгоритм исследования функции на четность.
6. Домашнее задание
Учебник П.11
Задачник № 11.11(в,г), 11.20
Приложение 1
Функция | D (f) | f(2) и f(– 2) | f(1) и f(– 1) |
Приложение 2
Исследовать на чётность функцию и схематически изобразить график
Карта 1. 1 2 3 | |
Карта 2. y = -1/2 x3 1 2 3 | |
Карта 3. y = -x2 +3x 1 2 3 | |
Карта 4. y = 1 2 3 |
Четные и нечетные функции: знать определение, график, формулу, свойства
Функция f(x) называется четной, если f(-x) = f(x) для всех действительных значений x и f(x) ) называется нечетной функцией, если f(-x) = -f(x) для всех действительных значений x. Четная функция и нечетная функция относятся к разным типам функций в математике. Четная функция в общем случае симметрична относительно оси y.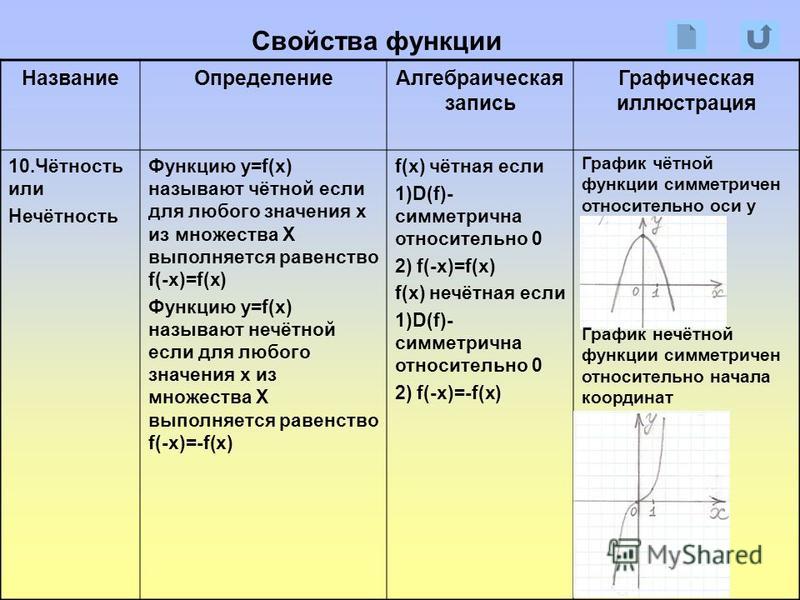 С другой стороны, нечетная функция симметрична относительно начала координат. Функцию можно определить как набор правил, которые связывают, как одна величина зависит от других величин. В этой статье мы постараемся узнать о четных и нечетных частях функции с определением, графиком, формулой, решенными примерами и различными свойствами.
С другой стороны, нечетная функция симметрична относительно начала координат. Функцию можно определить как набор правил, которые связывают, как одна величина зависит от других величин. В этой статье мы постараемся узнать о четных и нечетных частях функции с определением, графиком, формулой, решенными примерами и различными свойствами.
Четные и нечетные функции
Если у нас есть две переменные и мы можем сказать, что для каждого значения первой переменной есть только одно значение второй переменной, то мы можем гарантировать, что вторая переменная является функцией первой переменная. Давайте разберемся с определением четных и нечетных функций.
Четная функция
Функция обозначается f(x), где x — действительное число, которое можно разделить на четное или нечетное, как описано ниже.
Говорят, что функция f(x) является четной функцией, если мы подставляем -x на позицию x и получаем то же самое выражение, то есть f(x). Математически мы можем сказать, что f(x) называется четной функцией, если f(-x) = f(x) для всех действительных значений x.
Также узнайте здесь о четных числах.
Нечетная функция
В отличие от приведенного выше определения, f(x) называется нечетной функцией, когда мы подставляем -x на позицию x и получаем выражение как -f(x). Математически мы можем сказать, что f(x) называется нечетной функцией, если f(-x) = -f(x) для всех действительных значений x.
Узнайте здесь о различных концепциях отношений и функций.
Формула для четных и нечетных функций
Обычно функция записывается как f(x), которая далее читается как «функция f от x». В предыдущем заголовке мы читали об определении, теперь давайте сделаем шаг вперед и узнаем формулу или условия для четных и нечетных функций.
Формула четной функции
Формула четной функции выглядит следующим образом:
f(x) = даже если f(-x) = f(x)
ИЛИ
Уравнение f(-x) – f(x) = 0 верно для четной функции при всех значениях x.
Формула нечетной функции
Формула нечетной функции:
f(x) = нечетная, если -f(x) = f(-x) для всех значений x.
ИЛИ
Уравнение f(-x) + f(x) = 0 верно для нечетной функции при всех x.
Прочтите эту статью о домене и диапазоне функций.
График четных и нечетных функций
Четные и нечетные функции среди различных типов функций зависят от соотношения между входными и выходными условиями данной функции. Это означает, что для отрицательного значения домена, если диапазон равен диапазону исходной функции, то функция является четной. С другой стороны, для отрицательного значения домена, если диапазон также является отрицательным значением диапазона данной функции, то функция считается нечетной. Разберемся в чем дело с графиками.
График четной функции
График четной функции остается неизменным после отражения по оси Y. Это означает, что даже если мы перевернем график по вертикали, кривая останется прежней.
ИЛИ
Это можно понять, поскольку график четной функции симметричен относительно оси у. Это означает, что для любых двух противоположных входных значений x значение функции на оси y останется прежним.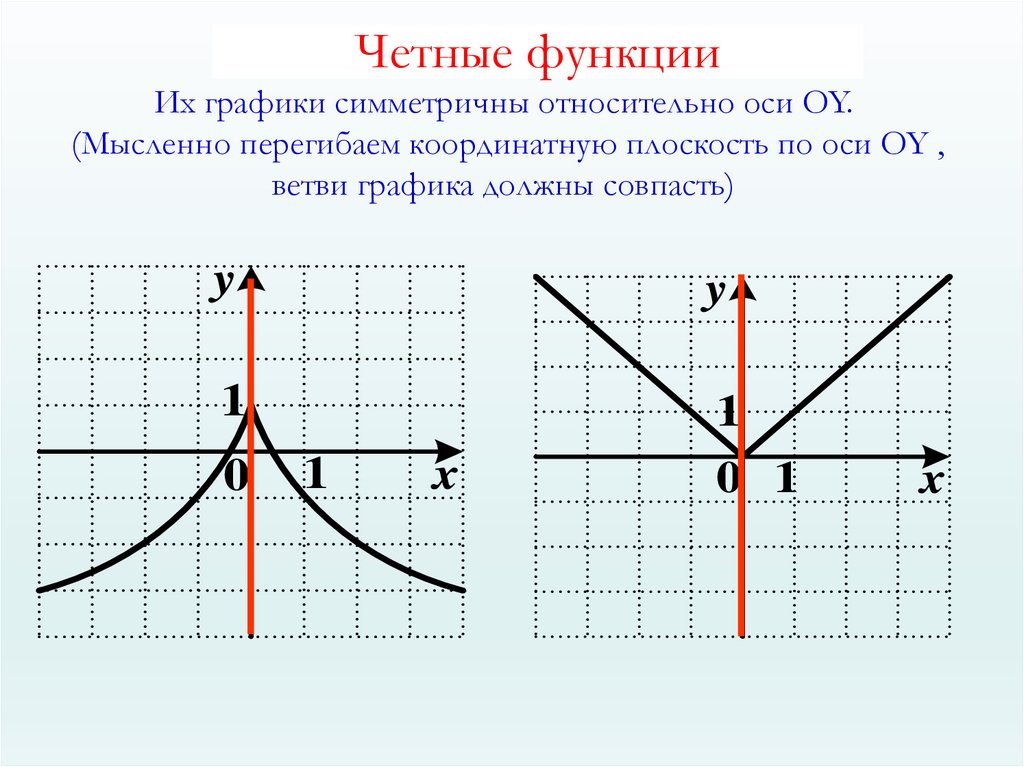 Посмотрите на изображение ниже, чтобы понять эти моменты визуально.
Посмотрите на изображение ниже, чтобы понять эти моменты визуально.
График нечетной функции
Подобно четной функции, график нечетной функции симметричен относительно начала координат. То есть график нечетной функции находится на одинаковой длине от начала координат (0,0), взятого в противоположных направлениях.
ИЛИ
Для любых двух противоположных входных значений x функция будет хранить противоположное значение по оси y. Ознакомьтесь с приведенным ниже графиком, чтобы понять обсуждаемые моменты.
Узнайте о четных и нечетных числах здесь. 9{11}\) и т. д. — все нечетные функции.
Тригонометрические функции можно разделить на четные и нечетные. Для шести основных тригонометрических соотношений; синус, cos, tan, cot, cosec и sec. Идентификация тригонометрических нечетных и четных функций выглядит следующим образом:
sin(-θ) = -sinθ, tan(-θ) = -tanθ, cot(-θ) = -cotθ и cosec(-θ) = -cosecθ. Следовательно, это нечетные функции.
Аналогично, cos(-θ) = cosθ, sec(-θ) = secθ. Следовательно, это четные функции.
Узнайте о тригонометрических соотношениях здесь. 9af(x)dx=0\)
Алгебраические свойства четных и нечетных функций
В предыдущем заголовке мы узнали о правилах интегрирования для нечетных и четных функций, далее мы узнаем о других правилах нечетных и четных функций .
Сложение и вычитание
- Сложение любых двух четных функций дает четную функцию.
- Аналогичным образом сумма любых двух нечетных функций является нечетной.
- Разностная операция, когда она выполняется между двумя четными функциями, результатом является четная функция.
- Точно так же разница между двумя нечетными функциями нечетна.
Умножение и деление
- Результат умножения любых двух четных функций четен.
- Кроме того, умножение любых двух нечетных функций является четным.
- Подобно умножению, деление двух четных функций является четным.

- Кроме того, деление любых двух нечетных функций также является четным.
Прочтите эту статью о типах отношений.
Во всех предыдущих свойствах обе функции были либо четными, либо нечетными. Но что, если один из них четный, а другой нечетный? Результат таких операций обсуждается ниже:
- Сумма или разность четных и нечетных функций не является ни четной, ни нечетной до тех пор, пока одна из заданных функций не является функцией нулевого типа.
- Произведение четных и нечетных функций нечетно.
- Аналогично, при делении четной и нечетной функции получается нечетная функция. 94+5x+6\)
Здесь мы можем сказать, что \(f(-x)\ne f(x)\ne-f(x)\)
То есть функция ни нечетная, ни четная.
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о четных и нечетных функциях
В.1 Как узнать, четная функция или нечетная?
Ответ 1 Если f (−x) = f (x), то функция называется четной. С другой стороны, если f (−x) = −f (x), функция нечетная.
Q.2 Что такое нечетная функция? Приведите пример.
Ответ 2 Если функция заканчивается тождественной противоположностью исходной функции, то функция является нечетной. То есть нечетные функции возвращают отрицательное значение при замене x на –x. Некоторыми примерами того же являются функции синуса, тангенса, раскладушки и косек. 9{2}\) и так далее.
В.4 В чем разница между четными и нечетными функциями?
Ответ 4 Основное различие между четной и нечетной функцией состоит в том, что график четной функции симметричен относительно оси y. Тогда как график нечетного типа функции симметричен относительно начала координат.
 к a оценивается как ноль. Это связано с тем, что области выше и ниже оси x идентичны.
к a оценивается как ноль. Это связано с тем, что области выше и ниже оси x идентичны.В.5 Что такое интеграция нечетных и четных функций?
Ответ 5 Интегрирование четной функции для предела от −a до a подразумевает две равные площади, поскольку график такой функции симметричен относительно оси y. Однако интегрирование нечетной функции для предела −a
Q.6 Как выглядит график четной функции?
Ответ 6 Для четного типа функции график симметричен относительно оси y по той причине, что f(–x) = f(x) для четного типа функции.
Скачать публикацию в формате PDFЧто такое четная функция? (Ответы на 5 часто задаваемых вопросов) – JDM Educational
Функции полезны в математике, и даже у функций есть определенные специальные свойства, облегчающие работу с ними.
Итак, что такое четная функция? Алгебраически четная функция f(x) — это функция, в которой f(-x) = f(x) для всех значений x в области определения функции.
 Визуально четная функция f(x) обладает симметрией относительно оси y (то есть график выглядит как зеркальное отражение слева и справа, отраженное поперек линии x = 0).
Визуально четная функция f(x) обладает симметрией относительно оси y (то есть график выглядит как зеркальное отражение слева и справа, отраженное поперек линии x = 0). Конечно, есть много способов идентифицировать четные функции и использовать их свойства.
В этой статье мы поговорим о том, что такое четные функции и как определить, что функция четная. Мы также ответим на некоторые распространенные вопросы о четных функциях.
Начнем.
Что влияет на стандартное отклонение
Включите JavaScript
Что влияет на стандартное отклонение
Что такое четная функция?
Четная функция — это функция, удовлетворяющая уравнению f(-x) = f(x) для каждого значения x в области определения функции. Это означает, что он будет иметь повторяющиеся значения y.
Но как выглядит четная функция? Что ж, с визуальной точки зрения четная функция имеет симметрию слева направо.
Если разрезать график пополам вертикально по линии x = 0, вы получите зеркальные изображения слева и справа.
. График функции f(x) = -x2: это четная парабола. Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии. См. приведенный ниже пример, представляющий собой график квадратичной функции f(x) = -x 2 :
См. приведенный ниже пример, представляющий собой график квадратичной функции f(x) = -x 2 :Вот некоторые типы четных функций:
- Функции-константы — также называемые горизонтальными линиями, эти функции имеют вид f(x) = c, где c — любое действительное число (константа).
- Квадратичная функция с b = 0 — этот особый тип параболы имеет вид f(x) = ax 2 + c, где a и c — действительные числа (за исключением того, что a не равно нулю).
- Функция косинуса — эти функции имеют вид f(x) = Acos(x) + B, где A и B — действительные числа (за исключением того, что A не равно нулю).
Полиномиальные функции только с четными показателями также являются четными функциями.
Давайте рассмотрим некоторые конкретные примеры четных функций, а также некоторые нечетные функции.

Пример 1. Функция четности (константа)
Возьмем функцию f(x) = 5. Эта функция всегда имеет значение 5, поэтому, безусловно, верно, что f(-x) = f(x) для любого значения х.
Вы можете увидеть симметрию слева направо (зеркальное отражение поперек вертикальной линии x = 0) на графике ниже.
График функции горизонтальной линии f(x) = 5 четный. Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.Пример 2: четная функция (квадратичная с b = 0)
Напомним, что квадратичная функция имеет форму f(x) = ax 2 + bx + c, где a не равно нулю. Если b = 0, то средний член «отсутствует» (на самом деле он равен нулю).
Возьмем функцию f(x) = 3x 2 + 5, которая имеет a = 3, b = 0 и c = 5. Мы можем доказать, что f(-x) = f(x) следующим образом, просто используя определение функции и правила показателей:
- f(x) = 3x 2 + 5 [исходная функция]
- f(-x) = 3(-x) 2 + 5 [подставьте –x для проверки четной функции ]
- f(-x) = 3x 2 + 5 [(-x) 2 = (-x)(-x) = +x 2 , так как произведение двух отрицательных чисел положительно]
- f(-x) = f(x) [поскольку f(x) = 3x 2 + 5]
Таким образом, эта квадратичная функция с b = 0 является четной функцией.

Вы можете увидеть симметрию слева направо (зеркальное отражение поперек вертикальной линии x = 0) на графике ниже.
График параболы f(x) = 3x 2 + 5, которая является четной функцией. Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.Пример 3. Нечетная функция (не горизонтальная линия)
Напомним, что линейная функция имеет вид f(x) = ax + b, где a не равно нулю. Если a не равно нулю, то эта функция нечетна.
Возьмем функцию f(x) = 2x – 7, которая имеет a = 2 и b = -7. Мы можем доказать, что f(-x) не равно f(x) для каждого x на одном примере: x = -1 и x = 1.
- Для x = 1: f(1) = 2(1) – 7 = -5
- Для x = -1: f(-1) = 2(-1) – 7 = -9
Поскольку -5 не равно -9, то f(1) не равно f( -1), а f(-x) не равно f(x) для каждого x в области.
Таким образом, эта строка не является четной функцией.
На графике ниже видно отсутствие симметрии слева направо (по вертикальной линии x = 0).
График линейной функции f(x) = 2x – 7 неровный. Симметрии относительно оси y нет (вертикальная линия x = 0), поскольку у нас нет зеркальных изображений слева и справа от этой линии.
Пример 4. Нечетная функция (кубический многочлен)
Напомним, что кубическая функция имеет вид f(x) = ax 3 + bx 2 + cx + d , где a не равно нулю. Такой функции не будет даже.
Возьмем функцию f(x) = 4x 3 – 7x 2 + 8x + 9, где a = 4, b = -7, c = 8 и d = 9. Мы можем доказать, что f(-x) не равно f(x) для каждого x на одном примере: x = -1 и x = 1.
- Для x = 1: f(1) = 4(1) 3 – 7(1) 2 + 8(1) + 9 = 4 – 7 + 8 + 9 = 14
- Для x = -1: f(-11) = 4(-1) 3 – 7(-1) 2 + 8(-1) + 9 = -4 – 7 – 8 + 9 = -10
Поскольку -14 не равно -10, то f(1) не равно f(-1) и f(-x) не равно f(x) при хотя бы одно значение x в домене.
Таким образом, эта кубическая функция не является четной функцией.

На графике ниже видно отсутствие симметрии слева направо (по вертикальной линии x = 0).
Кубическая функция f(x) = 4x 3 – 7x 2 + 8x + 9 не является четной. Симметрии относительно оси y нет (вертикальная линия x = 0), поскольку у нас нет зеркальных изображений слева и справа от этой линии.Как определить, является ли функция четной
Есть несколько способов определить, является ли функция четной:
- Алгебраически — для этого нужно провести доказательство, показав, что f(-x) такое же, как f(x).
- Графически — для этого необходимо построить график функции и посмотреть, симметричен ли график относительно оси y (то есть вертикальная линия x = 0).
- Из таблицы — для этого необходимо проверить каждую пару противоположных значений x и убедиться, что значения y совпадают.
Как определить, является ли функция четной алгебраически
Чтобы сказать, что функция является четной алгебраически, нам нужно сделать доказательство, используя данную функцию и определение четной функции.

Например, предположим, что у нас есть функция f(x) = x 4 – x 2 + 6.
Чтобы доказать, что эта функция четна алгебраически, нам нужно доказать, что f(-x) = f (x), так как это определение четной функции. Итак:
- f(-x) = (-x) 4 – (-x) 2 + 6 [используя определение f(x) и подставляя –x]
- f(-x) = x 4 – x 2 + 6 [поскольку отрицательное возведение в четную степень является положительным]
- f(-x) = f(x) [по определению , f(x) = x 4 – x 2 + 6]
Как определить четность функции по графику
график и посмотрите, есть ли зеркальные отражения слева и справа от оси у (вертикальная линия x = 0).
Например, пусть у нас есть функция четвертой степени f(x) = x 4 – 3x 2 + 2 (на фото ниже)
График функции четвертой степени f(x) = x 4 – 3x 2 + 2 четно. Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.
Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.Глядя на график, мы видим, что слева и справа от оси Y есть зеркальные изображения. Таким образом, функция четная (или симметричная относительно оси y).
Как узнать, является ли функция четной, по таблице
Мы также можем посмотреть на таблицу, чтобы определить, является ли функция четной. Нам нужно будет увидеть, одинаковы ли значения y для противоположных значений x.
For example, let’s say we have the following function table:
x f(x) -4 8 -3 5 — 2 2 -1 0 1 0 2 2 3 5 4 8 The y values are equal for opposite x values , так как:
- f(-4) = f(4) = 8
- f(-3) = f(3) = 5
- f(-2) = f(2) = 2
- f(-1) = f(1) = 0
Поскольку f(-x) = f(x) для каждой пары значений x в таблице, мы можем заключить, что график имеет вид четная функция.

Может ли четная функция быть отрицательной?
Четная функция может быть отрицательной. Возможно, самым простым примером является функция горизонтальной линии f(x) = -2.
Эта функция четная и отрицательная. Вы можете увидеть его график ниже.
График функции горизонтальной линии f(x) = -2 (постоянная функция), которая является четной и отрицательной для каждого значения x.Может ли четная функция быть взаимно однозначной (инъективной)
Четная функция не может быть взаимно однозначной. Причина в том, что всегда есть два разных значения x (входные данные), которые дают одно и то же значение y (выходное значение) для четной функции.
Подумайте об определении четной функции. В нем говорится, что f(-x) = f(x) для каждого значения x в домене.
Это говорит нам о том, что два разных входа (x и –x, если x не равен нулю) дадут один и тот же результат (то есть f(x)).
Функция «один к одному» имеет только один вход, который ведет к заданному выходу.

Таким образом, график четной функции всегда не пройдет тест горизонтальной линии.
Может ли четная функция иметь обратную?
Четная функция не может иметь обратной. Помните, что только инъективная (однозначная) функция может иметь обратную.
Поскольку четная функция не является взаимно однозначной, она не может иметь обратной.
Всегда ли сумма двух четных функций является четной функцией?
Сумма двух четных функций всегда является четной функцией. Мы можем доказать это в общем случае.
Допустим, у нас есть две четные функции, f(x) и g(x).
По определению четной функции:
- f(-x) = f(x)
- g(-x) = g(x)
Пусть их сумма есть функция h(x ) = f(x) + g(x). Чтобы доказать, что h(x) четно, нам нужно показать, что h(-x) = h(x):
- h(-x) = f(-x) + g(-x) [определение h(x) с подставленным –x]
- h(-x) = f(x) + g (-x) [поскольку f(-x) = f(x)]
- h(-x) = f(x) + g(x) [поскольку g(-x) = g(x)]
- h(-x) = h(x) [поскольку h(x) = f(x) + g(x)]
Таким образом, сумма двух четных функций также является четной функцией.

Вы можете добавить 3, 4 или столько четных функций, сколько хотите, и результирующая функция будет четной.
Может ли четная функция иметь точку перегиба?
Четная функция может иметь точку перегиба. Однако не все четные функции имеют точку перегиба.
Рассмотрим четную функцию f(x) = x 4 – 6x 2 .
Первая производная равна f’(x) = 4x 3 – 12x.
Вторая производная равна f’’(x) = 12x 2 – 12.
Вторая производная равна нулю, когда f’’(x) = 0, или:
- 12x 2 – 12 = 0
- 12x 2 = 12
- x 2 = 1
- x = +1 or -1
Between x = -1 and x = 1, f»(x) отрицательно (например, f»(0) = -12).
При x > 1 f’’(x) положительна (например, f’’(2) = 36).
Итак, знак f»(x) меняется с отрицательного на положительный при x = 1.



 y = -2x2 — 1
y = -2x2 — 1 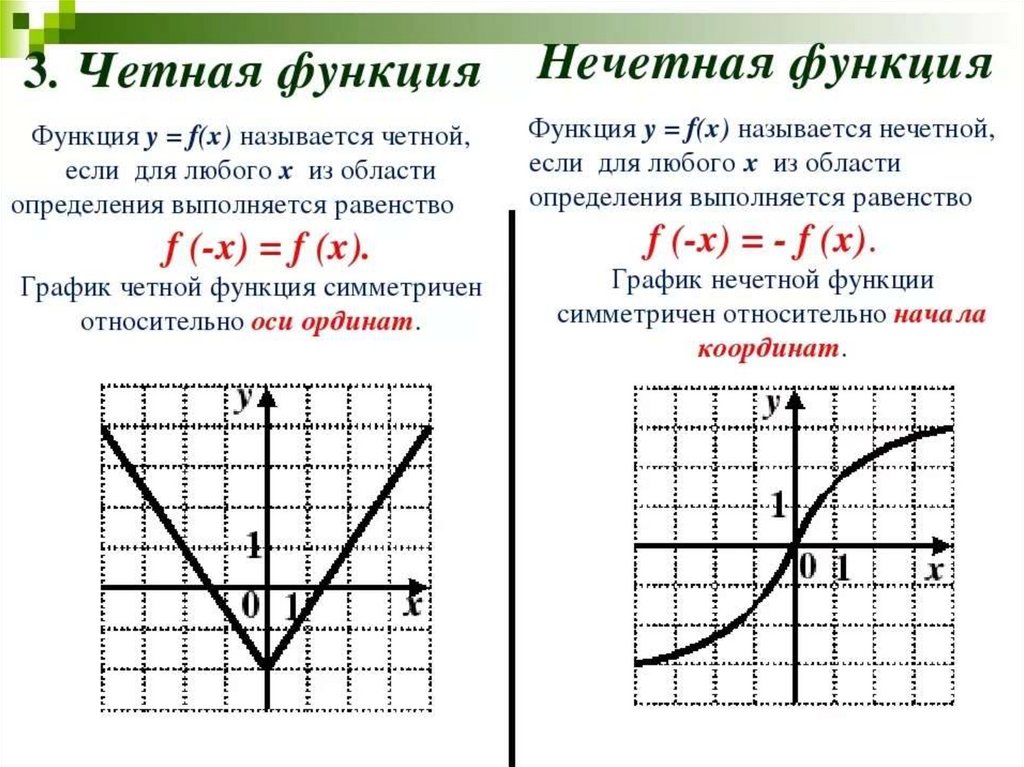
 к a оценивается как ноль. Это связано с тем, что области выше и ниже оси x идентичны.
к a оценивается как ноль. Это связано с тем, что области выше и ниже оси x идентичны.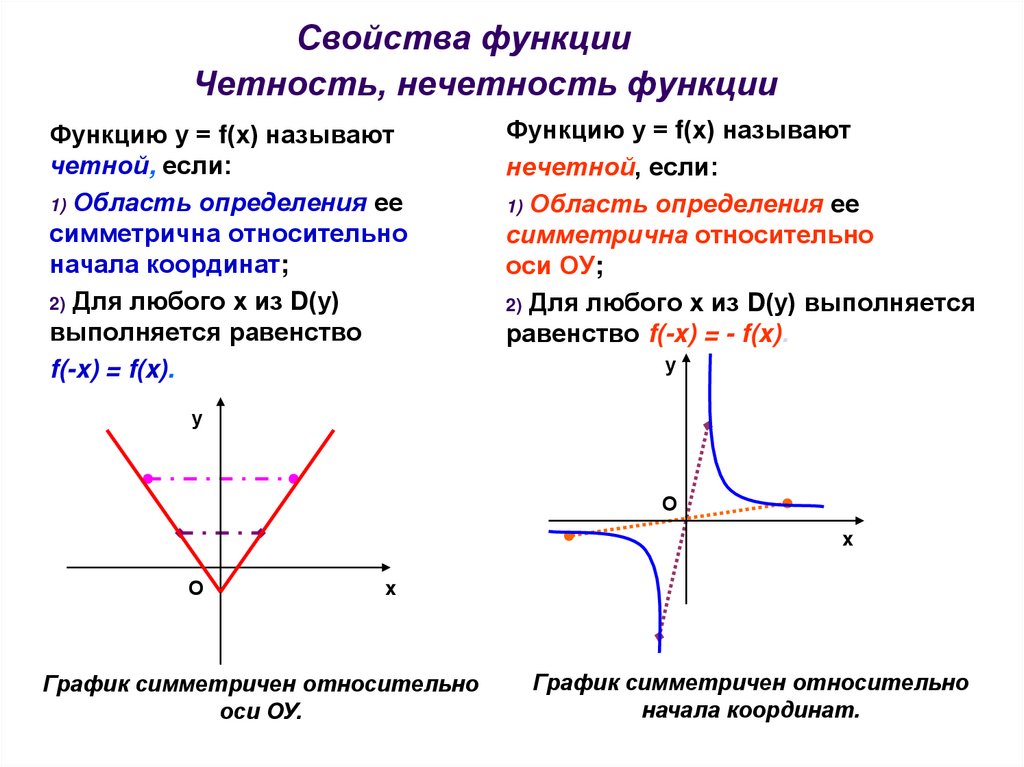 Визуально четная функция f(x) обладает симметрией относительно оси y (то есть график выглядит как зеркальное отражение слева и справа, отраженное поперек линии x = 0).
Визуально четная функция f(x) обладает симметрией относительно оси y (то есть график выглядит как зеркальное отражение слева и справа, отраженное поперек линии x = 0).  См. приведенный ниже пример, представляющий собой график квадратичной функции f(x) = -x 2 :
См. приведенный ниже пример, представляющий собой график квадратичной функции f(x) = -x 2 :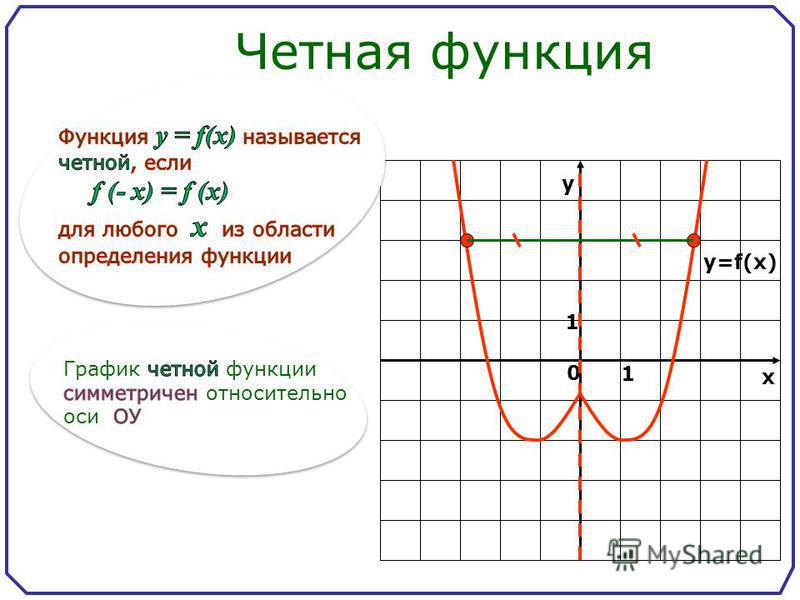

 Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.
Существует симметрия относительно оси y (вертикальная линия x = 0), поскольку у нас есть зеркальные изображения слева и справа от этой линии.