Нахождение обратной матрицы методом Гаусса
Получение обратной матрицы методом Гаусса относится к одному из точных (прямых) методов.
Пример 1
Алгоритм для поиска и нахождения обратной матрицы $A$ методом Гаусса:
$A = \left( \begin{array}{cc|cc} 1 & 2 \\ 3 & 5 \\ \end{array} \right)$
Сначала записывается матрица, от которой необходимо найти обратную, а рядом с ней через черту записывается единичная диагональная матрица того же размера, вот так:
$ \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\ 3 & 5 & 0 & 1 \\ \end{array} \right) $.
Теперь с помощью метода Гаусса находим верхнюю треугольную матрицу. Для этого, сначала, как правило, либо необходимо разделить верхнюю строку на её старший коэффициент, либо поменять верхнюю строку местами с какой-либо другой, у которой первый коэффициент равен единице, в нашем случае просто меняем местами верхнюю и нижнюю строки:
$ \left( \begin{array}{cc|cc} 1 & 2 & 0 & 1 \\ 3 & 5 & 1 & 0 \\ \end{array} \right) $.
Теперь верхнюю строку умножаем на $3$ и вычитаем из нижней:
$ \left( \begin{array}{cc|cc} 1 & 2 & 0 & 1 \\ 0 & -1 & 1 & -3 \\ \end{array} \right) $.
Теперь для получения единичной диагонали нужно обнулить элементы, находящиеся справа сверху, также эта часть метода зовётся методом Жордана-Гаусса. Для этого верхнюю строку складываем с нижней, умноженной на $2$:
$ \left( \begin{array}{cc|cc} 1 & 0 & 2 & -5 \\ 0 & -1 & 1 & -3 \\ \end{array} \right) $.
Делим нижнюю строку на $-1$, получаем:
$ \left( \begin{array}{cc|cc} 1 & 0 & 2 & -5 \\ 0 & 1 & -1 & 3 \\ \end{array} \right) $.
Обратная исходной матрица будет:
$ \left( \begin{array}{cc|cc} 2 & -5 \\ -1 & 3 \\ \end{array} \right) $.
Пример 2
Найти обратную матрицу методом Гаусса.
$A = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 5 & 4 \\ 0 & 1 & 0.5 \end{array} \right) $
Запишем нашу матрицу рядом с единичной:
$A = \left( \begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0\\ 2 & 5 & 4 & 0 & 1 & 0 \\ 0 & 1 & 1/2 & 0 & 0 & 1 \end{array} \right) $
Теперь найдём верхнюю треугольную матрицу, для этого сначала из средней строчки вычтем удвоенную верхнюю:
$A = \left( \begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 1 & 1/2 & 0 & 0 & 1 \end{array} \right) $.
Вычитаем из верхней строчки удвоенную вторую, а из третьей строчки просто вторую строку:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 7 & 5 & -2 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 0 & 2frac{1}{2} & 2 & -1 & 1 \end{array} \right) $.
Делим нижнюю строчку на $2\frac{1}{2}$:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 7 & 5 & -2 & 0\\ 0 & 1 & -2 & -2 & 1 & 0 \\ 0 & 0 & 1 & 0.8 & -0.4 & 0.4 \end{array} \right) $.
Теперь обнуляем элементы, находящиеся выше главной диагонали, для этого вычитаем из верхней строки третью, умноженную на $7$, а к средней строке добавляем третью, помноженную на $2$:
$A = \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -0.6 & 0.8 & -2.8\\ 0 & 1 & 0 & -0.4 & 0.2 & 0.8 \\ 0 & 0 & 1 & 0.8 & -0.4 & 0.4 \end{array} \right) $.
Обратная исходной матрице равна:
$A^{-1} = \left( \begin{array}{ccc} -0. 6 & 0.8 & -2.8\\ -0.4 & 0.2 & 0.8 \\ 0.8 & -0.4 & 0.4 \end{array} \right) $.
6 & 0.8 & -2.8\\ -0.4 & 0.2 & 0.8 \\ 0.8 & -0.4 & 0.4 \end{array} \right) $.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 15.12.2021
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
вычисление обратной матрицы онлайн
вычисление обратной матрицы онлайнВы искали вычисление обратной матрицы онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление обратной матрицы с помощью элементарных преобразований онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычисление обратной матрицы онлайн».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление обратной матрицы с помощью элементарных преобразований онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычисление обратной матрицы онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление обратной матрицы онлайн,вычисление обратной матрицы с помощью элементарных преобразований онлайн,вычислить обратную матрицу онлайн,вычислить обратную матрицу онлайн с подробным решением,как найти обратную матрицу 3 на 3 онлайн,как найти обратную матрицу онлайн,как найти обратную матрицу онлайн с решением,как сделать проверку обратной матрицы онлайн,калькулятор матриц обратная матрица,калькулятор матриц обратных,калькулятор матриц онлайн обратная матрица,калькулятор матрицы метод обратной матрицы,калькулятор матрицы метод обратной матрицы онлайн,калькулятор матрицы метод обратной матрицы онлайн калькулятор,калькулятор матрицы методом обратной матрицы,калькулятор матрицы методом обратной матрицы онлайн калькулятор,калькулятор матрицы обратной матрицы онлайн калькулятор,калькулятор матрицы онлайн методом обратной матрицы,калькулятор матрицы онлайн методом обратной матрицы онлайн,калькулятор метод обратной матрицы,калькулятор метод обратной матрицы онлайн,калькулятор найти обратную матрицу,калькулятор найти обратную матрицу онлайн,калькулятор нахождение обратной матрицы,калькулятор нахождения обратной матрицы,калькулятор обратная матрица,калькулятор обратной матрицы,калькулятор обратной матрицы онлайн,калькулятор обратной матрицы онлайн с решением,калькулятор обратной матрицы с решением,калькулятор обратные матрицы,калькулятор обратных матриц,калькулятор обратных матриц онлайн,калькулятор онлайн метод обратной матрицы,калькулятор онлайн найти обратную матрицу,калькулятор онлайн обернена матриця,матрица обратная к матрице системы онлайн калькулятор,матрица обратная матрица онлайн калькулятор,матрица обратная решение онлайн,матрицы калькулятор обратные,матрицы метод обратной матрицы онлайн,матрицы метод обратной матрицы онлайн калькулятор,матрицы обратная онлайн,матрицы обратная онлайн калькулятор,матрицы обратные онлайн,матрицы онлайн калькулятор метод обратной матрицы,матрицы онлайн метод обратной матрицы,матрицы решить методом обратной матрицы онлайн,матриця обернена онлайн,метод обратной матрицы калькулятор,метод обратной матрицы калькулятор онлайн,метод обратной матрицы онлайн,метод обратной матрицы онлайн калькулятор,метод обратной матрицы онлайн калькулятор с подробным решением,методом гаусса найти обратную матрицу онлайн,методом элементарных преобразований найти обратную матрицу онлайн,найти матрицу а 1 онлайн,найти матрицу обратную данной онлайн,найти матрицу обратную данной онлайн с решением,найти матрицу обратную методом гаусса онлайн,найти обратную,найти обратную матрицу данной онлайн,найти обратную матрицу калькулятор,найти обратную матрицу калькулятор онлайн,найти обратную матрицу методом гаусса онлайн,найти обратную матрицу методом элементарных преобразований,найти обратную матрицу методом элементарных преобразований онлайн,найти обратную матрицу онлайн,найти обратную матрицу онлайн калькулятор,найти обратную матрицу онлайн методом гаусса,найти обратную матрицу онлайн методом гаусса онлайн,найти обратную матрицу онлайн методом элементарных преобразований,найти обратную матрицу онлайн с подробным решением,найти обратную матрицу онлайн с подробным решением и проверкой,найти обратную матрицу онлайн с решением,найти обратную матрицу с помощью элементарных преобразований онлайн,найти обратную матрицу с проверкой онлайн с подробным решением,найти обратную матрицу с решением онлайн,найти обратные матрицы для матриц онлайн,найти союзную матрицу онлайн,нахождение матрицы методом обратной матрицы онлайн,нахождение обратной матрицы калькулятор,нахождение обратной матрицы калькулятор онлайн,нахождение обратной матрицы методом гаусса онлайн,нахождение обратной матрицы онлайн,нахождение обратной матрицы онлайн калькулятор,нахождение обратной матрицы онлайн методом гаусса,нахождение обратной матрицы онлайн с помощью элементарных преобразований,нахождение обратной матрицы онлайн с решением,нахождение обратной матрицы с помощью элементарных преобразований онлайн,нахождение обратной матрицы с решением онлайн,обернена матриця калькулятор онлайн,обернена матриця онлайн,обернена матриця онлайн калькулятор,обратить матрицу онлайн,обратная матрица калькулятор,обратная матрица калькулятор с решением,обратная матрица методом гаусса онлайн,обратная матрица методом элементарных преобразований онлайн,обратная матрица онлайн,обратная матрица онлайн калькулятор,обратная матрица онлайн калькулятор с подробным решением,обратная матрица онлайн методом гаусса,обратная матрица онлайн методом элементарных преобразований,обратная матрица онлайн решение,обратная матрица онлайн с подробным решением,обратная матрица онлайн с проверкой,обратная матрица онлайн с решением,обратная матрица проверка,обратная матрица решение онлайн,обратная матрица с проверкой онлайн,обратная матрица с решением онлайн,обратная матрицы калькулятор онлайн,обратная матрицы онлайн,обратная матрицы онлайн калькулятор,обратную матрицу посчитать,обратную матрицу решить онлайн,обратные матрицы калькулятор,обратные матрицы онлайн,обратные матрицы онлайн с решением,онлайн калькулятор матриц обратная матрица,онлайн калькулятор матриц обратных,онлайн калькулятор матрица обратная матрица,онлайн калькулятор матрицы метод обратной матрицы,онлайн калькулятор матрицы метод обратной матрицы онлайн,онлайн калькулятор матрицы методом обратной матрицы,онлайн калькулятор матрицы методом обратной матрицы онлайн,онлайн калькулятор метод обратной матрицы,онлайн калькулятор найти обратную матрицу,онлайн калькулятор нахождение обратной матрицы,онлайн калькулятор обернена матриця,онлайн калькулятор обратная матрица,онлайн калькулятор обратная матрицы,онлайн калькулятор обратной матрицы,онлайн калькулятор обратной матрицы с решением,онлайн калькулятор обратных матриц,онлайн матриця обернена,онлайн найти обратную матрицу методом гаусса,онлайн нахождение обратной матрицы методом гаусса,онлайн нахождение обратной матрицы с решением,онлайн обернена матриця,онлайн обратная матрица решение,онлайн обратная матрицы,онлайн поиск обратной матрицы,онлайн посчитать обратную матрицу,онлайн проверка матрицы,онлайн расчет обратной матрицы,онлайн решение матрицы методом обратной матрицы онлайн,онлайн решение матрицы обратной,онлайн решение матрицы с помощью обратной матрицы,онлайн решение матрицы с помощью обратной матрицы онлайн,онлайн решение методом обратной матрицы,онлайн решение методом обратной матрицы онлайн,онлайн решение обратная матрица,онлайн решение обратной матрицы,онлайн решение обратных матриц,онлайн решить методом обратной матрицы онлайн,онлайн решить обратную матрицу,поиск обратной матрицы онлайн,построение обратной матрицы онлайн,посчитать обратную матрицу,посчитать обратную матрицу онлайн,посчитать онлайн обратную матрицу,присоединенная матрица калькулятор онлайн,присоединенная матрица онлайн калькулятор,проверка обратной матрицы онлайн,проверка обратной матрицы онлайн с решением,рассчитать обратную матрицу онлайн,расчет обратной матрицы онлайн,решение матрица обратная,решение матрицы методом обратной матрицы калькулятор онлайн,решение матрицы методом обратной матрицы онлайн калькулятор,решение матрицы методом обратной матрицы онлайн с решением,решение матрицы методом обратной онлайн,решение матрицы обратной онлайн,решение матрицы онлайн методом обратной матрицы,решение матрицы онлайн методом обратной матрицы онлайн,решение матрицы с помощью обратной матрицы онлайн,решение обратная матрица онлайн,решение обратной матрицы онлайн,решение обратной матрицы онлайн с подробным решением,решение обратной матрицы онлайн с решением,решение обратных матриц онлайн,решение онлайн матрицы обратной,решение онлайн методом обратной матрицы,решение онлайн методом обратной матрицы онлайн,решение онлайн обратная матрица,решение онлайн обратной матрицы,решение онлайн обратных матриц,решить матрицу методом обратной матрицы онлайн,решить матрицу обратную,решить матрицу обратную онлайн,решить матрицу онлайн методом обратной матрицы,решить матрицы методом обратной матрицы онлайн,решить методом обратной матрицы онлайн калькулятор,решить обратную матрицу онлайн,решить онлайн матрицу методом обратной матрицы,решить онлайн обратную матрицу,союзная матрица онлайн.
Решить задачу вычисление обратной матрицы онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| A 1,1 = (-1) 1+1 |
|
∆ 1,1 = (-1 4-5 (-2)) = 6
| A 1,2 = (-1) 1+2 |
|
∆ 1,2 = -(2 4-(-2 (-2))) = -4
| A 1,3 = (-1) 1+3 |
|
∆ 1,3 = (2 5-(-2 (-1))) = 8
| A 2,1 = (-1) 2+1 |
|
∆ 2,1 = -(2 4-5 3) = 7
| A 2,2 = (-1) 2+2 |
|
∆ 2,2 = (-1 4-(-2 3)) = 2
| A 2,3 = (-1) 2+3 |
|
∆ 2,3 = -(-1 5-(-2 2)) = 1
| A 3,1 = (-1) 3+1 |
|
∆ 3,1 = (2 (-2)-(-1 3)) = -1
| A 3,2 = (-1) 3+2 |
|
∆ 3,2 = -(-1 (-2)-2 3) = 4
| A 3,3 = (-1) 3+3 |
|
∆ 3,3 = (-1 (-1)-2 2) = -3
Тогда обратную матрицу можно записать как:
| A -1 = 1 / 10 |
|
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Похожие на обратные по многим свойствам.
Энциклопедичный YouTube
1 / 5
✪ Как находить обратную матрицу — bezbotvy
✪ Обратная матрица (2 способа нахождения)
✪ Обратная матрица #1
✪ 2015-01-28. Обратная матрица 3×3
✪ 2015-01-27. Обратная матрица 2х2
Субтитры
Свойства обратной матрицы
- det
A
−
1
=
1
det
A
{\displaystyle \det A^{-1}={\frac {1}{\det A}}}
, где
det
{\displaystyle \ \det }
обозначает определитель .
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Способы нахождения обратной матрицы
Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:
Точные (прямые) методы
Метод Гаусса-Жордана
Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
Λ
1
⋅
⋯
⋅
Λ
n
⋅
A
=
Λ
A
=
E
⇒
Λ
=
A
−
1
{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}
. {-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}
где adj (A) {\displaystyle {\mbox{adj}}(A)} — присоединенная матрица ;
Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .
Использование LU/LUP-разложения
Матричное уравнение
A
X
=
I
n
{\displaystyle AX=I_{n}}
для обратной матрицы
X
{\displaystyle X}
можно рассматривать как совокупность
n
{\displaystyle n}
систем вида
A
x
=
b
{\displaystyle Ax=b}
. Обозначим
i
{\displaystyle i}
-ый столбец матрицы
X
{\displaystyle X}
через
X
i
{\displaystyle X_{i}}
; тогда
A
X
i
=
e
i
{\displaystyle AX_{i}=e_{i}}
,
i
=
1
,
…
,
n
{\displaystyle i=1,\ldots ,n}
,поскольку
i
{\displaystyle i}
-м столбцом матрицы
I
n
{\displaystyle I_{n}}
является единичный вектор
e
i
{\displaystyle e_{i}}
. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) . {-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
{-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}
Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .
Для того, чтобы найти обратную матрицу онлайн, вам потребуется указать размер самой матрицы. Для этого кликните на иконки «+» или «-» до тех пор, пока значение количества столбцов и строк вас не устроит. Далее введите в поля требуемые элементы. Ниже находится кнопка «Вычислить» — нажав её, вы получите на экране ответ с подробным решением.
В линейной алгебре довольно часто приходится сталкиваться с процессом вычисления обратной матрицы. Она существует только для невыраженных матриц и для квадратных матриц при условии отличного от нуля детерминанта. В принципе, рассчитать её не представляет особой сложности, особенно если вы имеете дело с небольшой матрицей. Но если нужны более сложные расчёты или тщательная перепроверка своего решения, лучше воспользуйтесь данным онлайн калькулятором. С его помощью вы оперативно и с высокой точностью решите обратную матрицу.
С его помощью вы оперативно и с высокой точностью решите обратную матрицу.
С помощью данного онлайн калькулятора вы сможете значительно облегчить себе задачу в плане расчётов. Кроме того, он помогает закрепить материал, полученный в теории – это своеобразный тренажёр для мозга. Не стоит рассматривать его, как замену вычислениям вручную, он может дать вам гораздо больше, облегчив понимание самого алгоритма. К тому же, лишняя перепроверка себя никогда не помешает.
Метод элементарных преобразований (методы Гаусса и Гаусса-Жордана для нахождения обратных матриц).
Высшая математика » Матрицы и определители » Обратная матрица » Метод элементарных преобразований.
Первая часть
Вторая часть
В первой части был рассмотрен способ нахождения обратной матрицы с помощью алгебраических дополнений. Здесь же мы опишем иной метод нахождения обратных матриц: с использованием элементарных преобразований.
Пусть нам задана квадратная матрица $A_{n\times{n}}$. {-1}$ не существует.
{-1}$ не существует.
Когда мы придём к последней строке, матрица до черты станет верхней треугольной, т.е. все элементы под главной диагональю будут равны нулю. Это будет означать конец прямого хода метода Гаусса.
Обратный ход метода Гаусса
На этом этапе мы поднимаемся по матрице «снизу вверх». Сначала используем последнюю строку $r_n$, затем предпоследнюю $r_{n-1}$ и так далее, пока не дойдём до первой строки. С каждой строкой выполняем однотипные операции.
Пусть, например, речь идёт о некоей k-й строке. Матрица, расположенная до черты, содержит в строке $r_k$ диагональный элемент $a_{kk}$. Если $a_{kk}=1$, то это нас вполне устраивает, а если $a_{kk}\neq{1}$, то просто умножаем строку $r_k$ на коэффициент $\frac{1}{a_{kk}}$, чтобы диагональный элемент стал равен 1. Затем с помощью строки $r_k$ обнуляем элементы k-го столбца, расположенные над строкой $r_k$.
Как только мы дойдём до первой строки, матрица до черты станет единичной, и алгоритм завершится. {-1}\right)$.
{-1}\right)$.
Метод Гаусса
Прямой ход метода Гаусса
Первый шаг
На первом шаге прямого хода мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов первого столбца, расположенных под первой строкой. Однако для тех преобразований, которые мы станем делать для обнуления элементов, удобно, когда ведущий элемент используемой строки равен 1 или -1. Почему это так, станет ясно из дальнейших действий. Чтобы ведущий элемент текущей строки стал равен -1, поменяем местами первую строку с одной из нижележащих строк – с второй строкой:
$$ \left(\begin{array}{ccc|ccc} -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \overset{r_1\leftrightarrow{r_2}}{\rightarrow} \left(\begin{array}{ccc|ccc} \boldred{-1} & 4 & -5 & 0 & 1 & 0\\ \normblue{-5} & 23 & -24 & 1 & 0 & 0\\ \normblue{9} & -40 & 43 & 0 & 0 & 1 \end{array}\right) $$
Теперь ведущий элемент первой строки стал равен -1 (я выделил этот элемент красным цветом).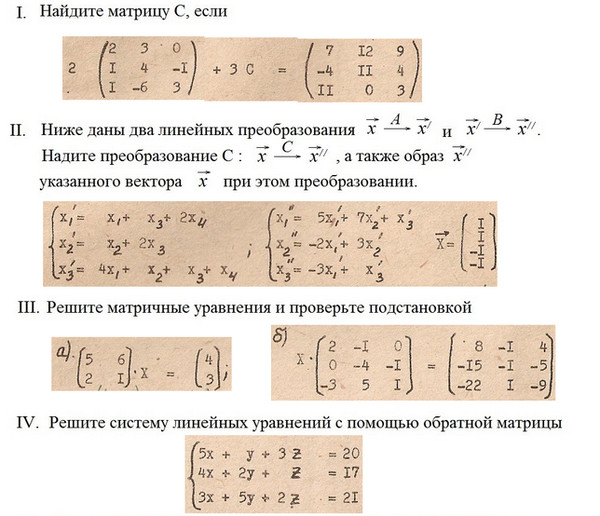 Приступим к обнулению ненулевых элементов первого столбца, лежащих под первой строкой (они выделены синим цветом). Для этого над строками матрицы нужно выполнить такие действия:
Приступим к обнулению ненулевых элементов первого столбца, лежащих под первой строкой (они выделены синим цветом). Для этого над строками матрицы нужно выполнить такие действия:
$$ \begin{aligned} &r_2-\frac{\normblue{-5}}{\boldred{-1}}\cdot{r_1}=r_2-5r_1;\\ &r_3-\frac{\normblue{9}}{\boldred{-1}}\cdot{r_1}=r_3+9r_1. \end{aligned} $$
Запись $r_2-5r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на пять. Результат записывают на место второй строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:
$$ r_2-5r_1 =(-5;\;23;\;-24;\;1;\;0;\;0)-5\cdot(-1;\;4;\;-5;\;0;\;1;\;0)=\\ =(-5;\;23;\;-24;\;1;\;0;\;0)-(-5;\;20;\;-25;\;0;\;5;\;0) =(0;\;3;\;1;\;1;\;-5;\;0) $$
Действие $r_3+9r_1$ выполняется аналогично. Первую строку мы не трогали, поэтому в новую матрицу она перейдёт без изменений:
Первую строку мы не трогали, поэтому в новую матрицу она перейдёт без изменений:
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ r_2-5r_1 \\ r_3+9r_1 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) $$
На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение. Кстати, теперь, я полагаю, ясно, зачем надо было менять местами строки. Если бы не смена мест строк, нам пришлось бы выполнять действия $r_2-\frac{1}{5}\cdot{r_1}$ и $r_3+\frac{9}{5}\cdot{r_1}$, что привело бы к появлению дробей. А легче, разумеется, работать с целыми числами, чем с дробями.
Второй шаг
На втором шаге прямого хода мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому можем приступать к обнулению ненулевых элементов второго столбца, расположенных под второй строкой:
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ r_3+4/3\cdot{r_2} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) $$
Матрица до черты стала верхней треугольной, поэтому прямой ход метода Гаусса окончен.
Пару слов насчёт действий со строками, которые мы выполняли на втором шаге. На первом шаге мы меняли местами строки, чтобы ведущий элемент первой строки стал равен -1. Здесь такая смена строк ничего не даст, так как доступна к обмену лишь третья строка, а у неё ведущий элемент тоже не равен ни 1, ни -1. В этом случае можно выполнить дополнительное преобразование со второй строкой: $r_2+r_3$:
На первом шаге мы меняли местами строки, чтобы ведущий элемент первой строки стал равен -1. Здесь такая смена строк ничего не даст, так как доступна к обмену лишь третья строка, а у неё ведущий элемент тоже не равен ни 1, ни -1. В этом случае можно выполнить дополнительное преобразование со второй строкой: $r_2+r_3$:
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ r_2+r_3 \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & -1 & -1 & 1 & 4 & 1\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) $$
После этого текущий шаг прямого хода будет продолжен без дробей. Можно было сделать и такое действие: $3r_3+4r_2$, тогда и необходимый элемент третьего столбца был бы обнулён, и дробей бы не появилось. Выполнять такие действия или нет – надо смотреть по ситуации. Если работы с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов прямого хода, то, возможно, лучше упростить себе расчёты и выполнить вспомогательное действие, чтобы потом не работать с дробями. К слову, если есть необходимость избавиться от дробей в некоей строке, то можно просто домножить данную строку на соответствующий коэффициент. Например, строку $\left(\frac{1}{3};\;-\frac{4}{5};\;2;0\right)$ можно домножить на число 15, тогда дроби исчезнут, и строка станет такой: $\left(5;\;-12;\;30;0\right)$.
Выполнять такие действия или нет – надо смотреть по ситуации. Если работы с дробями предвидится немного, то особого смысла в попытках их избежать нет. Если же нас ожидают ещё несколько шагов прямого хода, то, возможно, лучше упростить себе расчёты и выполнить вспомогательное действие, чтобы потом не работать с дробями. К слову, если есть необходимость избавиться от дробей в некоей строке, то можно просто домножить данную строку на соответствующий коэффициент. Например, строку $\left(\frac{1}{3};\;-\frac{4}{5};\;2;0\right)$ можно домножить на число 15, тогда дроби исчезнут, и строка станет такой: $\left(5;\;-12;\;30;0\right)$.
Обратный ход метода Гаусса
Первый шаг
На первом шаге обратного хода мы работаем с последней, т.е. третьей строкой матрицы. Посмотрим на диагональный элемент в третьей строке: он равен $-\frac{2}{3}$. Сделаем этот элемент единицей, домножив третью строку на $-\frac{3}{2}$, а затем с помощью третьей строки обнулим ненулевые элементы третьего столбца, расположенные над третьей строкой:
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ -3/2\cdot{r_3} \end{array} \rightarrow\\ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1+5r_3 \phantom{0}\\ r_2-r_3\\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) $$
Второй шаг
На втором шаге обратного хода мы работаем с предпоследней, т. е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $\frac{1}{3}$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:
е. второй строкой матрицы. Посмотрим на диагональный элемент во второй строке: он равен 3. Сделаем этот элемент единицей, домножив вторую строку на $\frac{1}{3}$, а затем с помощью второй строки обнулим ненулевой элемент второго столбца, расположенный над второй строкой:
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} \phantom{0}\\ 1/3\cdot{r_2} \\ \phantom{0} \end{array} \rightarrow\\ \left(\begin{array}{ccc|ccc} -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1-4r_2\\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 0 & 0 & -14 & -29/2 & -19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) $$
Третий шаг
Работаем с первой строкой. {-1}
=\left(\begin{array}{ccc}
14 & 29/2 & 19/2\\
1 & -1/2 & 1/2\\
-2 & -7/2 & -3/2 \end{array}\right)
$$
{-1}
=\left(\begin{array}{ccc}
14 & 29/2 & 19/2\\
1 & -1/2 & 1/2\\
-2 & -7/2 & -3/2 \end{array}\right)
$$
Если пропустить все пояснения, то решение будет таким:
$$ \left(\begin{array}{ccc|ccc} -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \overset{r_1\leftrightarrow{r_2}}{\rightarrow} $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ r_2-5r_1 \\ r_3+9r_1 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0} \\ r_3+4/3\cdot{r_2} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ -3/2\cdot{r_3} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1+5r_3 \phantom{0}\\ r_2-r_3\\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 3 & 0 & 3 & -3/2 & 3/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} \phantom{0}\\ 1/3\cdot{r_2} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} -1 & 4 & 0 & -10 & -33/2 & -15/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1-4r_2\\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} -1 & 0 & 0 & -14 & -29/2 & -19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} -1\cdot{r_1}\\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) $$
Теперь решим этот же пример методом Гаусса-Жордана.
Метод Гаусса-Жордана
Первый шаг
На первом шаге мы работаем с первой строкой. Первый элемент этой строки (число -5) не равен нулю, поэтому можем следовать стандартному алгоритму: домножить первую строку на $-\frac{1}{5}$, чтобы первый элемент стал равен единице, а затем обнулить все иные ненулевые элементы первого столбца. Однако, как и при решении методом Гаусса, удобно, когда ведущий элемент используемой строки равен 1 или -1. Поэтому как и на первом шаге метода Гаусса, поменяем местами первую строку с второй строкой:
$$ \left(\begin{array}{ccc|ccc} -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \overset{r_1\leftrightarrow{r_2}}{\rightarrow} \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ \normblue{-5} & 23 & -24 & 1 & 0 & 0\\ \normblue{9} & -40 & 43 & 0 & 0 & 1 \end{array}\right) $$
Теперь первый элемент первой строки стал равен -1. Чтобы этот элемент стал равен 1, домножим первую строку на -1, а потом обнулим все остальные ненулевые элементы первого столбца (они выделены в матрице выше синим цветом):
Чтобы этот элемент стал равен 1, домножим первую строку на -1, а потом обнулим все остальные ненулевые элементы первого столбца (они выделены в матрице выше синим цветом):
$$ \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} -1\cdot{r_1}\\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow\\ \rightarrow\left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ r_2+5r_1 \\ r_3-9r_1 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) $$
На этом первый шаг закончен. Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение.
Нулевых строк в матрице до черты не возникло, поэтому продолжаем решение.
Второй шаг
На втором шаге мы работаем с второй строкой. Второй элемент этой строки (число 3) не равен нулю, поэтому домножаем вторую строку на $\frac{1}{3}$, чтобы второй элемент стал равен единице, а затем обнуляем все иные ненулевые элементы второго столбца.
$$ \left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\1/3\cdot{r_2} \\\phantom{0}\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} r_1+4r_2\\ \phantom{0} \\ r_3+4r_2 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) $$
Замечание относительно облегчения работы с дробями, сделанное после второго шага прямого хода метода Гаусса, остаётся в силе и здесь.
Третий шаг
На третьем шаге мы работаем с третьей строкой. Третий элемент этой строки (число -2/3) не равен нулю, поэтому домножаем третью строку на $-\frac{3}{2}$, чтобы третий элемент стал равен единице, а затем обнуляем все иные ненулевые элементы третьего столбца.
$$ \left(\begin{array}{ccc|ccc} 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\\phantom{0} \\ -3/2\cdot{r_3}\end{array} \rightarrow\\ \rightarrow\left(\begin{array}{ccc|ccc} 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1-19/3r_3\\ r_2-1/3\cdot{r_3} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) $$
Матрица до черты стала единичной, преобразования завершены. {-1}
=\left(\begin{array}{ccc}
14 & 29/2 & 19/2\\
1 & -1/2 & 1/2\\
-2 & -7/2 & -3/2 \end{array}\right)
$$
{-1}
=\left(\begin{array}{ccc}
14 & 29/2 & 19/2\\
1 & -1/2 & 1/2\\
-2 & -7/2 & -3/2 \end{array}\right)
$$
Если пропустить все пояснения, то решение будет таким:
$$ \left(\begin{array}{ccc|ccc} -5 & 23 & -24 & 1 & 0 & 0\\ -1 & 4 & -5 & 0 & 1 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \overset{r_1\leftrightarrow{r_2}}{\rightarrow} \left(\begin{array}{ccc|ccc} -1 & 4 & -5 & 0 & 1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} -1\cdot{r_1}\\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ -5 & 23 & -24 & 1 & 0 & 0\\ 9 & -40 & 43 & 0 & 0 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ r_2+5r_1 \\ r_3-9r_1 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 3 & 1 & 1 & -5 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\1/3\cdot{r_2} \\\phantom{0}\end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} 1 & -4 & 5 & 0 & -1 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & -4 & -2 & 0 & 9 & 1 \end{array}\right) \begin{array} {l} r_1+4r_2\\ \phantom{0} \\ r_3+4r_2 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & -2/3 & 4/3 & 7/3 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\\phantom{0} \\ -3/2\cdot{r_3}\end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} 1 & 0 & 19/3 & 4/3 & -23/3 & 0\\ 0 & 1 & 1/3 & 1/3 & -5/3 & 0\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) \begin{array} {l} r_1-19/3r_3\\ r_2-1/3\cdot{r_3} \\ \phantom{0} \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & 0 & 0 & 14 & 29/2 & 19/2\\ 0 & 1 & 0 & 1 & -1/2 & 1/2\\ 0 & 0 & 1 & -2 & -7/2 & -3/2 \end{array}\right) $$
Ответ: $A^{-1}
=\left(\begin{array}{ccc}
14 & 29/2 & 19/2\\
1 & -1/2 & 1/2\\
-2 & -7/2 & -3/2 \end{array}\right)$. {-1}$, если
$A=\left(\begin{array}{cccc}
-2 & 3 & 0 & 1\\
-6 & 9 & -2 & 7\\
0 & -2 & -18 & 27\\
-4 & 5 & -8 & 14\end{array} \right)$.
{-1}$, если
$A=\left(\begin{array}{cccc}
-2 & 3 & 0 & 1\\
-6 & 9 & -2 & 7\\
0 & -2 & -18 & 27\\
-4 & 5 & -8 & 14\end{array} \right)$.
Решение
В предыдущем примере были даны подробные пояснения каждого шага как метода Гаусса, так и метода Гаусса-Жордана. В этом примере я стану комментировать лишь некие нюансы, которые возникнут в ходе решения.
Метод Гаусса
$$ \left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ -6 & 9 & -2 & 7 & 0 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ -4 & 5 & -8 & 14 & 0 & 0 & 0 & 1 \end{array} \right) \begin{array} {l} \phantom{0} \\ r_2-3r_1 \\ \phantom{0} \\ r_4-2r_1 \end{array} \rightarrow \left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end{array} \right) $$
Пора переходить ко второму шагу прямого хода метода Гаусса. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
$$ \left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end{array} \right) \overset{r_2\leftrightarrow{r_4}}{\rightarrow} \left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ r_3-2r_2 \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ \phantom{0} \\ r_4-r_3 \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1\\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} r_1-r_4 \\ r_2-12r_4 \\ r_3-3r_1 \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\\ 0 & 0 & -2 & 0 & 25 & -3 & 4 & -8\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ -1/2\cdot{r_3} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & -8 & 0 & 82 & -12 & 12 & -23\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} \phantom{0} \\ r_2+8r_3 \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & -1 & 0 & 0 & -18 & 0 & -4 & 9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} \phantom{0} \\ -1\cdot{r_2} \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 0 & 8 & -1 & 1 & -2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} r_1-3r_2 \\ \phantom{0} \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} -2 & 0 & 0 & 0 & -46 & -1 & -11 & 25\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} -1/2\cdot{r_1} \\ \phantom{0} \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array}\right) $$
Из последней матрицы получаем ответ:
$$ A^{-1} =\left(\begin{array}{cccc} 23 & 1/2 & 11/2 & -25/2\\ 18 & 0 & 4 & -9\\ -25/2 & 3/2 & -2 & 4\\ -7 & 1 & -1 & 2 \end{array}\right) $$
Метод Гаусса-Жордана
$$ \left(\begin{array}{cccc|cccc} -2 & 3 & 0 & 1 & 1 & 0 & 0 & 0\\ -6 & 9 & -2 & 7 & 0 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ -4 & 5 & -8 & 14 & 0 & 0 & 0 & 1 \end{array} \right) \begin{array} {l} -1/2\cdot{r_1} \\ \phantom{0} \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ -6 & 9 & -2 & 7 & 0 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ -4 & 5 & -8 & 14 & 0 & 0 & 0 & 1 \end{array} \right) \begin{array} {l} \phantom{0} \\ r_2+6r_1 \\ \phantom{0} \\ r_4+4r_1 \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end{array} \right) $$
Пора переходить ко второму шагу метода Гаусса-Жордана. На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
На этом шаге должна использоваться вторая строка, однако второй элемент данной строки равен нулю. Согласно алгоритму, нужно поменять местами вторую строку с одной из нижележащих строк, у которых второй элемент отличен от нуля. Поменяем местами вторую и четвёртую строки, а потом продолжим преобразования:
$$ \left(\begin{array}{cccc|cccc} 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \end{array} \right) \overset{r_2\leftrightarrow{r_4}}{\rightarrow} $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & -1 & -8 & 12 & -2 & 0 & 0 & 1 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ -1\cdot{r_2} \\ \phantom{0} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & -3/2 & 0 & -1/2 & -1/2 & 0 & 0 & 0\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & -2 & -18 & 27 & 0 & 0 & 1 & 0\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} r_1+3/2\cdot{r_2} \\ \phantom{0} \\ r_3+2r_2 \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & 0 & -2 & 3 & 4 & 0 & 1 & -2\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ -1/2\cdot{r_3} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & 0 & 12 & -37/2 & 5/2 & 0 & 0 & -3/2\\ 0 & 1 & 8 & -12 & 2 & 0 & 0 & -1 \\ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\\ 0 & 0 & -2 & 4 & -3 & 1 & 0 & 0 \end{array} \right) \begin{array} {l} r_1-12r_3 \\ r_2-8r_3 \\ \phantom{0} \\ r_4+2r_3 \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & 0 & 0 & -1/2 & 53/2 & 0 & 6 & -27/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9 \\ 0 & 0 & 1 & -3/2 & -2 & 0 & -1/2 & 1\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array} \right) \begin{array} {l} r_1+1/2\cdot{r_4} \\ \phantom{0} \\ r_3+3/2\cdot{r_4} \\ \phantom{0} \end{array} \rightarrow $$ $$ \rightarrow\left(\begin{array}{cccc|cccc} 1 & 0 & 0 & 0 & 23 & 1/2 & 11/2 & -25/2\\ 0 & 1 & 0 & 0 & 18 & 0 & 4 & -9\\ 0 & 0 & 1 & 0 & -25/2 & 3/2 & -2 & 4\\ 0 & 0 & 0 & 1 & -7 & 1 & -1 & 2 \end{array}\right) $$
Из последней матрицы получаем ответ:
$$ A^{-1} =\left(\begin{array}{cccc} 23 & 1/2 & 11/2 & -25/2\\ 18 & 0 & 4 & -9\\ -25/2 & 3/2 & -2 & 4\\ -7 & 1 & -1 & 2 \end{array}\right) $$
Ответ: $
A^{-1}
=\left(\begin{array}{cccc}
23 & 1/2 & 11/2 & -25/2\\
18 & 0 & 4 & -9\\
-25/2 & 3/2 & -2 & 4\\
-7 & 1 & -1 & 2
\end{array}\right)
$. {-1}$, если
$A=\left(\begin{array}{ccc}
1 & -2 & 5\\
-2 & 5 & -13\\
-3 & 4 & -9\end{array} \right)$.
{-1}$, если
$A=\left(\begin{array}{ccc}
1 & -2 & 5\\
-2 & 5 & -13\\
-3 & 4 & -9\end{array} \right)$.
Решение
В данном примере применим метод Гаусса.
$$ \left(\begin{array}{ccc|ccc} 1 & -2 & 5 & 1 & 0 & 0\\ -2 & 5 & -13 & 0 & 1 & 0\\ -3 & 4 & -9 & 0 & 0 & 1\end{array} \right) \begin{array} {l} \phantom{0} \\ r_2+2r_1 \\ r_3+3r_1 \end{array} \rightarrow\\ $$ $$ \rightarrow\left(\begin{array}{ccc|ccc} 1 & -2 & 5 & 1 & 0 & 0\\ 0 & 1 & -3 & 2 & 1 & 0\\ 0 & -2 & 6 & 3 & 0 & 1\end{array} \right) \begin{array} {l} \phantom{0} \\ \phantom{0} \\ r_3+2r_2 \end{array} \rightarrow \left(\begin{array}{ccc|ccc} 1 & -2 & 5 & 1 & 0 & 0\\ 0 & 1 & -3 & 2 & 1 & 0\\ 0 & 0 & 0 & 7 & 2 & 1\end{array}\right) $$
В матрице до черты появилась нулевая строка. {-1}$ не существует.
{-1}$ не существует.
Ответ: обратной матрицы не существует.
Первая часть
Вторая часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Обратная ⚠️ матрица методом Гаусса: алгоритм вычисления
Понятие обратной матрицы
Матрица A−1 считается обратной для матрицы A, если при умножении A−1 на исходную матрицу получится новая матрица E, на главной диагонали которой расположены единицы, а вокруг них – нули. Образованная матрица E является единичной диагональной матрицей и может быть записана с помощью формулы: E=A×A−1.
Инверсия матрицы существует лишь для квадратных матриц (с одинаковым количеством строк и столбцов) с детерминантом, не равном нулю. Такие матрицы называются невырожденными.
Наиболее наглядно обратная матрица рассматривается на примере матрицы 3×3. Ее возможно обобщить с аналогичными произвольными матрицами.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свойства обратных матриц
- Обратное значение обратной матрицы A−1 эквивалентно исходной матрице A: (A−1)−1=A.
- Определитель исходной матрицы A соответствует обратному значению детерминанта обратной матрицы A−1: |A|=1/|A−1|.
- Матрица, обратная матрице A, умноженной на коэффициент λ≠0, равна значению, полученному при умножении обратной матрицы A−1 и обратного значения коэффициента λ, то есть (λ×A)−1=A−1/λ.
- Обратное значение произведения обратимых матриц A и B с одинаковым числом строк и столбцов будет равно значению, полученному при умножении матриц, обратных исходным, то есть (A×B)−1=B−1×A−1.
- Обратная матрица транспонированной матрицы эквивалентна транспонированной обратной матрице (A−1)T=(AT)−1.

Метод Гаусса для решения
Метод Гаусса – это правило, применяющееся в решении СЛАУ (систем линейных алгебраических уравнений). Данный метод имеет следующие плюсы:
- Не нужно производить проверку системы уравнения на совместность.
- Можно решать системы уравнений со следующими условиями:
- при равенстве числа определителей и неизвестных переменных;
- при несовпадении количества детерминантов и неизвестных переменных;
- при определителе, равном 0.
- Ответ можно получить, выполнив относительно небольшое число вычислений.
Алгоритм решения
Исходная матрица имеет вид:
\(A=\begin{pmatrix}1&2\\3&5\end{pmatrix}\)
Нахождение обратной матрицы по правилу Гаусса необходимо выполнить в такой последовательности:
1. Записать матрицу, от которой необходимо выполнить преобразование в обратную. Рядом через вертикальную черту выполнить запись единичной диагональной матрицы аналогичного порядка:
Рядом через вертикальную черту выполнить запись единичной диагональной матрицы аналогичного порядка:
\(\left(\begin{array}{cc}1&2\\3&5\end{array}\left|\begin{array}{cc}1&0\\0&1\end{array}\right.\right)\)
2. Произвести поиск верхней треугольной матрицы по методу Гаусса. Это можно сделать двумя способами: разделить верхнюю строку на ее старший коэффициент или поменять верхнюю строку местами с той, где первый коэффициент равен 1. В данном примере поменяем верхнюю строку с нижней местами и получим:
\(\left(\begin{array}{cc}1&2\\3&5\end{array}\left|\begin{array}{cc}0&1\\1&0\end{array}\right.\right)\)
3. Выполним умножение верхней строки матрицы на 3 и вычтем полученные произведения из нижней:
\(\left(\begin{array}{cc}1&2\\0&-1\end{array}\left|\begin{array}{cc}0&1\\1&-3\end{array}\right.\right)\)
4. Данный шаг правила Гаусса именуют методом Жордана-Гаусса. В единичной диагонали, полученной в итоге предыдущих манипуляций, обнулим верхние правые элементы. {-1}=\begin{pmatrix}2&-5\\-1&3\end{pmatrix}\)
{-1}=\begin{pmatrix}2&-5\\-1&3\end{pmatrix}\)
Решение задач методом Гаусса
Пример
Найти инверсию матрицы третьего порядка:
\(A=\begin{pmatrix}2&3&7\\1&-5&2\\3&-1&9\end{pmatrix}\)
Решение:
1. Запишем справа от A единичную диагональную матрицу:
\(\left(\begin{array}{ccc}2&3&7\\1&-5&2\\3&-1&9\end{array}\left|\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right.\right)\)
Теперь необходимо выполнить преобразования, чтобы единичная диагональная матрица оказалась справа.
2. Первую и вторую строку поменяем местами:
\(\left(\begin{array}{ccc}1&-5&2\\2&3&7\\3&-1&9\end{array}\left|\begin{array}{ccc}0&1&0\\1&0&0\\0&0&1\end{array}\right.\right)\)
3. Вторую строку суммируем с первой, умноженной на −2. Третью строку сложим с первой, умноженной на −3:
\(\left(\begin{array}{ccc}1&-5&2\\0&13&3\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\1&-2&0\\0&-3&1\end{array}\right. \right)\)
\right)\)
4. Вторую сложим с третьей строкой, умноженной на −1:
\(\left(\begin{array}{ccc}1&-5&2\\0&-1&0\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\1&1&-1\\0&-3&1\end{array}\right.\right)\)
5. Выполним умножение второй строки на −1:
\(\left(\begin{array}{ccc}1&-5&2\\0&1&0\\0&14&3\end{array}\left|\begin{array}{ccc}0&1&0\\-1&-1&1\\0&-3&1\end{array}\right.\right)\)
6. Первую строку сложим с рядом чисел, полученных при умножении второй строки на 5. К третьей строке прибавим вторую строку, умноженную на −14:
\(\left(\begin{array}{ccc}1&0&2\\0&1&0\\0&0&3\end{array}\left|\begin{array}{ccc}-5&-4&5\\-1&-1&1\\14&11&-13\end{array}\right.\right)\)
7. Произведем деление третьей строки на 3:
\(\left(\begin{array}{ccc}1&0&2\\0&1&0\\0&0&1\end{array}\left|\begin{array}{ccc}-5&-4&5\\-1&-1&1\\\frac{14}3&\frac{11}3&\frac{-13}3\end{array}\right. {-1}=\begin{pmatrix}\frac{-43}3&\frac{-34}3&\frac{41}3\\-1&-1&1\\\frac{14}3&\frac{11}3&\frac{-13}3\end{pmatrix}\)
{-1}=\begin{pmatrix}\frac{-43}3&\frac{-34}3&\frac{41}3\\-1&-1&1\\\frac{14}3&\frac{11}3&\frac{-13}3\end{pmatrix}\)
метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l<j).
Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы:
- пустые клетки – нулевые элементы матрицы;
- заштрихованные клетки – произвольные элементы, которые могут быть как нулевыми, так и ненулевыми;
- черные квадратики – ненулевые элементы, которые называются угловыми элементами, «ступеньками» (в представленной рядом матрице такими элементами являются цифры –1, 5, 3, 8).

При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице.
Приведение матрицы к ступенчатой форме
Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя:
- перестановку строк местами;
- прибавление к одной строке другой строки, при необходимости умноженной на какое-либо число (можно также производить операцию вычитания).
Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду.
Для того чтобы решить задачу, будем следовать алгоритму:
- Удобно выполнять преобразования над такой матрицей, у которой первый элемент в верхнем углу с левой стороны (т. е. «ведущий» элемент) равен 1 или –1.
 В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами.
В нашем случае первый элемент в верхней строке равен 2, поэтому поменяем первую и вторую строчки местами. - Выполним операции вычитания, затронув строки № 2, 3 и 4. Мы должны получить в первом столбце под «ведущим» элементом нули. Для достижения такого результата: из элементов строчки № 2 последовательно вычтем элементы строчки № 1, умноженные на 2; из элементов строчки № 3 последовательно вычтем элементы строчки № 1, умноженные на 4; из элементов строчки № 4 последовательно вычтем элементы строчки № 1.
- Далее будем работать с укороченной матрицей (без столбца № 1 и без строки № 1). Новый «ведущий» элемент, стоящий на пересечении второго столбца и второй строки, равен –1. Переставлять строки не требуется, поэтому переписываем без изменений первый столбец и первую и вторую строки. Выполним операции вычитания, чтобы во втором столбце под «ведущим» элементом получить нули: из элементов третьей строчки последовательно вычтем элементы второй строчки, умноженные на 3; из элементов четвертой строчки последовательно вычтем элементы второй строчки, умноженные на 2.

- Осталось изменить последнюю строку. Из ее элементов вычтем последовательно элементы третьей строки. Таким образом мы получили ступенчатую матрицу.
Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ.
Матрицы и системы линейных уравнений
Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица.
СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных.
Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами.
Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение.
Несовместная СЛУ – система уравнений, которая не имеет решений.
Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже.
Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов.
Общая информация о методе Гаусса
В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные.
Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах».
Пример решения СЛУ методом Гаусса
Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке.
Алгоритм решения:
- Прямым ходом метода Гаусса приведем систему к ступенчатой форме, но для начала составим расширенную матрицу из числовых коэффициентов и свободных членов.
- Чтобы решить матрицу методом Гаусса (т. е. привести ее к ступенчатому виду), из элементов второй и третьей строчек последовательно вычтем элементы первой строчки. Получим в первом столбе под «ведущим» элементом нули. Далее поменяем вторую и третью строчки местами для удобства. К элементам последней строки прибавим последовательно элементы второй строчки, умноженные на 3.
- В результате вычисления матрицы методом Гаусса мы получили ступенчатый массив элементов. На его основе составим новую систему линейных уравнений. Обратным ходом метода Гаусса находим значения неизвестных членов. Из последнего линейного уравнения видно, что x3 равен 1.
 Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Подставляем это значение во вторую строчку системы. Получится уравнение x2 – 4 = –4. Отсюда следует, что x2 равен 0. Подставляем x2 и x3 в первое уравнение системы: x1 + 0 +3 = 2. Неизвестный член равен –1.
Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1.
Метод Гаусса – Жордана
В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов).
Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю).
Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю.
Основные шаги, на которых основывается метод Гаусса – Жордана:
- Взгляните на первую строку конкретной матрицы. Метод Гаусса – Жордана можно начинать применять, если первое значение не равно нулю. Если же на первом месте стоит 0, то поменяйте строки местами так, чтобы первый элемент имел отличное от нуля значение (желательно, чтобы число было ближе к единице).
- Разделите все элементы первой строки на первое число. У вас получится строка, которая начинается с единицы.
- Из второй строки вычтите первую строку, умноженную на первый элемент второй строки, т. е. в итоге у вас получится строка, которая начинается с нуля.
 Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент.
Аналогичные действия выполните с остальными строчками. Для того чтобы по диагонали получались единицы, делите каждую строку на ее первый ненулевой элемент. - В итоге вы получите верхнюю треугольную матрицу методом Гаусса — Жордана. В ней главная диагональ представлена единицами. Нижний угол заполнен нулями, а верхний угол – разнообразными значениями.
- Из предпоследней строки вычтите последнюю строчку, умноженную на необходимый коэффициент. У вас должна получиться строка с нулями и единицей. Для остальных строк повторите аналогичное действие. После всех преобразований получится единичная матрица.
Пример нахождения обратной матрицы методом Гаусса – Жордана
Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A.
Решение:
- Для начала найдем определитель матрицы методом Гаусса (det A). Если этот параметр не окажется равным нулю, то матрица будет считаться невырожденной.
 Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2.
Это позволит нам сделать вывод о том, что у A точно есть A-1. Для вычисления определителя преобразуем матрицу до ступенчатой формы элементарными преобразованиями. Подсчитаем число K, равное числу перестановок строк. Строки мы меняли местами всего 1 раз. Вычислим определитель. Его значение будет равно произведению элементов главной диагонали, умноженному на (–1)K. Результат вычисления: det A = 2. - Составим расширенную матрицу, добавив к исходной матрице единичную матрицу. Полученный массив элементов будем использовать для нахождения обратной матрицы методом Гаусса – Жордана.
- Первый элемент в первой строке равен единице. Нас это устраивает, т. к. не нужно переставлять строки и делить данную строку на какое-нибудь число. Начинаем работать со второй и третьей строками. Чтобы первый элемент во второй строке превратился в 0, отнимем от второй строки первую строчку, умноженную на 3. Из третьей строчки вычтем первую (умножения не требуется).
- В получившейся матрице второй элемент второй строчки равен –4, а второй элемент третьей строчки равен –1.
 Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу.
Поменяем строки местами для удобства. Из третьей строчки вычтем вторую строчку, умноженную на 4. Вторую строчку разделим на –1, а третью – на 2. Получим верхнюю треугольную матрицу. - Из второй строчки отнимем последнюю строчку, умноженную на 4, из первой строчки – последнюю строчку, умноженную на 5. Далее вычтем из первой строчки вторую строчку, умноженную на 2. С левой стороны мы получили единичную матрицу. Справа находится обратная матрица.
Пример решения СЛУ методом Гаусса – Жордана
На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана.
Решение:
- Составим расширенную матрицу. Для этого вынесем в таблицу коэффициенты и свободные члены.
- Решим матрицу методом Гаусса – Жордана. Из строки № 2 вычтем строку № 1. Из строки № 3 вычтем строку № 1, предварительно умноженную на 2.
- Поменяем местами строки № 2 и 3.
- От строки № 3 отнимем строку № 2, умноженную на 2.
 Разделим полученную третью строку на –1.
Разделим полученную третью строку на –1. - От строки № 2 отнимем строку № 3.
- От строки № 1 отнимем строку № 2, умноженную на –1. Сбоку у нас получился столбик, состоящий из цифр 0, 1 и –1. Из этого делаем вывод, что x1 = 0, x2 = 1 и x3 = –1.
При желании можно проверить правильность решения, подставив вычисленные значения в уравнения:
- 0 – 1 = –1, первое тождество из системы является верным;
- 0 + 1 + (–1) = 0, второе тождество из системы является верным;
- 0 – 1 + (–1) = –2, третье тождество из системы является верным.
Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения.
Онлайн-калькуляторы
Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи.
В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
-1=I, где I — единичная матрица.Результаты
Обратная матрица — dCode
Метки : Матрица
Поделиться
dCode и многое другое решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор обратного преобразования квадратной матрицы NxN
Загрузка. ..
..
(если это сообщение не исчезнет, попробуйте обновить эту страницу) 9{-1} = \left( \begin{bmatrix} \frac{e i-f h}{-c e g+b f g+c d h-a f h-b d i+a e i} & \frac{c h-b i}{-c e g+ b f g+c d h-a f h-b d i+a e i} & \frac{b f-c e}{-c e g+b f g+c d h-a f h-b d i+a e i} \\ \frac{f g-d i}{-c e g +b f g+c d h-a f h-b d i+a e i} & \frac{a i-c g}{-c e g+b f g+c d h-a f h-b d i+a e i} & \frac{c d-a f}{-c e g +b f g+c d h-a f h-b d i+a e i} \\ \frac{d h-e g}{-c e g+b f g+c d h-a f h-b d i+a e i} & \frac{b g-a h}{-c e g+b f g+c d h-a f h-b d i+a e i} & \frac{a e-b d}{-c e g+b f g+c d h-a f h-b d i+a e i} \end{bmatrix} \right) $$
Для того чтобы матрица была обратимой, необходимо, чтобы определитель инвертируемой матрицы не был равен нулю.
Как доказать, что матрица обратима?
Матрица обратима, если ее определитель отличен от нуля (отличен от 0). Итак, чтобы доказать, что матрица имеет обратную, вычислите определитель матрицы, если он отличен от 0, то матрица обратима.
Необратимая матрица называется сингулярной (инверсия невозможна). 9{-1} = I $.
Как вычислить модульную обратную матрицу?
Исходный код
dCode сохраняет за собой право собственности на исходный код «обратной матрицы». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «обратной матрицы», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «обратной матрицы». Матрицы» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Обратной матрицы» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Цитировать dCode
Копирование и вставка страницы «Инверсия матрицы» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Обратная матрица на dCode.fr [онлайн-сайт], получено 22 сентября 2022 г., https://www.dcode.fr/matrix-inverse
Сводка
- Калькулятор обратного преобразования квадратной матрицы NxN
- Калькулятор модульного обратного преобразования матрицы
- Как вычислить обратную обратимую матрицу?
- Как доказать, что матрица обратима?
- Как инвертировать матрицу с нулевым определителем?
- Как проверить, является ли матрица обратной другой?
- Как вычислить модульную обратную матрицу?
Похожие страницы
- Транспонирование матрицы
- Определитель матрицы
- Шифр Хилла
- Деление матрицы
- Вычитание матрицы
- Тенсорный продукт
- Matrix Direct Sum
- Список инструментов DCODE
Поддержка
- PayPal
- Patreon
- ESHRIX 9
. ,обратимый,единственный
,обратимый,единственный
Ссылки
▲
Обратная матрица с использованием исключения Гаусса-Жордана
М. Борна
В этом разделе мы видим, как работает исключение Гаусса-Жордана, на примерах.
Вы можете перезагружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел. Вы также можете выбрать матрицу другого размера (внизу страницы).
(Если вам сначала нужна предыстория, вернитесь к Введению в матрицы).
Выберите интересующий вас размер матрицы и нажмите кнопку .
Матрица А:
Матрица 2×2Матрица 3×3
Матрица 4×4
Матрица 5×5
Ниже приведен случайно сгенерированный пример.
Пользователи телефонов
ПРИМЕЧАНИЕ. Если вы пользуетесь телефоном, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть выражение целиком.
Найдите обратную матрицу A методом исключения Гаусса-Жордана.
Наша процедура
Мы пишем матрицу A слева и матрицу идентичности I справа, разделенную пунктирной линией, следующим образом. Результат называется дополненной 9.матрица 0192.
Мы добавили номера строк, чтобы было понятнее.
| 7 | 3 | 8 | |
| 10 | 12 | 4 | |
| 9 | 11 | 13 |
| 1 | 0 | 0 | Строка[1] | |
| 0 | 1 | 0 | Ряд[2] | |
| 0 | 0 | 1 | Ряд[3] |
Затем мы выполняем несколько операций над строками над двумя матрицами, и наша цель состоит в том, чтобы получить единичную матрицу на слева , например:
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 |
| ? | ? | ? | Строка[1] | |
| ? | ? | ? | Ряд[2] | |
| ? | ? | ? | Ряд[3] |
(Технически, мы уменьшаем матрицу A до сокращенной ступенчатой формы строки , также называемой канонической формой строки ).
Результирующая матрица справа будет обратная матрица из A .
Наша процедура работы со строками выглядит следующим образом:
- Получаем «1» в левом верхнем углу путем деления первой строки
- Затем мы получаем «0» в оставшейся части первого столбца
- Затем нам нужно получить «1» во второй строке, второй столбец
- Затем делаем все остальные записи во второй колонке «0».
Продолжаем в том же духе, пока слева не останется единичная матрица.
Давайте теперь найдем обратное.
Решение
Начнем с:
| 7 | 3 | 8 | |
| 10 | 12 | 4 | |
| 9 | 11 | 13 |
| 1 | 0 | 0 | Строка[1] | |
| 0 | 1 | 0 | Ряд[2] | |
| 0 | 0 | 1 | Ряд[3] |
Новый ряд [1]
Разделить строку [1] на 7 (чтобы получить «1» в желаемой позиции):
Это дает нам:
| 1 | 0,4286 | 1. 1429 1429 | |
| 10 | 12 | 4 | |
| 9 | 11 | 13 |
| 0,1429 | 0 | 0 | Строка[1] | |
| 0 | 1 | 0 | Ряд[2] | |
| 0 | 0 | 1 | Ряд[3] |
Новый ряд [2]
Row[2] − 10 × Row[1] (чтобы получить 0 в желаемой позиции):
10 − 10 × 1 = 0
12 − 10 × 0,4286 = 7,7143
4 − 10 × 1,1429 = -7,4286
0 − 10 × 0,1429 = -1,4286
1 − 10 × 0 = 1
0 − 10 × 0 = 0
Это дает нам нашу новую строку [2]:
| 1 | 0,4286 | 1.1429 | |
| 0 | 7,7143 | -7,4286 | |
| 9 | 11 | 13 |
| 0,1429 | 0 | 0 | Строка[1] | |
| -1,4286 | 1 | 0 | Ряд[2] | |
| 0 | 0 | 1 | Ряд[3] |
Новый ряд [3]
Row[3] − 9 × Row[1] (чтобы получить 0 в желаемой позиции):
9 — 9 х 1 = 0
11 — 9 х 0,4286 = 7,1429
13 — 9 х 1,1429 = 2,7143
0 — 9 х 0,1429 = -1,2857
0 — 9 х 0 = 0 9 9004 0 — 10004
Это дает нам нашу новую строку [3]:
| 1 | 0,4286 | 1. 1429 1429 | |
| 0 | 7,7143 | -7,4286 | |
| 0 | 7.1429 | 2,7143 |
| 0,1429 | 0 | 0 | Строка[1] | |
| -1,4286 | 1 | 0 | Ряд[2] | |
| -1,2857 | 0 | 1 | Ряд[3] |
Новый ряд [2]
Разделить строку [2] на 7,7143 (чтобы получить «1» в желаемой позиции):
Это дает нам:
| 1 | 0,4286 | 1.1429 | |
| 0 | 1 | -0,963 | |
| 0 | 7.1429 | 2,7143 |
| 0,1429 | 0 | 0 | Строка[1] | |
| -0,1852 | 0,1296 | 0 | Ряд[2] | |
| -1,2857 | 0 | 1 | Ряд[3] |
Новый ряд [1]
Строка[1] − 0,4286 × Строка[2] (чтобы получить 0 в нужной позиции):
1 -0,4286 × 0 = 1
0,4286 -0,4286 × 1 = 0
1,1429 -0,4286 × -0,963 = 1,5556
0,1429 -0,4286 × -0,1852 = 0,2222 2
0,4286 × 0,1852 = 0,22222 2
0 -0,4286 × 0,1852 = 0,2222 2
0,4286. 0
0
Это дает нам новую строку [1]:
| 1 | 0 | 1,5556 | |
| 0 | 1 | -0,963 | |
| 0 | 7.1429 | 2,7143 |
| 0,2222 | -0,0556 | 0 | Строка[1] | |
| -0,1852 | 0,1296 | 0 | Ряд[2] | |
| -1,2857 | 0 | 1 | Ряд[3] |
Новый ряд [3]
Строка[3] − 7,1429 × Строка[2] (чтобы получить 0 в нужной позиции):
0 — 7,1429 × 0 = 0
7,1429 — 7,1429х 1 = 0
2,7143 — 7,1429 х -0,963 = 9,5926
-1,2857 — 7,1429 х -0,1852 = 0,037
0 — 7,1429 х 0,1296 = -0,9259
1 — 9,0004 1 — 7,1429
Это дает нам нашу новую строку [3]:
| 1 | 0 | 1,5556 | |
| 0 | 1 | -0,963 | |
| 0 | 0 | 9,5926 |
| 0,2222 | -0,0556 | 0 | Строка[1] | |
| -0,1852 | 0,1296 | 0 | Ряд[2] | |
| 0,037 | -0,9259 | 1 | Ряд[3] |
Новый ряд [3]
Разделить строку [3] на 9,5926 (чтобы получить «1» в желаемой позиции):
Это дает нам:
| 1 | 0 | 1,5556 | |
| 0 | 1 | -0,963 | |
| 0 | 0 | 1 |
| 0,2222 | -0,0556 | 0 | Строка[1] | |
| -0,1852 | 0,1296 | 0 | Ряд[2] | |
| 0,0039 | -0,0965 | 0,1042 | Ряд[3] |
Новый ряд [1]
Строка[1] − 1,5556 × Строка[3] (чтобы получить 0 в нужной позиции):
1 -1,5556 × 0 = 1
0 -1,5556 × 0 = 0
1,5556 -1,5556 × 1 = 0
0,2222 -1,5556 × 0,0039 = 0,2162
-0,056 -1,5556 × -0,096 = 0,09464464 40004 -0,056 -1,5556 × -0,0966 = 0,504646464,056 4,5556 × 0,1062
-0,056 -1,5556 × -0,062
-0,056 -1,5556 × -0,062
-0,056 -1,5556 × -0,062
-0,056 -1. 0,1622
0,1622
Это дает нам новую строку [1]:
| 1 | 0 | 0 | |
| 0 | 1 | -0,963 | |
| 0 | 0 | 1 |
| 0,2162 | 0,0946 | -0,1622 | Строка[1] | |
| -0,1852 | 0,1296 | 0 | Ряд[2] | |
| 0,0039 | -0,0965 | 0,1042 | Ряд[3] |
Новый ряд [2]
Строка[2] − -0,963 × Строка[3] (чтобы получить 0 в нужной позиции):
0 — -0,963 х 0 = 0
1 — -0,963 х 0 = 1
-0,963 — -0,963 х 1 = 0 0 − -0,963 × 0,1042 = 0,1004
Это дает нам нашу новую строку [2]:
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 |
| 0,2162 | 0,0946 | -0,1622 | Строка[1] | |
| -0,1815 | 0,0367 | 0,1004 | Ряд[2] | |
| 0,0039 | -0,0965 | 0,1042 | Ряд[3] |
Мы достигли нашей цели, создав матрицу идентичности слева. Таким образом, мы можем заключить обратную матрицу A — правая часть расширенной матрицы:
Таким образом, мы можем заключить обратную матрицу A — правая часть расширенной матрицы:
На что обратить внимание
- В пояснении выше показаны все шаги. Обычно человек может пойти несколькими кратчайшими путями. Кроме того, иногда в правильной позиции уже есть «1» или «0», и в этих случаях нам не нужно ничего делать для этого шага.
- Всегда записывайте, что вы делаете на каждом этапе — очень легко заблудиться!
- Я показал результаты с точностью до 4 знаков после запятой, но максимально возможная точность использовалась повсюду. Имейте в виду, что небольшие ошибки округления будут накапливаться по всей задаче. Всегда используйте полную точность калькулятора! (Полностью используйте память вашего калькулятора.)
- Очень редко бывают странные результаты из-за внутреннего представления чисел в компьютере. То есть он может хранить «1» как 0,999999999872.
Видишь еще?
Вы можете вернуться наверх страницы и выбрать другой пример. 9{-1}$.
9{-1}$.
Обратная матрица 2 $\times$ 2
Пример 1. Найти обратную
$A = \left[ {\ begin {массив} {* {20} {c}} 1 и 3\\ 2 и 7 \end{array}} \right]$
Решение:
Шаг 1: Присоедините единичную матрицу к правой части $A$:
$ А = \ влево [ {\ begin {массив} {* {20} {c}} 1 и 3\\ 2 и 7 \конец{массив}\влево| {\начать{массив}{*{20}{с}} \цвет{синий}{1}&\цвет{синий}{0}\\ \цвет{синий}{0}&\цвет{синий}{1} \end{массив}} \right.} \right] $
Шаг 2: Применяйте операции со строками к этой матрице, пока левая сторона не уменьшится до $I$. Вычисления:
$$
\begin{выровнено}
&\ влево [ {\ begin {массив} {* {20} {c}}
\цвет{красный}{1}&\цвет{красный}{3}\\
{2 — \color{blue}{2} \cdot \color{red}{1}}&{7 — \color{blue}{2} \cdot \color{red}{3}}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
\цвет{красный}{1}&\цвет{красный}{0}\\
{0 — \color{blue}{2} \cdot \color{red}{1}}&{1 — \color{blue}{2} \cdot \color{red}{0}}
\end{array}} \right.} \right] \ \ Row2 = Row2 — \color{blue}{2} \cdot \color{red}{Row1} \\
&\ влево [ {\ begin {массив} {* {20} {c}}
1 и 3\\
0&1
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0\\
{- 2}&1
\end{массив}} \right. } \right] \\
&\ влево [ {\ begin {массив} {* {20} {c}}
{1 — \color{blue}{3} \cdot \color{red}{0}}&{3 — \color{blue}{3} \cdot \color{red}{1}}\\
\цвет{красный}{0}&\цвет{красный}{1}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
{1 — \color{blue}{3} \cdot \color{red}{( — 2)}}&{0 — \color{blue}{3} \cdot \color{red}{1}}\\
\цвет{красный}{ — 2}&\цвет{красный}{1}
\end{array}} \right.} \right] \ \ Row1 = Row1 — \color{blue}{3} \cdot \color{red}{Row2} \\
&\ влево [ {\ begin {массив} {* {20} {c}}
1&0\\
0&1
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
7&{ — 3}\\
{- 2}&1
\end{массив}} \right.} \right]
\end{выровнено}
$$
9{-1} = \left[ {\ begin {массив} {* {20} {c}}
7&{-3}\\
{-2}&1
\end{массив}} \right]$
} \right] \\
&\ влево [ {\ begin {массив} {* {20} {c}}
{1 — \color{blue}{3} \cdot \color{red}{0}}&{3 — \color{blue}{3} \cdot \color{red}{1}}\\
\цвет{красный}{0}&\цвет{красный}{1}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
{1 — \color{blue}{3} \cdot \color{red}{( — 2)}}&{0 — \color{blue}{3} \cdot \color{red}{1}}\\
\цвет{красный}{ — 2}&\цвет{красный}{1}
\end{array}} \right.} \right] \ \ Row1 = Row1 — \color{blue}{3} \cdot \color{red}{Row2} \\
&\ влево [ {\ begin {массив} {* {20} {c}}
1&0\\
0&1
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
7&{ — 3}\\
{- 2}&1
\end{массив}} \right.} \right]
\end{выровнено}
$$
9{-1} = \left[ {\ begin {массив} {* {20} {c}}
7&{-3}\\
{-2}&1
\end{массив}} \right]$
Необратимая матрица
Если $A$ необратима , то в левой части появится нулевая строка.
Пример 2: найти обратное число
$ А = \ влево [ {\ begin {массив} {* {20} {c}} 1&{ — 3}\\ {- 2}&6 \end{массив}} \right] $
Решение:
Шаг 1: Присоедините единичную матрицу к правой части A:
$
\ влево [ {\ {начать массив} {* {20} {с}}
1&{ — 3}\\
{- 2}&6
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
\цвет{синий}{1}&\цвет{синий}{0}\\
\цвет{синий}{0}&\цвет{синий}{1}
\end{массив}} \right. } \right]
$
} \right]
$
Шаг 2: Применение операций со строками
$ \ влево [ {\ {начать массив} {* {20} {с}} \цвет{красный}{1}&\цвет{красный}{ — 3}\\ { — 2 + \color{blue}{2} \cdot \color{red}{1}}&{6 + \color{blue}{2} \cdot \color{red}{( — 3)}} \конец{массив}\влево| {\начать{массив}{*{20}{с}} \цвет{красный}{1}&\цвет{красный}{0}\\ {0 + \color{blue}{2} \cdot \color{red}{1}}&{1 + \color{blue}{2} \cdot \color{red}{0}} \end{array}} \right.} \right]Row2 = Row2 + \color{red}{2} \cdot \color{blue}{Row1} $
$ \ влево [ {\ {начать массив} {* {20} {с}} 1&{ — 3}\\ \цвет{красный}{0}&\цвет{красный}{0} \конец{массив}\влево| {\начать{массив}{*{20}{с}} 1&0\\ 0&1 \end{массив}} \right.} \right]_{\color{red}{\leftarrow ZERO \ \ ROW}} $
Шаг 3: Вывод: Эта матрица необратима.
Обратная матрица 3 $\times$ 3
Пример 1. Найти обратную
$ А = \ влево [ {\ begin {массив} {* {20} {c}} 1&2&3\\ 2&5&3\\ 1&0&8 \end{массив}} \right] $
Решение:
Шаг 1: Присоедините единичную матрицу к правой части A:
$
\ влево [ {\ {начать массив} {* {20} {с}}
1&2&3\\
2&5&3\\
1&0&8
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
0&1&0\\
0&0&1
\end{массив}} \right. {R2 = R2 — \color {синий} {2} \cdot R1} \left[ {\begin{массив}{*{20}{c}}
1&2&3\\
{2 — \color{blue}{2} \cdot 1}&{5 — \color{blue}{2} \cdot 2}&{3 — \color{blue}{2} \cdot 3}\\
{1 \color{red}{-} 1}&{0 \color{red}{-} 2}&{8 \color{red}{-} 3}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
{0 — \color{blue}{2} \cdot 1}&{1 — \color{blue}{2} \cdot 0}&{0 — \color{blue}{2} \cdot 0}\\
{0 \color{red}{-} 1}&{0 \color{red}{-} 0}&{1 \color{red}{-} 0}
\end{массив}} \right.} \right]
$
9{} \left[ {\ begin {массив} {* {20} {c}}
1&2&3\\
0&1&{ — 3}\\
{0 \color{blue}{+ 2} \cdot 0}&{ — 2 \color{blue}{+ 2} \cdot 1}&{5 \color{blue}{+ 2} \cdot ( — 3) }
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
{- 2}&1&0\\
{ — 1 \color{blue}{+ 2} \cdot ( — 2)}&{0 \color{blue}{+ 2} \cdot 1}&{1 \color{blue}{+ 2} \cdot 0 }
\end{массив}} \right.} \right]
$
{R2 = R2 — \color {синий} {2} \cdot R1} \left[ {\begin{массив}{*{20}{c}}
1&2&3\\
{2 — \color{blue}{2} \cdot 1}&{5 — \color{blue}{2} \cdot 2}&{3 — \color{blue}{2} \cdot 3}\\
{1 \color{red}{-} 1}&{0 \color{red}{-} 2}&{8 \color{red}{-} 3}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
{0 — \color{blue}{2} \cdot 1}&{1 — \color{blue}{2} \cdot 0}&{0 — \color{blue}{2} \cdot 0}\\
{0 \color{red}{-} 1}&{0 \color{red}{-} 0}&{1 \color{red}{-} 0}
\end{массив}} \right.} \right]
$
9{} \left[ {\ begin {массив} {* {20} {c}}
1&2&3\\
0&1&{ — 3}\\
{0 \color{blue}{+ 2} \cdot 0}&{ — 2 \color{blue}{+ 2} \cdot 1}&{5 \color{blue}{+ 2} \cdot ( — 3) }
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
{- 2}&1&0\\
{ — 1 \color{blue}{+ 2} \cdot ( — 2)}&{0 \color{blue}{+ 2} \cdot 1}&{1 \color{blue}{+ 2} \cdot 0 }
\end{массив}} \right.} \right]
$
$
\ влево [ {\ {начать массив} {* {20} {с}}
1&2&3\\
0&1&{ — 3}\\
0&0&{ — 1}
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
1&0&0\\
{- 2}&1&0\\
{- 5}&2&1
\end{array}} \right. {R1 = R1 — 2 \cdot R2} \left[ {\begin{array} {*{20}{с}}
1&1&0\\
0&1&0\\
0&0&1
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
{- 40}&{16}&9{ — 1} = \ влево [ {\ begin {массив} {* {20} {c}}
{- 40}&{16}&9\\
{13}&{ — 5}&{ — 3}\\
5&{ — 2}&{ — 1}
\end{массив}} \right]
$
{R1 = R1 — 2 \cdot R2} \left[ {\begin{array} {*{20}{с}}
1&1&0\\
0&1&0\\
0&0&1
\конец{массив}\влево| {\начать{массив}{*{20}{с}}
{- 40}&{16}&9{ — 1} = \ влево [ {\ begin {массив} {* {20} {c}}
{- 40}&{16}&9\\
{13}&{ — 5}&{ — 3}\\
5&{ — 2}&{ — 1}
\end{массив}} \right]
$
Курсы PDF, Упражнения, Документы pdf, ppt, бесплатно PDF
Курсы PDF, Упражнения, Документы pdf, ppt, бесплатно PDF | PDFprof.com×
Титр
Корпус
ОШИБКА 404 Файл не найден
- Администрация
- Администрация
- Общественная администрация
- Общественная администрация
- Агролесоводство
- Агролесоводство
- Аллеманд
- Аллеманд
- Бак ST2S
- Андрагогия
- Андрагогия
- Драматическое искусство
- Драматическое искусство
- Художественные визуалы
- Художественные визуалы
- Астрономия
- Астрономия
- Бак
- БАК Математика
- BAC Physique Chimie
- БАК СЭС
- БАК СВТ
- Биохимия
- Биохимия
- Биографии
- Fiche de Cours
- Fiches de Revision
- География и история L
- Исторический антиквариат
- Современная история
- Европейский союз
- Ла Герр Фройд
- La Premiere Guerre Mondiale
- эпоха Возрождения
- Биология
- Биология
- Биология и физиопатология человека
- Бак ST2S
- Биотехнология
- Биотехнология
- Чими
- Чими
- Курсы и упражнения
- IP адрес
- Алгоритм
- Андроид
- годовые
- Bases des données
- Бюротик
- коммерция
- Коммуникация
- Совместимость
- Comptabilité Analytique
- Comptabilité générale
- Концепция и анализ
- курс 3ds max
- Курс Ада
- курс адрес ip
- алгоритм курса
- курс андроид
- курс ассемблера
- Кур Бак-сес
- курс баз де донне
- курс до-диез
- Курс коммерции
- Cours comptabilité
- курс друпал
- затмение
- Курс эконом-класса
- Курс Электрисите
- Курс Электроник
- курс эргономики
- курсы и упражнения 5e
- курсы и упражнения 6eme бесплатно
- курсы и упражнения html css
- курс и упражнения 1ère stmg
- курсы и упражнения 5eme
- Английский курс и упражнения
- Курсы и упражнения Excel 2010 бесплатно
- курсы и упражнения excel pdf
- большая секция курсов и упражнений
- курс превосходит
- Курс финансов
- курс фьюжн
- Курс Гестион
- курс канитель
- курс jquery
- курс labview
- курс языка c
- шепелявит
- Управление курсами
- Курсы маркетинга
- Курс Математики
- курс матлаб
- Кур Оберон
- цель курса c
- курс паскаль
- Курс PDF
- Курс телосложения
- курс pl sql
- кур питон
- курс qtcreator
- курс рубин
- Cours seconde
- Cours sixieme
- курс весна
- курс sql
- Статистика курса
- Курс статистики
- Терминал S
- Тройская улица
- курс unix linux
- курс вба
- курс визуальный базовый
- курс визуальной студии
- Курс Виндев
- курс слово
- Кутюр
- Криптография
- Дайверы
- Эконом
- Экономика pdf
- социальная экономия
- Электричество
- электроника
- эмс
- Этюд функции
- Совместимость экзаменов
- Экзамены по информатике
- маршрут упражнений
- Упражнения коммерции
- Совместимые упражнения
- Упражнения эконом
- упражнения
- Упражнения Финансы
- Упражнения
- Управление упражнениями
- Упражнения Маркетинг
- Упражнения по математике
- Упражнения pdf
- Упражнения телосложения
- Статистика упражнений
- слово упражнения
- Финансы
- Фискалите
- Гастрономия
- геополитика
- Жестион
- гуманитарии
- Информатика pdf
- Комбинация логики
- язык sql
- Усилители
- Les compteurs
- Конденсаторы
- диоды
- Фильтры
- английский язык
- Управление распределением и т.
 д.
д. - Управление человеческими ресурсами
- Управление рисками
- Управление pdf
- Стратегическое управление
- Цифровой маркетинг
- Маркетинговая часть
- Маркетинг pdf
- Маркетинговая стратегия
- Математика
- Математика 1эр S
- Терминал математики S
- микроэкономика
- модель отношений
- оракул
- Расходы по управлению
- телосложение
- Вероятности и статистика
- Программирование
- вопросник ле монд
- наук
- сэс
- сес бак
- Статистика
- Системы эксплуатации
- Тригонометрия
- учебник язык c
- учебник линукс
- учебник excel
- обучающая вспышка
- сервер виндовс 2003
- Курсы и упражнения PDF
- Achats et approvisionnement
- Рекламное действие
- Научная деятельность
- Актуальная экономика
- Администрация информационных систем
- Аэроспасьяль Эт Дефанс
- Агенты экономики
- Сельское хозяйство и лесное хозяйство
- Аллеманд
- Финансовый анализ
- Английский
- Anglais En Seconde Langue
- Анналы Бак эс
- анналес бак л
- анналы бак с
- Антропологические исследования автохтонов
- Антропология
- Apprendre Une Langue
- Ардуино
- Автоматизация
- бак финансы
- задний план
- бакалавриат
- залог рекламный
- Коммерческий баланс
- Биоинформатика
- Биоэтика
- ЧИМИ
- Амбулатория торговли
- Коммуникация и политика
- Коммуникации и реклама
- Comptabilité Et D’Audit
- курс xml
- Cours 2ème Bac
- Кур Араб
- курс назад
- Кур-бак-Л
- Cours bac s
- Кур Бэк ST2DA
- Курс бак STD2S
- Cours bac STI2D
- Cours bac STL
- Cours bac STMG
- Кур Банк
- Кур Шими
- Кур Компани
- курсы css
- Курс Эколь
- Cours École Primaire
- Cours École Secondaire
- Кур Экология
- Курс Энерги
- Изготовление курсов
- курс финансов
- Кур Фискалите
- Кур Геология
- Курс истории
- Кур Инженьери
- Cours L’Informatique
- Кур-ла-Физик
- Курс Логистик
- курс математики
- кур мериз
- Курс Метео
- Курс MPSI
- курс mysql
- трассировщик пакетов
- Курс PCSI
- курс философии
- Курсы физики
- программа курса
- Курс PSI
- Курс ПТ
- Курс ПТСИ
- схема курса
- Курс наук
- курс Tronc Commun
- курс веб-мастера
- Курсансе
- Круассан эконом
- Демография
- Демография и география
- Демография и статистика
- Devoirs Mathématiques
- Диплом по дисциплине
- экономика
- экономика
- экономия
- коммерческая экономия
- ECONOMIE CONCOMMATION ET épargne
- экономия образования
- экономия на строительстве
- экономия удовольствия и удовольствия
- Экономика и политика
- географическая экономия
- промышленная экономика
- экономическая институция
- мировая экономика
- денежная экономика
- сельская экономия
- Écriture de scénario et creation li
- Образование художественное
- Исламское образование
- образование телосложение образование»’
- Коммерческий эффект
- ЭЛЕКТРИЧЕСТВО
- электрический батимент
- электрический CAP
- электрический колледж
- электрический дебютант
- электрисите женераль
- электрическая промышленность
- электрический лицей
- электрическая первичная
- электрическое веселье
- ENA Национальные школы архитектуры
- ENAM Национальная школа сельского хозяйства
- ENCG Национальные школы торговли
- Энергия
- электрическая энергия
- ENSA Национальные школы наук
- Высшие национальные школы ENSAM
- испанский
- Статистика оценки
- этюды аллеманды
- Études allemandes et histoire
- Английские этюды
- арабские исследования
- Азиатские исследования языка и культуры
- Азиатские исследования
- Этюды автохтонов
- Каталанские этюды
- Классические этюды
- Классические и антропологические исследования
- маршевые этюды
- видео этюды игры
- Азиатские этюды
- Феминистские этюды
- Испанские этюды
- Международные исследования
- Итальянские этюды
- Латино-американские этюды
- Средневековые этюды
- Неоэллинские этюды
- Квебекские этюды
- Études religieuses (науки о ре
- экзамены бак с
- Упражнения
- доступ к упражнениям
- Упражнения для спины ES
- Упражнения на спину L
- Упражнения на спину
- Упражнения бак ST2DA
- Упражнения bac STD2S
- Упражнения bac STI2D
- Упражнения bac STL
- Упражнения бак СТМГ
- Упражнения де comptabilité analytiqu
- Exercices de comptabilité financière
- осуществляет финансы
- Упражнения
- Математические упражнения
- Упражнения МП
- Упражнения МПСИ
- Упражнения ПК
- Упражнения ПКСИ
- Философия упражнений
- программа упражнений
- Упражнения пси
- Упражнения ФТ
- Упражнения наук
- Упражнения СФЭ
- Упражнения SUP
- Упражнения ТСИ
- окна упражнений
- Факультет искусств и социальных наук
- Факультет наук
- Коммерческие финансы
- Банковские финансы
- Финансовый дебютант
- Финансы и совместимость
- Финансы количественные
- Финансовый солидер
- Финансирование проекта
- Факультеты медицины и фармакологии FMP
- Фонд коммерции
- французский
- Français langue seconde avancé
- Джин генерал
- география
- Экологическая география
- геополитика и политические науки
- Геостатистический
- Gestion de l’information numérique
- Прием серв.
 де санте
де санте - Партизанский маркетинг
- история
- История экономики
- История искусства
- Историческая география
- Гиперперсонализация
- IAV Institut Agronomique et Vétérin
- Входящий исходящий
- Индустри Химик
- информатика
- Информационная аппликация
- Психообразовательное вмешательство
- Инвестор
- ISEM Institut Supérieur d’Etudes Ma
- ISIC Высший институт информации
- ISPM Institut Supérieur des Pêches
- Высший институт науки ISSS
- Кинезиология и образование. физ.
- Язык и культура allemandes
- Английский язык и культура
- Арабский язык и культура
- Каталанский язык и культура
- Китайский язык и культура
- Язык и культура
- Греческий язык и культура
- Испанский язык и культура
- Японский язык и культура
- Латинский язык и культура
- Язык и культура португалоязычный
- Португальский язык и культура lusuph
- Английские языки и культуры
- Арабские языки и культуры
- Каталанские языки и культуры
- Греческие языки и культуры
- Испанские языки и культуры
- Неоэллинские языки и культуры
- Языки и культуры русские
- Letters et Sciences Humanes
- Письма, языки и культуры
- Littératures de langue française
- Littératures de langue française et
- Littératures et langues modernes
- Logiciels D’Entreprise
- Логистика и транспорт
- Макроэкономика
- Совместное управление
- Культура управления
- Менеджмент d’équipe
- Управление инновациями
- Управление знаниями
- Управление операциями
- Управление изменениями
- Этика управления
- Оперативное управление
- Участие в управлении
- Марж коммерческая
- Маркетинговый агропродовольственный
- Маркетинговая альтернатива
- Маркетинговая аналитика
- Маркетинг B2B
- Маркетинговый банк
- Маркетинговое сотрудничество
- Маркетинговая реклама
- Культура маркетинга
- Контент-маркетинг
- Массовый маркетинг
- Маркетинговые ассоциации
- Маркетинговая этика
- Маркетинговая этника
- Маркетинговые мероприятия
- Маркетинговый опыт
- Маркетинговая сенсорика
- Маркетинг территориальный
- математика
- Математика и информатика
- Математика здесь S
- МЕХАНИКА
- Мет.
 де ледук. физ. спорт.
де ледук. физ. спорт. - Микробиология и иммунология
- Микроменеджмент
- Мобильная коммерция
- Статистика моделирования
- Мультидисциплинарный
- Музыкальное образование
- Нейромаркетинг
- Когнитивная неврология
- Ондес
- ОПТИКА
- Ориентация и консультирование
- колебания
- Техническая логистика
- Рекламный спектакль
- философия
- Философия и классические исследования
- php курсы и упражнения pdf бесплатно
- телосложение
- Телосложение и информатика
- Physique-Chimie
- Коммерческая перспектива
- Психообразование,
- Психология и социология
- Реклама и маркетинг
- Recrutement et Gestion des Carrière
- Этнические отношения
- Промышленные отношения
- Природные ресурсы
- Ресурсы Pédagogiques Et En Class
- Ретаргетинг
- Агрономические науки
- биологические науки
- Когнитивные науки
- Науки о коммуникации
- наук о жизни
- инженерные науки
- Экономика и управление науками
- Науки экономические и социальные
- Науки и технологии Механика
- Математические науки
- Математические науки A
- Математические науки B
- Науки естественные и прикладные
- Религиозные науки
- Sécurité et études policières
- СЭС
- Социология Отношения Этники
- Статистика Зондажа
- Статистическая аппликация
- Статистический дебютант
- исчерпывающая статистика
- Неверная статистика
- Статистическая психология
- Коммерческая стратегия
- Стратегия предприятия
- Уличный маркетинг
- Субвенции, Des Bourses et Des Aid
- СВТ
- Tableau de bord et management de pe
- Электрик
- Промышленная технология
- Технологии
- Коммерческая реклама
- Курс Упражнения
- аргументация
- Бак де Франсэ 2013
- Бодлер
- Камю
- искренний
- диссертация
- дом Хуан
- описание изобретения
- принцесса де Клев
- цветочки зла
- мадам Бовари
- поэзия
- Упражнения на курсе PDF
- диссертация фр
- экспертная совместимость
- Недвижимость
- Информатика
- Ла Финанс
- мастер говядина
- Норм Ванкувер
- норм апа
- изнасилование
- раппорт де этап
- эти докторские
- Курс телосложения
- Курсы и упражнения
- Криминология
- Криминология
- Дизайн интерьера
- Дизайн интерьера
- Первая дидактика
- Первая дидактика
- Право
- Право
- Эконом
- Курсы и упражнения
- экономическая политика
- социальная экономия
- Экономика и поведение
- Бак про
- Образование
- Образование
- Éducation physActivité phys
- Éducation physActivité phys
- образование телосложение
- образование телосложение
- ЭЛЕКТРИЧЕСТВО
- Курсы и упражнения PDF
- электроника
- Алгебр де Буля
- Электромагнетизм
- Les Circuits RLC
- Предприятие
- Предприятие
- Управление
- Экологические исследования
- Экологические исследования
- Семейные исследования
- Семейные исследования
- Финансы
- Финансы
- Лесничество
- Лесничество
- французский
- Бак генерал
- Бак про
- Кур Франсэ
- французский
- Второй французский язык
- Второй французский язык
- Джин гражданский
- Джин гражданский
- Джин Электрик
- Джин Электрик
- Джин механический
- Джин механический
- География
- География
- Геронтология
- Геронтология
- Gestion de l’information
- Gestion de l\’information
- Gestion de l\’information
- Gestion de l’information
- Управление операциями
- Управление операциями
- Прием серв.
 де санте
де санте - Прием серв. де санте
- Gestion intégrée zone cotière
- Gestion intégrée zone cotière
- История
- Антиквариат
- История
- История Европы
- Histoire des États-Unis
- Глобальная история
- Гуманитарные науки
- Писание
- Наука о религиях
- Информациякоммуникация
- Информациякоммуникация
- информатика
- информатика
- инженерия
- Аэрокосмическая техника
- Электротехника
- информатика
- инженерия
- Промышленная техника
- Кинезиология и образование. физ.
- Кинезиология и образование.
 физ.
физ. - Язык по номиналу платит
- Язык по номиналу платит
- лингвистика
- лингвистика
- Литература
- Литература
- Управление
- Бак СТМГ
- Управление
- Управление рисками
- Маркетинг
- Маркетинг
- математический
- Этюд функции
- Математика
- Бак ST2S
- Бак СТИ2Д
- Курсы и упражнения PDF
- Enseignement des mathématiques
- Элементарная математика
- Мир труда
- Этика
- Пример де Plaidoirie
- Финансы и экономика
- Техника прогресса
- Синдикаты
- Музыка
- Музыка
- Питание и семейные исследования
- Питание и семейные исследования
- питаниепитание
- питаниепитание
- ofppt
- курс ppt
- PDF-документы
- Ноты для альт-саксофона
- Бас Ноты
- Барабаны и перкуссия для начинающих
- Пианино для начинающих
- Скрипка для начинающих
- Bien-être
- Ноты для блюза для гитары
- Блюз Ноты
- Ноты для виолончели
- курсы и упражнения Excel
- курсы и упражнения python
- Персонал по развитию
- Этническая принадлежность, раса и жанр
- Фантазия
- Историческая фантастика
- Ноты для флейты и пикколо
- Ноты для гитары
- Старая история
- История Мойен-Востока
- Европейская история
- Мировая история
- Ноты для гитары в стиле джаз и блюз
- Ноты для джазовой гитары
- Ноты для джазового фортепиано
- Коран и священные писания
- Классическая литература
- Мода и красота
- Ноты для гитары из фильмов и мюзиклов
- Питание и Вин
- Паранормальный
- Разделы поп и рок
- Перегородки для фортепиано
- Политика и актуальная информация
- Поп- и рок-бас-ноты
- Популярная культура
- Ноты для гитары R&B
- Отношения и родители
- Религиозные и праздничные ноты для гитары Mu
- Вегетарианские и веганские блюда
- Исторический роман
- Научная фантастика
- Ноты
- Ноты для трубы
- Ноты для укулеле
- Городское планирование и землепользование
- Ноты для скрипки
- Философия
- Отруи
- Курсы и упражнения PDF
- Искусство
- L’Inconscient et la Conscience
- Ла Либерте
- Религия
- Ле Бонёр
- детерминизм
- Ле Маль
- Le réel et la raison
- Ле Респект
- Ле Рир
- Труд и техника
- Телосложение
- Телосложение
- Физико-химия и математика
- Бак СТИ2Д
- Политика и интернационал
- военный
- Психология
- Фрейд
- Истерия
- Ла Восприятие
- La Perfectibilite
- Психология
- Психология Когнитивная
- Se Connaitre Soi Мем
- стресс
- Радиология
- Радиология
- Связи со сценой
- Force et Faiblesse
- Письмо о мотивации
- Религия и духовность
- атеизм
- буддизм
- христианство
- индуизм
- ислам
- иудаизм
- Религия
- Богословие
- Гуманитарные ресурсы
- Гуманитарные ресурсы
- Здоровье и культура
- Альтернатива медицине
- Научный лазарет
- Научный лазарет
- Наука политическая
- Наука политическая
- наук
- Астрономия
- Биология
- Чими
- Медицина
- Наука об окружающей среде
- наук де ла Терре
- наук о здоровье
- наук о здоровье
- Экономические и социальные науки
- Генеалогия
- социальные науки
- Антропология
- Психология
- Наука политическая
- социальные науки
- Социология
- Общество
- Помощник Суаньанте
- Ситуаеннете
- Поколение
- Иммиграция
- Liens Familiaux
- Социология
- Социология
- Статистика
- Статистика
- СВТ
- Бак генерал
- Сист.
 информация. организационные элементы
информация. организационные элементы - Сист. д \ ‘информация. организационные элементы
- Сист. д \ ‘информация. организационные элементы
- Сист. информация. организационные элементы
- Тех. медицинская лаборатория
- Тех. медицинская лаборатория
- Респираторная терапия
- Респираторная терапия
- токсикомания
- токсикомания
- перевод
- перевод
- Путешествие в соц.
- Путешествие в соц.
- Администрация
- Бак
- Бревет
- Конкурсы
- Дайверы
- Трудоустройство
- Формирование фише
- Fiche metier
- История
- Письмо о мотивации
- Ливр Блан
- Рапорт де стадии
- питание
- Архитектура
- Кинотеатр искусств
- Искусство ддд пластики
- Художественная литература
- Искусство Музыка
- Художественная фотография
- Художественная пластика
- Base de données
- Биология
- бюрократический
- Коммерческий коучинг
- Коммерческое общение
- Коммерция ддд интернэшнл
- Коммерческие дайверы
- Коммерция Экономика
- Коммерческий электронный маркетинг
- Коммерческий этюд на марше
- Коммерческие Финансы
- Международная коммерция
- Коммерческая логистика
- Управление торговлей
- Коммерческий маркетинг
- Коммерческие СМИ
- Коммерческая стратегия
- Коммерческий туризм и услуги
- Коммуникация
- курс 3ds max
- Курс 4D
- доступ к курсу
- Курс Аякс
- алгоритм курса
- курс андроид
- курс апертура
- Cours Architecture des ordinateurs
- курс жерех
- курс ассемблера
- Cours assembleur Cours informatique
- дерзость
- Курс аудита
- Автоматический курс
- курс баз де донне
- Курс биологии
- Курский мост
- курс с
- курс до-диез
- Курсы С/С++
- Курс Сиэль Компта
- Cours Ciel Devis фактура
- Cours Ciel Gestion Commerciale
- Курсы Cisco
- Кур Коболь
- Курс коммерции
- курс аналитической совместимости
- Cours comptabilite approfondie
- Cours comptabilité des entreprises
- Cours comptabilité des sociétés
- Общий курс совместимости
- Курсы криптографии
- курсы css
- Курс Дельфы
- Кур Друа
- курс друпал
- затмение
- Курс эконометри
- Курс эконом-класса
- Cours électricité автомобиль
- Cours électricité de base
- Электромеканская улица
- Электронный курс
- курс эргономики
- курс превосходит
- курс final cut pro
- Cours Finance de Marché
- Cours финансирует общественность
- Курс фискальных услуг
- курс фьюжн
- курс гаражной группы
- Cours Genie Civil
- курс
- Курсы управления проектами
- Cours gestion des approvvisionnements
- Cours gestion des entreprises
- Cours gestion des ressources humanes
- Cours gestion des risques
- курс канитель
- Бесплатные курсы
- курс html
- Курс гидравлики
- Курс Имови
- Курс информатики
- курс iphoto
- курс j2ee
- Кур Ява
- Курсы JAVA/J2EE
- курс javascript
- курс джумла
- курс jquery
- курс labview
- курс языка c
- Курс Лазаря
- Курсы Linux
- Курс ЛУА
- курс обслуживания ПК
- курс менеджмент
- Стратегия управления курсами
- курс маркетинга
- Курс маркетинговой стратегии
- Математический курс
- курс матлаб
- Курс медицины
- кур мериз
- Курс микроэкономики
- курс mysql
- цель курса c
- трассировщик пакетов
- курс паскаль
- курс перл
- Курс фотошоп
- курс php
- Cours physique chimie
- Курсы PL/SQL
- Курсы PowerPoint
- Курс вероятностей
- кур питон
- курс qtcreator
- Справочник по курсу
- Курс Резо
- Cours réseaux informatiques
- схема курса
- Cours Sécurité Informatique
- курс
- Курс звуковой кузницы
- Курсы SQL
- Статистика курса
- Cours système d’exploitation
- курс умл
- Курсы Unix
- курс unix linux
- курс вб нетто
- Курс VB/VB.
 NET
NET - курс вба
- курс визуальный базовый
- курс визуальной студии
- курс веб-мастера
- Курс Виндев
- Курсы Windows
- курс windows server
- курс слово
- Курсы XHTML
- курс xml
- курс xsl
- Право
- Право дел
- Конституционное право
- Droit Contrats типы
- Право ддд
- Европейское право
- Фискальное право
- Право недвижимости
- Международное право
- Уголовное право
- Право человеческих ресурсов
- Права общества
- Право труда
- Образование
- Совместимые упражнения
- Упражнения и исправления
- французский
- Французская аналитика
- Франсэ Биография
- Франсез Комментарий
- Общая французская культура
- французский ддд
- Французская диссертация
- Лекция Франсе Фиша
- Ревизия Francais Fiche bac
- Французская литература
- Французская философия
- Изобретение Francais Sujet d
- Совместимость с Gestion
- Gestion Controle de gestion
- Гестион Финанс
- Программирование жестов
- Gestion Ressources Humanes
- Высокие технологии
- Histoire geographie Droit
- Histoire geographie Fiche revision bac
- Историческая география
- Историческая география
- Индустри
- информатика
- Администрация информатики
- Информатический анализ объекта uml merise
- Информационная архитектура
- Информатик Бдд
- Информатика ддд
- Informatique Genie Logiciel
- Informatique Gestion de projet
- Информатическое программирование
- Informatique Reseaux информатики
- Информационная безопасность информационных систем
- Информатика Технологии
- Ланге Алеманд
- Английский язык
- Арабский язык
- Китайский язык
- Langue ddds des signes
- Испанский язык
- Язык итальянский
- Латинский язык
- Языки знаков
- логические
- Математика
- Медицина
- Администрация методологии
- Английская методология
- Методологический комментарий
- Методология коммуникации
- Общая методология культуры
- Методология Резюме
- Испанская методология
- Пересмотр методологии Fiche bac
- Методология Письмо о мотивации
- Математическая методология
- Мемуар методологии
- Методология анализа
- Методология Отчет о стадии
- Методология поддержки
- Методология Технология
- Музыка
- Фотография
- Physique-Chimie
- Программирование
- Рапорт де стадии
- Резо информатики
- Санте
- Английские науки
- наук Чими
- Электронные науки
- Управление науками
- Математические науки
- наук механика
- Науки Медицина
- Аптека наук
- Науки Телосложение
- наук Свт
- Социальная философия
- Социальная политика
- Социальная психология
- Гуманитарные социальные ресурсы
- Социальные науки
- Социальная социология
- Спорт
- Trucs et Astuces
Сайт использует файлы cookie для персонализации PUB,
Si vous continuez à utiliser ce site, nousceptrons que vous en êtes satisfait. Савуар плюс
Савуар плюс
Политика конфиденциальности — Политика конфиденциальности
шагов по использованию калькулятора обратной матрицы
- Автор: Tejasvee_S
- Последнее изменение 26-07-2022
- Автор Tejasvee_S
- Последнее изменение 26-07-2022
Калькулятор обратной матрицы — это математический инструмент, который выполняет все трудоемкие и сложные вычисления, необходимые для определения обратной матрицы за считанные секунды. Чтобы найти обратную матрицу, есть несколько методов и ярлыков. Для выполнения необходимой функции калькулятор обратной матрицы часто использует технику Гаусса-Жордана (также известную как элементарные операции со строками) и сопряженный метод. При использовании Калькулятора обратной матрицы вам не нужно выполнять все этапы расчета самостоятельно; просто введите соответствующие числа в калькулятор, и он сделает все остальное за считанные секунды. Давайте посмотрим, как использовать калькулятор обратной матрицы, используя инструкции в этом посте. Продолжайте читать, чтобы узнать больше.
Продолжайте читать, чтобы узнать больше.
Калькулятор обратной матрицы
В этой статье мы подробно обсудим Калькулятор обратной матрицы, его функции, принцип работы, примеры и т. д. Чтобы понять функциональность этого инструмента, во-первых, нам нужно понять все основные команды, связанные с ним. Например, вы должны четко понимать, что такое матрица и ее обратная сторона, компоненты матрицы, операции и математические методы, используемые для вычисления обратной матрицы. Итак, не теряя времени, прокрутите, чтобы получить всю важную информацию о Калькуляторе обратной матрицы, доступную на этой странице.
Читать о калькуляторе простых процентов
Что такое матрица и обратная матрица?
Матрица — это не что иное, как расположение чисел, символов, выражений или других математических объектов в виде строк и столбцов. Числа, символы или выражения, образующие матрицу, называются элементами матрицы или элементами матрицы. Горизонтальные и вертикальные линии элементов в матрицах называются строками и столбцами соответственно. «Матрицы» — форма множественного числа матрицы. Над матрицами можно выполнять такие математические операции, как сложение, вычитание и умножение.
«Матрицы» — форма множественного числа матрицы. Над матрицами можно выполнять такие математические операции, как сложение, вычитание и умножение.
Однако мы не можем разделить одну матрицу на другую; для деления мы используем концепцию обратной матрицы, которая обсуждается в последней части страницы. Значение матриц заключается в их многочисленных приложениях в статистике, экономике, технике, физике и других разделах математики.
Матрица может быть вещественной или сложной в зависимости от природы ее элементов. Например, ниже представлена действительная матрица, которая содержит все натуральные числа в качестве своих элементов:
.М=1–952,5–6,810
Размер матрицы
Общее количество строк и столбцов определяет размер матрицы. Нет ограничений на количество строк и столбцов, которые может иметь матрица (в стандартном смысле), если они являются положительными целыми числами. Матрица с m строками и n столбцами называется матрицей размера m × n или матрицей размера m на n, а m и n называются ее размерностями. Например, приведенная выше матрица M представляет собой матрицы 3 × 2, т. е. содержит 3 строки и 2 столбца. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей (m=n).
Например, приведенная выше матрица M представляет собой матрицы 3 × 2, т. е. содержит 3 строки и 2 столбца. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей (m=n).
Обратная матрица
Обратная матрица M равна M -1 только когда:
М × М -1 = М -1 × М = I
«I» представляет Матрицу идентичности, которая эквивалентна числу «1». Матрица идентичности 3 × 3 выражается как:
I=100010001
Матрица идентичности всегда квадратная по своей природе и имеет 1 по диагонали и 0 по всему остальному. Он может быть размером 2х2, или 3х3, 4х4 и так далее…
Для лучшего понимания давайте найдем, как вычислить обратную матрицу 2×2:
Обратная матрица M, abcd=1ad–bc d–b–ca
, где 1ad–b представляет определитель M.
Пример: обратная матрица 4276 = 14×6–7×26–7–24=1106–7–24=0,6–0,7–0,20,4
Теперь мы проверим Идентичность (A × A–1 = I), умножив матрицу на ее обратную, которую мы только что вычислили
=4276 0,6–0,7–0,20,4=4×0,6+7×-0,24×-0,7+7×0,42×0,6+6×-0,22×-0,7+6×0,4=2,4–1,4–2,8+2,81,2 –1,2–1,4+2,4=1001
Зачем нам нужно найти обратную матрицу?
Мы не можем выполнить операцию деления над матрицами. Таким образом, чтобы разделить матрицу на другую матрицу, мы можем умножить ее на обратную, что даст нам тот же результат, что и предполагалось получить после деления.
Таким образом, чтобы разделить матрицу на другую матрицу, мы можем умножить ее на обратную, что даст нам тот же результат, что и предполагалось получить после деления.
Что такое калькулятор обратной матрицы?
Как мы кратко объяснили выше в статье, это математический инструмент, который вычисляет обратную матрицу за считанные секунды, экономя наше драгоценное время и избавляя от беспокойных вычислений. Теперь вы все очень хорошо знаете о матрицах и их обратных, мы можем сосредоточиться на функциональности Калькулятора обратных матриц. Имейте в виду, что обратное можно вычислить только для квадратных матриц.
Как использовать калькулятор обратной матрицы?
Чтобы найти обратную матрицу с помощью онлайн-калькулятора обратной матрицы, выполните следующие действия:
- Шаг 1: Прежде всего, выберите размер квадратной матрицы (например, 4, 5 и т. д.)
- Шаг 2: Матрица с полями ввода введенного размера будет отображаться перед ты.
 Введите элементы матрицы в соответствующие места.
Введите элементы матрицы в соответствующие места. - Шаг 3: Нажмите кнопку «Рассчитать», чтобы найти результирующую обратную матрицу. Калькулятор обратной матрицы отобразит обработанный результат с подробным решением на экране за считанные секунды.
Примечание. Матричный калькулятор скоро будет встроен.
Продолжить расчет и пересчитать:
- Еще одна функция Калькулятора обратной матрицы, которую вы можете использовать, это вычисление или пересчет обратной матрицы другим методом. Нажмите соответствующую кнопку и выберите новый метод, который необходимо применить.
- Если вы решили продолжить расчет, метод будет применен к матрице результатов. Если выбран пересчет, метод будет использован для исходной матрицы.
Методы поиска обратной матрицы
Методы поиска обратной матрицы объясняются ниже:
1. Метод исключения Гаусса-Жордана Метод решения линейной системы уравнений. Это делается путем преобразования расширенной матрицы системы в сокращенную ступенчато-строковую форму с помощью операций со строками.
Это делается путем преобразования расширенной матрицы системы в сокращенную ступенчато-строковую форму с помощью операций со строками.
Используйте исключение Гаусса-Жордана для преобразования [ A | я ] в [ я | А -1 ].
Пример: следующие шаги приводят к 1234–1 12341001 → 120–210–31 → 1201103/2–1/2 → 1001–213/2–1/2, поэтому мы видим, что 1234–1= 1001–213/2– 1/2
2. Сопряженный методA–1 =1det A (сопряженная A) или A–1 =1det A (матрица кофакторов A)T
Пример: следующие шаги приводят к A–1 для A = 123145016Кофакторная матрица для A равна 245–4–1232–2–54, поэтому сопряженное значение равно 24–12–253–5–424. Поскольку det A = 22, получаем A–1 = 122 24–12–253–5–424 = 12/11–6/11–1/115/223/22–5/22–2/111/112/11
Учеба в Эмбибе
Воспользуйтесь следующими ресурсами и учитесь онлайн на Embibe.
В. Как найти обратную матрицу 3×3?
A. Для нахождения обратной матрицы 3×3 можно использовать два метода, а именно метод исключения Гаусса-Жордана и сопряженный метод. Эти методы были правильно объяснены на этой странице.
Эти методы были правильно объяснены на этой странице.
В. Может ли матрица иметь несколько инверсий?
Квадратная матрица не может иметь более одной мультипликативной обратной. Но если говорить о левой или правой инверсии неквадратной матрицы, у нее может быть много бесконечных инверсий.
В. Можете ли вы найти обратную неквадратную матрицу?
A. Нет, неквадратные матрицы (матрицы размера m на n, для которых m ≠ n) не имеют обратной. Если A имеет ранг m, то у него есть правая обратная: матрица B размером n на m такая, что AB = I. Квадратная матрица, которая не является обратимой, называется сингулярной или вырожденной. Квадратная матрица сингулярна тогда и только тогда, когда ее определитель равен 0,
В. Как найти обратную матрицу 2×2?
A. Ускоренный метод нахождения обратной матрицы 2×2 подробно обсуждается на этой странице.
В. Какая матрица не имеет обратной?
A. Матрица, определитель которой равен 0, называется сингулярной матрицей. Сингулярная матрица не имеет обратной.
Матрица, определитель которой равен 0, называется сингулярной матрицей. Сингулярная матрица не имеет обратной.
В. Каковы свойства обратной матрицы?
Если A неособая, то A -1 и (A -1 ) -1 = A.
Если A и B неособые матрицы, то AB неособая и. (AB) -1 = B -1 A -1 -1
Если A неособо, то. (А T ) -1 = (A -1 ) T
Если A и B — матрицы с. AB = I n , тогда A и B обратны друг другу.
РАСЧЕТ ЕЖЕМЕСЯЧНОГО EMI ОНЛАЙН
Это все, что вам нужно выучить в Калькуляторе обратной матрицы. Кроме того, вы можете изучить множество других тем, описанных на сайте embibe.com .
Практические вопросы по матрицам с советами и решениями
Калькулятор для конечных полей и линейной алгебры
Matrixer — это простой калькулятор, который может выполнять вычисления не только с действительными числами, но и с несколькими конечными полями, такими как F3, F4 или F8. Кроме того, как следует из названия, Matrixer может выполнять вычисления как с матрицами, так и с векторами.
Кроме того, как следует из названия, Matrixer может выполнять вычисления как с матрицами, так и с векторами.
Поле:
R (действительные числа)F2 (2 элемента)F3 (3 элемента)F4 (4 элемента)F5 (5 элементов)F7 (7 элементов)F8 (8 элементов)F9 (9 элементов)F11 (11 элементов) )F13 (13 элементов)F17 (17 элементов)F19 (19 элементов)
О нет! Matrixer обнаружил ошибку: 93\) Номера F4:
{1,2,3;4,5,6} представляет \(\begin{pmatrix}1 & 2 & 3 \\ 4 & 5 & 6\end{pmatrix}\)
[1,2,3,4] представляет \(\begin{pmatrix}1 \\ 2 \\ 3 \\ 4\end{pmatrix}\) Input Number 0 \(0\) 1 \(1\) a \(\alpha\) a+ 1 \(\alpha+1\)
F8 Numbers:
| Input | Number |
|---|---|
| 0 | \(0\) |
| 1 | \(1\) |
F9 Numbers:
| Input | Number |
|---|---|
| 0 | \(0\) |
| 1 | \(1\) |
| -1 | \ (-1 \) |
| J | \ (\ IOTA \) |
| J+1 | 7 \ IOTA+21219116 |
. | \(\йота-1\) |
| -j | \(-\йота\) 9{0.5} = \sqrt{4} = 2\) Например. в F5: {0,4,3;1,2,4}*{1,3;0,2;4,2} \(=\begin{pmatrix}0&4&3\\1&2&4\end{pmatrix}*\begin {pmatrix}1&3\\0&2\\4&2\end{pmatrix} = \begin{pmatrix}2&4\\2&0\end{pmatrix}\) в F4: {a,a+1;0,1}+{0,1;a,a} \(=\begin{pmatrix}\alpha&\alpha+1\\0&1\end{pmatrix}+\begin{ pmatrix}0&1\\\alpha&\alpha\end{pmatrix} = \begin{pmatrix}\alpha&\alpha\\\alpha&\alpha+1\end{pmatrix}\) Напр. в F5: {0,4,3;1,2,4}*[1,0,4] \(=\begin{pmatrix}0&4&3\\1&2&4\end{pmatrix}*\begin{pmatrix}1\\ 0\\4\end{pmatrix} = \begin{pmatrix}2\\2\end{pmatrix}\) Например. в F4: a*{1,1;1,1} \(=\alpha*\begin{pmatrix}1&1\\1&1\end{pmatrix}=\begin{pmatrix}\alpha&\alpha\\\alpha&\alpha \end{pmatrix}\) в F3: [2,1,2]*[2,2,0] \(=\begin{pmatrix}2\\1\\2\end{pmatrix}*\begin{pmatrix}2\\2\\ 0\end{pmatrix} = 0\) в R: [1,2,3]-[4,5,6] \(=\begin{pmatrix}1\\2\\3\end{pmatrix}-\begin{pmatrix}4\\5\\ 6\end{pmatrix} = \begin{pmatrix}-3\\-3\\-3\end{pmatrix}\) Например. Напр. в R: rowreduce({1,2,3,4;5,6,7,8;9,0,1,2}) \(=rowreduce(\begin{pmatrix}1&2&3&4\\5&6&7&8\\9&0&1&2\end {pmatrix}) = \begin{pmatrix}1&0&0&0\\0&1&0&-1\\0&0&1&2\end{pmatrix}\) Обратите внимание, что круглые скобки вокруг фигурных матричных скобок , а не можно опустить. Система однородных уравнений определяется как \(A*x=0\), где \(A\) – заданная матрица, а \(x\) – неизвестный вектор. в F9:solvehom({1,j,-j;1-j,0,-1}) \(=solvehom(\begin{pmatrix}1&\iota&-\iota\\1-\iota&0&-1\end{ pmatrix})\) приводит к Span: \[\langle\begin{pmatrix}-\iota-1\\-\iota-1\\1\end{pmatrix}\rangle\] Тривиальное решение : \[\begin{pmatrix}0\\0\\0\end{pmatrix}\] Матрица с уменьшенным числом строк: \[\begin{pmatrix}1&0&\iota+1\\0&1&\iota+1\end{pmatrix}\] Напр. Мультипликативный обратный элемент \(y\) числа \(x\) определяется как \(x* у=1\). в F4: мультиверсия(а) \(=мультинверсия(\альфа) = \альфа+1\) Напр. в R: мультиверсия(2) \(=мультинверсия(2) = 0,5\) Напр. в F7: мультиверсия ({1,5,3;3,4,1;6,2,5}) \(=мультинверсия(\begin{pmatrix}1&5&3\\3&4&1\\6&2&5\end{pmatrix}) = \ begin{pmatrix}6&3&0\\ 4&5&5\\ 1&0&1\end{pmatrix} \)  |


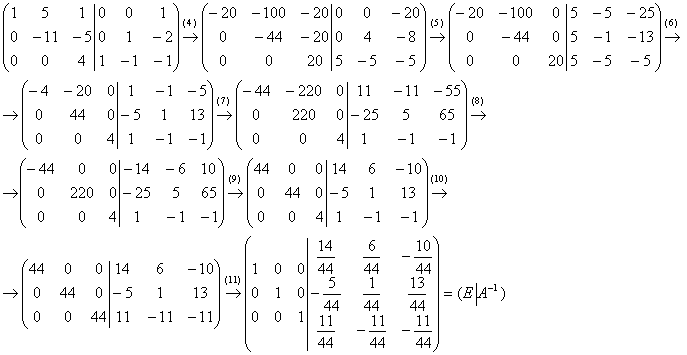
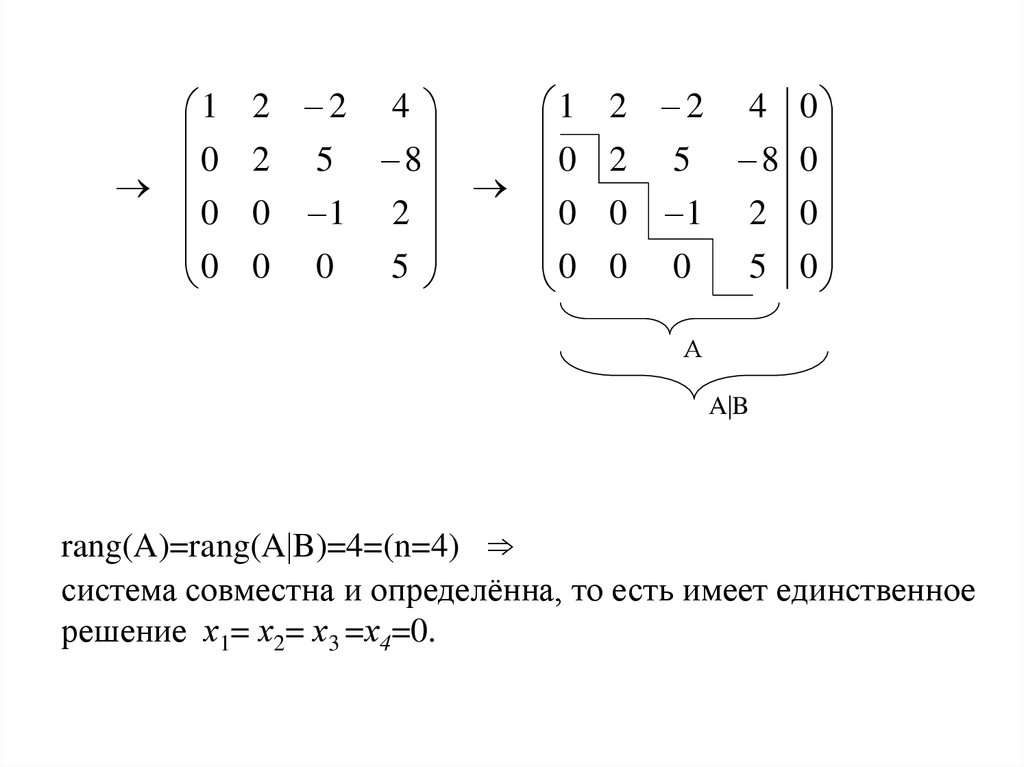


 Пусть дана неособенная матрица n -го порядка:
Пусть дана неособенная матрица n -го порядка:
 см. пример оформления .
см. пример оформления .
 {-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
{-1}b}
. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.