M в физике формула: Формула массы тела в физике

{n} m_{i}(1)$$

В классической механике считают:

масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.

Содержание

Инертная масса

Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:

$$\bar{F}=m \bar{a}(2)$$

где масса определяет инертные свойства материальной точки (инертная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.

{2}}}}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Какова масса 2м³ меди?

Решение. Будем считать, что медь однородна и для решения задачи используем формулу:

$$m=\rho V$$

При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ _Cu=8900 кг/м³ . Для расчета все величины известны. Проведем вычисления:

$m=8900 \cdot 2=17800$ (кг)

Ответ. $m=8900 \cdot 2=17800$ (кг)

Читать дальше: Формула момента силы.

Решение задач на расчет массы и объема тела. 7-й класс

org/Person»> Лебедев Алексей Васильевич

Разделы: Физика

Класс: 7

Цели урока.

1. Образовательные: систематизировать знания, имеющиеся у учащихся о понятиях: “плотность”, “масса”, “объем”, расширить область знаний о данных понятиях, выработка умения применять изученный материал для решения практических задач.

2. Развивающие: формирование логического мышления, продолжать развивать навык решения физических задач.

3. Воспитательные: привития учащимся к доброжелательному общению, взаимопомощи.

Тип урока: комбинированный.

Оборудование: 15 комплектов таблиц 1 и 2.

Ход урока

1. Организационный этап.

2. Актуализация знаний.

Деятельность учителя	Деятельность учеников
— Что такое плотность?	Физическая величина, которая показывает, какое количество вещества, содержится в единице объема.
— Что означает, плотность железа равна 6800 кг/м³? - Как можно найти плотность вещества? — От чего зависит масса тела?	Это означает, что масса 1 м³ железа равна 6800 кг. Чтобы найти плотность вещества нужно массу разделить на объем.
— Как найти массу тела?	Масса тела зависит от его объема и плотности вещества, из которого состоит данное тело.
— Как найти объем тела, если известна его масса и вещество, из которого состоит тело?	Чтобы найти массу тела нежно его плотность умножить на объем.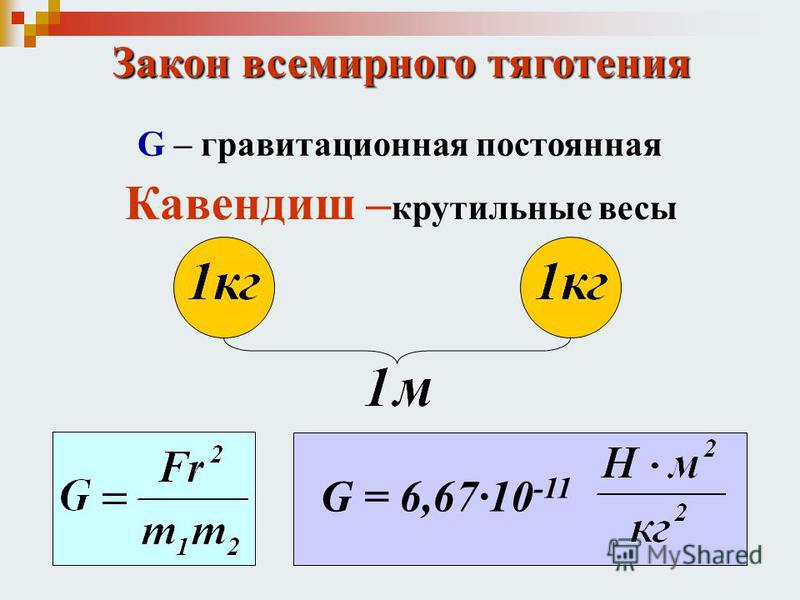 Чтобы найти объем тела, нужно его массу разделить на плотность.

3. Решение задач
1. Как будем выставлять оценку за работу на уроке по принципу сложения или вычитания?	По принципу сложения.
2. Таблица 1 (Приложение №1). На складе имеются грузы: мел, пробка, береза, лед, сталь. Каждый груз упакован в контейнеры по 2 м³. для перевозки этих грузов были вызваны пять автомобилей. Ваша задача распределить грузы по автомобилям.	Найти массу грузов.
— Что нужно сделать, чтобы распределить грузы по автомобилям?
— Как найти массу вещества, если известна его плотность и объём?	кг/м³
— В каких единицах измерена плотность вещества?	В килограммах
— В каких единицах будет вычислена масса?	В тоннах и килограммах
— В каких единицах выражена грузоподъемность автомобилей?	В тоннах, а для москвича в килограммах
— В каких единицах нужно получить массу грузов? Решите данную задачу и распределите грузы по автомобилям. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках (Приложение № 3) учеников делаются записи количества набранных баллов.	Ученики решают задачи и распределяют грузы.
3. Таблица 2 (Приложение № 2). Имеются пять различных жидкостей, которые имеют одинаковую массу. Эти жидкости нужно разлить по пяти различным сосудам. — Что нужно сделать, чтобы разлить жидкости по сосудам?	Найти объём жидкостей.
— Как найти объем, если известна масса вещества и его плотность?
— В каких единицах получится вычисленный объём?	в м³.
— В каких единицах дан объём сосудов?	В литрах и миллилитрах
— В каких единицах нужно получить объём жидкостей?	В литрах и миллилитрах
Решите данную задачу и распределите жидкость по сосудам. Учитель проверяет правильность выполненного задания у первого решившего ученика, и назначает его своим ассистентом. В карточках учеников делаются записи количества набранных баллов.	Ученики решают задачу.
4. Рефлексия.
— Какие физические понятия Вы использовали для выполнения заданий? Сравните количество баллов, которые вы выставили сами себе, с количеством баллов, которые вам выставили проверяющие. Какой вы можете для себя сделать вывод? Готовы ли вы к контрольной работе?	Масса, плотность, объем.

См. приложение 4 и приложение 5.

Домашнее задание: повторить 18-22.

23.07.2009

Формулы по физике 9 класса. Все формулы по физике за 9 класс с пояснениями и определениями

Закон	Формула	Определение	Единицы измерения
ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ
Вычисление перемещения	АВ² = АС² + ВС²	Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещения	S_x = x₂ – x₁		x₁ – начальная координата, [м] x₂ – конечная координата, [м] S_x – перемещение, [м]
Формула расчета скорости движения тела	v = s/t	Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.	v – скорость, [м/с] s – путь, [м] t – время, [c]
Уравнение движения	x = x₀ + v_xt		x0 – начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения тела	a = v — v₀⃗/t	Ускорение – физическая величина, которая характеризует быстроту изменения скорости.	a – ускорение, [м/с²] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] t – время, [c]
Уравнение скорости	v = v₀⃗+ at		v – конечная скорость, [м/с] v₀ – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Уравнение Галилея	S = v0t + at²/2		S – перемещение, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движении	x = x0 + v0t + at² /2		x0 – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с²] t – время, [c]
Первый закон Ньютона		Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютона	a = F ⃗/m	Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.	a – ускорение, [м/с²] F – сила, [Н] m – масса, [кг]
Третий закон Ньютона	\|F₁⃗ \|=\|F₂⃗\| F₁1 ⃗ = -F₂⃗	Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое	F – сила, [Н]
Формула для вычисления высоты, с которой падает тело	H=gt²/2		Н – высота, [м] t – время, [c] g ≈ 9,81 м/с² – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверх	h=v₀t — gt²/2		h – высота, [м] v₀ – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с² – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорением	P = m (g + a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения a – ускорение тела, [м/с²]
Формула для вычисления веса тела при движении вниз с ускорением	P = m (g – a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения a – ускорение тела, [м/с²]
Формула закона	F = Gm₁m₂/r²	Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.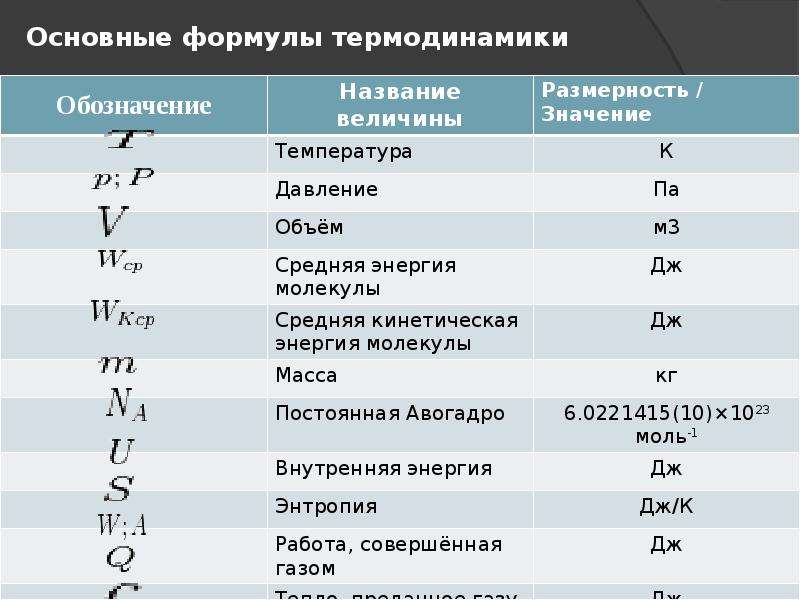	F – сила, [Н] G = 6,67 · 10^-11 [Н·м²/кг²] – гравитационная постоянная m – масса тела, [кг] r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетах	g = G M_пл/R_пл²		g – ускорение свободного падения, [м/с2] G = 6,67 · 10^-11 [Н·м²/кг² – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м]
Формула расчета ускорения свободного падения	g = GM₃/(R₃+H)²		g – ускорение свободного падения, [м/с2] G = 6,67 · 10^-11 [Н·м²/кг² – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м]
Формула расчета центростремительного ускорения	а=υ²/r		a – центростремительное ускорение, [м/с2] v – скорость, [м/с] r – радиус окружности, [м]
Формула периода движения по окружности	T = 1/ν = (2πr)/υ = t/N		Т – период, [с] ν – частота вращения, [с^-1] t – время, [с] N – число оборотов
Формула расчета угловой скорости	ω = 2π/T = 2πν = υr		ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения, [с^-1] r – радиус окружности, [м]
Формула импульса тела	p = mv	Импульсом называют произведение массы тела на его скорость.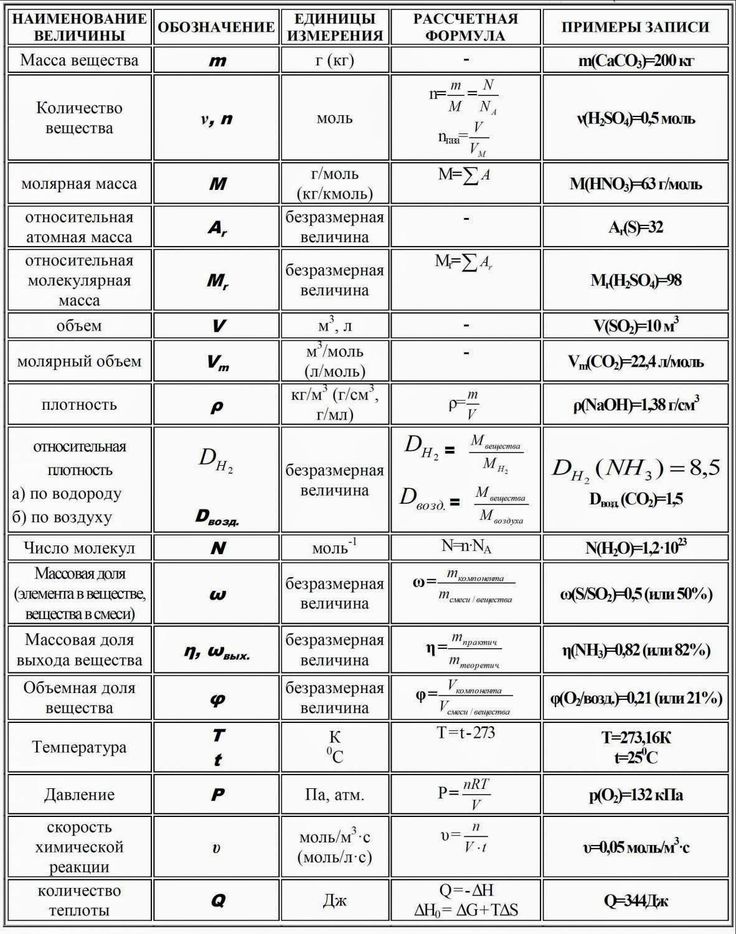	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с]
Формула закона сохранения импульса	p₁ + p₂ = p₁’ + p₂’ m₁v + m₂u = m₁v’ + m₂u’	Закон сохранения импульса: в замкнутой системе импульс всех тел остается величиной постоянной.	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость 1-го тела, [м/с] u – скорость 2-го тела, [м/с]
Формула импульса силы	P = Ft		p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c]
Формула механической работы	A = Fs	Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы	A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м]
Формула расчета мощности	N = A/t	Мощность – физическая величина, характеризующая быстроту совершения механической работы.	N – мощность, [Вт] A – работа, [Дж] t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)	η = A_п/A_з∙100	КПД – отношение полезной работы к затраченной работе.	A_п – полезная работа, [Дж] A_з – затраченная работа, [Дж]
Формула расчета потенциальной энергии	E_k = mv²/2	Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.	E_k – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергии	mv₁²/2 + mgh₁ = mv₂²/2 + mgh₂	Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.	m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения v₁ – скорость тела в начальный момент времени, [м/с] v₂ – скорость тела в конечный момент времени, [м/с] h₁ – начальная высота, [м] h₂ – конечная высота, [м]
Формула силы трения	F_тр = μmg	Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.	Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с² – ускорение свободного падения
Уравнение колебаний	x = A cos (ωt + φ₀)		А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ0 – начальная фаза, [рад]
Формула периода	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота колебании, [с^-1] t – время колебании, [с] N – число колебаний
Формула периода для математического маятника	T= 2π √L/g		Т – период, [с] g ≈ 9,81 м/с² – ускорение свободного падения L – длина нити, [м]
Формула периода для пружинного маятника	T = 2π √m/K		Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м]
Формула длины волны	λ = υТ = υ/ν		λ – длина волны, [м] Т – период, [с] ν – частота, [с^-1] υ – скорость волны, [м/с]
Формула расчета плотности тела	ρ=m/V	Плотность вещества – показывает, чему равна масса вещества в единице объема.	ρ – плотность, [кг/м³] m – масса, [кг] V – объем тела, [м³]
Формула гидростатического давления жидкости	p = ρgh		p – давление, [Па], [Н/м] ρ – плотность жидкости, [кг/м³] g ≈ 9,81 м/с² – ускорение свободного падения h – высота столба жидкости, [м]
Формула силы Архимеда	F_A = ρgV	Закон Архимеда: на всякое тело, погруженное в жидкость (газ(, действует выталкивающая сила, равная весу вытесненной жидкости (газа).	FА – сила Архимеда, [Н] ρ – плотность жидкости или газа [кг/м³] g ≈ 9,81 м/с² – ускорение свободного падения V – объем тела, [м³]
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Формула расчета силы Ампера	F_A = BIL sinα	Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником.	F_A – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м]
Формула расчета силы Лоренца	F_л = q B υ sinα	Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.	F_л – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с]
Формула радиуса движения частицы в магнитном поле	r = mυ/qB		r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с]
Формула для вычисления магнитного потока	Ф = B S cosα		Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м²]
Формула для вычисления величины заряда	q = It	Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.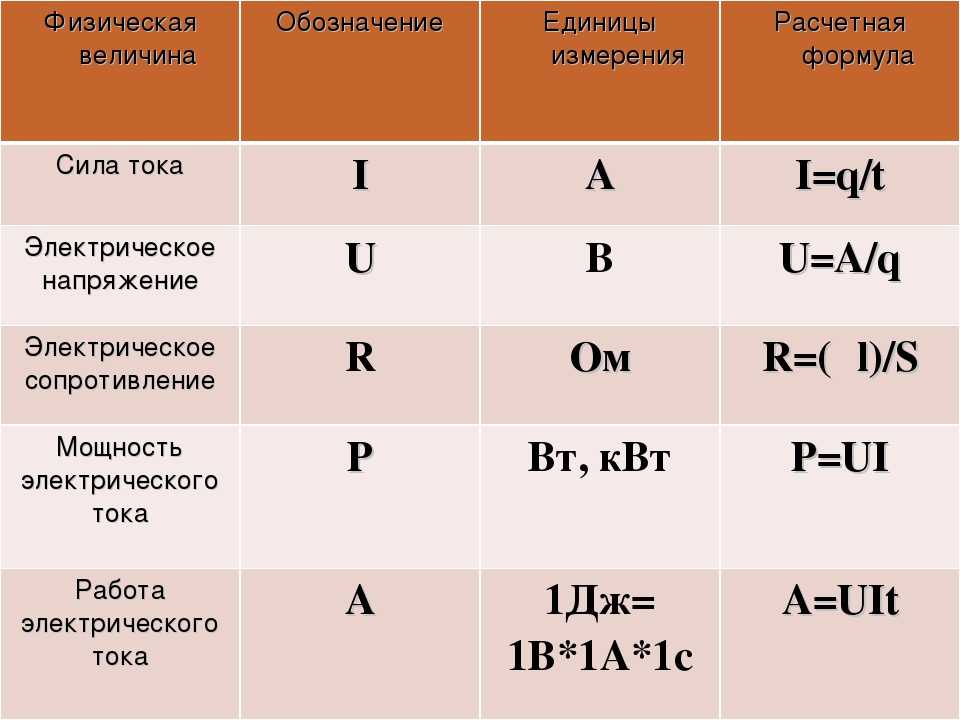	q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Закон Ома для участка цепи	I=U/R	Закон Ома: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Формула для вычисления удельного сопротивления проводника	R = ρ * L/S ρ = R * S/L	Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник.	ρ – удельное сопротивление вещества, [Ом·мм²/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [мм²] L – длина проводника, [м]
Законы последовательного соединения проводников	I = I₁ = I₂ U = U₁ + U₂ R_общ = R₁ + R₂	Последовательным соединением называется соединение, когда элементы идут друг за другом.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Законы параллельного соединения проводников	U = U₁ = U₂ I = I₁ + I₂ 1/R_общ = 1/R₁ +1/R₂	Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе.	I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом]
Формула для вычисления величины заряда.	q = It	Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику.	q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Формула для нахождения работы электрического тока	A = Uq A = UIt	Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д. Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле.	A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c]
Формула электрической мощности	P = A/t P = UI P = U²/R	Мощность – работа, выполненная в единицу времени.	P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом]
Формула закона Джоуля-Ленца	Q = I²Rt	Закон Джоуля-Ленца: при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.	Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом].
Закон отражения света		Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча.
Закон преломления	sinα/sinγ = n₂/n₁	При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого.	n – показатель преломления одного вещества относительно другого
Формула вычисления абсолютного показателя преломления вещества	n = c/v	Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде.	n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с]
Закон Снеллиуса	sinα/sinγ = v₁/v₂ = n	Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная.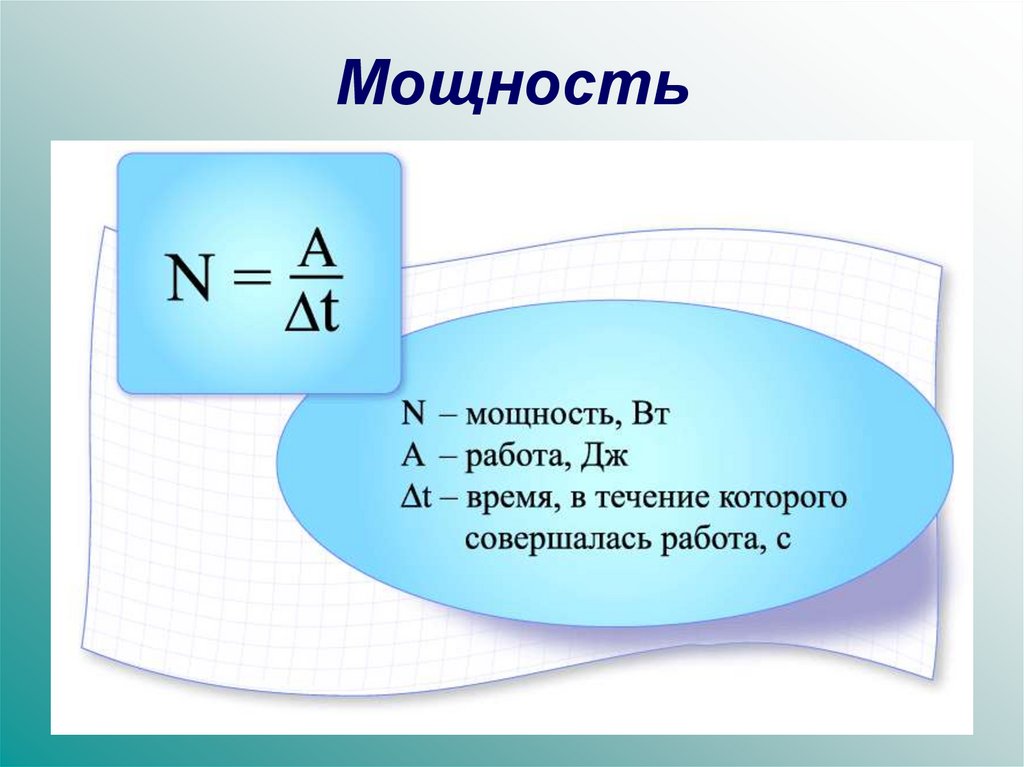	n – показатель преломления одного вещества относительно другого v – скорость света в данной среде, [м/с]
Показатель преломления среды	sinα/sinγ = n	Отношение синуса угла падения к синусу угла преломления есть величина постоянная.	n – показатель преломления среды
Формула оптической силы линзы	D = 1/F	Оптическая сила линзы – способность линзы преломлять лучи.	D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м]
Формула тонкой линзы	1/F = 1/d + 1/f		F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м]
СТРОЕНИЕ АТОМА И АТОМНОГО ЯДРА
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	М_я = М_А – Zm_e		M_я – масса ядра, [кг] М_А – масса изотопа , [кг] m_e – масса электрона, [кг]
Формула дефекта масс	∆m = Zm_p+ Nm_n – M_Я	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.	∆m – дефект масс, [кг] m_p – масса протона, [кг] m_n – масса нейтрона, [кг]
Формула энергии связи	Е_связи = ∆m c²	Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны).	Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·10⁸м/с – скорость света
Альфа распад	M/Z * X → 4/2 * α + M/Z — 4/2 * Y

Динамика | Формулы по физике

Инертность, масса, ускорение

Найти

Известно, что:

a1a2m2m1 =

Вычислить ‘a1’

Сила, масса, ускорение

Найти

Известно, что:

Fma =

Вычислить ‘F’

Сила тяжести

Найти

Известно, что:

Nmg =

Вычислить ‘N’

Сила трения

Найти

Известно, что:

F_трμN =

Вычислить ‘F_тр’

Сила трения

Найти

Известно, что:

F_трμmg =

Вычислить ‘F_тр’

Закон всемирного тяготения

Найти

Известно, что:

FGm1m2r =

Вычислить ‘F’

Центростремительное ускорение спутника

Найти

Известно, что:

avRh =

Вычислить ‘a’

Скорость спутника

Найти

Известно, что:

vGMRh =

Вычислить ‘v’

Первая космическая скорость (движение по круговой орбите)

Найти

Известно, что:

vgR =

Вычислить ‘v’

Вторая космическая скорость (преодоление гравитации)

Найти

Известно, что:

vgR =

Вычислить ‘v’

Третий закон Кеплера

Найти

Известно, что:

T1T2a1a2 =

Вычислить ‘T1’

Ускорение свободного падения на поверхности земли

Найти

Известно, что:

gGMR =

Вычислить ‘g’

Вес тела

Найти

Известно, что:

Pmg =

Вычислить ‘P’

Вес тела: невесомость

Найти

Известно, что:

Pmga =

Вычислить ‘P’

Вес тела: перегрузка

Найти

Известно, что:

Pmga =

Вычислить ‘P’

Время торможения

Найти

Известно, что:

tmvF_тр =

Вычислить ‘t’

Время торможения

Найти

Известно, что:

tvμg =

Вычислить ‘t’

Путь торможения

Найти

Известно, что:

smvF_тр =

Вычислить ‘s’

Путь торможения

Найти

Известно, что:

svμg =

Вычислить ‘s’

Сила трения качения

Найти

Известно, что:

F_трμNR =

Вычислить ‘F_тр’

Сила упругости

Найти

Известно, что:

F_упругkx =

Вычислить ‘F_упруг’

Кинетическая энергия вращающегося тела

Найти

Известно, что:

W_kJω =

Вычислить ‘W_k’

M в физике формула – Как в физике найти (m) формула

М в физике

Электродвигатель подъемного крана поднимает груз на высоту 18м за 50с. КПД установки составляет 50% . чему равна масса груза если известно что электродвигатель работает под напряжением 360 В и потребляет силу тока 20 А

Формула массы тела в физике

Определение и формула массы тела

В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.

Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна сумме масс всех отдельных частей системы (mi):

В классической механике считают:

масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела; выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.

Инертная масса

Где масса определяет инертные свойства материальной точки (инертная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки. при этом она носит название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести (Ft) избранного тела:

Где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.

Формула расчета массы через плотность тела

Масса тела может быть рассчитана как:

Где – плотность вещества тела, где интегрирование проводится по объему тела. Если тело однородное ( ), то масса может быть рассчитана как:

Масса в специальной теории относительности

В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:

Где E – полная энергия свободного тела, p — импульс тела, c – скорость света.

Релятивистская масса частицы определяется формулой:

Где m0 – масс покоя частицы, v – скорость движения частицы.

Основной единицей измерения массы в системе СИ является: [m]=кг.

Примеры решения задач

Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света). При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц до соударения равны m.

Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:

В нашем случае выполняется закон сохранения механической энергии. 2. ESLI TELO STOIT NA PODSTAVKE — VES TELA P = mg — SILA, S KOTOROI TELO DAVIT NA PODSTAVKU. A TI NE SMEESHSJA NAD LJUDJAMI, GIRL OR GUY? SMOTRI MNE. NAROD SIR, NO MUDR!

На тело массой 3кг действует сила F= 6н. Ускорение тела равно:

F=mg m-масса тела g-правильно 9,8(в учебниках говорят брать 10) Пример: Масса бруска 200г.; переводим в систему СИ: 0,2кг 0,2*9,8=1,96 Н Н-ньютон

Ускорение свободного падения

Mgh — это потенциальная энергия

F(cила) =m(массе) умноженой на h(ускорение свободного падения)

F=mg. F — сила тяжести. Где m — масса тела, g — ускорение свободного падения (9.8).

F(cила) =m(массе) умноженой на h(ускорение свободного падени

На тело массой 3кг действует сила F= 6н. Ускорение тела равно:

При ударе кулаком: F=mg. F — сила удара, m — масса тела, g — ускорение/скорость «вылета» кулака, легко доказывается на тренажере.

F=mg m-масса тела g-правильно 9,8(в учебниках говорят брать 10)

E=mgh — потенциальная энергия тела на высоте h от земли. 2/2

Гений (76570) F=mg F — сила тяжести где m — масса тела, g — ускорение свободного падения (9.8)

Определение и формула массы тела

В классической механике считают:

Инертная масса

Где масса определяет инертные свойства материальной точки (инертная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки. при этом она носит название гравитационной (тяжелой) массы.

Формула расчета массы через плотность тела

Масса тела может быть рассчитана как:

Масса в специальной теории относительности

В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:

Где E – полная энергия свободного тела, p — импульс тела, c – скорость света.

Релятивистская масса частицы определяется формулой:

Где m0 – масс покоя частицы, v – скорость движения частицы.

Основной единицей измерения массы в системе СИ является: [m]=кг.

Примеры решения задач

В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией. По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:

Где E1 – энергия первой частицы до удара, E2 – энергия второй частицы до соударения.

Закон сохранения энергии запишем в виде:

Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:

Задание. Какова масса 2м 3 меди?

Решение. Будем считать, что медь однородна и для решения задачи используем формулу:

При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной

Ответ. (кг)

Читать дальше: Формула момента силы.

Вы поняли, как решать? Нет?

Помощь с решением

Формула массы тела в физике.

Xn—-8sbanwvcjzh9e. xn--p1ai

25.03.2017 2:48:36

2017-03-25 02:48:36

Источники:

Https://xn—-8sbanwvcjzh9e. xn--p1ai/fizike/m-v-fizike-formula-kak-v-fizike-najti-m-formula. html

Ответы: что обозначает буква M в физике » /> » /> .keyword { color: red; }

М в физике

Зависит от контекста. В каждом разделе физики свое назначение. Со школы помню, что большая М обозначала массу Земли.

M = Масса, магнитное квантовое число, магнитный момент, эффективная масса, дефект массы, масса Планка

M = Момент силы, масса, вектор намагниченности, крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса

M = Масса, магнитное квантовое число, магнитный момент, эффективная масса, дефект массы, масса Планка

M Масса, магнитное квантовое число, магнитный момент, эффективная масса, дефект массы, масса Планка.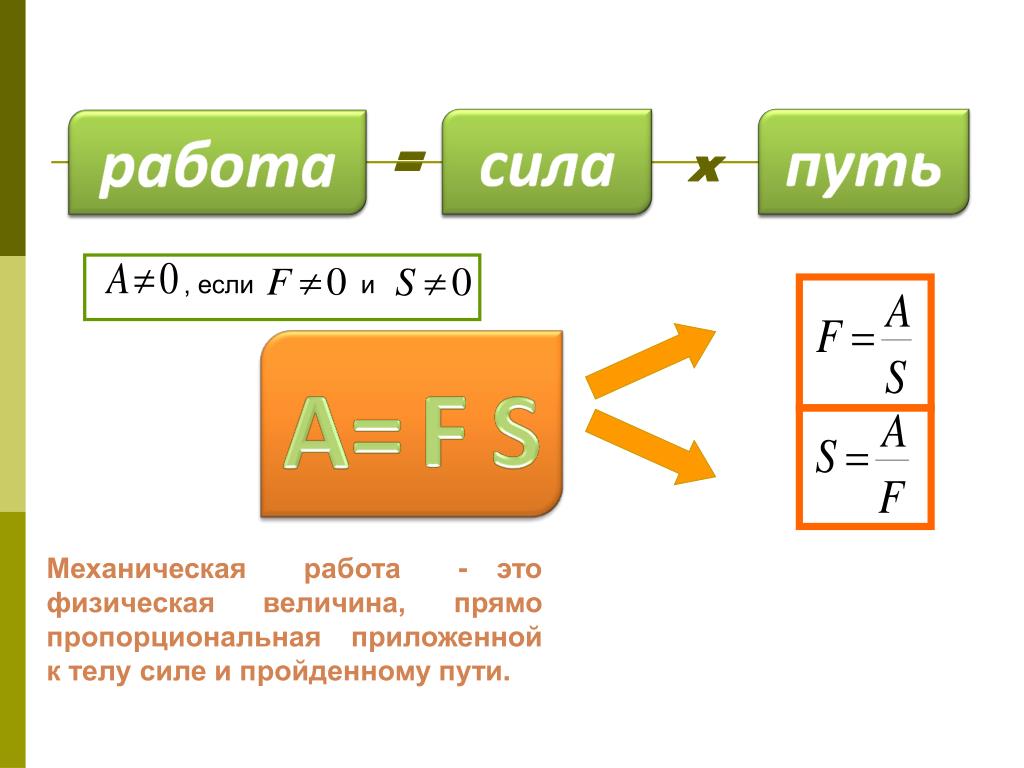

Otvet. mail. ru

31.10.2020 8:48:44

2020-10-31 08:48:44

Источники:

Https://otvet. mail. ru/question/33124669

Физ-мат класс » /> » /> .keyword { color: red; }

М в физике

Физические величины и единицы их измерения

Физическая величина	Единица измерения физической величины
Пространство и время
Длина	L, s, d	Метр	М
Площадь	S	Квадратный метр	М 2
Объем, вместимость	V	Кубический метр	М 3
Время	T	Секунда	С
Плоский угол	,	Радиан	Рад
Телесный угол	, ,	Стерадиан	Ср
Линейная скорость	V	Метр в секунду	М/с
Линейное ускорение	A, w	Метр в секунду в квадрате	М/с 2
Угловая скорость		Радиан в секунду	Рад/с
Угловое ускорение		Радиан в секунду в квадрате	Рад/с 2
Периодические явления, колебания и волны
Период	T	Секунда	С
Частота периодического процесса	V, f	Герц	Гц
Циклическая (круговая) частота		Радиан в секунду	Рад/с
Частота вращения	N	Секунда в минус первой степени	С -1
Длина волны		Метр	М
Волновое число	K	Метр в минус первой степени	М -1
Механика
Масса	M	Килограмм	Кг
Плотность		Килограмм на кубический метр	Кг/м 3
Удельный объем	V	Кубический метр на килограмм	М 3 /кг
Массовый расход	Qm	Килограмм в секунду	Кг/с
Объемный расход	QV	Кубический метр в секунду	М 3 /с
Импульс	P	Килограмм-метр в секунду	КгМ/с
Момент импульса	L	Килограмм-метр в квадрате в секунду	КгМ 2 /с
Момент инерции	J	Килограмм-метр в квадрате	КгМ 2
Сила, вес	F, Q	Ньютон	Н
Момент силы	M	Ньютон-метр	НМ
Импульс силы	I	Ньютон-секунда	НС
Давление, механическое напряжение	P,	Паскаль	Па
Работа, энергия	A, E, U	Джоуль	Дж
Мощность	N	Ватт	Вт
Тепловые явления
Температура	T	Кельвин	К
Температурный коэффициент		Кельвин в минус первой степени	К -1
Температурный градиент	GradT	Кельвин на метр	К/м
Теплота (количество теплоты)	Q	Джоуль	Дж
Удельная теплота	Q	Джоуль на килограмм	Дж/кг
Теплоемкость	C	Джоуль на кельвин	Дж/К
Удельная теплоемкость	C	Джоуль на килограмм-кельвин	Дж/(кгК)
Энтропия	S	Джоуль на килограмм	Дж/кг
Молекулярная физика
Количество вещества	V, n	Моль	Моль
Молярная масса	M,	Килограмм на моль	Кг/моль
Молярная энергия	Hмол	Джоуль на моль	Дж/моль
Молярная теплоемкость	Смол	Джоуль на моль-кельвин	Дж/(мольК)
Концентрация молекул	C, n	Метр в минус третьей степени	М -3
Массовая концентрация		Килограмм на кубический метр	Кг/м 3
Молярная концентра ция	Смол	Моль на кубический метр	Моль/м 3
Подвижность ионов	В,	Квадратный метр на вольт-секунду	М 2 /(ВС)
Электричество и магнетизм
Сила тока	I	Ампер	А
Плотность тока	J	Ампер на квадратный метр	А/м 2
Электрический заряд	Q, q	Кулон	Кл
Электрический дипольный момент	P	Кулон-метр	КлМ
Поляризованность	P	Кулон на квадратный метр	Кл/м 2
Напряжение, потенциал, ЭДС	U, ,	Вольт	В
Напряженность электрического поля	E	Вольт на метр	В/м
Электрическая емкость	C	Фарад	Ф
Электрическое сопротивление	R, r	Ом	Ом
Удельное электрическое сопротивление		Ом-метр	ОмМ
Электрическая проводимость	G	Сименс	См
Магнитная индукция	B	Тесла	Тл
Магнитный поток	Ф	Вебер	Вб
Напряженность магнитного поля	H	Ампер на метр	А/м
Магнитный момент	Pm	Ампер-квадратный метр	АМ 2
Намагниченность	J	Ампер на метр	А/м
Индуктивность	L	Генри	Гн
Электромагнитная энергия	N	Джоуль	Дж
Объемная плотность энергии	W	Джоуль на кубический метр	Дж/м 3
Активная мощность	P	Ватт	Вт
Реактивная мощность	Q	Вар	Вар
Полная мощность	S	Ват-ампер	ВтА
Оптика, электромагнитное излучение
Сила света	J, I	Кандела	Кд
Световой поток	Ф	Люмен	Лм
Световая энергия	Q	Люмен-секунда	ЛмС
Освещенность	E	Люкс	Лк
Светимость	M	Люмен на квадратный метр	Лм/м 2
Яркость	L, B	Кандела на квадратный метр	Кд/м 2
Энергия излучения	E, W	Джоуль	Дж
Акустика
Звуковое давление	P	Паскаль	Па
Объемная скорость	C, V	Кубический метр в секунду	М 3 /с
Скорость звука	V, u	Метр в секунду	М/с
Интенсивность звука	L	Ватт на квадратный метр	Вт/м 2
Акустическое сопротивление	Za, Ra	Паскаль-секунда на кубический метр	ПаС/м 3
Механическое сопротивление	Rm	Ньютон-секунда на метр	НС/м
Атомная и ядерная физика. Радиоактивность
Масса (масса покоя)	M	Килограмм	Кг
Дефект массы		Килограмм	Кг
Элементарный электрический заряд	E	Кулон	Кл
Энергия связи	Eсв	Джоуль	Дж
Период полураспада, среднее время жизни	T,	Секунда	С
Эффективное сечение		Квадратный метр	М 2
Активность нуклида	A	Беккерель	Бк
Энергия ионизирующего излучения	E, W	Джоуль	Дж
Поглощенная доза ионизирующего излучения	Д	Грей	Гр
Эквивалентная доза ионизирующего излучения	H, Дэк	Зиверт	Зв
Экспозиционная доза рентгеновского и гамма-излучения	Х	Кулон на килограмм	Кл/кг

Замечательный калькулятор единиц измерения на сайте Нолик. ру. Обязательно посмотрите!

Физические величины и единицы их измерения.

Fmclass. ru

27.08.2017 19:45:57

2017-08-27 19:45:57

Источники:

Https://fmclass. ru/phys. php? id=481dc3d678ac3

Формула по нахождению массы физика. Как найти массу в физике

Окружающее нас пространство наполнено разными физическими телами, которые состоят из разных веществ с различной массой. Школьные курсы химии и физики, ознакомляющие с понятием и методом нахождения массы вещества, прослушали и благополучно забыли все, кто учился в школе. Но между тем теоретические знания, приобретенные когда-то, могут понадобиться в самый неожиданный момент.

Вычисление массы вещества с помощью удельной плотности вещества. Пример – имеется бочка на 200 литров. Нужно заполнить бочку любой жидкостью, скажем, светлым пивом. Как найти массу наполненной бочки? Используя формулу плотности вещества p=m/V, где p – удельная плотность вещества, m – масса, V – занимаемый объем, найти массу полной бочки очень просто:

Меры объемов – кубические сантиметры, метры. То есть бочка на 200 литров имеет объем 2 м³.
Мера удельной плотности находится с помощью таблиц и является постоянной величиной для каждого вещества. Измеряется плотность в кг/м³, г/см³, т/м³. Плотность пива светлого и других алкогольных напитков можно посмотреть на сайте . Она составляет 1025,0 кг/м³.
Из формулы плотности p=m/V => m=p*V: m = 1025,0 кг/м³* 2 м³=2050 кг.

Бочка объемом 200 литров, полностью наполненная светлым пивом, будет иметь массу 2050 кг.

Нахождение массы вещества с помощью молярной массы. M (x)=m (x)/v (x) – это отношение массы вещества к его количеству, где M (x) – это молярная масса X, m (x) – масса X, v (x) – количество вещества X. Если в условии задачи прописывается только 1 известный параметр – молярная масса заданного вещества, то нахождение массы этого вещества не составит труда. Например, необходимо найти массу йодида натрия NaI количеством вещества 0,6 моль.

Молярная масса исчисляется в единой системе измерений СИ и измеряется в кг/моль, г/моль. Молярная масса йодида натрия – это сумма молярных масс каждого элемента: M (NaI)=M (Na)+M (I). Значение молярной массы каждого элемента можно вычислить по таблице, а можно с помощью онлайн-калькулятора на сайте : M (NaI)=M (Na)+M (I)=23+127=150 (г/моль).
Из общей формулы M (NaI)=m (NaI)/v (NaI) => m (NaI)=v (NaI)*M (NaI)= 0,6 моль*150 г/моль=90 грамм.

Масса йодида натрия (NaI) с массовой долей вещества 0,6 моль составляет 90 грамм.

Нахождение массы вещества по его массовой доле в растворе. Формула массовой доли вещества ω=*100%, где ω – массовая доля вещества, а m (вещества) и m (раствора) – массы, измеряемые в граммах, килограммах. Общая доля раствора всегда принимается за 100%, иначе будут погрешности в вычислении. Несложно из формулы массовой доли вещества вывести формулу массы вещества: m (вещества)=[ω*m (раствора)] /100%. Однако есть некоторые особенности изменения состава раствора, которые нужно учитывать при решении задач на эту тему:

Разбавление раствора водой. Масса вещества растворенного X не изменяется m (X)=m’(X). Масса раствора увеличивается на массу добавленной воды m’ (р)=m (р)+m (H 2 O).
Выпаривание воды из раствора. Масса растворенного вещества X не изменяется m (X)=m’ (X). Масса раствора уменьшается на массу выпаренной воды m’ (р)=m (р)-m (H 2 O).
Сливание двух растворов. Массы растворов, а также массы растворенного вещества X при смешивании складываются: m’’ (X)=m (X)+m’ (X). m’’ (р)=m (р)+m’ (р).
Выпадение кристаллов. Массы растворенного вещества X и раствора уменьшаются на массу выпавших кристаллов: m’ (X)=m (X)-m (осадка), m’ (р)=m (р)-m (осадка).

Алгоритм нахождения массы продукта реакции (вещества), если известен выход продукта реакции. Выход продукта находится по формуле η=*100%, где m (x практическая) – масса продукта х, которая получена в результате практического процесса реакции, m (x теоретическая) – рассчитанная масса вещества х. Отсюда m (x практическая)=[η*m (x теоретическая)]/100% и m (x теоретическая)=/η.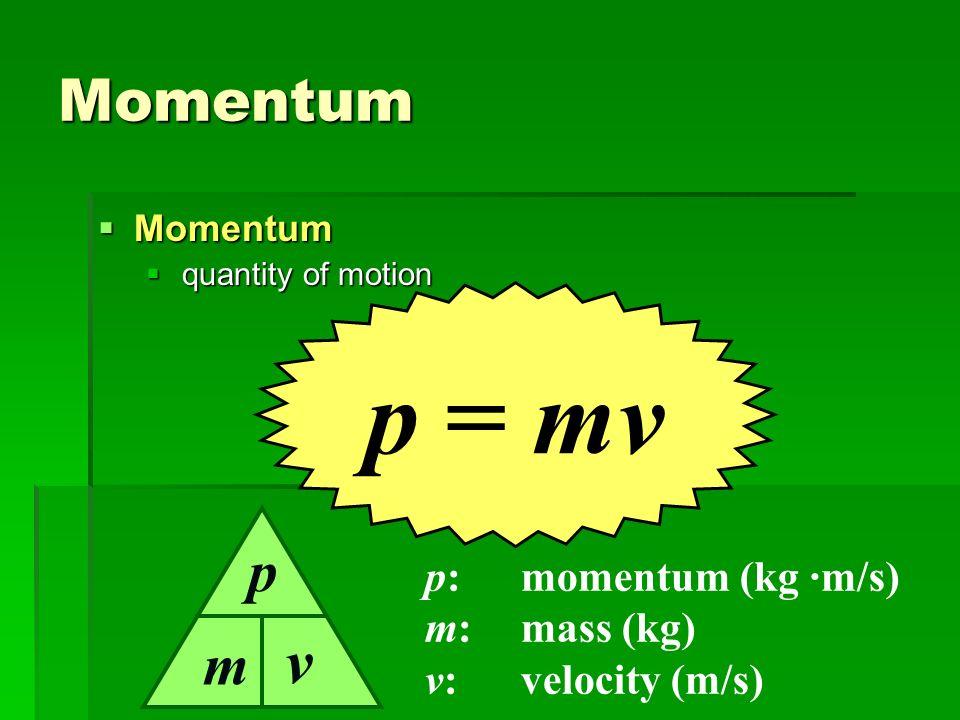 Теоретическая масса получаемого продукта всегда больше практической, в связи с погрешностью реакции, и составляет 100%. Если в задаче не дается масса продукта, полученного в практической реакции, значит, она принимается за абсолютную и равна 100%.

Варианты нахождение массы вещества – небесполезный курс школьного обучения, а вполне применяемые на практике способы. Каждый сможет без труда найти массу необходимого вещества, применяя вышеперечисленные формулы и пользуясь предлагаемыми таблицами. Для облегчения задания прописывайте все реакции, их коэффициенты.

Инструкция

Если нет возможности с точностью произвести измерение геометрических размеров тела, воспользуйтесь законом Архимеда. Для этого возьмите сосуд, имеющий шкалу (или деления) для измерения , опустите предмет в воду (в сам сосуд, снабженный делениями). Объем, на который увеличится содержимое сосуда, — и есть объем погруженного в него тела.

Если известны плотность d и объем V предмета, всегда можно найти его массу, пользуясь формулой: m=V*d. Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения СИ.

Вывод из приведенных формул следующий: чтобы получить искомое значение массы, зная плотность и объем, надо умножить значение объема тела на значение плотности вещества, из которого оно сделано.

Источники:

как находить массу

Массу тела обычно определяют экспериментально. Для этого берут груз, ставят его на весы и получают результат измерения. Но при решении физических задач, приведенных в учебниках, измерение массы по объективным причинам невозможно, зато имеются те или иные данные о теле. Зная эти данные, можно определить массу тела косвенно путем расчета.

Инструкция

Согласно этой таблице плотность составляет 2300 кг/м³. Тогда для того, чтобы найти массу бетонной плиты, потребуется простое алгебраическое действие: m = 15*2300 = 34500 кг, или 34.5 тонн. Ответ: масса бетонной плиты составляет 34. 5 тонн

Обратите внимание

Проводя расчет по указанной выше формуле, необходимо осознавать, что таким образом узнается масса покоя данного тела. Интересен факт того, что многие элементарные частицы обладают колеблющейся массой, которая зависит от скорости их движения. Если элементарная частица движется со скоростью тела, то эта частица является безмассовой (например, фотон). Если же скорость движения частицы ниже скорости света, то такая частица называется массивной.

Полезный совет

При измерении массы никогда нельзя забывать, в какой системе будет дан конечный результат. Имеется ввиду, что в системе СИ масса измеряется в килограммах, в то время как в системе СГС масса измеряется в граммах. Также масса измеряется в тоннах, центнерах, каратах, фунтах, унциях, пудах, а также во многих других единицах в зависимости от страны и культуры. В нашей стране, к примеру, массу издревле измеряли в пудах, берковцах, золотниках.

Источники:

масса бетонной плиты

К примеру, вам на зиму необходим минимум в 15 куб. метров березовых дров.
Ищите в справочной плотность березовых дров. Это: 650 кг/м3.
Вычисляйте массу, подставив значения в ту же формулу удельной плотности.

m = 650*15 = 9750 (кг)

Теперь, исходя из грузоподъемности и вместимости кузова, вы можете определиться с видом транспортного средства и количеством поездок.

Видео по теме

Обратите внимание

Люди постарше больше знакомы с понятием удельного веса. Удельная плотность вещества – это то же, что и удельный вес.

Бывают ситуации, когда необходимо вычислить массу жидкости , содержащейся в какой-либо емкости. Это может быть и во время учебного занятия в лаборатории, и в ходе решения бытовой проблемы, например, при ремонте или покраске.

Инструкция

Самый простой метод – прибегнуть к взвешиванию. Сначала взвесьте емкость вместе с , потом перелейте жидкость в другую емкость, подходящую по размерам, и взвесьте пустую тару. А затем остается лишь вычесть из большего значения меньшее, и вы получите

Масса как физическая величина — это параметр, характеризующий силу воздействия тела на гравитацию. Для расчета массы тела в физике требуется знать две его величины: плотность материала тела и его объем.

Инструкция

Пусть задано некое тело объемом V и плотностью его вещества p. Тогда его массу подсчитывают так:
m = p*V. Для наглядности приводится пример:
Пусть дан алюминиевый брусок объемом 5 куб. метров. Плотность алюминия составляет 2700 кг./куб. метр. В таком случае масса бруска составит:
m = 2700/5 = 540 кг.

Обратите внимание

Понятие массы часто путают с другой, не менее редко встречающейся, физической величиной — весом. Вес измеряется в н/м и характеризует силу, которая воздействует на точку опоры. Масса же, по своей природе, не имеет какой бы то ни было точки опоры, и воздействует, как было отмечено, лишь на гравитацию Земли.

Внимание, только СЕГОДНЯ!

Все интересное

Масса вещества m — это величина, равная произведению молярной массы вещества M и количества вещества n. Формула расчета усложняется, если и эти показатели придется рассчитывать через другие известные. Вам понадобитсяТаблица плотностей,…

Объем численно характеризует некоторую область пространства с заданными границами. В нескольких разделах математики его вычисляют по форме границ и размерам либо по площади сечения и координатам. Когда же говорят о физической формуле расчета объема,…

Вес и объем можно связать другой физической величиной, которая используется при расчете обоих вышеуказанных параметров, — массой. Но в одно действия этого не сделать, поэтому следует рассмотреть формулы расчета и объема и веса данного тела. …

Сила тяжести — это сила, которая действует на любое тело, находящееся вблизи поверхности Земли. Сила тяжести всегда направлена вертикально относительно горизонтальной поверхности. Определить силу тяжести достаточно легко. Инструкция …

Масса вещества — это та мера, с помощью которой воздействует тело на свою опору. Она измеряется в килограммах (кг), граммах (г), тоннах (т). Найти массу вещества, если известен его объем, очень легко. Вам понадобитсяЗнать объем данного вещества,…

Масса какого-либо тела является его важнейшей физической характеристикой.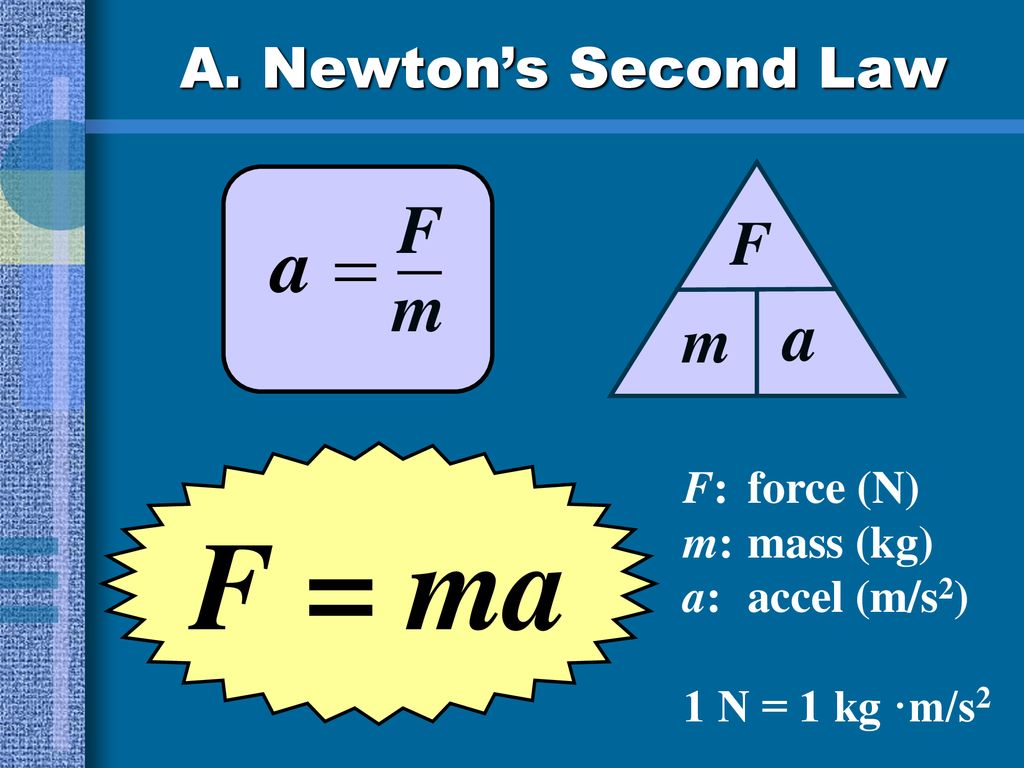 В современной физической науке есть разграничение понятия «масса»: гравитационная масса (как степень воздействия тела на земную гравитацию) и инертная масса (какое…

Наш мир трехгранен, это значит, что у всех тел в природе есть три характеристики: длина, ширина и высота. В совокупности эти величины объединяются в физической величине, называемой объемом тел. Науке известны несколько способов вычисления объема. …

Удельный вес — это показатель силы воздействия тела на точку ее опоры. Исходя из системы СИ, эта физическая величина измеряется в н/м Для нахождения удельного веса необходимо обладать лишь 4 данными. Вам понадобитсяP — вес тела;V — его объем;p…

Удельный вес какого-либо вещества — это характеристика данного вещества, показывающая величину его силы тяжести к заданной единице объема. В системе СИ он измеряется в н/м. В зависимости от исходных данных, удельный вес можно высчитать по-разному. …

Предметы, изготовленные из разных веществ, имеют разные массы. Физическую величину, показывающую, чему равна масса вещества в единице объема, называют плотностью вещества. Единицей плотности в Интернациональной системе единиц является килограмм,…

Массу тела обычно определяют экспериментально. Для этого берут груз, ставят его на весы и получают результат измерения. Но при решении физических задач, приведенных в учебниках, измерение массы по объективным причинам невозможно, зато имеются те или…

Любой предмет обладает массой и объемом. И это — аксиома. Но, помимо двух этих параметров, существует еще и третий — это плотность вещества, из которого состоит то или иное тело (жидкость). Зная плотность данного тела, достаточно легко перевести…

В окружающей нас природе масса взаимосвязана с объемом (мы имеем ввиду точные науки). Совершенно любое тело имеет и массу и объем. Масса представляет тяжесть тела, то есть его величину, а объем тела – это его реальные размеры. И благодаря этим двум параметрам мы можем вычислить или массу или объем. Так как найти объем через массу? Читайте об этом ниже.

Первая формула

Стоит отметить, что приведенные ниже правила пригодны как для физики, так и для химии.

Самая элементарная возможность нахождения нужного объема – это использовать плотность. То есть мы делим нашу массу на имеющийся объем. Вот формула: ρ = m/V. Из нее вытекает, что нужный объем составляет: V = m/ρ.

Запомните, что масса различных веществ в формуле может быть равной, даже если вещества не одинаковы, но объем всегда буде разным, также как и их плотности.

Вторая формула

Наука химия, имеет пример (модель) идеального газа: на одну моль с объемом (этот молярный объем всегда постоянен). Формула выглядит так: V = 22,4 моль на литр. Представленный газ всегда имеет этот объем при давлении и температуре (они постоянны). Если рассматривать этот вопрос со стороны науки физики, то он (объем) может меняться. Вот подходящие формулы: V м — молярный объем равен Vв — объем порции газа деленное на n в — количество вещества. (Vм = Vв/nв). А само количества вещества вычисляется благодаря формуле деления массы нужного вещества на молярную массу (nв = mв/Mв). Из этого следует что: Vв = Vм*mв/Mв.

Третья формула

Когда же в приведенной вам задаче предоставлена концепция самого вещества, то требуемый объем, вы можете легко выразить согласно формуле: c = n/V = m/M/V. В этой формуле М – это масса вещества (молярная).

Мы надеемся, что помогли вам, дорогие читатели, понять, как найти объем, зная массу предоставленного вещества. Желаем вам успехов в химии и физике.

Многие из нас в школьное время задавались вопросом: «Как найти массу тела»? Сейчас мы попытаемся ответить на этот вопрос.

Нахождение массы через его объем

Допустим, в вашем распоряжении есть бочка на двести литров. Вы намерены целиком заполнить ее дизельным топливом, используемом вами для отопления своей небольшой котельной. Как найти массу этой бочки, наполненной соляркой? Давайте попробуем решить эту простейшую на первый взгляд задачу вместе с вами.

Решить задачу, вещества через его объем, довольно легко. Для этого следует применить формулу удельной плотности вещества

где p является удельной плотностью вещества;

m — его массой;

v — занимаемым объемом.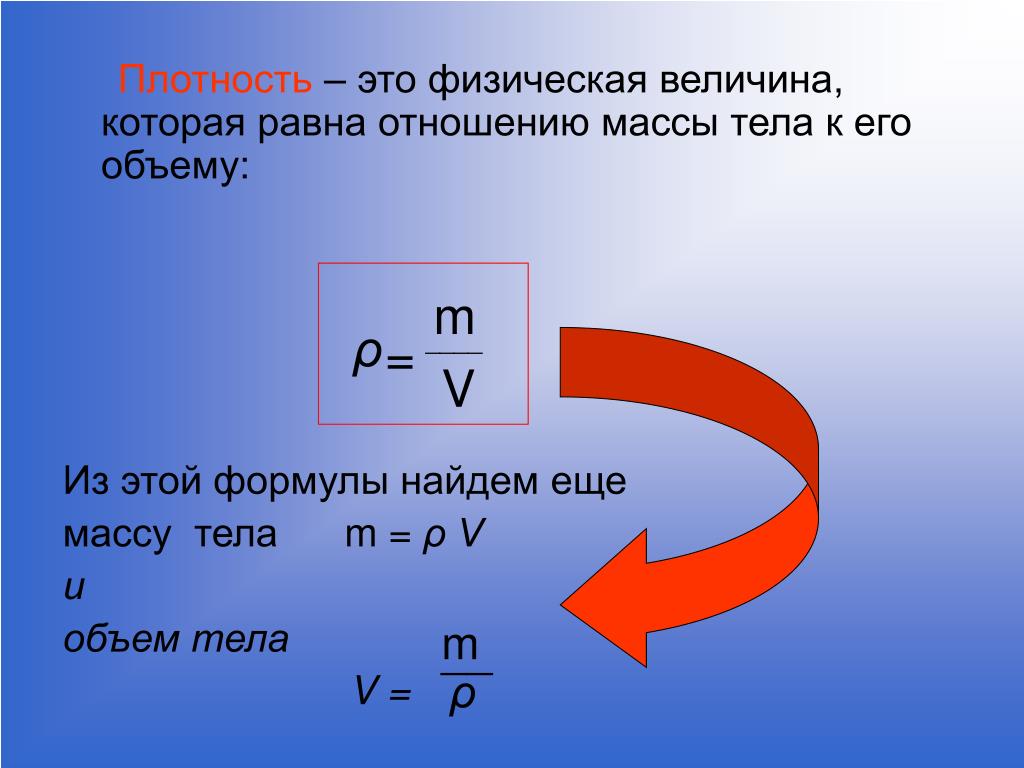

В качестве будут использоваться граммы, килограммы и тонны. Меры объёмов: сантиметры кубические, дециметры и метры. Удельная плотность будет вычисляться в кг/дм³, кг/м³, г/см³, т/м³.

Таким образом, в соответствии с условиями задачи в нашем распоряжении есть бочка объемом двести литров. Это значит, что ее объем равняется 2 м³.

Но вы хотите узнать, как найти массу. Из вышеназванной формулы она выводится так:

Сначала нам требуется найти значение р — удельной Найти данное значение можно, используя справочник.

В книге мы находим, что р = 860,0 кг/м³.

Затем полученные значения мы подставляем в формулу:

m = 860*2 = 1720,0 (кг)

Таким образом, ответ на вопрос, как найти массу, был найден. Одна тонна и семьсот двадцать килограммов — это вес двухсот литров летнего дизтоплива. Затем вы можете точно так же сделать приблизительный расчет общего веса бочки и мощности стеллажа под бочку с соляром.

Нахождение массы через плотность и объем

Очень часто в практических заданиях по физике можно встретить такие величины, как масса, плотность и объем. Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.

Предметы, которые вам будут нужны:

1) Рулетка.

2) Калькулятор (компьютер).

3) Емкость для измерения.

4) Линейка.

Известно, что у предметов с равным объемом, но изготовленных из различных материалов, будет разная масса (например, металл и дерево). Массы тел, которые изготовлены из определенного материала (без пустот), прямо пропорциональны объему рассматриваемых предметов. В противном случае, константа — это отношение массы к объему предметы. Этот показатель называется «плотностью вещества». Мы будем его обозначать буквой d.

Теперь требуется решить задачу, как найти массу в соответствии с формулой d = m/V, где

m является массой предмета (в килограммах),

V является его объемом (в метрах кубических).

Таким образом, плотность вещества является массой единицы его объема.

Если вам необходимо найти из которого создан предмет, то следует воспользоваться таблицей плотностей, которую можно найти в стандартном учебнике по физике.

Объем предмета вычисляется по формуле V = h * S, где

V — объем (м³),

H — высота предмета (м),

S — площадь основания предмета (м²).

В том случае, если вы не можете четко измерить геометрические параметры тела, то вам следует прибегнуть к помощи законов Архимеда. Для этого вам понадобится сосуд, у которого есть шкала, служащая для измерений объема жидкостей и опустить предмет в воду, то есть в сосуд, на котором есть деления. Тот объем, на который будет увеличено содержимое сосуда, является объемом тела, которое погружено в него.

Зная объем V и плотность d предмета, вы можете легко найти его массу по формуле m = d * V. Перед тем, как вычислить массу, требуется привести все измерительные единицы в единую систему, например, в систему СИ, являющуюся интернациональной измерительной системой.

В соответствии с вышеназванными формулами можно сделать следующий вывод: для нахождения требуемой величины массы с известным объемом и известной плотностью требуется умножить значение плотности материала, из которого изготовлено тело, на объем тела.

Уравнения и формулы физики — макеты

Физика заполнена уравнениями и формулами, которые имеют дело с угловым движением, двигателями Карно, жидкостями, силами, моментами инерции, линейным движением, простым гармоническим движением, термодинамикой, работой и энергией.

Вот список некоторых важных физических формул и уравнений, которые следует держать под рукой, упорядоченных по темам, чтобы вам не приходилось искать их.

Угловое движение

Уравнения углового движения применимы везде, где есть вращательные движения вокруг оси. Когда объект повернулся на угол θ с угловой скоростью ω и угловым ускорением α , то вы можете использовать эти уравнения, чтобы связать эти значения вместе.

Для измерения угла необходимо использовать радианы. Кроме того, если вы знаете, что расстояние от оси равно r, , то вы можете вычислить пройденное линейное расстояние, с , скорость, v , центростремительное ускорение, a _c и силу , Ф _с . Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.

Двигатели Карно

Тепловая машина берет тепло Q _h от высокотемпературного источника при температуре T _h и перемещает его к низкотемпературному стоку (температура T _{9 по курсу Q _c и при этом выполняет механическую работу, W . (Этот процесс можно обратить вспять, так что можно выполнить работу по перемещению тепла в противоположном направлении — тепловой насос.) Количество работы, выполняемой пропорционально количеству тепла, извлеченного из источника тепла, является КПД двигателя. Двигатель Карно является обратимым и имеет максимально возможный КПД, определяемый следующими уравнениями. Эквивалентом эффективности теплового насоса является коэффициент полезного действия.}

Жидкости

Объем А, В , жидкости с массой, м , имеет плотность, ρ . Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт _вода _{вытесненные} , создают направленную вверх выталкивающую силу, F _{плавучесть} . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.

Сил

Масса А, м , ускоряется со скоростью, a , из-за силы, F , действующей. Силы трения, F _F , пропорциональны нормальной силе между материалами, F _Н , с коэффициентом трения мк. Две массы, м ₁ и м ₂ , разделенные расстоянием, r , притягивают друг друга в пропорции гравитационная постоянная Г :

Моменты инерции

Вращательный эквивалент массы — это инерция, I , , которая зависит от того, как масса объекта распределена в пространстве. Здесь показаны моменты инерции для различных форм:

Диск, вращающийся вокруг своего центра:
Полый цилиндр, вращающийся вокруг своего центра: I = mr ²
Полая сфера, вращающаяся с осью, проходящей через ее центр:
Обруч, вращающийся вокруг своего центра: I = mr ²
Точечная масса, вращающаяся на радиусе r: I = mr ²
Прямоугольник, вращающийся вокруг оси вдоль одного края, где другой край имеет длину r :
Прямоугольник, вращающийся вокруг оси, параллельной одному краю и проходящей через центр, где длина другого края равна г :
Стержень, вращающийся вокруг оси, перпендикулярной ему и проходящей через его центр:
Стержень, вращающийся вокруг оси, перпендикулярной ей и через один конец:
Сплошной цилиндр, вращающийся вокруг оси вдоль ее центральной линии:
Кинетическая энергия вращающегося тела с моментом инерции I и угловой скоростью ω :
Угловой момент вращающегося тела с моментом инерции, I , а угловая скорость ω :

Линейное движение

Когда объект в положении x движется со скоростью v , и ускорением a, в результате перемещения s , каждый из этих компонентов связан следующими уравнениями:

Простое гармоническое движение

Определенные виды силы приводят к периодическому движению, когда объект повторяет свое движение с периодом, T , с угловой частотой ω, и амплитудой A . Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.

Термодинамика

Беспорядочные колебательные и вращательные движения молекул, составляющих объект вещества, обладают энергией; эта энергия называется тепловая энергия. Когда тепловая энергия перемещается из одного места в другое, она называется теплотой, Q . Когда объект получает некоторое количество тепла, его температура T , повышается.

Кельвина ( K ), Цельсия ( C ) и Фаренгейта (F ) — это температурные шкалы. Вы можете использовать эти формулы для преобразования одной температурной шкалы в другую:

Теплота, необходимая для изменения температуры массы, m , увеличивается с константой пропорциональности, c , называется удельной теплоемкостью.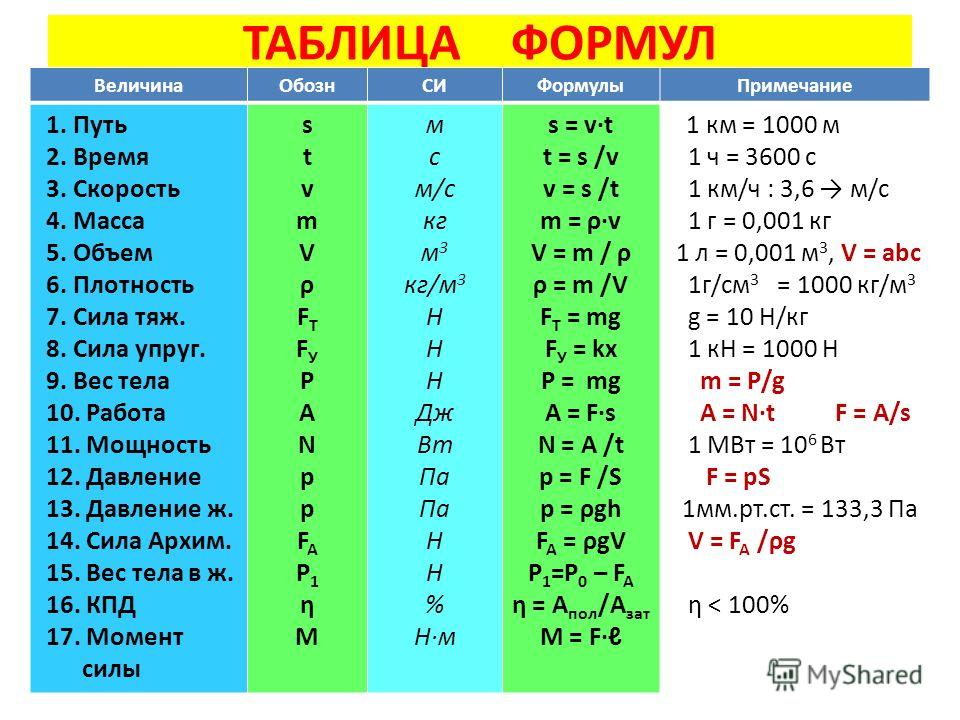 В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:

Давление, P , и объем, V , из n молей идеального газа при температуре T определяется по этой формуле, где R — газовая постоянная:

В идеальном газе средняя энергия каждой молекулы KE _avg пропорциональна температуре с постоянной Больцмана k :

Работа и энергия

Когда сила, F , перемещает объект на расстояние с , которое находится под углом Θ ,затем работа, W , выполнена. Импульс p является произведением массы m , и скорости v . Энергия, которой объект обладает благодаря своему движению, называется KE .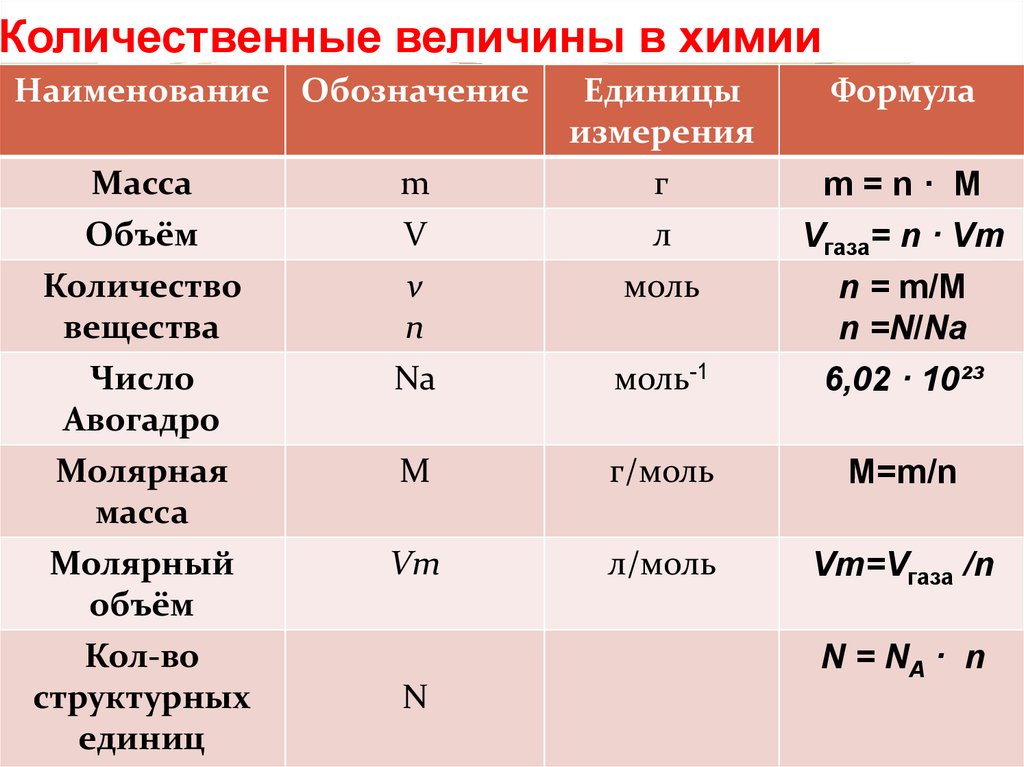

Какая формула массы?

Масса — это свойство физических объектов и мера устойчивости тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.

В отличие от относительных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством, которым объект обладает независимо от его отношения к другим вещам. Массу объекта можно рассчитать несколькими способами:

масса=плотность×объем (m=ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
масса=сила÷ускорение (m=F/a) . Согласно второму закону Ньютона (F=ma), ускорение тела прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающего приложение постоянной силы, обратно пропорциональна массе.
масса=вес÷ускорение свободного падения (м=Вт/г). Вес есть произведение ускорения массы в гравитационном поле. В зависимости от силы гравитационного ускорения вес будет разным.

Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в терминах других единиц, как джоуль (Дж) Ньютона (Н). Существуют и другие способы расчета массы объекта, но эти три формулы являются наиболее распространенными.

m=ρV

m=Вт/г

m=F/a

Единицы массы0413 (кг). Килограмм является единственной базовой единицей СИ с приставкой в названии (кило-). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре ее плавления. С 1889 года килограмм был переопределен как масса

Международного прототипа килограмма (IPK), физического артефакта, предназначенного для универсальной эталонной массы килограмма.

Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятым ИПК является цилиндр высотой 39 мм, изготовленный из специального платинового сплава.

«Слова тоже имеют подлинную субстанцию — массу, вес и удельный вес». — Тим О’Брайен

По состоянию на 2018 год килограмм является единственной единицей СИ, в которой физический объект является исходным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка. В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за новое определение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года..

Способы вычисления массы

Из плотности и объема

Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше его масса на единицу объема.

Например, вода имеет плотность 977 кг/м ³ при стандартной температуре и давлении. То есть один кубический метр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть 0,7 м ³ пробы воды. Какова масса этого образца?

Решение для массы дает нам:

m=ρV

m=(0,7 м ³ )(977 кг/м ³ ) = 683 кг

0. иметь массу 683 кг.

Некоторые объекты невероятно плотные. Нейтронная звезда, например, имеет среднюю плотность 1,1 х 10 ¹⁸ кг/м ³ . Одна чайная ложка нейтронной звезды на Земле весила бы около 100 миллионов тонн.

«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может только сокрушать своим весом». — Ханс фон Сект

From Force And Acceleration

Свойство массы понимается также как мера сопротивления физического объекта ускорению под действием внешней силы. Это понятие массы иногда называют инерционная масса . Инерция — это тенденция движущегося тела продолжать находиться в постоянном состоянии движения, поэтому инерционная масса — это мера того, насколько сильно инерционно тело и насколько трудно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом Ньютона F=ma. Это математическое соотношение говорит нам о том, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее. Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.

Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м/с ² . Какова масса металлического куба? Мы можем рассчитать массу, разделив величину силы на величину ускорения так:

м=F/a

м=(748 Н)/(21 м/с ² ) ≈ 35,62 кг

Итак, мы знаем, что металлический куб должен иметь массу 35,62 кг.

От веса

Строго говоря, вес и масса — разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, однако в физических науках они имеют разные значения. Масса — это неизменное свойство, которое не меняется от места к месту. Вес является мерой силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, т. Е. Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.

Соотношение между массой и весом выражается формулой W = mg, где g — мера ускорения свободного падения. Точное значение g зависит от местоположения. На Земле g имеет значение примерно 9,81 м/с ², а на Луне g составляет около 1,6 м/с ² . Выражение W=mg дает вес в ньютонах, в то время как повседневное понимание веса дается в фунтах (lbs) коэффициент преобразования из ньютонов в фунты составляет около 1 N=0,22 фунта.

Например, на поверхности Земли где г=90,81 м/с ² , 50-килограммовый объект будет иметь вес в фунтах:

W=(50kg)(9,81м/с ² )=490,5N

Преобразование ньютонов в фунты дает нам:

490,5 Н(0,22 фунта/1 Н)≈ 108 фунтов

И наоборот, на Луне, где g имеет значение 1,6 м/с ² , объект массой 50 кг будет весить:

W=50(кг) (1,6 м/с ² )(0,22 фунта/1 Н) ≈ 18 фунтов

Тот же 50-килограммовый объект весит 108 фунтов на Земле и 18 фунтов на Луне.

Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как: 2 )≈ 83,4 кг

Итак, 180-фунтовое тело на Земле имеет массу около 84,3 кг.

Массово-энергетическая эквивалентность

Очень долгое время ученые считали, что массу объекта можно считать полностью независимой от других его свойств. Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E=mc ² , где c — скорость света в вакууме.

E=mc ² говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c ² . Поскольку c = 3 000 000 м/с, c ² является чрезвычайно большим фактором. Следовательно, даже крошечная частица массы содержит подавляющее количество внутренней энергии. Для сравнения, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам тротила — мощности атомной бомбы, сброшенной на Хиросиму.

«Любой дурак может знать. Суть в том, чтобы понять». — Альберт Эйнштейн

В некоторых физических процессах, таких как деление ядер или движение тела в интенсивном гравитационном поле, материя преобразуется в энергию и высвобождается в виде большого количества света и тепла. В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, высвобождаемой во время таких реакций.

Скажем, 30 кг урана (Ur) помещают в ядерный реактор. При делении примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?

0,1% от 30 кг это 0,3 кг. Подключение этого к уравнению Эйнштейна дает нам:

E = (0,3 кг) (3 000 000) ² = (0,3) (8,98755179 × 10 ¹⁶) = 2,69626554 × 10 ¹⁶ J 000. 101013930139000

0004000400040004000. 100193 16 Дж. кг (0,6 фунта) вещества в энерговыделение 2,69626554 × 10 ¹⁶ Дж энергии. Это количество примерно равно взрыву более 6 миллионов тонн тротила (12 миллиардов фунтов), что достаточно, чтобы полностью сровнять с землей даже самые крупные города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, какая-то реакция деления высвобождает 1,6178 × 10 ¹⁶ джоулей энергии. Какое количество массы перешло в энергию при этом процессе? Using our handy-dandy mass-energy equivalence formula we can determine:
1.6178 × 10 ¹⁶ J =m(8.98755179 × 10 ¹⁶ )
(1.6178 × 10 ¹⁶ )/8.98755179 × 10 ¹⁶ )=m
m ≈ 0,18 кг
Итак, около 0,18 кг массы было преобразовано в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы с их уравнениями, описывающими поведение элементарных частиц. В частности, их уравнения предсказывали, что некоторые частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может генерироваться взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют часть энергии. Поле Хиггса преобразует эту энергию в энергию массы, которая проявляется как свойство массы, которое мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса создаст новую частицу, крошечный бозон, названный бозоном Хиггса. Ускоритель частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглер были удостоены Нобелевской премии по физике за свою теоретическую работу над частицей.
Что такое масса? — Определение, единицы, формула и примеры

Массу лучше всего понимать как количество материи, присутствующей в любом объекте или теле. Все, что мы видим вокруг себя, имеет массу. Например, стол, стул, ваша кровать, футбольный мяч, стакан и даже воздух имеют массу. При этом все объекты легкие или тяжелые из-за своей массы. На этом уроке мы узнаем, что такое масса, как ее вычислить, и ее примеры, открывая при этом интересные факты о ней.
1. Что такое масса?
2. Что такое единица массы?
3. Разница между массой и весом
4. Часто задаваемые вопросы по Mass
Что такое масса?
В физике масса — это основное свойство материи и одна из фундаментальных величин. Масса определяется как количество вещества, присутствующего в теле. Единицей массы в системе СИ является килограмм (кг). Формулу массы можно записать так:
Масса = Плотность × Объем
Примечание : Масса тела постоянна; он не меняется в любое время. Только в определенных крайних случаях, когда от тела отдается или отнимается огромное количество энергии, масса может воздействовать. Например, при ядерной реакции крошечное количество вещества превращается в огромное количество энергии, это уменьшает массу вещества.
Что такое единица массы?
Существуют различные единицы измерения массы, такие как килограммы, граммы, фунты, фунты и т. д., но единицей массы в системе СИ является «килограмм» или кг. Каждая единица массы может быть преобразована в другие единицы с помощью соответствующей формулы преобразования, не затрагивающей смысла и сути измеряемой величины.
Примечание. 1 кг равен 2,20462 фунта.
Разница между массой и весом
Люди часто путают массу и вес, и в конечном итоге используют эти два термина как синонимы. Однако масса и вес — это два разных термина, и важно понимать разницу между ними. Разница между массой и весом показана в приведенной ниже таблице.
Масса Вес
Определение Масса определяется как количество вещества в веществе Вес определяется как количество силы, действующей на массу объекта из-за ускорения под действием силы тяжести.
Обозначение Масса представлена буквой «М».
Масса представлена буквой «W».
Формула •Масса тела всегда постоянна.
• Один из способов расчета массы: масса = объем × плотность. •Вес является мерой гравитационной силы, действующей на массу.
• Формула веса: Вес = масса × ускорение свободного падения
Единица измерения Единицей массы в системе СИ является «килограмм». Единицей веса в системе СИ является ньютон (Н).
Количество Тип •Масса является базовой величиной.
• Масса имеет только величину и, следовательно, является скалярной величиной 90 636. •Вес является производной величиной.
• Вес имеет как величину, так и направление (к центру тяжести) и, следовательно, является векторной величиной.
Измерительный прибор Массу можно легко измерить с помощью любых обычных весов.
Например, балочный баланс, рычажный баланс, панорамный баланс и т. д. Вес можно измерить с помощью пружинных весов или по приведенной выше формуле.
Знаете ли вы, что у нас разный вес на Земле, на Луне и в космосе? Однако наша масса везде одинакова.
Теперь давайте посмотрим на некоторые важные факты, связанные с массой:
Масса имеет только величину, следовательно, это скалярная величина.
Вес имеет как величину, так и направление; это векторная величина.
Массу также можно определить как «энергию, запасенную в частицах».
Масса представляет собой общее количество атомов или частиц, которые оно содержит.

Пример 1: Сэм на Земле весит 1000 фунтов. На какой-нибудь другой планете вес Сэма составил бы 38 % от земного. Сколько бы Сэм весил на этой планете?
Решение: Мы знаем, что вес Сэма на Земле составляет 1000 фунтов, а его вес на другой планете будет составлять 38 % от земного. Следовательно, вес Сэма на другой планете = 38 % × его вес на Земле = 0,38 × 1000 фунтов = 380 фунтов
Пример 2: Масса объекта составляет 6000 фунтов. Вычислите его массу в тоннах.
Решение: Мы знаем, что 1 тонна = 2000 фунтов. Таким образом, 6000 фунтов = 6000/2000=3 тонны.
Пример 3: У Дамиана есть книга массой 2,2 кг. Каков вес книги на Земле?
Решение:
Масса учебника = 2,2 кг, ускорение свободного падения = 92\)
Вес учебника = 21,56 Н
Следовательно, вес учебника на Земле равен 21,56 Н.

перейти к слайду
перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы по Mass
Имеет ли воздух массу?
Да, воздух имеет массу. Например, надутый воздушный шар весит тяжелее, чем сдутый воздушный шар, что доказывает, что воздух внутри надутого воздушного шара имеет массу.
Масса и объем одинаковы?
Масса — это количество материи, из которой состоит объект. Объем — это количество свободного места, которое занимает объект. Следовательно, масса и объем не совпадают.
Плотность и масса — одно и то же?
Масса измеряет количество вещества, присутствующего в веществе. Плотность показывает количество вещества в данном пространстве для вещества. Плотность и масса могут быть такими же, как единица объема.
Вес и масса — одно и то же?
Нет, вес и масса не одно и то же. Вес – это сила, действующая на тело, а масса – это количество вещества в теле. Вес может изменяться в зависимости от силы, в то время как масса постоянна.
Что такое единица массы в СИ?
Единицей массы в системе СИ являются килограммы (кг).
Что такое формула массы?
Формула, используемая для расчета массы объекта: Плотность × Объем.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Массовый рабочий лист
Импульс
Спортивный диктор говорит: «Переходя к матчу всех звезд, команда «Чикаго Уайт Сокс» имеет импульс ». Заголовки гласят: «Чикаго Буллз набирает обороты 90 876 – 90 877». Тренер накачивает своей команде в перерыве, говоря: «У вас есть импульс ; критическая необходимость заключается в том, чтобы вы использовали этот импульс и похоронили их в этой третьей четверти». некоторое усилие, чтобы остановиться Команда, которая имеет большой импульс, действительно движется и будет трудно остановить . Импульс — это физический термин, он относится к количеству движения, которое имеет объект. спортивная команда это на ходу имеет импульс. Если объект находится в движении ( в движении ), то он имеет импульс.
Импульс можно определить как «массу в движении». Все объекты имеют массу; поэтому, если объект движется, то у него есть импульс — его масса движется. Величина импульса, которую имеет объект, зависит от двух переменных: насколько движется объект и как быстро движется объект . Импульс зависит от переменных массы и скорости. С точки зрения уравнения, импульс объекта равен массе объекта, умноженной на скорость объекта.
Импульс = масса • скорость
В физике количество импульса обозначается строчными буквами p . Таким образом, приведенное выше уравнение можно переписать как
p = m • v
, где m — масса, а v — скорость. Уравнение показывает, что импульс прямо пропорционален массе объекта и прямо пропорционален скорости объекта.
Единицами импульса будут единицы массы, умноженные на единицы скорости. Стандартной метрической единицей импульса является кг•м/с. В то время как кг•м/с является стандартной метрической единицей импульса, существует множество других единиц, которые являются приемлемыми (хотя и не общепринятыми) единицами импульса. Примеры включают кг•ми/ч, кг•км/ч и г•см/с. В каждом из этих примеров единица массы умножается на единицу скорости, чтобы получить единицу импульса. Это согласуется с уравнением для импульса.
Импульс как векторная величина
Импульс является векторной величиной . Как обсуждалось в предыдущем разделе, векторная величина — это величина, которая полностью описывается как величиной, так и направлением. Чтобы полностью описать импульс 5-килограммового шара для боулинга, движущегося на запад со скоростью 2 м/с, вы должны включить информацию как о величине, так и о направлении шара для боулинга. , а не достаточно, чтобы сказать, что мяч имеет импульс 10 кг•м/с; импульс мяча равен не полностью описан, пока не будет дана информация о его направлении. Направление вектора импульса совпадает с направлением скорости мяча. В предыдущем разделе было сказано, что направление вектора скорости совпадает с направлением движения объекта. Если шар для боулинга движется на запад, то его импульс можно полностью описать, сказав, что он равен 10 кг•м/с в западном направлении. Как векторная величина, импульс объекта полностью описывается как величиной и направление .

Уравнение импульса как руководство к размышлению
Из определения импульса становится очевидным, что объект имеет большой импульс, если велики его масса и скорость. Обе переменные одинаково важны для определения импульса объекта. Представьте, что грузовик Mack и роликовые коньки движутся по улице с одинаковой скоростью. Значительно большая масса грузовика Mack придает ему значительно больший импульс. Тем не менее, если бы грузовик Mack находился в состоянии покоя, то инерция наименее массивного роликового конька была бы наибольшей. Импульс любого покоящегося объекта равен 0. Покоящиеся объекты делают , а не имеют импульс — у них нет никакой «движущейся массы». Обе переменные — масса и скорость — важны при сравнении количества движения двух объектов.
Уравнение импульса может помочь нам подумать о том, как изменение одной из двух переменных может повлиять на импульс объекта. Рассмотрим физическую тележку массой 0,5 кг, нагруженную одним кирпичом массой 0,5 кг и движущуюся со скоростью 2,0 м/с. Полная масса загруженной тележки составляет 1,0 кг, а ее импульс равен 2,0 кг•м/с. Если вместо этого тележка была загружена тремя 0,5-килограммовыми кирпичами, то общая масса загруженная тележка будет весить 2,0 кг, а ее импульс будет равен 4,0 кг·м/с. Удвоение массы приводит к удвоению импульса.
Аналогично, если бы тележка весом 2,0 кг имела скорость 8,0 м/с (вместо 2,0 м/с), то тележка имела бы импульс 16,0 кг•м/с (вместо 4,0 кг•м/с). ). четырехкратное увеличение скорости на дает четырехкратное увеличение импульса на . Эти два примера иллюстрируют, как уравнение p = m•v служит «руководством к мышлению» и , а не просто .0877 a « подключи и пей рецепт решения алгебраических задач.»

Проверьте свое понимание
Выразите свое понимание концепции и математики импульса, ответив на следующие вопросы. Нажмите кнопку, чтобы просмотреть ответы.
1. Определить импульс а…
а. Полузащитник массой 60 кг движется на восток со скоростью 9 м/с.
б. Автомобиль массой 1000 кг движется на север со скоростью 20 м/с.
в. Первокурсник массой 40 кг движется на юг со скоростью 2 м/с.

2. Автомобиль обладает импульсом 20 000 единиц. Каким был бы новый импульс автомобиля, если бы…
а. его скорость удвоилась.
б. его скорость утроилась.
в. его масса была удвоена (за счет добавления большего количества пассажиров и большей нагрузки)
д. и его скорость удвоилась, и его масса удвоилась.

3. По футбольному полю бегут полузащитник (m = 60 кг), тайт-энд (m = 90 кг) и линейный игрок (m = 120 кг). Рассмотрим их модели бегущей строки ниже.
Сравните скорости этих трех игроков. Во сколько раз скорость полузащитника и тайт-энда больше скорости лайнмена?

У какого игрока самый большой импульс? Объяснять.

Следующий раздел:
Перейти к следующему уроку:
1.4 Анализ размеров | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
Находить размерности математического выражения, включающего физические величины.
Определите, является ли уравнение, включающее физические величины, размерно-согласованным.
Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. (Рисунок) перечислены основные величины и символы, используемые для их измерения. {g} [/latex] для некоторых степеней [латекс] a,b,c,d,e,f, [/латекс] и 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
Базовые количества и их размеры
Базовое количество Символ размера
Длина л
Масса М
Время Т
Текущий я
Термодинамическая температура Θ
Количество вещества Н
Сила света Дж
Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Точно так же, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Важность концепции размерности проистекает из того факта, что любое математическое уравнение, связывающее физические величины, должно быть размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:
Каждый член выражения должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными. Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь запомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2} [/латекс] и [латекс] 2\pi r. [/latex] Одно выражение — это длина окружности круга радиусом r , а другое — его площадь. Но что есть что?
Стратегия
Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
[латекс] [2\pi r]=[2]·[\pi ]·[r]=1·1·\text {L}=\text{L,} [/latex]
, так как константы [latex] 2 [/latex] и [latex] \pi [/latex] безразмерны, а радиус [latex] r [/latex ] — это длина. Мы видим, что [латекс] 2\pi r [/латекс] имеет размерность длины, что означает, что он никак не может быть площадью.
Мы исключаем [латекс] 2\pi r [/латекс], потому что его размерность не соответствует площади. Мы видим, что [латекс] \pi {r}^{2} [/латекс] согласуется по размерам с областью, поэтому, если нам нужно выбирать между этими двумя выражениями, [латекс] \пи {г}^{2} [/latex] — это то, что нужно выбрать. {2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
Стратегия
В соответствии с определением размерной согласованности нам необходимо проверить, что каждый член данного уравнения имеет те же размерности, что и другие члены этого уравнения, и что аргументы любых стандартных математических функций безразмерны.
Решение
В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})]=1.\hfill \end{массив} [/latex]
Два термина имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».
Значение
Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Проверьте свое понимание
Соответствует ли размерность уравнения v = at ?
Показать решение
Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :
[латекс] [ \frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]
Точно так же, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла v по отношению к t — это просто размерность v , умноженная на размерность t :
[латекс] [\int vdt]=[v]·[t]. [/latex]
По тем же соображениям аналогичные правила справедливы для единиц физических величин, полученных из других величин путем интегрирования или дифференцирования.
Резюме
Размерность физической величины — это просто выражение основных величин, из которых она получена.
Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2}; [/latex] (c) [latex] v=s\text{/}t; [/latex] (d) [latex] a=v\text{/}t. [/latex]
Показать решение
Рассмотрим физические величины [латекс] m, [/латекс] [латекс] s, [/латекс] [латекс] v, [/латекс] [латекс] а, [/латекс] и [латекс] t [/латекс ] с размерами [ м ] = M, [ s ] = L, [ v ] = LT ^–1 , [ a ] = LT ^–2 , и [ t 90 ] T. Предполагая, что каждое из следующих уравнений размерностно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv ² ; в) р = mv ; (г) Вт = мсд ; (e) L = mvr .
Предположим, что количество [латекс] s [/латекс] — это длина, а количество [латекс] t [/латекс] — это время. Предположим, что величины [латекс] v [/латекс] и [латекс] а [/латекс] определены как v = ds / dt и a = dv / dt . а) Какова размерность числа 9?{–3}, [/latex] и [t] = T. (a) Какова размерность [latex] \int \rho dV? [/latex] (b) Каков размер dV / dt ? в) Каков размер [латекс] \rho (dV\text{/}dt)? [/latex]
Формула длины дуги говорит, что длина [латекс] s [/латекс] дуги, опирающейся на угол [латекс] Ɵ [/латекс] в окружности радиусом [латекс] r [/латекс], определяется выражением уравнение [латекс] s=rƟ. [/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством размерности 1 или чистым числом
Калькулятор силы | Как найти силу?
, созданный Джулией Жулавиньской
, рассмотренным Стивеном Вудлингом
Последнее обновление: 26 апреля 2022 г.
СОДЕРЖА сила?
Что такое чистая сила?
Часто задаваемые вопросы
Калькулятор силы поможет вам рассчитать силу по второму закону Ньютона. Читать до узнать, что такое сила , а какие виды сил есть в классической механике . Мы также объясним , как найти силу в упражнениях, используя формулу силы . В конце мы также проиллюстрируем , что такое чистая сила , на простом примере.
Если вам нужно найти конкретную силу, возможно, вам поможет один из этих калькуляторов:
Калькулятор второго закона Ньютона
Калькулятор гравитационной силы
Калькулятор нормальной силы
Вычислитель центробежной силы
Вычислитель трения
Калькулятор натяжения
Калькулятор плавучести
Вычислитель давления
Калькулятор силы Лоренца
Калькулятор электромагнитной силы на проводе
Калькулятор магнитной силы между проводами
Калькулятор поверхностного натяжения
Определение силы и уравнение силы
Что такое сила?
Сила — это любое взаимодействие, которое, если ему не противодействовать, может изменить движение объекта .
Если спросить: «Что такое сила?» нефизик, вероятно, подумал бы о том, чтобы толкать и тянуть. Физик подумал бы об изменении скорости объекта. Чтобы понять почему, давайте посмотрим на уравнение силы:
a = m / F ,
где:
a ускорение объекта, выраженное в метрах в секунду в квадрате [м/с ² ] ;
m – масса объекта в килограммах [кг]; и
F — сила, измеряемая в ньютонах [Н].
Ускорение — это изменение скорости во времени . И, как видно из формулы силы, чем больше сила, тем больше ускорение. Так, если что-то ускоряется, например, автомобиль, то оно может передать значительную силу при столкновении с другим автомобилем. Эта сила пропорциональна массе автомобиля и его (остановочному) ускорению. Другим примером может служить сила удара человека, когда масса и ускорение тела прямо пропорциональны силе удара.
Чтобы использовать калькулятор силы, введите две из этих переменных: массу, ускорение или силу в любых единицах и получите недостающее число в мгновение ока.
Если вы рассчитываете силу самостоятельно, всегда используйте систему СИ, чтобы избежать ошибок. Что такое единица силы в системе СИ? Это Newton [N] , названный в честь Исаака Ньютона — математика, физика и первооткрывателя гравитации. В основных единицах СИ один ньютон равен:
1 Н = 1 кг * м/с ²
Чтобы узнать больше о единицах силы, воспользуйтесь нашим конвертером силы.
Законы движения Ньютона
Ньютон вывел три закона движения, которые объясняют движение всех физических объектов. Они являются основой всей классической механики , которая также известна как ньютоновской механики .
Первый закон Ньютона
Объект останется в покое или продолжит равномерное движение, если на него не воздействует внешняя сила.
Второй закон Ньютона
Сила, действующая на объект, равна массе, умноженной на ускорение этого объекта: F = m * a .
Третий закон Ньютона
Когда одно тело действует с силой на второе тело, второе тело действует на первое тело с силой, равной по величине и противоположной по направлению (на всякое действие всегда есть равное, но противоположное противодействие).
Типы сил
Все силы в классической механике подчиняются трем законам движения Ньютона.
Гравитационная сила — это притяжение между любыми двумя объектами с ненулевой массой . Вы ходите по земле, а не плывете благодаря этой силе — гравитации. На него влияет все, что вас окружает, например, экран, на котором вы это читаете. Он такой маленький; это незаметно.
Нормальная сила это реакция на силу гравитации — прекрасный пример третьего закона Ньютона. Когда вы стоите, вы воздействуете на пол силой (равной силе гравитации). Пол воздействует на вас с такой же силой.
Трение — это сила, противодействующая движению . Она пропорциональна нормальной силе, действующей между объектом и землей. Зимой вы наносите песок на обледенелые поверхности, чтобы увеличить трение и предотвратить скольжение.
Натяжение представляет собой осевую силу, которая проходит через веревки, цепи, пружины и другие объекты при внешнем натяжении . Например, если вы выгуливаете свою собаку, и она тянет вас вперед, это создает напряжение на ее поводке.
Центробежная сила — это сила, действующая на вращающийся объект . Вы когда-нибудь были на карусели? Вы помните чувство выталкивания наружу? Центробежная сила вызвала это чувство.
Давление является мерой силы, приложенной к поверхности . Если вы надуваете воздушный шар, частицы воздуха внутри оказывают давление на воздушный шар. Все частицы испытывают одинаковую силу, поэтому шарик надувается равномерно.
Как найти силу?
Давайте рассмотрим несколько упражнений, чтобы вас ничем не удивить на уроке физики.
1. Найти ускоряющую и тормозящую (останавливающую) силу:
Гепард имеет массу 50 кг. Он разгоняется из состояния покоя до 50 км/ч за 3 секунды. Затем он начинает плавно замедляться и останавливается через 8 секунд.
Ускоряющая сила:
Сначала найдите ускорение:
50 км/ч равно 13,89м/с (мы рассчитали это с помощью преобразователя скорости).
Ускорение равно разности скоростей во времени:
а = (13,89 м/с - 0) / 3 с = 4,63 м/с ²
Рассчитать ускоряющую силу:
F _a = m * a = 50 кг * 4,63 м/с ² = 231,5 Н
Сила торможения:
а = (0 - 13,89 м/с) / 8 с = -1,74 м/с ²
Ф _r = 50 кг * -1,74 м/с ² = -87 Н
Тормозящая сила отрицательна, поскольку направлена противоположно ускоряющей силе.
2. Какая сила необходима для ускорения тела (m = 2 кг) на 8 м/с ² ? А если объект в три раза тяжелее? Как это влияет на силу?
Если масса в три раза тяжелее, то и сила должна быть в три раза больше.
Что такое чистая сила?
Сила является вектором . Это значит, что оно имеет значение и направление. Вот почему вы не можете добавить его как обычные числа (скаляры).
Чистая сила (F _N ) представляет собой сумму векторов всех отдельных сил, действующих на объект . Например, давайте посмотрим на падающий мяч. На него влияет сила тяжести (F _G = 5 Н), сопротивление воздуха (F _R = 1 Н) и боковая сила, вызванная ветром (F _W = 2 Н).
Сначала найдите результирующую силу горизонтальных сил. Они имеют противоположное направление, поэтому частично компенсируют друг друга:
F _H = F _G - F _R = 5N - 1 N = 4N
Теперь найдите суммарную силу двух оставшихся сил.
Здесь можно посчитать по теореме Пифагора (в прямоугольном треугольнике: a ² + b ² = с ² ). Чтобы узнать больше о сложении векторов, перейдите к калькулятору сложения векторов.
F _H ² + F _W ² = F _N ² 4 ² + 2 ² = F _N ² 16 + 4 = Ж _Н ² F _N ² =20 Ф _Н = √20 Ж _Н = 2√5
Суммарная сила, действующая на шар, равна 2√5 Н.
Теперь, когда вы знаете три закона движения Ньютона и определение силы, взгляните на один из калькуляторов, перечисленных в начале. Там мы подробно объясняем все виды сил. Недавно мы также провели забавный эксперимент, в ходе которого проверяли, что выиграет гонку — туалетная бумага или бутылка? Посмотрите его, чтобы узнать кое-что о моменте инерции массы и ускорении!
FAQ
Как найти ускорение с учетом силы и массы?
Разделить силу на массу .
Не забудьте использовать базовые единицы СИ. Значит, ньютонов силы и килограммов массы.
Наслаждайтесь своим ускорением в метров в секунду в квадрате .
Является ли вес силой?
Вес — это другое название гравитационной силы . В физике масса и вес не одно и то же. Масса – это свойство объекта. Он сопротивляется любым изменениям в движении. Вес – это сила, действующая на массу из-за гравитации . На Земле, если ваша масса составляет 70 килограммов, ваш вес составляет около 700 ньютонов (точно 686,5 ньютонов).
Является ли сила вектором?
Сила является вектором . Это означает, что он определяется как величиной , так и направлением . Скаляры, как масса или длина, определяются только величиной. Итак, если вы приложите к объекту две силы, вы не сможете сложить их, как скаляры. Вам нужно принять во внимание направление и найти чистая сила — векторная сумма сил.
Какова формула силы?
Формула силы определяется вторым законом движения Ньютона :
Сила, действующая на объект, равна массе, умноженной на ускорение этого объекта: F = m ⨉ a.
Чтобы использовать эту формулу, вам нужно использовать единицы СИ: ньютонов для силы, килограммов для массы и метров в секунду в квадрате для ускорения.
Что происходит, когда две силы действуют в одном направлении?
Когда две силы действуют в одном направлении, они складываются в и создают результирующую силу, равную их сумме.
Как связаны сила и движение?
Сила — это любое взаимодействие, которое, если ему не противодействовать, может изменить движение объекта. Без внешней силы движущийся объект будет продолжать двигаться с постоянной скоростью и направлением, а объект, находящийся в состоянии покоя, останется в покое. Если приложить внешнюю неуравновешенную силу, объект изменит движение, изменив свою скорость и/или направление.
Связь между силой и движением определяется законами движения Ньютона .
Какие бывают силы?
Виды сил в физике:
Контактные силы — Нормальная сила, приложенная сила, сила трения, сила натяжения, сила сопротивления воздуха; и
Бесконтактные силы — Гравитационная сила, электрическая сила, магнитная сила.
Является ли ускорение силой?
Ускорение не является силой . Ускорение – это изменение скорости во времени. Как и сила, ускорение является вектором, поэтому оно имеет как величину, так и направление. Согласно второму закону движения Ньютона ускорение пропорционально силе: F = m ⨉ a. Направление ускорения объекта определяется направлением чистой силы, действующей на этот объект.
Может ли результирующая сила быть отрицательной?
Суммарная сила может быть как положительной, так и отрицательной . Чистая сила представляет собой сумму векторов всех отдельных сил, действующих на объект. Силы всегда положительны по модулю, но, чтобы облегчить вычисление результирующей силы, мы предполагаем, что силы, направленные в противоположные стороны, имеют разные знаки. Обычно говорят, что силы, направленные вправо, положительны, а влево – отрицательны. Итак, если у вас есть две силы, противоположные по направлению, действующие на объект, и результирующая сила направлена влево, вы можете сказать, что результирующая сила отрицательна.
В чем разница между уравновешенными и неуравновешенными силами?
Уравновешенные силы имеют одинаковую величину, но противоположное направление . Они уравновешивают друг друга, поэтому уравновешивают друг друга . Классическим примером уравновешенных сил может быть гравитационная сила и нормальная сила, действующие на объект, расположенный на горизонтальной поверхности. Уравновешенные силы не вызывают изменения направления или скорости объекта.
Неуравновешенные силы не имеют одинаковой величины . Если на объект действует неуравновешенная сила, она воздействует на движение объекта . Например, если что-то падает, это происходит из-за силы гравитации. Сила сопротивления воздуха противодействует гравитации, но не уравновешивает ее, если объект слишком тяжелый.
Вызывают ли уравновешенные силы изменение движения?
Уравновешенные силы не вызывают изменения движения . Две силы уравновешены, когда они имеют одинаковую величину и противоположное направление, поэтому они уравновешивают друг друга. Вместе они не влияют на скорость или направление движения объекта.
No related posts.