Задания по математике для 1 класса — интересные задачи по математике для 1 класса
Четыре причины полюбить математику с 1 класса
Развитие логического мышления
Математика учит анализировать данные, устанавливать взаимосвязи и находить оптимальное решение. Эти навыки помогут справиться не с одной жизненной задачей.
Достижение успеха в любой профессии
Умение оперировать цифрами нужно не только экономистам. Математика необходима даже в таких творческих профессиях, как архитектор и фотограф.
Повышение авторитета в своем окружении
В школе разбирающийся в математике ребенок будет пользоваться уважением сверстников, а вне учебы не позволит обмануть себя, например, на кассе в магазине.
Развитие коммуникативных навыков
Неочевидно, но факт: те, у кого все хорошо с математикой, более стройно, логично и последовательно излагают свои мысли. А значит, с ними приятнее общаться.
Какой должна быть математике для учеников 1 класса?
Подана небанально и в игровой форме
В Умназии все задания представлены в интерактивном формате с красочными иллюстрациями и приятной озвучкой. Дети проходят сюжетную игру, по ходу которой им приходится решать математические и логические задачи.
Не перегружает ребенка
Каждый урок посвящен отдельной теме и длится около 30-40 минут.
Ребенок может заниматься в любое время и делить уроки так, как ему удобно. Начать можно даже с 5-10 минут в день!
Развивает логику и креативность
Ребенок научится решать математические и логические задачи не быстрее, а рациональнее. Умение находить верные и порой нестандартные решения не раз пригодится и за пределами школы.
Какие задачи по математике для 1 класса предлагает Умназия?
Задачи на классификацию
Поиск закономерностей
Математические задачи на логику
Задачи на истину и ложь
Волшебные квадраты
Математические ребусы
Задачи на переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи на скорость
Задачи, решаемые методом перебора
Геометрические задачи
Начать заниматься
Примеры заданий по математике для 1 класса
Задача 1
Коллекция фантиков у Маши очень разрослась, и Маша решила собрать их все в отдельный альбом, разделив по группам: шоколадные, ириски, карамельки, самые редкие и так далее.
Какое минимальное количество линий для этого могла провести Маша?
Решить задачу
Задача 2
Финн, Джейк, принцесса Пупырка, Снежный Король и Марселина соревновались в метании мармеладок. Известно, что Финн метнул свою мармеладку ближе, чем Джейк. Пупырка метнула мармеладку дальше всех, а Марселина показала самый плохой результат. Снежный Король забросил мармеладку дальше Джейка.
Можешь ли ты сказать, кто из соревнующихся оказался на третьем месте?
Решить задачу
Задача 3
Главу семьи зовут Антон Петрович. Его сыновей зовут Дмитрий и Антон, а внуков — Мирон и Антон.
Какое наименьшее число Антонов Антоновичей может быть в этой семье?
Решить задачу
Решать задачи по математике для 1 класса
Познакомьтесь с форматом курса «Математическое мышление».
Пройдите сюжетную игру и решите три математические задачи!
Решать задачи
В Умназии дети развивают логическое мышление, решая увлекательные сюжетные задачи по математике
Продуманная программа
Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением
Увлекательные задания
Ребенок решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу.
Никакой скуки! Ни одно задание не повторяется!
Дипломы и награды
В конце каждого курса ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!
Решение задач по математике в 1 классе
Первоклассников еще рано грузить сложными примерами и скучной теорией, а вот развивать у них математическое мышление — самое время. Хороший инструмент для этого — несложные, но требующие смекалки и творческого подхода математические задачи.
Идеально, если материал всего урока подается в форме игры или сюжетной истории. Подолгу сидеть за занятиями не стоит — хватит и 10 минут в день.
Купите курс математики для детей со скидкой 40 % уже сейчас
Задачи математики для 1 класс
Описание
Помогает вам практиковаться и улучшать свои математические навыки.
Более 570 математических проблем для 1-го класса с разной сложностью.
Все категории задач бесплатны. Если вы оцениваете нашу работу или хотите прекратить рекламу, вы можете сделать это, нажав кнопку «Остановить рекламу». Таким образом, мы сможем добавить новые задачи.
Приложение содержит:
+ Сложение и вычитание до 10
+ Сложение и вычитание до 20
+ Сравнение чисел
+ Что верное?
+ Сложение десяток
+ Пропущенные числа в ряду
+ Текстовые задачи до 10
+ Текстовые задачи до 20
+ Сложение трех чисел
Задачи делятся на категории сложности.
Языки:
Болгарский, русский, английский, испанский, немецкий, французский, итальянский, польский, турецкий, китайский (традиционный), китайский (упрощенный), хинди, португальский, украинский, индонезийский, японский, вьетнамский, иврит, греческий, голландский, чешский, корейский, Норвежский, арабский, венгерский, румынский, шведский, тайский, малайский, датский.
По вопросам и комментариям: [email protected].
Используются следующие ресурсы:
Designed by Terdpongvector / Freepik
https://www.freepik.com/terdpongvector/
Designed by brgfx / Freepik
https://www.freepik.com/brgfx
Версия 3.4
Новые задачи
Исправление ошибок
Оценки и отзывы
Оценок: 633
Реклама
Купили игру за 229₽ а реклама так и не отключилась!!!!!!! Очень хорошее приложение, НО РЕКЛАМА ПРОСТО ВЫВОДИТ ИЗ СЕБя!! Поэтому купили приложение, НО ИЗМЕНЕНИЙ НЕТ!!!!!
Писала вам ранее это сообщение.
После вашего ответа, все равно такая же ситуация.… невозможно заниматься.!!!! Покупка не восстанавливается, и не обновляется…. деньги потратили, а толку нет…. Обидно(((
… невозможно заниматься.!!!! Покупка не восстанавливается, и не обновляется…. деньги потратили, а толку нет…. Обидно(((
Здравствуйте. Приносим извинения за доставленные неудобства. Пожалуйста, напишите нам по адресу [email protected], чтобы бесплатно отправить вам ваучеры.
Круто
Круто
The best game
My kids love this so much. I think it will play the main role in their future. Thanks for these kind of apps. I am a programmer and I know it’s not easy for you guys. Thanks a lot. If there were 10 starts I would choose ten.
Hello, thank you for the kind words really mean a lot to us.
Калин М.
We wish you luck.Разработчик Kalin M указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Геопозиция
- Идентификаторы
- Данные об использовании
- Диагностика
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов.
Подробнее
Информация
- Провайдер
- Kalin M
- Размер
- 52,6 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © Ina Mihaleva
- Цена
- Бесплатно
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Математика в 1 классе — что должен уметь ребенок?
Общемировое развитие не стоит на месте, поэтому требования к человеку и его возможностям постоянно возрастают.
В том числе и к такой категории населения как школьники. Им необходимо трудится практически без отдыха, чтобы выдерживать конкуренцию своих ровесников.
Уровень знаний первоклассников также стал довольно высоким. У школ нет жестких требований к будущим ученикам, но все же вчерашние детсадовцы должны быть подготовлены к основным предметам. Ребенку будет легче учиться в первом классе, если он будет знать буквы и звуки, сможет читать по слогам, правильно держать ручку, а еще лучше уметь писать буквы и хорошо знать алфавит. Что касается математики в первом классе, то также есть некоторые требования: нужно знать простые геометрические фигуры, считать до 10, а лучше до 20, понимать, что такое прямой и обратный порядковый счет, ориентироваться на листе бумаги.
Важна как образовательная, так и моральная готовность детей. Родители волнуются за будущего первоклашку, ведь, даже зная все, что нужно, он может растеряться и занервничать. А школьные собеседования именно для того и проводятся, чтобы преподаватели могли понять, насколько способный и подготовленный ребенок.
Как помочь выучить ребенку школьную программу по математике в первом классе?
Многие родители с первого класса стремятся приучить детей учиться хорошо – получать одни пятерки. Но при этом забывают сделать акцент на том, что самое главное – это получать знания. Даже у первоклассников часто возникает проблема, что оценки хорошие, а знаний очень мало. Ведь несложно просто зазубрить материал, чтобы хорошо ответить у доски на следующий день. Сложно – понять и разобраться в теме, чтобы закрепить ее навсегда.
Поэтому родители должны донести до детей, что самое главное – понять математику, научиться применять ее в жизни, осознанно выполнять упражнения, не решать примеры на занятиях механически, а только с полным пониманием и без спешки. Для осознанного обучения также помогает развитие логики и нестандартного критического мышления. Благодаря им ученику будет легче понять математику и применять ее законы в жизни.
Задания по математике в 1 классе
Обучение первоклассников в основном строится на том, что дети изучали на уроках подготовки к школе.
Повторяется уже пройденное, а усложнение материала происходит очень постепенно.
Задания по математике в 1 классе – это изучение прямой, точки, ломанной, простых геометрических фигур, счет как письменный, так и в уме. Учитывая, что основа алгебры – это таблица умножения, то в первом классе происходит подготовка к ее изучению: нарабатываются фундаментальные знания, которые во втором классе позволяют освоить таблицу умножения.
Кроме этого, конечно, ученики учатся находить фигуры в окружающем мире, расширяют свой кругозор, стараются применять в жизни счет, который уже освоили. Также они решают ребусы, головоломки, легкие занимательные задачи, самые простые примеры. Несмотря на то, что это школа, учителя стараются преподать материал интересно, а задания подобрать увлекательные и в игровой форме.
Математические ребусы и задачи на сообразительность
Кроме изучения цифр, правил и обучения счету, важно давать малышу решать различные ребусы и головоломки. Именно нестандартные задачи помогают ребенку развивать свой мозг, научиться находить решение, не боятся трудностей, применять математические хитрости.
Простые примеры помогут только отработать навык арифметических вычислений, а развиваться дальше можно только лишь используя нестандартное мышление.
Современная методика «Амаматика» от Академии развития интеллекта AMAKids включает в себя онлайн-платформу и игровые тренажеры по математике, которые позволяют развивать сразу все способности детей в области математики.
Чтобы научить учеников легко решать задачи любой сложности, а также применять «царицу наук» в жизни, в наших учебниках и пособиях предложены интересные задания с пропущенными числами, неизбитые кроссворды и головоломки, математические ребусы за 1 класс и для детей постарше, увлекательные лабиринты, задачи на сообразительность. Умея применять нестандартные способы решения, ребенок не испытывает страх перед заданиями повышенной сложности. Он с интересом берется за любую задачку.
Тренажер по математике 1 класс
Платформа и тренажер Амаматика помогут не только преуспевать в школе, но и научат находить подход к сложным заданиям, обучат финансовой грамотности и основам программирования, помогут развить аналитическое мышление, пространственное воображение.
Математика – сложный предмет, но, если структурировано подходить к обучению и придерживаться проверенной методики, школьник сможет понять и закрепить даже самые непростые темы.
На нашей удобной онлайн-платформе ученики могут подтянуть любое математическое направление – нужно лишь зайти в требующийся раздел и начать выполнять упражнения. Тренажер по математике для первого класса обеспечит правильное понимание предмета и заложит необходимые азы для дальнейшего обучения.
Также на игровой платформе есть разделы с арифметикой, геометрией, задачами, а также заданиями по финансовой грамотности, программированию и играми на развитие логики, памяти и внимания. Амаматика – эффективные и удобные курсы для современных детей.
Логические задачи для 1 класса по математике, с ответами | Для детей 7
Задачи на логику с ответами для 1 класса ( детей 7-8 лет)
Логические задачи по математике
Ответы на задачи п.1
Логические задачи на предположение с ответами и решением
Логические задания для 1 класса
Игры на логику для 1 класса
Логические задачи для 1 класса в картинках (для детей от 6 лет)
Упражнения, игры и задачи, которые помогут школьникам развивать логическое мышление.
Согласитесь, умение мыслить логически всегда будет актуальным. Навыки логического мышления пригодятся детям в любой сфере жизни: на уроках, дома, при выборе будущей профессии. Ведь для успешной сдачи экзаменов просто необходимо не только владеть материалом, но и иметь развитые навыки логического, критического и креативного мышления!
Возможности развития логического мышления безграничны. Используя их, мы не только тренируем свой интеллект, но и совершенствуем навыки коммуникации и учимся помогать другим. Кроме того, от уровня развития нашей логики зависит и скорость реагирования на жизненные вызовы. А это прекрасно помогает сохранять время и силы.
Задачи на логику 1 класс с ответами
Логические задачи — нестандартные задания по математике длядетей 7 — 8 лет
1. Летели воробьи и уселись на столбце. Если бы сели по одному, то остался бы без места воробей, а если бы по два, то свободным был бы столбец. Сколько было воробьев? Сколько столбцов?
2. Одна белочка насобирала 9 сыроежек и 6 маслят и разделилась со второй — дала ей 8 грибов.
Какое наименьшее число сыроежек могла получить вторая белочка?
3. Сидело 6 Воробьев и 4 ласточки. 9 птичек полетело. Сколько воробьев осталось?
4. Когда дети выстроились в ряд, то Коля увидел, что он стоит пятым от правого края и третьим от левого. Сколько детей выстроилось?
5. На ветке сидело несколько птичек. После того, как 4 птички полетели, на ветке осталось на 2 птицы больше, чем полетело. Сколько птичек сидело на ветке?
6. Андрюша и Аленка удили рыбу. Увидев, что у Аленки мало рыбы, мальчик дал ей столько рыбин, сколько у нее было. Впоследствии Аленка поймала 7 Рыбин, отдала долг Андрюше и у нее стало 10 рыбин. Сколько Рыбин было у Аленки изначально?
7.Какое число можно написать вместо точек 1, 3; 2 …; 3, 5, если придерживаться установленной закономерности?
8. Один грузовой автомобиль за один раз может перевозить вмещает два станка. Сколько нужно таких автомобилей, чтобы перевезти 7 станков.
9. Найдите три числа, удовлетворяющие условию: каждое следующее число на 1 больше предыдущего, а одно из них равно сумме двух других.
10. Летели гуси, а навстречу им — гусь «Добрый день, десять гусей!»- молвил он. «Нет, нас не десять. Если бы ты был с нами да еще двое гусей, то тогда было бы 10», — ответили гуси. Сколько летело гусей?
11.В комнате были стулья на 3-х и 4-х ножках. Сколько было каких стульев, если всего ножек — 10?
12. Имеем два сосуда: в один вмещается 8, а во второй — 5 стаканов воды. Как, пользуясь ими, отмерить два стакана воды?
13. У Юрки сегодня день рождения. Он моложе своей сестры, которой исполнилось 7 лет. Сколько лет может быть Юре?
14. Аленка и Коля поставили на полочку 5 игрушек. Коля сказал, что он поставил столько же игрушек, сколько поставила Лена. Не ошибся ли он?
15. Светлана и Василий пришли утром в класс, а там уже было 4 ученицы. Сколько всего учениц стало в классе? Можете ли вы сказать, сколько всего стало детей?
16. В ящике вперемешку лежат 10 синих и 10 красных носков. Сколько надо вынуть носков, не глядя, чтобы получилась пара одного цвета?
17.
Аленка живет на четвертом этаже. Когда она возвращается на улицу, то с этажа на этаж поднимается за полминуты. Сколько времени тратит Леночка, чтобы подняться по лестнице в свое жилище?
18. На лесопильном заводе машина отрезает от бревна за 1 мин кусок дерева длиной 1 м. За сколько минут она разрежет на такие куски бревно длиной 10 м?
19.Бабушке надо зажарить 6 котлет, а на сковородке умещается только 4. Каждую котлету надо жарить 6 мин на одной стороне и 5 мин на второй. Сколько времени нужно для того, чтобы зажарить 6 котлет на этой сковородке?
20. Внук спросил у дедушки: «сколько тебе лет?» Дедушка ответил: «Если проживу еще половину того, что я прожил, да еще один год, то мне будет 100 лет». Сколько лет дедушке?
21. Есть два бидона вместимостью 2 л и 7 л. Как с их помощью набрать из реки 3 л воды?
22. Трое друзей: Андрюша, Назарчик и Дима удили рыбу. Больше всего рыб поймал Андрюша, а меньше всего — Дима. Количество Рыбин, которые поймал каждый, выражается одноцифровым числом.
Сколько рыб мог поймать каждый из мальчиков, если вместе они поймали 20?
23.Почтовый индекс сказочной страны Берендеево выражен четырехзначным числом, в котором цифры не повторяются. Сумма двух чисел, обозначаемых двумя средними цифрами, равна 15, а число, обозначенное крайней левой цифрой, втрое меньше числа, обозначенного правой крайней. Каким может быть индекс?
24. У Олеси было три куклы: Анечка, Марийка и Оля. Каждая из них жила в одном из трех домиков. Первый домик был с высокой крышей и маленьким окном. Вторая хатка — с высокой крышей и большим окном, третий — с низкой крышей и большим окном. Анечка и Маша жили в домиках с большим окном, а Маша и Оля — в домиках с высокой крышей. Нужно отгадать, в какой хатке живет каждая кукла.
25. Катруся, Софийка, Галинка и Наденька родились 2 марта, 17 мая, 2 июня, 20 марта. Софийка и Галинка родились в одном месяце, а у Галинки и Катруси день рождения одного числа. Кто когда родился?
Ответы на логические задачи:
1.
Воробьев-4, столбцов — 3.
2.Наименьшее число сыроежек вторая белочка получит, если первая отдаст ей все собранные маслята. Итак, это будет 2 сыроежки (8-6=2).
3. Не осталось ни одного воробья, если все улетели. А если полетят 4 ласточки и еще 5 воробьев, то останется 1 воробей.
4.5+2=7 или 3+4=7.
5.Осталось — 4+2=6, сидело — 6+4=10.
6.10-7=3 (рыбы).
7.Сумма чисел, одинаково удаленных от начала и конца, стала и равна 6.
1+5=6; 3+3=6, поэтому вместо квадратика надо записать 4 (2 + 4=6).
8.7=2+2+2+1; требуется 4 автомобиля.
9. Один, два, три, поскольку 3=2+1.
10.10=1+2+7 следовательно, летело 7 гусей.
11.10=3+3+4 значит, было 2 стула на 3-х ножках и 1 стул на 4-х ножках.
12.Надо наполнить сосуд, что вмещает 5 стаканов, и всю воду из нее вылить в сосуд, вмещающий 8 стаканов. Сюда можно долить еще 3 стакана (8-5=3), поэтому в сосуде на 5 стаканов останется 2 стакана воды (5-3=2).
13.6, 5, 4, 3, 2, 1.
14.Да, ошибся, потому что число 5 не может состоять из одинаковых чисел.
15. Стало 5 учениц и 6 детей.
16.3.
17.1 мин с (30+30+30).
18.9 мин.
19.За 17 мин.
20.Дедушке 66 лет.
21. налить в семилитровый бидон сначала 2 л воды, затем еще половину двухлитрового (2+1=3).
22.
Андрюша 9 8 9 9
Назарчик 8 7 7 6
Дима 3 5 4 5
23.1, 7, 8, 3; 3, 7, 8, 9; 2, 7, 8, 6; 1, 6, 9, 3.
24. Анечка живет в третьем домике, Машенька — во второй, а Оля — в первой.
25. Катя-2 июня, Софийка-20 марта, Галинка-2 марта, Наденька — 17 мая.
Логические задачи на предположение для использования на уроках математике в 1 класса (с ответами и решением)
Задача № 1
На новогоднем празднике танцевала одна из девочек 1-А класса: Татьяна, Елена или Наталья. Когда же их спросили девочки 1-Б кто из них танцевал, то Татьяна сказала, что танцевала она. Елена сказала, что она не танцевала. А Наталка, которая всегда
говорит правду сказала, что одна из девушек говорит правду, а другая неправду. Кто же из девочек танцевал на празднике?
Решение и ответ:
1) Предположим, что Татьянка сказала правду, то есть она танцевала, тогда Аленка сказала неправду, а значит и она танцевала, а это противоречит условию задачи где сказано, что только одна из девочек танцевала.
2) Предположим, что Елена сказала правду, то есть Елена не танцевала, тогда Татьяна сказала неправду, значит и она не танцевала. Из этого следует, что танцевала другая девочка — Наталья.
Задача № 2
Три одноклассника — Алексей, Василий и Сергей занимаются в разных школьных кружках: хореографическом, математическом и баскетбольном. На вопрос, кто какой кружок посещает, они ответили:
Алексей :»я посещаю хореографический».
Василий: «Я – не хореографический».
Сережа : «я – не математический».
Какой кружок посещает каждый из мальчиков, если известно, что только один из них сказал правду?
Решение и ответ:
1) предполагаем, что Алексей сказал правду, то есть он посещает хореографический кружок, тогда Василий и Сергей сказали неправду, а
значит Василий тоже посещает хореографический кружок, а это противоречит условию задачи, где сказано, что дети занимаются в разных кружках.
2) Предположим, что Василий говорит правду, то есть он не посещает хореографический кружок, тогда Алексей и Сергей говорят неправду, а значит Алексей не посещает хореографический тоже, а Сергей посещает математический.
То есть ни один из ребят не посещает хореографический, что
опять противоречит условию.
3) предположим, что Сергей сказал правду, тогда Алексей и Василий сказали неправду.
Поэтому следует, что Василий посещает хореографический кружок. Так как Сергей не посещает математический то он посещает баскетбольный кружок. Тогда кружок по математике посещает Алексей.
Задача № 3
Один из трех братьев испачкал скатерть.
— Кто испачкал скатерть? — спросила бабушка.
— Василь не ставил пятно, — сказал Лесик, — это сделал Петрик.
— Это Василь запятнал скатерть, а не Лесик, — сказал Петрик.
— Не сердись, бабушка. Я знаю, что Петрик не мог этого сделать, это я испачкал скатерть, – возразил Василько.
Выяснилось, что двое мальчиков дважды сказали правду, а один дважды соврал. Кто поставил пятно?
Ответ и решение:
Исходя из условия, мы имеем:
Лесик: Василько нет, это сделал Петрик
Петрик: Василько запятнал, а не Лесик
Василько: Петрик нет, это сделал я (Василько)
1) Предположим, что дважды солгал Лесик.
Тогда Василько запятнал скатерть, а не Петрик. В этом случае две другие ответы правильные и не противоречат тому, что это сделал Вася.
Ответ: Скатерть запятнал Василь.
Задача № 4
В соревновании по бегу участвовали три бегуна: Авдиенко, Василенко и Семенюк. Перед началом соревнования один зритель сказал, что Авдиенко придет первым, второй – что Семенюк не будет последним, а третий – что Василенко первым финиширует. После завершения соревнований выяснилось, что один из зрителей угадал, а двое других-ошиблись. Как завершились соревнования, если известно, что все три бегуна закончили бег с разным результатом?
Решение и ответ:
Все предположения выпишем отдельно.
1-й : Авдиенко первым,
2-й : Семенюк не последний,
3-й : Василенко не первым.
1) Предположим что угадал 1-й зритель, то есть, Авдиенко придет первым. Тогда другие предположения ошибочны. И отсюда следует, что Семенюк
придет последним, а Василенко, как и Авдиенко, тоже первым, что противоречит условию задачи, где сказано, что бег закончили с разным результатом.
2) Предположим что 2-й зритель угадал, то есть » Семенюк не будет последним». Тогда предположения первого и третьего зрителей ошибочны, а это
означает, что Авдиенко не первый финиширует, а Василенко первым. Исходя из предположения, что Семенюк не последним придет, то он вторым, а Авдиенко третьим.
Ответ: 1-й – Василенко; 2-й – Семенюк; 3-й – Авдиенко.
Логические задания для 1 класса
Задание №1: Какая из данных фигур (треугольник, квадрат, круг) «лишняя» (отличается от остальных)? Чем она отличается? (Ответ: третья фигура «лишняя».
Задание № 2. Чем отличаются изображенные ряды? А) 1 3 5 7 9 11 13… Б) 2 4 6 78 10
Задание №3. Как разрезать фигуру на 2 части, чтобы из них можно было сложить прямоугольник?
Задание №4. В сумке у мамы находятся яблоки, лимоны и апельсины, всего 10 штук. Сколько в сумке отдельно яблок, лимонов и апельсинов, если количество яблок на 7 больше, чем лимонов? (Ответ: 8 яблок, 1 лимон, 1 апельсин).
Задание №5.
На ветке сидело 5 синиц и 7 воробьев. 6 птичек улетело. Полетел ли хотя один воробей? (Ответ: да, улетел, потому что синиц всего 5, и если все они улетели, то тогда среди птиц, которые улетели был воробей).
Задание №6. Что больше — 5 единиц второго разряда или 8 единиц первого разряда?
Заданиена логику: «Соотнесенные выражения» (для детей 7-8 лет)
Фразеологизмы – это универсальное средство для тренировки мышления. Они развивают не только логику, но и критическое и креативное мышление, воображение и фантазию детей. Кроме того, устоявшиеся изречения помогают нам изъясняться лаконично, ярко и остроумно.
Приведите детям такое устойчивое выражение и попросите выбрать из нескольких предложенных фраз ту, которая бы лучше отражала содержание фразеологизма. Например:
Опять двадцать пять –
а) если хочешь что-то получить — надо платить;
б) Снова то же самое, все время одно и то же;
в) что-то стоит 25 .
Правильный ответ: Снова то же самое, все время одно и то же.
Варианты заданий:
Манна небесная –
а) неожиданные жизненные блага;
б) очень вкусная каша;
в) Иногда с неба может упасть что-то полезное.
Как собака на сене –
а) чувствовать себя очень комфортно;
б) достигать небывалого успеха;
в) ни себе, ни другим.
Для усложнения задания можно дать детям больше вариантов ответов на каждое задание.
Задания на логику «Объединяем в группы» (для детей 7-8 лет)
Заранее подготовьте перечень понятий или терминов, касающихся различных аспектов или даже тематических блоков вашего предмета. Их количество и сложность определяются индивидуально (в зависимости от возраста детей и уровня их подготовки). Задача для детей: объединить в группы слова, которые имеют общие признаки или характеристики. Дети также должны сказать, по какому критерию они относят то или иное слово к определенной понятийной группе.
Проведение этого упражнения можно успешно сочетать с проработкой учебного материала по любому предмету.
Например, на уроке истории:
Слова: ярлык, вече, курган, меч, крепостное право, копье, князь, изгой, летопись, цех, казак, булава, мушкет, поместье.
Из этих слов, скажем, можно составить группу «оружие»: меч, копье, булава, мушкет. Также дети могут предложить собственные критерии для группировки. Так, меч, копье и булава являются холодным оружием, а мушкет – огнестрельным.
Игровые задания на логику для 1 класса
Игра «Один, два, не собьюсь»
Выходят участники. Поочередно считают, начиная с 1, а вместо числа, кратного 3, говорят «не собьюсь». Победителем будет тот, кто назовет большее натуральное число. Например: один, два не собьюсь, четыре, пять, не собьюсь, семь, восемь, не собьюсь. .).
Игра «Выиграй приз».
Нужно с завязанными глазами срезать приз. Если участник, срезавший приз, даст правильный ответ на математический вопрос, привязанный к этому призу, он забирает этот приз.
Игра «Веселая рыбалка»
На полу класса обводят контуры озера, в которое помещают рыбок.
К рыбке скрепкой прикрепляются задания. Участник берет удочку. (На конце лески — Магнит). И ловит рыбку. Дав правильный ответ на вопрос — забирает рыбку.
Игра «Кто быстрее посчитает до 25»
На доске две одинаковые таблицы с числами от 1 до 25. Кто из учеников первым закончит счет, тот победил.
Игра «Не собьюсь».
Капитаны по очереди делают по 10 шагов и на каждом шагу называют:
- примеры на сложение;
- примеры на вычитание.
Игра «Футбол».
На доске нарисованы футбольные ворота, мячи с примерами. Роль вратаря выполняет определенная цифра. Судья — ученик, который очень хорошо считает. Дети вычисляют примеры на мячиках. Если выбрали такой пример, что ответ совпадает с цифрой — вратарем, гол считается забитым.
Игра «Кто чем пообедает?»
Зайчик с разными цифрами: перед ним рисунки капусты, моркови, свеклы, яблок с написанными примерами. Найти ответы к примерам.
Игра «Прибавляем-отнимаем»
Предложите детям интересное и необычное занятие, которое сочетает элементы математики и филологии, а также тренирует логическое мышление.
Вместо привычных для детей чисел здесь используются слова. И именно с ними дети должны осуществить математические действия. Например:
Сложение
Задание: Бу + оттенок = цветок, который еще не распустился.
Ответ: Бу + тон = бутон.
Вычитание
Задание: Вид транспорта – о = единица измерения.
Ответ: Метро-о = метр.
Примеры логических задач
к + полосатое насекомое = прическа девушки (коса)
у + имя египетского бога Солнца = победный возглас (ура)
м + суп из рыбы = насекомое (муха)
за + дом за городом = требует решения (задача)
ав + томат = оружие (автомат)
ко + ее играет актер = король
емкость – а = там хранят деньги (банк)
помидор-ат = отдельная книга (том)
Математические домики
Математические задачи прекрасно развивают логическое мышление. Например, можно использовать игру «математические домики», которая является интересным и полезным занятием. Обратите внимание, что ее сложность может варьироваться в зависимости от уровня знаний детей и от опыта ее использования.
Первый уровень:
Поставь в свободное окошко домика нужный знак математического действия, чтобы число на крыше было ответом.
Второй уровень:
Запиши в свободные окошки нужный знак математического действия и такое число, чтобы результатом было число на крыше. Такие задачи дают возможность подобрать несколько вариантов решения. Дополнительно можно дать задание подобрать максимальное количество вариантов, которые бы соответствовали числам одного домика.
Дети могут тренировать логическое мышление не только на уроках, но и дома, играя с друзьями или путешествуя. Главное-объяснить ученикам, что это интересно и совсем не сложно! Кроме того, такие занятия можно связать с изучением учебного материала. Обязательно попробуйте создать собственные игры и упражнения.
Логические задачи для 1 класса в картинках (для детей от 6 лет)
Логические задачи для 1 класса
Из книги выпало несколько листов. На первой выпавшей странице стоит номер 5, а на последней номер 10.
Сколько листов выпало из книги?
———————————
В группе 15 детей. 10 детей любят мороженое, 9 человек — конфеты. Как это может быть?
———————————
В лесу елок больше, чем берез, а берез больше, чем осин. Чего больше: елок или осин? Почему?
———————————
В комнате стояли табуретки и стулья. У каждой табуретки 3 ножки, а у стула — 4.
Всего табуреток и стульев было 5, а ножек у них было 18.
Сколько было табуреток и стульев?
———————————
В книжке 12 страниц. Сколько цифр понадобилось, чтобы пронумеровать все страницы?
Сколько из них единичек? А если в книге 20 страниц?
———————————
Полный бидон с молоком весит 10 килограммов, а наполненный до половины — 6 килограммов.
Сколько весит пустой бидон?
———————————
У трёх девочек вместе было 20 карандашей. У Ани и Оли вместе было 15 карандашей. У Оли и Кати вместе было 12 карандашей.
Сколько карандашей у каждой девочки?
———————————
Нарисуй три прямых и отметь на каждой из них по две точки так, чтобы отмеченных точек было 5.
———————————
У Маши и у Лены кукол поровну, а у Пети машинок в два раза больше, чем кукол у Лены.
Чего больше: машинок у Пети или кукол у Лены и Маши вместе?
———————————
Коля, Вася и Боря играли в шашки. Каждый из них сыграл две партии. Сколько всего партий было сыграно?
———————————
В квартирах 1, 2, и 3 живут белый, черный и рыжий котята. В квартире 1 — не черный.
Белый — не в квартире 1 и не в квартире 2. Кто где живет?
———————————
У мальчика сестер и братьев поровну. Кого в семье больше: сыновей или дочерей? На сколько?
———————————
По дороге один за другим идут 5 детей. За каждым мальчиком, кроме последнего, идёт девочка.
Сколько девочек идут по дороге?
———————————
Каждый из троих взрослых ведёт за руку двоих детей.
Сколько детей идут со всеми взрослыми?
———————————
Я придумала два числа. Когда я их сложила, то получила 6. Когда же из одного вычла другое, то снова получила 6.
Что же это за числа?
———————————
В коробке 8 пирожных. Сколько пирожных надо взять из коробки, чтобы в ней осталось 5 пирожных?
———————————
Катя задумала число, прибавила к нему 5 и получила 15. Какое число задумала Катя?
———————————
На яблоне было 10 яблок, Садовник разрешил детям сорвать с яблони по 1 яблоку. На яблоне осталось 6 яблок.
Сколько было детей?
———————————
Поезд состоит из 10 вагонов. Петя сел в пятый вагон от начала поезда, а Федя – в пятый вагон от конца.
В одном ли вагоне они едут?
———————————
Плитка шоколада состоит из 6 квадратных долек.
Сколько разломов нужно сделать, чтобы разломить эту плитку на отдельные дольки?
———————————
Пётр сын Сергея, а Сергей – сын Фёдора.
Кем приходится Пётр Фёдору?
———————————
В саду яблонь на 3 больше, чем груш. Яблонь 7. Сколько груш?
———————————
У Зины на 4 открытки меньше, чем у Гали. У Зины 6 открыток. Сколько открыток у Гали?
———————————
Меня зовут Иваном Сергеевичем, а моего деда (отца моего отца) – Петром Николаевичем. Запишите имя и отчество моего отца.
———————————
Красный шнур на 1м длиннее зелёного и на 2м длиннее синего. Длина зелёного шнура 5м. Найди длину зелёного шнура.
———————————
На вешалке висят головные уборы; шляп на 1 больше, чем беретов. Шляп 8. Сколько шапок и сколько беретов?
———————————
Уменьшаемое больше вычитаемого на 2. Чему равна разность?
———————————
Угадайте, сколько лет моему дедушке, если через 15 лет мы будем отмечать его семидесятилетие.
———————————
Разность двух чисел равна вычитаемому.
Придумайте такие числа и запишите пример.
———————————
Разность двух чисел равна 0. Придумайте и запишите пример.
———————————
Из куска проволоки согнули квадрат со стороной 6 см.
Потом проволоку разогнули и согнули из неё треугольник с равными сторонами.
Найти длину стороны треугольника.
———————————
В первый день турист прошел 2 км, а в каждый следующий – на 2 км больше, чем в предыдущий.
Сколько он прошел в седьмой день? Сколько он прошел за 8 дней?
ГДЗ по математике 1 класс учебник Моро, Волкова 2 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Степанова С. В.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
Решебник — страница 13Готовое домашнее задание
Номер 1.
1) У Мити 5 вагончиков.
У Кости на 2 вагончика меньше, чем у Мити. Сколько вагончиков у Кости?
2) У Мити 5 вагончиков, а у Кости ☐ вагончика. Сколько всего вагончиков у этих мальчиков? Дополни условие, используя ответ предыдущей задачи.
Ответ: Задача 1:
5 ‒ 2 = 3 (в.) ‒ у Кости.
Ответ: 3 вагончика.
Задача 2:
5 + 3 = 8 (в.) − всего у этих ребят. Ответ: 8 вагонов.
Номер 2.
У Лены было 7 книг со сказками. Она принесла 2 из них в классную библиотечку. Сколько книг со сказками осталось у Лены?
Ответ: Было – 7 к. Отнесла – 2 к. Осталось – ? к. 7 − 2 = 5 (к.) – осталось у Лены. Ответ: 5 книг.
Номер 3.
Сравни примеры в каждом столбике. По какому правилу они составлены? Запиши еще по одному примеру и вычисли.
Ответ:
Первый столбик: чем больше число которое отнимаем, тем значение примера меньше.
7 − 1 = 6
7 − 2 = 5
7 − 3 = 4
7 − 4 = 3
Второй столбик: чем больше число, которое прибавляем, тем больше сумма
5 + 1 = 6
5 + 2 = 7
5 + 3 = 8
5 + 4 = 9
Третий столбик: чем меньше число, которое прибавляем, тем сумма меньше.
6 + 4 = 10
6 + 3 = 9
6 + 2 = 8
6 + 1 = 7
Четвертый столбик: чем меньше число, которое вычитаем, тем значение примера больше.
9 − 4 = 5
9 − 3 = 6
9 − 2 = 7
9 − 1 = 8
Номер 4.
Сравни рисунки и объясни, что сделали ребята.
Ответ: Игрок стал вратарем. Вратарь – игроком.
Задание внизу страницы
Ответ:
3 + 4 = 7
9 > 10 ‒ 2, потому что 9 > 8
8 = 4 + 4
8 ‒ 3 > 4, потому что 5 > 5
6 < 5 + 3, потому что 6 < 8
7 = 10 ‒ 3
Задание на полях страницы
Нарисуй узор и раскрась.
Ответ:
Рейтинг
👇 Выберите другую страницу 👇
1 часть
| Учебник Моро | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
Ваше сообщение отправлено!
+
Ознакомьтесь с этими 50 задачами дня по математике для первоклассников
Начните свой ежедневный урок математики со словесной задачи дня по математике — это отличный способ подготовить почву для обучения.
Все мы знаем, что юным ученикам трудно понять текстовые задачи, даже если часть задачи, связанная с математическими операциями, является базовой.
Включайте эти математические задачи для первого класса один раз в день в начале вашего математического блока, чтобы развить уверенность, навыки критического мышления и обучающееся сообщество. Студенты привыкнут читать медленно, чтобы понять смысл, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли!
Рассматриваемые темы включают сложение, вычитание, умножение и сравнение. Все, что вам нужно сделать, это опубликовать одну из этих математических задач для первого класса на доске или экране проектора. Тогда пусть дети взять его оттуда!
Хотите весь этот набор текстовых задач в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь.
1.
У меня было 6 карандашей, и мой учитель дал мне еще 4. Сколько карандашей у меня сейчас?
2. Собака Джины получила 3 угощения в воскресенье и 0 угощений в понедельник. Сколько всего угощений получил щенок Джины?
3. Джоэл пошел в зоопарк со своей семьей. В первый же час он увидел медведя, 2 тигров и 3 львов. Сколько животных увидел Джоэл в свой первый час в зоопарке?
4. Джексон рассортировал свои машинки по цвету. У него 6 синих машин, 5 зеленых машин и 4 черных машины. Сколько всего машин у Джексона?
5. У Бена 2 зеленых и 4 желтых шарика. Сколько всего шариков у него?
6. В семье Кларков трое детей. Тине 3 года, Джошуа 4 года, а Саманте 7 лет. Если сложить все их возрасты, какова сумма детей Кларков?
7. Если вы пойдете купаться и с вами придут 6 ваших друзей, сколько всего друзей будет плавать?
8. У мамы Рэйчел были цветы в вазе. 3 цветка завяли, и мама Рэйчел вынула их из вазы.
Теперь в вазе 5 цветов. Сколько цветов было в вазе изначально?
9. У кошки Хейден родились котята. 3 котенка были серыми, 2 котенка пятнистыми и 7 котят черными. Сколько котят было у кошки Хейден?
10. Педро принес с игровой площадки 3 красных и 6 желтых листьев. Сколько всего листьев у него?
11. Габриэлла прочитала 3 книги в понедельник, 6 книг во вторник и 4 книги в среду. Сколько всего книг прочитала Габриэлла?
12. Если у вас 3 кошки, 2 морские свинки и кролик. Сколько милых маленьких носиков у них всего?
13. Если утром на земле лежит 3 дюйма снега, а к обеду выпадает еще 3 дюйма снега. Сколько дюймов снега выпало в тот день?
14. У моей кошки 4 лапы и у собаки моего брата 4 лапы. Сколько всего лап?
15. У меня было 10 копеек, но я потерял 2 из них. Сколько копеек у меня сейчас?
16. За лето Сантьяго прочитал 7 книг. Райан прочитал 5 книг. На сколько больше книг Сантьяго прочитал, чем Райан?
17.
Андрей наклеил 10 наклеек на свой блокнот. Когда он пришел в школу, он заметил, что некоторые наклейки отвалились. Сейчас у Андрея на блокноте всего 6 наклеек. Сколько наклеек упало с блокнота Андрея?
18. Николь любит помогать маме собирать помидоры в саду. Она насчитала в саду 9 помидоров. 6 помидоров были красными, а остальные зелеными. Николь и ее мама собрали все красные помидоры. Сколько зеленых помидоров Николь и ее мама оставили в саду?
19. У нас с сестрой есть 20 пенни. Если у моей сестры 10 пенни, сколько пенни будет у меня?
20. В зоопарке было 8 тигров. 3 тигра переехали в другой зоопарк. Сколько тигров осталось?
21. Эстер прочитала 3 стихотворения. Магенна прочитал еще несколько стихов. Всего они прочитали 7 стихотворений. Сколько стихов прочитал Магена?
22. Отец Хейли купил 8 чизбургеров. Хейли съела 1 из них. Сколько чизбургеров осталось у отца Хейли?
23. Если вы сварите 7 яиц в воде, и количество яиц, которые всплывут, на одно больше, чем количество, которое утонет, сколько яиц всплывет?
24.
Рашид любит есть мармеладки. Его любимые мармеладки — желтые. В его сумке было 12 мармеладок. Рашид убрал все желтые мармеладки и съел их, оставив в своей сумке 6 мармеладок. Сколько желтых драже съел Рашид?
25. У учителя физкультуры было 5 баскетбольных мячей. На следующей неделе учитель физкультуры получил несколько новых баскетбольных мячей. Сейчас у учителя физкультуры 9баскетбольные мячи. Сколько новых баскетбольных мячей получил учитель физкультуры?
26. У Джамала 6 игрушечных самолетов, а у его брата 4 игрушечных самолета. На сколько игрушечных самолетов у Джамала больше, чем у его брата?
27. У Антонио есть шарики. Его брат Алекс дает ему еще 5. Теперь у Антонио 8 шариков. Сколько шариков было у Антонио в начале?
28. Если у вас есть упаковка из 8 мелков, и вы даете своему другу 3 из них для использования во время рисования. Сколько карандашей сейчас у тебя в упаковке?
29. У Эмили есть 4 розовых ластика и несколько белых ластиков.
Всего у нее 7 ластиков. Сколько белых ластиков у Эмили?
30. Энджел подает пиццу на свой день рождения. В пицце 12 кусочков. Ангел и ее гости съедают 8 кусочков пиццы. Сколько кусочков пиццы осталось?
31. Если у вас на полу 9 игрушек, а у вашего младшего брата 6 игрушек на полу. Сколько у тебя еще игрушек на полу?
32. В классе 8 окон. На некоторых окнах есть украшения, на 2 из них нет направлений. Сколько окон украшено украшениями?
33. В субботу вы принесли домой рыбу из зоомагазина. Если 15 из ваших 18 рыб имеют полосы. Сколько ваших рыб без полосок?
34. На вершину забора прилетело 8 птиц. Некоторые птицы улетели, а 6 птиц остались. Сколько птиц улетело?
35. На полке Ноя было 6 книг. Оливия взяла несколько книг. Сейчас на полке 2 книги. Сколько книг взяла Оливия?
36. У Итана несколько папок в рюкзаке и 4 папки на столе. Всего у него 8 папок. Сколько папок в его рюкзаке?
37.
У Лиама 8 футболок. На 5 из них изображены супергерои, а остальные сплошные цвета. Сколько футболок Лиама однотонных?
38. Мэри собирала пазл из 20 частей. Закончив, она обнаружила, что там всего 18 штук. Сколько штук пропало?
39. У Николаса 7 кузенов. Некоторые из его двоюродных братьев — девочки, а трое его двоюродных братьев — мальчики. Сколько двоюродных сестер у Николая?
40. Снег шел 6 часов в понедельник и 4 часа во вторник. Сколько еще часов шел снег в понедельник?
41. Мама Чарли испекла на десерт 12 шоколадных печений. Чарли съел 2 печенья, а его мама и 1 печенье. Сколько шоколадных печений осталось?
42. У Мелани 16 фиолетовых ручек. У Данте 10 синих ручек. У Мелани на ____ больше ручек, чем у Данте.
43. У Софии в банке 75 пенни. Сколько еще пенни ей понадобится, чтобы в ее банке было 100 пенни?
44. На столе стояло 9 чашек газировки. Некоторые чашки были опрокинуты, а 6 еще стояли.
Сколько чашек газировки было опрокинуто?
45. У Грифона 20 настольных игр. Некоторые из них были под его кроватью, а 15 — в шкафу. Сколько настольных игр было под кроватью Гриффина?
46. Антонио заметил 3 оленей, сидящих на вершине холма, но все, что он мог видеть, это их глаза. Сколько всего глаз увидел Антонио?
47. Десмонд увидел 5 кроликов. Он пересчитал все их уши. Сколько кроличьих ушей насчитал Десмонд?
48. Кэти пересчитала все пальцы на ногах, а затем она пересчитала все пальцы на ногах своей мамы. Сколько всего пальцев Кэти насчитала?
49. Что весит больше? Рыжая лисица весом 15 фунтов или дикая индейка весом 24 фунта?
50. Кто больше весит: 150-килограммовый белохвостый олень или 110-килограммовый кенгуру?
Нравятся эти задачи по математике для первого класса? Посетите наш центр первого класса, чтобы получить еще больше ресурсов.
Получите версию этих текстовых задач в формате PPT.
IXL | Учим математику в 1 классе
IXL | Изучайте математику в 1 классе1
Счетный обзор — до 10
2
Подсчитайте, чтобы заполнить десять кадров
3
Счетный обзор — до 20
4
Счет десятков и единиц — до 20
5
Рассчитывайте на десять кадров — до 40
6
Пропустить счет двойками
7
Пропустить счет пятерками
8
Пропустить счет десятками
9
Пропустить счет двойками, пятерками и десятками
10
Счет — до 100
11
Счет десятков и единиц — до 99
12
Счет двойками, пятерками и десятками
13
Счет вперед — до 100
14
Счет в обратном порядке — до 100
15
Счет вперед — до 120
16
Счет в обратном порядке — до 120
17
Количество строк — до 100
18
Количество строк — до 120
19
Подсчет на сотню диаграммы
20
Счет по числовой схеме — до 120
21
Сотня диаграмма
22
Четным или нечетным
23
Определите числа как четные или нечетные
24
Четные или нечетные числа в числовых рядах
25
Какое четное или нечетное число стоит перед или после?
26
Шаблоны с пропуском счета — с таблицами
27
Последовательности — считать вверх и вниз на 1
28
Последовательности — счет вверх и вниз на 1, 2, 5 и 10
29
Порядковые номера
30
Написание чисел словами — преобразование слов в цифры
31
Написание чисел словами — преобразование цифр в слова
32
Римские цифры I, V, X
1
Складываем кубиками — суммирует до 10
2
Добавить с картинками — сумма до 10
3
Сложение предложений до 10: какая модель подходит?
4
Сложение предложений до 10: что показывает модель?
5
Сложение предложений с использованием числовых линий — сумма до 10
6
Превратите слова в дополнительное предложение — суммирует до 10
1
Добавление 1
2
Добавление 2
3
Добавление 3
4
Добавление 4
5
Добавление 5
6
Добавление 6
7
Добавление 7
8
Добавление 8
9
Добавление 9
10
Добавление 0
1
Сложение фактов — суммирует до 10
2
Составьте число, используя сложение — сумма до 10
3
Завершите добавочное предложение — сумма до 10
4
Способы составить число — сложение предложений до 10
5
Сложение словесных задач с картинками — сумма до 10
6
Словесные задачи на сложение — сумма до 10
7
Сложение предложений для текстовых задач — сумма до 10
8
Сложение предложений с использованием числовых линий — сумма до 20
9
Сложение фактов — суммирует до 20
10
Составьте число, используя сложение — сумма до 20
11
Завершите дополнительное предложение — сумма до 20
12
Словесные задачи на сложение — сумма до 20
13
Сложение предложений для текстовых задач — сумма до 20
14
Связанные дополнительные факты
15
Дополнительные предложения: правда или ложь?
16
Дополнительные предложения: что верно?
17
Используйте модели для добавления двузначного и однозначного числа — без перегруппировки
18
Добавить однозначное число к двузначному — без перегруппировки
19
Перегруппировка десятков и единиц — способы составить число
20
Перегруппировать десятки и единицы
21
Используйте модели для добавления двузначного и однозначного числа — с перегруппировкой
22
Добавление однозначного числа к двузначному — с перегруппировкой
23
Задачи на сложение слов — однозначные плюс двузначные числа
24
Сложение предложений для текстовых задач — однозначные плюс двузначные числа
25
Используйте модели для добавления двузначных чисел — без перегруппировки
26
Складывать двузначные числа без перегруппировки — суммируется до 100
27
Используйте модели для добавления двузначных чисел с перегруппировкой
28
Складывание двузначных чисел с перегруппировкой — суммирует до 100
1
Добавить двойников — с моделями
2
Добавить двойников
3
Добавить двойников — закончить предложение
4
Добавить, используя удвоения плюс один
5
Добавить, используя удвоения минус один
6
Добавьте три числа — используйте двойные числа
7
Сделайте десять, чтобы добавить — с моделями
8
Закончи предложение сложением — сделай десять
9
Сделайте десять, чтобы добавить
10
Сложите три числа — получится десять
11
Используйте модели для сложения числа, кратного десяти, и однозначного числа
12
Сложите число, кратное десяти, и однозначное число
13
Сложите два кратных десяти
14
Используйте модели, чтобы добавить число, кратное десяти, и двузначное число
15
Сложите число, кратное десяти, и двузначное число
16
Добавьте три числа
17
Сложите три числа — словесные задачи
1
Вычитание кубиками — до 10
2
Вычитание с картинками — до 10
3
Предложения с вычитанием до 10: какая модель подходит?
4
Предложения с вычитанием до 10: что показывает модель?
5
Вычитание предложений с использованием числовых строк — до 10
6
Превратите слова в предложение с вычитанием — до 10
7
Вычесть ноль и все
1
Вычитание 1
2
Вычитание 2
3
Вычитание 3
4
Вычитание 4
5
Вычитание 5
6
Вычитание 6
7
Вычитание 7
8
Вычитание 8
9
Вычитание 9
10
Вычитание 0
1
Вычитание фактов — до 10
2
Составьте число с помощью вычитания — до 10
3
Способы сделать число — вычитание предложений до 10
4
Способы вычитания из числа — вычитание предложений до 10
5
Завершите предложение с вычитанием — до 10
6
Задания на вычитание с картинками — до 10
7
Проблемы со словами на вычитание — до 10
8
Предложения на вычитание для текстовых задач — до 10
9
Вычитание предложений с использованием числовых строк — до 20
10
Вычитание фактов — до 20
11
Составьте число с помощью вычитания — до 20
12
Завершите предложение с вычитанием — до 20
13
Проблемы со словами на вычитание — до 20
14
Предложения на вычитание для текстовых задач — до 20
15
Связанные факты вычитания
16
Предложения с вычитанием: правда или ложь?
17
Предложения с вычитанием: что верно?
18
Вычесть однозначные числа из двузначных чисел
1
Соотнесите предложения на сложение и вычитание
•
Новинка! Вычитание обратным счетом — до 10
•
Новинка! Вычитание обратным счетом — до 20
2
Вычесть по счету — до 10
3
Вычесть по счету — до 20
4
Вычитание двойников
5
Вычитание кратных десяти
6
Вычесть кратное десяти
1
Сложение и вычитание — способы сделать число
2
Какой знак делает числовое предложение верным?
3
Семейства фактов
4
Факты сложения и вычитания — до 10
5
Факты сложения и вычитания — до 20
6
Предложения со сложением и вычитанием: что верно?
7
Десять больше или меньше
8
Складывать и вычитать десятки
1
Задачи Word с неизвестным изменением — до 10
2
Проблемы Word с неизвестным запуском — до 10
3
Словесные задачи с одним неизвестным дополнением — до 10
4
Задачи Word с обоими неизвестными дополнениями — до 10
5
Словесные задачи на сложение и вычитание — до 10
6
Словесные задачи на сложение и вычитание — до 20.
7
Сложение и вычитание предложений для текстовых задач — до 20
8
Задачи на сравнение слов до 10: на сколько больше или меньше?
9
Задачи на сравнение слов до 10: какая сумма больше?
10
Задачи на сравнение слов до 10: какая сумма меньше?
11
Задачи на сравнение слов до 10
1
Сравнение: больше или меньше?
•
Новинка! Сравнение: на сколько больше или меньше?
2
Сравните числа до 10, используя слова
3
Сравните числа до 10, используя символы
4
Сравните числа до 100, используя слова
5
Сравните числа до 100, используя символы
6
Сравните числа до 100: текстовые задачи
1
Оценка с точностью до десяти
1
Поместите модели до 20
2
Запишите числа в виде десятков и единиц до 20
3
Размещение моделей до 100
4
Преобразование между десятками и единицами — кратными десяти
5
Запишите числа в виде десятков и единиц
1
Слева, посередине и справа
2
Верх, середина и низ
3
Расположение в сетке
4
Над и под
5
Рядом и рядом
1
Какой рисунок-график правильный?
2
Интерпретировать графические изображения
3
Какая таблица учета правильная?
4
Интерпретация итоговых диаграмм
5
Какая таблица правильная?
6
Интерпретировать данные в таблицах
7
Интерпретация гистограмм I
8
Интерпретация гистограмм II
9
Какой столбчатый график правильный?
1
Читать термометр
2
Сравните предметы: длину и высоту
3
Широкий и узкий
4
Легкий и тяжелый
5
Держит более-менее
6
Сравните размер, вес и вместимость
7
Измеряйте длину предметами
8
Измерьте длину кубами
9
Измерьте высоту кубиками
10
Измерьте с помощью дюймовой линейки
11
Какая обычная единица длины подходит?
12
Привычные единицы длины: текстовые задачи
13
Какая обычная единица веса подходит?
14
Измерьте с помощью сантиметровой линейки
15
Какая метрическая единица длины подходит?
16
Метрические единицы длины: текстовые задачи
17
Какая метрическая единица веса подходит?
1
Названия и номиналы обычных монет
2
Названия и номиналы всех монет
3
Считайте копейки, пятаки и десять центов
4
Считайте пенни, пятаки, десять центов и четверти
5
Эквивалентные группы монет
6
Обмен монет — с картинками
7
Обмен монет
8
Деньги — проблемы со словами
9
Покупки: хватит ли денег?
10
Сравните денежные суммы
11
Наименьшее количество монет
1
Введение в шаблоны
2
Найдите следующую фигуру в шаблоне
3
Завершить шаблон
4
Сделать выкройку
5
Шаблоны выращивания
6
Найдите следующую форму в растущем шаблоне
7
Найдите следующую строку в растущем шаблоне
1
Больше, меньше и равновероятно
2
Определенные, вероятные, маловероятные и невозможные
1
Подсчет фигур на диаграмме Венна
2
Сортировка фигур в диаграмму Венна
3
Расставь числа по порядку — до 100
1
Сопоставьте цифровые часы и время
2
Сопоставьте аналоговые часы и время
3
Сопоставьте аналоговые и цифровые часы
4
Чтение часов и запись времени
5
ЯВЛЯЮСЬ.
или П.М.6
Время повседневных событий
7
Сравните часы
8
Время и часы: текстовые задачи
9
Дни недели
10
Времена года
11
Месяцы года
12
Читать календарь я
13
Читать календарь II
или П.М.1
Назовите двухмерную форму
2
Выберите двумерные фигуры
3
ромбы
4
Считаем стороны и углы
5
Сравните стороны и углы
6
Квадратные углы
7
Равные стороны
8
Открытые и закрытые формы
9
Переворачивать, поворачивать и скользить
10
Симметрия
11
Создавайте двухмерные фигуры
1
Двумерные и трехмерные формы
2
Назовите трехмерную форму
3
Кубы и прямоугольные призмы
4
Выберите трехмерные фигуры
5
Подсчет вершин, ребер и граней
6
Сравните вершины, ребра и грани
7
Определение форм, вычерченных из твердых тел
8
Определение граней трехмерных фигур
9
Формы повседневных предметов I
10
Формы повседневных предметов II
1
Равные части — половинки и четверти
2
Равные части — половинки, трети и четверти
3
Определить половинки
4
Определить трети
5
Определить четверти
6
Определите половинки и четверти
7
Определите половинки, трети и четверти
8
Сделать половинки
9
Сделать трети
10
Сделать четверти
11
Сделать половинки и четверти
12
Делайте половинки, трети и четверти
13
Делайте половинки и четвертинки разными способами
14
Простые дроби: какую дробь изображает фигура?
50 Возможные задачи дня по математике для первоклассников
Распространите любовь
Начните свои ежедневные уроки математики с задач дня по математике Word — это отличный способ отложить учебу.
Словесные задачи обычно представляют собой сложную тему для понимания молодыми учащимися, даже если математический аспект прост.
Ежедневно добавляйте эти первоклассные задачи по математике в начале математического блока, чтобы развить критическое мышление, уверенность в себе и создать обучающееся сообщество. Студенты будут медленно адаптироваться к смыслу, а также взаимодействовать с ключевыми деталями. Мотивируйте учащихся записывать уравнения текстовых задач и рисовать картинки, чтобы объяснить свои мысли, так как это помогает им найти выход, когда они застряли.
Включены темы сложения, умножения, вычитания и сравнения. Ваша задача — написать на доске одну из этих первоклассных задачек по математике. Затем позвольте детям сделать необходимое.
50 Математические задачи для первого класса
- У меня было шесть карандашей. Если мой учитель дал мне еще четыре, сколько у меня карандашей?
- Собака Джины съела три лакомства в воскресенье и 0 в понедельник. Сколько всего лакомств съела собака Джины?
- Джоэл отправился в зоопарк со своей семьей. В первый час он увидел медведя, трех львов и двух тигров. Сколько животных увидел Джоэл за первый час своего пребывания в зоопарке?
- Джексон расположил свои машинки по цвету. У Джексона шесть синих, четыре черных и пять зеленых машин. Сколько всего машин у Джексона?
- У Бена есть два зеленых и четыре желтых воздушных шара. Сколько всего шариков у Бена?
- У нас в семье Кларк трое детей. Тине три года, Джошуа четыре, а Саманте семь. Какую сумму вы сложите с возрастом троих детей?
- Если вы идете плавать, и 6 ваших приятелей приходят, сколько пловцов?
- Цветок в вазе раньше был для мамы Рэйчел. Три цветка упали, и мама Рэйчел велела их убрать. Сейчас в вазе пять свежих цветов. Сколько цветов уже было в вазе?
- У кошки Хейдена были котята. Три были серыми, двухпятнистыми и семеро черными. Сколько всего котят было у кошки Хейден?
- Педро взял с игровой площадки три красных и шесть желтых листьев. Сколько всего листьев у Педро?
- Габриэлла изучила три книги в понедельник, шесть во вторник и четыре в среду. Сколько всего книг было прочитано?
- Должны ли у вас быть три кошки, две морские свинки и один кролик. Сколько у них всего маленьких носиков?
- Если утром на землю кладут 3 дюйма снега, к обеду мы снова добавим еще три дюйма. Сколько дюймов снега у нас в этот день?
- У моего кота четыре лапы, а у собаки моего брата четыре лапы. Сколько всего лап?
- У него есть 10 монет, но он потерял 2 из них. Сколько копеек у него сейчас?
- За лето Джейсон прочитал семь книг. Кларк тоже прочитал пять книг. На сколько больше книг Джейсон прочитал, чем Кларк?
- Дрейк наклеил на свой блокнот десять наклеек. Но когда он пришел в школу, он заметил, что некоторые наклейки отвалились. Сейчас у Дрейка на блокноте всего шесть наклеек. Сколько наклеек упало с блокнота Дрейка?
- Николь любит помогать маме собирать помидоры в их семейном саду. Она собрала в саду девять помидоров. Шесть из них были красными, а остальные зелеными. Затем они выбрали все красные помидоры. Сколько зеленых помидоров осталось в саду?
- У нас с сестрой есть 30 пенни. Если у меня есть 10 пенни, сколько пенни у моей сестры?
- В зоологическом саду было восемь тигров. Трое из них переехали в другой зоопарк. Сколько тигров осталось?
- Матвей прочитал три стихотворения. Марта читала немного больше, чем Матфей. Всего они прочитали семь стихотворений. Сколько стихов прочитала Марта?
- Отец Хейли купил восемь бутербродов. Хейли съела 1 из них. Сколько бутербродов осталось у отца Харли?
- Если сварить семь яиц, то количество всплывающих яиц будет на одно больше, чем утонувших. Сколько яиц всплывает?
- Рашид любит драже. Его любимые — желтые. В его сумке было 12 драже. Сколько желтых драже съел Рашид?
- У инструктора физкультуры было пять баскетбольных мячей. На следующей неделе он добавил несколько новых; теперь их девять. Сколько новых баскетбольных мячей получил инструктор физкультуры?
- У Сахида шесть игрушечных машинок, а у его брата Камала на четыре машинки больше, чем у него. На сколько машинок у Сахида больше, чем у его брата Камала?
- У Эндрю есть шарики. Его младший брат дает ему еще пять. Теперь у Эндрю восемь шариков. Сколько шариков было у Андрея изначально?
- Должны ли вы иметь упаковку из 8 мелков, и вы предлагаете 3-2 своим друзьям использовать их во время рисования? Сколько карандашей осталось у тебя сейчас в рюкзаке?
- У Джейн есть четыре розовых ластика и несколько синих ластиков. Всего у нее семь ластиков. Сколько синих ластиков у Джейн?
- Лайла подает пиццу на свой день рождения. В пицце 12 кусочков. Лайла и ее гость съели восемь кусочков пиццы. Сколько пицц у нас осталось?
- Подумайте, есть ли у вас девять игрушек, а у вашего брата шесть. Сколько еще игрушек у тебя будет?
- В классе восемь окон. Где на некоторых окнах есть украшения, на 2 из них нет направлений. Сколько классных комнат украшено?
- В пятницу вы купили рыбу в зоомагазине. Предположим, что 15 из 18 рыб имеют полосы. У скольких рыб нет полос?
- 8 птиц сели на вершину забора. Некоторые птицы улетели, а шесть остались. Сколько птиц улетело?
- На полке у Натана шесть книг. Ной взял несколько книг. Теперь на полке осталось две книги. Сколько книг взял Ной?
- У Лэрда несколько папок в рюкзаке и пять на столе. Всего у него восемь папок. Сколько папок в его рюкзаке?
- У Лиама восемь шорт. На пяти есть изображения супергероев, а на остальных — сплошные цвета. Сколько шорт у Лиама однотонных?
- Эвелин собирала пазл из 20 деталей. Починив ее, она поняла, что там всего 18 штук. Сколько штук пропало?
- У Натана семеро двоюродных братьев. Некоторые из них — девочки, а трое его двоюродных братьев — мальчики. Сколько двоюродных сестер у Натана?
- Снег шел 7 часов в понедельник и 5 часов во вторник. Сколько еще часов шел дождь и снег в понедельник?
- Мама Дэна испекла на десерт десять шоколадных печений. Дэн съел два печенья, а его мама съела одно печенье. Сколько шоколадных печений осталось?
- У Анджелы 16 фиолетовых ручек. У Алекса десять зеленых ручек. У Анджелы на ___ больше ручек, чем у Алекса.
- У Доры в банке 75 пенни. Сколько пенсов ей понадобится, чтобы на ее банковском счету было 100 пенсов?
- на столе стояло 9 стаканов газировки. Некоторые чашки были опрокинуты, а шесть еще стояли. Сколько стаканов газировки было опрокинуто?
- У Чарльза есть 20 настольных игр. Часть находилась под его кроватью, а 15 — в шкафу. Сколько настольных игр было под кроватью Чарльза?
- Романо увидел трех оленей, сидящих на вершине холма, но все, что он мог видеть, это их глаза. Сколько всего глаз видел Романо?
- Эллиот увидел пять кроликов. Он пересчитал все их уши. Сколько кроличьих ушей насчитал Эллиот?
- Катя пересчитала все свои пальцы на ногах и пальцы своей мамы тоже. Сколько всего пальцев насчитала Катя?
- Что имеет больший вес? Рыжая лиса весом 15 фунтов или индюк весом 24 фунта?
- Что имеет больший вес? Кенгуру весом 110 фунтов или белохвостый олень весом 150 фунтов.
Сколько всего лакомств съела собака Джины?
Сколько всего листьев у Педро?
Она собрала в саду девять помидоров. Шесть из них были красными, а остальные зелеными. Затем они выбрали все красные помидоры. Сколько зеленых помидоров осталось в саду?
Сколько новых баскетбольных мячей получил инструктор физкультуры?
Сколько классных комнат украшено?
Дэн съел два печенья, а его мама съела одно печенье. Сколько шоколадных печений осталось?
Как решить математический рисунок с фруктами
- Пользователи Твиттера не могут решить домашнее задание первоклассника по математике.
- Передовая педагогика стремится выявить различные идеи детей (буквально!), чтобы исследовать, как они думают.
- Развитие критического мышления и ежедневной математической грамотности помогает учащимся более гибко изучать математику.
На прошлой неделе The N ew Yorker Хелен Рознер поделилась тупо написанной детской математической задачей, и Интернет отреагировал соответствующим образом:
Просмотреть всю публикацию в Твиттере
(Бен прав, но это трудно объяснить в одном твите.)
Просмотреть полную публикацию в Твиттере
Прав ли Билл Шиллито из Университета Оглторп? W шляпа означает ли эта математическая задача?
➗ Вы любите цифры.
И мы тоже. Давайте вместе покопаемся в цифрах.
Общая задача следует общепринятой в настоящее время формуле с обновленными математическими методиками различных видов. Родитель, который не читал или просто не получил нужных материалов для понимания педагогики, вырывает ролик из контекста и смеется над тем, какой он кажется ерундой. В этом случае домашнее задание использует язык, который учащиеся, вероятно, выучили в классе.
Математический рисунок — это визуализированная детская версия того, как они считали бы такие объекты, как кубики или даже свои пальцы в реальной жизни. Например, они рисуют круги, соответствующие количеству объектов в вопросе. Затем они также рисуют отношения, обводя некоторые объекты, зачеркивая некоторые, помещая их в разные группы и так далее.
Если это звучит как довольно сложный материал, это так и не так — дети тяготеют к такому типу мышления, но для взрослых вне областей, таких как комбинаторика или теория множеств, это можно найти почти исключительно в инфографике.
📚
Лучшие книги по математикеМорские книги Бесконечные силы: как исчисление раскрывает секреты Вселенной
Скидка 28%
Прочитать
Базовые книги Искусство статистики: как учиться на основе данных
Скидка 13%
Прочитать
Кредит: AmazonMariner Books Радость x: Путеводитель по математике, от единицы до бесконечности
Сейчас скидка 12%
Читать сейчас
Кредит: AmazonДавайте рассуждать о том, что такое математические рисунки, и почему этот вид педагогики набирает обороты для математики. Математика, в частности, уязвима для многих болевых точек в образовании. Озабоченные математикой учителя начальной школы сообщают об этом беспокойстве ученикам и влияют на их результаты, и это еще до того, как чему-то научат.
В книге 2005 г. Как студенты учатся: математика в классе , которая сама по себе является продолжением некоторые другие известные книги по психологии об обучении, эксперты сосредотачиваются на способах вовлечения учащихся в математику, чтобы показать, как они думают о задачах.
Дети усваивают числа более осязаемым способом, например, видят количество вещей, расставленных на прилавке, или считают на пальцах.
Другие математические задачи
- Сможете ли вы решить эту вирусную головоломку с треугольниками?
- Как решить возмутительную вирусную математическую задачу
- Удивительная математика внутри кубика Рубика
Поскольку отношения между реальной, исчисляемой, удерживаемой вещью и числительными, которые вы начинаете писать в своей домашней работе по математике, не всегда ясны, по словам экспертов, некоторые учащиеся сталкиваются с трудностями просто из-за того, что пытаются поделиться своими мыслями о том, как решать задачи. .
Детей старшего возраста поощряют демонстрировать свои работы, хотя, честно говоря, это больше похоже на способ выявить мошенничество, чем на изучение их мышления. Математическая педагогика говорит, что разговор с младшими детьми через их мысли также очень помогает. «Такое общение о математическом мышлении может помочь каждому в классе понять данную концепцию или метод, потому что оно разъясняет противоположные подходы, некоторые из которых ошибочны, но часто по интересным причинам», — пишут авторы в Как учатся студенты .
Это точка ключа . Если вы когда-либо посещали Princeton Review или другие курсы подготовки к экзаменам, вы знаете, что один из основных способов, которым писатели заманивают тестируемых в ловушку неверных ответов, — это предложение чего-то почти правильного. Если вы допустили одну распространенную и ключевую ошибку, ваша работа направит вас к ложным ответам. И понимание различных распространенных ошибок в мышлении — отличный способ помочь детям обдумать свои варианты в среде, которая не наказывает их за то, что они все обдумали. Здесь в Popular Mechanics , мы на Team Math Drawing.
Итак, теперь, когда вы освоились с математическими рисунками и исчисляемыми вещами, снова взгляните на задачу. Как бы вы решили это? Расскажите в комментариях. 💬 ⬇Кэролайн Делберт
Кэролайн Делберт — писатель, заядлый читатель и пишущий редактор в Pop Mech. Она также энтузиаст практически всего.
Ее любимые темы включают ядерную энергию, космологию, математику повседневных вещей и философию всего этого.
Математика для первоклассников — обучение и практика математики для первоклассников
[«`#», «Моя учетная запись»]Учащиеся заглядывают внутрь сложения и вычитания, применяя понимание разрядного значения к двузначным операциям.
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 5
Pre-kindergartenKindergartenКласс 1Класс 2Класс 3Класс 4Класс 50002 Учащиеся изучают сложение до 5, используя конкретные объекты, абстрактные объекты и уравнения. Они изучают значение и правильное использование знаков + и =, а также термины «сложение» и «сумма».
Подсчитайте два слагаемых и определите сумму
Учащиеся определяют, сколько в каждой из двух групп, а затем сколько всего в сумме до 5. Они завершают утверждение «X и X дают X», перетаскивая сумму на место
Определить общее количество объектов и определить два его слагаемых
Учащиеся определяют общее количество предметов двух цветов, а затем определяют количество предметов каждого цвета.
Они завершают утверждение «X и X составляют X», перетаскивая сумму на место
Использование знаков + и = в уравнении
Учащиеся знакомятся со знаками + и = и используют их для составления простых уравнений
Определять слагаемые и сумма в уравнении
Учащиеся знакомятся с терминами «сложение» и «сумма». Они определяют слагаемые и сумму в уравнениях
Составление уравнения сложения по картинке
Учащиеся находят сумму уравнения сложения по показанным объектам. Затем они составляют уравнение на основе показанных объектов
Представление объектов с помощью кубиков
Учащиеся перетаскивают цветные кубики, чтобы сопоставить объекты. Затем они определяют набор цветных кубиков, соответствующих заданным объектам
Составляют уравнения сложения на основе кубиков и решают уравнения с кубиками и без них
Учащиеся составляют уравнение сложения на основе цветных кубиков и решают его сумму. Они используют уравнения, чтобы показать, что существует более одного способа представления суммы.
Затем учащиеся решают уравнения сложения без показанных кубов
Решение уравнений сложения
Учитывая выражение сложения, учащиеся определяют сумму. Затем они решают уравнения на сложение
Тема B: Счет от встроенных чисел
Учащиеся изучают сложение до 10, используя конкретные объекты, абстрактные объекты, уравнения и числовые связи. Они решают проблемы с отсутствующими слагаемыми и начинают представлять и решать задачи со словами.
Прибавление 0 к числу
Учащиеся прибавляют ноль к однозначному числу. Они решают уравнения, в которых ноль — первое слагаемое, а когда — второе слагаемое
Используйте знак + в уравнении и найдите сумму
Учащиеся складывают однозначные числа, представленные цветными кубиками. Они выбирают знак +, чтобы завершить уравнение и определить сумму
Смоделировать и решить уравнение сложения
Учащиеся используют цветные кубики для представления слагаемых в уравнении, а затем определяют сумму
Запишите уравнение сложения на основе модели, чтобы показать более одного способа получить заданную сумму
Учащиеся пишут уравнение сложения, чтобы соответствовать заданной модели кубиков.
Они повторяют этот навык с другим уравнением с той же суммой и замечают, что существует более одного способа показать эту сумму
Показать более одного способа получить заданную сумму
Учащиеся составляют уравнение сложения, чтобы соответствовать заданной модели кубиков. Затем они создают другую модель куба с той же суммой и записывают уравнение, замечая, что существует несколько способов показать эту сумму
Решить уравнение сложения (всего до 7)
Учащиеся определяют сумму для уравнений сложения с двумя слагаемыми и суммирует до 7
Определите части уравнения сложения
Учитывая уравнение сложения, учащиеся определяют первое слагаемое, второе слагаемое, знак плюс и сумму
Запишите уравнение сложения на основе модели и создайте модель, показывающую более одного способа получения заданной суммы.
Учащиеся пишут уравнение сложения, соответствующее заданной модели кубиков. Затем они создают еще одну модель куба с той же суммой и записывают уравнение, замечая, что существует несколько способов показать эту сумму
Решают уравнения сложения до 10 с моделью или без нее
Учащиеся выбирают, просматривать куб или нет модель, чтобы решить уравнения сложения до 10, а затем решить
Решение уравнения сложения (сумма до 10)
Учащиеся определяют сумму уравнений сложения с двумя слагаемыми и суммы до 10
Моделирование и решение задачи на сложение с объектами
Учащиеся пишут и решают уравнение сложения на основе цветных объекты.
Затем они используют объекты, как указано, для моделирования сценария сложения, записывают его в виде уравнения и решают за весь период
Моделируют и решают задачу на сложение с помощью кубов
уравнение и решить для суммы
Написать и решить уравнение сложения на основе задачи со словами
Учащиеся составляют уравнение на основе сценария сложения и решить его
Определить отсутствующее слагаемое на основе модели кубов
Ученики определяют отсутствующее второе слагаемое в уравнении на основе цветных кубиков. Во-первых, подсказки направляют их к части модели, чтобы найти ответ. Затем учащиеся решают без подсказки
Определяют недостающее слагаемое на основе модели кубов
Учащиеся определяют недостающее второе слагаемое в уравнении на основе модели кубов. Во-первых, подсказки направляют их к части модели, чтобы найти ответ. Затем учащиеся решают без подсказки
Определяют недостающее слагаемое в уравнении (Часть 1)
Учащиеся определяют отсутствующее второе слагаемое в уравнении
Определяют отсутствующее слагаемое в уравнении (Часть 2)
Учащиеся определяют отсутствующее второе слагаемое в уравнении, выбирая, решать ли немедленно или моделировать с помощью кубов.
Затем они определяют недостающее первое или второе слагаемое в уравнении 9.0003
Определение отсутствующего слагаемого в уравнении
Учащиеся тренируются в решении отсутствующего второго слагаемого в уравнении сложения
Выберите два слагаемых, чтобы получить заданную сумму или модель с кубиками. Они определяют, какое из двух уравнений верно. Затем учащиеся выбирают два слагаемых, чтобы получить заданную сумму
Решают уравнения сложения отсутствующих слагаемых
Учащиеся определяют отсутствующее второе слагаемое в уравнении
Определите слагаемые с суммой 10
Учащиеся определяют, какое из двух слагаемых с суммами до 10 является правильным. Они определяют пары слагаемых, сумма которых равна 10
Определите числовую связь
Учащиеся определяют общее количество объектов, а затем два его слагаемых в зависимости от цвета. Они перетаскивают эти значения в числовую связь. Затем учащиеся находят числовую связь среди трех изображений.
Постройте числовую связь на основе модели кубиков
Учащиеся составляют числовую связь на основе модели цветных кубиков, а затем записывают ее в виде уравнения сложения. Затем учащиеся сначала пишут уравнение на основе модели кубов и строят числовую связь 9.0003
Постройте числовую связь на основе модели кубиков и заполните ее уравнение сложения.
На основе модели цветных кубиков учащиеся заполняют отсутствующее слагаемое в числовой связи и связанное с ней уравнение сложения. Затем они завершают всю числовую связь на основе модели кубов
Постройте модель, числовую связь и уравнение
Учащиеся создают двухцветную модель кругов. Они строят числовую связь на основе модели и определяют недостающее слагаемое или сумму в соответствующем уравнении 9.0003
Завершите связку чисел
Учащиеся определяют недостающее слагаемое в связке чисел. Затем они определяют два сложения, которые завершают числовую связь с заданной суммой.
Завершите числовую связь, чтобы показать более одного способа достижения заданной суммы.
Затем они определяют два разных слагаемых, чтобы завершить числовую связь с той же суммойОпределить отсутствующее слагаемое в числовой связи
Учащиеся находят отсутствующее сложение в связке чисел для нескольких связей чисел с одинаковой суммой
Тема C: Развитие беглости сложения в пределах 10
Учащиеся укрепляют свое понимание сложения в пределах 10 и лежащих в его основе концепций по мере разработки более эффективных стратегий решить проблемы. Они используют сценарии сложения с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Определение отсутствующего слагаемого в уравнениях с суммой и их оборотными фактами
Вычисление отсутствующего слагаемого в уравнениях, которые в сумме дают максимальное значение 10 с визуальной поддержкой. Также вычислите отсутствующее слагаемое в уравнениях, которые в сумме дают максимальное значение 10, используя оборотные факты, или переключите слагаемые, которые в сумме дают максимальное значение 10
Запишите модель блоков с основанием 10 в качестве уравнения сложения
Используйте блоки с основанием 10 и /или оборотные факты, чтобы завершить уравнение сложения.
Эти уравнения будут в сумме давать 10 каждый раз, когда
Определите отсутствующее слагаемое в уравнениях, представляющих собой оборотные факты с суммами 4, 5, 6 и 7. mssing addends
Нахождение отсутствующего слагаемого в уравнении
Нахождение отсутствующего слагаемого в уравнении. Учащиеся будут использовать интерактивную игру, которая поможет им найти отсутствующие слагаемые
Определить отсутствующее слагаемое в уравнениях, объединенных в пары фактов оборота с суммами 6, 7, 8 и 9.
Определите отсутствующее слагаемое в уравнениях, сумма которых равна 6, 7, 8 или 9. Учащиеся также будут использовать оборотные факты для определения пропущенных слагаемых
Выберите правильную сумму для выражения сложения
Выберите один из двух вариантов ответа для каждое числовое выражение, которое им дано. Каждое числовое выражение в сумме дает один из двух ответов
Определите отсутствующее слагаемое в уравнениях, объединенных как оборотные факты с суммами 9 и 10
Определите отсутствующее слагаемое в уравнениях, сумма которых равна 9или 10.
Учащиеся также будут использовать оборотные факты для выявления пропущенных дополнений
Тема D: Стратегии декомпозиции для вычитания
Учащиеся укрепляют свое понимание вычитания в пределах 10 и лежащих в его основе концепций по мере того, как они создают более эффективные стратегии решения задач. Они исследуют взаимосвязь между сложением и вычитанием и все чаще работают с 0 как с вычитаемым и разностью. Они используют сценарии вычитания с объектами, шаблонами блоков с основанием 10, числовой прямой и уравнениями, чтобы усилить отношения между семействами фактов. Они опираются на имеющиеся знания о составе чисел 6-10 по мере перехода от конкретного к абстрактному.
Запишите сценарий на основе объектов в виде уравнения вычитания с разностью 0 (Часть 1)
Запишите уравнения вычитания, используя два числа. Они напишут эти уравнения вычитания, чтобы они соответствовали картинке, которую им дали
Запишите сценарий числовой строки как уравнение вычитания -0
Узнайте, что вычитание 0 из числа дает вам число, которое вы начали с использования числовой строки.
Студенты должны будут идентифицировать как числа, которые вычитаются, так и разницу, основанную на сценарии числовой строки 9.0003
Запишите сценарий числовой прямой как уравнение вычитания с разностью 0
Узнайте, что вычитание числа из самого себя дает разность 0 с помощью числовой строки. Они определят разницу после того, как им будет предложено поработать с числовой строкой
Определить пропущенные числа в уравнениях вычитания с разницей 0
Решить отсутствующие элементы в уравнениях вычитания, которые приводят к разнице 0. Определить одно из чисел что приводит к разнице в 0 или самой разнице в 0 в зависимости от примера
Вычитание путем перемещения объекта назад по числовой прямой и решение связанного уравнения, которое показывает вычитание из 3, 4 или 5
Вычитание чисел из 3, 4 или 5 с помощью числовой строки. Иногда учащимся будет предложено заполнить один отсутствующий элемент в уравнении вычитания после взаимодействия со сценариями числовой прямой.
Запишите сценарий числовой строки как уравнение, которое показывает вычитание из 3, 4 или 5
4 или 5 с помощью числовой строки. Учащимся будет предложено заполнить все элементы уравнения вычитания, включая уменьшаемое, символ операции, вычитаемое и разность 9.0003Запишите сценарий, основанный на объектах, как уравнение вычитания с разностью 0 (Часть 2)
Используйте сценарий, иллюстрированный картинками, для завершения уравнений вычитания. Учащиеся введут уменьшаемое, вычитаемое и разность для каждого уравнения вычитания
Используйте блоки с основанием 10 для представления сценариев вычитания с объектами в пределах 5 и определяйте шаблоны блоков с основанием 10, которые представляют сценарии вычитания с объектами в пределах 5
Выберите число кубов с основанием 10, которые соответствуют количеству удаленных объектов в сценарии, проиллюстрированном рисунками. Оставшаяся разница должна совпадать с количеством оставшихся изображений более
Решите уравнения, основанные на модели блоков с основанием 10, чтобы вычесть 1 или все, кроме 1
Щелкните количество кубов с основанием 10, которое нужно вычесть из суммы, чтобы получить разницу в заданном вам уравнении вычитания.
После этого учащиеся будут вводить разность в уравнении вычитания
Записать модель блоков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 6
Заполнить слагаемые и суммы в уравнениях, которые дают в сумме 6, учитывая сценарий, иллюстрированный основанием 10 кубов. Затем учащиеся завершат два уравнения на вычитание, используя 6 и сложения из первого уравнения 9.0003
Запишите модель блоков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 7 или 8
Заполните сложения и суммы в уравнениях, которые дают в сумме 7 или 8, учитывая сценарий, иллюстрируемый кубами с основанием 10. Затем учащиеся выполнят два уравнения на вычитание, используя числа 7 или 8 и слагаемые из первого уравнения.
Вычитание путем перемещения объекта назад по числовой прямой и решение связанного уравнения, которое показывает вычитание в пределах 7
Вычитание чисел из 7 с помощью числовой строки . Затем учащимся будет предложено заполнить разницу уравнений вычитания
Запишите модель блоков с основанием 10 в виде двух связанных уравнений, которые показывают вычитание из 9 или 10
Вставьте сложения и суммы в уравнениях, которые дают в сумме 9 или 10.
учитывая сценарий, иллюстрируемый кубами с основанием 10. Затем учащиеся завершат два уравнения на вычитание, используя 9 или 10 и слагаемые из первого уравнения.
Определите пропущенные числа в уравнениях на вычитание из 9
Используя кубы с основанием 10, вставьте пропущенное слагаемое и просуммируйте для уравнений сложения, которые в сумме дают 9. Кроме того, используйте кубы с основанием 10, чтобы заполнить пропущенное вычитаемое и разницу в уравнениях вычитания, которые начинаются с уменьшаемого числа 9
Тема E: Переместительное свойство сложения и знак равенства
Учащиеся узнают о переместительном свойстве сложения, сравнивая сложение выражения с теми же слагаемыми, но в другом порядке. Кроме того, учащиеся тренируются составлять выражения, равные друг другу, вставляя пропущенное слагаемое. Наконец, учащиеся знакомятся со знаком равенства как способом показать, что два выражения равны или одинаковы.
Решите простые уравнения на сложение и убедитесь, что изменение порядка слагаемых не меняет сумму.
С помощью наглядных материалов учащиеся считают и складывают предметы. Затем объекты меняются местами, чтобы показать, что сумма одинакова. Затем учащиеся решают задачи на сложение, используя только числа, и замечают, что изменение порядка слагаемых не меняет сумму
Исследуйте выражения и закрепляйте свойство перестановочности сложения
Учащиеся узнают, что такое выражение. Затем учащиеся сопоставляют выражения с одинаковой суммой, хотя порядок слагаемых меняется
Составляйте равные выражения и решайте уравнения с одинаковыми слагаемыми в другом порядке.
Учащиеся тренируются заполнять пробелы в выражении, чтобы сделать его равным другому выражению. Затем учащиеся практикуются в решении уравнений сложения, которые имеют одинаковые слагаемые и суммы.
Определяют и составляют равные и неравные выражения сложения
Учащиеся решают уравнения с одинаковой суммой, но разными слагаемыми. Затем учащиеся решают уравнения, чтобы увидеть, равны они или нет.
Учащиеся практикуют алгебраическое мышление, заполняя пропущенное сложение, в результате чего два выражения будут равны 9.0003
Использование знака равенства для отображения и создания выражений равенства (Часть 1)
Учащиеся учатся использовать знак равенства для отображения выражений равенства. Затем учащиеся тренируются заполнять одно отсутствующее сложение, чтобы уравнение было верным, с прямыми инструкциями
Используйте знак равенства, чтобы отображать и составлять выражения равенства (Часть 2)
Учащиеся тренируются заполнять одно отсутствующее сложение, чтобы уравнение было верным
Определить являются ли числовые предложения истинными и ложными
Учащиеся упражняются в определении истинных и ложных числовых предложений. Некоторые примеры требуют добавления, а другие нет
Тема F: Развитие беглости вычитания в пределах 10
Учащиеся закрепляют взаимосвязь между сложением и вычитанием и взаимосвязь между семействами фактов.
Они используют знакомые предметы, кубики с основанием 10, числовую прямую и уравнения, чтобы исследовать состав чисел 3-10. Они строят скорость и точность со всеми +/- фактами в пределах 10.
Определите модель числового ряда, которая представляет сценарий вычитания, заданный словами
Посмотрите на три возможных сценария числового ряда, данные вам. Затем выберите тот, который представляет уравнение вычитания, записанное словами
Найдите недостающие числа в уравнениях вычитания из 4, 5 и 6
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания начинается с 4, 5 или 6
Определите недостающие числа в уравнениях вычитания из 6 и 7
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания будет начинаться либо с 6, либо с 7
Выберите соответствие выражения вычитания и разности
Используя сценарии, иллюстрированные рисунками, сопоставьте выражения вычитания с соответствующими разностями.
Упражнение заканчивается, когда вы переходите от одного игрового поля к другому
Определите недостающие числа в уравнениях вычитания из 7 и 8
Используя сценарии, иллюстрированные кубиками с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания будет начинаться либо с 7, либо с 8
Найдите недостающие числа в уравнениях вычитания из 8 и 9
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания. Каждое из уравнений вычитания начинается либо с 8, либо с 9
Определите недостающий элемент в уравнении вычитания
Определите, какие элементы отсутствуют в уравнениях вычитания. По мере того, как вы заполняете недостающие элементы уравнений вычитания, головоломка будет медленно решаться
Найдите недостающие числа в уравнениях вычитания из 9 и 10
Используя сценарии, проиллюстрированные кубами с основанием 10, заполните недостающие элементы уравнений вычитания.
Каждое уравнение вычитания начинается с 9 или 10
МОДУЛЬ 2. Знакомство с размещением значений путем сложения и вычитания в пределах 20
Тема A: Подсчет или прибавление десяти для решения неизвестных результатов и общих неизвестных задач
Учащиеся закрепляют свои понимание «десятки» и «единицы» при сортировке, подсчете, сложении и вычитании. Они используют объекты, блоки с основанием 10, числовую прямую и десятичную рамку. Они практикуют различные стратегии, чтобы добавить через 10 и улучшить беглость с +/- фактами в пределах 20.
Закрепить знания о числах 11-20, добавив одну цифру к числу десять
Учащиеся выберут правильное сложение, чтобы заполнить таблицу, а затем отработают навыки сложения, введя правильную сумму
Откройте для себя сложения, чтобы получить десять
Откройте для себя сложения с суммой десять. Найдите недостающее слагаемое в сумме десять и заполните таблицу чисел
Определите недостающее сложение
Учащиеся продемонстрируют свои навыки, найдя недостающее сложение, чтобы составить уравнение
Практика с десятью кадрами
Щелкайте и перетаскивайте капли, чтобы завершить десять кадров.
Добавьте оставшиеся капли к десяти рамкам, чтобы определить сумму
Используйте десять рамок, чтобы изучить уравнения и определить сумму
Используя десять рамок, учащиеся считают объекты, чтобы определить слагаемые. Затем учащиеся заполняют десятикадр и используют наглядные материалы, чтобы решить уравнение
Используйте блоки с основанием десять, чтобы получить десять, затем найдите сумму
Нажмите и перетащите блоки с основанием десять, чтобы сначала составить стержень из десяти. Затем учащиеся будут считать свободные блоки и добавлять их к стержню, чтобы определить сумму
Используйте блоки с основанием десять, чтобы определить сумму
Определите количество блоков, необходимых для сборки стержня. Используйте блок с основанием десяти, чтобы определить сумму данного уравнения
Введение в уравнения с тремя слагаемыми
Используйте блоки разного цвета, чтобы найти слагаемые, равные десяти. Затем добавьте оставшееся слагаемое к десяти, чтобы найти сумму.
Введите ответ на уравнение
Разложить слагаемые, чтобы получилось десять, затем сложить, чтобы найти сумму
Разложите одно сложение, чтобы добавить правильное количество блоков в другую группу, чтобы получилось десять. Добавьте десять к оставшимся блокам, чтобы решить уравнение
Продолжение практики разложения слагаемых для решения уравнения
Разложите одно слагаемое, чтобы получить десять. Добавьте десять к оставшимся блокам, чтобы решить уравнение. Введите сумму в уравнение
Продемонстрируйте знание пропущенного сложения, чтобы получить десять
Введите пропущенное сложение, чтобы завершить уравнение с суммой десяти
Решение с помощью числовой связи
Решение уравнений путем разложения и нахождения десяти без использования визуальных манипуляций. Введение в использование числовых связей для решения уравнения
Использование числовых связей для решения уравнений сложения
Используя числовые связи, определите, как нужно разделить слагаемое, чтобы получить десять.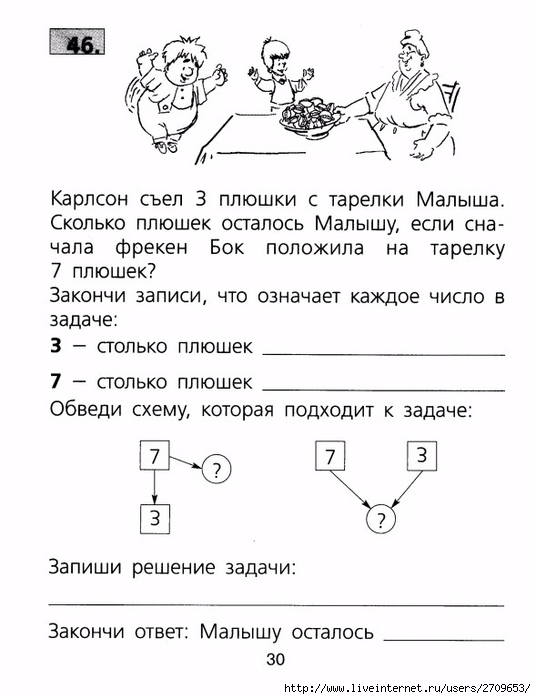
Добавьте остаток от деления к десятке, чтобы найти сумму
Продолжение практики использования числовых связей для решения уравнений сложения
Использование числовых связей для нахождения суммы уравнения сложения
Продемонстрировать навыки или попрактиковаться с помощью
Учащимся предоставляется возможность решать уравнения с помощью или без помощи
Решать уравнения сложения с суммами 11-16 для объединения объектов
Решать уравнение сложения для объединения двух объектов в один
Решите уравнения сложения с суммами 11-16
Решите уравнение сложения для создания боевого костюма
Решите уравнения сложения с перегруппировкой
Решите уравнение на сложение, чтобы выиграть математическую битву.
Тема B: Подсчитайте или вычтите из десяти, чтобы решить неизвестный результат и общее количество неизвестных задач
Учащиеся изучают стратегии сложения и вычитания по десяти. Они используют знакомые модели блоков с основанием 10, числовую прямую и десять кадров, чтобы проиллюстрировать смысл операций.
Завершите серию связанных уравнений для вычитания 10 на основе модели блоков с основанием 10
Используя модель куба с основанием 10, вы начнете со значения больше 10. Затем вы будете вычитать 1, 2, 3 , и 4 от этого начального числа
Решите уравнения на вычитание через 10, используя числовую прямую
Используя числовую прямую и начав с числа больше 10, вы составите уравнения на вычитание. Скорее всего, вы получите разницу менее 10 каждый раз.
Смоделируйте и решите уравнения вычитания для 10, используя объекты в десятичной рамке
Имея коробку или контейнер из 10 объектов с дополнительными объектами вне коробки или контейнера, вы закончит уравнения вычитания. Вы начнете с общего количества объектов больше 10 каждый раз
Смоделируйте и решите уравнения вычитания по десятичной системе с использованием блоков с основанием 10 (Часть 1)
Используя модель куба с основанием 10, завершите уравнения вычитания. Начните с более чем 10 кубов каждый раз, когда эта область сортируется в столбце десятков и единиц. Затем удалите числовые кубы, эквивалентные числу, которое вы вычитаете из большего числа.
Смоделируйте и решите уравнения вычитания для 10, используя блоки с основанием 10 (Часть 2)
Используя модель куба с основанием 10, завершите уравнения вычитания. Начните с более чем 10 кубов каждый раз, когда эта область сортируется в столбце десятков и единиц. Затем удалите числовые кубики, эквивалентные числу, которое вы вычитаете из большего числа 9.0003
Решите уравнения на вычитание в пределах 20
Используйте модель с основанием 10. Начальное количество кубиков будет эквивалентно уменьшаемому. Десять кубиков будут размещены в столбце десятков, остальные кубики в столбце единиц. Определите, сколько еще кубиков вам нужно удалить из столбца десятков до e
Решите уравнения вычитания через 10
Без использования каких-либо наглядных пособий вы будете решать уравнения вычитания. Каждый раз, когда уравнение начинается с числа больше 10
Решите уравнения вычитания 2-значного минус 1-значного через 10
Используя интерактивные иллюстрации, учащиеся будут решать уравнения вычитания. Все эти уравнения вычитания будут двузначными числами минус однозначные числа
Тема C: Разнообразные задачи с разложением подростковых чисел на 1 десяток и несколько единиц
Учащиеся изучают разрядное значение, складывая и вычитая 10. Они используют множественные представления ( объекты, десятикадр, числовая линия, блоки с основанием 10 и уравнения), чтобы перейти от конкретного к абстрактному. Учащиеся строят свою беглость с +/- фактами внутри, усиливая основную концепцию обмена и используя стратегию «отдыха» на 10. Они также решают +/- задачи, в которых все единицы или все десятки складываются или вычитаются.
Решите уравнения на вычитание, содержащие число 10
Используя модель куба с основанием 10, учащиеся будут решать уравнения на сложение и вычитание. Перед завершением каждого уравнения кубы будут добавляться и вычитаться на экране
Завершать уравнения, которые добавляют или вычитают все десятки или все единицы с моделью блоков с основанием 10 и без нее
С использованием и без использования кубов с основанием 10 вы будете выполнить уравнения сложения и вычитания. Когда используются числовые кубы с основанием 10, они будут либо добавлены, либо вычтены из общей суммы перед завершением уравнений вычитания 9.0003
Добавляйте единицы к числам во второй десятке, используя блоки с основанием 10
Используя кубики с основанием 10, которые расположены в столбцах десятков и единиц, чтобы отразить первое слагаемое, вы будете добавлять числовые кубики к столбцу единиц, равному второму слагаемому . После сложения числовых кубов вы определите окончательную сумму
Вычтите из чисел 11-20, используя блоки с основанием 10 кубов из столбца единиц, равных вычитаемому. После того, как вы уберете числовые кубики, вы определите окончательную разницу
Решите +/- уравнения, в которых используются числа из второго десятка и однозначное число (Часть 1)
В этом упражнении вы вычислите разницу в уравнениях на вычитание. Каждое уравнение включает вычитание однозначных чисел из двузначных чисел
Определение недостающего слагаемого для получения суммы 20 с моделью блоков с основанием 10 и без нее
Используя модель куба с основанием 10, вы определяете, сколько кубов нужно добавить равно 20 числовых кубов. Затем вы завершите соответствующее уравнение сложения
Решите уравнения +/-, в которых используются числа из второго десятка и однозначное число (Часть 2)
В этом упражнении вы будете решать уравнения на сложение и вычитание с двузначным числом меньше 20 и однозначным числом. После правильного ответа на каждое уравнение будет отображаться анимированная иллюстрация.
МОДУЛЬ 3. Упорядочивание и сравнение измерений длины в виде чисел
Тема A: Косвенное сравнение в измерении длины
Учащиеся используют знакомые, реальные объекты, чтобы развить чувство сравнения длины. Они определяют самый длинный, самый короткий, длинный и короткий среди объектов, даже если они не выровнены.
Определите, какой из двух объектов длиннее или короче, и выровняйте объекты, чтобы сравнить их длину.
Сравните длины двух объектов, нажав на более длинный или более короткий из двух вариантов, как указано. Узнайте, как выравнивать объекты, чтобы иметь возможность более точно оценивать длину
Определите утверждение, которое правильно сравнивает длину двух объектов
Выберите правильное утверждение, которое сравнивает длины двух объектов. Даны три варианта оператора
Определить самый короткий или самый длинный объект в невыровненном наборе из трех объектов
Выберите самый длинный или самый короткий объект, как указано, из трех вариантов. Объекты не выровнены
Упорядочить набор выровненных объектов по длине
Перетащите 3 или 4 объекта, чтобы упорядочить их по длине или высоте
Подсчет расстояний в блоках на карте и сравнение
Подсчет расстояний по сетке карты . Введите значение расстояния. Затем сравните два расстояния и укажите, одно из них длиннее или короче другого
Подсчитайте расстояния в блоках на карте и создайте путь, который длиннее или короче заданных путей
Потренируйтесь считать расстояния по сетке карты. Затем создайте путь короче или длиннее заданного пути
Тема B: Нестандартные единицы длины
Учащиеся используют скрепки в качестве нестандартной единицы длины для измерения объектов. Они узнают, что единицы измерения должны измерять расстояние от конечной точки до конечной точки без пробелов или перекрытий.
Счет для измерения длины объектов
Узнайте, как измерять длину объектов, используя нестандартные единицы измерения. Скрепки используются для измерения письменных принадлежностей. Введите количество скрепок, равное длине предмета
Измерение длины объектов от одной конечной точки до другой без зазоров и перекрытий
Узнайте, как измерять длину объектов от одной конечной точки до другой, используя нестандартные единицы измерения. Скрепки используются для измерения без зазоров или перекрытия. Введите количество скрепок, равное длине объекта
Определите, какой из двух объектов измерен правильно
Выберите правильный способ измерения длины по двум картинкам. Скрепки используются как нестандартный блок. Затем введите значение измерения
Правильное измерение длины объектов с помощью укладочных единиц
Измерение длины объектов с помощью скрепок в качестве нестандартной единицы. Единицы измерения должны быть правильно размещены между конечными точками
Тема C: Интерпретация данных
Учащиеся считают реальные объекты и используют подсчетные отметки или гистограммы для их представления. Они интерпретируют данные, представленные в таблицах и графиках, и используют их, чтобы найти общее количество, на сколько больше и на сколько меньше.
Делать отметки для подсчета до 5 объектов
Узнайте, как использовать метки для учета наблюдений. Введите значение, представленное подсчетными метками
Определите общее количество подсчетных меток (Часть 1)
Потренируйтесь в интерпретации значения, представленного подсчетными метками. Введите число, показанное на подсчетах
Определите общее количество отметок (Часть 2)
Интерпретируйте значение отметок как часть гоночной игры. Ввод правильного значения продвигает персонажа вперед в гонке.2141
Создайте таблицу для подсчета животных, изображенных на картинке. Интерпретация значений контрольных отметок на диаграмме и нахождение суммы двух значений
Интерпретация данных в таблице с помощью контрольных отметок (уровень 2)
Определите значение контрольных отметок на диаграмме, а затем определите, какой элемент появился больше или меньше всего . Затем найдите сумму трех значений на диаграмме
Интерпретация данных в гистограмме с 1 категорией
Узнайте, как создать и прочитать гистограмму для одной категории
Создайте гистограмму с двумя категориями и используйте ее для интерпретации данных.
Создайте гистограмму из двух категорий. Определите, какая категория содержит больше или меньше. Найдите разницу между двумя категориями
Интерпретация данных на гистограмме из 3 категорий (Часть 1)
Интерпретация значений, представленных тремя гистограммами. Сравните значения и найдите сумму всех трех категорий
Интерпретация данных на гистограмме с 3 категориями (Часть 2)
Попрактикуйтесь в интерпретации данных, представленных на гистограмме с 3 категориями. Определите, какая полоса показывает определенное число и сумму двух категорий
МОДУЛЬ 4. Размещение значения, сравнения, сложения и вычитания до 40
Тема A: Десятки и единицы
Учащиеся дополнительно изучают понятие о том, что двузначное число состоит из круглого числа (десятки) плюс единицы. Они определяют итоги, разлагают числа, складывают и вычитают. Учащиеся используют знакомые объекты, блоки с основанием 10, десятичные кадры, уравнения и названия чисел вместе с карточками разрядов. Обратите внимание, что используемые «монеты» предназначены для закрепления концепции десятков, пятерок и единиц, а не для распознавания монет.
Прибавление десятков к 40 на основе модели блоков с основанием 10
Имея стержни из 10 кубиков с основанием 10, вы посчитаете количество кубиков десятками. Во время выполнения части этого задания вы сначала определите количество десятков, а затем укажите, сколько кубиков в общей сложности с максимальным общим числом кубиков 40
Определить общее количество до 90 путем подсчета стержней с основанием 10
Данные стержни с основанием 10 10 кубиков, вы будете считать количество кубиков десятками. Во время части этого задания вы сначала определите количество десятков, а затем укажете, сколько всего кубиков, максимум 9.0 кубиков
Определить общее количество объектов путем подсчета объектов с заполнением десяти рамок или без них
В этом упражнении вы определите общее количество объектов, показанных путем заполнения десяти рамок. Под десятикадром я подразумеваю коробку, вмещающую не более 10 предметов.
Определить двузначные круглые числа
Это задание связано с математической идеей круглых чисел или чисел, оканчивающихся на ноль. Учитывая группу чисел, вы определите, какие числа будут считаться круглыми
Определить сумму до 40 путем подсчета десятков и единиц с использованием блоков с основанием 10.
Кубы с основанием 10, рассортированные по палочкам по 10, и оставшиеся кубики, рассортированные по разрозненным одиночным кубикам, подсчитайте количество кубиков. Запишите количество десятков, затем количество единиц и укажите общее количество кубиков. Максимальная сумма будет 40
Определить общее количество до 40 путем подсчета десятков и единиц, используя объекты в десятирамках
Объекты рассортированы по 10 коробкам, а оставшиеся объекты рассортированы по разбросанным одиночным объектам, подсчитайте количество кубиков. Укажите количество десятков, затем количество единиц и укажите общее количество объектов. Максимальная сумма будет 40
Определить итоги путем подсчета десятков и единиц с использованием разбросанных и разнородных объектов в десятикадров
Объекты рассортированы по 10 коробкам, а оставшиеся объекты рассортированы по разбросанным одиночным объектам, подсчитайте количество кубиков. Укажите количество десятков, затем количество единиц и укажите общее количество предметов.
Определите общее количество «монет», используя цифры 10, 5 и 1 значения (10 центов, 5 центов, 1 цент). Затем вы посчитаете количество денег, которое у вас есть в каждой задаче 9.0003
Представлять числа до 40, используя палочки и кубики с основанием 10.
Вам дадут несколько стержней из кубиков с основанием 10 и несколько кубиков с основанием 10. Затем вам будет предложено выбрать определенное количество кубов из большего количества, с которым вы начинаете. Максимальное значение, которое вам нужно будет отсчитать, будет 40
Определите названия чисел до 40 в числовой строке
В этом упражнении вам будет предоставлена числовая строка с существующими числами. Затем вам нужно будет назвать числа, которые следуют за теми, которые уже находятся в строке чисел. Максимальное значение наибольшего числа, которое вам потенциально придется назвать, равно 40 9.0003
Определите отсутствующее число до 40 в числовой строке и определите его письменное название
Вам будет предоставлена числовая строка с существующими номерами. Вам нужно будет заполнить пробелы в числовой строке отсутствующим числом. Затем вам нужно будет назвать эти числа. Максимальное значение наибольшего числа, которое вам нужно назвать, равно 40
Разложите двузначные числа до 40 на десятки и единицы с моделью блоков с основанием 10 и без нее
Вам будут даны различные двузначные числа. Вам будет предложено разложить каждое число на десятки и единицы, или вам будет предложено начать разложение и определить число, которое соответствует каждому разложению
Разложите двузначные числа до 40 в круглое двузначное число плюс единицы
В этом упражнении вам будут даны монеты разного номинала (10 центов, 5 центов, 1 цент). Затем вы подсчитаете количество денег, которое у вас есть в каждой задаче
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 1)
Вы будете добавлять 1 к различным двузначным числам меньше чем 40 в этой деятельности. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения сложения
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 2)
В этом упражнении вы будете прибавлять 10 к различным двузначным числам меньше 40. Вы будете использовать блоки с основанием 10 для моделирования каждого уравнения сложения
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 3)
Вы будете вычитать 1 из различных двузначных чисел меньше 40 в этой деятельности. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения вычитания
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 4)
В этом упражнении вы будете вычитать 10 из различных двузначных чисел меньше 40. Вы будете использовать блоки с основанием 10 для моделирования каждого уравнения вычитания
Решать уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10 (Часть 5)
Вы будете прибавлять 10, прибавлять 1 к, вычитать 1 и вычтите 10 из различных двузначных чисел в этом упражнении. Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения
Тема B: Сравнение пар двузначных чисел
Учащиеся сравнивают и упорядочивают числа, укрепляя свое понимание разрядности и последовательности. Они используют знакомые блоки с основанием 10, числовую прямую и начинают использовать знаки неравенства.
Выровняйте разбросанный набор пронумерованных непоследовательных объектов в порядке возрастания
Вам будет предоставлена разрозненная группа объектов с номерами на них. Затем вам будет предложено расположить эти объекты в линию в порядке 9.0003
Сравните два набора разбросанных объектов, используя > или
< с визуальным пособиемВам будут предоставлены две отдельные группы объектов для сравнения. Вы выберете, какая группа имеет большее количество объектов с помощью наглядного пособия
Выровняйте разрозненный набор пронумерованных, непоследовательных объектов в порядке убывания
Вам будет предоставлена разрозненная группа объектов с номерами на них. Затем вам будет предложено расположить эти объекты в ряд в порядке убывания
Определить пропущенные круглые числа в числовой строке, пронумерованной десятками
Вам будет дана числовая строка, пронумерованная десятками. Затем вам нужно будет заполнить пробелы круглыми числами
Сравните два двузначных числа, используя >,
< или = с моделью блоков с основанием 10 и без нее Вам будут даны два двузначных числа. Затем вы будете использовать знаки неравенства и равенства, чтобы указать, какое число больше, используя числовые блоки с основанием 10 в качестве наглядного пособия.
Поместите двузначные числа в числовую строку
Имея числовую строку, вы будете размещать числа на ней в реальном времени. Каждое число будет двузначным числом.
Сравнение двузначных чисел с использованием знаков
<, = или > с моделью числовой прямой и без нееВ этом упражнении вы будете сравнивать пары двузначных чисел. Сначала вы поместите каждое число в числовую строку, прежде чем определить, какое число больше
Сравните двузначные числа, используя
<, = или >В этом упражнении вы будете сравнивать пары двузначных чисел. Вы будете использовать знаки неравенства и равенства в каждом примере для сравнения чисел
Тема C: Сложение и вычитание десятков
Учащиеся работают с круглыми числами, чтобы закрепить понимание разряда на 10 больше и на 10 меньше. Они используют уравнения и числовую прямую для решения задач на сложение и шаблонов счета.
Решите уравнения сложения, которые добавляют круглые числа к 40
В этом упражнении вы будете складывать пары круглых чисел. Максимальное значение каждой суммы будет 40
Посчитайте назад на 10 по числовой прямой (Часть 1)
Для этого действия будет предоставлена числовая строка. Вам будет дан номер, отмеченный на линии, чтобы начать. Затем, следуя пометкам на числовой строке, вы будете считать в обратном порядке на десятки, чтобы заполнить пропущенное число для каждой задачи. . Вам будет дан номер, отмеченный на линии, чтобы начать. Затем, следуя пометкам в строке чисел, вы будете считать в обратном порядке на десятки, чтобы заполнить 2 пропущенных числа для каждой задачи
Тема D: Добавление десятков или единиц к двузначному числу
Учащиеся полагаются на растущее понимание обмена на модель и решают задачи на сложение двузначных чисел с обменом, используя знакомые модели и новые стратегии.
Решите уравнения, которые добавляют или вычитают 1 или 10 с использованием и без моделирования с использованием блоков с основанием 10
В этом упражнении вы будете добавлять однозначные числа к различным двузначным числам меньше 40. Вы будете использовать числовые блоки с основанием 10 для моделирования каждого уравнения сложения
Смоделируйте и решите уравнения сложения, которые добавляют однозначное число к двузначному, используя числовую прямую
В этом упражнении вы будете складывать однозначные числа к двузначным числам. Вам будет разрешено использовать числовую прямую, чтобы помочь с этими уравнениями сложения
Решите уравнения, которые добавляют однозначное число к двузначному числу (Часть 1)
Вы будете добавлять однозначные числа к двузначным числам в эта деятельность. Однако вам не разрешается использовать числовую прямую или любые другие наглядные пособия, чтобы помочь с этими уравнениями сложения
Выберите соответствующее выражение сложения и сумму
В этом упражнении вы будете складывать однозначные числа с двузначными числами. Вы будете использовать игровую доску, чтобы решать свои проблемы. Как только вы дойдете до другой стороны игрового поля, вы выиграете.
Определите недостающее слагаемое, чтобы сложить его с числом в следующем раунде с моделью блоков с основанием 10 и без нее
В этом упражнении вы будете решать, какое число добавьте к данному двузначному числу, чтобы перейти к следующему круглому номеру. Вы будете делать это с помощью и без помощи базовой 10-кубической модели 9.0003
Определите отсутствующее слагаемое, чтобы добавить его к следующему круглому числу, и решите уравнение (Часть 1)
В этом упражнении вы будете решать, какое число добавить к заданному двузначному числу, чтобы перейти к следующему круглому числу после размещение двузначного числа на числовой прямой. Вы будете делать это с помощью числовой строки
Определите недостающее слагаемое, чтобы добавить к следующему округленному числу, и решите уравнение (Часть 2)
В этом упражнении вы будете решать, какое число добавить к задано двузначное число, чтобы перейти к следующему раунду. Вы будете делать это без использования каких-либо наглядных пособий
Определите отсутствующее слагаемое, чтобы добавить его к следующему круглому числу, и решите уравнение (часть 3)
С помощью числовой строки вы определите, что нужно добавить к заданному двузначному числу, чтобы получить следующее круглое число. Вам также нужно будет выяснить, какая первая цифра этого круглого числа
Моделируйте и решайте двузначные уравнения сложения с обменом, используя блоки с основанием 10
Используя модель куба с основанием 10, вы будете решать уравнения сложения. Вы решите, сколько второго слагаемого потребуется, чтобы получить первое слагаемое для следующего круглого числа. Затем вы добавите оставшуюся сумму, чтобы получить окончательную сумму
Решите уравнения сложения через 10, используя числовую прямую
Используя числовую прямую, вы будете решать уравнения сложения. Вы решите, сколько второго слагаемого потребуется, чтобы получить первое слагаемое для следующего круглого числа. Затем вы сложите оставшиеся блоки, чтобы получить окончательную сумму
Решите уравнения сложения через 10, разделив слагаемое, чтобы получить десять
Без использования каких-либо наглядных пособий, вы будете решать уравнения сложения. Вы решите, сколько вторых слагаемых потребуется, чтобы получить первое сложение для следующего круглого числа. Затем вы добавите оставшиеся блоки, чтобы получить окончательную сумму
Решите уравнения для сложения однозначного числа с двузначным (Часть 2)
В этом упражнении вы будете складывать однозначные числа с двузначными числами. Вы будете использовать интерактивную иллюстрацию, чтобы мотивировать вас, когда вы будете решать эти уравнения сложения. Максимальное значение суммы будет 40
Тема E: Добавление десятков и единиц к двузначному числу
Учащиеся синтезируют свои знания из предыдущей темы, чтобы складывать десятки и единицы к двузначному числу. Они поддерживаются знакомой моделью блоков с основанием 10 и пошаговым руководством.
Смоделируйте и решите уравнения сложения двузначных чисел в пределах 40, используя кубики с основанием 10.
В этом упражнении вы будете использовать кубы с основанием 10. Вы будете складывать пары двузначных чисел вместе. Максимальное значение этих сумм будет 40
Решите двузначные уравнения сложения в пределах 40 с моделированием и без него с использованием блоков с основанием 10
Для этого задания не будет наглядных пособий. Вы будете складывать пары двузначных чисел вместе. Максимальное значение этих сумм будет 40
Решите уравнения сложения двузначных чисел с заменой путем сложения десятков и единиц по отдельности
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это, разделив десятки и единицы в числах и сложив их отдельно. Максимальное значение этих сумм будет 40
Решите уравнения сложения двузначных чисел
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это без каких-либо наглядных пособий. Максимальное значение этих сумм будет 40
Смоделируйте и решите уравнения сложения 2-значных чисел с обменом, используя блоки с основанием 10 (Часть 1)
В этом упражнении вы будете использовать модель куба чисел с основанием 10, чтобы складывать пары двузначных чисел. Вы будете разделять числа на десятки и единицы, используя числовые кубики в качестве наглядного пособия.
Моделируйте и решайте уравнения сложения двузначных чисел с заменой элементов с основанием 10 (Часть 2)
Вы будете складывать пары двузначных чисел. чисел с использованием кубов с основанием 10. Первое сложение будет разделено на десятки и единицы перед началом каждой задачи. Рассортируйте второе слагаемое по десяткам и единицам перед добавлением пары двузначных чисел
Решите уравнения сложения двузначных чисел с заменой путем сложения десятков и единиц по отдельности
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это, разделив десятки и единицы в числах и сложив их отдельно. Максимальное значение этих сумм будет 40
Решите уравнения, которые складывают двузначные числа через 10
В этом упражнении вы будете складывать пары двузначных чисел. Вы сделаете это без каких-либо наглядных пособий. Максимальное значение этих сумм, возможно, будет больше 40
МОДУЛЬ 5. Идентификация, составление и разбиение фигур
Тема A: Атрибуты фигур
Учащиеся изучают основные атрибуты фигур: линии, замкнутые фигуры, стороны и углы. Они учатся определять треугольники, прямоугольники, квадраты, трапеции и шестиугольники.
Определение линий
Научитесь различать линии. Выберите линии в различных ориентациях из группы, содержащей линии и кривые
Определение изогнутых линий
Научитесь определять кривые. Выберите кривые в различных ориентациях и формах из группы, содержащей линии и кривые
Определение закрытых фигур
Определение открытых и закрытых фигур. Выберите все незамкнутые или закрытые фигуры из набора, содержащего обе формы
Определите фигуры с заданным количеством сторон
Выберите все фигуры с заданным количеством сторон из набора, содержащего множество закрытых фигур
Подсчитайте количество сторон и углов фигур
Назовите признаки треугольника, прямоугольника и шестиугольника. Выберите открытую или замкнутую форму и укажите, сколько у нее сторон и углов.
Определение шестиугольников
Изучение характеристик шестиугольника. Затем выберите те фигуры, которые являются шестиугольниками
Определите треугольники, прямоугольники, квадраты и шестиугольники
Сортируйте треугольники, прямоугольники, квадраты и шестиугольники, нажав на существо, которое ест каждый из этих типов фигур
Определите трапецию
Научитесь определять трапецию. Выберите трапецию из двух четырехугольников, затем укажите признаки трапеции
Нарисуйте заданные фигуры
Попрактикуйтесь в рисовании различных фигур в соответствии с указаниями на доске для колышков
Определите данные фигуры
Выберите имя многоугольника из двух вариантов
Определите формы повседневных предметов
Получив изображение объекта реального мира, выберите правильное название многоугольника из 4 вариантов
Тема Б: Половинки и четверти прямоугольников и окружностей
Учащиеся учатся определять и считать равные части в разделенной фигуре. Они узнают названия половин и четвертей и используют эти названия для идентификации фигур, разделенных на части.
Определить фигуру, которая разделена на половинки (Уровень 1)
Решить, какая из двух одинаковых или разных фигур разделена на две равные части, называемые половинками
Определить фигуру, которая разделена на половинки (Уровень 2)
Решить какая из двух одинаковых или разных фигур разделена пополам
Определить количество равных частей в разделенной фигуре
Дана фигура, разделенная на равные части, определить общее количество равных частей до 4
Определить фигуру, которая разделена на четверти
Решить, какая из двух одинаковых или разных фигур разделена на четыре равные части, называемые четвертями
Тема C: Использование половинок для определения времени
ход и идентификация времени. Они изучают части часов и различные типы обозначения времени: X:XX, X часов, X-тридцать и половина первого X.
Определять части часов и время с точностью до часа на часах
Имея цифровые или аналоговые часы, учащиеся определяют время с точностью до часа, а также часовую и минутную стрелки
Определяют ежедневный и ежечасный ход времени
Понимают, что день длится с полуночи до полуночи, и как выглядит это время на аналоговых часах. Определение времени с точностью до часа по аналоговым часам
Определение времени с точностью до часа на цифровых и аналоговых часах
Определение времени с точностью до часа на цифровых или аналоговых часах. Выберите одни из трех цифровых часов, которые соответствуют времени на аналоговых часах
Определение времени с точностью до часа на аналоговых часах
Выберите одни из трех аналоговых часов, которые показывают заданное время с точностью до часа. Переместите часовую стрелку часов, чтобы показать заданное время.
Определите количество минут на аналоговых часах
Определите, сколько минут прошло на аналоговых часах. Понимать, что в часе 60 минут, а в получасе 30 минут
Определять время с точностью до получаса на аналоговых часах и использовать соответствующий язык (Часть 1)
Студенты изучают концепцию получаса на аналоговых часах. Они также изучают язык половины X. Затем учащиеся учатся определять время с точностью до получаса на аналоговых часах
Определять время с точностью до получаса на аналоговых часах и использовать соответствующий язык (Часть 2)
Учащиеся учатся говорить X тридцать в качестве альтернативы половине X. Затем учащиеся тренируются определять время с точностью до получаса на аналоговых часах и выбирать правильное соответствие цифровому времени
Определять время с точностью до получаса на цифровых и аналоговых часах
Определить время с точностью до получаса на аналоговых и цифровых часах, используя X-тридцать и половину десятого. Показывать время с точностью до часа или получаса на аналоговых часах
Определить время на часах
Определить время до час или полчаса на аналоговых или цифровых часах, набрав или выбрав время. Используйте обозначение X-тридцать, половина первого X, X часов или X:XX
МОДУЛЬ 6. Поместите значение, сравнение, сложение и вычитание до 100
Тема A: Числа до 120
Учащиеся используют знакомые представления (объекты, десятичные кадры, десятичные блоки, числовую прямую, карточки с разрядными значениями, названия чисел и уравнения), чтобы расширить свое понимание разрядных значений на более высокие числа в пределах 100. Они начинают строить свою мысленную модель сто диаграммы, понимая взаимосвязь между числами в столбцах и строках. Они укрепляют понимание того, что двузначные числа состоят из круглого числа (или десятков) плюс единицы.
Определить отсутствующее круглое число до 100 в числовой строке и определить его письменное название
В этом упражнении вы будете использовать числовую прямую. Вы будете называть числа по десяткам, начиная с нуля и заканчивая 100
Расположите круглые числа, как цифрами, так и прописью, на вертикальной числовой строке
В этом упражнении вы будете размещать круглые числа от нуля до 100 на числе линия. Цифры будут написаны на дирижаблях, которые вы «приземлитесь» на числовой линии
Определите двузначные суммы на основе блоков с основанием 10 и карточек с номиналом
Для этого задания будут использоваться кубики с основанием 10. Вам будет предоставлено определенное количество 10 кубиков с числами и определенное количество кубиков с отдельными числами, чтобы определить общее количество кубиков с числами 9.0003
Определить 2-значное количество объектов в блоках из десяти кадров или с основанием 10
Вам будут даны группы из 10 объектов, расположенных в 10-кадрах, а также отдельные объекты за пределами 10-кадров. Затем вы будете использовать 10-кадры и отдельные объекты для подсчета общего количества объектов
Определить общее количество путем подсчета объектов с заполнением или без заполнения десятикадров
Десятокрамки будут использоваться для помощи в определении общего количества объектов для эта деятельность. Вы закончите заполнение как можно большего количества 10-кадров и добавите оставшиеся объекты в объекты, расположенные в 10-кадрах
Представление заданного двузначного числа с помощью блоков с основанием 10
Для этого задания будут использоваться кубы с основанием 10. Вы будете использовать 10-кубические стержни и отдельные числовые кубики для представления суммы, указанной в каждой задаче.
Определить двузначные круглые числа
В этом упражнении вы будете выбирать круглые числа, меньшие или равные 100. Вам будет дана группа чисел, и вам нужно будет выбрать круглые числа из каждой группы
Разложить двузначные числа на круглое число плюс единицы
Для начала этой деятельности вам будет предоставлена серия двузначных чисел до 100. Вы разобьёте каждое число на круглое число и однозначное число.
Определите двузначное количество блоков с основанием 10, подсчитав десятки и единицы
Для этого упражнения будет использоваться модель куба числа с основанием 10. Вам будет предоставлено определенное количество 10-кубовых палочек и отдельных числовых кубиков. Затем вы определите, сколько всего кубиков
Определите общее количество, считая десятки и единицы, используя разбросанные и неодинаковые предметы в десятикадровом формате
Для этого задания будут использоваться группы похожих и непохожих объектов, расположенных внутри и вне 10-кадров. Затем вы подсчитаете общее количество объектов в целом.
Разложите двузначные числа на десятки и единицы с моделью блоков с основанием 10 и без нее
Для этого задания будут использоваться кубы с основанием 10. С помощью этой модели числового куба разложите двузначные числа. Каждое число будет либо представлено числовыми кубами в начале, либо вам придется представлять каждое число числовыми кубами перед 9-м числом.0003
Решите +/- 1 и +/- 10 уравнений с моделью блоков с основанием 10 и без нее
В этом упражнении вы будете прибавлять 10, прибавлять 1, вычитать 1 и вычитать 10 из различных двузначных чисел. . Вы не сможете использовать числовые блоки с основанием 10 для моделирования каждого уравнения. Максимальное значение каждой окончательной суммы будет 99
Считайте вперед и назад в пределах десяти по числовой строке
Числовая строка будет использоваться, чтобы помочь Вам со счетом в прямом и обратном порядке. По мере того, как вы будете считать вперед и назад, вы будете заполнять данные пробелы в числовой строке, предоставленной
Выровняйте разрозненный набор пронумерованных непоследовательных объектов в порядке возрастания
С помощью наглядного пособия вы будете располагать числа в порядке возрастания. Числа в этом упражнении будут меньше 100
Выровняйте разрозненный набор пронумерованных непоследовательных объектов в порядке убывания
С помощью наглядного пособия вы будете располагать числа в порядке убывания. Числа в этом упражнении будут меньше 100
Сравните двузначные суммы с набором из 10, 5 и 1 монет
Имея определенную сумму денег в монетах в 1 цент, 5 центов и 10 центов и группу предметов с различной ценой, вы определите, какой предмет вы можете купить на указанную сумму денег
Определить пропущенные числа на сотенной диаграмме
В начале этого задания вам будет предоставлена в основном заполненная таблица чисел в порядке от 1 до 100. Затем вы заполните пропуски недостающими числами
Определите на 10 меньше, на 10 больше, на 1 меньше и 1 больше на сотенной таблице с ограниченной нумерацией
В начале этого задания вам будет предоставлена слегка заполненная таблица чисел в порядке от 1 до 100. Затем вы заполните пропуски недостающими числами
Добавление круглых чисел с использованием блоков и полос
Для этого упражнения будет использоваться модель кубов с основанием 10. Вы будете добавлять пары двузначных чисел. Максимальное значение каждой суммы будет меньше 100.
Сложение и вычитание круглых чисел
Для этого задания будет использоваться модель кубов с основанием 10. В этом упражнении вы будете добавлять круглые числа. Максимальное значение каждой суммы будет 90
Решите уравнения для сложения двузначных чисел через 10
В центре внимания этого упражнения будет сложение пар двузначных чисел. Некоторые проблемы связаны с использованием фактов оборота. Если вы ответите на вопрос неправильно, вы будете использовать числовые кубы с основанием 10, чтобы помочь ответить на вопрос правильно
Решите уравнения, которые добавляют или вычитают круглое число, используя таблицу сотен
Для этого упражнения будет предоставлена таблица сотен, чтобы завершить сложение и проблемы с вычитанием. Вы будете складывать и вычитать круглые числа из некруглых двузначных чисел
Определите пропущенные числа в столбцах таблицы с ограниченной нумерацией.
В начале этого задания вам будет предоставлена таблица сотен. Вам нужно будет заполнить столбцы этой таблицы, отсчитывая по десяткам в каждом столбце
Определите еще 1 и еще 10 на сотенной диаграмме с ограниченной нумерацией
В этом упражнении вам будет дана сотенная диаграмма. Вы будете добавлять единицу или десять к каждому числу, указанному в таблице, чтобы перейти от одной стороны диаграммы к другой 9.0003
Завершите и решите уравнения, которые добавляют или вычитают круглое число, используя диаграмму сотен.
В этом упражнении вам будет дана диаграмма сотен. Вы будете использовать эту таблицу для помощи в добавлении круглых чисел к некруглым числам
Определите пропущенные числа в сотенной таблице и разложите их на десятки и единицы
Для этого упражнения вам будет предоставлена сотенная таблица. Вы определите, какое число должно быть введено в пустое место на сотенной диаграмме. Затем вы разложите это же число на десятки и единицы
Считать вперед от 100 и выше 100 в числовой строке
Вам будет предоставлена числовая строка с большинством заполненных значений. Вам нужно будет заполнить пробелы, двигаясь вперед по числовой строке, используя числа, указанные на числовая строка уже. Вы будете вводить значения, которые время от времени превышают 100
Посчитайте в обратном порядке от 100 и выше 100 в числовой строке
Вам будет предоставлена числовая строка с большинством заполненных значений. Вам нужно будет заполнить пробелы, перемещая назад по числовой строке, используя числа, уже представленные в числовой строке. Вы будете предоставлять значения, которые превышают 100 раз в 9 раз.0003
Определите отсутствующее трехзначное число в числовой строке и его письменное название.
Для этого действия будет предоставлена числовая строка с уже помеченными большинством значений. Для каждого вопроса вы будете заполнять одно пропущенное значение. Затем вы будете называть число словами
Определить общее количество объектов в десяти кадрах за пределами 100
Вам будут предоставлены объекты, предварительно рассортированные по 10 кадрам, и некоторые объекты, которые отложены в сторону сами по себе . Вам нужно будет определить, сколько объектов находится в коробках и сколько в стороне, чтобы определить общее количество объектов
Подсчитайте палочки с основанием 10 сверх 100
Кубики с основанием 10, сгруппированные в палочки длиной 10 кубов, будут доступны в начале этого задания. Затем вам нужно будет определить, сколько всего кубиков. Каждый раз ответом будет круглое число.
Определяйте суммы, превышающие 100, используя плоскость с основанием 10, стержни и кубики
Кубики с основанием 10, сгруппированные в 10 кубиков, стержни вместе с отдельными кубиками будут даны вам в начале игры. эта деятельность. Используйте оба этих наглядных пособия, чтобы подсчитать общее количество кубиков. Некоторые ответы на вопросы будут более 100
Тема B: Прибавление к 100 Использование разрядных значений Понимание
Учащиеся используют знакомые блоки с основанием 10, числовой ряд и уравнения для работы с круглыми числами. Для решения задач они полагаются на счет, позиционное значение и навыки сложения/вычитания. Учащиеся используют знакомые манипуляторы для решения задач на сложение двузначных чисел с обменом и без обмена. Они также решают задачи на вычитание двузначных чисел без обмена.
Решайте уравнения, прибавляя или вычитая 10 из круглого числа 9 или из него2141
В этом упражнении вы будете прибавлять и вычитать 10 из круглых чисел. Вы будете использовать кубики с основанием 10, чтобы помочь с некоторыми задачами, но некоторые задачи не позволяют использовать эти кубики
Сложение и вычитание круглых чисел с моделью блоков с основанием 10 и без нее
Сложение и вычитание круглых чисел будет в центре внимания этого занятия. Вы будете использовать числовые кубики с основанием 10, чтобы помочь с некоторыми задачами, но некоторые задачи не позволяют использовать эти кубики
Запишите и решите уравнения, которые добавляют круглое число к двузначному числу на основе модели блоков с основанием 10.
Целью этого упражнения будет добавление круглого числа к другим двузначным числам. Вы смоделируете эти уравнения сложения, используя числовые кубы с основанием 10
Запишите и решите уравнения, которые вычитают круглое число из двузначного числа на основе модели блоков с основанием 10
Вычитание круглого числа из других двузначных чисел будет основной акцент в этом упражнении. Вы смоделируете эти уравнения сложения, используя числовые кубы с основанием 10 9. 0003
Моделируйте и решайте уравнения, которые добавляют круглое число к двузначному числу, используя блоки с основанием 10. Вы будете добавлять круглые числа к другим двузначным числам.
Моделируйте и решайте уравнения для сложения двух двузначных чисел, используя блоки с основанием 10.
Моделирование и решение уравнений сложения будет основной целью этого занятия. Вы будете складывать пары двузначных чисел вместе
Моделирование и решение уравнений сложения двух двузначных чисел с использованием блоков с основанием 10.
Моделирование и решение уравнений сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубов вам нужно для представления второго числа, прежде чем складывать пару чисел.
Смоделируйте и решите уравнения для сложения двух двузначных чисел с использованием блоков с основанием 10.
Смоделируйте и решите уравнения сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубиков вам нужно для представления второго числа, прежде чем складывать пару чисел
Сложите 10 с помощью десятичной рамки (в пределах 100)
Вам будет предоставлено определенное количество объектов, чтобы начать это задание. Какое-то их количество будет помещено в 10-кадровые коробки, а какое-то нет. Вам необходимо определить, сколько всего объектов
Смоделировать и решить уравнения сложения двузначных чисел с обменом и без, используя блоки с основанием 10
Кубы с основанием 10 будут использоваться для сложения пар двузначных чисел в этом упражнении. Вы будете сортировать кубы по столбцам десятков и единиц, прежде чем в конечном итоге сложить пару чисел вместе
Моделируйте и решайте уравнения сложения двузначных чисел с обменом и без, используя блоки с основанием 10.
Моделируйте и решайте уравнения сложения. Сложите пары двузначных чисел вместе. Одно из двух чисел будет смоделировано для вас с помощью кубов с основанием 10. Определите, сколько кубиков вам нужно для представления второго числа, прежде чем складывать пару чисел
Решить уравнения сложения двузначных чисел с заменой и без замены путем сложения десятков и единиц по отдельности
Сложение пар из двух двузначных чисел — цель этого упражнения. . Однако числа будут разделены на десятки и единицы, чтобы вы могли добавить их отдельно, прежде чем вычислить окончательную сумму
Тема C: Монеты и их номиналы
Учащиеся изучают орел и решку монеты пенни, никеля, десятицентовой монеты и четвертака. Они узнают ценность каждой монеты, как считать их коллекцию и как считать смешанную коллекцию монет. Учащиеся сопоставляют изображение монеты, имя и номинал.
Определите монету и ее стоимость.
Изучите внешний вид обеих сторон монеты. Поймите его стоимость как один цент и рассчитайте общую стоимость до 6 пенни
Определите десятицентовую монету и ее стоимость
Исследуйте внешний вид монеты с обеих сторон. Поймите ее стоимость как десять центов и рассчитайте общую стоимость до 6 десятицентовиков
Сопоставьте пенни или десятицентовую монету с ее названием, внешним видом и стоимостью
Выберите название монеты, изображение и достоинство, которые все представляют десятицентовую монету или пенни
Определить общую стоимость набора десятицентовиков и пенни
При заданном наборе десятицентовиков и пенни введите общую стоимость
Обмен одной десятицентовой монеты на десять пенни
Считай и меняй пенни на десять центов. Используйте пенни и десятицентовики, чтобы показать в общей сложности 12 центов двумя разными способами.
Определите монету и ее стоимость
Изучите внешний вид обеих сторон монеты. Поймите ее стоимость как пять центов и рассчитайте общую стоимость до 6 пятицентовых монет
Сопоставьте пенни, пятицентовую монету или десятицентовую монету с ее названием, внешним видом и стоимостью (Часть 1)
Определите, соответствует ли название монеты показанному изображению. Сопоставьте пенни, десять центов и пятицентовиков с их названием и номиналом 9.0003
Сопоставьте пенни, никель или десятицентовик с их названием, внешним видом и номиналом (Часть 2)
Определите, соответствует ли показанная монета заданному названию. Сопоставьте пенни, десятицентовики и пятицентовые монеты с их названием и номиналом
Определите пенни, пятицентовые монеты или десятицентовые монеты по цвету или размеру
Определите пенни, пятицентовые монеты и десятицентовые монеты из коллекции монет, даже если детали монет размыты
Обмен пенни, пятицентовика и десятицентовика
Подсчет и обмен пенни, пятицентовика и десятицентовика. Подсчитайте сумму коллекции пятаков и пенни
Показать заданную сумму, используя пятаки и пенни
Получив общее значение, выберите пятаки и пенни, чтобы получить сумму
Определите четвертак и его стоимость
Исследуйте внешний вид обеих сторон четверти. Поймите его стоимость как двадцать пять центов. Сортировка пенни, пятицентовиков, десятицентовиков и четвертаков по номиналу
Математика для первого класса: Дополнение
Первый класс — очень важный год, когда учащиеся закладывают прочный фундамент на пути к математическим знаниям. Одной из наиболее фундаментальных областей математики, которую необходимо освоить учащимся, являются основные операции. Студентам нужно МНОГО возможностей для практики, чтобы стать опытными в освоении фактов сложения. В этом занятии по математике учащиеся будут использовать различные практические математические игры и практические страницы NO PREP, чтобы помочь достичь мастерства.
В этом разделе по математике учащиеся научатся:
*Складывать в пределах 20, чтобы решать текстовые задачи
*Решать текстовые задачи на сложение 3 чисел (сложение)
*Применять коммутативные и ассоциативные свойства сложение
*Сложение в пределах 20 и демонстрация беглости сложения в пределах 10
*Разложение и составление чисел
*Понимание значения знака равенства и истинности или ложности уравнений
*Нахождение неизвестного числа в задаче на сложение
*Используйте различные стратегии, чтобы быстрее решать математические задачи.
Развлекательный модуль «Математика для первоклассников 2» содержит 31 практический математический центр и 88 практических страниц, которые помогут научить, закрепить и освоить базовое сложение до 20 .0003
Модуль 4: Разрядное значение
Модуль 5: Геометрия
Модуль 6: Измерение
Модуль 7: Деньги
Модуль 8: Расчет времени
Модуль 9: Графики и данные
СОХРАНИТЕ $$$!
ВКЛЮЧЕНЫ ВСЕ 9 УСТАНОВОК!
ДАВАЙТЕ ПОСМОТРИМ НА МАТЕМАТИЧЕСКИЕ ЦЕНТРЫ ДЛЯ БЛОКА 2 В ДЕЙСТВИИ…
ЦЕНТР НОМЕР 1: ДОБАВЛЕНИЕ СУММ КЛИП КАРТОЧКИ
Прочтите каждую дополнительную задачу Если сумма проблемы совпадает с суммой в середине карточки, обрежьте ее.
ЦЕНТР НОМЕР 2: ДОБАВЛЕНИЕ ВРАЩЕНИЯ И ГРАФИКА
Вращение спиннера. Решите задачу и нарисуйте сумму.
ЦЕНТР НОМЕР 3: БРОСИТЬ, ДОБАВИТЬ И НАКРЫТЬ
Бросьте кубик. Решите задачу на сложение в ряду выпавшего числа. Запишите ответ в протокольный лист.
ЦЕНТР НОМЕРА 4: ОБВЕДИТЕ СУММЫ
Обведите числа, которые в сумме дают указанную сумму. Раскрась звездочку для каждого найденного набора. Напишите числовое предложение.
ЦЕНТРАЛЬНАЯ ЦИФРА 5: СДЕЛАЙТЕ 10 И ДОБАВЬТЕ
Посмотрите на первую цифру. Решите, какое число нужно прибавить, чтобы получилось 10, и запишите его в первый пузырь. Затем завершите числовое соединение. Заполните уравнение, используя новые числа.
ЦЕНТР НОМЕР 6: Я ШПИОН ДОПОЛНИТЕЛЬНЫЕ ФАКТЫ
Используя увеличительное стекло, найдите дополнительные факты на картинке. Решите задачи и запишите.
ЦЕНТРАЛЬНЫЙ НОМЕР 7: ДОПОЛНЕНИЕ ДО 20
Переверните карту. Используйте данные манипуляторы, чтобы решить задачу на сложение.
ЦЕНТР НОМЕР 8: СУММЫ МОРОЖЕНОГО
Решите задачи на шариках мороженого и рассортируйте их по правильным конусам мороженого.
ЦЕНТР НОМЕР 9: СЛОЖЕНИЕ КРЕСТИКИ-НОЛИКИ
По очереди с другом решайте задачи на сложение. Каждый игрок использует свой цвет, чтобы написать ответы. Выигрывает тот, кто первым наберет три подряд.
ЦЕНТРАЛЬНЫЙ НОМЕР 10: ГОЛОВОЛОМКИ С КАРАНДАШАМИ
Сопоставьте задачу с суммой, чтобы решить головоломку с карандашом.
ЦЕНТРАЛЬНЫЙ НОМЕР 11: ФАКТЫ
Вращайте оба спиннера. Сложите числа и запишите математический факт. Затем напишите флип-флоп факт.
ЦЕНТР НОМЕР 12: ДОМИНО ФАКТЫ
Выберите домино. Запишите задачу на сложение. Поменяйте местами числа, чтобы показать свойство коммутативности.
ЦЕНТР НОМЕР 13: ДЕСЯТЬ ПЛЮС ВАШ ВРАЩАТЕЛЬ
Вращайте спиннер. Добавьте десять к числу, которое вы раскрутили. Закройте сумму на доске.
ЦЕНТР НОМЕР 14: ДВОЙНАЯ ИГРА
Играйте с несколькими игроками. По очереди бросайте кубик. Переместите свою игровую фишку на количество делений в вашем броске. Решите задачу на сложение. Если вы ответили правильно, закрасьте место маркером. Если вы ошиблись, оставьте поле пустым.
ЦЕНТР НОМЕР 15: ДУБЛЫ ПЛЮС 1 НАСТОЛЬНАЯ ИГРА
Играйте с несколькими игроками. По очереди бросайте кости. Переместите свою игровую фишку на количество делений в вашем броске. Решите задачу на сложение. Если вы ответили правильно, закрасьте место маркером. Если вы ответили неправильно, оставьте поле пустым.
ЦЕНТРАЛЬНАЯ ЦИФРА 16: ПАРЫ ПО ДЕСЯТКАМ И БОЛЬШЕ
Найдите на полоске два числа, которые в сумме дают десять. Обведите числа. Затем добавьте третью цифру. Запишите свой ответ в регистрационном листе.
ЦЕНТРАЛЬНАЯ ЦИФРА 17: ДОБАВЬТЕ ОТСУТСТВУЮЩЕЕ ДОБАВЛЕНИЕ
Напишите число, которое нужно прибавить к верхнему числу, чтобы получилось 10. Сложите числа. Запишите свой ответ в регистрационном листе.
ЦЕНТР НОМЕР 18: ДОМИНО: НАЙТИ РАВНОЕ
Выбери домино. Добавьте точки. Найдите другую костяшку домино с такой же суммой. Запишите оба уравнения в регистрационный лист.
ЦЕНТРАЛЬНОЕ НОМЕР 19: УРАВНЕНИЯ — ИСТИНА ИЛИ ЛОЖЬ
Определите, верны или нет уравнения сложения. Отсортируйте их по правильной карточке. Запишите свои ответы в регистрационном листе.
ЦЕНТРАЛЬНЫЙ НОМЕР 20: ЗАПОМНИТЕ-СООТВЕТИТЕ СУММУ
Положите все карты лицевой стороной вниз. Игроки по очереди переворачивают по две карты. Если суммы карт совпадают, игрок получает обе карты. Запишите эквивалентные уравнения на листе для записей.
ЦЕНТРАЛЬНОЕ НОМЕР 21: УРАВНЕНИЯ БАЛАНСИРОВКИ
Найдите две задачи на сложение, которые имеют одинаковую сумму для балансировки на шкале. Поместите их на весы и запишите уравнения на листе для записей.
ЦЕНТРАЛЬНЫЙ НОМЕР 22: DUBLES PLUS 1
Каждый из двух игроков переворачивает карту и закрывает соответствующее число на игровом поле. Продолжайте, пока доска не будет заполнена.
ЦЕНТРАЛЬНЫЙ НОМЕР 23: ДУБЛЫ ПЛЮС 2
Каждый из двух игроков переворачивает карту и закрывает соответствующее число на игровом поле. Продолжайте, пока доска не будет заполнена.
ЦЕНТРАЛЬНЫЙ НОМЕР 24: СРАВНИТЕ СУММЫ С 10
Переверните карточку. Добавьте числа. Решите, будет ли сумма меньше, больше или равна 10. Рассортируйте карты на коврике.
ЦЕНТРАЛЬНЫЙ НОМЕР 25: ДОПОЛНЕНИЕ ДЛЯ БОУЛИНГА
Бросьте два кубика и сложите их. Вычеркните 1 или 2 кегли, сумма которых равна вашему броску. Продолжайте играть, пока не сможете устранить сумму. Запишите свой окончательный счет на шаре для боулинга. Идеальный результат равен 0.
ЦЕНТРАЛЬНОЕ ЧИСЛО 26: ОТСУТСТВУЮЩИЕ ДОБАВЛЕНИЯ
Завершите уравнение, вставив пропущенное слагаемое.
ЦЕНТРАЛЬНЫЙ НОМЕР 27: ДОПОЛНЕНИЕ ДЛЯ ПИЦЦЫ
Сосчитайте количество пепперони. Добавьте число в углу. Найдите соответствующее уравнение.
ЦЕНТРАЛЬНЫЙ НОМЕР 28: ДОМИНО ФАКТЫ
Выберите домино из стопки. На листе для записей нарисуйте точки. Напишите семью фактов для домино.
ЦЕНТРАЛЬНЫЙ НОМЕР 29: ВРАЩАЙТЕ И ДОБАВЬТЕ 3 ЧИСЛА
Вращайте спиннер. Напишите число в поле. Сложите три числа вместе.
ЦЕНТР НОМЕР 30: ЗАДАЧИ 3 ДОПОЛНЕНИЯ
Выберите 4 задачи из стопки. Покажите, как вы их решили, на листе для записи.
ЦЕНТРАЛЬНЫЙ НОМЕР 31: ЗАДАЧИ С ОТСУТСТВУЮЩИМИ ДОБАВЛЕНИЯМИ
Выберите 4 задачи со словами из стопки. Покажите, как вы их решили, на листе для записи.
В БЛОК 2 НЕ ВКЛЮЧЕНО 88 СТРАНИЦ ПОДГОТОВИТЕЛЬНЫХ ПРАКТИК
К каждой странице прилагается стандарт уровня обучения, чтобы вы ТОЧНО знали, что изучаете! Вы можете быть уверены, что ВСЕ стандарты для первого класса соблюдаются!
Давайте взглянем на некоторые страницы NO PREP «в действии»…
HOW DO I ORGANIZE THE UNITS?
Я решил хранить математические центры в контейнерах Sterilite, потому что они не занимают слишком много места.