Производная e x 2x 3. Производная e в степени x и показательной функции
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное)
 Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
12. Производная арктангенса Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной
функции как производной простой функции. Поэтому
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Вычисление производной — одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:- Таблица производных экспоненциальных и логарифмических функций

Производные простых функций
1. Производная от числа равна нулюс´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. nx. Формулы производных высших порядков.
nx. Формулы производных высших порядков.
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′
= e x
.
Производная показательной функции с основанием степени a
равна самой функции, умноженной на натуральный логарифм от a
:
(2) .
Вывод формулы производной экспоненты, e в степени x
Экспонента — это показательная функция, у которой основание степени равно числу e
,
которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e
в степени x
:
y = e x
.
Эта функция определена для всех .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .
Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.
Сделаем подстановку .
Тогда ;
.
В силу непрерывности экспоненты,
.
Поэтому при ,
.
В результате получаем:
.
Сделаем подстановку .
Тогда .
При ,
.
И мы имеем:
.
Применим свойство логарифма (5):
.
Тогда
.
Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a
.
Мы считаем, что и .
Тогда показательная функция
(8)
Определена для всех .
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции
и логарифма
.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.
Отсюда видно, что производная n-го порядка также равна исходной функции:
.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a
:
.
Мы нашли ее производную первого порядка:
(15) .
Дифференцируя (15), получаем производные второго и третьего порядка:
;
.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на .
Поэтому производная n-го порядка имеет следующий вид:
.
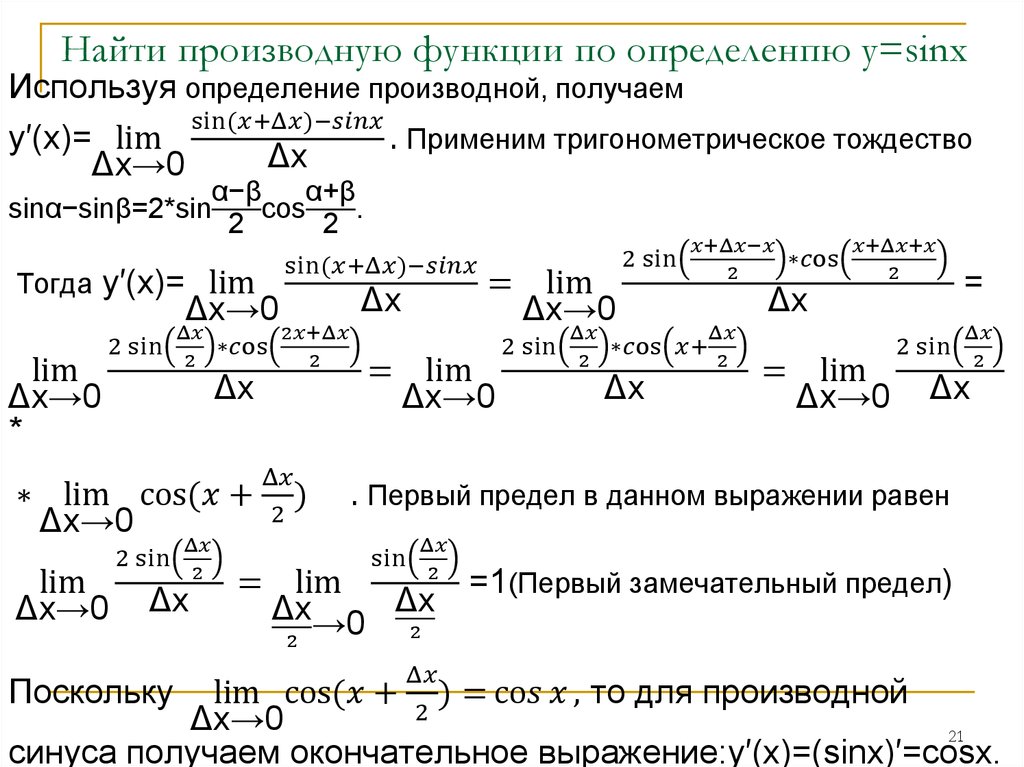
Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.
Производная по переменной x от синуса x равна косинусу x:
(sin
x)′ = cos
x
.
Доказательство
Для вывода формулы производной синуса, мы воспользуемся определением производной:
.
Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и ,
то
(4) .
Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
;
.
Тогда
;
;
;
.
Теперь сделаем подстановку .
При ,
.
Применим первый замечательный предел (1):
.
Сделаем такую же подстановку и используем свойство непрерывности (2):
.
Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):
.
Формула производной синуса доказана.
Примеры
Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2
x
и y = sin 3
x
.
Пример 1
Найти производную от sin 2x .
Решение
Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.
Применяем .
.
Здесь .
Ответ
(sin 2x)′ = 2 cos 2x.
Пример 2
Найти производную от синуса в квадрате:
y = sin 2
x
.
Решение
Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.
.
Здесь .
Можно применить одну из формул тригонометрии. Тогда
.
Ответ
Пример 3
Найти производную от синуса в кубе:
y = sin 3
x
.
Производные высших порядков
Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.
Найдем производную второго порядка, используя формулу производной сложной функции :
.
Здесь .
Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на .
Тогда производная n-го порядка имеет вид:
(5) .
Докажем это, применяя метод математической индукции.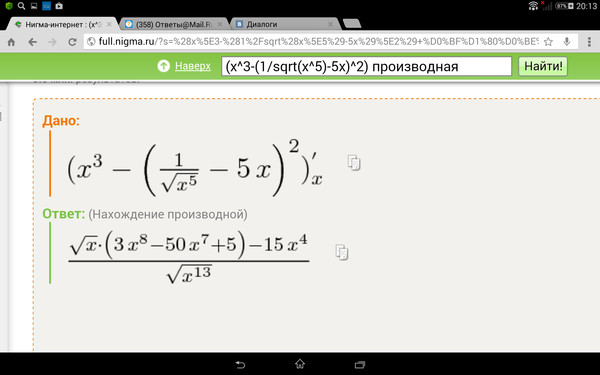
Мы уже проверили, что при , формула (5) справедлива.
Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .
Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:
.
Здесь .
Итак, мы нашли:
.
Если подставить ,
то эта формула примет вид (5).
Формула доказана.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) .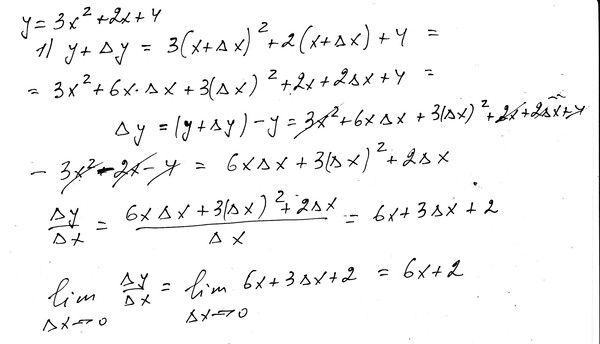 Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Производная функции y 4. Правила вычисления производных
Дата: 10.05.2015
Правила дифференцирования.
Чтобы найти производную от любой функции, надо освоить всего три понятия:
2. Правила дифференцирования.
3. Производная сложной функции.
Именно в таком порядке. Это намёк.)
Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.
Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.
Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.
Такое понимание очень помогает избежать каши в голове.
Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:
В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.
Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала — самые простые.
Найти производную функции y=sinx — x 2
Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U , а x 2 — функция V. Имеем полное право написать:
y» = (sinx — x 2)» = (sinx)»- (x 2)»
Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:
Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:
y» = (sinx)» — (x 2)» = cosx — 2x
Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.
А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:
Найти производную функции y=sinx — x 2 +cosx — x +3
Смело пишем:
y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3 )»
В конце урока дам советы по облегчению жизни при дифференцировании.)
Практические советы:
1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.
2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.
3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4. nx. Формулы производных высших порядков.
nx. Формулы производных высших порядков.
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′
= e x
.
Производная показательной функции с основанием степени a
равна самой функции, умноженной на натуральный логарифм от a
:
(2) .
Вывод формулы производной экспоненты, e в степени x
Экспонента — это показательная функция, у которой основание степени равно числу e
,
которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e
в степени x
:
y = e x
.
Эта функция определена для всех .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .
Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.
Сделаем подстановку .
Тогда ;
.
В силу непрерывности экспоненты,
.
Поэтому при ,
.
В результате получаем:
.
Сделаем подстановку .
Тогда .
При ,
.
И мы имеем:
.
Применим свойство логарифма (5):
.
Тогда
.
Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a
.
Мы считаем, что и .
Тогда показательная функция
(8)
Определена для всех .
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции
и логарифма
.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.
Отсюда видно, что производная n-го порядка также равна исходной функции:
.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a
:
.
Мы нашли ее производную первого порядка:
(15) .
Дифференцируя (15), получаем производные второго и третьего порядка:
;
.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на .
Поэтому производная n-го порядка имеет следующий вид:
.
Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.
Производная по переменной x от синуса x равна косинусу x:
(sin
x)′ = cos
x
.
Доказательство
Для вывода формулы производной синуса, мы воспользуемся определением производной:
.
Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и ,
то
(4) .
Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
;
.
Тогда
;
;
;
.
Теперь сделаем подстановку .
При ,
.
Применим первый замечательный предел (1):
.
Сделаем такую же подстановку и используем свойство непрерывности (2):
.
Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):
.
Формула производной синуса доказана.
Примеры
Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2
x
и y = sin 3
x
.
Пример 1
Найти производную от sin 2x .
Решение
Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.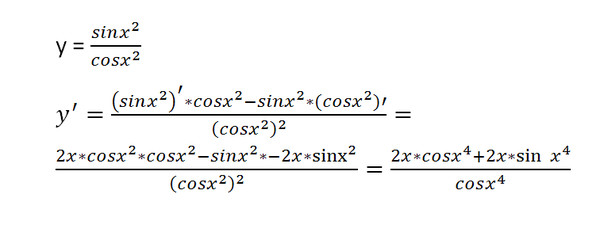
Применяем .
.
Здесь .
Ответ
(sin 2x)′ = 2 cos 2x.
Пример 2
Найти производную от синуса в квадрате:
y = sin 2
x
.
Решение
Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.
.
Здесь .
Можно применить одну из формул тригонометрии. Тогда
.
Ответ
Пример 3
Найти производную от синуса в кубе:
y = sin 3
x
.
Производные высших порядков
Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.
Найдем производную второго порядка, используя формулу производной сложной функции :
.
Здесь .
Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на .
Тогда производная n-го порядка имеет вид:
(5) .
Докажем это, применяя метод математической индукции.
Мы уже проверили, что при , формула (5) справедлива.
Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .
Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:
.
Здесь .
Итак, мы нашли:
.
Если подставить ,
то эта формула примет вид (5).
Формула доказана.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.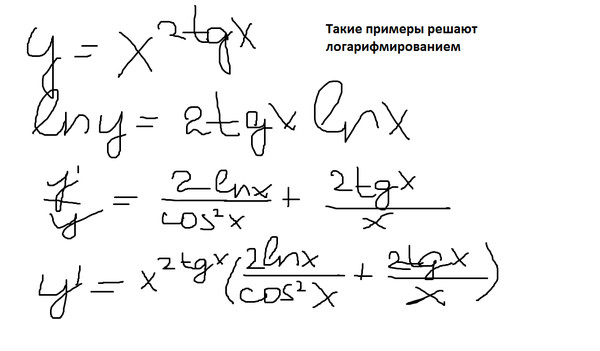 К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Поиск производной математической функции называется дифференцированием. Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе сайт у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса.
А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис сайт призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также сайт отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, — сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение.
Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, — сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени.
Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени. От бессмысленных и долгих расчетов вы можете избавиться, если воспользуетесь нашим онлайн сервисом. Благодаря ему производная будет вычислена за считанные секунды.
От бессмысленных и долгих расчетов вы можете избавиться, если воспользуетесь нашим онлайн сервисом. Благодаря ему производная будет вычислена за считанные секунды.
Задание 11 ЕГЭ по математике Профиль. Исследование функций
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
Нахождение точек максимума и минимума функций
1. Найдите точку максимума функции
Найдем производную функции.
Приравняем производную к нулю. Получим:
Исследуем знаки производной.
В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции
Ответ: 17.
2. Найдите точку минимума функции
Найдем производную функции.
Приравняем производную к нулю.
Определим знаки производной.
В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции
Ответ: 1.
Исследование сложных функций
3. Найдите точку максимума функции
Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.
Так как функция монотонно возрастает, точка максимума функции будет при том же , что и точка максимума функции А ее найти легко.
при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .
Заметим, что точку максимума функции можно найти и без производной.
Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при
Ответ: — 4.
4. Найдите абсциссу точки максимума функции
Напомним, что абсцисса — это координата по
Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.
Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции
Это вершина квадратичной параболы
Нахождение наибольших и наименьших значений функций на отрезке
5. Найдите наибольшее значение функции на отрезке
Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.
Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.
Найдем знаки производной.
В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.
Ответ: 12.
6. Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю.
при
Найдем знаки производной.
Точка — точка минимума функции . Точка не лежит на отрезке Поэтому
и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.
Ответ: -11.
7. Найдите наименьшее значение функции на отрезке
Иногда перед тем, как взять производную, формулу функции полезно упростить.
Мы применили формулу для логарифма произведения. при
Если то Если , то
Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке
Ответ: 4.
8. Найдите наибольшее значение функции на отрезке
Найдем производную функции
Приравняем производную к нулю:
. Поскольку если
Найдем знаки производной на отрезке
При знак производной меняется с «плюса» на «минус».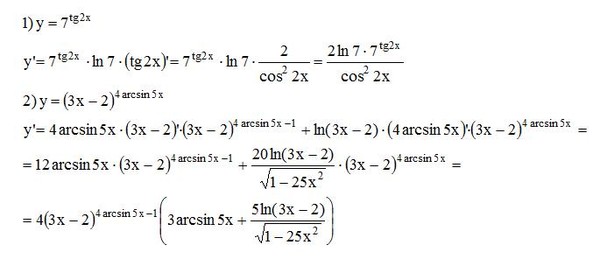 Значит, — точка максимума функции
Значит, — точка максимума функции
Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и
Мы нашли, что
Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.
Ответ: 4.
9. Найдите наименьшее значение функции на отрезке [0;2].
Снова сложная функция. Запишем полезные формулы:
Найдем производную функции
если Тогда
При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции
Ответ: -7.
10. Найдите наибольшее значение функции на отрезке
Как всегда, возьмем производную функции и приравняем ее к нулю.
По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки
На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки
В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при
Ответ: 12.
11.Найдите наименьшее значение функции на отрезке
Найдем производную функции и приравняем ее к нулю. — нет решений.
Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.
Поскольку , получим, что для всех , и функция монотонно возрастает при
Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при
Ответ: 6
Производной » задачи
производная »
Найти значение производной заданной функции в указанной точке x0 а) y=e^x/x+1 x0=0
б) y=e^0,5x-3 x0=4
Решение: А) у = е ^ х / х + 1 = 0 x0 б) у = е ^ 0. 2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможнораскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможнораскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
Решение: F(x) = — x² +3|x-1| +2 ; x∈ [ -2 ;2]
a) f(x) = — x² -3(x-1) +2 = -x² -3x +5 x∈ [ -2 ;1] *** = — (x +3/2)² +29/4 ***f (x) = -2x -3 ;
f (x) + —
———— -2 ——————— — 3/2 ——— 1
f(x) ↑ max ↓
f( -3/2) = — (-3/2)² — 3*(-3/2) +5 = 29/4 .
b) f(x) = — x² +3(x-1) +2 = — x² +3x -1 ;x∈ [ 1 ;2]
*** f(x) = — (x — 3/2)² +5/4 ; парабола : вершина А(3/2 ; 5) ; ветви вниз ***f(x) = — 2x +3 ;
f (x) + —
— 1 ——————- 3/2 ———————- 2
f(x) ↑ max ↓
f(3/2) = -(3/2)² +3*(3/2) -1 = 5/4
f(- 2) = 7 ; f( -3/2) =29/4 ; f(1) =1 ; f(3/2) =5/4 ; f(2) =1.
сравнивая эти данные заключаем
max f(x) = f(-3/2) =7,25.
x∈[ -2 ;2]min f(x) = f(1) =f(2) = 1.
x∈[ -2 ;2]
ответ : 7,25 ; 1.
——————————————-
P.S. x=1 критическая точка ( производная в этой точке не существует) ;
выясняется точка минимума (производная левее от x=1 отрицательно ,
а правее от нее положительно [при переходе знак меняется от «- » к «+») .
и еще; для этой функции не стоит применить «артиллерию» , достаточно
выделить полный квадрат (элементарно исслед кв функ).
Постройте график .
Найдите производную функции f(x)=(xв 4 степени-1)*(х в 4 степени+1)
Решение: f(x)=(x⁴-1)(x⁴+1)=x⁸-1f’(x)=8x⁷
.
 2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможно раскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможно раскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
Решение: F(x) = — x² +3|x-1| +2 ; x∈ [ -2 ;2]
a) f(x) = — x² -3(x-1) +2 = -x² -3x +5 x∈ [ -2 ;1] *** = — (x +3/2)² +29/4 ***
f (x) = -2x -3 ;
f (x) + —
-2 — 3/2 — 1
f(x) ↑ max ↓
f( -3/2) = — (-3/2)² — 3*(-3/2) +5 = 29/4.
b) f(x) = — x² +3(x-1) +2 = — x² +3x -1 ;x∈ [ 1 ;2]
*** f(x) = — (x — 3/2)² +5/4 ; парабола : вершина А(3/2 ; 5) ; ветви вниз ***
f(x) = — 2x +3 ;
f (x) + —
— 1 — 3/2 — 2
f(x) ↑ max ↓
f(3/2) = -(3/2)² +3*(3/2) -1 = 5/4
f(- 2) = 7 ; f( -3/2) =29/4 ; f(1) =1 ; f(3/2) =5/4 ; f(2) =1.
сравнивая эти данные заключаем
max f(x) = f(-3/2) =7,25.
x∈[ -2 ;2]
min f(x) = f(1) =f(2) = 1.
x∈[ -2 ;2]
ответ : 7,25 ; 1.
—
P.S. x=1 критическая точка ( производная в этой точке не существует) ;
выясняется точка минимума (производная левее от x=1 отрицательно,
а правее от нее положительно [при переходе знак меняется от «- » к «+»).
и еще; для этой функции не стоит применить «артиллерию», достаточно
выделить полный квадрат (элементарно исслед кв функ).
Постройте график .
Темы школьной программы — математика 5-11 класс. Таблица производных и правила дифференцирования функций
Таблица производных в алгебре нужна для решения целого ряда различных прикладных задач.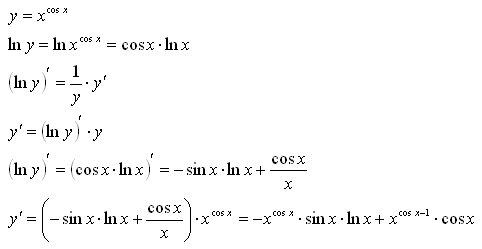 Поскольку смысл производной иначе интерпретируется как «скорость изменения», то, каждый раз, беря производную, мы находим величину на ступеньку более «быструю», чем та, от которой мы берем производную. Например, беря производную от y(x) по x, мы фактически находим скорость изменения координаты y в зависимости от изменения координаты x, а беря производную от скорости изменения координаты y в зависимости от координаты x, мы находим ускорение.
Поскольку смысл производной иначе интерпретируется как «скорость изменения», то, каждый раз, беря производную, мы находим величину на ступеньку более «быструю», чем та, от которой мы берем производную. Например, беря производную от y(x) по x, мы фактически находим скорость изменения координаты y в зависимости от изменения координаты x, а беря производную от скорости изменения координаты y в зависимости от координаты x, мы находим ускорение.
Содержание
Что такое производная функции
Например, при использовании производной в физике, мы знаем, что производная расстояния s по времени — это скорость. Потому что скорость — это величина, характеризующая быстроту изменения расстояния в зависимости от времени. А производная скорости — ничто иное как ускорение, так как ускорение — это величина, характеризующая быстроту изменения скорости.
Поскольку производная находится по формуле: , то бесконечное количество различных функций усложняют задачу дифференцирования, так как удобно функцию, которую можно представить из различных элементарных функций, дифференцировать основываясь на уже выведенных выражениях для производных этих элементарных функций.
Характеристика производной и ее смысл
Производная характеризует быстроту изменения функции в зависимости от изменения аргумента.
Таблица производных
Таким образом, чтобы работать с производными, необходима таблица производных элементарных функций. Руководствуясь этой таблицей, можно взять производную от какой угодно функции. Но прежде чем работать с таблицей — нужно знать как брать производную функции, есть определенные правила дифференцирования, которые представим в таблице.
Правила дифференцирования
| № правила | Название правила | Правило дифференцирования |
| 1 | Производная постоянной величины | , С-постоянная |
| 2 | Производная суммы | . |
| 3 | Производная произведения постоянной на функцию | , С — постоянная |
| 4 | Производная переменной x | |
| 5 | Производная произведения двух функций | |
| 6 | Производная деления двух функций | |
| 7 | Производная сложной функции |
Таблица производных простых и сложных функций
Теперь таблица производных для элементарных и для сложных функций.
| Номер формулы | Название производной | Основные элементарные функции | Сложные функции |
| 1 | Производная натурального логарифма по x | ||
| 2 | Производная логарифмической функции по основанию a | ||
| 3 | Производная по x в степени n | ||
| 4 | Производная квадратного корня | ||
| 5 | Производная a в степени x | ||
| 6 | Производная e в степени x | ||
| 7 | Производная синуса | ||
| 8 | Производная косинуса | ||
| 9 | Производная тангенса | ||
| 10 | Производная котангенса | ||
| 11 | Производная арксинуса | ||
| 12 | Производная арккосинуса | ||
| 13 | Производная арктангенса | ||
| 14 | Производная арккотангенса |
Примеры нахождения производных
Пример 1
Пользуясь формулами и правилами дифференцирования, найти производную функции: .
Решение:
Мы использовали правило 2 дифференцирования суммы. Теперь найдем производную каждого слагаемого:
По формуле 3 «производная по x в степени n» (у нас в степени 2).
По правилам дифференцирования 3 и 4.
По первому правилу дифференцирования «производная постоянной равна нулю»
Итак, получим: .
Пример 2
Найти производную функции
Решение:
Находим производную, пользуясь правилам дифференцирования 6.
Ответ:
Пример 3
Найти производную функции
Решение: здесь все просто, мы возьмем производную из таблицы производных.
Ответ:
Пример 4
Найдите производную функции
Решение: Здесь мы уже имеем не простую функцию, а сложную функцию и брать производную мы будем по формуле 8 таблицы производных для сложных функций.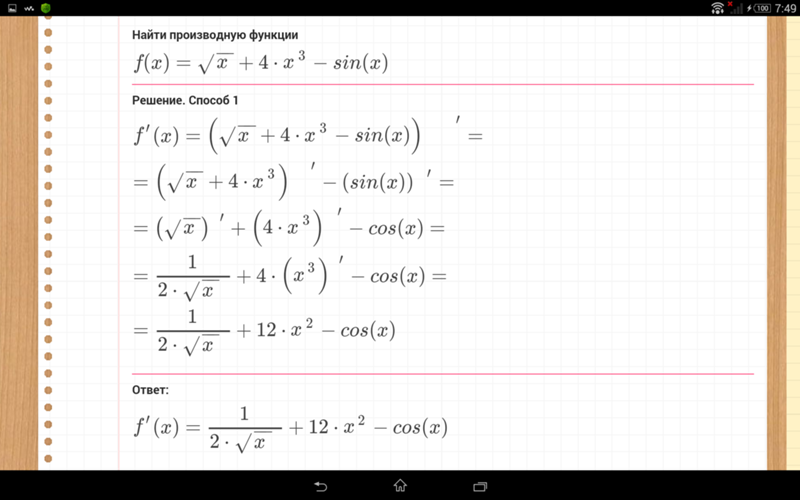
Ответ:
Пример 5
Пользуясь правилами дифференцирования и таблицей производных, найдите производную функции
Решение: У нас сложная функция, так как под корнем стоит не просто , а квадратная функция.
То есть мы имеем функцию вида .
Возьмем производную этой функции:
Ответ:
Пример 6
Найдите скорость тела, если траектория его движения задана уравнением м
Решение: скорость тела — это первая производная траектории по времени: . м/с.
Находим скорость тела:
Ответ: 3 м/с.
Итак, таблица производных и правила дифференцирования дают возможность легко брать производные и простых, и сложных функций.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Как дифференцировать экспоненциальные функции — Mathsathome.
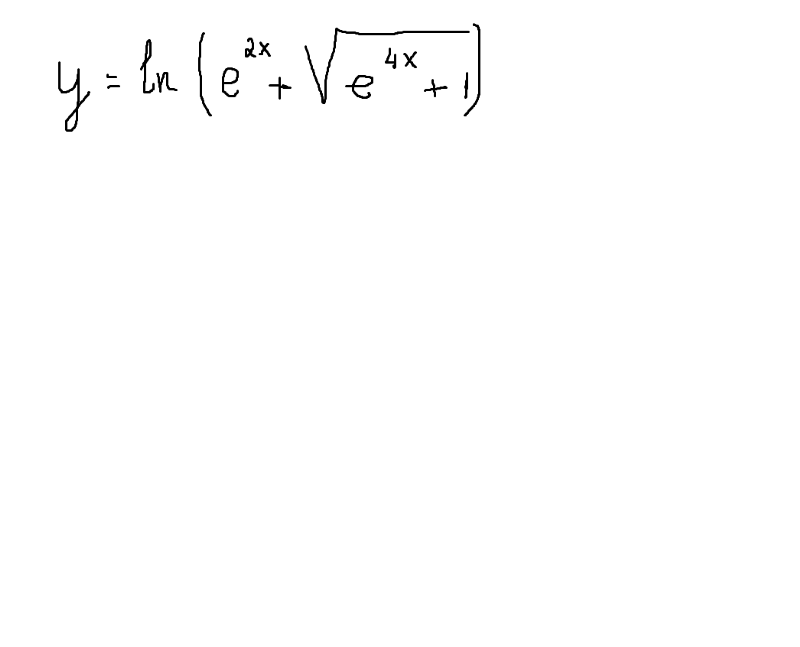 com
comДеривативы экспоненциальных функций: видео урок
Как дифференцировать E
x. Поэтому е в степени х остается неизменным при дифференцировании. Это единственная функция, имеющая это свойство. Производная от e kx это ke кх . Для e x , k = 1, поэтому производная от e x равна e x .
Поскольку производная e x равна e x , график производной e x выглядит идентично e x .
| Exponential Function | Derivative |
| y=e x | y’=e x |
| y=e kx | y’=k. e KX e KX |
| y = E F (x) | y ‘= f’ (x) .e F (x) |
| Y = A x | Y ‘= Ln. (a).a x |
Как дифференцировать показательную функцию
Чтобы дифференцировать показательную функцию, скопируйте показательную функцию и умножьте ее на производную степени. Например, чтобы дифференцировать f(x)=e 2x , возьмите функцию e 2x и умножьте ее на производную степени 2x. Производная от 2x равна 2. Следовательно, производная от f(x)=e 2x равно f'(x)=2e 2x .
Производная от e 2x равна 2e 2x .
Правило дифференцирования экспоненциальной функции состоит в том, что для f(x)=e u производная равна f'(x)=u’.e u .
u — функция, находящаяся в степени экспоненты, а u’ — производная этой функции.
Другими словами, правило дифференцирования показательной функции состоит в умножении исходной показательной функции на производную от ее степени.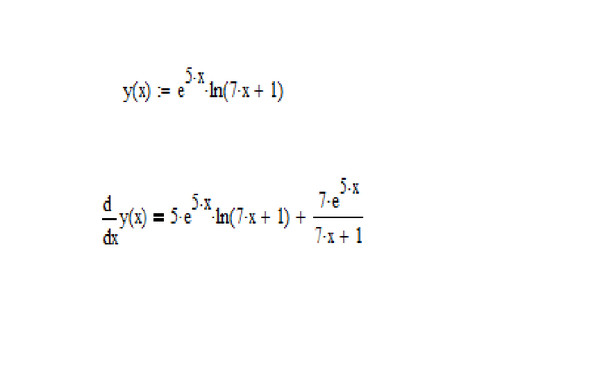
Правило дифференцирования экспоненциальных функций таково: если f(x)=e u , то f'(x)=u’.e u , где u — функция в степени экспоненты, а u’ — производная этой функции. Для f(x)=e 2x , u = 2x и u’ = 2. Следовательно, f'(x)=2e 2x .
Примеры дифференцирования экспоненциальных функций
Чтобы дифференцировать любую экспоненциальную функцию, продифференцируйте степень и умножьте ее на исходную функцию.
Это может быть записано математически как когда , .
В качестве альтернативы это можно записать как когда , .
Например, продифференцируйте f(x) = e 3x .
u — степень экспоненты, равная 3x.
u’ — производная от u. Дифференцируя 3x, получаем u’ = 3.
Подставляя u = 3x и u’ = 3 в f’(x) = u’.e u , получаем f’(x) = 3e 3x .
Например, дифференцировать f(x)=e x 2 .
u = x 2 и, следовательно, u’ = 2x.
Следовательно, f'(x) = u’ . e u становится f'(x) = (2x).e x 2 .
Например, дифференцировать f(x)=e x 2 +3x .
u = x 2 +3x и, следовательно, u’ = 2x+3.
Следовательно, f'(x) = (2x+3).e x 2 +3x .
Например, дифференцировать f(x) = e 1 / x .
Если степень экспоненциальной функции представляет собой дробь, перепишите ее в виде индекса.
1 / x можно переписать как x -1 . Запись этой дроби в виде индекса позволяет нам дифференцировать ее.
u = x -1 и, следовательно, u’ = -x -2 .
Следовательно, f'(x) = (-x -2 )e x -1 .
Это также может быть записано как или .
Например, дифференцировать e sin(x) .
u = sin(x) и, следовательно, u’ = cos(x).
Следовательно, f'(x) = cos(x). e sin(x) .
e sin(x) .
Вот несколько примеров дифференцирования показательных функций с решениями.
| Exponential Function | Derivative |
| e x | e x |
| e kx | ke kx |
| e 3x | 3e 3x |
| 5e 2x | 10e 2x |
| e x 2 | (2x).e x 2 |
| e (2x 3 -x 2 ) | (6x 2 -2x) .e (2x 3 -x 2 ) |
| E -x | -E -x |
| E SIN (X) | |
| E (X) | |
| E . e sin(x) |
Цепное правило с экспоненциальными функциями
Цепное правило используется для дифференциации функции от функции. Цепное правило гласит, что .
Цепное правило гласит, что .
Правило дифференцирования экспоненциальных функций можно использовать в сочетании с цепным правилом.
Например, продифференцируйте y = sin(e x ).
Мы можем записать это как y = sin(u), где u = e x .
Следовательно, и .
Используя цепное правило и так далее, .
Правило произведения с экспоненциальными функциями
Правило произведения гласит, что для функции производная равна .
Наше правило дифференцирования экспонент можно использовать вместе с правилом произведения.
Например, продифференцируйте y=xe x .
Здесь u = x и v = e x .
Поэтому и .
Используя правило произведения, производная равна .
Мы можем разложить на множители член e x так, что .
Правило частных с экспоненциальными функциями
Правило частных .
Вот пример использования правила отношения для дифференцирования экспоненциальных функций.
Дифференцировать .
По правилу частных u — это функция от числителя, а v — функция от знаменателя.
u = e x и так далее.
v = x и, следовательно, .
Подставив эти значения в правило отношения, .
Это можно упростить, разложив член e x .
.
Неявное дифференцирование e
xyЧтобы дифференцировать e xy , используйте f'(x)=u’.e u , где u = xy.
Используйте правило произведения, чтобы неявно дифференцировать степень «xy».
Неявное дифференцирование говорит нам, что производная от y равна y’.
Если u = xy, правило произведения дает нам u’ = (1)(y)+(x)(y’), что упрощается до u’ = y + xy’.
Следовательно, производная e xy равна (y+xy’)e xy .
Если , то .
- Используйте неявное дифференцирование, чтобы дифференцировать xy, чтобы получить y + xy’.
- Собрать вместе y членов
- Разложить на множители y членов
- Решить уравнение для y’
Доказательство производной e является собой.

- Предположим, что y = e x
- Возьмем натуральный логарифм обеих частей так, что ln|y|=x
- Дифференцируя обе по x, получаем ( 1 / y )( dy / dx ) = 1
- Умножая обе части на 2dy 9dx , получаем 209 9dx = y
- Substituting y = e x , the result is dy / dx = e x
Derivative of e
𝑥 using first principlesThe derivative of е х можно найти, используя дифференцирование по первым принципам.
Формула первых принципов гласит, что функцию градиента можно найти с помощью .
- Если , то .
- Термин может быть записан как .
- Тогда формула первых принципов становится .
- Термин может быть вынесен за скобки, чтобы дать нам .

- Теперь этот лимит можно разделить на два лимита.
- , потому что в .
- Поскольку , мы можем видеть, что , что равно 1.
- становится
Доказательство производной e
𝑥 с использованием рядаe x можно записать в виде степенного ряда
Например, 1 дифференцируется в 0, x дифференцируется в 1, x 2 / 2 дифференцируется в x и так далее.
Поскольку в этом степенном ряду бесконечное число членов, ряд остается неизменным при дифференцировании.
дифференцируется в
Как дифференцировать f(𝑥) = a
𝑥Производная от x есть x ln(a). Это правило верно для любого значения больше 0. Например, если y=2 x , то dy / dx = 2 x ln(2).
Например, если y = 5 x , то dy / dx = 5 x ln(5).
Доказательство производной
𝑥Производная от y=a x может быть доказана заменой a на e ln(a) .
y=a x становится и сила может быть снижена перед ln, чтобы сделать .
Мы можем дифференцировать это, используя наше правило дифференцирования экспонент: становится .
Вот так вот, .
Получаем .
Мы можем переместить перед числом (а) обратно в степень числа (а). Мы получаем .
Теперь и так . 92 раза?
Производная функции — это функция, которая сообщает вам скорость изменения исходной функции в любой конкретной точке этой функции. Можно думать о производной функции как о мере того, насколько чувствителен выход исходной функции к небольшим изменениям ее входа. Производная говорит нам, как быстро функция изменяется в любой момент времени. Таким образом, производные полезны для моделирования ситуаций, связанных со скоростями изменения, такими как смещение, скорость и ускорение.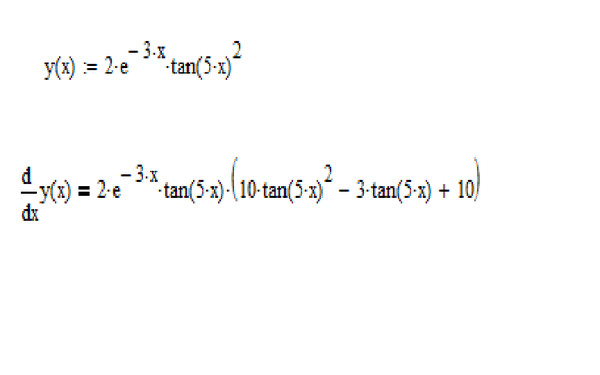
Производную функции:
можно определить по специальному правилу нахождения производной функции в виде e x . Общее правило:
Таким образом, используя это правило, мы можем определить, что:
, который является Derivative of
. равно ƒ'(x) = 2 e 2x . Эта производная говорит нам о скорости изменения выходных данных исходной функции при изменении входных данных. По сути, два уравнения говорят нам, что выход функции ƒ(x) = e 2x увеличивается в 2 раза e 2x на вход. Итак, если наше значение x равно единице, подстановка этого значения в уравнение дает нам:
Эти уравнения говорят нам о двух вещах. Во-первых, в точке x=1 функция ƒ(x) имеет выход e 2 . Во-вторых, производная говорит нам, что в точке x=1 выход ƒ(x) изменяется в 2 e 2 .
Что такое производная?
Как указывалось ранее, производная функции является мерой того, насколько чувствителен выход функции к изменениям ее входа. Производная ƒ(x) измеряет скорость изменения выхода ƒ(x) по отношению к изменениям x.
Представьте себе простой случай, когда у нас есть линейное уравнение y =2x+3. Далее выберем два набора координат x y, которые попадают на эту прямую: (1,5) и (2,7). Какова скорость изменения функции по x между этими двумя точками? Мы можем выяснить это, вычислив:
Это означает, что между этими двумя точками выход функции изменяется в 2 раза. Обратите внимание, что это значение 2 также равно наклону линейного уравнения y =2 х +3.
На самом деле, для любых двух точек уравнения y =2x+3 скорость изменения всегда будет равна 2. Это означает, что в каждой точке нашей функции выход функции увеличивается в раз 2 относительно х. Между прочим, это дает нам наше первое правило для нахождения производных: в случае, когда ƒ(x) является некоторой линейной функцией y= mx+ b :
That is, for any linear function in the form y= mx+ b , the derivative of that function is equal to the slope м . Если мы подумаем о линейных уравнениях, выражающих некоторую скорость изменения y по отношению к изменениям x, наклон функции m дает нам эту скорость изменения, так как для каждого входа скорость изменения выхода изменяется на a коэффициент 2,
Если мы подумаем о линейных уравнениях, выражающих некоторую скорость изменения y по отношению к изменениям x, наклон функции m дает нам эту скорость изменения, так как для каждого входа скорость изменения выхода изменяется на a коэффициент 2,
Процесс нахождения производной для функции более высокой степени (например, x 2 , x 3 ) обобщает этот процесс нахождения наклона между двумя точками и находит предельное значение, к которому отношение Δy/Δx приближается, когда Δx становится произвольным маленький. В результате производная функции в какой-то точке, по сути, говорит нам о наклоне графика в одной точке. Это также проявляется в том, что производная функции в некоторой точке дает наклон линии, касательной к графику в этой точке.
Хорошо, это все хорошо, но как нам найти скорость изменения функции вроде ƒ(x)=x 2 в каждый момент времени? В отличие от уравнения типа y = m x + b, скорость изменения функции ƒ(x) = x 2 не является постоянной и меняется в каждой точке. Как мы фиксируем скорость изменения такого рода функции мощности?
Как мы фиксируем скорость изменения такого рода функции мощности?
Помните, что в случае линейного уравнения мы нашли скорость изменения уравнения, найдя отношение изменения x к изменению y (Δy/Δx). Начнем с функции ƒ(x)= x 2 . Выбирая два значения для x, мы получаем ƒ(1)=1 и ƒ(2) = 4. Решение для Δy/Δx дает нам (4-1)/(2-1)=4. Наклон линии, проходящей между этими двумя точками, равен 4. Теперь представьте, что мы повторили этот процесс, выбрав значения x очень близко друг к другу, скажем, 1 и 1,5. Это дает нам:
Что, если мы подойдем еще ближе? Как насчет 1 и 1.1? Подстановка этих значений дает нам:
А как насчет 1 и 1.01?: Это дает нам:
Обратите внимание, что по мере того, как Δx становится сколь угодно малым, отношение Δy/Δx приближается к некоторому значению, в данном случае к 2. В графических терминах это означает, что если мы продолжаем выбирать все меньшие и меньшие разности x , мы все ближе и ближе аппроксимируем наклон функции в одной точке. Это в конечном итоге даст нам производную функции в этой точке, которая равна 2.
Это в конечном итоге даст нам производную функции в этой точке, которая равна 2.
Итак, мы только что нашли способ аппроксимировать производную функции в одной точке. Производная функции может быть аппроксимирована рядом меньших и меньших Δx, приближающихся к точке. Это дает нам общее определение для получения производной значения, записанного в предельной записи; то есть:
По сути, это уравнение говорит, что производная ƒ(a) равна пределу, к которому приближается отношение Δy/Δx, когда h становится бесконечно малым. Значение ч , очень близкое к 0, даст вам хорошее приближение наклона графика в этой точке. Идея состоит в том, что по мере того, как мы выбираем все меньшие и меньшие значения для h, мы все ближе и ближе подходим к наклону касательной в этой точке функции. Это формальное определение производной, и его можно использовать для получения производной функция — т.е. функция, которая сопоставляет все входные значения со скоростью изменения исходной функции в некоторый момент времени.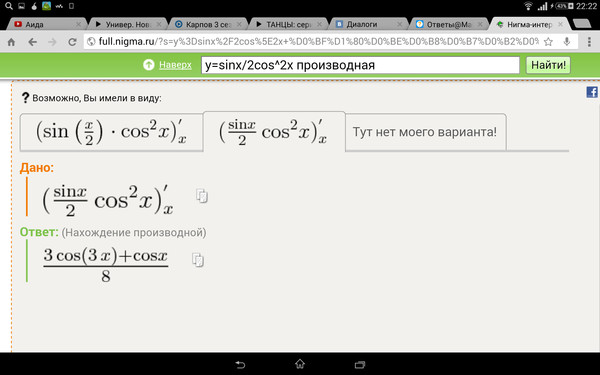
Вернемся к нашей функции ƒ(x)=x 2 . Если мы подключим эту функцию к нашему определению производной, мы сможем получить производную функцию для ƒ(x)=x 2 . Это дает нам:
. Утверждение:
.0931
Поскольку в этом уравнении предполагается, что h представляет собой очень, очень маленькое значение, мы можем по существу проигнорировать любой h в уравнении и упростить его следующим образом:
, производная функция ƒ(x) = x 2 равна ƒ'(x) = 2x. Скорость изменения функции x 2 в любой точке x равна 2x. Таким образом, при x=1 ƒ'(1)=2, при x=2, ƒ'(2)=4, при x=3, ƒ'(3)=6 и так далее. Функция производной дает скорость изменения исходной функции в каждой точке по отношению к изменениям входного значения. Для каждого значения x на этом графике функция изменяется со скоростью, пропорциональной 2x.
Общие правила вычисления производных
Первое правило касается производной постоянной функции. Для любой функции, которая дает постоянный результат, производная этой функции равна 0. Это:
Поскольку постоянная функция дает только один и тот же результат, она никогда не меняется, поэтому ее скорость изменения всегда равна 0. Итак, если ƒ(x)=7, то ƒ'(x)=0.
Далее, обобщая предыдущий процесс получения производной x 2 до любого полинома n-й степени дает нам общее правило для нахождения производной полиномиальных членов:
Это называется степенным правилом и может использоваться для вычисления производных полиномов разной степени. Используя правило степени, мы можем определить, что производная x 3 равна 3x 2 , производная x 4 равна 4x 3 и так далее.
Для экспоненциальных функций можно найти производную, умножив саму функцию на натуральный логарифм основания. Это:
Это:
Это называется правилом экспоненты . Правило экспоненты — это более обобщенная версия специального правила нахождения производной от e x . Из всех функций f(x) = e x — единственная функция, производная которой равна самой себе. То есть наклон всей линии, касательной к графику e x , равен всего лишь e x .
Четыре приведенных выше выражения являются наиболее распространенными правилами нахождения производных выражений. Кроме того, существуют правила, регулирующие сочетание функций и их производных. Например, существует правило сумм , то есть:
Правило сумм говорит нам, что если некоторая функция h является суммой двух других функций f и g, то производная от h равна сумме производные f и g. Правило сумм позволяет нам найти производную каждого члена в полиномиальном уравнении и сложить их вместе, чтобы получить полную производную. Например, представьте ƒ(x)= x 3 +4x 2 -3x. Правило сумм говорит нам, что производная этой функции будет равна сумме производных составляющих ее функций, поэтому ƒ'(x)=3x 2 +8x-3
Например, представьте ƒ(x)= x 3 +4x 2 -3x. Правило сумм говорит нам, что производная этой функции будет равна сумме производных составляющих ее функций, поэтому ƒ'(x)=3x 2 +8x-3
Далее следует правило произведения , которые дают формулу для нахождения производных произведения функций. Правило произведения:
Правило произведения говорит нам, что производная произведения двух функций равна первой функции, умноженной на производную второй, плюс вторая функция, умноженная на производную первой. Таким образом, производная от ƒ(x)=sin(x)x 2 будет ƒ'(x)=sin(x)2x + x 2 cos(x). Вы можете запомнить этот порядок правила произведения с мнемоникой «левое право, правое право» (LDR RDL)
Наконец, цепное правило , которое описывает производную композиции функций. Если какая-то функция является композицией двух других, то цепное правило говорит нам, что производная составной функции равна производной первой функции при вычислении в g(x), умноженной на производную от g(x). Символически это:
Символически это:
Цепное правило позволяет нам поместить функцию в функцию и получить производную этой составной функции.
Используя эти правила, можно вычислить производные большинства стандартных полиномиальных уравнений. Некоторые функции более сложны, но четкое применение приведенных выше правил должно позволить вам разделить слои любой функции с действительным знаком, чтобы получить ее производную.
6. Производная показательной функции
М. Борна 9х`
Что это значит? Это означает, что наклон совпадает со значением функции (значение и ) для всех точек на графике.
Пример: Возьмем пример, когда x = 2. В этот момент значение y равно e 2 ≈ 7,39.
Поскольку производная от e x равна e x , то наклон касательной при x 9x`, показывающий тангенс при x=2. `
`
Теперь посмотрим, верно ли это при некоторых других значениях x .
123-1-2-31234567xy(−2, 0,135)slope = 0,135Открыть изображение на новой страницеКогда `x=-2,` `y=»slope»~~0,135`.
12345-1-212345678xy(0, 1)slope = 1Открыть изображение на новой страницеКогда `x=0`, `y=»slope»=1`.
2468101214162468101214161820xy(3, 20.1)slope = 20.1Открыть изображение на новой страницеКогда `x=3,` `y=»slope»~~20.1`.
Мы видим, что в каждом случае 9(-x)sinx.`
Мы увидим больше таких кривых в Дифференциальных уравнениях второго порядка, в следующем разделе исчисления.
Нужна помощь в решении другой задачи по тригонометрии? Попробуйте решение проблем.
Отказ от ответственности: IntMath.com не гарантирует точность результатов. Решатель задач предоставлен Mathway.
Закажите одного из наших репетиторов из Лиги плюща, чтобы помочь вам освоить математику и улучшить свои оценки.
Образование: Компьютерные науки и математика, Стэнфордский университет
Предметы: Алгебра, геометрия, триггер, исчисление, доп. Исчисление, подготовка к SAT/ACT
Исчисление, подготовка к SAT/ACT
Биография: Привет! Меня зовут Лигия, мне очень нравится наставлять других, и я работала репетитором по математике в Стэнфорде. Я также интересуюсь физическими науками и провожу исследования с использованием машинного обучения в биологических проблемах. Мне нравится теннис, бразильская музыка и любое рукоделие.
Тариф: 100 долл. США/час
Производные экспоненциальной и логарифмической функций
Подход
к
C A L C U L U S
Содержание | Главная
14
Производная от ln x
Производная от e с функциональным показателем
Производная от ln u ( x )
Общее правило власти
В СИСТЕМЕ НАТУРАЛЬНЫХ ЛОГАРИФМОВ в качестве основания используется число, называемое e; это система, которую мы используем во всей теоретической работе. (В следующем уроке мы увидим, что e равно примерно 2 . 718.) Система натуральных логарифмов отличается от системы десятичных логарифмов, в основе которой лежит 10 и которая используется в большинстве практических работ.
(В следующем уроке мы увидим, что e равно примерно 2 . 718.) Система натуральных логарифмов отличается от системы десятичных логарифмов, в основе которой лежит 10 и которая используется в большинстве практических работ.
Обозначим логарифмическую функцию с основанием e как «ln х ».
ln x = log e x .
y = ln x подразумевает e y = x .
Другими словами, эта логарифмическая функция —
у = пер х
— имеет обратную экспоненциальную функцию,
у = е х .
Вот обратные соотношения:
ln e x = x и e ln x = x .
А сам логарифм основания всегда равен 1:
лн е = 1.
(Тема 20 предварительного исчисления.)
Функция y = ln x непрерывна и определена для всех положительных значений х . Оно будет подчиняться обычным законам логарифмов:
Оно будет подчиняться обычным законам логарифмов:
1 . ln ab = ln a + ln b .
| 2 . номер | а б | = ln a − ln b . |
3 . № и n = n ln a .
(Тема 20 предварительного исчисления.)
Как и все правила алгебры, они подчиняются правилу симметрии.
Например,
n ln a = ln a n .
Производная от ln x
Теперь мы применим определение производной, чтобы доказать:
| д дх | л х | = | 1 х |
. В ходе доказательства будет значительно упрощено, если мы определим основание системы натуральных логарифмов, число, которое мы называем e, следующим пределом:
Предел в доказательстве будет иметь тот же вид.
Позже мы будем называть переменную x , а не v . А на следующем уроке, при замене переменной с на на , следует знакомое определение.
Вот коэффициент разности:
| по 2-му закону; | |||
| = | при умножении на x / x ; | |
| = | в соответствии с 3-м законом. | |
Теперь мы берем предел, поскольку ч приближается к 0.
| = |
| Ограничение не распространяется на | 1 х | , потому что ч это переменная |
| приближается к 0. | 1 х | – постоянный коэффициент. |
Теперь мы определим этот предел как основание натуральных логарифмов, число, которое мы будем называть e. (Этот предел указан выше, с v = ; когда 0, 0.)
Следовательно,
| = | ||
| = | ||
| = | ||
Что мы и хотели доказать.
Чтобы убедиться, что этот предел —
— то есть e существует, поскольку x приближается к 0, вот график
y имеет определенное значение, так как x приближается к 0. И в следующем уроке мы увидим, что это приблизительно 2,718.
Производная от e x
Сейчас мы докажем:
| д дх | е х | = e x |
«Производная е х по отношению к х
равно е x ».
С г = е x является обратным y = ln x , мы можем получить его производную следующим образом:
| г | = | е х | ||
| подразумевает | п г | = | ln e x | = x . |
Следовательно, взяв производную от обеих сторон относительно x и применив цепное правило к ln y :
| = | 1. | ||
| г’ | = | и . | |
| То есть | |||
| = | е х . | ||
e x является собственной производной.
Что это значит? Это подразумевает значение экспоненциального роста. Ибо мы говорим, что количество растет «экспоненциально», когда оно растет в 9 раз.1911 скорость , что пропорционально его размеру. Чем он больше в любой момент времени, тем быстрее он растет в это время. Типичным примером является население. Чем больше будет индивидуумов, тем больше будет рождений и, следовательно, тем больше будет скорость изменения населения — числа рождений в каждом году.
Все экспоненциальные функции имеют вид a x , где a — основание. Следовательно, сказать, что скорость роста пропорциональна его размеру, значит сказать, что производная a x пропорционально a x .
| д дх | x | = тыс. лет назад x лет назад x | , |
, где k — константа пропорциональности. (Урок 39алгебры.) Когда мы вычислим эту производную ниже, мы увидим, что эта константа становится ln a .
| д дх | x | = ln a · a x | . |
В системе натуральных логарифмов, в которой e — это основание, у нас есть самая простая возможная константа, а именно 1.
| д дх | е х | = e x . |
Производная от e с функциональным показателем
Когда y = e u ( x ) , то по цепочке:
То есть
«Производная от e с функциональным показателем
равно e с этим показателем, умноженным на
производную от этого показателя».
Пример 1. Вычислите производную e 2 x + 3 .
| Решение . |
Задача 1. Вычислить производную от e x 2 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
e x 2 · 2 x = 2 x e x 2
Задача 2. Вычислите производную от следующего.
а) e sin x . e sin x cos x
б) e −x . e — x (-1) = -e — x
c) x 2 e x . x 2 e x + 2 x e x
Согласно правилу продукта.
| г) | Согласно частному правилу: |
Производная от ln u ( x )
Когда y = ln u ( x ), то по цепному правилу:
То есть
| Пример 2. |
| Пример 3. | д дх | ln sin x | = | 1 sin x | · cos x | = | cos x sin x | = детская кроватка x . |
Пример 4. Найдите производную от ln x 2 .
Раствор . Мы можем применить законы логарифмов:
| д дх | л x 2 | = | д дх | 2 ln x , 3-й закон, | |||
| = | 2 | д дх | л х | ||||
| = | 2 х | . | |||||
| Пример 5. Найти производную от ln | . x 3 x − 4 | . |
Решение . Согласно 2-му закону:
| д дх | в | x 3 x − 4 | = | д дх | [ln x — ln (3 x — 4)] |
| = | |||||
| = | |||||
| = | |||||
Задача 3. Дифференцируйте следующее.
а) в x 3 . | д дх | ln x 3 = | д дх | 3 дюйма x | = | 3 х |
| b) (ln x ) 3 . | 3 (пер. x ) 2 · | 1 х | = | 3(ln x ) 2 x |
| c) ln (3 x 2 − 4 x ). | 1 3 x 2 − 4 x | · (6 х — 4) | = | 6 x − 4 3 x 2 − 4 x |
| d) ln (3 x − 4) 2 . | 1 (3 x − 4) 2 | · 2(3 x − 4) · 3 | = | 6(3 х — 4) (3 х — 4) 2 | = | 6 3 x − 4 |
e) ln cos x . | 1 cos x | (−sin x ) | = | − | sin x cos x | = | −загар x |
| Задача 4. Вычислить производную от ln | . 2 х | . |
| д дх | п | 2 х | = | д дх | (ln 2 — ln x ) = 0 — | 1 х | = − | 1 х |
Задача 5. Производная от log a x .
Согласно правилу перехода с базы e на другую базу a :
Тема 20 предварительного исчисления.
Вычислить предел этой производной
а) когда x больше 1 и становится больше.
Эта производная приближается к 0, то есть становится меньше.
б) когда x меньше 1 и становится меньше.
Эта производная становится больше.
Общее силовое правило
Теперь мы можем доказать, что производная от f ( x ) = x n , где n — любой рациональный показатель, выглядит следующим образом:
| д дх | x нет | = n x n −1 |
Пусть
| г | = | x n . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Затем | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| п г | = | n ln x (3-й закон). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поэтому при взятии производной по x : | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | нет x | |||
| так что | ||||
| г | = | нет x | · г | |
| = | нет x | · x п | ||
| = | n x n −1 . | |||
Именно это мы и хотели доказать.
(Если n равно 0, то x 0 = 1, константа; ее производная равна 0. Если n иррационально, потребуется рациональное приближение.)
Если n иррационально, потребуется рациональное приближение.)
| Задача 6. Вычислить производную от |
Производное от a x
Докажем:
| д дх | x | = ln a · a x |
«Производная экспоненциальной функции с основанием a
равно натуральному логарифму по основанию
. экспоненциальная функция враз больше.»
Пусть
| г | = | и х . | |||
| Тогда после натурального логарифма обеих частей: | |||||
| ln y | 5 | = | x ln a . (3-й закон) (3-й закон) | ||
| Следовательно, | |||||
| = | |||||
| Но по правилу цепочки: | |||||
| = | |||||
| Следовательно, | |||||
| = | по и . | ||||
| = | п а | ||||
| г’ | = | ln a · y | |||
| То есть | |||||
| = | ln a · a x . | ||||
Это то, что мы хотели доказать.
| Пример 6. | д дх | 2 x | = ln 2 · 2 x . |
Задача 7. Вычислите производную от y = 10 5 x .
По цепному правилу:
Следующий урок: оценка e
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Производная и интеграл показательной функции
Производная экспоненты
Получение производной
Прежде чем вывести производную, необходимо сделать несколько предварительных замечаний. Отзывать
что число e определяется пределом как x
приближается к 0 из
Отзывать
что число e определяется пределом как x
приближается к 0 из
е(х) = (1 + x) 1/x
Если мы подставим Dx для x и пусть Dx быть маленьким тогда
(1 + Дх) 1/ D x @ e
Обе стороны Дкс мощность получаем
(1 + Дх) @ e D x
Сейчас пришло время найти производную экспоненциальной функции f(x) = e x
Определение говорит США
Мы показали следующую теорему
г.
Теорема (Производная от e x ) Если |
Примеры
Найдите производную от
e 2 x
х е х
Раствор
Мы используем цепное правило с
и = e u u = 2 x
Что даету ‘ = е у и ‘ = 2
Так что( е 2 х )’ = ( e u )(2) = 2 e 2 x
Мы используем правило произведения:
( х е х )’ = ( x )’ ( e x ) + x ( e x )’
= e x + x e x
Упражнения:
Найдите производные от
3 e 4x
e x
х 2
Приложение
Поперечное сечение нижней половины яичной скорлупы может быть моделируется уравнением
у = е х/4 + е -х/4 -4 < х < 4
где
x — горизонтальное измерение и
y — вертикальное измерение, измеряемое в сантиметрах. Что такое
расстояние по вертикали от дна скорлупы до середины скорлупы?
Что такое
расстояние по вертикали от дна скорлупы до середины скорлупы?
Решение
Первый нам нужно найти дно раковины. Здесь будет оболочка получается минимум. Чтобы найти минимум, возьмем производную и примем ее равен нулю. Мы используем цепное правило, чтобы получить
y’ = 1/4 e x/4 — 1/4 e -x/4 = 0
е х/4 — е -х/4 = 0 Умножение по 4
e x/4 = е -x/4
х/4 = -x/4
x = 0
Подключение дает
y(0) = e 0/4 + e -0/4 = 1 + 1 = 2
Чтобы обеспечить минимальное возьмем вторую производную
y» = 1/16 e x/4 + 1/16 e -x/4
Заглушка в 2 для х дает
y»(2) = 1/16 e 2/4 + 1/16 e -2/4
Какой
положительно (поскольку экспоненты всегда положительны).

 2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможнораскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможнораскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
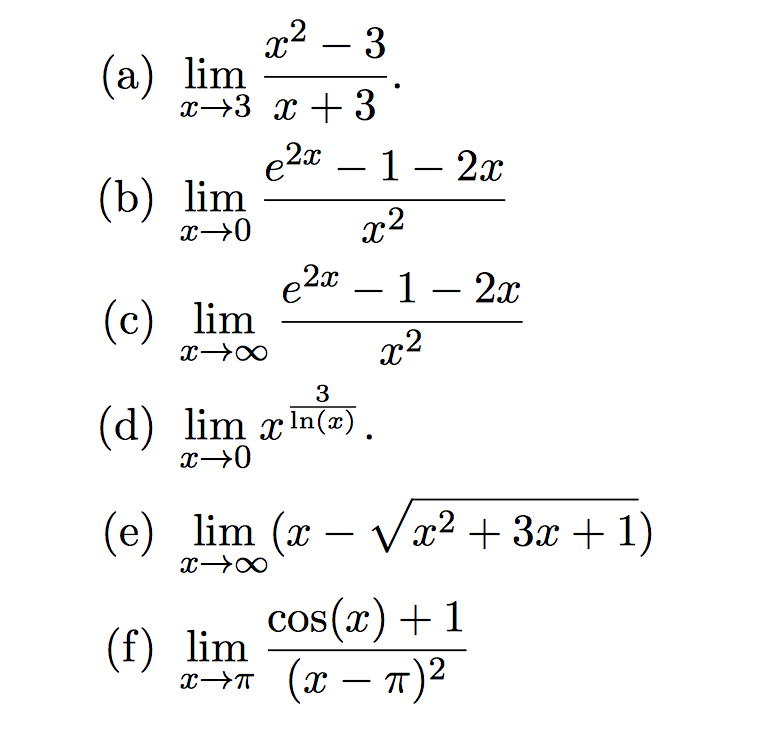 2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможно раскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
2+3|x-1|+2 на отрезке [-2;2] больше не понимаю как найти производную от данной функции, возможно раскрыть модуль по определению и взять поочередно производную и еще, куда нужно подставлять полученные x чтоб найти значение производной?
