| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | tan(45) | ||
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Помогите пожалуйста квадратный участок со стороной 90 м, ограждённый сеткой, делят на 4 участка прямоугольной формы.1) хватит ли 200 погонных метров
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
какой цифрой оканчивается значение 2017 в степени 2016
Пользуйтесь нашим приложением
Алгебра и начала анализа в 10-м классе «Решение тригонометрических уравнений»
Цель: закрепить навык решения
тригонометрических уравнений.
Работа учащихся состоит из нескольких этапов. Чтобы получить оценку “3”, необходимо пройти 4 этапа, чтобы получить оценку “4” — 5 этапов, чтобы получить оценку “5” — 6 этапов. На каждом этапе ученик встретится с указаниями учителя о том, что нужно знать и уметь, или краткими пояснениями к выполнению заданий.
Прочитав указания учителя, ученик выполняет самостоятельные работы данного этапа, проверяет ответы, сверяя с ответами, которые предоставляет учитель. Если допущены ошибки, то ученик их исправляет и решает задания другого варианта, аналогичные тем, где он допустил ошибки. После этого можно переходить к следующему этапу.
1 этап.
Цель: закрепить решение простейших тригонометрических уравнений.
Указания учителя.
Вспомните основные правила решения тригонометрических уравнений.
(учебник А. Н.Колмогорова и др. с. 69 – 73)
Н.Колмогорова и др. с. 69 – 73)
Выполните письменно самостоятельную работу (10 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) cos x = 1/2 | 1) sin x = -1/2 |
| 2) sin x = -/2 | 2) cos x = /2 |
| 3) tg x = 1 | 3) ctg x = -1 |
| 4) cos (x+) = 0 | 4) sin (x – /3) = 0 |
| 5) 2 cos x = 1 | 5) 4 sin x = 2 |
| 6) 3 tg x = 0 | 6) 5 tg x = 0 |
| 7) sin 4x = 1 | 7) cos 4x = 0 |
2 этап.
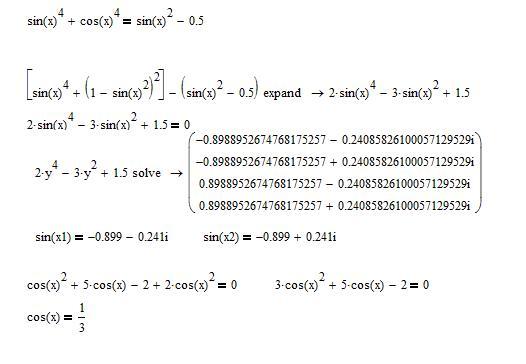
Цель: закрепить умения решать тригонометрические уравнения методом сведения к квадратному.
Указания учителя.
Метод сведения к квадратному состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x) или комбинацию функций обозначить через y, получив при этом квадратное уравнение относительно y.
Пример. 4 – cos2 x = 4 sin x
Так как cos2 x = 1 – sin2 x, то
4 – (1 – sin2 x) = 4 sin x,
3 + sin2 x = 4 sin x,
sin2 x — 4 sin x + 3 = 0,
Пусть y = sin x, получим уравнение
y 2 — 4 y +3 = 0
у1=1; у2=3.
sin x =1 или sin x = 3,
x = /2 + 2 n, n= Z, решений нет.
Ответ: x = /2 + 2 n, n= Z.
Выполните письменно самостоятельную работу (10 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) tg2 x — 3 tg x + 2 = 0; | 1) 2 + cos2 x — 3 cos x = 0; |
| 2) 2 cos2 x + 5 sin x – 4 = 0; | 2) 4 — 5 cos x — 2 sin2 x =0; |
| 3) (1 — cos 2x)/2 + 2 sin x = 3; | 3) (1 — cos 2x)/2 + 2 sin x = 3. |
3 этап.
Цель: закрепить навык решения тригонометрических уравнений методом разложения на множители.
Указания учителя.
Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит несколько множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, данный множитель можно представить в виде совокупности более простых уравнений.
Пример. 2 sin3 x — cos 2x — sin x = 0
Сгруппируем первый член с третьим, а cos 2x = cos2 x — sin2 x.
(2sin3 x — sin x) – (cos2 x — sin x) = 0,
Вынесем из выражения, стоящего в первой скобке sin x, а cos2 x = 1 — sin x.
sin x (2sin2 x – 1) – (1 — 2 sin2 x) = 0,
sin x (2sin2 x – 1) + (2 sin2 x — 1) = 0,
(2 sin2 x — 1) • ( sin x + 1) = 0.
| 2 sin2 x – 1 = 0 | или | sin x + 1 = 0 |
| sin2 x = 1/2, | sin x = — 1 | |
| sin x = ±1/v2 |
Ответ: x1 = ± /4 + n, n = Z, x2 = — /2 +2k, k = Z.
Выполните письменно самостоятельную работу (10 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) sin2 x — sin x = 0, | 1) ctg2 x — 4 ctg x = 0, |
| 2) 3 cos x + 2 sin 2x = 0, | 2) 5 sin 2x — 2 sin x = 0. |
4 этап.
Цель: закрепить навык решения однородных уравнений
Указания учителя.
Однородными называются уравнения вида a sin x + b cos x = 0,
a sin2 x + b sin x cos x + c cos2 x = 0, и т.д., где a, b, c – числа.
Пример 1. 5 sin x — 2 cos x = 0
Поделим обе части уравнения cos x (или на sin x). Предварительно докажем,
что cos x 0 (или sin x 0). (Пусть cos x = 0, тогда 5 sin x — 2 • 0 = 0, т.е. sin x = 0; но этого не может быть, так как sin2 x + cos2 x = 1).
Значит, можно делить на cos x:
5 sin x /cos x — 2 cos x / cos x = 0 / cos x. Получим уравнение
5 tg x – 2 = 0
tg x = 2/5,
x = arctg 2/5 + n, n = Z.
Ответ: x = arctg 2/5 + n, n = Z.
Аналогично решаются однородные уравнения вида
a sin2 x + b sin x cos x + c cos2 x = 0, их решение
начинается с того, что обе части уравнения
делятся на cos2 x (или на sin2 x).
Пример 2. 12 sin2 x + 3 sin 2x — 2 cos2 x = 2.
Данное уравнение не является однородным, но его можно преобразовать в однородное, заменив 3 sin 2x на 6 sin x cos x и число 2 на 2sin2 x + 2cos2 x.
Приведя подобные члены, получим уравнение
10sin2 x + 6sin x cos x — 4 cos2 x = 0.
(Пусть cos x = 0, тогда 10sin2 x = 0, чего не может быть, т.к. sin2 x + cos2 x = 1, значит, cos x 0).
Разделим обе части уравнения на cos2 x.
10 tg2 x +6 tg x — 4 = 0,
tg x = -1 или tg x = 2/5,
x = — /4 + n, n = Z, x = arctg 2/5 + k, k = Z.
Ответ: x1 = — /4 + n, n = Z, x2 = arctg 2/5 + k, k = Z.
Выполните письменно самостоятельную работу (10 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) sin x — cos x = 0, | 1) 5sin x +6cos x = 0, |
| 2) sin2 x — sin 2x = 3 cos2 x, | 2) 3sin2 x — 2sin 2x +5cos2 x = 2. |
5 этап.
Указания учителя.
Вы прошли 4 этапа, теперь вам самостоятельно придется выбрать метод решения уравнений. Вспомните основные тригонометрические формулы.
(Учебник А.Н.Колмогорова и др. с. 7 — 9)
Выполните письменно самостоятельную работу (20 минут)
Решите уравнения:
| 1 вариант | 2 вариант |
| 1) cos 2x -5 sin x – 3 = 0, | 1) cos 2x + 3 sin x = 2, |
| 2) sin 2x + cos 2x = 0, | 2) sin 2x — cos 2x = 0, |
| 3) cos2 x — cos 2x = sin x, | 3) 6 — 10cos2 x + 4cos 2x = sin 2x, |
| 4) sin 4x — cos 2x = 0, | 4) cos x cos 2x = 1, |
| 5) 5 — 5 cos (/2 — x ) = 2 cos2 ( – x), | 5) cos2 (/2 + x ) — cos2 (2 + x) = /2. |
6 этап.
Указания учителя.
Молодцы! Вы прошли 5 этапов. Целью вашей дальнейшей работы является применение своих знаний и умений в более сложных ситуациях.
Выполните письменно самостоятельную работу
(Задания даются в одном варианте, т.к. их решают не все учащиеся. Время, отводимое на эту работу, определяется учителем (ситуацией на уроке)).
Решите уравнения:
- sin 6x + cos 6x = 1 — sin 3x,
- 29 — 36 sin2 (x – 2) — 36 cos (x – 2) = 0,
- 2sin x cos x + – 2 cos x — v3 sin x = 0,
- sin 4x = 2 cos2 x – 1,
- sin x (sin x + cos x ) = 1,
- 1/(1 + cos2 x) + 1/(1 + sin2 x) =16/11.
Подсказки:
- Воспользуйтесь формулой двойного угла для sin 6x, cos 6x.
- Обозначьте x – 2 = y, решите уравнение, сведя его к
квадратному с помощью формулы sin2 y = 1 — cos2
y.

- Сгруппируйте первое и третье слагаемое, примените разложение на множители.
- Воспользуйтесь формулой двойного угла для sin 4x, cos 4x, формулой понижения степени 2cos2 x – 1 = cos 2x.
- Раскройте скобки, примените основное тригонометрическое тождество.
- Приведите дроби к общему знаменателю, затем используйте основное тригонометрическое тождество sin2 x + cos2 x = 1, сведите уравнение к квадратному.
Оцените свои работы самостоятельно.
Домашнее задание:
Если вы выполнили задания всех этапов, то дома № 163-165 – любое уравнение (учебник А.Н.Колмогорова и др. с. 333)
Если вы выполнили задания 5 этапов, то дома задания 6 этапа.
Если вы выполнили задания 4 этапов, то дома задания 5 этапа, и т.д.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как найти тригонометрию загара?
Содержание
- Как делать Cos Sin Tan?
- Какова формула для cos sin Tan?
- Как запомнить точные значения sin, cos и TAN?
tan (θ) = y/x (где x и y — координаты точек на единичной окружности) Используя свойства треугольника 30-60-90, мы можем найти остальные стороны, Прилегающая сторона угол в √3 раза больше противоположной стороны. А гипотенуза в 2 раза больше противоположной стороны. И гипотенуза становится = 2 единицы. [8]
А гипотенуза в 2 раза больше противоположной стороны. И гипотенуза становится = 2 единицы. [8]
Точно так же, как найти sin cos tan? Как найти значения Sin Cos Tan ? Чтобы запомнить тригонометрические значения, приведенные в приведенной выше таблице, выполните следующие действия: Сначала разделите числа 0,1,2,3 и 4 на 4, а затем извлеките положительные корни из всех этих чисел. Следовательно, мы получаем значения для синусоидальных отношений , то есть 0, ½, 1/√2, √3/2 и 1 для углов 0°, 30°, 45°, 60° и 90°. [3]
Во-вторых, как делать Cos Sin Tan? sin = o/h cos = a/h tan = o/a Часто вспоминается как: soh cah toa. Пример. Найдите длину стороны x на рисунке ниже: Угол равен 60 градусов. Дана гипотенуза и нужно найти прилежащий катет. Эта формула, которая соединяет эти три, такова: cos (угол) = смежный / гипотенуза, следовательно, cos60 = x / 13, следовательно, x = 13 × cos60 = 6,5 [3]
Аналогично, какова формула для cos sin Tan?
- SIN A = противоположная сторона/гипотенуза
- COS A = соседняя сторона/гипотеновая сторона
- TAN A = противоположная сторона/соседняя сторона
8
444
4
4
4
4
4
4
4
4924
- 89н.
- Сначала разделите числа 0,1,2,3 и 4 на 4, а затем извлеките положительные корни из всех этих чисел.
- Следовательно, мы получаем значения для синусоидальных отношений, т.е.,½,1/√2,√3/2 и 1 для углов 0°,30°,45°,60° и 90°
- Теперь запишите значения синуса в градусах в обратном порядке от до , чтобы получить значения косинуса для тех же углов.
- S в θ = О позит/Гипотенуза
- C os θ = А близлежащий/Гипотенуза
- T an θ = Противоположный/А близлежащий
- синус: Синус угла равен и определяется как отношение стороны, противоположной (перпендикулярной стороне) к этому углу, к гипотенузе.

- косинус : Косинус угла равен , определяемому как отношение стороны, прилегающей к этому углу, к гипотенузе.
- тангенс: Тангенс угла равен , определяемому как отношение стороны, противоположной этому углу, к стороне, примыкающей к этому углу.
- Сначала разделите на чисел 0,1,2,3 и 4 на 4, а затем извлеките из положительных корней из всех этих чисел.
- Следовательно, мы получаем значения для синусоидальных отношений, т.
 е.,½,1/√2,√3/2 и 1 для углов 0°, 30°, 45°, 60° и 90°
е.,½,1/√2,√3/2 и 1 для углов 0°, 30°, 45°, 60° и 90° - Теперь напишите значений синусоидальных градусов в обратном порядке, чтобы получить значений косинуса для одинаковых углов.
- Тождества Пифагора sin 2X+cos 2X = 1 1+tan 2X = sec 2X 1+cot 2X = csc 2X
- Тождества отрицательного угла sin (-X) = – sin X, нечетная функция csc (-X) = – csc X, нечетная функция cos (-X) = cos X, четная функция sec (-X) = sec .
 ..
.. - Кофункции Тождества sin (π/2 – X) = cos X cos (π/2 – X) = sin X tan (π/2 – X) = кроватка X кроватка (π/2 – X) …
- Формулы половинного угла.
 Если A/2 находится в первом или втором квадранте, в формуле используется положительный знак. …
Если A/2 находится в первом или втором квадранте, в формуле используется положительный знак. … - Двойной и Формулы тройного угла
- Сумма и Разность углов
- Формулы кратного угла
- Произведение К Формулы сумм
- Суммы по Формулы произведений
- Периодические тождества
- Закон синусов
- Закон косинусов
- Тождества произведений. Узнайте больше о тригонометрических формулах и приложениях на BYJU’S. …
- Желто-коричневый A = sin A/ cos A
- Cot A = cos A/ sin A
- Sin A = tan A/sec A
- Cos A = sin A/ tan A
- Sec A = tan A/ sin A
- Cosec A = sec A/ tan A
- mathopenref.com, Калькулятор тангенса 📐 — вычисляет tan(x) для градусов или радианов.
- studytonight.com, Тригонометрические функции (определение, графики, решение и ….
- studytonight.com, Тригонометрические функции (определение, графики, решение и .
 …
… - Тригонометрические функции — Википедия, mathsisfun.com.
- Отношения между sin, cos, tan — Студенческая комната, thestudentroom.co.uk.
- Тригонометрические функции — Википедия, mathsisfun.com.
- Тригонометрические функции — Википедия, mathsisfun.com.
- netexplanations.com, Какова формула для sin cos и tan ….
- Как выразить sin3x через cosx — Quora, youtube.com.
- Как найти cos от sin в математике — Quora, quora.com.
- Формула закона синуса и косинуса — формула и объяснение, mechamath.com.
- wikihow.com, Как запомнить тригонометрическую таблицу: 11 шагов (с иллюстрациями). г.
- Что такое формула Cos(A + B)? — Матемеризация, cuemath.com.
- Формула Sin Cos Tan — изучите формулу для расчета коэффициента Sin Cos Tan…, cuemath.com.
- Значение sin, cos, tan, cot при 0, 30, 45, 60, 90 — Таблица тригонометрии,teachoo.com.
- Синус и косинус — визуальное объяснение, codevscolor.
 com.
com. - Поделиться:
Для решения проблемы потери атрибута времени после преобразования матрицы временных рядов предлагается метод преобразования, основанный на матрице Грама, который преобразует временные ряды в изображения во временной области без потерь и использует метод порогового шумоподавления для фильтрации нормальный фоновый шум 11, 12 .

Чтобы повысить скорость сходимости сети, в слой свертки CNN вводится матрица ядра свертки Теплица 13 , а произведение матрицы матрицы Теплица используется для замены традиционной операции свертки.
Предложена модель T-CNN, которая вводит тройную сеть 14 в полносвязном слое для вычисления функции разности между одним и тем же классом и разными классами и оптимизирует функцию квадратичных потерь модели CNN для улучшения классификации. точность.
г.- (1)
Вейвлет-разложение сигналов. Вейвлет выбирается для определения вейвлет-разложения на уровне S , а затем для сигналов выполняется вычисление вейвлет-разложения на уровне S .
- (2)
Пороговое квантование высокочастотных коэффициентов при вейвлет-разложении.
 Из слоя 1 в слой S выбирается пороговое значение для высокочастотных коэффициентов каждого слоя для порогового квантования. Пороговая функция, используемая в этой статье, рассчитывается по формуле:
Из слоя 1 в слой S выбирается пороговое значение для высокочастотных коэффициентов каждого слоя для порогового квантования. Пороговая функция, используемая в этой статье, рассчитывается по формуле:$$ \lambda = \sigma \sqrt {2\ln N} $$
(2)
, где \(\sigma = M/0,6745\) обозначает медиана абсолютного значения коэффициента вейвлет-разложения первого уровня. Поскольку функция гауссовского распределения P(|x|< 0,6745σ) приблизительно равна 0,5, следовательно, 0,6745 является корректирующим коэффициентом стандартного отклонения гауссовского шума и является фиксированным значением. N обозначает длину сигнала.
- (3)
Вейвлетная реконструкция сигналов. По низкочастотным коэффициентам слоя S и квантованным высокочастотным коэффициентам первого слоя до S -го слоя вейвлет-разложения сигнал восстанавливается вейвлетом.
9{\prime} = \frac{{x — x_{min} }}{{x_{max} — x_{min} }} $$
(3)
, где x обозначает данные, подлежащие нормализации, x ´ обозначает нормализованный результат, x min представляет минимальное значение в данных временного ряда, а x max представляет максимальное значение в данных временного ряда. С помощью преобразования нормализации данных все данные могут быть нормализованы до [0,1]. Например, на рис. 1 показан нормализованный временной ряд 9239.5 T ´ = { t 1 ´, t 2 ´, t 3 ´,…, t n ´} calculated by уравнение (3), абсцисса – время t , а ордината – порог Tv .
Рисунок 1Временные ряды.
Полноразмерное изображение
Преобразование изображения во временной области на основе матрицы Грама
Атрибут времени является важным атрибутом для определения классификации.
 Из-за различных атрибутов времени различные регулярные распределения представлены в хронологическом порядке. Поэтому в этой статье предлагается преобразование изображения во временной области на основе матрицы Грама. Этот метод может сохранять атрибуты времени и преобразовывать временной ряд в N × N двумерная матрица без потерь.
Из-за различных атрибутов времени различные регулярные распределения представлены в хронологическом порядке. Поэтому в этой статье предлагается преобразование изображения во временной области на основе матрицы Грама. Этот метод может сохранять атрибуты времени и преобразовывать временной ряд в N × N двумерная матрица без потерь.Матрица Грама G представляет собой матрицу, состоящую из скалярного произведения каждой пары векторов в виде уравнения (4):
$$ G знак равно \left( {\begin{array}{*{20}c} {\left\langle {a_{1}, a_{1}} \right\rangle} & {\ влево\langle {a_{1}, a_{2}} \right\rangle} & {…} & {\left\langle {a_{1}, a_{n}} \right\rangle} \\ { \left\langle {a_{2}, a_{1}} \right\rangle} & {\left\langle {a_{2}, a_{2}} \right\rangle} & {…} & { \left\langle {a_{2}, a_{n}} \right\rangle} \\ {\begin{array}{*{20}c} .\\ .\\ .\\ \end{array} } & {\begin{массив}{*{20}c} .\\ .\\ .\\ \end{массив}} & {\begin{массив}{*{20}c} .\\ .\\ . \\ \end{массив}} & {\begin{массив}{*{20}c} .
 \\ .\\ .\\ \end{массив}} \\ {\left\langle {a_{n} , a_{1} } \right\rangle} & {\left\langle {a_{n}, a_{2}} \right\rangle} & {…} & {\left\langle {a_{n}, a_{n} } \right\rangle } \\ \end{array} } \right) $$ 9{\prime}GZ = \left({x_{1},x_{2}…x_{n}} \right)\left({\begin{array}{*{20}c} {\left\ langle {a_ {1}, a_ {1}} \ right \ rangle } & {\ left \ langle {a_ {1}, a_ {2}} \ right \ rangle} & {…} & {\ left \ langle {a_ {1}, a_ {n}} \ right \ rangle} \\ {\ left \ langle {a_ {2}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {2 } ,a_{2} } \right\rangle } & {…} & {\left\langle {a_{2} ,a_{n} } \right\rangle } \\ {\begin{array}{* {20}c} . {\ begin {array} {* {20} c} . \\ . \\ . \\ \ end {array} } & {\ begin {array} {* {20} c} . \\ . \\ . \ \ \ end {array} } \\ {\ left \ langle {a_ {n}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {n}, a_ {2}} \ right \ rangle} & {…} & {\left\langle {a_{n}, a_{n}} \right\rangle} \\ \end{array}} \right)\left({\begin{array} {*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right) $$ 9{n} a_{i} x_{i} } \right) \ge 0 $$
\\ .\\ .\\ \end{массив}} \\ {\left\langle {a_{n} , a_{1} } \right\rangle} & {\left\langle {a_{n}, a_{2}} \right\rangle} & {…} & {\left\langle {a_{n}, a_{n} } \right\rangle } \\ \end{array} } \right) $$ 9{\prime}GZ = \left({x_{1},x_{2}…x_{n}} \right)\left({\begin{array}{*{20}c} {\left\ langle {a_ {1}, a_ {1}} \ right \ rangle } & {\ left \ langle {a_ {1}, a_ {2}} \ right \ rangle} & {…} & {\ left \ langle {a_ {1}, a_ {n}} \ right \ rangle} \\ {\ left \ langle {a_ {2}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {2 } ,a_{2} } \right\rangle } & {…} & {\left\langle {a_{2} ,a_{n} } \right\rangle } \\ {\begin{array}{* {20}c} . {\ begin {array} {* {20} c} . \\ . \\ . \\ \ end {array} } & {\ begin {array} {* {20} c} . \\ . \\ . \ \ \ end {array} } \\ {\ left \ langle {a_ {n}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {n}, a_ {2}} \ right \ rangle} & {…} & {\left\langle {a_{n}, a_{n}} \right\rangle} \\ \end{array}} \right)\left({\begin{array} {*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right) $$ 9{n} a_{i} x_{i} } \right) \ge 0 $$где Z ´ GZ представляет собой положительно определенную квадратичную форму, а G обозначает положительно определенную матрицу.
 Положительно определенная матрица может сохранять свойство матрицы путем вычисления собственных значений. После преобразования временного ряда по матрице Грама атрибуты времени могут быть сохранены. Результат преобразования в форму матрицы Грама показан в уравнении. (5):
Положительно определенная матрица может сохранять свойство матрицы путем вычисления собственных значений. После преобразования временного ряда по матрице Грама атрибуты времени могут быть сохранены. Результат преобразования в форму матрицы Грама показан в уравнении. (5):$$ G_{t} = \left( {\begin{array}{*{20}c} {\left\langle {t_{1},t_{1}} \right\rangle} & {\left\langle {t_{1}, t_{2}} \right\rangle} & {…} & {\left\langle {t_{1}, t_{n}} \right\rangle} \\ {\left\langle {t_{2}, t_{1}} \right\rangle} & {\left\langle {t_{2}, t_{2}} \right\rangle} & {… } & {\ left \ langle {t_ {2}, t_ {n}} \ right \ rangle} \\ {\ begin {array} {* {20} c} . \\ . \\ . \\ \ end { массив} } & {\begin{массив}{*{20}c} .\\ .\\ .\\ \end{массив}} & {\begin{массив}{*{20}c} .\\ . \\ . \\ \end{массив} } & {\begin{массив}}{*{20}c} .\\ .\\ . n} ,t_{1} } \right\rangle } & {\left\langle {t_{n} ,t_{2}} \right\rangle} & {…} & {\left\langle {t_{ n} ,t_{n} } \right\rangle } \\ \end{array} } \right) $$
(5)
where G t denotes the time series after Gram matrix conversion, < t i , t j > is the inner product pair of временной ряд, а n — длина временного ряда.
 Внутренний продукт представляет корреляцию между двумя точками, G t вещественной симметричной матрицей. Слева направо от первой строки и сверху вниз от первой колонки в G t корреляция между первой точкой и последующими точками временного ряда увеличивается со временем. Точно так же вторая строка и второй столбец представляют собой корреляцию между второй точкой и последующими точками. Таким образом, матрица G t слева вверху справа внизу представляет порядок расположения корреляций между двумя точками с увеличением времени. Атрибут времени временного ряда сохраняется в матрице Грама.
Внутренний продукт представляет корреляцию между двумя точками, G t вещественной симметричной матрицей. Слева направо от первой строки и сверху вниз от первой колонки в G t корреляция между первой точкой и последующими точками временного ряда увеличивается со временем. Точно так же вторая строка и второй столбец представляют собой корреляцию между второй точкой и последующими точками. Таким образом, матрица G t слева вверху справа внизу представляет порядок расположения корреляций между двумя точками с увеличением времени. Атрибут времени временного ряда сохраняется в матрице Грама.Поскольку временной ряд T является одномерным и имеет прямоугольную систему координат, для расчета пары внутренних произведений требуется двумерная информация об абсциссе и ординате. Поэтому, чтобы лучше сохранить атрибут времени временного ряда, мы используем полярную систему координат для вычисления пар внутреннего произведения временного ряда.
 {\prime}} ) $$ 9{\prime}}\) обозначает нормированный временной ряд, i — отметка времени во временном ряду, n — длина временного ряда, \(\theta_{i}\) — угол точка временного ряда в полярной системе координат, а \(r_{i}\) — радиус точки временного ряда в полярной системе координат. Таким образом, каждая точка временного ряда может быть представлена уравнениями. (6 и 7).
{\prime}} ) $$ 9{\prime}}\) обозначает нормированный временной ряд, i — отметка времени во временном ряду, n — длина временного ряда, \(\theta_{i}\) — угол точка временного ряда в полярной системе координат, а \(r_{i}\) — радиус точки временного ряда в полярной системе координат. Таким образом, каждая точка временного ряда может быть представлена уравнениями. (6 и 7).На рисунке 2 показано кодирование T ´ в полярных координатах на рисунке 1. Процесс кодирования для 0,5:
Рисунок 2Полярные координаты временного ряда.
Полноразмерное изображение
Согласно формуле. (6), arccos (0,5) = 60º; i = 3; N = 5; согласно уравнению (7), радиус равен 0,6. Таким образом, (0,6, 60°) является результатом кодирования.
Со временем радиус точки становится все больше и больше, и она постепенно удаляется от центра круга. Полярное кодирование может полностью сохранить атрибут времени за счет увеличения радиуса, а численное изменение может быть представлено изменением угла.
 Поэтому, как показано в уравнении (8), новая матрица Грама может быть получена с использованием отношения углов в полярных координатах между двумя точками временного ряда:
Поэтому, как показано в уравнении (8), новая матрица Грама может быть получена с использованием отношения углов в полярных координатах между двумя точками временного ряда:$$ G_{t} = \left( {\begin{array}{*{20}c} {\cos (\theta_{1} + \theta_{1})} & {\cos(\theta_{ 1} + \ theta_ {2} )} & {…} & {\ cos (\ theta_ {1} + \ theta_ {n} )} \\ {\ cos (\ theta_ {2} + \ theta_ {1 } )} & {\ cos (\ theta_ {2} + \ theta_ {2} )} & {…} & {\ cos (\ theta_ {2} + \ theta_ {n})} \\ {\ begin {массив}{*{20}c} .\\ .\\ .\\ \end{массив} } & {\begin{массив}{*{20}c} .\\ .\\ .\\ {массив}} & {\begin{массив}{*{20}c} .\\ .\\ .\\ \end{массив}} & {\begin{массив}{*{20}c} .\\ . \\ . {…} & {\cos (\theta_{n} + \theta_{n} )} \\ \end{array} } \right) $$ 9{2} — 1\) матрицы G t , а диагональ матрицы G t расположена по порядку.
По мере перемещения матрицы Грама из верхнего левого угла в нижний правый угол значения временных рядов располагаются в матрице последовательно.
 Другими словами, мы сохраняем атрибут времени временного ряда и кодируем измерение времени в геометрической структуре матрицы. Каждое значение матрицы эквивалентно пикселю изображения, и каждый временной ряд преобразуется в изображение во временной области с помощью матрицы Грама.
Другими словами, мы сохраняем атрибут времени временного ряда и кодируем измерение времени в геометрической структуре матрицы. Каждое значение матрицы эквивалентно пикселю изображения, и каждый временной ряд преобразуется в изображение во временной области с помощью матрицы Грама.Изображение во временной области Классификация T-CNN
Как упоминалось выше, временные ряды преобразуются в изображения во временной области Gram, а изображения во временной области Gram используются в качестве входной матрицы сверточных нейронных сетей для классификации. Чтобы решить проблемы сложных вычислений и низкой скорости обучения сверточных нейронных сетей, мы предлагаем метод, основанный на теплицевом матричном произведении, для замены операции свертки слоя свертки, и вводим идею триплетной сети в функцию потерь для повысить эффективность и точность классификации.
Свертка на основе умножения теплицевых матриц
Операция свертки на основе произведения теплицевых матриц показана на рис.
Рисунок 3 3. На рис. 3 темно-синий квадрат представляет ядро свертки, а светло-синий квадрат представляет свертываемую матрицу. . Ядро свертки имеет размер 2 × 2, несвернутая матрица — 3 × 3, размер шага — 1. Традиционная свертка показана в верхней части рис. 3. размер шага равен 1, и для свертки требуется четыре обхода всей матрицы. После каждого обхода ядро свертки и матричная часть с его повторяющейся суммой перемножаются и накапливаются, а полученное значение является результатом локальной свертки в соответствующей позиции. Поскольку традиционная свертка должна пройти через все изображение, вычислительная сложность высока.
3. На рис. 3 темно-синий квадрат представляет ядро свертки, а светло-синий квадрат представляет свертываемую матрицу. . Ядро свертки имеет размер 2 × 2, несвернутая матрица — 3 × 3, размер шага — 1. Традиционная свертка показана в верхней части рис. 3. размер шага равен 1, и для свертки требуется четыре обхода всей матрицы. После каждого обхода ядро свертки и матричная часть с его повторяющейся суммой перемножаются и накапливаются, а полученное значение является результатом локальной свертки в соответствующей позиции. Поскольку традиционная свертка должна пройти через все изображение, вычислительная сложность высока.Сверточные вычисления.
Изображение в натуральную величину
Как показано в нижней части рис. 3, на основе свертки произведения матрицы Теплица каждая матрица процесса 3 × 3, полученная матрицей обхода ядра свертки, расширяется в соответствии с порядком строк для получения 4 × 1 × 9-строчная матрица, образующая большую матрицу H .
 Затем матрица свертки расширяется до вектора-столбца 9 × 1 X в соответствии с порядком расположения строк. Произведение большой матрицы H , построенный ядром свертки, и вектор-столбец X , построенный матрицей свертки, эффективно заменяет вычисление свертки. В частности, матрица ядра свертки H состоит из 6 небольших матриц, которые представляют собой соответственно матрицу в красном поле и матрицу в желтом поле, а также нулевую матрицу в двух белых частях.
Затем матрица свертки расширяется до вектора-столбца 9 × 1 X в соответствии с порядком расположения строк. Произведение большой матрицы H , построенный ядром свертки, и вектор-столбец X , построенный матрицей свертки, эффективно заменяет вычисление свертки. В частности, матрица ядра свертки H состоит из 6 небольших матриц, которые представляют собой соответственно матрицу в красном поле и матрицу в желтом поле, а также нулевую матрицу в двух белых частях.На рис. 3 матрица в красной рамке соответствует форме определения матрицы Теплица. Точно так же матрица в желтом поле и нулевая матрица являются теплицевыми матрицами. Таким образом, построенная матрица ядра свертки представляет собой большую теплицевую матрицу, состоящую из нескольких малых теплицевых матриц. Произведение матрицы Теплица используется для замены традиционной операции свертки. Ядро свертки напрямую встраивается в матрицу ядра свертки без обхода изображения в порядке размера шага, а произведение двух матриц вычисляется для уменьшения вычислительной сложности.

Определение 2 Матрица Теплица. Матрица с одинаковыми элементами на каждой диагональной линии слева вверху справа внизу является матрицей Теплица, которая обладает свойствами \(A_{i,j} = A_{i + 1,j + 1} = а_{i — j}\). Математически
$$ A = \left( {\begin{array}{*{20}c} {a_{0}} & {a_{- 1}} & {a_{- 2}} & {.. .} & {…} & {a_{{ — \left( {n — 1} \right)}} } \\ {a_{1} } & {a_{0} } & {a_{ — 1} } & \ddots & {} & \vdots \\ {a_{2} } & {a_{1} } & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & {a_{- 1} } & {a_{- 2} } \\ \vdots & {} & \ddots & {a_{1} } & {a_{0} } & {a_{- 1} } \\ {a_{n — 1} } & {…} & {…} & {a_{2} } & {a_{1} } & {a_{0} } \\ \end{массив} } \ справа) $$
(9)
Построение матрицы ядра свертки Теплица
Чтобы заменить вычисление свертки операцией умножения матрицы Теплица, матрица ядра свертки H строится как матрица ядра свертки Теплица H t . Для любой матрицы ядра свертки следующим образом:
$$ H = \left( {\begin{array}{*{20}c} {h_{11}} & {h_{12}} & \cdots & {h_{ 1D} } \\ {h_{21} } & {h_{22}} & \cdots & {h_{2D} } \\ \vdots & \vdots & \vdots & \vdots \\ {h_{C1} } & {h_{C2} } & \cdots & {h_{CD} } \\ \end{массив} } \right) $$
(10)
Соответствующие шаги построения матрицы ядра свертки Теплица следующие:
- (1)
Малая матрица Теплица генерируется из каждого элемента строки матрицы ядра свертки.
 Поскольку размер матрицы ядра свертки равен C × D , матрица ядра свертки H делится на C тёплицевых матриц: H 0 , H 1 , H 2 , H 3 , …, H c -1 , where H 0 is the нулевая интерполяция элемента h 11 в первой строке и первом столбце H , количество вставленных нулей равно количеству столбцов в матрице ядра свертки H минус 1, и берется результат интерполяции как первый ряд из Н 0 . Затем h 12 интерполируется как вторая строка в соответствии со свойствами матрицы Теплица до тех пор, пока не будут сформированы 2 × D -1 строк и завершено построение H 0 . По аналогии, H i является матрицей, полученной путем интерполяции \(i — 1\) элементов строки H . Например, матрица ядра свертки имеет вид \(H = \left[ {\begin{array}{*{20}c} 1 & 2 \\ 3 & 4 \\ \end{array}} \right]\), затем H делится на две матрицы \(H_{0} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 2 & 1 \\ 0 & 2 \\ \end{array } } \right]\) и \(H_{1} = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 4 & 3 \\ 0 & 4 \\ \end{array } } \Правильно]\).
Поскольку размер матрицы ядра свертки равен C × D , матрица ядра свертки H делится на C тёплицевых матриц: H 0 , H 1 , H 2 , H 3 , …, H c -1 , where H 0 is the нулевая интерполяция элемента h 11 в первой строке и первом столбце H , количество вставленных нулей равно количеству столбцов в матрице ядра свертки H минус 1, и берется результат интерполяции как первый ряд из Н 0 . Затем h 12 интерполируется как вторая строка в соответствии со свойствами матрицы Теплица до тех пор, пока не будут сформированы 2 × D -1 строк и завершено построение H 0 . По аналогии, H i является матрицей, полученной путем интерполяции \(i — 1\) элементов строки H . Например, матрица ядра свертки имеет вид \(H = \left[ {\begin{array}{*{20}c} 1 & 2 \\ 3 & 4 \\ \end{array}} \right]\), затем H делится на две матрицы \(H_{0} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 2 & 1 \\ 0 & 2 \\ \end{array } } \right]\) и \(H_{1} = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 4 & 3 \\ 0 & 4 \\ \end{array } } \Правильно]\).
- (2)
Малая матрица Теплица, полученная на шаге (1), преобразуется в матрицу Теплица большого размера:
$$ H_{t} = \left( {\begin{array}{*{20}c} {H_{0}} & 0 & {…} & 0 & 0 \\ {H_{1} } & {H_{0} } & \ddots & \vdots & \vdots \\ {H_{2} } & {H_{1} } & \ddots & 0 & 0 \\ \vdots & {H_{2} } & \ddots & {H_{0} } & 0 \\ {H_{c — 2} } & \vdots & \ddots & {H_{1} } & {H_{0} } \\ {H_{c — 1 } } & {H_{c — 2} } & \vdots & {H_{2} } & {H_{1} } \\ 0 & {H_{c — 1} } & {H_{c — 2}} & \vdots & {H_{2}} \\ 0 & 0 & {H_{c — 1}} & {H_{c — 2}} & \vdots \\ \vdots & \vdots & \vdots & {H_{c — 1} } & {H_{c — 2} } \\ 0 & 0 & 0 & \cdots & {H_{c — 1} } \\ \end{array} } \right) $$
(11)
В примере на шаге (1) \(H_{t} = \left[ {\begin{array}{*{20}c} {H_{0}} & 0 \\ {H_{1}} & {H_{0} } \\ 0 & {H_{1} } \\ \end{array} } \right]\) получается по уравнению.
 (11), где 0 представляет нулевую матрицу 3 × 2,
(11), где 0 представляет нулевую матрицу 3 × 2,
Свертка теплицевой матрицы
После получения матрицы ядра тёплицевой свертки из раздела 8 «Построение матрицы ядра тёплицевой свертки» традиционная свертка может быть заменена умножением тёплицевой матрицы с использованием уравнения. (12).
$$ X*H = H_{t} \times X_{T} $$
(12)
где \(X = \left( {\begin{array}{*{20}c} {x_ {11} } & {x_{12}} & \cdots & {x_{1B} } \\ {x_{21} } & {x_{22}} & \cdots & {x_{2B}} \\ \vdots & \vdots & \vdots & \vdots \\ {x_{A1} } & {x_{A2} } & \cdots & {x_{AB} } \\ \end{array} } \right)\) обозначает матрицу быть свернутым, \(H = \left( {\begin{array}{*{20}c} {h_{11}} & {h_{12}} & \cdots & {h_{1D}} \\ { h_{21} } & {h_{22} } & \cdots & {h_{2D} } \\ \vdots & \vdots & \vdots & \vdots \\ {h_{C1} } & {h_{C2}} & \cdots & {h_{CD} } \\ \end{array} } \right)\) обозначает ядро свертки, H t — матрица ядра свертки Теплица в разделе «Построение матрицы ядра свертки Теплица», а X T — вектор-столбец, полученный путем расположения всех элементов матрицы X 92 в порядке строк.
 {T}\).
{T}\).Затем расчетный вектор столбца перезаписывается в матрицу 3 × 3 в соответствии с M = A + C — 1 = 3 и N = B + D — = B + D — = B + D — = B + D — = B + D — . совпадает с результатами вычисления свертки.
Мы используем умножение матриц Теплица, чтобы эффективно заменить операцию свертки. С точки зрения временной сложности размер входного изображения во временной области составляет A × B , а размер ядра свертки равен C × D . Операция свертки требует, чтобы ядро свертки непрерывно обходило изображение во временной области и вычисляло A × B × C × D -кратное умножение.
При использовании умножения теплицевых матриц требуется вычислить умножение матриц только один раз. Из рис. 3 видно, что в каждой строке матрицы имеется большое количество нулей, которые не нужно вычислять.
 Таким образом, фактическое вычисление каждой строки равно C × D , номер строки – это время прохождения ядра свертки, и приблизительно умножить A × B × C × D раз. Таким образом, во время расчета сумма расчета двух методов примерно одинакова. Однако, когда в традиционную свертку каждый раз вводится новое изображение во временной области, в расчете возникает большое количество операций сдвига, что значительно увеличивает время расчета.
Таким образом, фактическое вычисление каждой строки равно C × D , номер строки – это время прохождения ядра свертки, и приблизительно умножить A × B × C × D раз. Таким образом, во время расчета сумма расчета двух методов примерно одинакова. Однако, когда в традиционную свертку каждый раз вводится новое изображение во временной области, в расчете возникает большое количество операций сдвига, что значительно увеличивает время расчета.Несмотря на то, что для построения матрицы Теплица требуется некоторое время, для умножения матриц Теплица требуется построить соответствующую матрицу Теплица только один раз в соответствии с заданным ядром свертки, а затем можно напрямую выполнить вычисление умножения матрицы на всех входных изображениях во временной области, чтобы получить результат свертки. Таким образом, для наборов данных с большим количеством наборов выборок и наборов тестов время операции свертки будет значительно сокращено.

Классификация моделей T-CNN 9{i} } \right)\) — фактический результат выборки. Модель CNN непрерывно регулирует параметры \(\omega\) и \(b\) путем обучения минимизации \(R\left({\omega,b} \right)\). Уравнение (13) представляет собой функцию квадратичных потерь традиционной модели сверточной нейронной сети, которая учитывает только категорию самого изображения и не учитывает различия между разными категориями. Поэтому мы улучшим его позже.
CNN использует метод градиентного спуска для настройки параметра \(R(\omega ,b)\), как показано в уравнениях. (14) и (15):
$$ \omega_{ij} = \omega_{ij} — a\frac{\partial }{{\partial \omega_{ij}}}R\left({\omega ,b} \right) $$
(14)
$$ b_{ij} = b_{ij} — a\frac{\partial }{{\partial b_{ij} }}R\left( {\omega ,b} \right) $$
(15)
, где a — скорость обучения, а \(R\left ({\omega,b} \right)\) — функция потерь CNN. Уравнения (14) и (15) используются для обновления значений сетевых параметров \(\omega\) и \(b\).
 Метод расчета – метод градиентного спуска. Другими словами, значения \(\omega\) и \(b\) могут быть получены, когда производная функции потерь равна 0,9.1826
Метод расчета – метод градиентного спуска. Другими словами, значения \(\omega\) и \(b\) могут быть получены, когда производная функции потерь равна 0,9.1826Для повышения точности классификации в функцию потерь CNN для ограничения введена сеть Triplet, а также предложена модель T-CNN, основанная на функции потерь Triplet. Идея модели T-CNN состоит в том, чтобы одновременно вводить три изображения домена, два из которых принадлежат одному классу, а одно — другому классу. Модель T-CNN может получить характеристику изображений во временной области путем обучения и может получить функцию разности признаков \(L_{1}\) двухвременных изображений из одного и того же класса и функцию разности характеристик \(L_{ 2} \) двукратных образов доменов из разных классов. Затем \(L_{1} \) и \(L_{2} \) используются для настройки параметров модели T-CNN. \(L_{1} \) и \(L_{2}\) показаны в уравнениях. (16 ) и (17) соответственно: 9{\left( l \right)}\) — это выходное значение различных классов. Функции различия характеристик изображения показаны в уравнении настройки.
 (18).
(18).$$ L_{T} = \max (0,L_{1} — L_{2} + \gamma ) $$
(18)
где \(\gamma\) представляет минимальное расстояние разности между разными классами и между классами (в этой статье установлено значение 0,1). В эксперименте этой статьи сравнительный эксперимент проводился путем изменения значения \(\gamma\), а значение \(\gamma\) составляло 0,01, 0,05, 0,1, 0,2 и 0,5 соответственно. Эксперимент показал, что 0,1 был лучшим экспериментальным результатом. В каждой обратной итерации L T постепенно приближается к нулю. Как показано на рис. 4, когда функция различия признаков L 1 одного и того же класса изображений больше, чем функция различия признаков L 2 изображений разных классов за вычетом параметра α , L T больше нуля, и модель корректируется в обратном порядке, чтобы сделать L 1 меньше, а L 2 больше. Ссылка 21 подтвердила, что функция тройных потерь может сделать выборки одного типа близкими друг к другу, а выборки разных типов — далекими друг от друга.
Рисунок 4
Диаграмма регулировки разницы характеристик. (Он используется для иллюстрации тройной функции потерь, предложенной в этой статье. Программное обеспечение — Microsoft Office Visio).
Изображение в полный размер
На рис. 4 A и P относятся к одному классу, а N не принадлежит к тому же классу, что и A и P . Перед корректировкой расстояние между A и P больше, чем между A и N , а функция разности L T больше нуля. Таким образом, параметры модели должны быть скорректированы в обратном порядке. После регулировки расстояние между A и N становится больше, а расстояние между A и P становится меньше.
Согласно уравнениям. (16) и (17), в каждой обратной итерации видно, что L 1 уменьшат разность признаков того же класса, а L 2 сделают признак разница разных классов больше.
 На этой основе предлагается тройная функция потерь, как показано в уравнении. (19):
На этой основе предлагается тройная функция потерь, как показано в уравнении. (19):$$ L\left( {\omega ,b} \right) = R\left( {\omega ,b} \right) + \alpha L_{1} — \beta L_{2} $ $
(19)
где \(R\left( {\omega ,b} \right)\) обозначает функцию квадратичных потерь CNN, \(\alpha\) и \(\beta\) — коэффициенты весовой доли больше нуля. В эксперименте мы проверили значения \(\alpha\) и \(\beta\). Значения \(\альфа\) были 0,1, 0,01, 0,3, 0,4 и так далее, а значения \(\бета\) были 0,9, 0,99, 0,7, 0,6 и так далее. После нескольких экспериментов было установлено, что значения \(\альфа\) и \(\бета\) составляют 0,4, 0,6 соответственно, а экспериментальный эффект был наилучшим. L 1 — функция разности признаков того же класса, а L 2 — функция разности признаков разных классов. Таким образом, новая остаточная ошибка каждого слоя по алгоритму обратного распространения выглядит следующим образом: }L\left( {\omega ,b} \right) $$
(20)
$$ b_{ij} = b_{ij} — a\frac{\partial }{{\partial b_{ij} }}L\влево( {\omega ,b} \вправо) $$
(21)
Модель T-CNN, основанная на сети Triplet, добавляет функцию различия признаков между одним и тем же классом и функцию различия признаков между разными классами в функцию кросс-энтропийных потерь, которая позволяет параметрам быстрее извлекать признаки с большими различиями в процессе корректировки веса параметра.
 Частная производная \(L\left({\omega,b} \right)\) может выполнить вычисление невязки обратного распространения для получения новых параметров \(\omega\) и \(b\). Каждая итерация больше склоняется к направлению градиентного спуска, что может ускорить сходимость модели и повысить эффективность классификации.
Частная производная \(L\left({\omega,b} \right)\) может выполнить вычисление невязки обратного распространения для получения новых параметров \(\omega\) и \(b\). Каждая итерация больше склоняется к направлению градиентного спуска, что может ускорить сходимость модели и повысить эффективность классификации.Структура модели T-CNN, используемая в этой статье, представляет собой 5 × 5 сверток из 128 нейронов в первом слое, 5 × 5 сверток из 128 нейронов во втором слое, максимальный объединяющий слой 2 × 2 в третьем слое, 3 × 3 свертка из 256 нейронов в четвертом слое, 3 × 3 свертка из 256 нейронов в пятом слое, максимальный объединяющий слой 2 × 2 в шестом слое, 1024 нейрона в слое полной связи в седьмом слое. Функция потерь — это функция потерь на основе триплета, функция активации — сигмовидная функция, а диапазон значений функции — (0,1). На рис. 5 показана структура модели. Алгоритм классификации временных рядов T-CNN показан в Алгоритме 1.
Рисунок 5Структура модели классификации T-CNN.

Полноразмерное изображение
Эксперименты
Набор экспериментальных данных включает 6 наборов данных UCR2018 и наборов данных о микроземлетрясениях, которые содержат три типа временных рядов волновых форм событий шахтных микросейсмических сигналов. Набор данных включает данные временных рядов разного размера, длины и категории. Размер тренировочного набора составляет 60 % от общего набора данных, а размер тестового набора — 40 % от общего набора данных, а модель обучения — Tensorflow. Аппаратно-программная среда эксперимента представлена в табл. 1.
Таблица 1 Программно-аппаратная среда.Полноразмерная таблица
Наборы экспериментальных данных показаны в Таблице 2. После применения вейвлет-метода шумоподавления в этой статье тип и длина набора данных микроземлетрясений, содержащего шум, не изменятся, но сама длина неодинакова, поэтому не повлияет на структуру набора данных.
Таблица 2 Экспериментальные наборы данных.
Полноразмерная таблица
Чтобы предотвратить локальную сверхконвергенцию, структура сверточной нейронной сети снабжена двумя сверточными слоями. Сверточный слой 1 использует ядро свертки размером 5 × 5, а максимальный размер окна объединения составляет 3 × 3.Сверточный слой 2 использует ядро свертки размером 3 × 3, а максимальный размер окна объединения составляет 2 × 2. За сверточным слоем 2 следует стандартный полносвязный слой. Функция активации этого уровня использует ReLU, что обеспечивает быструю сходимость модели CNN. Функция потерь использует функцию потерь Triplet. Изображение во временной области, выводимое моделью T-CNN, равно p = { p 1 , p 2 , p 3 }, where p 1 , p 2 , and p 3 represent вероятности трех классов в наборе данных соответственно. Класс = T ( max ( p )) используется для классов оценки, где функция T является пороговой функцией, а порог устанавливается равным 0,8 после повторных экспериментов.
 Когда max ( p ) превышает пороговое значение, установленное функцией T , выводится класс изображения во временной области. Чтобы сделать экспериментальные результаты более надежными, в эксперименте используется десятикратная перекрестная проверка, а конечный результат составляет в среднем 10-кратную. Модель T-CNN настраивается на оптимальное состояние за счет непрерывной прямой проводимости, в которой основными регулируемыми параметрами являются скорость обучения и время итерации. Во время этого эксперимента скорость обучения установлена на 0,005, а время итерации регулируется.
Когда max ( p ) превышает пороговое значение, установленное функцией T , выводится класс изображения во временной области. Чтобы сделать экспериментальные результаты более надежными, в эксперименте используется десятикратная перекрестная проверка, а конечный результат составляет в среднем 10-кратную. Модель T-CNN настраивается на оптимальное состояние за счет непрерывной прямой проводимости, в которой основными регулируемыми параметрами являются скорость обучения и время итерации. Во время этого эксперимента скорость обучения установлена на 0,005, а время итерации регулируется.Сравнение точности классификации
Точность представляет собой отношение числа правильно классифицированных образцов к общему количеству образцов. На рис. 6 показано сравнение точности классификации по восьми различным моделям классификации. Сравниваемыми методами являются преобразователь, аппроксимация символьной агрегации (SAX), шейплет, динамическое преобразование времени (DTW), коллектив ансамблей на основе преобразования (COTE), инвариантное расстояние сложности (CID) и метод классификации CNN.
Рисунок 6
Сравнение точности классификации.
Изображение в натуральную величину
Экспериментальные результаты сравнения точности классификации при различных наборах данных представлены в Таблице 3.
Таблица 3 Сравнительная таблица точности классификации.Полноразмерная таблица
Из рис. 6 и таблицы 3 известно, что модель T-CNN преобразует временные ряды в изображения во временной области с помощью матрицы Грама, она может полностью сохранять временные характеристики временных рядов , и его точность классификации значительно выше, чем у других методов. 9{{n_{c} }} n_{ji} }} $$
(22)
где \(n_{ij}\) — количество выборок, предсказанное как j--й класс в классе i , а \(n_{c}\) — количество классов примеров. Затем вычислите среднюю точность всех классов, чтобы получить среднюю точность классификации. На рис. 7 показано сравнение точности классификации.
Рисунок 7
Сравнение точности классификации.
Изображение в полный размер
Экспериментальные результаты сравнения точности классификации при различных наборах данных представлены в таблице 4. 9{{n_{c} }} n_{ij} }} $$
(23)
где \(n_{ij}\) — количество выборок, предсказанное как j--й класс в классе i , а \(n_{c}\) — количество классов примеров. Затем вычислите средний отзыв всех классов, чтобы получить средний отзыв классификации. Рисунок 8 представляет собой сравнение отзыва классификации.
Рисунок 8Сравнение полноты классификации.
Изображение в натуральную величину
Экспериментальные результаты сравнения полноты классификации при различных наборах данных представлены в таблице 5.
Таблица 5 Сравнение отзыва классификации.Полноразмерная таблица
Из рис. 8 и таблицы 5 модель T-CNN использует матрицу Грама для преобразования временных рядов без потерь и улучшает функцию потерь, поэтому полнота классификации близка к полноте метода COTE.
 и превосходит другие методы.
и превосходит другие методы.Сравнение точности свертки Теплица и традиционной свертки
В этом разделе сравнивается точность свертки, основанной на матричном произведении Теплица, и традиционной свертки. В экспериментальном процессе для расчета свертки берется размер ядра свертки, а длина временного ряда последовательно перехватывается от 10 до 100. Размер изображения во временной области, преобразованный на основе матрицы Грама, составляет от 10*10 до 100*100. Сравнение точности свертки Теплица и традиционной свертки для свертки изображений во временной области разных размеров показано на рис. 9.. По оси абсцисс — количество итераций, по оси ординат — точность.
Рисунок 9Сравнение времени выполнения свертки.
Изображение в полный размер
Из рис. 9 видно, что после нескольких экспериментов, после 70 итераций обучающая выборка может дать хороший эффект, а точность на тестовой выборке достигает 90% и имеет тенденцию быть стабильной.
 точность как традиционной свертки, так и свертки Теплица плавно изменяется между размером изображения 10 и 40 во временной области. При размере изображения более 40 во временной области точность двух сверток увеличивается быстрее. В целом, при размере изображения от 10*10 до 100*100 точность тёплицевой свертки выше, чем у традиционной операции свертки, поэтому сходимость тёплицевой свертки происходит быстрее. Следовательно, свертка Теплица, предложенная в этой статье, может ускорить обучение модели.
точность как традиционной свертки, так и свертки Теплица плавно изменяется между размером изображения 10 и 40 во временной области. При размере изображения более 40 во временной области точность двух сверток увеличивается быстрее. В целом, при размере изображения от 10*10 до 100*100 точность тёплицевой свертки выше, чем у традиционной операции свертки, поэтому сходимость тёплицевой свертки происходит быстрее. Следовательно, свертка Теплица, предложенная в этой статье, может ускорить обучение модели.Заключение
В этой статье предлагается метод классификации временных рядов T-CNN, основанный на матрице Грама. Метод сначала очищает временные ряды с помощью порога вейвлета, а затем преобразует временные ряды без потерь во временные изображения с помощью матрицы Грама, атрибут времени сохраняется для повышения точности классификации. И на этой основе в модели T-CNN предлагается ввести в слой свертки матрицу сверточного ядра Теплица, заменить операцию свертки умножением двух матриц и ввести функцию различия признаков одного класса и разных классов для улучшения функция потерь CNN полносвязного слоя, а эффективность классификации повышается.

- (1)
 Также спросили, как запомнить точные значения sin, cos и TAN?
Также спросили, как запомнить точные значения sin, cos и TAN?[5]
Как сделать Cos Sin Tan?
Тогда что такое sin, cos и Tan для новичка?
[2] [2] между грехом, соз и Тан?
[7]
Также вопрос: что такое тан с точки зрения sin и cos? Тангенс x определяется как его синус , разделенный на его косинус : tan x = sin x cos x . Котангенс x определяется как косинус x, деленный на синус x: cot x = cos x sin x . Нажмите, чтобы увидеть полный ответ [2]
Кроме того, как вручную найти значения Sin Cos и TAN?
[2]
г. Какова формула для cos sin Tan?
Аналогично, как найти тригонометрию загара? tan (θ) = y/x (где x и y — координаты точек единичной окружности) Используя свойства треугольника 30-60-90, мы можем найти остальные стороны. Сторона, примыкающая к угол в √3 раза больше противоположной стороны. А гипотенуза в 2 раза больше противоположной стороны. И гипотенуза становится = 2 единицы. [8]
Из них, как выразить грех через Cos?
[5]
Далее, Как найти COS с помощью Sin? — TanX = SinX/CosX — CotX = CosX/SinX — Sin (квадрат)X + Cos (квадрат)X = 1 [4]
Точно так же люди спрашивают: что такое закон sin и cos? Правила синуса и косинуса , также называемые синусом и косинусом , используются для нахождения решения косоугольного треугольника. Это треугольник, который не является прямоугольным треугольником. В этом треугольнике все углы острые или только один тупой. Закон синуса (правило синуса ) Есть два случая, когда мы используем г. Синус г. Правило. ААС или АСК; SSA [5]
Как запомнить точные значения sin, cos и TAN?
Также вопрос, какова формула для cos?
[7]
Точно так же можно спросить: что такое формулы sin cos tan?
[6]
Учитывая это, каковы значения sin и cos? cosec θ = 1/sin θ.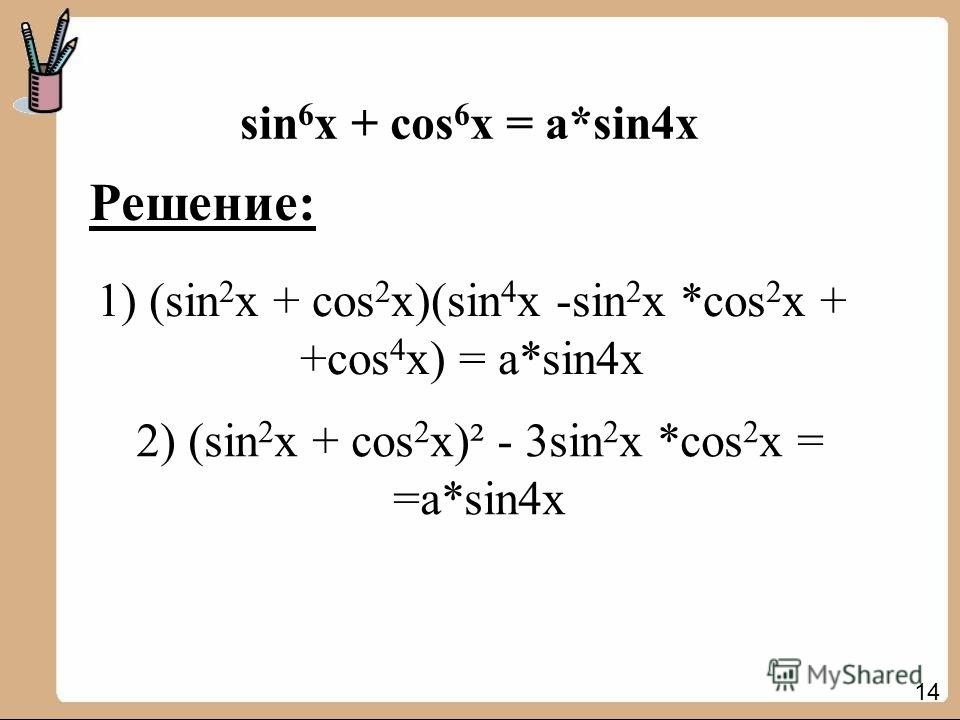 За грех, мы знаем. 0, 1/2, 1/√2, √3/2, 1. Значит, для cosec будет. cosec 0° = 1 / sin 0° = 1/0 = не определено = ∞. cosec 30° = 1 / sin 40° = 1/(1/2) = 2. cosec 45° = 1 / sin 45° = 1/(1/√2) = √2. cosec 60° = 1 / sin 60° = 1/(√3/2) = 2/√3. косек 90° = 1 / sin 90° = 1/1 = 1. [1]
За грех, мы знаем. 0, 1/2, 1/√2, √3/2, 1. Значит, для cosec будет. cosec 0° = 1 / sin 0° = 1/0 = не определено = ∞. cosec 30° = 1 / sin 40° = 1/(1/2) = 2. cosec 45° = 1 / sin 45° = 1/(1/√2) = √2. cosec 60° = 1 / sin 60° = 1/(√3/2) = 2/√3. косек 90° = 1 / sin 90° = 1/1 = 1. [1]
Учитывая это, как найти Sin из COS? Sin Cos формулы основаны на сторонах прямоугольного треугольника. Sin и Cos являются основными тригонометрическими функциями наряду с функцией тангенса в тригонометрии. Синус угла равен отношению противолежащего катета к гипотенузе, а косинус угла равен отношению прилежащего катета к гипотенузе. [4]
Ссылки
Тригонометрические тождества — если да, то чему они эквивалентны 92 х$. Добавить комментарий
обязательно ответьте на вопрос . Предоставьте подробности и поделитесь своими исследованиями!Xem thêm: Tên Cac Hành Tinh Bằng Tiếng Anh Về Vũ Trụ, Từ Vựng Tiếng Anh Về Hệ Mặt Trời
Используйте quansulienminh.vnJax для форматирования уравнений. ссылка на quansulienminh.vnJax.
Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов.
Черновик сохранен
Черновик удален
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь, используя Google
Зарегистрируйтесь, используя Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Отправить
Опубликовать как гость
Имя
Электронная почта Обязательно, но никогда не отображалась
Опубликовать как гость
Имя
Электронная почта
Обязательно, но никогда не отображалась
Опубликовать свой ответ Отменить
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, конфиденциальностью политика и политика в отношении файлов cookie
Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками тригонометрия или задайте свой вопрос.

Популярные на Meta
27 голосов · комментарий · статистика
Похожие 92\right)\,\right)$ без калькулятора
Hot Network Questions больше горячих вопросов
Лента вопросов
Подписаться на RSS
Лента вопросов Чтобы подписаться на эту RSS-ленту, скопируйте и вставьте этот URL в программу чтения RSS.
quansulienminh.vnematics
Компания
Сеть Stack Exchange
дизайн сайта / логотип © 2021 Stack Exchange Inc; вклады пользователей под лицензией cc by-sa. ред.2021.8.13.39972
quansulienminh.vnematics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой использования файлов cookie.
Метод классификации временных рядов T-CNN на основе матрицы Грама.
 1824 1 . В последние годы, с развитием компьютерных технологий, временные ряды стали все более широко применяться, например, для мониторинга стихийных бедствий, анализа безопасности, изменения климата, фондовых фондов и других областей. Как классифицировать временные ряды 2,3,4 было трудным моментом в области интеллектуального анализа данных. Например, в системах мониторинга и раннего оповещения шахтных аварий используются микросейсмические датчики, установленные вокруг шахт, для хранения данных в реальном времени. Эти аварии на шахтах обычно длятся от нескольких секунд до более 10 с. Классификация этих событий помогает обобщить особенности различных типов бедствий 5 , что имеет большое значение для анализа данных и предотвращения стихийных бедствий.
1824 1 . В последние годы, с развитием компьютерных технологий, временные ряды стали все более широко применяться, например, для мониторинга стихийных бедствий, анализа безопасности, изменения климата, фондовых фондов и других областей. Как классифицировать временные ряды 2,3,4 было трудным моментом в области интеллектуального анализа данных. Например, в системах мониторинга и раннего оповещения шахтных аварий используются микросейсмические датчики, установленные вокруг шахт, для хранения данных в реальном времени. Эти аварии на шахтах обычно длятся от нескольких секунд до более 10 с. Классификация этих событий помогает обобщить особенности различных типов бедствий 5 , что имеет большое значение для анализа данных и предотвращения стихийных бедствий. Существующие методы классификации временных рядов в основном используют аппроксимацию символьного агрегирования (SAX) 6 и нейронную сеть свертки (CNN) 7, 8 , но игнорируют атрибут времени, и точность классификации невысока. Поэтому для решения вышеуказанных проблем в этой статье предлагается метод классификации временных рядов T-CNN, основанный на матрице Грама 9 . Сеть CNN заменяет ядра свертки большого размера путем каскадирования нескольких ядер свертки малого размера, так что нейроны нескольких ядер свертки малого размера и одного ядра свертки большого размера имеют одинаковое восприятие, что не только эффективно уменьшает количество сетевых параметров, но также увеличивает нелинейное преобразование и сетевая глубина сети. Он может извлекать более сложные и абстрактные расширенные функции и повышать точность классификации моделей. Предлагаемый метод сохраняет атрибут времени и улучшает функцию квадратичных потерь 10 модели CNN на уровне полного соединения для повышения точности и эффективности классификации. Основные материалы этой статьи следующие:
Поэтому для решения вышеуказанных проблем в этой статье предлагается метод классификации временных рядов T-CNN, основанный на матрице Грама 9 . Сеть CNN заменяет ядра свертки большого размера путем каскадирования нескольких ядер свертки малого размера, так что нейроны нескольких ядер свертки малого размера и одного ядра свертки большого размера имеют одинаковое восприятие, что не только эффективно уменьшает количество сетевых параметров, но также увеличивает нелинейное преобразование и сетевая глубина сети. Он может извлекать более сложные и абстрактные расширенные функции и повышать точность классификации моделей. Предлагаемый метод сохраняет атрибут времени и улучшает функцию квадратичных потерь 10 модели CNN на уровне полного соединения для повышения точности и эффективности классификации. Основные материалы этой статьи следующие:
Родственные работы
В настоящее время исследователи изучили классификацию временных рядов и получили некоторые научные достижения.
Чжун и др. 15 предложил SAX, который делил серию на сегменты и преобразовывал каждый сегмент в соответствующую букву для классификации. В этом методе использовалась идея агрегирования для эффективного уменьшения размерности и повышения эффективности классификации. Однако этот метод потерял большое количество точек данных во временном ряду, и точность классификации этого метода была невысокой. Син и др. 16 предложил метод точки поворота тренда (TTP), который извлекал характеристику тренда самого временного ряда и требовал статистического анализа экстремальных точек и точек перегиба каждого временного ряда. Этот метод хорошо повлиял на наборы данных с определенными правилами, но не на наборы данных с большими колебаниями тренда.
Однако этот метод потерял большое количество точек данных во временном ряду, и точность классификации этого метода была невысокой. Син и др. 16 предложил метод точки поворота тренда (TTP), который извлекал характеристику тренда самого временного ряда и требовал статистического анализа экстремальных точек и точек перегиба каждого временного ряда. Этот метод хорошо повлиял на наборы данных с определенными правилами, но не на наборы данных с большими колебаниями тренда.
Марион и др. 17 предложил метод расстояния во временной области (TDD), который отражал сходство путем вычисления евклидова расстояния между различными последовательностями. Чем ближе расстояние, тем выше сходство. Скорость классификации этого метода была высокой, но точность классификации была низкой. Марко и др. 18 предложил метод интервальной классификации, который разделял временные ряды на интервалы равной длины, вычислял среднее значение и стандартное отклонение каждого интервала и использовал для классификации машины опорных векторов.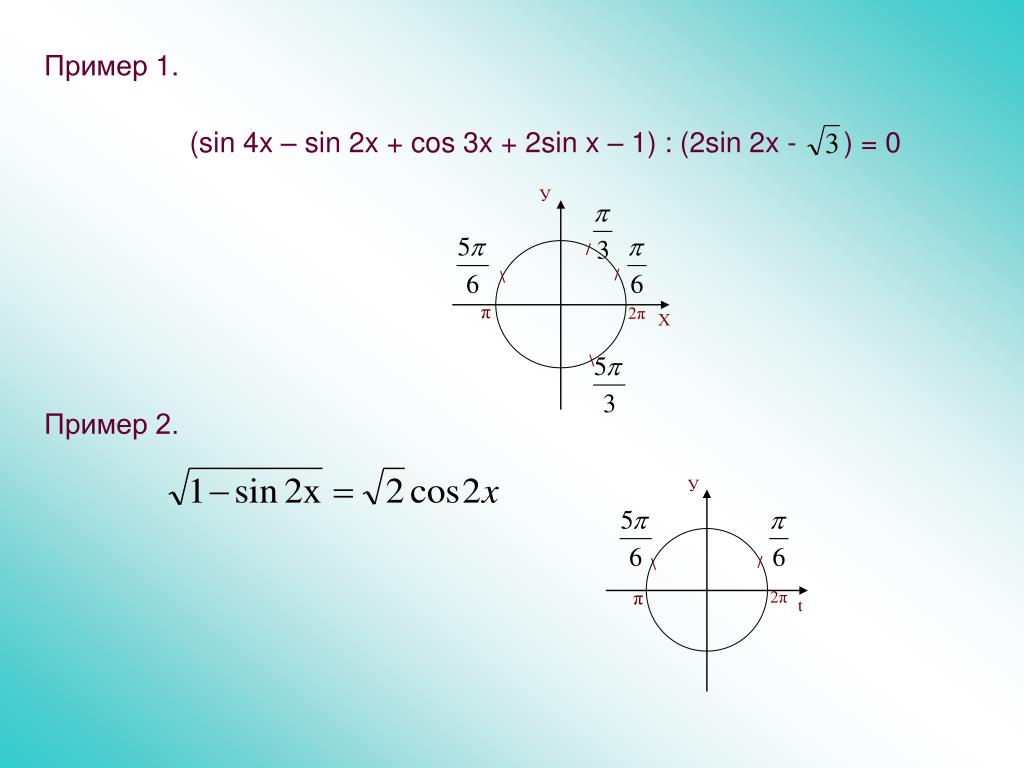 Этот метод рассматривал временной ряд как набор дискретных точек данных и терял атрибут времени.
Этот метод рассматривал временной ряд как набор дискретных точек данных и терял атрибут времени.
Франциско и др. 19 предложил метод Shapelet для поиска Shapelet из временных рядов известных меток классов, чтобы отразить соответствующие признаки классификации. Этот метод имеет высокую точность классификации, но временная сложность извлечения Shapelet высока, а эффективность классификации низка. Чен и др. 20 предложил метод классификации, основанный на сверточных нейронных сетях, которые использовали CNN для эффективной классификации временных рядов. Однако тренировочный процесс этого метода был сложным и не учитывал временной атрибут.
Для решения вышеупомянутых проблем в этой статье предлагается метод классификации временных рядов T-CNN, основанный на матрице Грама, который преобразует временные ряды в изображения во временной области без потерь и сохраняет атрибуты времени. Предлагаемая модель T-CNN, основанная на сверточных нейронных сетях, вводит в модель изображения во временной области, повышая точность классификации.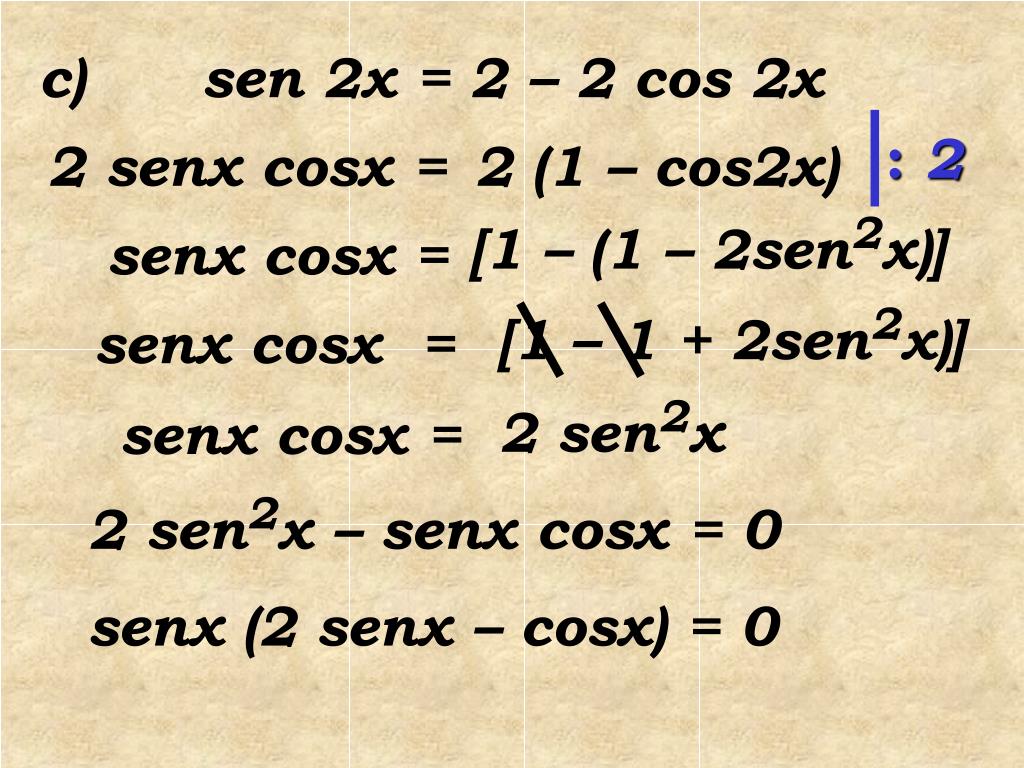
Преобразование временных рядов по матрице граммов
События временных рядов представляют собой не одну или несколько точек данных аномального восприятия, а серию дискретных точек данных, которые соответствуют пороговому диапазону во временной области, и события одного и того же класса имеют схожие характеристики.
Определение 1 События временного ряда: набор непрерывных аномальных данных, инициированный первым выбросом во временном ряду, который превышает пороговый диапазон и длится в течение определенного периода времени. Это можно представить как:
$$ E = \{ \left( {e_{1} ,e_{2} ,e_{3} ,…,e_{n} } \right)\left| {\forall я \in \left({1,2,3,…,n} \right),} \right|e_{i} | > \phi \} $$
(1)
где \(e_{i}\) представляет выброс в событии, а \(\phi\) обозначает заданный пороговый диапазон.
Согласно определению 1 каждое событие временного ряда имеет атрибуты времени. Стремясь к отсутствию атрибута времени в существующих методах классификации временных рядов, мы вводим метод преобразования матрицы Грама для реализации преобразования временных рядов без потерь.
Нормальная фильтрация шума
После преобразования матрицы Грама гистограмма изображения во временной области представляет собой нормальное распределение. Наличие нормального шума напрямую влияет на преобразование изображений во временной области. Следовательно, прежде чем использовать матрицу Грама для преобразования временных рядов, данные сначала предварительно обрабатываются, а затем используется метод шумоподавления с пороговым значением вейвлета для фильтрации нормального фонового шума, переносимого данными.
Шаги метода вейвлет порогового шумоподавления следующие:


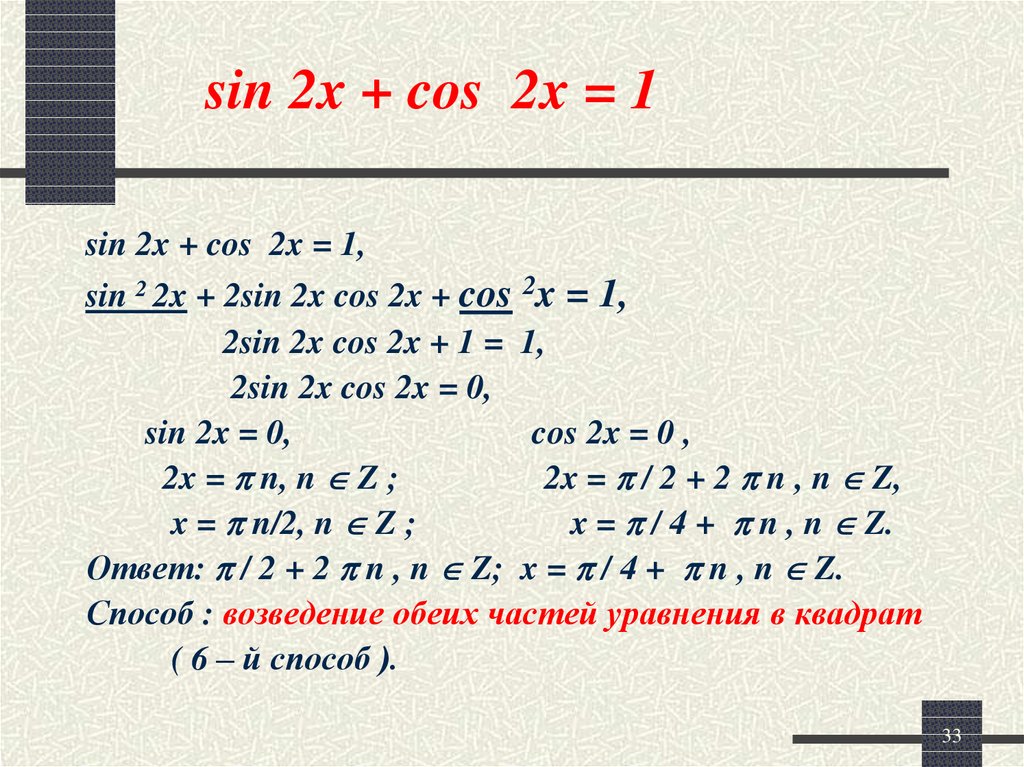

 е.,½,1/√2,√3/2 и 1 для углов 0°, 30°, 45°, 60° и 90°
е.,½,1/√2,√3/2 и 1 для углов 0°, 30°, 45°, 60° и 90° ..
.. Если A/2 находится в первом или втором квадранте, в формуле используется положительный знак. …
Если A/2 находится в первом или втором квадранте, в формуле используется положительный знак. …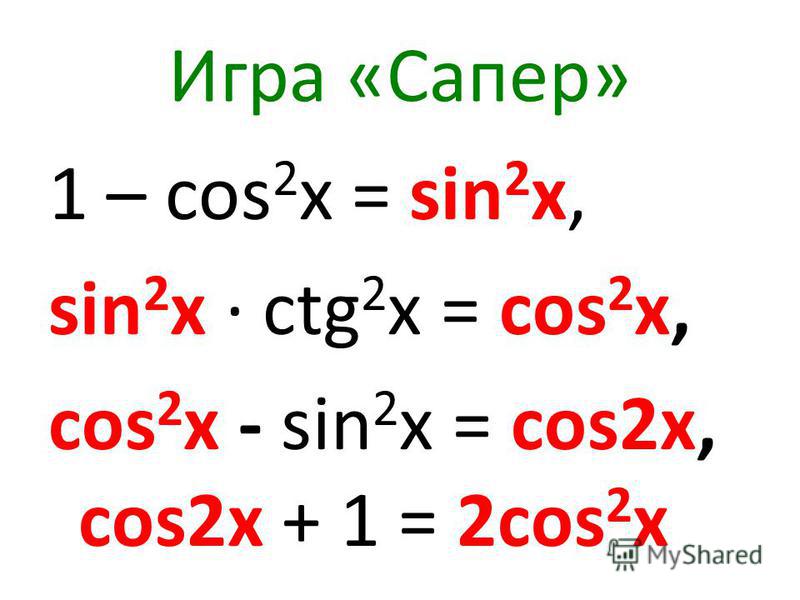 …
… com.
com.
 Из слоя 1 в слой S выбирается пороговое значение для высокочастотных коэффициентов каждого слоя для порогового квантования. Пороговая функция, используемая в этой статье, рассчитывается по формуле:
Из слоя 1 в слой S выбирается пороговое значение для высокочастотных коэффициентов каждого слоя для порогового квантования. Пороговая функция, используемая в этой статье, рассчитывается по формуле:
 Из-за различных атрибутов времени различные регулярные распределения представлены в хронологическом порядке. Поэтому в этой статье предлагается преобразование изображения во временной области на основе матрицы Грама. Этот метод может сохранять атрибуты времени и преобразовывать временной ряд в N × N двумерная матрица без потерь.
Из-за различных атрибутов времени различные регулярные распределения представлены в хронологическом порядке. Поэтому в этой статье предлагается преобразование изображения во временной области на основе матрицы Грама. Этот метод может сохранять атрибуты времени и преобразовывать временной ряд в N × N двумерная матрица без потерь. \\ .\\ .\\ \end{массив}} \\ {\left\langle {a_{n} , a_{1} } \right\rangle} & {\left\langle {a_{n}, a_{2}} \right\rangle} & {…} & {\left\langle {a_{n}, a_{n} } \right\rangle } \\ \end{array} } \right) $$ 9{\prime}GZ = \left({x_{1},x_{2}…x_{n}} \right)\left({\begin{array}{*{20}c} {\left\ langle {a_ {1}, a_ {1}} \ right \ rangle } & {\ left \ langle {a_ {1}, a_ {2}} \ right \ rangle} & {…} & {\ left \ langle {a_ {1}, a_ {n}} \ right \ rangle} \\ {\ left \ langle {a_ {2}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {2 } ,a_{2} } \right\rangle } & {…} & {\left\langle {a_{2} ,a_{n} } \right\rangle } \\ {\begin{array}{* {20}c} . {\ begin {array} {* {20} c} . \\ . \\ . \\ \ end {array} } & {\ begin {array} {* {20} c} . \\ . \\ . \ \ \ end {array} } \\ {\ left \ langle {a_ {n}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {n}, a_ {2}} \ right \ rangle} & {…} & {\left\langle {a_{n}, a_{n}} \right\rangle} \\ \end{array}} \right)\left({\begin{array} {*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right) $$ 9{n} a_{i} x_{i} } \right) \ge 0 $$
\\ .\\ .\\ \end{массив}} \\ {\left\langle {a_{n} , a_{1} } \right\rangle} & {\left\langle {a_{n}, a_{2}} \right\rangle} & {…} & {\left\langle {a_{n}, a_{n} } \right\rangle } \\ \end{array} } \right) $$ 9{\prime}GZ = \left({x_{1},x_{2}…x_{n}} \right)\left({\begin{array}{*{20}c} {\left\ langle {a_ {1}, a_ {1}} \ right \ rangle } & {\ left \ langle {a_ {1}, a_ {2}} \ right \ rangle} & {…} & {\ left \ langle {a_ {1}, a_ {n}} \ right \ rangle} \\ {\ left \ langle {a_ {2}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {2 } ,a_{2} } \right\rangle } & {…} & {\left\langle {a_{2} ,a_{n} } \right\rangle } \\ {\begin{array}{* {20}c} . {\ begin {array} {* {20} c} . \\ . \\ . \\ \ end {array} } & {\ begin {array} {* {20} c} . \\ . \\ . \ \ \ end {array} } \\ {\ left \ langle {a_ {n}, a_ {1}} \ right \ rangle} & {\ left \ langle {a_ {n}, a_ {2}} \ right \ rangle} & {…} & {\left\langle {a_{n}, a_{n}} \right\rangle} \\ \end{array}} \right)\left({\begin{array} {*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right) $$ 9{n} a_{i} x_{i} } \right) \ge 0 $$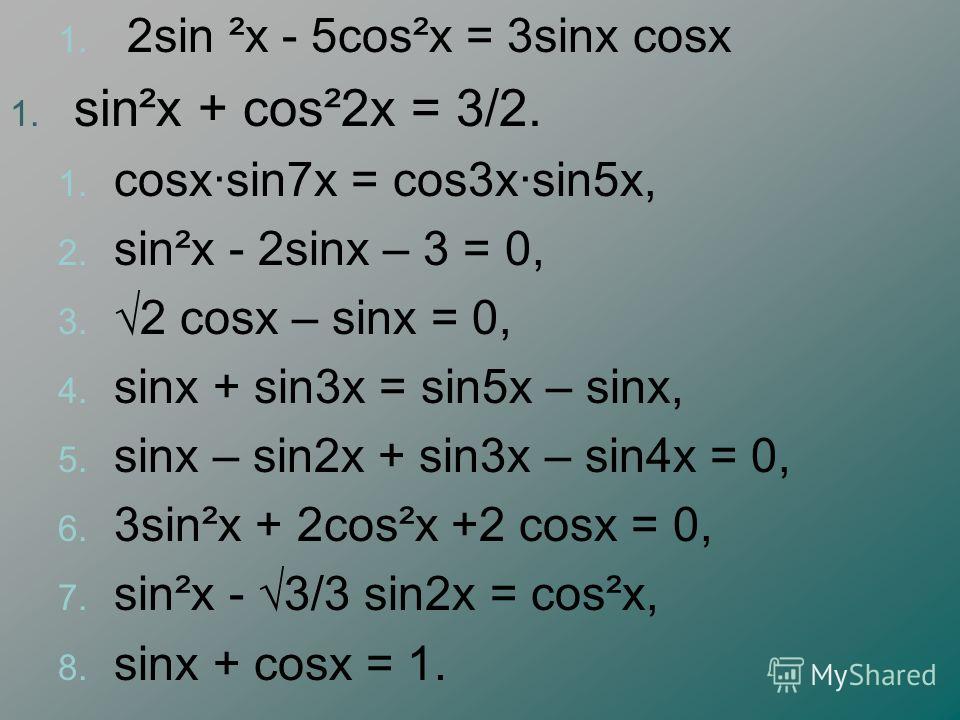 Положительно определенная матрица может сохранять свойство матрицы путем вычисления собственных значений. После преобразования временного ряда по матрице Грама атрибуты времени могут быть сохранены. Результат преобразования в форму матрицы Грама показан в уравнении. (5):
Положительно определенная матрица может сохранять свойство матрицы путем вычисления собственных значений. После преобразования временного ряда по матрице Грама атрибуты времени могут быть сохранены. Результат преобразования в форму матрицы Грама показан в уравнении. (5): Внутренний продукт представляет корреляцию между двумя точками, G t вещественной симметричной матрицей. Слева направо от первой строки и сверху вниз от первой колонки в G t корреляция между первой точкой и последующими точками временного ряда увеличивается со временем. Точно так же вторая строка и второй столбец представляют собой корреляцию между второй точкой и последующими точками. Таким образом, матрица G t слева вверху справа внизу представляет порядок расположения корреляций между двумя точками с увеличением времени. Атрибут времени временного ряда сохраняется в матрице Грама.
Внутренний продукт представляет корреляцию между двумя точками, G t вещественной симметричной матрицей. Слева направо от первой строки и сверху вниз от первой колонки в G t корреляция между первой точкой и последующими точками временного ряда увеличивается со временем. Точно так же вторая строка и второй столбец представляют собой корреляцию между второй точкой и последующими точками. Таким образом, матрица G t слева вверху справа внизу представляет порядок расположения корреляций между двумя точками с увеличением времени. Атрибут времени временного ряда сохраняется в матрице Грама. {\prime}} ) $$ 9{\prime}}\) обозначает нормированный временной ряд, i — отметка времени во временном ряду, n — длина временного ряда, \(\theta_{i}\) — угол точка временного ряда в полярной системе координат, а \(r_{i}\) — радиус точки временного ряда в полярной системе координат. Таким образом, каждая точка временного ряда может быть представлена уравнениями. (6 и 7).
{\prime}} ) $$ 9{\prime}}\) обозначает нормированный временной ряд, i — отметка времени во временном ряду, n — длина временного ряда, \(\theta_{i}\) — угол точка временного ряда в полярной системе координат, а \(r_{i}\) — радиус точки временного ряда в полярной системе координат. Таким образом, каждая точка временного ряда может быть представлена уравнениями. (6 и 7). Поэтому, как показано в уравнении (8), новая матрица Грама может быть получена с использованием отношения углов в полярных координатах между двумя точками временного ряда:
Поэтому, как показано в уравнении (8), новая матрица Грама может быть получена с использованием отношения углов в полярных координатах между двумя точками временного ряда: Другими словами, мы сохраняем атрибут времени временного ряда и кодируем измерение времени в геометрической структуре матрицы. Каждое значение матрицы эквивалентно пикселю изображения, и каждый временной ряд преобразуется в изображение во временной области с помощью матрицы Грама.
Другими словами, мы сохраняем атрибут времени временного ряда и кодируем измерение времени в геометрической структуре матрицы. Каждое значение матрицы эквивалентно пикселю изображения, и каждый временной ряд преобразуется в изображение во временной области с помощью матрицы Грама. 3. На рис. 3 темно-синий квадрат представляет ядро свертки, а светло-синий квадрат представляет свертываемую матрицу. . Ядро свертки имеет размер 2 × 2, несвернутая матрица — 3 × 3, размер шага — 1. Традиционная свертка показана в верхней части рис. 3. размер шага равен 1, и для свертки требуется четыре обхода всей матрицы. После каждого обхода ядро свертки и матричная часть с его повторяющейся суммой перемножаются и накапливаются, а полученное значение является результатом локальной свертки в соответствующей позиции. Поскольку традиционная свертка должна пройти через все изображение, вычислительная сложность высока.
3. На рис. 3 темно-синий квадрат представляет ядро свертки, а светло-синий квадрат представляет свертываемую матрицу. . Ядро свертки имеет размер 2 × 2, несвернутая матрица — 3 × 3, размер шага — 1. Традиционная свертка показана в верхней части рис. 3. размер шага равен 1, и для свертки требуется четыре обхода всей матрицы. После каждого обхода ядро свертки и матричная часть с его повторяющейся суммой перемножаются и накапливаются, а полученное значение является результатом локальной свертки в соответствующей позиции. Поскольку традиционная свертка должна пройти через все изображение, вычислительная сложность высока. Затем матрица свертки расширяется до вектора-столбца 9 × 1 X в соответствии с порядком расположения строк. Произведение большой матрицы H , построенный ядром свертки, и вектор-столбец X , построенный матрицей свертки, эффективно заменяет вычисление свертки. В частности, матрица ядра свертки H состоит из 6 небольших матриц, которые представляют собой соответственно матрицу в красном поле и матрицу в желтом поле, а также нулевую матрицу в двух белых частях.
Затем матрица свертки расширяется до вектора-столбца 9 × 1 X в соответствии с порядком расположения строк. Произведение большой матрицы H , построенный ядром свертки, и вектор-столбец X , построенный матрицей свертки, эффективно заменяет вычисление свертки. В частности, матрица ядра свертки H состоит из 6 небольших матриц, которые представляют собой соответственно матрицу в красном поле и матрицу в желтом поле, а также нулевую матрицу в двух белых частях.
 Поскольку размер матрицы ядра свертки равен C × D , матрица ядра свертки H делится на C тёплицевых матриц: H 0 , H 1 , H 2 , H 3 , …, H c -1 , where H 0 is the нулевая интерполяция элемента h 11 в первой строке и первом столбце H , количество вставленных нулей равно количеству столбцов в матрице ядра свертки H минус 1, и берется результат интерполяции как первый ряд из Н 0 . Затем h 12 интерполируется как вторая строка в соответствии со свойствами матрицы Теплица до тех пор, пока не будут сформированы 2 × D -1 строк и завершено построение H 0 . По аналогии, H i является матрицей, полученной путем интерполяции \(i — 1\) элементов строки H . Например, матрица ядра свертки имеет вид \(H = \left[ {\begin{array}{*{20}c} 1 & 2 \\ 3 & 4 \\ \end{array}} \right]\), затем H делится на две матрицы \(H_{0} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 2 & 1 \\ 0 & 2 \\ \end{array } } \right]\) и \(H_{1} = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 4 & 3 \\ 0 & 4 \\ \end{array } } \Правильно]\).
Поскольку размер матрицы ядра свертки равен C × D , матрица ядра свертки H делится на C тёплицевых матриц: H 0 , H 1 , H 2 , H 3 , …, H c -1 , where H 0 is the нулевая интерполяция элемента h 11 в первой строке и первом столбце H , количество вставленных нулей равно количеству столбцов в матрице ядра свертки H минус 1, и берется результат интерполяции как первый ряд из Н 0 . Затем h 12 интерполируется как вторая строка в соответствии со свойствами матрицы Теплица до тех пор, пока не будут сформированы 2 × D -1 строк и завершено построение H 0 . По аналогии, H i является матрицей, полученной путем интерполяции \(i — 1\) элементов строки H . Например, матрица ядра свертки имеет вид \(H = \left[ {\begin{array}{*{20}c} 1 & 2 \\ 3 & 4 \\ \end{array}} \right]\), затем H делится на две матрицы \(H_{0} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 2 & 1 \\ 0 & 2 \\ \end{array } } \right]\) и \(H_{1} = \left[ {\begin{array}{*{20}c} 3 & 0 \\ 4 & 3 \\ 0 & 4 \\ \end{array } } \Правильно]\).
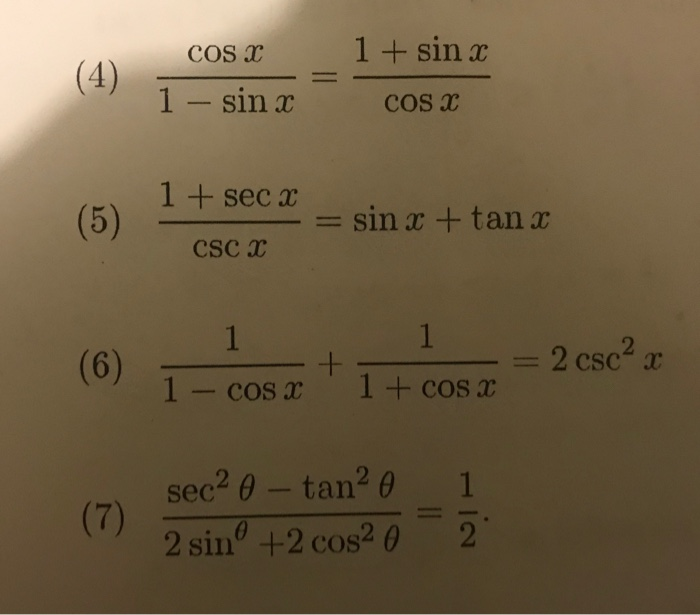 (11), где 0 представляет нулевую матрицу 3 × 2,
(11), где 0 представляет нулевую матрицу 3 × 2, {T}\).
{T}\). Таким образом, фактическое вычисление каждой строки равно C × D , номер строки – это время прохождения ядра свертки, и приблизительно умножить A × B × C × D раз. Таким образом, во время расчета сумма расчета двух методов примерно одинакова. Однако, когда в традиционную свертку каждый раз вводится новое изображение во временной области, в расчете возникает большое количество операций сдвига, что значительно увеличивает время расчета.
Таким образом, фактическое вычисление каждой строки равно C × D , номер строки – это время прохождения ядра свертки, и приблизительно умножить A × B × C × D раз. Таким образом, во время расчета сумма расчета двух методов примерно одинакова. Однако, когда в традиционную свертку каждый раз вводится новое изображение во временной области, в расчете возникает большое количество операций сдвига, что значительно увеличивает время расчета.
 Метод расчета – метод градиентного спуска. Другими словами, значения \(\omega\) и \(b\) могут быть получены, когда производная функции потерь равна 0,9.1826
Метод расчета – метод градиентного спуска. Другими словами, значения \(\omega\) и \(b\) могут быть получены, когда производная функции потерь равна 0,9.1826 (18).
(18).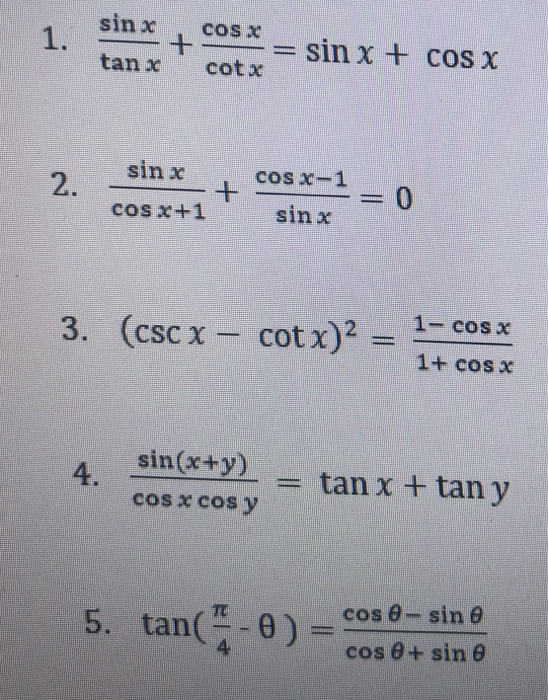
 На этой основе предлагается тройная функция потерь, как показано в уравнении. (19):
На этой основе предлагается тройная функция потерь, как показано в уравнении. (19): Частная производная \(L\left({\omega,b} \right)\) может выполнить вычисление невязки обратного распространения для получения новых параметров \(\omega\) и \(b\). Каждая итерация больше склоняется к направлению градиентного спуска, что может ускорить сходимость модели и повысить эффективность классификации.
Частная производная \(L\left({\omega,b} \right)\) может выполнить вычисление невязки обратного распространения для получения новых параметров \(\omega\) и \(b\). Каждая итерация больше склоняется к направлению градиентного спуска, что может ускорить сходимость модели и повысить эффективность классификации.

 Когда max ( p ) превышает пороговое значение, установленное функцией T , выводится класс изображения во временной области. Чтобы сделать экспериментальные результаты более надежными, в эксперименте используется десятикратная перекрестная проверка, а конечный результат составляет в среднем 10-кратную. Модель T-CNN настраивается на оптимальное состояние за счет непрерывной прямой проводимости, в которой основными регулируемыми параметрами являются скорость обучения и время итерации. Во время этого эксперимента скорость обучения установлена на 0,005, а время итерации регулируется.
Когда max ( p ) превышает пороговое значение, установленное функцией T , выводится класс изображения во временной области. Чтобы сделать экспериментальные результаты более надежными, в эксперименте используется десятикратная перекрестная проверка, а конечный результат составляет в среднем 10-кратную. Модель T-CNN настраивается на оптимальное состояние за счет непрерывной прямой проводимости, в которой основными регулируемыми параметрами являются скорость обучения и время итерации. Во время этого эксперимента скорость обучения установлена на 0,005, а время итерации регулируется.

 и превосходит другие методы.
и превосходит другие методы. точность как традиционной свертки, так и свертки Теплица плавно изменяется между размером изображения 10 и 40 во временной области. При размере изображения более 40 во временной области точность двух сверток увеличивается быстрее. В целом, при размере изображения от 10*10 до 100*100 точность тёплицевой свертки выше, чем у традиционной операции свертки, поэтому сходимость тёплицевой свертки происходит быстрее. Следовательно, свертка Теплица, предложенная в этой статье, может ускорить обучение модели.
точность как традиционной свертки, так и свертки Теплица плавно изменяется между размером изображения 10 и 40 во временной области. При размере изображения более 40 во временной области точность двух сверток увеличивается быстрее. В целом, при размере изображения от 10*10 до 100*100 точность тёплицевой свертки выше, чем у традиционной операции свертки, поэтому сходимость тёплицевой свертки происходит быстрее. Следовательно, свертка Теплица, предложенная в этой статье, может ускорить обучение модели.