Вычисление отрицательных чисел и положительных: Сложение Чисел с Разными Знаками

Как рассчитать среднее значение с отрицательными и положительными числами • BUOM

Автор: редакционная команда Indeed

30 июня 2021 г.

Изучение того, как вычислить среднее среди набора чисел, может помочь вам определить среднее число в данных. Это может быть полезно при попытке определить средние продажи или расходы или любой другой средний показатель.

В этой статье мы обсудим, что такое среднее значение, и разницу между средним значением и медианой. Затем мы объясним, как вычислить среднее значение, даже если есть отрицательные числа.

Какое значение?

Среднее значение относится к среднему числу, рассчитанному в рамках определенного набора данных. Его можно использовать в любой ситуации, когда вам было бы полезно понять среднее значение набора данных, например затрат или доходов. Зная средний расход или доход в определенном наборе данных, вы можете лучше позиционировать себя, чтобы увеличить свою прибыль или сбережения.

Как рассчитать среднее

Существует простой способ расчета среднего числа в наборе данных.

Среднее значение = сумма всех значений данных, деленная на количество значений данных.

Вот пошаговые инструкции для расчета среднего:

1. Определите все числа в вашем наборе данных

Начните с набора чисел, которые вы проверили на предмет точности и репрезентативности данных, которые вы пытаетесь проанализировать.

2. Сложите все числа, чтобы получить общую сумму.

Сложите все числа в вашем наборе данных, чтобы получить общую сумму.

3. Разделите общую сумму на количество значений данных, чтобы найти среднее значение.

После добавления всех сумм в набор данных разделите сумму на количество значений данных. Допустим, вы сделали 10 покупок в командировке. Сначала вы должны сложить общую стоимость 10 покупок, а затем разделить эту сумму на 10, поскольку это количество покупок, которые вы сделали в поездке.

Как вычислить среднее с использованием отрицательных чисел

Вы можете вычислить среднее значение, даже если в наборе данных есть отрицательные числа. Выполните следующие шаги, чтобы вычислить среднее значение с отрицательными числами:

1. Узнайте, сколько отрицательных чисел существует в наборе данных

Если вы видите отрицательные числа в наборе данных, убедитесь, что вы знаете, сколько у вас есть, прежде чем приступать к расчету. Добавление отрицательного числа к общей сумме аналогично вычитанию числа, поэтому важно правильно выполнить этот шаг.

2. Сначала сложите все положительные числа

Разделите положительные и отрицательные числа, чтобы найти сумму положительных чисел перед вычитанием отрицательных чисел.

3. Вычислить отрицательные числа

Теперь, когда у вас есть общее количество положительных чисел, вычтите отрицательные числа из набора данных, чтобы получить общее количество. Опять же, объединение отрицательных чисел с положительной суммой аналогично вычитанию. Если ваша начальная сумма положительных чисел равна 80, а у вас есть -35 из расчета ваших отрицательных чисел, то вы вычисляете это уравнение: 80 — 35 = 45.

4. Разделить на количество цифр в наборе данных

Чтобы получить среднее значение, разделите сумму на количество значений, которые вы сложили вместе. Используя предыдущий пример, если у вас есть общая сумма из девяти чисел или значений, вы должны разделить 45 на 9, чтобы получить среднее значение 5.

Примеры вычисления среднего с положительными и отрицательными числами

Давайте взглянем на несколько расчетов среднего положительного и отрицательного чисел:

Вычисление среднего с использованием положительных чисел

Если мы используем финансовый пример, скажем, доход от трех сделанных вами инвестиций включает 2000 долларов, 7000 долларов и 12000 долларов. Сложите эти три числа и разделите на 3, чтобы получить среднее значение.

(2000 долларов США + 7000 долларов США + 12000 долларов США или 21000 долларов США / 3 = 7000 долларов США.

Вы заработали средний (средний) доход в размере 7000 долларов на свои инвестиции.

Вычисление среднего с использованием отрицательных и положительных чисел

Допустим, вы сделали шесть инвестиций, но две из них убыточны. Эти потери будут отображаться в вашем наборе данных как отрицательные числа, тогда как четыре положительных числа показывают прибыль от ваших инвестиций. Мы скажем, что четыре положительных числа включают в себя 4000 долларов, 9000 долларов, 6000 долларов и 10000 долларов, а две инвестиции составляют -3000 долларов и -2000 долларов.

Сначала добавим положительные числа:

$4000 + $9000 + $6000 + $10000 = $29000 прибыли

Теперь посчитаем отрицательные числа:

-3000 долларов США + -2000 долларов США = -5000 долларов США

Затем вычтите 5 000 долларов из 29 000 долларов, чтобы получить 24 000 долларов.

Наконец, разделите 24 000 долларов на шесть, так как это общее количество инвестиций. В этом примере вы зарабатываете в среднем 4000 долларов за одну инвестицию.

В чем разница между средним, медианой и модой?

Среднее значение, медиана и мода — это три разных способа анализа набора данных. Среднее значение — это среднее значение суммы чисел в наборе данных, и его лучше всего использовать с числами, близкими по диапазону. Медиана — это среднее значение в наборе данных, и ее лучше всего использовать, когда у вас есть несколько чисел, выходящих за рамки нормы. А мода — это число или значение, которое появляется чаще всего, что может помочь вам определить тенденции.

Пример среднего, медианы и моды

Вот пример вычисления среднего значения, медианы и моды из одного и того же набора значений данных:

Как владелец антикварного магазина, вы совершили пять продаж за один день:

Медиана: медианой этих значений является среднее число: 700 долларов США.

Среднее значение: среднее значение этих значений представляет собой сумму всех значений, деленную на количество значений: 2700 долларов США, деленное на 5 = 540 долларов США.

Режим: режим этих значений — 125 долларов, потому что это число встречается чаще всего.

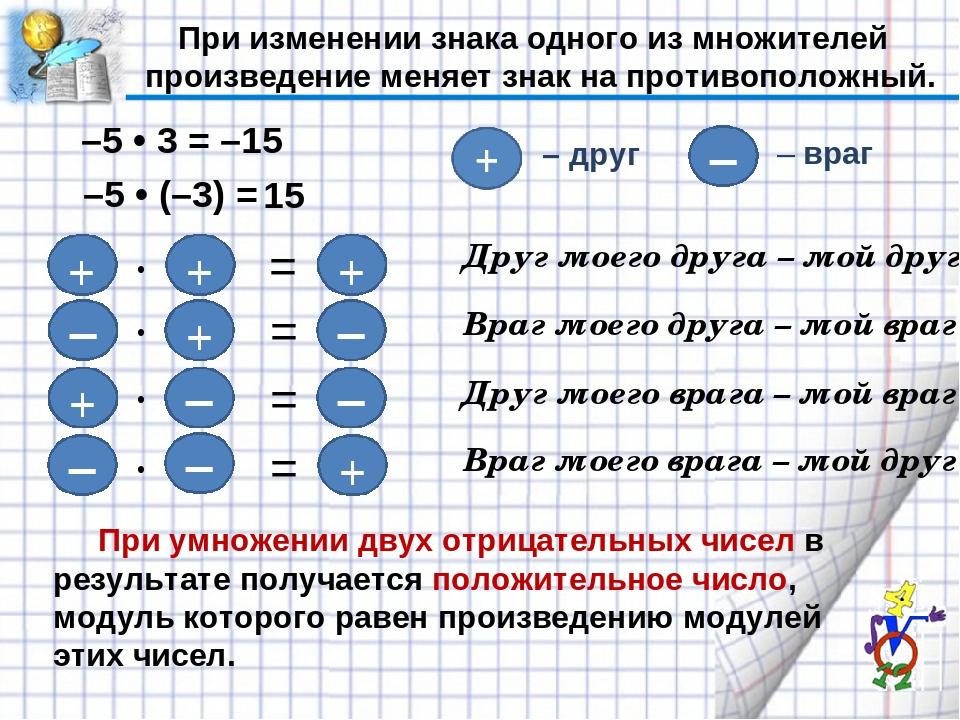
Умножение положительных и отрицательных чисел. 6 класс

1. Урок математики в 6 классе по теме: «Умножение положительных и отрицательных чисел».

УРОК МАТЕМАТИКИ
В 6 КЛАССЕ ПО ТЕМЕ:
«УМНОЖЕНИЕ ПОЛОЖИТЕЛЬНЫХ И
ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ».
КЛИМКОВА ЛЮДМИЛА НИКОЛАЕВНА,
УЧИТЕЛЬ МАТЕМАТИКИ
МБОУ «ШКОЛА – ИНТЕРНАТ №1» Г. РЯЗАНЬ

2. Цели урока:

ЦЕЛИ УРОКА:
ФОРМИРОВАНИЕ УУД:
• ЛИЧНОСТНЫХ-МОТИВАЦИЯ К ИЗУЧЕНИЮ ПРЕДМЕТА;
• ПОЗНАВАТЕЛЬНЫХ – ПОИСК И ВЫДЕЛЕНИЕ НУЖНОЙ ИНФОРМАЦИИ;
• РЕГУЛЯТИВНЫХ – ДЕЙСТВИЯ ПРОГНОЗИРОВАНИЯ, КОНТРОЛЯ, ОЦЕНКИ И САМООЦЕНКИ;
• КОММУНИКАТИВНЫХ – ВОСПРОИЗВОДИТЬ ТЕКСТ С УЧЁТОМ ПОСТАВЛЕННОЙ УЧЕБНОЙ
ЗАДАЧИ, НАХОДИТЬ В ТЕКСТЕ ИНФОРМАЦИЮ, НЕОБХОДИМУЮ ДЛЯ РЕШЕНИЯ
ПОСТАВЛЕННОЙ ЗАДАЧИ.

3. Задачи урока:

ЗАДАЧИ УРОКА:
ОБРАЗОВАТЕЛЬНЫЕ:
СОСТАВИТЬ АЛГОРИТМ УМНОЖЕНИЯ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ;
НАУЧИТЬ ПРИМЕНЯТЬ АЛГОРИТМ В ПРОЦЕССЕ ВЫПОЛНЕНИЯ УПРАЖНЕНИЙ;
ФОРМИРОВАТЬ НАВЫКИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ;
РАЗВИВАЮЩИЕ:
РАЗВИВАТЬ ЛОГИЧЕСКОЕ МЫШЛЕНИЕ, МАТЕМАТИЧЕСКУЮ РЕЧЬ, ВЫЧИСЛИТЕЛЬНЫЕ НАВЫКИ, СООБРАЗИТЕЛЬНОСТЬ, ВНИМАТЕЛЬНОСТЬ;
РАЗВИВАТЬ УМЕНИЕ ПРИМЕНЯТЬ ПОЛУЧЕННЫЕ ЗНАНИЯ К РЕШЕНИЮ ПРИКЛАДНЫХ ЗАДАЧ;
ВОСПИТЫВАЮЩИЕ:
ВОСПИТАНИЕ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА К ПРЕДМЕТУ;
ВОСПИТЫВАТЬ АКТИВНОСТЬ, САМОСТОЯТЕЛЬНОСТЬ, ЧУВСТВА ВЗАИМОПОМОЩИ И ТОВАРИЩЕСТВА У ОБУЧАЮЩИХСЯ, СТРЕМЛЕНИЕ К
САМОСОВЕРШЕНСТВОВАНИЮ.

4. Техническое и методическое обеспечение урока.

ТЕХНИЧЕСКОЕ И МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
УРОКА.
• 1.НОУТБУК,
• 2. ПРОЕКТОР,
• 3.ЭКРАН,
• 4.ПРЕЗЕНТАЦИЯ УРОКА,
• 5. ИНДИВИДУАЛЬНЫЕ ДОСКИ,
• 6. ИНДИВИДУАЛЬНЫЕ КАРТОЧКИ,
• 7.УЧЕБНАЯ ТАБЛИЦА

5. Высказывание:

ВЫСКАЗЫВАНИЕ:
• «ЗНАНИЕ –САМОЕ ПРЕВОСХОДНОЕ ИЗ ВЛАДЕНИЙ ЧЕЛОВЕКА.
• ВСЕ СТРЕМЯТСЯ К НЕМУ, САМО ЖЕ ОНО НЕ ПРИХОДИТ».
АЛЬ – БЕРУНИ

6. Устные упражнения

УСТНЫЕ УПРАЖНЕНИЯ
1.ЧТО НАЗЫВАЕТСЯ МОДУЛЕМ ЧИСЛА А?
2.ЧЕМУ РАВЕН МОДУЛЬ ПОЛОЖИТЕЛЬНОГО ЧИСЛА?
3. ЧЕМУ РАВЕН МОДУЛЬ ОТРИЦАТЕЛЬНОГО ЧИСЛА?
4.КАК СЛОЖИТЬ ОТРИЦАТЕЛЬНЫЕ ЧИСЛА?
5.КАК СЛОЖИТЬ ДВА ЧИСЛА С РАЗНЫМИ ЗНАКАМИ?
6. КАКИЕ ЧИСЛА НАЗЫВАЮТСЯ ПРОТИВОПОЛОЖНЫМИ?
7. КАК ВЫЧЕСТЬ ОТРИЦАТЕЛЬНЫЕ ЧИСЛА?
8.ВЫЧИСЛИТЬ:
1 ВАРИАНТ: 1) -3,4+ 2=
2) -1,2 +(-3)=
3) 2-7=
2 ВАРИАНТ: 1) -4,1 +5=
2) -3,5 +(-2)=
4) 3-8=

7. Ответы:

ОТВЕТЫ:
1 вариант
2 вариант
1) –3,4+2=- 1,4
1) -4,1 +5= 0,9
2) -1,2 +(-3)= -4,2
2) -3,5 + (-2) = -5,5
3) 2-7 = -5
3) 3-8 = -5
1 вариант
Ответ
2 вариант
1)-18+(-25)
а)43, б) -43, в)7, г)-7
1)-32+(-17)
а)15 б) -15 в) -49 г)49
2)23+(-47)
а)70, б) -70, в)24, г)-24
2)27+(-48)
а) -21 б)21 в) -75 г) 75
3)-5,1+6,7
а)11,8 б)1,6 в) -11,8 г) -1,6
3) -2,4+7,5
а) -5,1 б)5,1
4) 34-(-29)
а)63 б) -63 в)5 г) -5
4) 24-(-38)
а) -62 б) -14 в)14 г)62
Ответ
в)9,9 г) -9,9

9.

Ответы тестаОТВЕТЫ ТЕСТА
№
1 вариант
2 вариант
1
б
в
2
г
а
3
б
а
4
а
г

10. Проблема

ПРОБЛЕМА
ПРАКТИЧЕСКАЯ ЗАДАЧА:
• УРОВЕНЬ ВОДЫ В РЕКЕ ОКЕ ИЗМЕНЯЕТСЯ КАЖДЫЕ СУТКИ:
1) НА 4 ДМ;
2)НА -3 ДМ;
КАК ИЗМЕНИТЬСЯ УРОВЕНЬ ВОДЫ В РЕКЕ ЗА 3 СУТОК В КАЖДОМ СЛУЧАЕ?
РЕШЕНИЕ:
1)
4·3=
2)
-3·3=?

11. Тема урока

ТЕМА УРОКА
УМНОЖЕНИЕ
ПОЛОЖИТЕЛЬНЫХ И
ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ.

12. Работа с учебником:

РАБОТА С УЧЕБНИКОМ:
• 1 ПРОЧИТАТЬ ПРАВИЛО УМНОЖЕНИЯ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ.
СТРАНИЦА 190
2.ПРОЧИТАТЬ ПРАВИЛО УМНОЖЕНИЯ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ.
СТРАНИЦА 191
3. ПРОЧИТАТЬ ПРАВИЛО ПО ГРАММАТИКЕ
СТРАНИЦА 192
1.ПРАВИЛО УМНОЖЕНИЯ ЧИСЕЛ С РАЗНЫМИ ЗНАКАМИ:
ЧТОБЫ ПЕРЕМНОЖИТЬ ДВА ЧИСЛА С РАЗНЫМИ ЗНАКАМИ, НАДО ПЕРЕМНОЖИТЬ МОДУЛИ
ЭТИХ ЧИСЕЛ И ПОСТАВИТЬ ПЕРЕД ПОЛУЧЕННЫМ ЧИСЛО ЗНАК «-».
ПРИМЕР:
-4,2 ·2=-(4,2·2)=-8,4
10·(-1,3)=-(10·1,3)=-13
-0,3·0,3=-(0,3·0,3)=-0,09
2. ПРАВИЛО УМНОЖЕНИЯ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ:
ЧТОБЫ ПЕРЕМНОЖИТЬ ДВА ОТРИЦАТЕЛЬНЫХ ЧИСЛА, НАДО ПЕРЕМНОЖИТЬ ИХ МОДУЛИ.
ПРИМЕР:
-3,5·(-100)=3,5·100=350
-0,04·(-0,2)=0,04·0,2=0,008

14. Это надо запомнить!

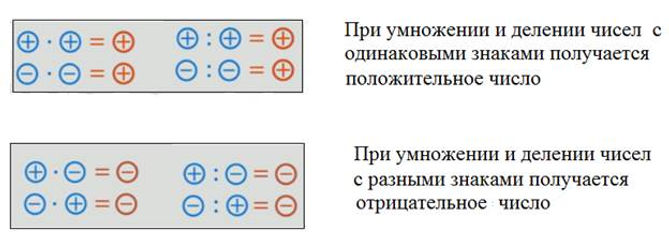
ЭТО НАДО ЗАПОМНИТЬ!
• ПРАВИЛО ЗНАКОВ:
• (+)·(+)=(+)
• (+)·(-)=(-)
• (-)·(+)=(-)
• (-)·(-)=(+)

15. Физкультурная пауза.

ФИЗКУЛЬТУРНАЯ ПАУЗА.
• ДРУЖНО С ВАМИ МЫ СЧИТАЛИ И ПРО ЧИСЛА РАССУЖДАЛИ.
• А ТЕПЕРЬ МЫ ДРУЖНО ВСТАЛИ , СВОИ КОСТОЧКИ РАЗМЯЛИ.
• НА СЧЁТ РАЗ КУЛАК СОЖМЁМ, НА СЧЁТ ДВА В ЛОКТЯХ СОЖМЁМ.
• НА СЧЁТ ТРИ – ПРИЖМЁМ К ПЛЕЧАМ, НА 4 – К НЕБЕСАМ.
• ХОРОШО ПРОГНУЛИСЬ, И ДРУГ ДРУГУ УЛЫБНУЛИСЬ.
• ПРО ПЯТЁРКУ НЕ ЗАБУДЕМ –ДОБРЫМИ ВСЕГДА МЫ БУДЕМ.
• НА СЧЁТ ШЕСТЬ ПРОШУ ВСЕХ СЕСТЬ.

16. Тренируем внимание и память.

ТРЕНИРУЕМ ВНИМАНИЕ И ПАМЯТЬ.
1 вариант
2 вариант
— 1,5·(-100)
— 2,5·100
-9+10
-8+9
-2,5·2
-1,3·(-2)

17. Задание на дом.

ЗАДАНИЕ НА ДОМ.
• П.35 –ВЫУЧИТЬ ПРАВИЛА И ТАБЛИЦУ
• №1121(1,2 СТОЛБИК)
• №1123(1 СТОЛБИК)
• ДОПОЛНИТЕЛЬНО №1146 (ДЛЯ ЖЕЛАЮЩИХ)
• 0СНОВНАЯ ГРУППА. ИНДИВИДУАЛЬНАЯ РАБОТА С УЧИТЕЛЕМ.
• ВЫЧИСЛИТЬ:
• №1
• 1) -3,8·10
• 2) 67,9·(-100)
• 3) -0,09·(-10)
• №2
• 1) -1,2·(-0,2)
• 2) 0,5·(-0,3)
• 3) -2,5·0,02
• ВТОРАЯ ГРУППА. ВОЗМОЖНА КОНСУЛЬТАЦИЯ У УЧИТЕЛЯ.
• РАБОЧАЯ ТЕТРАДЬ: СТРАНИЦА 26, Р-10
• ТРЕТЬЯ ГРУППА: САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ИНДИВИДУАЛЬНЫМ КАРТОЧКАМ.

19. Рефлексия. Подведение итогов урока. Самооценка урока.

РЕФЛЕКСИЯ.
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. САМООЦЕНКА
УРОКА.
• ЧТО НОВОГО УЗНАЛИ НА УРОКЕ?
• ПРЕДЛАГАЮ ОЦЕНИТЬ СТЕПЕНЬ ДОСТИЖЕНИЯ ЦЕЛИ УРОКА: НА
ВСЕ ЛИ ВОПРОСЫ НАЙДЕНЫ ОТВЕТЫ.
• НАД КАКИМИ ВОПРОСАМИ НАДО РАБОТАТЬ НА СЛЕДУЮЩЕМ
УРОКЕ?
• НА ИНДИВИДУАЛЬНЫХ ДОСКАХ ПОСТАВЬТЕ СЕБЕ ОТМЕТКУ,
ОЦЕНИВ СВОЮ РАБОТУ НА УРОКЕ И СТЕПЕНЬ УСВОЕНИЯ НОВОГО
МАТЕРИАЛА.
СПАСИБО ЗА УРОК!

нормализация — вычисление расстояния до 1 (положительные и отрицательные числа)

спросил 4 года 8 месяцев назад

Изменено 4 года, 8 месяцев назад

Просмотрено 1к раз

$\begingroup$

У меня есть, как я полагаю, очень простой вопрос.

У меня есть диапазон чисел от 81 до -6, что соответствует racios pop. рост/градостроительство городов. Идеальное соотношение было бы = 1. Поэтому мне нужно рассчитать расстояние до 1 (идеальное значение), чтобы увидеть, какой город ближе к идеальному значению. Если бы я имел дело только с положительными числами, я бы знал, как это сделать, однако недостаток математических знаний не позволяет мне решить эту задачу.

Надеюсь, вы мне поможете. Большое спасибо,

Марта

• нормализация
• алгоритмы
• дистанционные функции

$\endgroup$

$\begingroup$

Все, что вам нужно сделать, это вычислить абсолютное значение разницы между числами.

Пример:

абс(76-1) = 75

абс(-5-1) = 6

Абсолютное значение числа, независимо от того, положительное оно или отрицательное, представляет собой расстояние до начала координат. В вашем случае «начало» равно 1, поэтому вам нужно включить это при расчете расстояния.

Дополнительную информацию об абсолютном значении см. здесь.

$\endgroup$

0

$\begingroup$

Отрицательные коэффициенты здесь имеют смысл, потому что городское население может сократиться. (Вопрос: бывают ли случаи, когда и прирост населения, и городское строительство отрицательны?)

Хотя @sdiabr верно с точки зрения арифметики, что соотношение $|$ $-\ 1|$ является допустимой шкалой, я был бы удивлен если либо это, либо соотношение $-\ 1$, либо соотношение всегда было лучшей шкалой для работы, например. для построения графиков результатов или регрессионного моделирования.

Кубический корень из отношения $-\ 1$ или asinh(отношение $-\ 1$) или знак(отношение $-\ 1$) log(|отношение $-\ 1$|) могут быть полезными шкалами. Графики лучше маркировать отношениями в том виде, в котором они были записаны.

$\endgroup$

5

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Расчет процентного изменения для отрицательных чисел в Excel

Итог: Узнайте, как создавать формулы процентного изменения в Excel с отрицательными числами.

Уровень навыка:  Средний

В своем последнем посте я поделился макросом для быстрого создания формул процентного изменения. Я также объяснил две формулы, которые мы можем использовать для расчета процентного изменения.

Формула №1

 =(новое значение – старое значение) / старое значение 

Формула #2

 =(новое значение/старое значение) – 1 

Обе эти формулы дадут один и тот же результат, когда числа положительны . Тот, который вы используете, — это просто вопрос личных предпочтений.

Цель формулы процентного изменения состоит в том, чтобы позволить нам проводить сравнения производительности между двумя или более элементами. Это могут быть периоды времени, объекты, категории, предприятия и т. д. Эту формулу также можно использовать для расчета процентов скидок.

Загрузите файл

Загрузите файл, чтобы продолжить.

Формула процентного изменения для отрицательных чисел. zipDownload

Что делать, если числа отрицательные?

После небольшого исследования я не нашел хорошего способа рассчитать процентное изменение, когда либо старое число, либо новое число отрицательно. Определенно есть формулы, которые вы можете использовать, но они, похоже, дают неверные или вводящие в заблуждение результаты.

The Wall Street Journal опубликовал старый справочник по отчетам о прибылях и убытках, в котором говорится следующее:

Процентное изменение чистой прибыли — это изменение за тот же период по сравнению с прошлым годом. Изменение в процентах не предоставляется , если либо последний период, либо период прошлого года содержит чистый убыток [отрицательное число] . На странице дайджеста, если компания публикует прибыль за последний период по сравнению с убытком за прошлый период, процентное изменение представлено как «P». Точно так же, если компания публикует убыток в последнем периоде по сравнению с прибылью в прошлом году, процентное изменение представлено как «L».

Эта статья может быть устаревшей, так как я обнаружил, что последние финансовые страницы WSJ используют метод ABS (подробнее об этом ниже) для расчета процентного изменения, но дело в том, что процентное изменение отрицательных чисел может привести к вводящим в заблуждение результатам.

Как насчет метода ABS (абсолютного)?

Один из распространенных способов расчета процентного изменения с отрицательными числами — сделать знаменатель в формуле положительным. Функция ABS используется в Excel для изменения знака числа на положительный или его 9.0087 абсолютное значение .

Вот формула, которая обычно используется:

 =(новое значение – старое значение) / ABS(старое значение) 

Технически эта формула работает для получения числа процентного изменения с правильным знаком (положительным/отрицательным). Однако я считаю, что дает вводящие в заблуждение результаты .

Изображение ниже содержит пример этого. Старое значение отрицательное, а Новое значение положительное.

• Когда значение изменяется от -10 до 50, изменение суммы составляет +60, а процентное изменение составляет 600%.
• Когда значение изменяется от -60 до 50, изменение суммы составляет +110, а процентное изменение составляет 183,3% не имеет смысла для меня.

  Если бы вы просто смотрели на цифры процентного изменения, вы бы подумали, что у кофе дела обстоят лучше, чем у пирожных. В то время как на самом деле торты получили огромную прибыль по сравнению с предыдущим периодом, намного больше, чем кофе.

  Та же проблема возникает, когда числитель (новое значение) отрицательный. Вот еще один пример, который приводит к вводящим в заблуждение результатам.

  В этом примере пирожные имели большее отрицательное изменение значения, но меньшее процентное изменение, чем кофе.

  Но я всегда использовал метод ABS!!!

  Я знаю, я тоже. Я видел, как этот метод использовался на протяжении всей моей карьеры, и похоже, что Wall Street Journal даже использует его. Я заметил это в некоторых показателях их роста на этой странице финансовой отчетности Bank of America.

  Трудно сказать, что использовать формулу ABS совершенно неправильно. Но хорошо знать, что результаты могут вводить в заблуждение. Так что используйте его с осторожностью! 😉

  Альтернативные расчеты процентного изменения с отрицательными числами

  Вот несколько способов проверить наличие отрицательного числа и предоставить альтернативный результат.

  Метод №1: Нет результата для отрицательных чисел

  Первое, что мы можем сделать, это проверить, является ли число отрицательным, а затем отобразить текст, сообщающий читателю, что расчет процентного изменения невозможен.

  Следующая формула делает это с функцией ЕСЛИ и функцией МИН.

   =ЕСЛИ(МИН(старое значение, новое значение)<=0,"--",(новое значение/старое значение)-1) 

  Вот как работает формула:

  1. Логическая проверка функции ЕСЛИ (MIN(старое значение, новое значение)<=0) находит минимальное из двух значений и проверяет, меньше ли значение или равно нулю. Результат будет либо ИСТИНА, либо ЛОЖЬ.
  2. Если результат TRUE, то существует отрицательное число (или ноль). В этом случае мы можем отобразить некоторый текст, чтобы сообщить читателю. Это может быть что угодно. Я просто использовал два тире «-». Вы также можете заставить его возвращать ошибку N/A с помощью функции NA() или любой другой текст, который позволяет читателю узнать, что процентное изменение не может быть рассчитано.
  3. Если результат FALSE, то формула процентного изменения используется для возврата процентного изменения двух положительных чисел.

  Эта формула также обрабатывает деление на ноль (#ДЕЛ/0!), поэтому нам не нужно заключать ее в функцию ЕСЛИОШИБКА.

  Метод № 2: Показать положительное или отрицательное изменение

  В справочнике Wall Street Journal говорится, что его отчеты о доходах отображают «P» или «L», если есть отрицательное число, и компания опубликовала прибыль или убыток.

  Мы могли бы использовать ту же методологию, чтобы сообщить нашим читателям, было ли изменение положительным (P) или отрицательным (N), когда одно из значений отрицательное.

  Следующая формула проверяет это с помощью дополнительной функции ЕСЛИ.

   =ЕСЛИ(МИН(старое значение, новое значение)<=0,ЕСЛИ((новое значение - старое значение)>0,"P","N"),(новое значение/старое значение)-1) 

  Вот как работает формула:

  1. Мы начинаем с той же логической проверки, чтобы определить, существует ли отрицательное значение, используя функцию MIN.
  2. Затем используется вторая функция ЕСЛИ, чтобы определить, является ли изменение от старого к новому положительным или отрицательным.
     ЕСЛИ((новое значение – старое значение)>0, "P", "N")
     Этот оператор IF возвращает «P» для положительного изменения и «N» для отрицательного изменения.
  3. Если оба числа положительные, то для отображения результата используется формула процентного изменения.

  Другие методы процентного изменения с отрицательными значениями?

  Вычислить процентное изменение при использовании отрицательных чисел непросто. Метод ABS, вероятно, используется чаще всего, но он может давать вводящие в заблуждение результаты.

  No related posts.