Синус и косинус. Тангенс и котангенс
В данной теме мы разберем такие понятия, как синус и косинус, тангенс и котангенс. Сразу отметим, что раньше все вышеописанные термины выражались путем соотношения конкретных сторон треугольника, имеющего прямой угол.
Следовательно, можем дать определение нашим тригонометрическим функциям:
- Так синус угла, обозначаемый как sin a — это частное противолежащего катета угла к гипотенузе.
- Косинус же угла, который записывается cos a — это частное уже прилежащего катета угла к все той же гипотенузе.
- Тангенс угла, записываемый как tg a — это частное синуса к косинусу или противолежащего катета к прилежащему.
- Котангенс угла с обозначением ctg a — это частное косинуса к синусу или прилежащего катета к противолежащему.
Важно
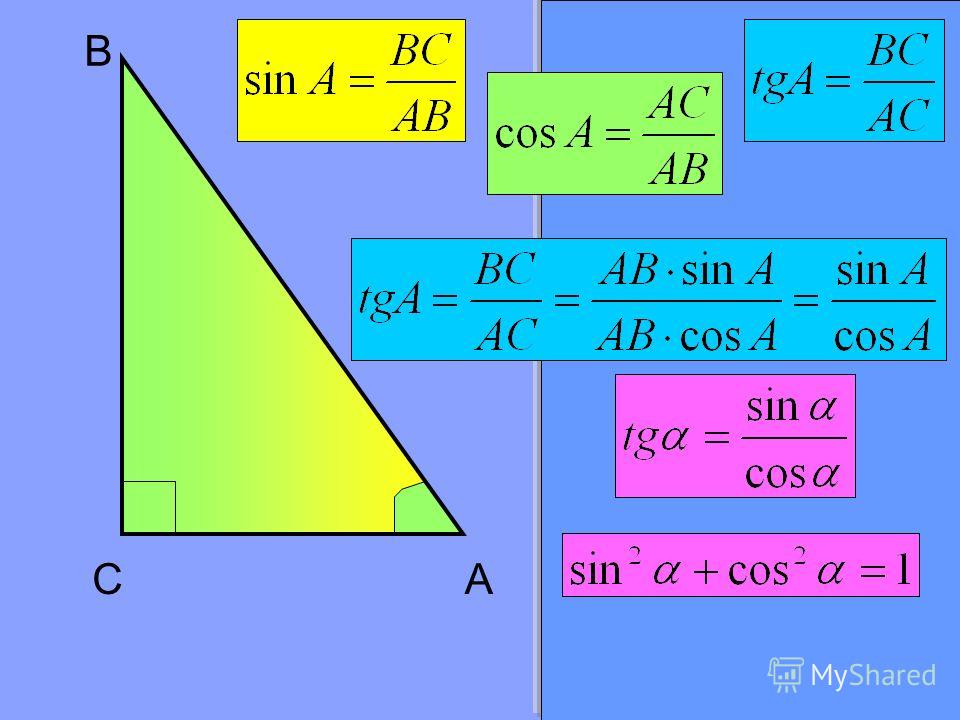
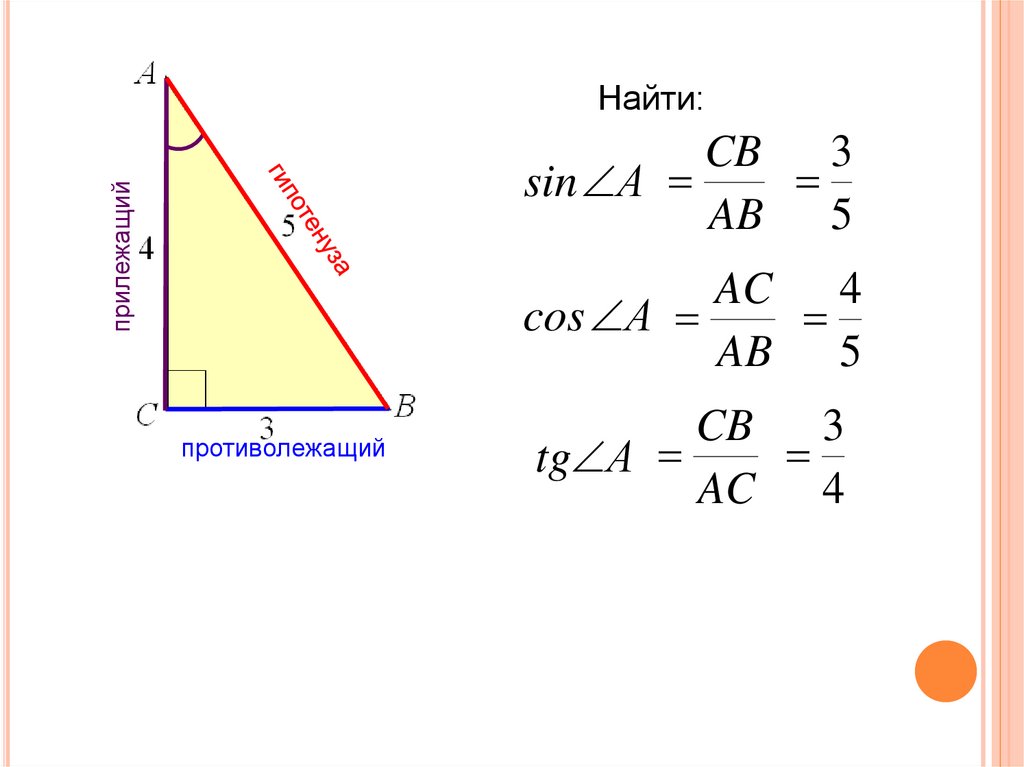
Вышеописанные определения составлены относительно острого угла прямоугольного треугольника. Пример можете увидеть на рисунке, представленном ниже.
Как мы видим, треугольник обладает прямым углом, который обозначен точкой C. Тогда синусом острого угла A будет отношение стороны BC (катет) к стороне AB (гипотенуза).
Необходимо помнить, что знание определений всех рассматриваемых нами функций в совокупности с данными о длине сторон треугольника помогут нам в вычисление значений этих самых функций.
Также отметим, что синус и косинус, а именно их значения заключены в интервал от -1 до 1 включительно. Говоря простым языком, функции не выходят за рамки указанных чисел. С тангенсом и котангенсом другая ситуация: их область значений — это все действительные числа или, как еще говорят, вся числовая прямая.
Все вышеперечисленные определения сформулированы относительно острых углов, но не стоит забывать и о таком понятии, как угол поворота. Он, в отличие от острых углов, не имеет градусных ограничений.
Угол поворота, как правило, может быть выражен как в виде всевозможных натуральных чисел, лежащих на интервале (-∞; +∞), так и в виде радиан.
Исходя из угла поворота, синусу, косинусу, тангенсу и котангенсу можно дать еще один вариант терминов. Но для начала рассмотрим следующий рисунок:
На нем изображена уже привычная для нас окружность, удовлетворяющая все необходимые для ее построения условия.
Возьмем точку A с координатами (1; 0) и провернем ее вокруг центра окружности на определенный угол, пусть будет a. В итоге мы должны оказаться в некоторой точке A1. Теперь можем дать нашим функциям определение, которое формируется относительно координат точки A1(x; y):
- sin a = y;
- cos a = х;
- tg a = y/x;
- ctg a = x/y.
Важно
Если синус и косинус свойственны всем углам поворота, то тангенс и котангенс нет. Как мы уже знаем, для их вычисления нам необходимо x поделить на y или наоборот. Однако это невозможно, если полученная после поворота точка имеет абсциссу (0; 1) или (0; -1).
С углом поворота разобрались, поэтому теперь перейдем к обычным числам.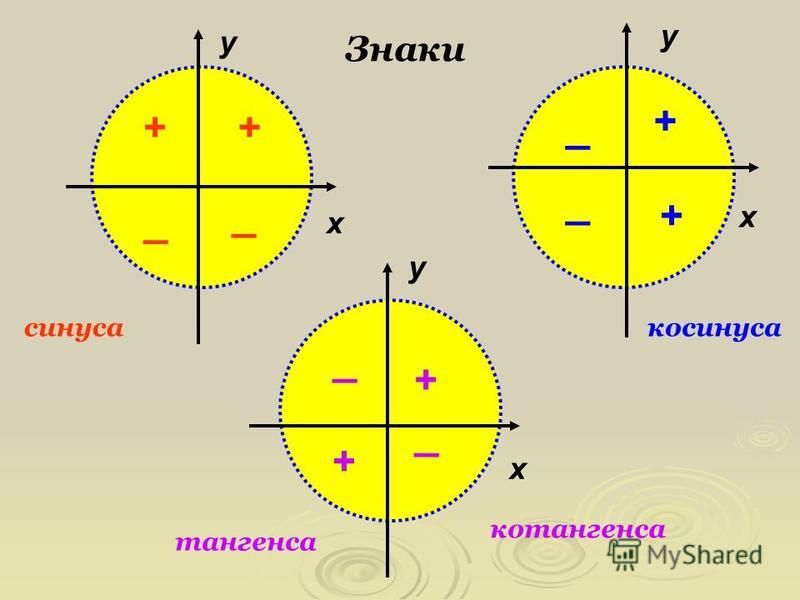
Определение
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Для наглядности приведем пример: синус числа 12 равен синусу угла поворота величиной 12 рад. Но помимо этого способа определений функций существует еще один. Ему как раз стоит уделить чуть больше внимания.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Как раз через координаты этой точки и будут вычисляться значения рассматриваемых нами функций.
Исходная точка, откуда мы будем двигаться, это точка A, имеющая координаты (1; 0).
Для получения положительного числа t требуется двигаться по окружности против часовой стрелки, а для отрицательного числа t — по окружности по часовой стрелки.
Теперь перейдем непосредственно к нашим терминам:
- Синус числа t — ордината точки единичной окружности, соответствующей числу t.
 sin t = y
sin t = y - Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
- Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t = y/x = sin t/cos t. Для котангенса необходимо поменять местами числитель и знаменатель.
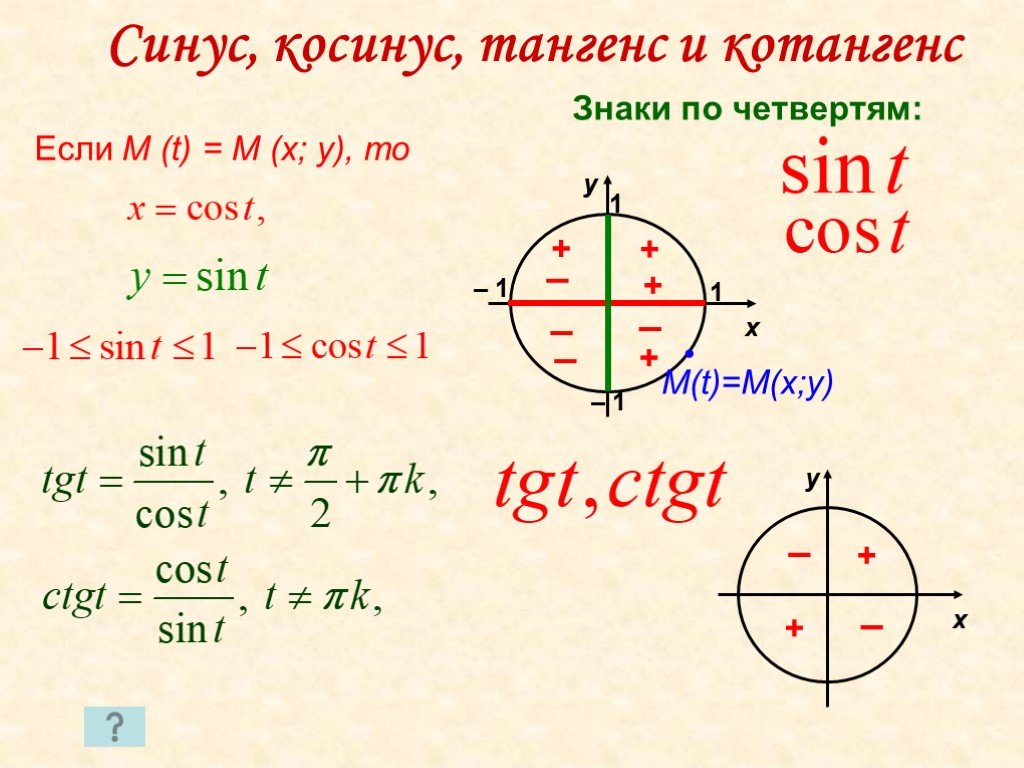
И в заключении ознакомимся с таблицей основных формул, касаемых рассматриваемых нами тригонометрических функций:
Данная шпаргалка очень полезна на уроках математики, особенно в первые дни, после изучения данной темы. Благодаря ей вы сможете быстро ознакомиться с основными формулами и применить их в решаемой задаче. Поэтому настоятельно рекомендуем ее распечатать или написать от руки, что будет еще лучше. При необходимости туда можно добавить еще какую-то полезную информацию о данных функциях.
Как уже было сказано выше, представленная таблица не отражает всех свойств функции, поэтому запишем их так.
Свойство №1
sin (-t) = -sin t;
cos (-t) = cos t;
tg (-t) = — tg t;
ctg (-t) = — ctg t.
Свойство №2
sin (t + 2πk) = sin t;
cos (t + 2πk) = cos t, где k ∈ Z.
Свойство №3
sin (t + π) = -sin t;
cos (t + π) = -cos t;
tg (t + πk) = tg t;
ctg (t + πk) = ctg t, где k ∈ Z.
Свойство №4
sin (t + π/2) = cos t;
cos (t + π/2) = sins t.
Подведем теперь итог нашего занятия:
- Обозначили наименование для декартовых координат;
- Дали несколько вариантов определений для изучаемых нами формул;
- Поговорили о свойствах формул;
- Ознакомились с таблицей самых распространенных значений формул.
Таким образом, данная тема требует заучивание множества формул и определений. Это необходимо делать в обязательном порядке, так как иначе вы не сможете на достаточном уровне освоить предоставленный вам материал. Также стоит особое внимание уделять практике решения задач с изученными формулами.
Поделиться статьей в соцсетях
Остались вопросы?
Наши репетиторы помогут
Остались вопросы?
Преобразование графика котангенса — концепция
Котангенс — это обратная триггерная функция функции тангенса, которую можно определить как cot(theta)=cos(theta)/sin(theta).
косинус синус котангенс четные и нечетные функции период добавления пи-идентификаций вертикальные асимптоты
Я хочу поговорить о преобразованиях графика котангенса, но сначала давайте рассмотрим кое-что о котангенсе. y равно котангенсу тета помните, что котангенс такой же, как косинус тета над синусом тета это важное тождество, и нам нужно будет развить несколько фактов о котангенсе, например, котангенс четен или нечетен? Ну, мы можем использовать тот факт, что косинус четный, а синус нечетный.
Теперь и косинус, и синус свойства, что если вы добавите пи к входу, вы получите противоположный результат. Таким образом, это может быть минус косинус тета по сравнению с минус синус тета. Теперь минусы сократятся, и вы просто получите котангенс тета. Поэтому, если вы добавите число пи, вы получите точно такой же вывод, это означает, что котангенс периодичен с периодом пи, поэтому нам нужно это знать. Хорошо, давайте начнем составлять таблицу значений котангенса; давайте начнем с 0, теперь котангенс равен косинусу относительно синуса, синус 0 равен 0.
Теперь позвольте мне работать в обратном направлении, позвольте мне дать нам немного места здесь, котангенс тета. Я вернусь к отрицательному числу пи больше 4, потому что функция узла котангенса, котангенс отрицательного числа пи больше 4 будет противоположен котангенсу числа пи больше 4. 4. Таким образом, мы получим отрицательную 1 здесь также потому, что у него есть период пи, если я добавлю к этому число пи, что даст мне 3 пи на 4, я получу тот же результат. И я действительно могу использовать периодичность, чтобы получить остальную часть вывода, если я добавлю к этому пи, до 0 я получу пи. Я получаю тот же вывод undefined, на самом деле это один полный период функции котангенса.
 Итак, я могу начать строить графики, позвольте мне начать с построения вертикальных асимптот, там будет вертикальная асимптота для x=0 и для x=pi. Итак, один из них здесь, а другой здесь, что происходит между ними?
Итак, я могу начать строить графики, позвольте мне начать с построения вертикальных асимптот, там будет вертикальная асимптота для x=0 и для x=pi. Итак, один из них здесь, а другой здесь, что происходит между ними? При пи больше 2 мы получаем 0, это пи больше 2, при пи больше 4 мы получаем 1 и при 3 пи больше 4 мы получаем отрицательную 1. Теперь вспомните форму тангенса, котангенс имеет очень похожую форму, он получил это вид изогнутой формы и, конечно, имеет асимптотическое поведение. Итак, это грубая форма графика котангенса. Теперь, если вы хотите нарисовать больше, помните, что это один период, все, что вам нужно сделать, это продублировать этот период. Я могу взять все это и сдвинуть вправо, а при сдвиге вправо все сдвигается вправо, включая асимптоту. Так, например, когда я сдвигаю это вправо, эта асимптота также сдвигается вправо. Итак, я получаю еще один при x = 2 pi, и я также могу сместиться влево, эта асимптота, сдвинутая влево, дает мне x, равное отрицательному pi. Итак, позвольте мне сдвинуть каждую из этих точек вправо, эта точка, сдвинутая вправо, дает мне точку на 3 пи больше 2, эту здесь, эту я поставлю здесь, и мы просто используем периодичность в этой точке.
Я сдвину это влево. Я получаю точку здесь, здесь, здесь и это 3 периода функции котангенса. Итак, вы заметите, что на самом деле было очень легко разработать ключевые точки для этой функции, все, что мне нужно было сделать, это помнить, что котангенс равен косинусу относительно синуса, и это позволило мне найти нули функции, а также где функция была неопределенной. Очень легко узнать, что котангенс числа пи на 4 равен 1, потому что косинус и синус оба являются корнем 2 на 2. Я также использовал тот факт, что котангенс был нечетным, чтобы получить это значение, а затем я использовал периодичность и превратил это значение в значение в 3 pi больше 4. И это все, что вам нужно: 0, pi больше 4, pi больше 2, 3 pi больше 4 и pi, и как только вы получите полный период, используйте периодичность, чтобы расширить график в обоих направлениях.
Тригонометрические функции
В Show My Work можно ввести следующие тригонометрические обозначения.
коробки.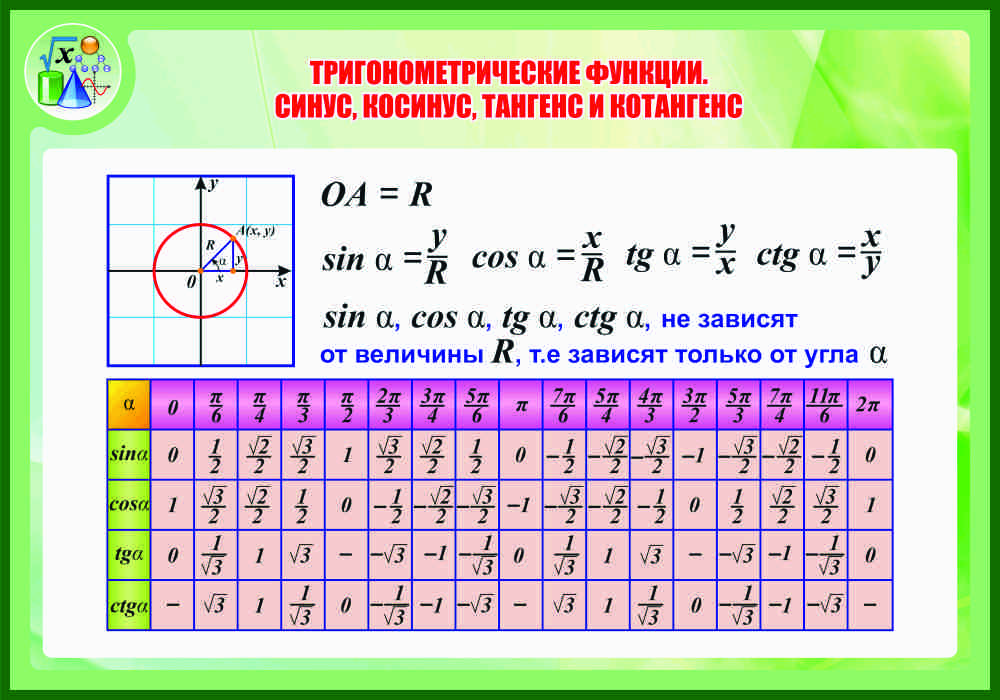

 sin t = y
sin t = y