Вычисление приближенно с помощью дифференциала
С одной стороны, вычисление дифференциала значительно проще, чем вычисление приращения, с другой стороны, dy≈∆y и допускаемая при этом погрешность может быть сделана сколь угодно малой за счет уменьшения ∆x. Эти обстоятельства позволяют во многих случаях заменять ∆y величиной dy. Из приближенного равенства dy≈∆y, учитывая, что ∆y = f(x) – f(x0), а dy=f’(x0)(x-x0), получимf(x) ≈ f(x0) + f’(x0)(x–x0), (1)
Пример№1. Вычислить .
Решение. Взяв функцию , имеем: . Полагая x0=16 (выбираем сами, чтобы корень извлекался), ∆x = 0,02, получим:
Пример №2. Вычислить значение функции f(x) = ex в точке x=0.1.
Решение. В качестве x0 возьмем число 0, то есть x0=0, тогда ∆x=x-x0 =0.
Отметим еще одно важное свойство дифференциала. Формула для нахождения дифференциала dy=f’(x)dx верна как в случае, когда x – независимая переменная, так и в случае, когда x – функция от новой переменной t. Это свойство дифференциала называется свойством инвариантности его формы. Например, для функции y=tg(x) дифференциал запишется в виде независимо от того, является ли x независимой переменной или функцией. В случае, если x – функция и конкретно задана, например x=t2, то вычисление dy можно продолжить, для чего найдем dx=2tdt и подставим в ранее полученное выражение для dy:
.
Если вместо формулы (2) воспользовались бы неинвариантной формулой (1), то в случае, когда x – функция, мы не могли бы подобным образом продолжить вычисление dy, так как ∆x, вообще говоря, не совпадает с dx.
Пример №3
Извлечь квадратный корень из 3654.
Решение. Надо найти значение функции при x=3654. Легко вычисляются значения f(x) и при x=3600. Формула (1) при a=3600, h=54 дает . Здесь все знаки верны.
Пример №4. Найти 102,1.
Решение. Полагаем f(x)=10x , так что . Формула (1) при a=2, h=0,1 дат:
.
Этот результат грубоват (с точностью до четвертой значащей цифры 102,1=125,9).
Если таким же образом вычислить 102,01 (теперь h=0,01), получим 102,3. Здесь все знаки верны.
Пример №5. Найти без таблиц tg 46о.
Решение. Полагаем f(x)=tg x, a=45о, h=1о=0,0175 радиана; тогда имеем: . Значит, tg 45о=1+2·0,0175=1,0350.
Неверен только последний знак; из таблиц имеем tg 46
Полезно заметить следующие приближенные формулы (a-малая величина):
, ; (2)
, ; (3)
, ; (4)
, ; (5)
, ; (6)
Формулы (2)-(6) являются частными случаями формулы (1+a)n≈1+na; последняя получается из (1), если положить f(x)=xn, a=1,h=a.
ln(1+a)≈a, ln(1-a)≈-a; (7)
ea≈1+a, ; (8)
sin a≈a, , tg a≈a; (9)
4. Приближенные вычисления с помощью дифференциала
Теорема. Если функция дифференцируема в точке x, причем f ‘(x) 0, то при Δx —> 0 приращение Δy и дифференциал dy функции являются эквивалентными бесконечно малыми.
На этой теореме и основано применение дифференциала к приближенным вычислениям. Известно, что любую из двух эквивалентных бесконечно малых можно приближенно заменить другой. Следовательно,
Δy ≈ dy. (9)
Абсолютная и
относительная погрешности этого
равенства могут быть сделаны сколь
угодно малыми при достаточно малом
. Структура
дифференциала обычно значительно проще
структуры приращения функции, в силу
чего формула (9) широко применяется в
приближенных вычислениях.
5. Частные производные и полный дифференциал
5.1. Частные производные. Пусть (x, у) — произвольная фиксированная точка из области определения z =f(x, у). Рассмотрим предел
.
Этот предел (если он существует) называется частной производной (1-го порядка) данной функции z по переменной x в точке (x, у). Производная обозначается одним из символов: .
Частные производные функции z = f(x, у) сами представляют собой некоторые функции переменных x и у.
Таким образом, частная производная функции z = f(x, у) по аргументу x есть производная этой функции по x при постоянном значении у. Аналогично, есть производная функции z = f(x, у) по у в предположении, что x является константой.
Частные производные
функции нескольких переменных определяются
как производные этой функции по одному
из них при условии, что остальные
переменные считаются постоянными.
5.2. Полный дифференциал. Пусть Р(x, у) — данная точка, а Р'(х+Δх, у+Δу) — близкая точка, отвечающая приращениям аргументов Δх и Δу. Полным приращением функции z = f(x, у) в точке Р называется разность Δz =
f(Р’) – f(Р) = f(x + Δx, у + Δу) – f(x, у). Если приращение Δz можно представить в виде Δz = АΔх + BΔу + ε, где ε — бесконечно малая более высокого порядка по сравнению с расстоянием ρ = между точками Р и Р’ (т.е. ε / ρ —> 0 при ρ —> 0), то функция z = f(x, у) называется дифференцируемой в точке Р, а главная линейная часть ее приращения AΔx + ВΔу = dz называется полным дифференциалом функции в точке Р. Функция, имеющая дифференциал в каждой точке некоторой области D, называется дифференцируемой в этой области.Если функция дифференцируема, то необходимо, чтобы выполнялись равенства:
A = , B = .
Достаточным
условием дифференцируемости является
наличие непрерывных частных
производных.
Так как приращения
независимых переменных совпадают с их
дифференциалами, т. е. Δx
= dx,
Δу = dу,
то дифференциал функции z
.
6. Понятие неопределенного интеграла, свойства.
При изучении дифференциального исчисления рассматрива- лась задача нахождения производной или дифференциала по заданной функции у = F(х), т. е. необходимо было найти f(x) = = F'(х) или dF(х) = F'(х)dх = f(х)dх. Можно поставить обратную задачу: восстановить продифференцированную функ- цию, т.е., зная производную f(x) (или дифференциал f(x) dx), найти такую функцию F(х), чтобы F'(х) = f(x). Например, пусть известна скорость перемещения точки υ = υ(t), а надо найти закон ее перемещения S = S’ (t), причем S'(t) = υ (t). Эта задача оказывается значительно более трудной, чем задача дифференцирования. Для решения подобных задач вводятся новые понятия и действия.
Определение 1.
Например, для f(x) = х2 первообразная F(х) = x3/3, так как F'(х) = (x3/3)’ = х2; для f(x) = соs x первообразной будет F(х) = sin х, потому что F'(х) = (sin x)’ = соs x, что совпадает с f(x).
Всегда ли существует первообразная для заданной функции f(x)? Ответ положителен, если эта функция непрерывна на (а,b). Кроме того, первообразных бесчисленное множество и отличаются они друг от друга только постоянным слагаемым. Действительно, sin x + 2, sin x – 2, sin x + с, — все эти функции будут первообразными для соs x (производная от постоянной величины равна 0).
Определение 2. Выражение F(х)
+ С, где
С —
произвольная постоянная величина,
определяющее множество первообразных
для функции f(x),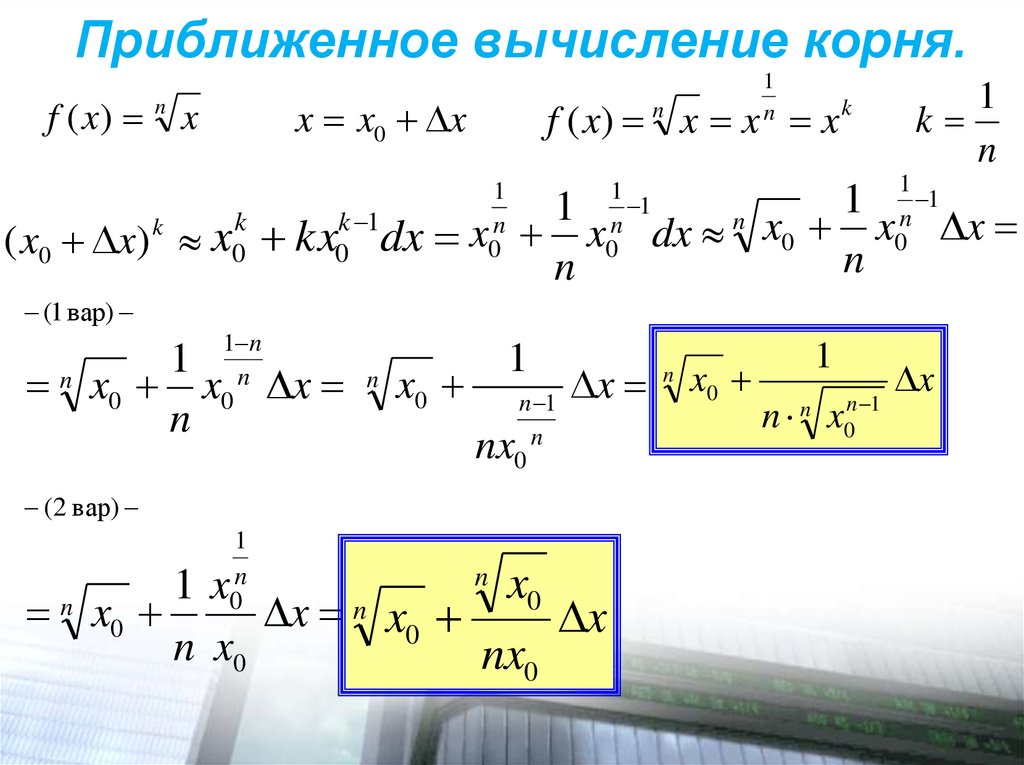 
е. = F(х)
+ С,
где знак
—
знак неопределенного интеграла, f(x)
— называется подынтегральной
функцией, f(x)
dx — подынтегральным
выражением, x
— переменной интегрирования.
Определение 3. Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием этой функции.
Интегрирование — действие, обратное дифференцированию, его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ с точностью до постоянной. Придавая постоянной величине С конкретные значения С1, С2, Сз, получим различные функции:
y1(х) = F(х) + С1
, у2(х) = F(х) + С2, y3(х) = F(х) + С3, каждая из которых
задает на координатной плоскости кривую,
называемую интегральной. Все графики
интегральных кривых сдвинуты относительно
друг друга вдоль оси ОУ.
Следовательно,
геометрически неопределенный интеграл
представляет собой семейство интегральных
кривых (рис. 4).
Рис. 4
Итак, введены новые понятия (первообразной и неопределенного интеграла) и новое действие (интегрирование), но как все-таки находить первообразную? Чтобы легко было ответить на этот вопрос, надо в первую очередь составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она получается в результате обращения соответствующих формул дифференцирования. Например, если (sin x)’ = соs х, то соs х dх
Обычно в таблицу включаются и некоторые интегралы, полученные после применения простейших методов интегрирования.
Свойства неопределенных интегралов
Рассмотрим
простейшие свойства неопределенного
интеграла, которые позволят
интегрировать не только основные
элементарные функции.
1. Производная от неопределенного интеграла равна подынтегральной функции:
.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
3. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
Пример 1.
Пример 2.
Постоянный множитель можно выносить за знак интеграла:
Пример 3.
Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
Пример 4.
Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если
,
то
,
где u
= φ(x)
– произвольная функция, имеющая
непрерывную производную.
Это свойство
называется инвариантностью.
Пример 5. , поэтому
, .
Сравнить с .
В интегральном исчислении нет универсального способа интегрирования. Применение различных методов приводит данный интеграл к табличному, который надо узнать с учетом свойства инвариантности. Полезно прочитать табличный интеграл, обращая внимание на то, где находится переменная интегрирования (в показателе степени, в знаменателе, под знаком синуса и т. д.).
Mathwords: Аппроксимация по дифференциалам
Mathwords: Аппроксимация по дифференциалам
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Метод использует касательную
линия при известном значении функции
аппроксимировать график функции.
В этом методе Δ x и
Δ и представляют
изменения x и y для функции и dx и dy представляют
изменения x и y для касательной.
Обратите внимание, что \(f’\left( x \right) = \frac{1}{{2\sqrt x }}\).
Линейные аппроксимации: аппроксимация дифференциалами
Идея здесь в «геометрических» терминах состоит в том, что кривую можно аппроксимировать касательной к ней прямой. Из Конечно, это приближение годится только «вблизи» точки касание и так далее. Так что единственная формула здесь тайно формула для касательной к графику функции. Есть некоторые хлопоты из-за того, что существует так много разных вариантов символов для напиши это.
Мы можем написать несколько формул: Пусть $f$ будет
функцию и фиксируем точку $x_o$. Идея состоит в том, что за $x$ «около»
$x_o$ имеем «приблизительное» равенство $$f(x)\приблизительно f(x_o)+f'(x_o)(x-x_o)$$
Мы делаем , а не пытаемся прояснить, что или «рядом» или
«приблизительно» означает в данном контексте. Что действительно верно, так это то, что
для заданного значения $x$ количество
$$f(x_o)+f'(x_o)(x-x_o)$$ точно $y$-координата строки касательной к
график в $x_o$.
Заявление об аппроксимации имеет много парафраз в различных выбор символов, и человек должен уметь распознавать все их. Например, один из наиболее традиционных парафраз, который вводит немного глупые, но такие традиционные обозначения, следующий один. Мы могли бы также сказать, что $y$ является функцией $x$, заданной по $y=f(x)$. Позволять $$\Delta x = \hbox{ небольшое изменение в $x$}$$ $$\Delta y= \hbox{ соответствующее изменение в $y$ }=f(x+\Delta x)-f(x)$$
Тогда утверждение состоит в том, что $$\Delta y\приблизительно f'(x)\,\Delta x$$
Иногда некоторые тексты вводят следующие сомнительные
(но традиционно популярная!) нотация:
$$dy = f'(x)\;dx = \hbox{ приближение к изменению $y$}$$
$$dx = \Дельта x$$
и назовем $dx$ и $dy$ «дифференциалами» . А потом весь этот
процедура «аппроксимация дифференциалами» . А не
особенно поучительный парафраз, используя предыдущую нотацию,
$$dy\приблизительно \Дельта y.$$
Даже если вы видите, что люди пишут это, не делайте этого.
Другие парафразы с различными символами: $$f(x+\Delta x)\приблизительно f(x) + f'(x)\Delta x$$ $$f(x+\delta)\приблизительно f(x) + f'(x)\delta$$ $$f(x+h)\приблизительно f(x) + f'(x)h$$ $$f(x+\Delta x)-f(x)\приблизительно f'(x)\Delta x$$ $$y+\Delta y\приблизительно f(x)+f'(x)\Delta x$$ $$\Delta y\приблизительно f'(x)\Delta x$$
Немного истории: Еще 20$ или 30$ лет назад, калькуляторы не были широко доступны, и особенно обычно не умеет вычислять тригонометрические, экспоненциальные и логарифмические функции. В этом контексте расплывчатые и ненадежные «приближение», обеспечиваемое «дифференциалами», безусловно, стоило того. во многих ситуациях.
Напротив, теперь, когда довольно сложные калькуляторы широко распространены
доступны, некоторые вещи, которые когда-то казались разумными, больше не являются. За
например, очень традиционный тип вопроса — «приблизительно
$\sqrt{10}$ по дифференциалам». Разумный современный ответ
было бы просто ввести «$1,0,\sqrt{}$» на вашем калькуляторе и получить
ответ сразу до 10 знаков после запятой.
Но это было возможно
только относительно недавно.
Пример 1
Например, аппроксимируем $\sqrt{17}$ на дифференциалы. Чтобы эта проблема вообще имела смысл 9{1/2}$. Тем не менее мы представьте, что мы делаем это «вручную», и тогда, конечно, мы можем «легко вычислить» функцию $f$ и ее производную $f’$ в точке $x=16$, которая находится «около» $18$. Таким образом, здесь $$\Дельта х=18-16=2$$ и $$\sqrt{18}=f(18)\приблизительно f(16)+f'(16)\Дельта x=\sqrt{16}+{1\over 2}{ 1 \over \sqrt{16 }}\cdot 2=4+{1\over 4}.$$
Почему бы не использовать «хорошую» точку $25 $ как «рядом» указывает на найти $\sqrt{18}$? Ну, в общих чертах, чем дальше ваше «хорошее» Дело в том, что хуже будет аппроксимация. Да, это правда, что мы понятия не имею, насколько хороша или плоха аппроксимация все равно .
Несколько разумнее использовать эту идею для , а не .
числовая работа, а скорее сказать что-то вроде $$\sqrt{x+1}\приблизительно
\sqrt{x}+{1\over 2}{ 1 \over \sqrt{x}}$$ и $$\sqrt{x+h}\примерно
\sqrt{x}+{1\over 2}{ 1 \over \sqrt{x }}\cdot h.
$$ Утверждение такого рода
больше, чем может дать любой конкретный численный пример, потому что он
дает отношение , сообщая, насколько изменяется выход для данного изменения в введите , в зависимости от того, что 9о\cdot {2\pi\более 360}$$
$$={1\over 2}+{\sqrt{3} \over 2} {2\pi\over 360}$$ Очевидно, мы
к также представьте, что мы знаем или можем легко найти $\sqrt{3}$ (по дифференциалам?), а также значение $\pi$. Да ,
это большая проблема по сравнению с простым ударом кулаком
кнопок, и с современной точки зрения может показаться бессмысленным.
Пример 4
Аппроксимация $\ln(x+2)$ «дифференциалами» через $\ln x$ и $x$: это нечисловой вопрос несколько больше разумный. Возьмем $f(x)=\ln\,x$, так что $f'(x)={1\over x}$. затем $$\Дельта х=(х+2)-х=2$$ и по формулам выше $$\ln(x+2)=f(x+2)\приблизительно f(x)+f'(x)\cdot 2=\ln\,x+{2\over x}.$$
Пример 5
Аппроксимация $\ln\,(e+2)$ через дифференциалы: Использование
$f(x)=\ln\,x$ снова, так что $f'(x)={1\over x}$.