Математический анализ. (Виленкин)
Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств.  8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2.  Метод разложения на множители. Метод разложения на множители.3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 3. Сокращение показателей и приведение корней к общему показателю. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений.  8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 2. Выражение степенных сумм 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости.  § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  Комбинаторные задачи. Продолжение Комбинаторные задачи. Продолжение§ 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
Степень с рациональным показателем
Урок 5. Алгебра 10 класс ФГОС
Из данного видеоурока мы узнаем, что подразумевают под понятием «степень с рациональным показателем». А также рассмотрим основные свойства степеней.
Конспект урока «Степень с рациональным показателем»
Вам
уже знакомы понятия степени числа с натуральным и целым показателями. Напомним,
что
Напомним,
что
В свою очередь, степенью с отрицательным целым показателем называется , где , – натуральное число.
.
Однако в алгебре существует ещё и понятие степени, у которой показатель не целое, а дробное число. Итак, попытаемся записать как некоторую степень числа а, то есть .
Мы знаем, что . Исходя из того, что мы представили , то получим, что . По свойству возведения степени в степень имеем . Откуда видим, что произведение . Следовательно, .
Тогда получаем, что . По свойству возведения корня n-й степени в степень получим, что .
Например,
.
Сделаем
вывод: если —
натуральное число, причём ,
—
целое число и частное является
целым числом, то при справедливо
равенство .
Пусть , причём — целое число. Отсюда . Тогда .
Если же частное не является целым числом, то степень числа а, где , определяют так, чтобы выполнялась формула , то есть и в этом случае считают, что .
Таким образом, формула справедлива для любого целого числа и любого натурального числа и положительного основания степени .
Например,
.
Напомним, что рациональное число – это число вида , где – целое, – натуральное число. Тогда по формуле получаем .
Таким образом, степень определена для любого рационального показателя и любого положительного основания а.
Если рациональное число , то выражение имеет смысл не только при положительном основании степени, но и при , причём . Поэтому считают, что при .
Пользуясь
формулой ,
степень с рациональным показателем можно представить в виде корня
и наоборот.
Запомните! Степенью числа с рациональным показателем , где – целое число, а – натуральное, причём , называется число .
Замечание: из определения степени с рациональным показателем сразу следует, что для любого и любого рационального число – положительно.
Любое
рациональное число допускает различные записи его в виде дроби. По основному
свойству дроби частное можно
представить, как частное ,
где
и
–
натуральные числа, –
целое число. Тогда при любом справедливо
равенство.
Что легко доказать применяя свойства корней.
Имеем.
Заметим, что при отрицательном основании степени рациональная степень числа а не определяется. Отрицательные числа нельзя возводить в рациональную степень, не являющуюся целым числом.
А
теперь перейдём к основным свойствам степени и покажем, что все свойства
степени с натуральным показателем верны для степени с любым рациональным
показателем и положительным основанием.
А именно для любых рациональных чисел и и любых и верны равенства:
1. .
2. .
3. .
4. .
5. .
Для доказательства этих свойств нужно воспользоваться определением степени с рациональным показателем и свойствами корней.
Докажем первое свойство.
1. .
Итак, пусть , , где и – натуральные числа, и – целые числа.
Нам нужно доказать, что .
Приведём дроби к общему знаменателю , .
По определению степени с рациональным показателем имеем .
Аналогичным образом можно доказать и все остальные свойства степени с рациональным показателем.
А теперь давайте приступим к практической части нашего урока.
Задание. Найдите значения выражения .
Решение.
.
Предыдущий урок 4 Арифметический корень натуральной степени
Следующий урок 6 Степень с действительным показателем
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 10 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
6.
 2.3.1: Уравнение Аррениуса — Химия LibreTexts
2.3.1: Уравнение Аррениуса — Химия LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1443
- Стивен Лоуэр
- Университет Саймона Фрейзера
Общеизвестно, что химические реакции протекают быстрее при более высоких температурах. Молоко скисает гораздо быстрее, если хранить его при комнатной температуре, а не в холодильнике; масло летом прогоркает быстрее, чем зимой; а яйца варятся быстрее на уровне моря, чем в горах. По той же причине хладнокровные животные, такие как рептилии и насекомые, обычно более вялые в холодные дни.
Причину этого понять несложно. Тепловая энергия связывает направление с движением на молекулярном уровне.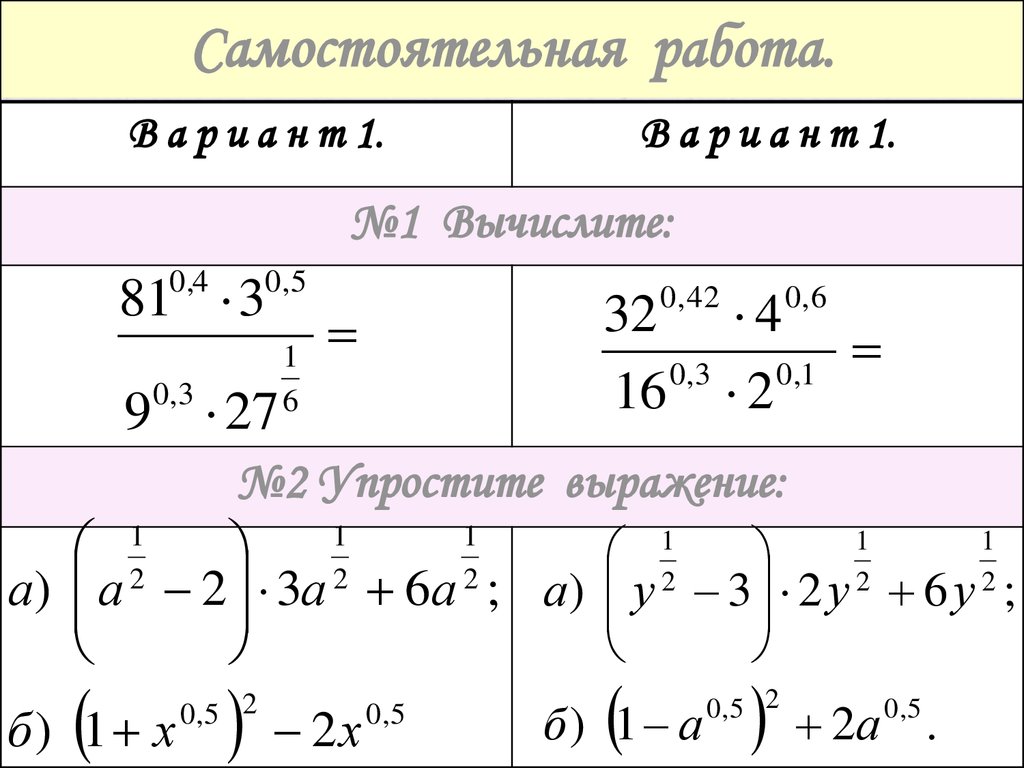 По мере повышения температуры молекулы движутся быстрее и сталкиваются более энергично, что значительно увеличивает вероятность разрыва связей и перегруппировок. Будь то теория столкновений, теория переходного состояния или просто здравый смысл, обычно ожидается, что химические реакции протекают быстрее при более высоких температурах и медленнее при более низких температурах.
По мере повышения температуры молекулы движутся быстрее и сталкиваются более энергично, что значительно увеличивает вероятность разрыва связей и перегруппировок. Будь то теория столкновений, теория переходного состояния или просто здравый смысл, обычно ожидается, что химические реакции протекают быстрее при более высоких температурах и медленнее при более низких температурах.
К 1890 году было общеизвестно, что более высокие температуры ускоряют реакции, часто удваивая скорость при повышении температуры на 10 градусов, но причины этого были неясны. Наконец, в 1899 году шведский химик Сванте Аррениус (1859-1927) объединил понятия энергии активации и закона распределения Больцмана в одно из важнейших соотношений физической химии:
Найдите минутку, чтобы сосредоточиться на значении этого уравнения, пренебрегая Коэффициент на данный момент. Во-первых, обратите внимание, что это еще одна форма экспоненциального закона затухания, обсуждавшаяся в предыдущем разделе этой серии статей. Здесь «затухает» не концентрация реагента как функция времени, а величина константы скорости как функция показателя степени –E a / RT . И какое значение имеет эта величина? Вспоминая, что RT — это средняя кинетическая энергия , становится очевидным, что показатель степени — это просто отношение энергии активации E a к средней кинетической энергии. Чем больше это отношение, тем меньше скорость (отсюда и знак минус). Это означает, что высокая температура и низкая энергия активации способствуют большим константам скорости и, таким образом, ускоряют реакцию. Поскольку эти члены входят в экспоненту, их влияние на скорость весьма существенно.
Здесь «затухает» не концентрация реагента как функция времени, а величина константы скорости как функция показателя степени –E a / RT . И какое значение имеет эта величина? Вспоминая, что RT — это средняя кинетическая энергия , становится очевидным, что показатель степени — это просто отношение энергии активации E a к средней кинетической энергии. Чем больше это отношение, тем меньше скорость (отсюда и знак минус). Это означает, что высокая температура и низкая энергия активации способствуют большим константам скорости и, таким образом, ускоряют реакцию. Поскольку эти члены входят в экспоненту, их влияние на скорость весьма существенно.
На двух приведенных ниже графиках показано влияние энергии активации (обозначенной здесь как E ‡ ) на константу скорости. Даже скромная энергия активации 50 кДж/моль снижает скорость в 10 9 раз.{-E_a/RT}\right) \label{2} \\[4pt] &= \left(\dfrac{-E_a}{R}\right) \left(\dfrac{1}{T}\right) + \ln A \label{3} \end{align} \]
Уравнение \ref{3} имеет вид \(y = mx + b\) — уравнение прямой линии.
\[ \ln k=\ln A — \dfrac{E_{a}}{RT} \nonumber \]
где температура является независимой переменной, а константа скорости является зависимой переменной. Таким образом, если бы кто-то получил набор данных различных значений \(k\), константы скорости определенной химической реакции при различной температуре \(T\), можно было бы построить график \(\ln (k)\) в зависимости от \( 1/Т\). Затем по графику можно определить наклон линии и понять, что это значение равно \(-E_a/R\). Затем можно найти энергию активации, умножив на -R, где R — газовая постоянная.
Это дает простой способ определения энергии активации по значениям k , наблюдаемым при различных температурах, путем построения графика \(\ln k\) как функции \(1/T\).
Пример \(\PageIndex{1}\): Изомеризация циклопропана
Для изомеризации циклопропана в пропилен
были получены следующие данные (расчетные значения выделены розовым цветом): Т, °С
 11
11Комментарий : Эта энергия активации высока, что неудивительно, поскольку для открытия циклопропанового кольца необходимо разорвать углерод-углеродную связь. (Энергия связи C – C обычно составляет около 350 кДж / моль.) Вот почему реакцию необходимо проводить при высокой температуре.
Расчет \(E_a\) без графика
Поскольку график ln k -vs.-1/ T дает прямую линию, часто удобно оценивать энергию активации из экспериментов только при двух температурах. Чтобы увидеть, как это делается, рассмотрим, что
\[\begin{align*} \ln k_2 -\ln k_1 &= \left(\ln A — \frac{E_a}{RT_2} \right)\left(\ln A — \frac{E_a}{ RT_1} \right) \\[4pt] &= \color{red}{\boxed{\color{black}}{\frac{E_a}{R}\left( \frac{1}{T_1}-\frac{ 1}{T_2} \right) }}} \end{align*} \]
Член ln- A исключается путем вычитания выражений для двух членов ln- k . ) Решение выражения на право на энергию активации дает
) Решение выражения на право на энергию активации дает
\[ E_a = \dfrac{R \ln \dfrac{k_2}{k_1}}{\dfrac{1}{T_1}-\dfrac{1}{T_2}} \nonumber \]
Пример \(\PageIndex{2}\)
Широко используемое эмпирическое правило для температурной зависимости скорости реакции заключается в том, что повышение температуры на десять градусов примерно удваивает скорость. Обычно это неверно, особенно когда необходимо разорвать прочную ковалентную связь. Какой должна быть энергия активации для реакции, которая демонстрирует такое поведение?
Решение
Центрируйте десятиградусный интервал при 300 K. Подстановка в приведенное выше выражение дает 9{–1} \end{align*} \]
Пример \(\PageIndex{3}\)
Приготовление яйца вкрутую в Лос-Анджелесе занимает около 3,0 минут, но на большей высоте Денвера, где вода кипит при 92°C, время приготовления 4,5 минуты. Используйте эту информацию для оценки энергии активации коагуляции белка яичного альбумина.
Решение
Отношение констант скорости на высотах Лос-Анджелеса и Денвера составляет 4,5/3,0 = 1,5, а соответствующие температуры равны \(373 \; \rm{K }\) и \(365\; \ гм{К}\). С нижними индексами 2 и 1, относящимися к Лос-Анджелесу и Денверу соответственно: 9{–1}} \end{align*} \]
С нижними индексами 2 и 1, относящимися к Лос-Анджелесу и Денверу соответственно: 9{–1}} \end{align*} \]
Комментарий : Это низкое значение кажется разумным, поскольку термическая денатурация белков в первую очередь связана с разрушением относительно слабых водородных связей; никакие ковалентные связи не разрываются (хотя дисульфидные связи могут мешать этой интерпретации).
Предэкспоненциальный множитель
До этого момента предэкспоненциальный член \(A\) в уравнении Аррениуса (уравнение \ref{1}) игнорировался, поскольку он не связан напрямую с температурой и энергия активации, которая является основным практическим использованием уравнения.
Однако, поскольку \(A\) умножает экспоненциальный член, его значение явно вносит вклад в значение константы скорости и, следовательно, скорости. Напомним, что экспоненциальная часть уравнения Аррениуса выражает долю молекул реагентов, которые обладают достаточной кинетической энергией, чтобы вступить в реакцию в соответствии с законом Максвелла-Больцмана. Эта доля может варьироваться от нуля почти до единицы, в зависимости от величин \(E_a\) и температуры.
Эта доля может варьироваться от нуля почти до единицы, в зависимости от величин \(E_a\) и температуры.
Если бы эта дробь была равна 0, закон Аррениуса сократился бы до
\[k = A \nonumber \]
Другими словами, \(A\) — это доля молекул, которые реагируют, если либо энергия активации равна нулю, либо если кинетическая энергия всех молекул превышает \(E_a \) — правда, редкий сценарий (хотя безбарьерные реакции были охарактеризованы).
Что ограничивало бы константу скорости, если бы не требовалась энергия активации? Наиболее очевидным фактором будет скорость, с которой молекулы реагентов вступают в контакт. Это можно рассчитать с помощью кинетической молекулярной теории, и оно известно как частота- или коэффициент столкновения , \(Z\).
В некоторых реакциях важна относительная ориентация молекул в точке столкновения, поэтому можно определить геометрический или стерический фактор (обычно обозначаемый \(\rho\)) . В общем, мы можем выразить \(A\) как произведение этих двух факторов:
В общем, мы можем выразить \(A\) как произведение этих двух факторов:
\[A = Z\rho \nonumber \]
Значения \(ρ\) вообще очень трудно оценить; иногда их оценивают путем сравнения наблюдаемой константы скорости с константой, в которой \(A\) считается таким же, как \(Z\).
Выводы
Экспоненциальный член в уравнении Аррениуса подразумевает, что константа скорости реакции увеличивается экспоненциально, когда энергия активации уменьшается. Поскольку скорость реакции прямо пропорциональна константе скорости реакции, скорость также увеличивается экспоненциально. Поскольку реакция с малой энергией активации не требует много энергии для достижения переходного состояния, она должна протекать быстрее, чем реакция с большей энергией активации.
Кроме того, уравнение Аррениуса подразумевает, что скорость некаталитической реакции больше зависит от температуры, чем скорость катализируемой реакции. Это связано с тем, что энергия активации некаталитической реакции больше, чем энергия активации соответствующей катализируемой реакции. Поскольку экспоненциальный член включает энергию активации в качестве числителя и температуру в качестве знаменателя, меньшая энергия активации будет иметь меньшее влияние на константу скорости по сравнению с большей энергией активации. Следовательно, скорость некаталитической реакции больше зависит от изменения температуры, чем катализируемой реакции.
Поскольку экспоненциальный член включает энергию активации в качестве числителя и температуру в качестве знаменателя, меньшая энергия активации будет иметь меньшее влияние на константу скорости по сравнению с большей энергией активации. Следовательно, скорость некаталитической реакции больше зависит от изменения температуры, чем катализируемой реакции.
Математика при исключении константы A
Чтобы исключить константу \(A\), должны быть известны две температуры и/или константы скорости. Зная это, можно написать следующие уравнения:
\[ \ln k_{1}=\ln A — \dfrac{E_{a}}{k_{B}T_1} \label{a1} \]
в \(T_1\) и
\[ \ln k_{2}=\ln A — \dfrac{E_{a}}{k_{B}T_2} \label{a2} \]
в \(T_2 \). Переписывая уравнение \ref{a2}:
\[ \ln A = \ln k_{2} + \dfrac{E_{a}}{k_{B}T_2} \label{a3} \]
и подставьте \(\ln A\) в уравнение \ref{a1}:
\[ \ln k_{1}= \ln k_{2} + \dfrac{E_{a}}{k_{B }T_2} — \dfrac{E_{a}}{k_{B}T_1} \label{a4} \]
Это упрощает до:
\[\begin{align*} \ln k_{1} — \ ln k_{2} &= -\dfrac{E_{a}}{k_{B}T_1} + \dfrac{E_{a}}{k_{B}T_2} \\[4pt] \ln \dfrac{k_ {1}}{k_{2}} &= -\dfrac{E_{a}}{k_{B}} \left (\dfrac{1}{T_1}-\dfrac{1}{T_2} \right ) \end{align*} \]
Резюме
Заметив, что скорость многих химических реакций зависит от температуры, Аррениус разработал следующее уравнение для характеристики реакций, зависящих от температуры: 9{\frac{-E_{a}}{RT}}} \nonumber \]
или
\[\ln k=\ln A — \frac{E_{a}}{RT} \nonumber \]
со следующими терминами:
\(k\): Константа скорости химической реакции
- В единицах с -1 (для 1 ст константа скорости порядка) или М -1 с -1 (для 2 и скорость заказа постоянная)
\(A\): предэкспоненциальный фактор или частотный фактор
- Специально относится к столкновению молекул
- Определяет частоту столкновения молекул в правильной ориентации и с достаточной энергией, чтобы инициировать реакцию.

- Этот фактор определяется экспериментально, так как он варьируется в зависимости от различных реакций.
- В единицах л моль -1 с -1 или М -1 с -1 (для 2 и порядка константы скорости) и с -1 (для 1 3 порядка скорости 9 постоянная)
- Поскольку коэффициент частоты А связан с молекулярным столкновением, он зависит от температуры
- Трудно экстраполировать предэкспоненциальный коэффициент, поскольку lnk является линейным только в узком диапазоне температур
\(E_a\): Энергия активации – это пороговая энергия, которую должны приобрести реагенты, прежде чем они достигнут переходного состояния.
- Находясь в переходном состоянии, реакция может идти в прямом направлении к продукту(ам) или в обратном направлении к реагенту(ам).
- Реакции с большой энергией активации требуется гораздо больше энергии для достижения переходного состояния.

- Точно так же реакция с небольшой энергией активации не требует столько энергии для достижения переходного состояния.
- В единицах кДж/моль.
- -E a /RT напоминает закон распределения Больцмана.
\(R\): газовая постоянная.
- Значение 8,314 Дж/моль К.
\(T\): Абсолютная температура, при которой происходит реакция.
- В единицах Кельвина (К).
Проблемы
- Найдите энергию активации (в кДж/моль) реакции, если константа скорости при 600 К равна 3,4 М -1 с -1 и 31,0 при 750 К.
- Найдите константу скорости, если температура 289 К, энергия активации 200 кДж/моль и предэкспоненциальный множитель 9 М -1 с -1
- Найдите новую константу скорости при 310 К, если константа скорости равна 7 М -1 с -1 при 370 К, энергия активации равна 900 кДж/моль
- Рассчитайте энергию активации, если предэкспоненциальный множитель равен 15 M -1 с -1 , константа скорости равна 12M -1 с -1 и равна 22K
- Найдите новую температуру, если константа скорости при этой температуре равна 15M -1 с -1 , а при температуре 389K константа скорости равна 7M -1 с 1 , энергия активации равна 600 кДж/моль
Растворы
1. 9{-1})(289\text{K})} + \ln 9\)
9{-1})(289\text{K})} + \ln 9\)
k = 6,37X10 -36 M -1 с -1
k 2 =1.788X10 -24 M -1 s -1
4. Используйте уравнение K = AE -EA /RT
12 = 15E -EA /(8.314) 25. 25.
EA = 40,82J /MOL
EA = 40,82J /MOL
EA = 40,82J /MOL
EA = 40,82J /MOL
. ln(k 1 /k 2 )=-Ea/R(1/T 1 -1/T 2 )
ln(15/7)=-[(600 X 1000) /8.314](1/T 1 — 1/389)
T 1 = 390,6K
Ссылки
- Chang, Raymond. 2005. Физическая химия для биологических наук. Саусалито (Калифорния): Университетские научные книги.
 п. 311-347.
п. 311-347. - Сигал, Ирвин. 1975. Кинетика ферментов. John Wiley & Sons, Inc., стр. 931-933.
- Эймс, Джеймс. 2010. Лекция 7 Chem 107B. Калифорнийский университет в Дэвисе.
- Лейдлер, Кит. «Развитие уравнения Аррениуса». J. Chem. Образовательный , 1984, 61 (6), стр. 494
- Логан, С.Р. «Происхождение и состояние уравнения Аррениуса». J. Chem. Образовательный , 1982, 59 (4), стр. 279
Авторы и авторство
- Гвиневьев Дель Мундо, Карим Мусса, Памела Чача, Флоренс-Дамилола Одуфалу, Галактика Мудда, Кан, Чин Фунг Кельвин
Эта страница под названием 6.2.3.1: Уравнение Аррениуса распространяется под лицензией CC BY и была создана, изменена и/или курирована Стивеном Лоуэром с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Стивен Лоуэр
- Лицензия
- СС BY
- Показать страницу TOC
- № на стр.
- Теги
- Уравнение Аррениуса
- источник@http://www.chem1.com/acad/webtext/virtualtextbook.html
Интуитивное понимание формулы Эйлера – лучшее объяснение0042 мнимый показатель степени
до синуса и косинуса! И каким-то образом подключение пи дает -1? Может ли это когда-нибудь быть интуитивно понятным?Не согласно математику 1800-х годов Бенджамину Пирсу:
Совершенно парадоксально; мы не можем этого понять, и мы не знаем, что это значит, но мы доказали это, и поэтому мы знаем, что это должно быть правдой.
Арх, от такого отношения моя кровь закипает! Формулы — это не магические заклинания, которые нужно запоминать: мы должны, должны, должны найти озарение. Вот мой: 9{i \pi} = -1$, спросите их о i в i -й степени. Если они не могут это обдумать, формула Эйлера остается для них магическим заклинанием.
Обновление: Во время написания я подумал, что видео может помочь объяснить идеи более ясно:
Понимание cos(x) + i * sin(x)
Знак равенства перегружен. Иногда мы имеем в виду «установить одну вещь на другую» (например, x = 3), а иногда мы имеем в виду «эти две вещи описывают одну и ту же концепцию» (например, $\sqrt{-1} = i$).
Формула Эйлера является последней: она дает две формулы, которые объясняют, как двигаться по кругу. Если мы рассмотрим круговое движение с помощью тригонометра и пройдём x радиан:
- cos(x) — это координата x (горизонтальное расстояние)
- sin(x) — координата y (расстояние по вертикали)
Оператор
— это умный способ объединить координаты x и y в одно число. Аналогия «комплексные числа двумерны» помогает нам интерпретировать одно комплексное число как позицию на окружности.
Аналогия «комплексные числа двумерны» помогает нам интерпретировать одно комплексное число как позицию на окружности.
Когда мы устанавливаем x равным $\pi$, мы перемещаемся на $\pi$ единиц по внешней стороне единичного круга. Поскольку общая длина окружности равна $2\pi$, старое доброе $\pi$ находится на полпути, что дает нам -1.
Неато: Правая часть формулы Эйлера ($\cos(x) + i \sin(x)$) описывает круговое движение с мнимыми числами. Теперь давайте выясним, как e часть уравнения решает эту задачу.
Что такое воображаемый рост?
Объединение координат x и y в комплексное число сложно, но выполнимо. Но что значит воображаемая 9{\ln(3) \cdot 4} = 81$
Вместо того, чтобы видеть числа сами по себе, вы можете думать о них как о чем-то, до чего нужно «дорасти». Действительные числа, такие как 3, дают процентную ставку ln(3) = 1,1, и это то, что е «собирает» по мере своего развития, постоянно увеличиваясь.
Регулярный рост прост: он продолжает «толкать» число в том же самом направлении, в котором оно двигалось. 3 × 3 толкает в исходном направлении, делая его в 3 раза больше (9).
3 × 3 толкает в исходном направлении, делая его в 3 раза больше (9).
Воображаемый рост отличается: «проценты», которые мы зарабатываем, идут в другом направлении! Это похоже на реактивный двигатель, который был привязан сбоку — вместо того, чтобы двигаться вперед, мы начинаем толкаться в 9 часов.0 градусов.
Прелесть постоянного ортогонального (перпендикулярного) толчка в том, что он не ускоряет и не замедляет вас — он вращает вас! Взяв любое число и умножив его на и , мы не изменим его величину, а только направление, которое оно указывает.
Интуитивно, вот как я вижу непрерывный воображаемый темп роста : «Когда я расту, не толкай меня вперед или назад в том направлении, в котором я уже иду. Вместо этого вращай меня.»
Но разве мы не должны вращаться все быстрее и быстрее? 9{\ln(2)x}$, что означает мгновенный рост со скоростью ln(2) в течение «x» секунд.
И эй — если бы наша скорость роста была в два раза выше, 2ln(2) против ln(2), это выглядело бы так же, как рост в два раза дольше (2x против x). Магия e позволяет нам поменять местами скорость и время; 2 секунды в ln(2) — это такой же рост, как 1 секунда в 2ln(2).
Магия e позволяет нам поменять местами скорость и время; 2 секунды в ln(2) — это такой же рост, как 1 секунда в 2ln(2).
Теперь представьте, что у нас есть некоторая чисто воображаемая скорость роста (Ri), которая поворачивает нас, пока мы не достигнем i, или 90 градусов вверх. Что произойдет, если мы удвоим эту скорость до 2Ri, не закрутится ли круг?
Нет! Имея скорость 2Ri, мы просто вращаемся в два раза быстрее или, альтернативно, вращаемся со скоростью R в два раза дольше, но остаемся на круге. Вращение в два раза дольше означает, что теперь мы повернуты лицом на 180 градусов.
Как только мы осознаем, что некоторая экспоненциальная скорость роста может привести нас от 1 к i, увеличение этой скорости только еще сильнее раскрутит нас. Мы никогда не выйдем из круга.
Однако, если наша скорость роста комплексная (a+bi против Ri), то действительная часть (a) будет увеличивать нас, как обычно, а мнимая часть (bi) вращает нас. Но не будем заморачиваться: формула Эйлера $e^{ix}$ примерно равна 9i$), мы просто умножаем наш неявный темп роста на i. Таким образом, вместо того, чтобы расти со старым добрым значением ln(3), мы растём со значением ln(3) * i.
Таким образом, вместо того, чтобы расти со старым добрым значением ln(3), мы растём со значением ln(3) * i.
Верхняя часть экспоненты изменяет неявную скорость роста нижней части.
Важные детали
Давайте посмотрим поближе. Помните это определение e :
Что $\frac{100\%}{n}$ представляет процентную долю, которую мы зарабатывали в каждый микроскопический период. Мы предположили, что процентная ставка равна 100 % в реальном измерении, но что, если она равна 100 % в воображаемом направлении?
Теперь наш недавно сформированный интерес добавляется к нам в направлении 90 градусов. Удивительно, но это не меняет нашу длину — это хитрая концепция, потому что она создает треугольник, в котором гипотенуза должна быть больше. Мы имеем дело с пределом, и дополнительное расстояние находится в пределах указанной нами погрешности. Это то, чем я хочу заняться в другой раз, но поверьте мне на слово: непрерывный перпендикулярный рост заставит вас вращаться. Это сердце синуса и косинуса, где ваше изменение перпендикулярно вашему текущему положению, и вы двигаетесь по кругу.
Это сердце синуса и косинуса, где ваше изменение перпендикулярно вашему текущему положению, и вы двигаетесь по кругу.
Мы применяем i единиц роста бесконечно малыми шагами, каждый из которых толкает нас под углом 90 градусов. Нет вращения «все быстрее и быстрее» — вместо этого мы ползаем по периметру на расстояние |i| = 1 (величина i).
И эй — расстояние, пройденное по кругу, равно углу в радианах! Мы нашли другой способ описать круговое движение!
Чтобы получить круговое движение: Непрерывно меняйтесь, вращаясь под углом 90 градусов (иначе воображаемая скорость роста).
Итак, формула Эйлера гласит: «Экспоненциальный воображаемый рост описывает круг». И этот путь такой же, как движение по кругу с использованием синуса и косинуса в воображаемой плоскости.
В данном случае слово «экспоненциальный» сбивает с толку, потому что мы движемся по кругу с постоянной скоростью. В большинстве дискуссий предполагается, что экспоненциальный рост имеет кумулятивный, усугубляющий эффект. i$
i$
Это сложно — это не наш стандартный формат. Но помните,
Нам нужен начальный рост в 3 раза в конце периода или мгновенная скорость ln(3). Но появляется i и изменяет скорость ln(3) на «i * ln(3)»: немного быстрее, чем 100% непрерывный рост, поскольку e составляет около 2,718. Но нет, и закрутили нас: теперь мы трансформируемся с воображаемой скоростью, что означает, что мы просто вращаемся. Если 9i$, какова мгновенная скорость роста, представленная i в качестве базы?
Хрм. Обычно мы делаем ln(x), чтобы получить скорость роста, необходимую для достижения x в конце 1 единицы времени. Но по воображаемой ставке? Нам нужно обдумать это.
Для того, чтобы начать с 1 и вырасти до i , нам нужно начать ротацию с самого начала. Как быстро? Нам нужно получить 90 градусов (пи/2 радиана) за 1 единицу времени. Таким образом, наша ставка равна $i \frac{\pi}{2}$. Помните, что наша скорость должна быть воображаемой, поскольку мы вращаемся, а не растем! Обычный старый $\frac{\pi}{2}$ составляет около 1,57 и приводит к регулярному росту. 1$). 1 единица времени дает нам оборот $-\frac{\pi}{2}$ радиан (-90 градусов) или -i!
1$). 1 единица времени дает нам оборот $-\frac{\pi}{2}$ радиан (-90 градусов) или -i!
И, просто для удовольствия, если мы возведем этот сумасшедший результат в квадрат:
Это «всего лишь» удвоенное вращение: 2 — это обычное число, поэтому скорость вращения удваивается до полных -180 градусов в единицу времени. . Или вы можете посмотреть на это как на поворот на -90 градусов дважды подряд.
На первый взгляд, это действительно странные показатели. Но с нашими аналогиями мы можем принять их спокойно.
Сложный рост
Мы можем иметь реальный и воображаемый рост одновременно: реальная часть увеличивает нас, а мнимая часть нас вращает: 9{2,3 + 0,93i}$.
Почему это полезно?
Формула Эйлера дает нам другой способ описать движение по окружности. Но мы уже могли сделать это с помощью синуса и косинуса — что особенного?
Все дело в перспективе. Синус и косинус описывают движение в терминах сетки , отображая горизонтальные и вертикальные координаты.
В формуле Эйлера используются полярные координаты — каковы ваши угол и расстояние? Опять же, есть два способа описать движение: 9{ix}$ можно преобразовать в синус и косинус, мы можем переписать формулы в триггерах как вариации e, что очень удобно (нет необходимости запоминать sin(a+b), вы можете вывести его — подробнее в другой раз) . И прекрасно, что каждое число, действительное или комплексное, является разновидностью e.
Но полезность, сентиментальность: самым важным результатом является осознание того, что непонятные уравнения могут стать интуитивно понятными при правильных аналогиях. Не позволяйте красивым уравнениям, таким как формула Эйлера, оставаться магическим заклинанием — опирайтесь на известные вам аналогии, чтобы увидеть идеи внутри уравнения.
Счастливая математика.
Приложение
Демонстрация экрана была интересной, и отзывы определенно приветствуются. Я думаю, что это помогает идеям всплывать, а просмотр статьи помог мне найти пробелы в моей интуиции.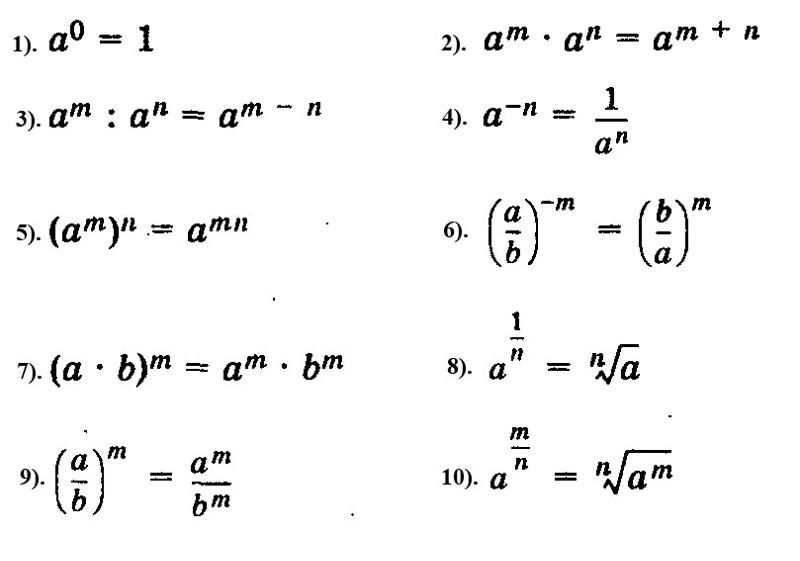



 п. 311-347.
п. 311-347.