Видеоурок по физике 8 класс тема Функция y kx её свойства и график.
Рациональные дроби
Квадратные корни
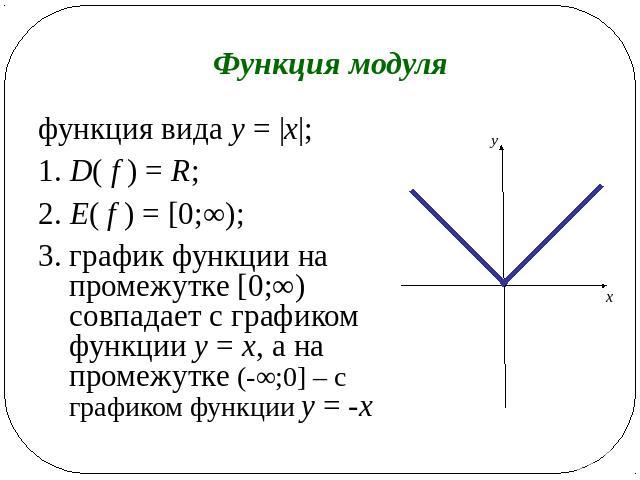
Модуль
Квадратные уравнения
Рациональные уравнения
Иррациональные уравнения
Неравенства
Показать все темы
7 8 9 10 11
Поделиться
0
0
07:17
В данном видеоуроке мы познакомимся с новой функцией y=k/x, которую также называют функцией обратной пропорциональности. Коэффициент k может принимать любые значения, кроме k=0, при этом х никогда не будет равен 0.
Коэффициент k может принимать любые значения, кроме k=0, при этом х никогда не будет равен 0.
| Функция y=k/x, её свойства и график |
Пройти тест |
16.9. Постройте график функции у = |x|. С помощью графика найдите… Алгебра Мордкович 8 класс – Рамблер/класс
16.9. Постройте график функции у = |x|. С помощью графика найдите… Алгебра Мордкович 8 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
16. 9. Постройте график функции у = |x|. С помощью графика найдите:
9. Постройте график функции у = |x|. С помощью графика найдите:
а) значения у при х = 5; 0; -2,5;
б) значения х, если у = 7; 3; 1;
в) наименьшее и наибольшее значения функции на отрезке [-4; -1];
г) значения х, при которых функция убывает, возрастает.
ответы
решение тут такое
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее.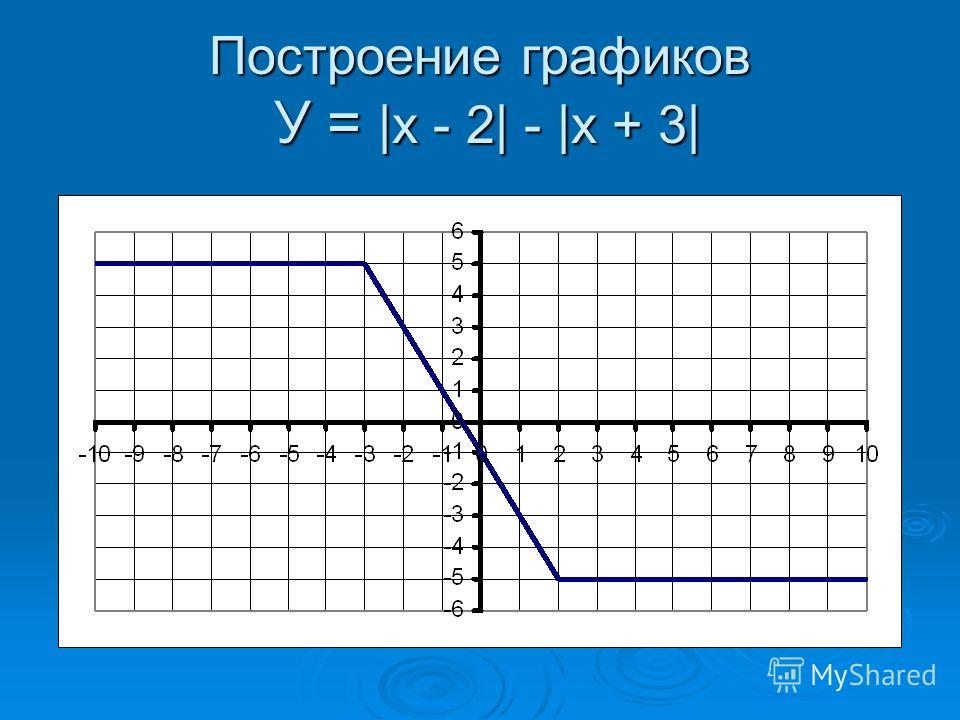 ..)
..)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые).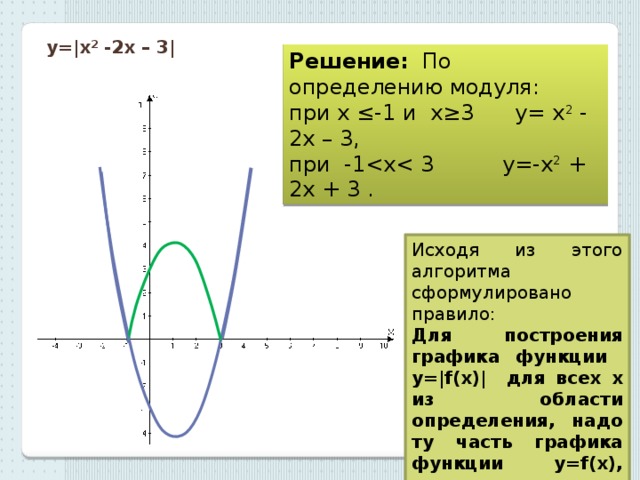 (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Модуль 12 — Правила дифференциации
В этом уроке вы будете использовать функцию TI-83 Numeric Derivative для построения графиков производных различных функций. Эти графики дадут подсказки для правил дифференцирования. Аналитическое подтверждение этих правил можно найти в большинстве книг по математическому анализу.
Производная от y = sin x
График функции y = sin x и его производная. Изучите график производной и определите, как он соотносится с графиком функции.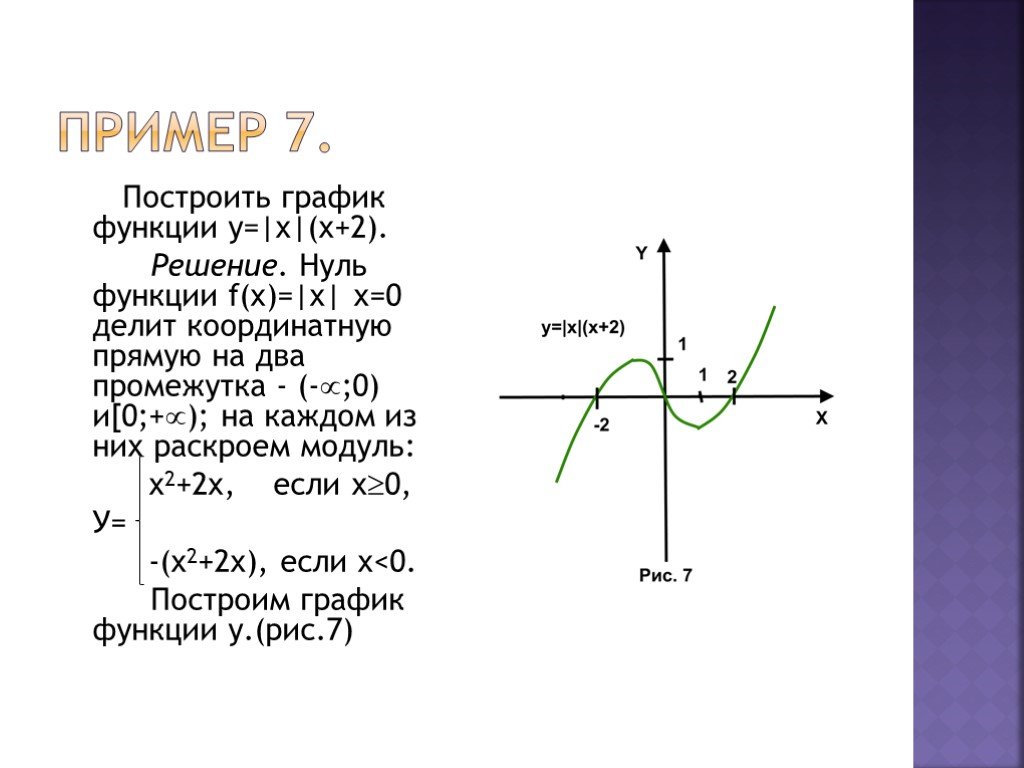 Обратите внимание на значения производной, когда функция возрастает и когда она убывает.
Обратите внимание на значения производной, когда функция возрастает и когда она убывает.
- Убедитесь, что ваш калькулятор находится в радианном режиме. Введите Y 1 = sin(X) и Y 2 = nDeriv(Y 1 ,X,X).
- Измените стиль графика Y 1 на «толстый».
- Отобразите оба графика в смотровое окно.
12.1.1 Когда график y = sin х увеличивается, что верно относительно его производной? Когда график y = sin x уменьшается, что верно в отношении его производной? Щелкните здесь, чтобы получить ответ.
12.1.2 Каково значение производной, когда y = sin x имеет точку поворота? Щелкните здесь, чтобы получить ответ.
12.1.3 Сделайте предположение о том, какой функцией может быть производная от y = sin x . Введите предполагаемую функцию в Y 3
Введите предполагаемую функцию в Y 3
Вы должны обратиться к книге по математическому анализу для аналитического определения производной y = sin x , чтобы подтвердить свою гипотезу.
Производная от y = cos x
График y = cos x и его производная в том же окне просмотра.
- Измените Y 1 на cos(X). Придерживайтесь «толстого» графического стиля.
- Отобразите оба графика в смотровое окно.
12.1.4 Сделайте предположение о производной y = cos x . Обеспечьте графическую поддержку вашей гипотезы, нарисовав график вашей функции в Y 3 , чтобы увидеть, дает ли он тот же график, что и производная. Щелкните здесь, чтобы получить ответ.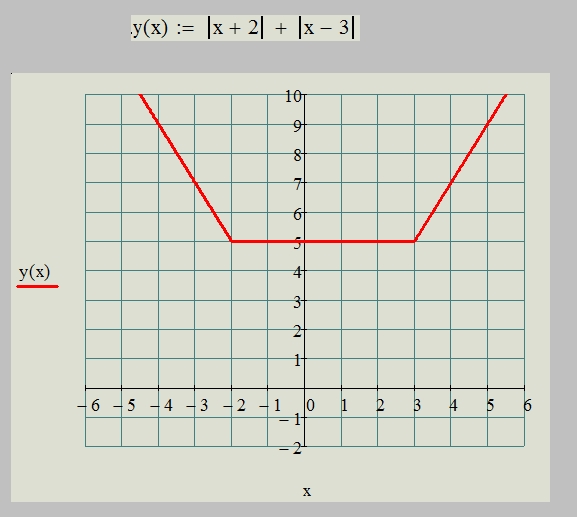
Обратитесь к книге по математическому анализу, чтобы подтвердить свою гипотезу о производной y = cos x .
Процедура, использованная выше, может быть расширена для включения более общих форм знакомых функций.
Производная от y = sin kx
Определите форму производной y = sin kx , исследуя форму с различными значениями k . Сначала исследуйте производную от y = sin 2 x .
- Введите Y 1 = sin(2X) и Y 2 = nDeriv(Y 1 ,X,X)
- Установите стиль графика Y 1 на «толстый».
- Отобразите оба графика в смотровое окно.
12.1.5 Какова амплитуда производной? Каков период производной? Щелкните здесь, чтобы получить ответ.
12.1.6 Напишите уравнение для производной y
 0023 3 , что должно соответствовать графику Y 2 . Щелкните здесь, чтобы получить ответ.
0023 3 , что должно соответствовать графику Y 2 . Щелкните здесь, чтобы получить ответ.12.1.7 График y = sin 3 x и его числовая производная. Сделайте предположение о функции, представляющей производную. Нарисуйте свою гипотезу вместе с числовой производной. Они одинаковы?
Повторите этот процесс для y = sin 4 x . Щелкните здесь, чтобы получить ответы.
12.1.8 Как вы думаете, какой может быть производная от y = sin kx , где k — константа? Щелкните здесь, чтобы получить ответ.
Производная от y = cos kx
12.1.9 Используйте предыдущие графические процедуры, чтобы сделать и подтвердить гипотезы для производных следующего:
г = cos 2 х
у = cos 3 х
у = cos 4 х
Щелкните здесь, чтобы получить ответы.
12.1.10 Основываясь на ваших предыдущих ответах, какова производная от y = cos( kx ), если k является константой? Щелкните здесь, чтобы получить ответ.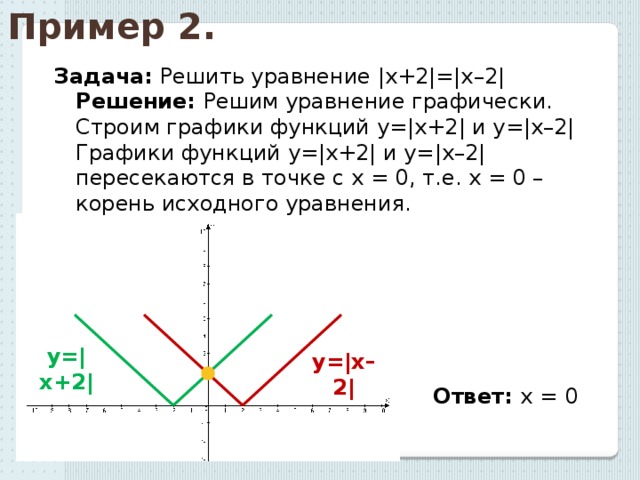 9(это функция «2 nd » выше .
9(это функция «2 nd » выше .
- Отобразите оба графика в окне [-3, 3, 1] x [-5, 5, 1].
Кажется, есть только один график.
12.1.11 Используйте функцию трассировки и клавиши со стрелками, чтобы перемещаться к различным точкам на графиках и переходить назад и вперед между Y 1 и Y 2 с помощью клавиш со стрелками вверх и вниз. Что вы обнаружите? Щелкните здесь, чтобы получить ответ.
| |||
12.1.12 Используйте свое открытие, чтобы сделать предположение о производной y = е x . Щелкните здесь, чтобы получить ответ.
Производная от y = e kx
Иногда трудно решить, равны ли две функции, глядя на их графики. Это помогает сравнить их значения с помощью таблиц.
12.1.13 Используйте таблицы и графические методы этого урока, чтобы обнаружить производные следующих функций:
y = e 2 x
y = e 3 x
y = e 4 x
Щелкните здесь, чтобы получить ответ.
12.1. 14 Основываясь на ваших результатах, какова производная от y = e kx ? Щелкните здесь, чтобы получить ответ.
14 Основываясь на ваших результатах, какова производная от y = e kx ? Щелкните здесь, чтобы получить ответ.
Цепное правило
Во многих производных этого урока есть закономерность.
12.1.15 Основываясь на этих производных, какой может быть производная от y = f ( kx ), где k — константа, а f — неизвестная функция? Щелкните здесь, чтобы получить ответ.
Ответ на предыдущий вопрос является частным случаем теоремы, называемой Цепным правилом для производных . Найдите это правило в учебнике по математическому анализу и посмотрите, как оно применимо к этому уроку.
Модуль 10 Граф радикальных функций
Результат обучения
- График радикальных функций с использованием таблиц и преобразований
Вы также можете построить график радикальных функций (например, функций квадратного корня), выбрав значения для x и нахождение точек, которые будут на графике. Опять же, полезно иметь некоторое представление о том, как будет выглядеть график.
Опять же, полезно иметь некоторое представление о том, как будет выглядеть график.
Подумайте об основной функции квадратного корня, [latex]f(x)=\sqrt{x}[/latex]. Взгляните на таблицу значений для x и y , а затем постройте график функции. Обратите внимание, что все значения x в таблице являются правильными квадратами. Поскольку вы извлекаете квадратный корень из x , использование полных квадратов имеет больше смысла, чем простое нахождение квадратных корней из [latex]0, 1, 2, 3, 4[/latex] и т. д.
| х | f ( x ) |
|---|---|
| [латекс]0[/латекс] | [латекс]0[/латекс] |
| [латекс]1[/латекс] | [латекс]1[/латекс] |
| [латекс]4[/латекс] | [латекс]2[/латекс] |
| [латекс]9[/латекс] | [латекс]3[/латекс] |
| [латекс]16[/латекс] | [латекс]4[/латекс] |
Вспомните, что x никогда не может быть отрицательным, потому что, когда вы возводите в квадрат действительное число, результат всегда положительный. Например, [латекс]\sqrt{49}[/латекс] означает «найти число, квадрат которого равен [латекс]49[/латекс]». Поскольку не существует действительного числа, которое мы можем возвести в квадрат и получить отрицательное значение, функция [latex]f(x)=\sqrt{x}[/latex] будет определена для [latex]x>0[/latex].
Например, [латекс]\sqrt{49}[/латекс] означает «найти число, квадрат которого равен [латекс]49[/латекс]». Поскольку не существует действительного числа, которое мы можем возвести в квадрат и получить отрицательное значение, функция [latex]f(x)=\sqrt{x}[/latex] будет определена для [latex]x>0[/latex].
Взгляните на график.
Как и в случае с параболами, умножение и сложение чисел вносят некоторые изменения, но основная форма остается той же. Вот некоторые примеры.
Умножение [латекс]\sqrt{x}[/латекс] на положительное значение изменяет ширину полупараболы. Умножение [латекс]\sqrt{x}[/латекс] на отрицательное число дает вторую половину горизонтальной параболы.
В следующем примере мы покажем, как умножение радикальной функции на константу может изменить форму графика.
Пример
Сопоставьте каждую из следующих функций с графиком, который она представляет.
а) [латекс]f(x)=-\sqrt{x}[/латекс]
b)[латекс]f(x)=2\sqrt{x}[/latex]
c) [латекс]f(x)=\dfrac{1}{2}\sqrt{x}[/latex ]
1)
2)
3)
Показать решение
Добавление значения вне радикально перемещает график вверх или вниз.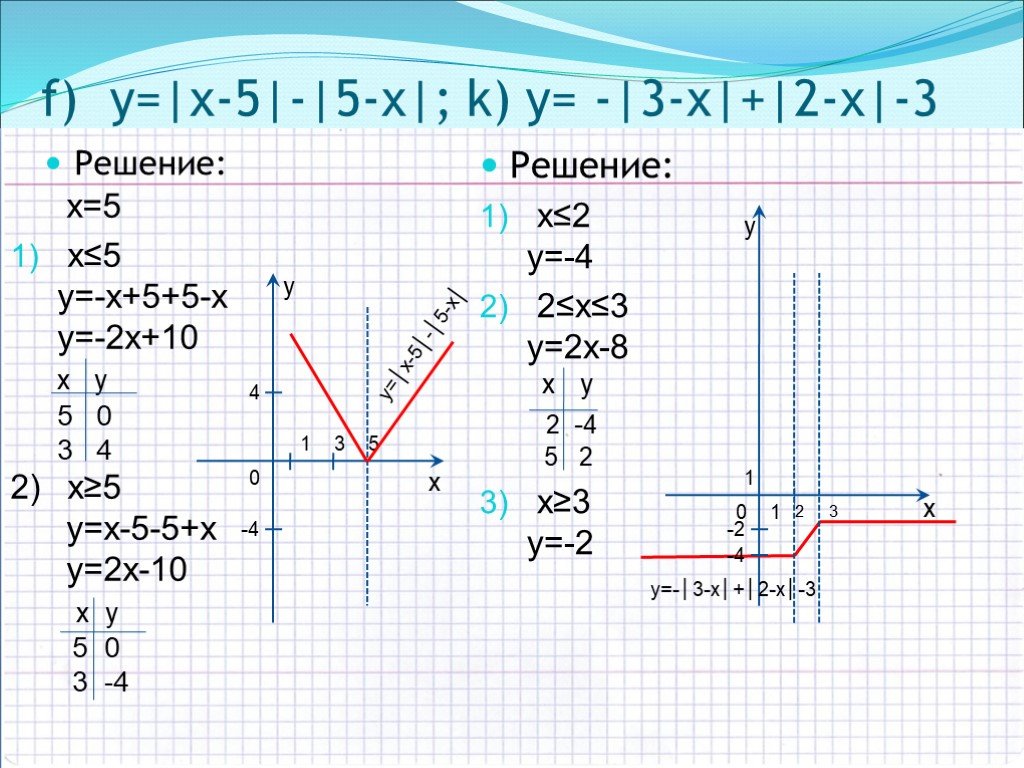 Думайте об этом как о добавлении значения к основному значению y [латекс] \sqrt{x}[/латекс], поэтому добавленное положительное значение перемещает график вверх.
Думайте об этом как о добавлении значения к основному значению y [латекс] \sqrt{x}[/латекс], поэтому добавленное положительное значение перемещает график вверх.
Пример
Сопоставьте каждую из следующих функций с графиком, который она представляет.
а) [латекс] f(x)=\sqrt{x}+3[/латекс]
б)[латекс] f(x)=\sqrt{x}-2[/латекс]
1)
2)
Показать решение
Добавление значения внутри радикально перемещает график влево или вправо. Думайте об этом как о добавлении значения к x , прежде чем извлекать квадратный корень, так что значение y перемещается в другое значение x . Например, для [latex]f(x)=\sqrt{x}[/latex] квадратный корень равен [latex]3[/latex], если [latex]x=9[/латекс]. Для [latex]f(x)=\sqrt{x+1}[/latex] квадратный корень равен [latex]3[/latex], когда [latex]x+1[/latex] равен [latex]9[ /latex], поэтому x равно [latex]8[/latex]. Изменение x на [latex]x+1[/latex] сдвигает график влево на [latex]1[/latex] единицу (от [latex]9[/latex] до [latex]8[/latex] ).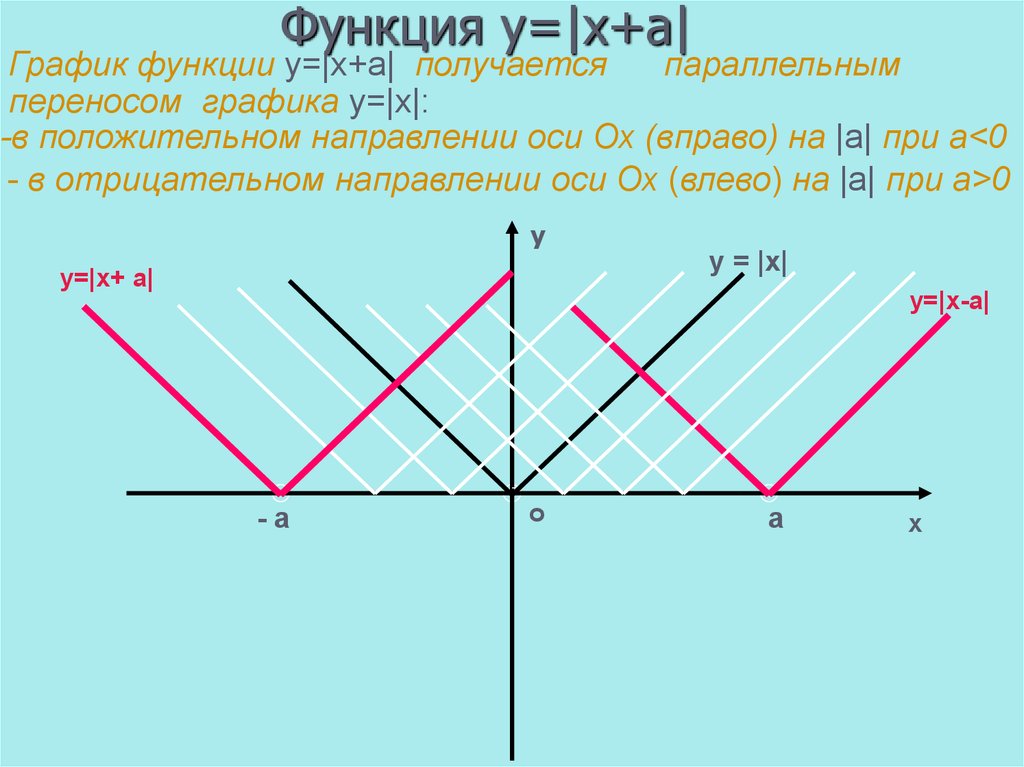

 0023 1 и Y 2 . Это позволяет сравнивать значения Y 1 и Y 2 для выбранных значений x .
0023 1 и Y 2 . Это позволяет сравнивать значения Y 1 и Y 2 для выбранных значений x .