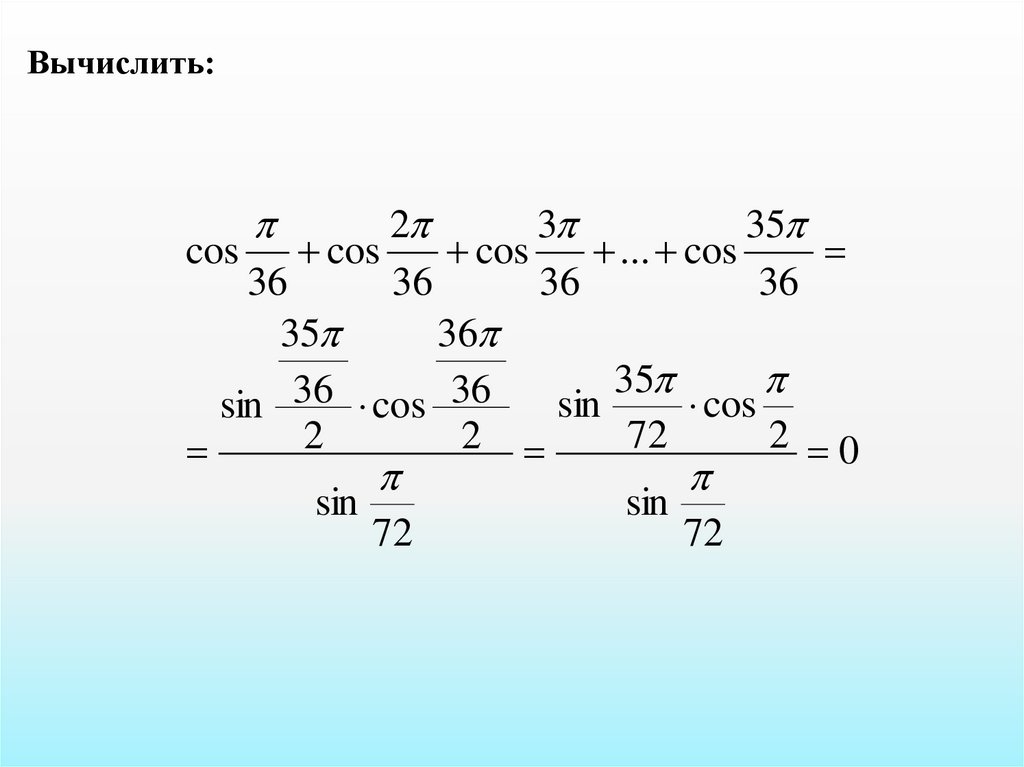
Вычисление тригонометрических выражений: Вычисление значений тригонометрических выражений

Содержание

Вычисление значений тригонометрических выражений

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-09-09

Вычисление значений тригонометрических выражений. В этой статье мы рассмотрим несколько примеров на вычисление значений тригонометрических выражений. В одной из статей уже были представлены такие примеры, посмотрите. Что необходимо знать, понимать и уметь применять?

Это формулы приведения, формулы периодичности тригонометрических функций, чётность нечётность, знаки тригонометрических функций в четвертях тригонометрической окружности, и конечно же, как всегда, требуется внимательность при вычислениях.

Периодичность тригонометрических функций.

Подробно саму теорию о периодичности здесь разъяснять не стану, будет отдельная статья, напомню вам только сами формулы:

*Наименьший положительный период функции синус составляет 2Пи или 360⁰

*Наименьший положительный период функции косинус составляет 2Пи или 360⁰

*Наименьший положительный период функции тангенс составляет Пи или 180⁰

*Наименьший положительный период функции котангенс составляет Пи или 180⁰

Если вы знакомы с тригонометрической окружностью и тригонометрические функции основательно изучили, то понятие периодичности вам знакомо и смысл ясен.

Чётность и нечётность тригонометрических функций, кратко:

Рассмтотрим примеры.

*Общая рекомендация! Сначала выделяйте период и «избаляйтесь» от него, а уже затем применяйте свойство четности (нечётности) и формулы приведения.

64771. Найдите

Применим свойство периодичности синуса и формулу его приведения:

Вычислим cos α. Это можем сделать используя основное тригонометрическое тождество:

Определим знак косинуса для интервала (3П/2;2П). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы (и наоборот) можно посмотреть здесь. Значение косинуса в этой четверти положительное, поэтому:

Таким образом, 8∙cos α = 8∙0,8 = 6,4

Второй способ:

Вычисляем cos α, получаем 0,8. Таким образом:

Ответ: 6,4

64897. Найдите

Применим формулу приведения для косинуса:

Вычислим sin α. Из основного тригонометрического тождества следует, что:

Определим знак синуса для интервала (0;π/2). Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:

Таким образом, –15∙sin α = –15∙0,96 = – 14,4

Ответ: – 14,4

65031. Найдите

Применим свойства нечётности тангенса, свойство его периодичности и формулу приведения:

Вычислим котангенс угла:

Таким образом

Ответ: – 0,8

65429. Найдите значение выражения

Используем свойство периодичности косинуса и формулу приведения синуса:

Ответ: – 2

65489. Найдите значение выражения

Используем периодичность синуса, свойство чётности косинуса и формулу приведения косинуса:

Ответ: 8

64695. Найдите значение выражения:

Решение:

Ответ: 1

26784. Найдите

Посмотреть решение

26785. Найдите

Посмотреть решение

26786. Найдите

Посмотреть решение

26792. Найдите значение выражения

Посмотреть решение

26793. Найдите значение выражения

Посмотреть решение

26783. Найдите значение выражения

Посмотреть решение

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Выражения | ЕГЭ-№6Тригонометрия

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

ЕГЭ Профиль №4. Вычисление значений тригонометрических выражений — math200.ru

ЕГЭ Профиль №4. Вычисление значений тригонометрических выраженийadmin2022-08-28T09:56:35+03:00

Скачать файл в формате pdf.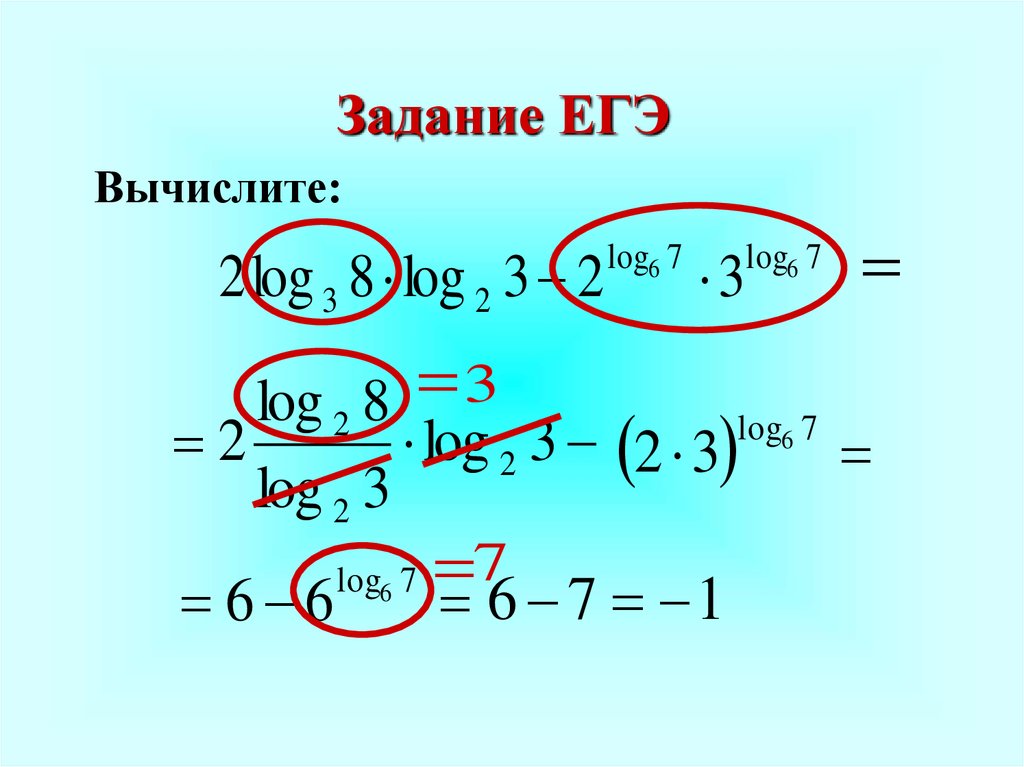 \circ }\)

Ответ

ОТВЕТ: 10.

Задача 28. Найдите \({\text{tg}}\alpha \), если \(\cos \alpha = \frac{1}{{\sqrt {10} }}\) и \(a \in \left( {\frac{{3{\\\pi }}}{2};\;2{\\\pi }} \right)\)

Ответ

ОТВЕТ: — 3.

Задача 29. Найдите \({\text{tg}}\alpha \), если \(\sin \alpha = — \frac{5}{{\sqrt {26} }}\) и \(\alpha \in \left( {{\\\pi };\;\frac{{3{\\\pi }}}{2}} \right)\)

Ответ

ОТВЕТ: 5.

Задача 30. Найдите \(3\cos \alpha \), если \(\sin \alpha = — \frac{{2\sqrt 2 }}{3}\) и \(\alpha \in \left( {\frac{{3{\\\pi }}}{2};\;2{\\\pi }} \right)\)

Ответ

ОТВЕТ: 1.

Задача 31. Найдите \(7\sin \alpha \), если \(\cos \alpha = \frac{{3\sqrt 5 }}{7}\) и \(\alpha \in \left( {1,5{\\\pi };\;2{\\\pi }} \right)\)

Ответ

ОТВЕТ: — 2.

Задача 32. Найдите \(24\cos 2\alpha \), если \(\sin \alpha = — 0,2\)

Ответ

ОТВЕТ: 22,08.

Задача 33. Найдите \(\frac{{10\sin 6\alpha }}{{3\cos 3\alpha }}\), если \(\sin 3\alpha = 0,6\)

Ответ

ОТВЕТ: 4.

Задача 34. Найдите значение выражения \(\frac{{3\cos \left( {{\\\pi } — \beta } \right) + \sin \left( {\frac{{\\\pi }}{2} + \beta } \right)}}{{\cos \left( {\beta + 3{\\\pi }} \right)}}\)

Ответ

ОТВЕТ: 2.

Задача 35. Найдите значение выражения \(\frac{{2\sin \left( {\alpha — 7{\\\pi }} \right) + \cos \left( {\frac{{3{\\\pi }}}{2} + \alpha } \right)}}{{\sin \left( {a + {\\\pi }} \right)}}\)

Ответ

ОТВЕТ: 1.

Задача 36. Найдите значение выражения \(5{\text{tg}}\left( {5{\\\pi } — \gamma } \right) — {\text{tg}}\left( { — \gamma } \right)\), если \({\text{tg}}\gamma {\text{ = 7}}\)

Ответ

ОТВЕТ: — 28.

Задача 37. Найдите \(\sin \left( {\frac{{7{\\\pi }}}{2} — \alpha } \right)\), если \(\sin \alpha = 0,8\) и \(a \in \left( {\frac{{\\\pi }}{2};\;{\\\pi }} \right)\)

Ответ

ОТВЕТ: 0,6. 2}\alpha = 6\)

Ответ

ОТВЕТ: 1,5.

Задача 41. Найдите \(\frac{{3\cos \alpha — 4\sin \alpha }}{{2\sin \alpha — 5\cos \alpha }}\), если \({\text{tg}}\alpha {\text{ = 3}}\)

Ответ

ОТВЕТ: — 9.

Задача 42. Найдите \(\frac{{10\cos \alpha + 4\sin \alpha + 15}}{{2\sin \alpha + 5\cos \alpha + 3}}\), если \({\text{tg}}\alpha {\text{ = }} — {\text{2}}{\text{,5}}\)

Ответ

ОТВЕТ: 5.

Задача 43. Найдите \({\text{tg}}\alpha \), если \(\frac{{6\sin \alpha — 2\cos \alpha }}{{4\sin \alpha — 4\cos \alpha }} = — 1\)

Ответ

ОТВЕТ: 0,6.

Задача 44. Найдите \({\text{tg}}\alpha \), если \(\frac{{3\sin \alpha — 5\cos \alpha + 2}}{{\sin \alpha + 3\cos \alpha + 6}} = \frac{1}{3}\)

Ответ

ОТВЕТ: 2,25.

Задача 45. Найдите значение выражения \(7\cos \left( {{\\\pi } + \beta } \right) — 2\sin \left( {\frac{{\\\pi }}{2} + \beta } \right)\), если \(\cos \beta = — \frac{1}{3}\)

Ответ

ОТВЕТ: 3.

Задача 46. Найдите значение выражения \(5\sin \left( {\alpha — 7{\\\pi }} \right) — 11\cos \left( {\frac{{3{\\\pi }}}{2} + \alpha } \right)\), если \(\sin \alpha = — 0,25\)

Ответ

ОТВЕТ: 4.

Задача 47. Найдите \(3\cos 2\alpha \), если \(\cos \alpha = \frac{1}{2}\)

Ответ

ОТВЕТ: — 1,5.

Поддержать нас

Упростить тригонометрическое выражение — Онлайн калькулятор тригонометрии

Упрощение триггера, онлайн-исчисление

Резюме:

Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.

simple_trig онлайн

Описание :

Этот калькулятор позволяет с помощью различных тригонометрических формул от до вычислить тригонометрическое выражение .

Тригнометрические выражения — это выражения, включающие функции синуса, косинуса, функции тангенса…

Для упрощения тригонометрических выражений калькулятор использует различные формулы тригонометрии, вот несколько примеров формул тригонометрические, используемые калькулятором:

`AA x в RR, k в ZZ`,

`sin(-x)= -sin(x)`
`sin(x+2*k*pi)=sin(x)`
`sin(pi-x)=sin(x)`
`sin(pi+x)=-sin(x)`
`sin(pi/2-x)=cos(x)`
`sin(pi/2+x)=cos(x)`

`cos(-x)= cos(x)`
`cos(x+2*k*pi)=cos(x)`
`cos(pi-x)=-cos(x)`
`cos(pi+x)=-cos(x) `
`cos(pi/2-x)=sin(x)`
`cos(pi/2+x)=-sin(x)`

`tan(-x)= -tan( x)`
`tan(x+k*pi)=tan(x)`
`tan(pi-x)=-tan(x)`
`tan(pi+x)=tan(x) `
`tan(pi/2-x)=1/tan(x)`
`tan(pi/2+x)=-1/tan(x)`

Это лишь небольшой пример из многих тригонометрических формул, используемых этим тригонометрическим калькулятором.

Когда калькулятор упрощает тригонометрическое выражение, он указывает формулы, используемые для получения результата, в разделе, предназначенном для деталей расчетов.

Чтобы упростить тригонометрическое выражение , введите выражение для упрощения и примените функцию simple_trig. Таким образом, для упрощения следующего выражения `cos(x+pi)+2*sin(x)` введите simple_trig(`cos(x+pi)+2*sin(x)`) , после вычисления возвращается упрощенная форма тригонометрического выражения.

В этом другом примере показано, как вычислить тригонометрическое выражение `cos(pi-x)`: simple_trig(`cos(pi-x)`) .

Тригонометрический калькулятор может упростить не только буквенно-цифровые выражения, но и чисто числовые выражения.

Синтаксис:

simple_trig(выражение), где выражение представляет тригонометрическое выражение, которое нужно упростить.

Примеры:

simple_trig(`cos(x+pi)`) возвращает `-cos(x)`

Вычислите онлайн с помощью Simplize_trig (тригонометрический калькулятор)

См. также

Список связанных калькуляторов:

Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.

Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
Тангенс: тангенс. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

Список связанных упражнений:

Тригонометрические вычисления. Целью этого математического упражнения является вычисление выражений, содержащих синусы, косинусы и замечательные углы.

Напоминания о курсах, калькуляторы, упражнения и игры: Тригонометрические функции, Алгебраические вычисления

Объяснение урока: Вычисление тригонометрических функций с помощью калькулятора

В этом объяснении мы узнаем, как находить значения тригонометрических функций с помощью калькулятора.

Тригонометрия — одна из наиболее часто используемых областей математики, используемая в навигации, вычислительной технике, механике и во многих других областях. По этой причине большинство калькуляторов имеют стандартную возможность вычисления тригонометрических выражений.

В качестве примера воспользуемся калькулятором для расчета грех35∘. Первое, что нам нужно сделать, это убедиться, что наш калькулятор установлен в режим «градусы»; это часто делается войдя в меню «настройка» или «режим», а затем выбрав опцию для градусов (иногда сокращенно до град ). Некоторые калькуляторы будут иметь символ D вверху, указывающий, что они измеряют заданные углы в градусов. Затем мы можем оценить sin35∘, нажав кнопку кнопку «sin» на калькуляторе, а затем 35. Это дает нам следующее:

Важно отметить, что большинство калькуляторов округляют ответ до определенного числа знаков после запятой, но калькулятор выходное значение вряд ли будет точным; у нас может быть sin35=0,57357….∘

Как и в случае с письменной математикой, важно закрывать круглые скобки в конце тригонометрического выражения. Затем, выражение в скобках будет аргументом тригонометрической функции.

Мы можем округлить это значение до трех знаков после запятой, заметив, что четвертая десятичная цифра — 5, поэтому мы округляем, чтобы найти sin35≈0,574,∘

Аналогичным образом можно вычислить другие тригонометрические функции. Для функции косинуса мы используем «cos» кнопку, а для функции касательной мы используем кнопку «tan». Мы могли бы оценить cos35∘ и tan35∘ таким же образом. Это дает нам следующее:

Таким образом, с точностью до трех знаков после запятой имеем costan35≈0,819,35≈0,700.∘∘

Мы можем использовать это для вычисления любого тригонометрического выражения, аргументы которого приведены в степени; однако мы часто работаем с углы измеряются в градусах, минут и секунды. Чтобы вычислить тригонометрическое выражение с измеренным углом в градусах, минут и секунд, мы сначала преобразуем угол в градусов. Для этого мы помним, что 1 градус равен 60 минут, что, в свою очередь, равно 3‎ ‎600 секунд: 1=60′=3600′′.∘

Следовательно, если нам дан угол 𝑑𝑚′𝑠′′∘, мы можем записать этот угол в градусах как 𝑑+𝑚60+𝑠3600.∘

Это дает нам следующую формулу результата для преобразования угла, заданного в минуты и секунд в одну, указанную в градусов.

Формула: преобразование угла из минут и секунд в градусы

Если 𝑑𝑚′𝑠′′∘ — это угол, градусов, минут и секунд, то мы можем преобразовать этот угол в градусов по формуле 𝑑𝑚′𝑠′′=𝑑+𝑚60+𝑠3600. ∘∘

Например, 354′13∘ можно записать как 35+460+133600.∘

Мы можем использовать это преобразование для вычисления тригонометрических функций с помощью калькулятора, аргумент которого указан в градусов, минут и секунды. Вычислять tan(354′13′′)∘, мы конвертируем угол в градусах, а затем введите полученное выражение в калькулятор: tantan(354′13′′)=35+460+133600∘∘

С точностью до трех знаков после запятой имеем тангенс(354′13′′)≈0,702,∘

Теперь давайте рассмотрим несколько примеров использования калькулятора для вычисления различных тригонометрических выражений.

Пример 1. Использование калькулятора для нахождения косинуса угла, измеренного в градусах

Используйте калькулятор для нахождения cos56,3∘ четыре десятичных знака.

Ответ

Чтобы вычислить это тригонометрическое выражение с помощью калькулятора, сначала отметим, что аргумент приведен в градусов. Убеждаемся, что наш калькулятор настроен в режим «градусы», а затем используйте кнопку «cos», чтобы оценить cos56,3∘; мы получили cos56.3=0.5548444274….∘

Чтобы округлить до четырех знаков после запятой, нам нужно посмотреть на пятую десятичную цифру. Мы видим, что это 4, что меньше 5, поэтому мы округляем вниз. Это дает нам cos56,3=0,55484…≈0,5548,∘

Отсюда с точностью до четвертого знака после запятой имеем cos56,3≈0,5548∘.

Пример 2. Использование калькулятора для нахождения синуса угла, измеренного в градусах, минутах и секундах

Вычислить sin5538′24′′∘ давая ответ до четырех знаков после запятой.

Ответ

Чтобы вычислить синус угла, воспользуемся калькулятором. Для этого мы сначала удостоверимся, что наш калькулятор настроен на Режим «градусы». Затем нам нужно преобразовать аргумент в степени. Напомним, что угол 𝑑𝑚′𝑠′′∘ (градусы, минут и секунды) можно преобразовать в градусов по формуле 𝑑𝑚′𝑠′′=𝑑+𝑚60+𝑠3600. ∘∘

Следовательно, имеем 5538′24′′=55+3860+243600,∘∘ что упрощает дать 5538′24′′=55,64.∘∘

Следовательно, имеем sinsin5538′24′′=55,64,∘∘ который мы можем ввести в калькулятор, чтобы получить sinsin5538′24′′=55,64=0,8255077185….∘∘

Чтобы округлить это число до четырех знаков после запятой, мы проверяем пятую десятичную цифру, которая равна 0, поэтому мы округляем в меньшую сторону, чтобы получить sin5538′24′′=0,82550…≈0,8255,∘

Следовательно, с точностью до четвертого знака после запятой имеем sin5538′24≈0,8255∘.

Пример 3. Использование калькулятора для нахождения тангенса угла, измеренного в градусах и минутах

Найти с точностью до 4 знаков после запятой значение загар3848′∘.

Ответ

Чтобы определить значение тригонометрической функции, где аргумент измеряется в градусов, минуты, и секунд, мы будем использовать калькулятор. Мы начинаем с убедитесь, что калькулятор установлен в режим «градусы», часто обозначается символом D на экране.

Аргумент, который нам дан в градусах, минуты, и секунд, поэтому мы преобразуем это в градусов. Для этого напомним следующую формулу преобразования: 𝑑𝑚′𝑠′′=𝑑+𝑚60+𝑠3600.∘∘

Это дает нам 3848′=3848′0′′=38+4860+03600=38,8.∘∘∘∘

Следовательно, tantan3848′=38.8.∘∘

Затем мы можем оценить это с помощью калькулятора, нажав кнопку «tan»: tantan3848′=38,8=0,8040206426….∘∘

Чтобы округлить до четырех знаков после запятой, мы проверяем пятую десятичную цифру, которая равна 2, поэтому мы округляем в меньшую сторону, чтобы получить tan3848′=0,80402…≈0,8040,∘

Отсюда с точностью до четвертого знака после запятой имеем tan3848′≈0,8040∘.

В нашем следующем примере мы определим, верно ли неравенство, включающее тригонометрические функции, проверив значения с помощью калькулятора.

Пример 4. Использование калькулятора для сравнения значений косинуса двух углов, измеренных в градусах

Определите, верно или нет следующее утверждение:

coscos2510∘∘.

Ответ

Чтобы определить, верно ли неравенство, нам нужно будет вычислить тригонометрические выражения с обеих сторон неравенства. Мы можем сделать это с помощью калькулятора. Убеждаемся, что калькулятор настроен на «градусы», а затем используйте «cos» кнопку для вычисления косинуса угла, измеренного в градусов. У нас есть coscos25=0,906307787…,10=0,984807753….∘∘

Мы видим, что косинус 10∘ больше косинуса 25∘. Следовательно, утверждение верно.

В следующих двух примерах мы будем вычислять тригонометрические выражения с помощью калькулятора.

Пример 5. Использование калькулятора для нахождения синуса угла, измеренного в градусах

Использование калькулятора для нахождения sin6.4∘ до четырех знаков после запятой.

Ответ

Чтобы вычислить это тригонометрическое выражение с помощью калькулятора, сначала заметим, что угол дан в градусов. Мы убеждаемся, что наш калькулятор настроен на режим «градусы», а затем использовать «грех» кнопку для оценки выражения. Мы получили sin6.4=0,1114689322….∘

Чтобы округлить до четырех знаков после запятой, нам нужно посмотреть на пятую десятичную цифру. Мы видим, что это 6, что больше 5, поэтому мы округляем, получая sin6,4=0,11146…≈0,1115,∘

Следовательно, с точностью до четвертого знака после запятой имеем sin6,4≈0,1115∘.

Пример 6. Использование калькулятора для нахождения косинуса угла, измеренного в градусах, минутах и секундах

Вычислить cos8036′36′′∘ ответ до четырех знаков после запятой.

Ответ

Нас просят вычислить косинус угла; мы можем сделать это с помощью калькулятора. Сначала мы убеждаемся, что наш калькулятор установлен в режим градусов. Затем нам нужно преобразовать аргумент в градусов. Напомним, что угол 𝑑𝑚′𝑠′′∘ (градусы, минут и секунды) можно преобразовать в градусов по формуле 𝑑𝑚′𝑠′′=𝑑+𝑚60+𝑠3600.∘∘

Следовательно, имеем 8036′36′′=80+3660+363600=80,61.∘∘∘

Следовательно, имеем coscos8036′36′′=80,61,∘∘ который мы можем ввести в калькулятор, чтобы получить coscos8036′36′′=80,61=0,1631537704….∘∘

Чтобы округлить это число до четырех знаков после запятой, мы проверяем пятую десятичную цифру, которая равна 5, поэтому мы округляем, чтобы увидеть cos8036′36′′=0,16315…≈0,1632,∘

Отсюда с точностью до четвертого знака после запятой имеем cos8036′36≈0,1632∘.

В наших последних двух примерах мы будем вычислять тригонометрические выражения, включающие несколько тригонометрических выражений, используя Калькулятор.

Пример 7. Использование калькулятора для вычисления выражения, содержащего значения тригонометрических функций

Вычислить sincossin(31)+(25)(33)∘∘∘, что дает ваш ответ с точностью до двух знаков после запятой.

Ответ

Мы можем вычислить каждую тригонометрическую функцию в выражении отдельно с помощью калькулятора; однако это может привести к ошибкам округления. Поэтому, если возможно, лучше делать все расчеты одновременно или использовать кнопку памяти на калькуляторе, чтобы запомнить точное значение. Мы устанавливаем наш калькулятор на режиме «градусы» и оценить всю выражение сразу, соблюдая порядок операций:

Получаем sincossin(31)+(25)(33)=2.60970252….∘∘∘

Чтобы округлить до двух знаков после запятой, мы проверяем третью десятичную цифру, которая равна 9, поэтому мы округляем, чтобы увидеть sincossin(31)+(25)(33)=2,609…≈2,61.∘∘∘

Следовательно, с точностью до двух знаков после запятой выражение равно 2,61.

Пример 8. Использование калькулятора для вычисления выражения, содержащего тригонометрические функции углов, измеренных в градусах и минутах

Вычислить sincos(1835′)+(1835′)∘∘, что дает ваш ответ с точностью до двух знаков после запятой.

Ответ

Мы можем вычислить синус и косинус углов, заданных в градусах, минут и секунд с помощью калькулятора. Мы могли бы оценить каждый термин отдельно, а затем добавить результаты, но это может привести к ошибке округления, поэтому нам потребуется использовать функцию памяти на калькуляторе, чтобы использовать точные значения. Другой вариант — провести все расчеты сразу на калькуляторе. Для этого нам нужно преобразовать аргументы в градусов.

Напомним, что угол 𝑑𝑚′𝑠′′∘ (градусы, минуты, и секунды) можно преобразовать в градусов по формуле 𝑑𝑚′𝑠′′=𝑑+𝑚60+𝑠3600.∘∘

Следовательно, 1835′=1835′0′′=18+3560+03600=22312.∘∘∘∘

Затем мы можем вычислить выражение в нашем калькуляторе, не забывая заключать аргумент в круглые скобки. Мы получили последующий: sincossincos(1835′)+(1835′)=22312+22312=1,266544753….

Вычисление тригонометрических выражений: Вычисление значений тригонометрических выражений

Вычисление значений тригонометрических выражений