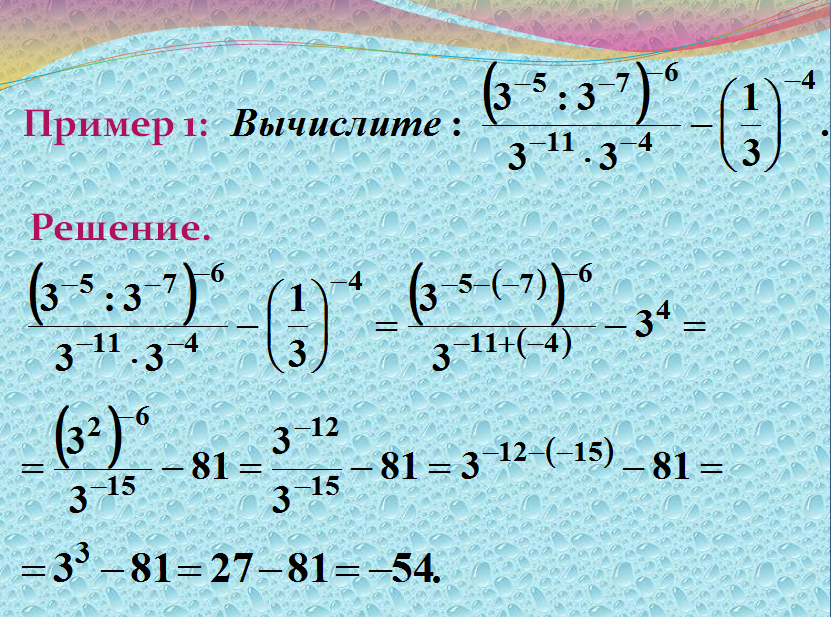Вычисления и преобразования: Задание 6 ЕГЭ по математике. Вычисления и преобразования

Задача 9 Вычисления и преобразования ЕГЭ 2021 Практика.

Задача 9 Вычисления и преобразования ЕГЭ 2021 Практика. | Университет СИНЕРГИЯ

В задание 9 ЕГЭ математика профильный уровень нужно найти значения алгебраических выражений. Раздел содержит 15 заданий. Во всех нужно найти численные значения выражений. При решении задач нужно применять формулы приведения, разности квадратов, использовать свойства показательной и степенной функций и т. п. Задания 1, 2, 12 — 15 содержат тригонометрические выражения, задания 9 — 11 — логарифмы. К заданиям приведены ответы и краткие указания по решению.

Этот документ можно скачать по ссылке

Курс подготовки к ЕГЭ и ОГЭ. Идёт набор!

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c  политикой конфиденциальности.

Какую профессию можно получить, сдав обществознание и английский

25.10.2022

Из чего складывается проходной балл

30. 06.2022

Что значит первичный балл в ЕГЭ

14.06.2022

Самые высокооплачиваемые профессии, связанные с биологией

14.06.2022

Распределение баллов ЕГЭ по русскому языку

14.04.2022

Куда можно поступить после 9 класса с обществознанием и информатикой

28.03.2022

Смотреть все

Всё нужное в твоём телефоне

Скачай приложение и узнавай самую актуальную информацию

ПОДБЕРИ КУРС ЕГЭ И ОГЭ

Ответь на пять вопросов и узнай, где будешь учиться!

Подобрать программу

Образование для карьеры

К каким профессиям вы более склонны?

ТехническимГуманитарнымТворческимМедицинским

Какой у вас уровень образования?

Без образованияШкола 9-11 классКолледжБакалавриатМагистратураАспирантура

Какой формат обучения вам подходит?

ОчноЗаочноОнлайнПо выходным дням

Вас интересуют бюджетные места?

ДаНет

И последний вопрос. Вы из Москвы?

ДаНет

Мы подобрали вам программу обучения

Заполните форму, чтобы узнать больше о программе и наших предложениях

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от  Университета «Синергия» и соглашаюсь c политикой конфиденциальности

Уважаемый посетитель!

Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в  30-дневный срок ответим на указанный вами адрес электронной почты

Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое

Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Симферополь Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород

Тип обращения Вопрос Предложение Благодарность Жалоба

Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое

* Все поля обязательны для заполнения

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c  политикой конфиденциальности

Вычисления и преобразования.

Логарифмические выражения | ЕГЭ по математике (профиль)

Все для самостоятельной подготовки к ЕГЭ

Зарегистрироваться

Русский язык Математика (профильная) Математика (базовая) Обществознание Физика История Биология Химия Английский язык Литература Информатика География

Задания Варианты Теория

Простейшие уравнения Вычисления и преобразования. Логарифмические выражения Логарифмические уравнения Начала теории вероятностей Вычисления и преобразования выражений Тригонометрия. Основные тождества и формулы приведения Тригонометрия.

Преобразование выражений Тригонометрия. Простейшие уравнения Планиметрия. Четырехугольники Планиметрия. Задачи на окружности Планиметрия. Вписанная и описанная окружность Производная. Дифференцирование, физический смысл производной Производная. Геометрический смысл Производная. Производная сложной функции Производная. Исследование функции Задачи с прикладным содержанием Текстовые задачи. Задачи на движение Текстовые задачи. Проценты, совместная работа Текстовые задачи. Смеси и сплавы, прогрессии Стереометрия. Параллелепипед. Пирамида. Призма Стереометрия. Цилиндр. Конус. Шар Стереометрия. Комбинация тел Тригонометрические уравнения Уравнения Стереометрия Стереометрия. 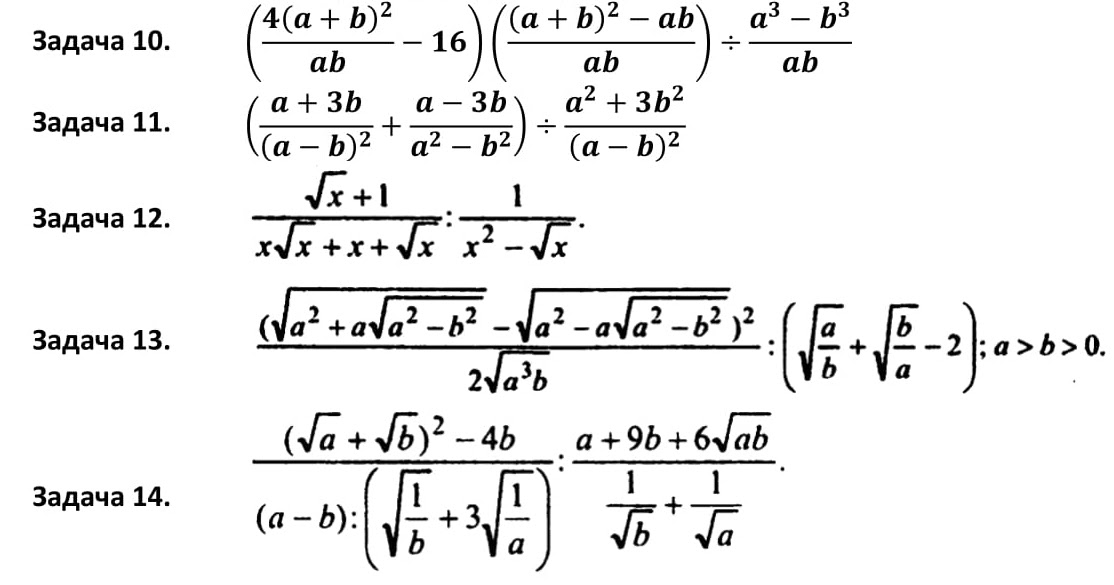{{1}/{4}}={1}/{4}=0.25$

Ответ: $0.25$

Практика: решай 6 задание и тренировочные варианты ЕГЭ по математике (профиль)

Составим твой персональный план подготовки к ЕГЭ

Преобразование данных: определение и методы

Преобразование данных — это когда определенная комбинация математических операций (таких как сложение или умножение) применяется к каждой отдельной точке данных в наборе. Это особенно полезно для облегчения нашей жизни при работе со сложными числами. При преобразовании данных важно знать, как преобразование влияет на статистические параметры, такие как показатели центральной тенденции (т. е. среднего) и дисперсии (т. е. стандартного отклонения).

Почему мы преобразовываем данные в статистику?

Предположим, мы хотим найти среднее значение четырех чисел: 305, 306, 305 и 310. Мы могли бы использовать калькулятор, чтобы вычислить это.

305+304+305+3104=12244=306

Но есть способ намного проще. Это можно сделать даже без калькулятора. Вместо этого мы могли бы вычесть 300 из каждого из четырех значений. Теперь значения данных равны 5, 4, 5 и 10, а их среднее значение равно 6. Конечно, 6 не является средним значением исходных точек данных, но если мы добавим обратно 300, которые мы вычли, мы получим 306. Это среднее значение, которое мы вычислили с помощью калькулятора, но вместо этого мы использовали преобразование данных .

Методы и приемы преобразования статистических данных

Существует несколько методов и приемов преобразования статистических данных, чтобы ими было легче манипулировать и интерпретировать. Здесь мы рассмотрим преобразование данных путем сложения и преобразование данных путем умножения.

Преобразование данных путем сложения

Безусловно, самый простой метод отслеживания того, что происходит с точками данных, — назначить новую переменную к формуле преобразования. В общем случае для преобразования данных сложением эта формула будет иметь вид y=x-a.

Давайте посмотрим на это в контексте нашего предыдущего примера. Мы можем присвоить исходные точки данных переменной x, что даст нам преобразованную переменную y. Теперь мы можем узнать среднее значение y, которое известно как y¯(‘y-bar’). В предыдущем примере, где мы вычли 300, a будет равно 300.

Стоит отметить, что в экзаменационных вопросах почти всегда указывается формула преобразования, которую необходимо применить. В случае, если они не указывают, попытайтесь подумать о том, как вы можете уменьшить размер данных и упростить их обработку.

Шаг 1. Чтобы найти новые точки данных значения y, используйте формулу:

y=x-300.

Точки данных x со значениями следующие: x1=305,x2=304,x3=306,x4=310.

Таким образом, y -значение данных точек: -300=310-300=10

Шаг 2. Найдите среднее значение: y=y1+y2+y3+y44=5+4+5+104=6

Шаг 3. Чтобы преобразовать y обратно в x, используйте формулу y=x-300, чтобы найти среднее значение точек исходных данных:

y=x-300=6,

, следовательно, x=300+ 6=306.

Итак, среднее значение найдено. Но как насчет стандартного отклонения, σx? Во-первых, давайте вычислим стандартное отклонение y, yx.

Шаг 1. Используйте формулу стандартного отклонения:

σy=∑(yi-y)2N.

(Напомним, N – это количество точек данных, yi – каждая точка данных, а y – среднее значение y.

Шаг 2. Используйте значения y, которые мы нашли ранее, 5, 4, 5, 10, и просуммируйте квадраты отклонений от среднего, 6.

∑(yi-y)2=(5 -6)2+(4-6)2+(5-6)2+(10-6)2=1+4+1+16=22

Шаг 3. Найти стандартное отклонение:

σy =224=2,3452 до 5 ст.ф.

А как насчет σx (стандартное отклонение точек данных x значений)?

Шаг 1. Используйте формулу стандартного отклонения:

σx=∑(xi-x)2N.

Шаг 2. Используйте исходные значения для x, 305, 304, 305, 310 и просуммируйте квадраты отклонений от среднего, 306.

∑(xi-x)2=(305-306) 2+(304-306)2+(305-306)2+(310-306)2=1+4+1+16=22

Шаг 3. Найдите стандартное отклонение:

σx=224= от 2,3452 до 5 ст.ф.

Обратите внимание, что стандартные отклонения значений x и y равны . W Почему при добавлении числа к каждой точке данных стандартное отклонение одинаково, а среднее значение отличается? Почему преобразования по-разному влияют на статистические параметры?

Интуитивно, поскольку стандартное отклонение является мерой разброса, его значение должно сохраняться, даже если все точки данных выше. Мы можем видеть в примере, что, поскольку сумма квадратов отклонений от среднего не меняется, не изменится и стандартное отклонение при использовании формулы преобразования y=x-a.

Важно помнить, что преобразование данных путем сложения или вычитания не меняет стандартное отклонение. Математически говоря, a не влияет на стандартное отклонение исходного и преобразованного наборов данных.

Преобразование данных путем умножения

Допустим, у нас есть другой набор точек данных: 152, 160, 128, 136. Потенциально мы могли бы вычесть число из них, но другим возможным подходом было бы деление каждой точки на число, b , тем самым используя формулу преобразования y=xb.

В отличие от преобразования сложением, стандартное отклонение необходимо декодировать так же, как и среднее значение.

Мы можем одновременно использовать умножение и сложение, и в этом случае формула будет иметь вид y=x-ab

Попробуем найти среднее значение и стандартное отклонение, используя эту формулу.

Шаг 1: Чтобы найти новые значения y, используйте формулу y=x8.

Шаг 2: Найдите преобразованное среднее значение, y=1528+1608+1288+13684=19+20+16+174=18

Шаг 3: Найдите среднее значение точек исходных данных, x=y ×8=18×8=144.

Шаг 4: Найдите преобразованное стандартное отклонение,

σy=∑(yi-18)24=12+22+22+124=104=1,5811 до 5 ст.

Шаг 5: Наконец, найдите стандартное отклонение точек исходных данных: σx=8×1,5811…=12,649 до 5 s.f.

Обратите внимание, что параметр b повлиял на стандартное отклонение .

Преобразование данных — основные выводы

• Преобразование данных — это математические операции, применяемые к каждой точке данных в наборе.
• Формула соединяет исходные точки данных с преобразованными точками данных.
  • Для преобразования сложением: y=x-a
  • Для преобразования путем умножения: y=xb
  • Для одновременного сложения и умножения: y=x-ab
• Значение a не влияет на стандарт отклонение, но влияет на среднее значение.
• Значение b влияет как на стандартное отклонение, так и на среднее значение.

Формулы для функций преобразования — ArcGIS Pro

Доступно с лицензией Spatial Analyst.

В этом разделе объясняются формулы, используемые для функций преобразования в инструменте «Перемасштабировать по функции». Формулы функции преобразования представлены в виде выражений алгебры карт Spatial Analyst.

Определена общая формула для каждой функции преобразования. По умолчанию общая формула изменена, чтобы соответствовать минимуму (нижний порог) и максимуму (верхний порог) входного набора данных. Как определяются параметры по умолчанию, также представлено ниже.

Используя общую формулу, можно определить любое количество функциональных кривых и захватить любую часть функциональной кривой. В версии формулы по умолчанию есть только одна кривая для функции, которая соответствует минимуму и максимуму входного набора данных. В результате, помимо применения линейного масштабирования преобразованных значений, данные, представленные в разных единицах измерения, например, в градусах Цельсия или Фаренгейта, будут давать одинаковые выходные значения оценки.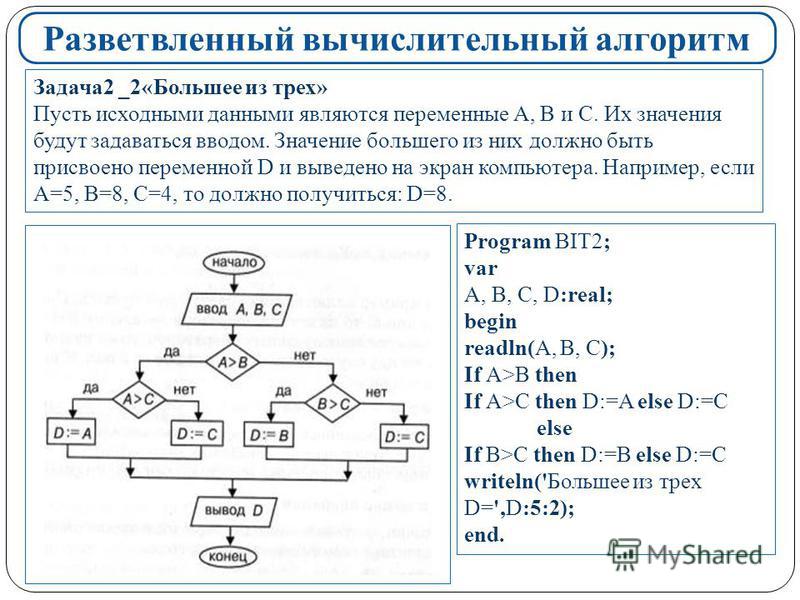

Применение функции преобразования

Концептуально шаги для применения функции преобразования следующие:

1. Укажите входной набор данных и параметры функции.
2. Применение формулы преобразования.
3. Линейно масштабируйте преобразованные значения по шкале оценки.

Уравнение линейного преобразования, используемое для масштабирования преобразованных значений до шкалы оценки на шаге 3, выглядит следующим образом.

 ScaledY = fromScale + (Y - min(Y)) * r 

где:

• Y = F(In) — преобразованное значение по формуле F, которое отображается в следующих общих формах:
• In — входное значение
• r — результат (toScale — fromScale) / (max(Y) — min(Y))
• min(Y) — минимальное значение Y
• max(Y) — максимальное значение Y
• fromScale — минимум оценочной шкалы (например, 1 )
• toScale — максимальное значение оценочной шкалы (например, 10)

Экспоненциальное

Ниже приведены формулы и значения по умолчанию для функции экспоненциального преобразования.

Общая форма

Общая форма формулы выглядит следующим образом.

 Exp((In – inShift) * baseFactor) 

где:

• In — входное значение
• inShift — значение, вычитаемое из входных значений
• baseFactor — множитель для сдвинутых входных значений, который определяет, насколько круто возрастает экспоненциальная функция

Значения по умолчанию

Значения inShift и baseFactor по умолчанию рассчитываются следующим образом.

 inShift = Con(toScale > fromScale, A, B) 

 baseFactor = Con(toScale > fromScale, C, D) 

где:

• A = (minIn * Ln(toScale) — maxIn * Ln(fromScale)) / (Ln(toScale) — Ln(fromScale))
• B = (minIn * Ln(fromScale) — maxIn * Ln(toScale) ) / (Ln(из масштаба) — Ln(в масштабе))
• C = (Ln(в масштабе) — Ln(из масштаба)) / (maxIn — minIn)
• D = (Ln(fromScale) — Ln(toScale)) / (maxIn — minIn)
• Ln — логарифм значения с основанием e
• minIn — минимум входных данных
• maxIn — максимум input

Gaussian

Ниже приведены формулы и значения по умолчанию для функции преобразования Gaussian.

Общая форма

Общая форма формулы выглядит следующим образом.

 Exp(-Spread * Square(In - MidPoint)) 

где:

• Spread — параметр распространения, который управляет крутизной спада от средней точки.
• In — входное значение.
• MidPoint — параметр средней точки, определяющий центр кривой Гаусса. значения Spread и MidPoint по умолчанию рассчитываются следующим образом.

   Распространение = Ln(10) * 4 / Pow(MidPoint - minIn, 2) 

   MidPoint = (maxIn + minIn) / 2 

  где:

  • Ln(10) — логарифм 10 по основанию e
  • Pow(MidPoint — minIn, 2) — значение MidPoint — minIn в степени 2
  • minIn — минимум входных данных
  • maxIn — максимум input

  Large

  Ниже приведены формулы и значения по умолчанию для функции преобразования Large.

  Общая форма

  Общая форма формулы выглядит следующим образом.

   1,0 / (1,0 + Pow(In/MidPoint, - Spread)) 

  где:

  • In — входное значение
  • MidPoint — параметр средней точки, определяющий точку перехода функции
  • Spread — параметр спреда, определяющий скорость увеличения и уменьшения предпочтения значения Spread и MidPoint рассчитываются, как показано ниже.

     Распространение = 5 

     Средняя точка = (maxIn + minIn) / 2 

    , где:

    • minIn — минимум ввода
    • maxIn — максимальное значение на входе.

    Linear

    Ниже приведены формулы и значения по умолчанию для функции линейного преобразования.

    Общий вид

    Ниже приведены общие формы формулы в зависимости от типа наклона:

    Положительный наклон (Мин.

    < Макс.):
    — Min) / Diff))

    Отрицательный наклон (Min > Max):

     Con(In > Min, 0, Con(In < Max, 1, (In - Min) / Diff)) 

    где:

    • In — входное значение
    • Min — указанный минимум, который устанавливает первую точку, через которую должна пройти линейная функция
    • Max — указанный максимум, который устанавливает вторую точку, через которую должна пройти линейная функция
    • Diff equals Макс. - Мин.

    Значения по умолчанию

    Значения по умолчанию Мин. и Макс. рассчитываются, как показано ниже.

     Мин. = minIn 

     Макс. = maxIn 

    где:

    • minIn — минимум ввода
    • maxIn — максимум ввода

    Логарифм

    Ниже приведены формулы и значения по умолчанию для функции преобразования логарифма.

    Общая форма

    Общая форма формулы выглядит следующим образом.

     Ln((In – inShift) * baseFactor) 

    где:

    • In — входное значение
    • InShift — значение, вычитаемое из входных значений
    • baseFactor — это множитель сдвинутых входных значений, который управляет возрастанием функции логарифма.

       inShift = Con(toScale > fromScale, A, B) 

       baseFactor = Con(toScale > fromScale, C, D) 

      где:

      • A = (minIn * Exp(toScale) - maxIn * Exp(fromScale)) / (Exp(toScale) - Exp(fromScale))
      • B = (minIn * Exp(fromScale) - maxIn * Exp(toScale) ) / (Exp(из масштаба) - Exp(в масштабе))
      • C = (Exp(toScale) - Exp(fromScale)) / (maxIn - minIn)
      • D = (Exp(fromScale) - Exp(toScale)) / (maxIn - minIn)
      • Exp - экспонента значение с основанием e
      • minIn — минимум ввода
      • maxIn — максимум ввода

      LogisticDecay

      Ниже приведены формулы для функции преобразования Logistic Decay.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       C / (1 + A * Exp((In – Min) * B)) 

      Определения параметров в формуле такие же, как в LogisticGrowth.

      В уравнении LogisticGrowth экспоненциальные расчеты определяются по отрицательному значению для экспоненциального расчета: Exp( - (In - Min) * B).

      LogisticGrowth

      Ниже приведены формулы и значения по умолчанию для функции преобразования Logistic Growth.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       C / (1 + A * Exp( - (In – Min) * B)) 

      где:

      • Min — указанный минимум, который контролирует начальную точку логистического роста
      • C — мощность или верхняя горизонтальная асимптота
      • A определяет точку пересечения, когда In = Min
      • B определяет основание экспоненциальной функции Exp

      Значения по умолчанию

      Значения по умолчанию C, A и B определяются следующим образом.

       C = 100 

       A = C / yInterceptPercent - 1 

       B = Ln(A) / (0,5 * (Макс. + Мин.) - Мин.) 

      , где:

      • yInterceptPercent — это процент перехвата y, разделенный на C, который по умолчанию равен 1 для LogisticGrowth и 99 для LogisticDecay
      • Min — указанный минимум, который по умолчанию установлен на минимальное значение ввода
      • Max — указанный максимум, который по умолчанию установлен на максимальное значение входа
      • Ln(A) — логарифм А с основанием e
      • 0,5 * (Макс. + Мин.) — координата x точки перегиба y = C/2, делая точку перегиба в середине Min и Max

      MSLarge

      Ниже приведены формулы и значения по умолчанию для функции преобразования MSLarge.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       Con(In > nMeans, 1 - (nStdv / (In - nMeans + nStdv)), 0) 

      , где:

      • In — входное значение
      • nMeans равно meanMultiplier * mean
      • nStdv равно STDMultiplier * std, где std относится к стандартному отклонению среди всего населения

      Значения по умолчанию

      По умолчанию для параметров meanMultiplier и STDMultiplier установлено значение 1.

      MSSmall

      Ниже приведены формулы и значения по умолчанию для функции преобразования MSSmall.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       Con(In > nMeans, nStdv / (In - nMeans + nStdv), 1) 

      где:

      • In — входное значение
      • nMeans равно meanMultiplier * mean
      • nStdv равно STDMultiplier * std, где std относится к стандартному отклонению среди всего населения.

      Значения по умолчанию

      По умолчанию оба параметра meanMultiplier и STDMultiplier установлены на 1.

      Near

      Ниже приведены формулы и значения по умолчанию для функции преобразования Near.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       1,0 / (1,0 + Разброс * Pow(In - MidPoint, 2)) 

      где:

      • In — входное значение
      • Spread — параметр распространения, который управляет крутизной спада от средней точки
      • MidPoint — параметр средней точки, определяющий центр кривой

      Значения по умолчанию

      значения Spread и MidPoint рассчитываются следующим образом.

       Распространение = 36 / Pow(MidPoint - minIn, 2) 

       MidPoint = (maxIn + minIn) / 2 

      , где:

      • Pow(MidPoint - minIn, 2) — значение MidPoint — minIn в степени 2
      • minIn — минимум ввода
      • maxIn — максимум ввода

      Power

      Ниже приведены формулы и значения по умолчанию значения для функции преобразования мощности.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       Pow(In – inShift, Exponent) 

      где:

      • In — входное значение
      • inShift — значение, вычитаемое из входных значений
      • Экспонента — это экспонента для повышения функции до

      Значения по умолчанию

      Значения inShift и Exponent по умолчанию рассчитываются следующим образом.

       inShift = Con(toScale > fromScale, A, B) 

      где:

      • A = Con(fromScale == 1, minIn - 1, minIn)
      • B = Con(toScale == 1, minIn - 1 , minIn)
      • minIn — минимум ввода
      • maxIn — максимум ввода

       Exponent = Con(toScale > fromScale, C, D) 

      где:

      • C = Con(fromScale == 0, C1, Con(fromScale == 1, C2, 2))
      • C1 = Con(toScale <= 1, 1, Ln(toScale) / (maxIn - inShift))
      • C2 = Ln(toScale) / Ln(maxIn - inShift)
      • D = Con(toScale == 0, D1, Con(toScale == 1, D2, 2))
      • D1 = Con(fromScale <= 1 , 1, Ln(fromScale) / (maxIn - inShift))
      • D2 = Ln(fromScale) / Ln(maxIn - inShift)
      • Ln - логарифм значения с основанием e
      • minIn - минимум ввода
      • maxIn — максимальное значение ввода

      Small

      Ниже приведены формулы и значения по умолчанию для функции преобразования Small.

      Общая форма

      Общая форма формулы выглядит следующим образом.

       1,0 / (1,0 + Pow(In/MidPoint, Spread)) 

      где:

      • In — входное значение
      • MidPoint — параметр средней точки, определяющий точку перехода функции
      • Spread — параметр спреда, определяющий, как быстро уменьшается и увеличивается предпочтение0168

      Значения по умолчанию

      Значения Spread и MidPoint по умолчанию рассчитываются следующим образом.

       Распространение = 5 

       Средняя точка = (maxIn + minIn) / 2 

      , где:

      • minIn — минимум ввода
      • maxIn — максимум ввода

      SymmetricLinear

      Ниже приведены формулы и значения по умолчанию для функции симметричного линейного преобразования.

      Общая форма

      Общие формы формулы для различных типов уклонов следующие.

      Для положительных наклонов (мин. < макс.):

       Con(In < Min , 0, Con(In < MidP, (In - Min) / HDiff, Con(In > Max, 0, (Max - In) / HDiff) ))) 

      Для отрицательных наклонов (Min > Max):

       Con(In < Max, 1, Con(In < MidP, (In - MidP) / HDiff, Con(In > Min, 1, (MidP - In ) / HDiff))) 

      где:

      • In — входное значение
      • Min — указанный минимум, который устанавливает одну точку, через которую функция SymmetricLinear должна пройти
      • Max — указанный максимум, который устанавливает другую точку, через которую должна пройти функция SymmetricLinear
      • Diff равно Max-Min
      • HDiff равно 0,5 * Diff
      • MidP равно Min + HDiff

      Значения по умолчанию

      Значения по умолчанию Мин. и Макс. рассчитываются следующим образом.

       Мин. = minIn 

       Макс.
      No related posts.