Вычислить десятичный логарифм калькулятор онлайн: Калькулятор десятичный логарифм

Содержание

Как вычислить десятичный логарифм числа. Десятичный логарифм: как вычислить

Нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными . При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg , а не log ; при этом число десять, определяющие основание, не указывают. Так, заменяем log 10 105 на упрощенное lg105 ; а log 10 2 на lg2 .

Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.

Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.

Целая часть десятичного логарифма числа а именуется характеристикой , а дробная — мантиссой этого логарифма.

Характеристика десятичного логарифма числа а указывается как , а мантисса как {lg а }.

Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно = 0, {lg 2} ≈ 0,3010.

Подобно и для lg 543,1 ≈2,7349. Соответственно, = 2, {lg 543,1}≈ 0,7349.

Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.

Характерные признаки десятичных логарифмов.

Первый признак десятичного логарифма. целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.

Возьмем, lg 100 = 2, lg 1 00000 = 5.

Обобщенно, если

То а = 10 n , из чего получаем

lg a = lg 10 n = n lg 10 = п

Второй признак. Десятичный логарифм положительной десятичной дроби , показанный единицей с предыдущими нулями, равен — п , где п — численность нулей в представлении этого числа, учитывая и нуль целых.

Рассмотрим, lg 0,001 = — 3, lg 0,000001 =-6.

Обобщенно, если

То a = 10 -n и получается

lga= lg 10 n =-n lg 10 =-п

Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.

Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.

И правда, 10

lg 10

1 .

Отсюда следует,

lg 75,631 = 1 +б,

Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем

п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.

Так, {lg 0,0053} = {lg 0,53} = {lg 0,0000053}.

Степень отдельно взятого числа называется математическим термином, придуманным несколько столетий назад. В геометрии и алгебре встречается два варианта — десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.

Особенности и важные признаки

На данный момент различают десять известных математических качеств. Самыми распространенными и востребованными из них являются:

Подкоренной log, разделенный на величину корня, всегда такой же, как и десятичный логарифм √.

Произведение log всегда равно сумме производителя.
Lg = величине степени, перемноженной на число, которое в нее возводится.
Если от log делимого отнять делитель, получится lg частного.

Кроме того, есть уравнение, основанное на главном тождестве (считается ключевым), переход к обновленному основанию и несколько второстепенных формул.

Вычисление десятичного логарифма — довольно специфическая задача, поэтому к интегрированию свойств в решение необходимо подходить осторожно и регулярно проверять свои действия и последовательность. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.

Разновидности математического термина

Главные отличия математического числа «спрятаны» в основании (a). Если оно имеет показатель 10, то это десятичный log. В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.

Логарифмы десятичного типа получили широкое применение при вычислении сложных формул. Составлены целые таблицы, облегчающие расчеты и наглядно показывающие процесс решения задачи. При этом перед непосредственным переходом к делу нужно возвести log в К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности.

Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.

Два вида формулы

Все типы и разновидности задач на вычисление ответа, имеющие в условии термин log, обладают отдельным названием и строгим математическим устройством. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.

Разница и терминология

Оба главных показателя обладают собственными особенностями, отличающими числа друг от друга:

Десятичный логарифм. Важная деталь числа — обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью — log x или lg x.
Натуральный. Если его основанием является знак «e», представляющий собой константу, идентичную строго рассчитанному уравнению, где n стремительно движется к бесконечности, то приблизительный размер числа в цифровом эквиваленте составляет 2.72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
Разные. Кроме основных логарифмов встречаются шестнадцатиричные и двоичные виды (основание 16 и 2 соответственно). Есть еще сложнейший вариант с базовым показателем 64, подпадающий под систематизированное управление адаптивного типа, с геометрической точностью производящее расчет итогового результата.

Терминология включает в себя следующие величины, входящие в алгебраическую задачу:

значение;
аргумент;
основание.

Вычисление log числа

Есть три способа быстро и в устной форме сделать все необходимые расчеты по нахождению интересующего результата с обязательным правильным итогом решения. Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени. Такой вариант подсчета создан на основе двух математических фактов:

произведение и сумма log всегда имеют одинаковый показатель;
логарифм, взятый из числа от одного до десяти, не может превышать величину в 1 пункт.

Если ошибка в вычислении все-таки происходит, то она никогда не бывает меньше одного в сторону вычитания.
Точность повышается, если учесть, что lg с основанием три имеет итоговый результат — пять десятых от единицы. Поэтому любое математическое значение больше 3 автоматически добавляет к ответу один пункт.

Практически идеальная точность достигается, если под рукой есть специализированная таблица, которую можно легко применять в своих оценочных действиях. С ее помощью можно выяснить, чему равен десятичный логарифм до десятых процентов от оригинального числа.

История вещественного log

Шестнадцатый век остро испытывал потребности в более сложных исчислениях, чем было известно науке того времени. Особенно это касалось деления и умножения многозначных цифр с большой последовательностью, в том числе дробей.

В конце второй половины эпохи сразу несколько умов пришли к выводу о сложении чисел с помощью таблицы, которая сопоставляла две и геометрическую. При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.

Первое упоминание об lg состоялось в 1614 году. Это сделал любитель-математик по фамилии Непер. Стоит отметить, что, несмотря на огромную популяризацию полученных результатов, в формуле была сделана ошибка из-за незнаний некоторых определений, появившихся позже. Она начиналась с шестого знака показателя. Наиболее близки к пониманию логарифма были братья Бернулли, а дебютное узаконивание произошло в восемнадцатом столетии Эйлером. Он же и распространил функцию в область образования.

История комплексного log

Дебютные попытки интегрировать lg в широкие массы делали на заре 18-го века Бернулли и Лейбниц. Но целостных теоретических выкладок они так и не сумели составить. По этому поводу велась целая дискуссия, но точного определения числу не присваивали. Позже диалог возобновился, но уже между Эйлером и Даламбером.

Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.

Таблицы

Свойства числа указывают на то, что многозначные цифры можно не перемножать, а найти их log и сложить посредством специализированных таблиц.

Особенно ценным этот показатель стал для астрономов, которые вынуждены работать с большим набором последовательностей. В советское время десятичный логарифм искали в сборнике Брадиса, выпущенного в 1921 году. Позже, в 1971 году, появилось издание Веги.

Логарифмирование — это операция, обратная возведению в степень. Если вы задаетесь вопросом, в какую степень нужно возвести 2, чтобы получить 10, то вам на помощь придет логарифм.

Обратная операция для возведения в степень

Возведение в степень — это повторяющееся умножение. Для возведения двойки в третью степень нам потребуется вычислить выражение 2 × 2 × 2. Обратная операция для умножения — это деление. Если верно выражение, что a × b = c, то обратное выражение b = a / c так же верно. Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.

Понятие логарифма

Давайте попробуем решить простое уравнение вида 2 x = 16. Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.

Теперь попробуем решить 2 x = 20. Сколько раз нужно умножить двойку на саму себя, что бы получить 20? Это сложно, ведь 2 4 = 16, а 2 5 = 32. Рассуждая логически, корень этого уравнения располагается между 4 и 5, причем ближе к 4, возможно 4,3? Математики не терпят приблизительных вычислений и хотят знать точный ответ. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.

Выражение log2 20 читается как логарифм 20 по основанию 2. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.

Таким элегантным способом вы можете решить любое простое показательное уравнение. Например, для уравнений:

4 x = 125, x = log4 125;
12 x = 432, x = log12 432;
5 x = 25, x = log5 25.

Последний ответ x = log5 25 математикам не понравится. Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5 2 = 25. Поэтому для уравнения вида 5 x = 25, x = 2.

Десятичный логарифм

Десятичный логарифм — это функция по основанию 10. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.

Натуральный логарифм

Натуральный логарифм — это функция по основанию e. В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.

В какую степень нужно возвести число e, чтобы получить 10? Ответом был бы loge 10, но математики обозначают натуральный логарифм как ln, поэтому ответ будет записан как ln10. Тоже самое с выражениями loge 35 и loge 40, верная форма записи которых – ln34 и ln40.

Антилогарифм

Антилогарифм — это число, которому соответствует значение выбранного логарифма. Простыми словами, в выражении loga b антилогарифмом считается число b a . Для десятичного логарифма lga, антилогарифм равен 10 a , а для натурального lna антилогарифм равняется e a . По сути, это тоже возведение в степень и обратная операция для логарифмирования.

Физический смысл логарифма

Нахождение степеней — чисто математическая задача, но для чего нужны логарифмы в реальной жизни? В начале развития идеи логарифмирования данный математический инструмент использовался для сокращения объемных вычислений. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.

Логарифмы нашли применение и в сфере изображения графических процессов. Если требуется нарисовать график функции, которая принимает значения 1, 10, 1 000 и 100 000, то маленькие значения будут невидны и визуально они сольются в точку около нуля. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.

Физический же смысл логарифмирования — это описание временных процессов и изменений. Так, логарифм по основанию 2 позволяет определить, сколько требуется удвоений начального значения для достижения определенного результата. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.

Наша программа представляет собой сборник из четырех онлайн-калькуляторов, которые позволяют вычислить логарифм по любому основанию, десятичную и натуральную логарифмическую функцию, а также десятичный антилогарифм. Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.

Примеры из реальной жизни

Школьная задача

Как было сказано выше, иррациональные значения по типу log2 345 не требуют дополнительных преобразований, и такой ответ полностью удовлетворит учителя математики. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:

log7 65 — иррациональное число;
log3 243 — целое число 5;
log5 95 — иррациональное;
log8 512 — целое число 3;
log2 2046 — иррациональное.

Таким образом, значения log3 243 и log8 512 вам потребуется переписать как 5 и 3 соответственно.

Потенцирование

Потенцирование — это нахождение антилогарифма числа. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:

для n = 1 antlog = 10;
для n = 1,5 antlog = 31,623;
для n = 2,71 antlog = 512,861.

Непрерывный рост

Натуральный логарифм позволяет описывать процессы непрерывного роста. Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.

Поиск количества удесятирений

Допустим, за 30 лет количество персональных компьютеров увеличилось с 250 000 до 1 миллиарда. Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.

Заключение

Несмотря на сложность логарифмов и нелюбовь детей к ним в школьные годы, этот математический инструмент находит широкое применение в науке и статистике. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.

Добро пожаловать в калькулятор логарифмов онлайн.

Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. Уж лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте основание с числом. Калькулятор логарифмов чем то, схож с калькулятором факториалов, который автоматически выдает несколько решений.
В данном калькуляторе, вам предстоит заполнить всего два поля. Поле для числа и поле для основания. Ну что ж, давайте попробуем обуздать калькулятор на практике. К примеру, вам нужно найти log 2 8 (логарифм 8-ми по основанию 2 или логарифм по основанию 2 числа 8, не пугайтесь разного произношения).

Итак, вводим 2 в поле «введите основание», а 8 вводим в поле «введите число». После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат.

Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Калькулятор десятичных логарифмов — это калькулятор, который ищет десятичный логарифм с основанием 10 онлайн.
Калькулятор натуральных логарифмов — этот калькулятор, который ищет логарифм по основанию e онлайн.
Калькулятор двоичных логарифмов – это калькулятор, который находит логарифм по основанию 2 онлайн.

Немного теории.

Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b.

Иногда используется обозначение log b .
Основание, то есть «а» всегда находится внизу. Так как оно всегда возводится в степень.
А теперь собственно, определение самого логарифма:
Логарифмом положительного числа b по основанию a (где a>0, a≠1)называется степень, в которую нужно возвести число а, чтобы получить число b. Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным. В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:

Возведение в степень	Логарифмирование

	log 10 1000 = 3;
	log 03 0,0081=4;

А операция обратная логарифмированию это – Потенцирование.
Помимо вещественного логарифма, основанием которого может быть какое угодно число(помимо отрицательных чисел, нуля и единицы), существует логарифмы с постоянным основанием. Например, десятичный логарифм.
Десятичный логарифм числа – это логарифм с основанием 10, который записывается как lg6, или lg14. Выглядит как орфографическая ошибка или даже как опечатка, в которой пропущена латинская буква «о».
Натуральный логарифм – это логарифм с основанием равный числу е, например ln7, ln9, е≈2,7. Существует еще двоичный логарифм, который не так важен в математике, как в теории информации и информатике. Основанием двоичного логарифма является 2. Например: log 2 10.
Десятичные и натуральные логарифмы обладают теми же свойствами, что и логарифмы чисел с любым положительным основанием.

Новые функции онлайн калькулятора

Добрый день.

Продолжаем улучшать наш конструктор веб-форм и калькуляторов, и добавлять все новые и новые функции. Сегодня хотим рассказать о новых математических функциях, которые теперь можно использовать в своих формулах для расчетов, а их накопилось немало.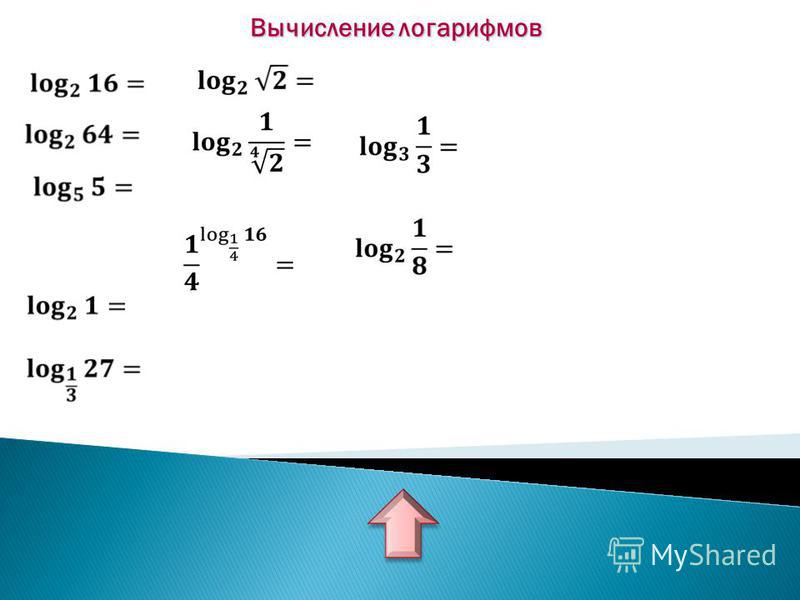

На данный момент в своих расчетах можно использовать вот такие функции:

round()	Возвращает число, округлённое к ближайшему целому
ceil()	Округляет число до ближайшего большего целого
floor()	Округляет число до ближайшего меньшего целого
roundUp()	Округляет число до ближайшего числа, кратного заданному
min()	Возвращает наименьшее из нескольких чисел
max()	Возвращает наибольшее из нескольких чисел
medium()	Возвращает среднее из нескольких чисел
today()	Возвращает количество секунд от текущей даты
datetime()	Возвращает количество секунд от текущей даты и времени
strlen()	Возвращает количество символов в строке
pow()	Возведение числа в степень
ln()	Натуральный логарифм
lg()	Десятичный логарифм
log()	Логарифм числа по произвольному основанию
sin()	Синус угла в радианах
cos()	Косинус угла в радианах
tan()	Тангенс угла в радианах
ctg()	Котангенс угла в радианах
mod()	Остаток от деления двух чисел
countYears()	Возвращает количество лет от разности двух дат
countMonths()	Возвращает количество месяцев от разности двух дат
countDays()	Возвращает количество дней от разности двух дат
year()	Извлекает год из даты
month()	Извлекает месяц из даты
day()	Извлекает день из даты
countRemainingDays()	Возвращает количество оставшихся дней от разности двух дат
countRemainingMonths()	Возвращает количество оставшихся месяцев от разности двух дат
date()	Возвращает количество секунд от даты из переданных параметров (год, месяц, день)
dateValue()	Возвращает суммарное число всех цифр даты

С некоторыми функциями вы уже знакомы из наших прошлых статей. Сегодня же мы хотели подробно остановиться вот на этих функциях: roundUp(), mod(), countYears(), countMonths(), countDays(), year(), month(), day(), countRemainingDays(), countRemainingMonths(), date(), dateValue().

Читайте также: Подробная инструкция по созданию калькулятора для сайта

Большинство из этих функций добавляют новые возможности при работе с датой. Но обо всем по порядку.

dateValue(date)

Данная функция возвращает суммарное число всех цифр даты. Обычно это используется в нумерологии, чтобы посчитать число даты рождения. Пример:

dateValue('1985-08-20') = 1 + 9 + 8 + 5 + 0 + 8 + 2 + 0 = 33 = 3 + 3 = 6

roundUp(a, b)

Данная функция округляет число a до ближайшего большего числа, кратного числу b. Пример:

roundUp(4, 3) = 6;
roundUp(5, 3) = 6;
roundUp(7, 3) = 9.

mod(a, b)

Данная функция возвращает остаток от деления числа a на число b. Пример:

mod(10, 3) = 1;
mod(10, 2) = 0;
mod(35, 4) = 3.

Если число b = 1, а число a дробное, то функция mod() возвращает дробную часть числа a:

mod(3.45, 1) = 0.45.

countYears(date1, date2)

Данная функция возвращает количество полных лет от разности двух дат: date1 и date2. Пример:

countYears('2022-01-25', '2020-01-25') = 2;
countYears('2022-01-25', '2020-01-26') = 1; //(не хватает одного дня для полных двух лет)
countYears('2022-01-25', '2019-06-26') = 2;

countMonths(date1, date2)

Данная функция возвращает количество полных месяцев от разности двух дат: date1 и date2. Пример:

countMonths('2022-01-25', '2021-11-25') = 2;
countMonths('2022-01-25', '2019-06-26') = 30.

countDays(date1, date2)

Данная функция возвращает количество дней от разности двух дат: date1 и date2. Пример:

countDays('2022-01-25', '2021-12-25') = 31;
countDays('2022-01-25', '2019-06-26') = 944.

year(date)

Данная функция извлекает год из даты. Пример:

year('2022-01-25') = 2022;
year('1985-11-03') = 1985.

month(date)

Данная функция извлекает месяц из даты. Пример:

month('2022-01-25') = 1;
month('1985-11-03') = 11;

day(date)

Данная функция извлекает день из даты. Пример:

day('2022-01-25') = 25;
day('1985-11-03') = 3;

countRemainingDays(date1, date2)

Данная функция возвращает количество оставшихся дней от разности двух дат, за вычетом полных лет и месяцев. Эту функцию очень удобно использовать при расчёте возраста пользователя по дате рождения. Пример:

countRemainingDays('2022-01-25','1985-08-20') = 5; 
countRemainingDays('2022-01-25','1985-08-25') = 0;
countRemainingDays('2022-01-25','1985-08-26') = 30;

countRemainingMonths(date1, date2)

Данная функция возвращает количество оставшихся месяцев от разности двух дат, за вычетом полных лет и дней. Эту функцию очень удобно использовать при расчёте возраста пользователя по дате рождения. Пример:

countRemainingMonths('2022-01-25','1985-08-20') = 5; 
countRemainingMonths('2022-01-25','1985-01-20') = 0;
countRemainingMonths('2022-01-25','1985-04-24') = 9;
countRemainingMonths('2022-01-25','1985-04-26') = 8;

date(year, month, day)

Данная функция формирует дату из переданных параметров (год, месяц, день), которую можно использовать в других функциях и расчетах (любая дата конвертируется в метку unix timestamp — количество секунд, прошедших с полуночи 1 января 1970 года).

Давайте рассмотрим несколько реальных примеров из жизни.

Сколько дней осталось до Нового года?

В качестве примера, рассчитаем, сколько дней осталось до Нового года. В этом нам помогут функции: countDays(date1, date2), today() и year().

Как вы помните, функция countDays(date1, date2) возвращает количество дней от разности двух дат. В нашем случае:

date1 — дата Нового года
date2 — текущая дата

В самом простом случае наша формула будет выглядеть вот так:

countDays(date(2022,12,31), today())

Но это не очень удобно, так как год 2022 у нас прописан вручную и его нужно будет менять на 2023 через 1 год, чтобы все корректно считалось. Но здесь нам на помощь приходит функция year() которая извлекает год из даты. Используя эту функцию мы можем переписать нашу формулу следующим образом:

countDays(date(year(today()),12,31), today())

Т.е. используя запись year(today()) — мы динамически получаем год из текущей даты. Точно также можно комбинировать и все остальные функции.

Сколько дней осталось до дня рождения?

Давайте рассмотрим еще один пример: пользователь в форме вводит свою дату рождения и нам нужно посчитать, сколько дней осталось до его ДР. В этом нам помогут все те же функции, которые мы рассматривали в прошлом примере, а именно countDays(date1, date2) возвращает количество дней от разности двух дат. В нашем случае:

date1 — здесь нам нужно сформировать дату, где день и месяц будет указан тот, который пользователь ввел в форму, а год необходимо использовать текущий. Например, если дата рождения 1985-08-20, то нам необходимо получить такую дату: 2022-08-20 и именно до этой даты нужно считать количество оставшихся дней.
date2 — текущая дата

Итак, наша формула может выглядеть вот так:

countDays(date(year(today()), month(поле1), day(поле1)), today())

Где поле №1 — это поле из формы, куда пользователь вводит свою дату рождения.

На сегодня это все. А каких функций не хватает вам, для ваших калькуляторов?

Калькулятор логарифмов — логарифм и антилогарифм (натуральный, основание e, 2, 10)

Да – это умный калькулятор логарифмов, который помогает вычислять логарифмы и обратное логарифмическое по любой системе счисления. Итак, начнем с термина «логарифм».

Что такое логарифм?

С точки зрения математики, логарифмическая (логарифмическая) операция называется операцией, обратной возведению в степень, что означает, что (логарифмическое число) — это показатель степени, до которого было возведено другое фиксированное число, известное как «основание», для получения числа . Однако вы можете выполнять любые вычисления логарифмов с помощью калькулятора логарифмов. В частности, логарифм числа x по основанию b — это показатель степени, в которую нужно возвести b, чтобы получить x. Другими словами, логарифм y по основанию b является решением y данного уравнения:

= x

И для любых x и b есть:

x =

Логарифмические правила:

Логарифмическое произведение:

(x*y =) (x*y)

Правило логарифмического частного:

(x/y) = (x) – (y)

Правило логарифмической степени:

) = y*(x)

основание логарифма: 6m00052 900
(c) = 1/(b)
Правило изменения основания логарифма:
(x) = (x)/ (b)
Несколько именованных логарифмов:
Логарифм десятичный. такие науки, как физика и химия. Люди, которые относятся к области науки или техники, часто используют калькулятор базы журналов для выполнения расчетов базы журналов
.
Натуральный логарифм — этот логарифм имеет основание числа e (число Эйлера, 2,71828), он часто используется в физике и математике из-за его более простой производной, студенты часто используют калькулятор натурального логарифма для вычисления натурального логарифма
Двоичный логарифм — этот логарифм имеет основание 2, вы можете вычислить log2 с помощью калькулятора log base 2, этот log2 широко используется в информатике, например, для представления единиц данных
При использовании приведенного выше логарифмического калькулятора вам просто нужно ввести «основание» 10 для десятичного логарифма, 2 для двоичного логарифма и оставить поле основания пустым для вычисления натурального логарифма.
Калькулятор логарифмов:
Логарифмическая форма или калькулятор логарифмов — важный инструмент, который помогает вычислить любой тип логарифма действительного числа по любому основанию. Проще говоря, этот качественный инструмент работает как решатель логов, чтобы понять, как решать логарифмы любого числа. Кроме того, вы можете вычислить обратный логарифм, используя этот калькулятор обратного логарифма для действительного числа по отношению к заданным или натуральным базовым значениям.
Как использовать:
Журналы дел Расчеты:
Прежде всего, вы должны выбрать опцию «Журнал» в раскрывающемся меню
Затем вы должны ввести номер в специальное поле
Сразу после этого вы должны ввести числовую систему в данное поле
Наконец, нажмите кнопку расчета этого калькулятора логарифмов, чтобы получить результаты
Вычисления антилогарифмических задач:
Здесь сначала вы должны выбрать опцию «Антилог» из выпадающего меню
Затем вы должны ввести число в данное поле
Далее вы должны ввести числовую базу в специальное поле
После этого нажмите кнопку вычисления антилогарифмического калькулятора, чтобы получить значение обратного логарифма
Примечание. Этот калькулятор расширяющихся логарифмов эффективно находит логарифм или антилогарифм любого числа по заданному основанию. 92 = 64.
Люди также спрашивают:
Что такое вход в калькулятор?
Функция «Журнал» на научном или графическом/научном калькуляторе — это клавиша, которая позволяет пользователю выполнять вычисление логарифмов. Логарифмы — это способы, помогающие определить, какие показатели степени нужно умножать на определенное число. Как правило, функция журнала на большинстве калькуляторов работает одинаково!
Как считать логарифмы?
Вы должны выразить члены в десятичных логарифмах, отношение представлено как log mn = log m + log n.
Например:
Выражение 100 × 1000:
Однако его можно вычислить, найдя логарифмы 100 (2) и 1000 (3), тогда вам следует сложить логарифмы вместе (5), сразу после этого нужно посмотреть его антилогарифм (100 000) в таблице.
Как найти значение журнала 2?
Предположим, что необходимо вычислить log2 числа «12», то есть log2 (12). Чтобы вычислить логарифм по основанию 2 числа (y), вы должны разделить логарифм y на логарифм 2.
Чему равно log10?
В математическом выражении log10(x) эквивалентно log(10,x). Логарифм по основанию (10) выражается для всех комплексных аргументов x ≠ 0. log10(x) , здесь необходимо переписать логарифмы по основанию 10 в математических терминах натурального логарифма i:e log10(x) = ln (х)/ln(10) .
Что такое Антилог?
В соответствии с термином логарифма антилогарифм называется обратной функцией логарифма, поэтому log(b) x = y. Вы можете записать это в экспоненциальной записи, так что антилогарифм (b) y = x подразумевает = x.
Например:
Если лог 39.2 = 1.5933, то антилог 1.5933 = 39.2
Как преобразовать лог в антилог?
Во-первых, вы должны отметить основание вашего логарифма
Далее вы должны возвести обе части уравнения к этому основанию, это удалит логарифм. Например: y = log 15(8) становится 15y = 8
И решить оставшееся уравнение
Примеры преобразования между логами и антилогами: 9-3
Как вычислить логарифм с произвольным основанием?
Если вы хотите определить лог по произвольной базе, то вам нужно придерживаться следующих правил:
logₐ(x) = ln(x) / ln(a)
logₐ(x) = lg( x) / lg(a)
Кроме того, для его расчета можно использовать приведенный выше калькулятор журнала с основанием 10 или калькулятор натурального журнала!
Заключительные слова:
Калькулятор логарифмических уравнений будет принят во внимание для понимания запросов (образование K-12) или для понимания концепции показателей и журналов. Также вы можете использовать этот инструмент исчисления, алгебры, вероятности и многих других областей науки и жизни.
логарифмический калькулятор с основанием 4 | ICalc
Log Base 4 Calculator (Калькулятор логарифма 4) находит результат функции логарифмирования по основанию 4; Вычислить логарифмическое основание 4 числа.

Что такое номер

Список журналов ₄ таблицы значений функций, журнал по основанию 4 чисел.
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 1 (log ₄ (1)) = 0,0000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 2 (log ₄ (2)) = 0,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 3 (log ₄ (3)) = 0,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 4 (log ₄ (4)) = 1,0000000000
Согласно калькулятору Log Base 4, значение log base 4 из 5 (log ₄ (5)) = 1,1609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 6 (логарифм ₄ (6)) = 1,2924812504
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 7 (логарифм ₄ (7)) = 1,4036774610
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 8 (log ₄ (8)) = 1,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 9 (log ₄ (9)) = 1,5849625007
логарифмической базы 4 из 11 (логарифм ₄ (11)) = 1,7297158093
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 12 (логарифм ₄ (12)) = 1,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 13 (log ₄ (13)) = 1,8502198591
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 14 (log ₄ (14)) = 1,
74610
Согласно калькулятору Log Base 4, значение log Base 4 из 15 (log ₄ (15)) = 1,9534452978
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 16 (логарифм ₄ (16)) = 2,0000000000
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 17 (логарифм ₄ (17)) = 2,0437314206
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 18 (log ₄ (18)) = 2,0849625007
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 19 (log ₄ (19)) = 2,1239637567
логарифмической базы 4 из 21 (логарифм ₄ (21)) = 2,1961587114
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 22 (логарифм ₄ (22)) = 2,2297158093
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 23 (log ₄ (23)) = 2,2617809780
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 24 (log ₄ (24)) = 2,2924812504
. логарифмической базы 4 из 26 (логарифм ₄ (26)) = 2,3502198591
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 27 (логарифм ₄ (27)) = 2,3774437511
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 28 (log ₄ (28)) = 2,4036774610
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 29 (log ₄ (29)) = 2,4289_{6
Согласно калькулятору Log Base 4, значение log base 4 из 30 (log ₄ (30)) = 2,4534452978
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 31 (логарифм ₄ (31)) = 2,4770981552
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 32 (логарифм ₄ (32)) = 2,5000000000
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 33 (log ₄ (33)) = 2,5221970597
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 34 (log ₄ (34)) = 2,5437314206
. логарифмической базы 4 из 36 (логарифм ₄ (36)) = 2,5849625007
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 37 (логарифм ₄ (37)) = 2,6047266828
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 38 (log ₄ (38)) = 2,6239637567
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 39 (log ₄ (39)) = 2,6427011094
Согласно калькулятору Log Base 4, значение log base 4 из 40 (log ₄ (40)) = 2,6609640474
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 41 (логарифм ₄ (41)) = 2,6787760023
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 42 (логарифм ₄ (42)) = 2,6961587114
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 43 (log ₄ (43)) = 2,7131323774
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 44 (log ₄ (44)) = 2,7297158093
. логарифмической базы 4 из 46 (логарифм ₄ (46)) = 2,7617809780
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 47 (логарифм ₄ (47)) = 2,7772944258
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 48 (log ₄ (48)) = 2,7924812504
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 49 (log ₄ (49)) = 2,8073549221
Согласно калькулятору Log Base 4, значение log base 4 из 50 (log ₄ (50)) = 2,8219280949
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 51 (логарифм ₄ (51)) = 2,8362126710
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 52 (логарифм ₄ (52)) = 2,8502198591
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 53 (log ₄ (53)) = 2,8639602273
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 54 (log ₄ (54)) = 2,8774437511
логарифмической базы 4 из 56 (логарифм ₄ (56)) = 2,
74610
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 57 (логарифм ₄ (57)) = 2,9164450071
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 58 (log ₄ (58)) = 2,9289_{6
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 59 (log ₄ (59)) = 2,9413215247
Согласно калькулятору Log Base 4, значение log base 4 of 60 (log ₄ (60)) = 2,9534452978
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 61 (логарифм ₄ (61)) = 2,9653686688
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 62 (логарифм ₄ (62)) = 2,9770981552
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 63 (log ₄ (63)) = 2,9886399617
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 64 (log ₄ (64)) = 3,0000000000
Согласно калькулятору Log Base 4, значение log base 4 of 65 (log ₄ (65)) = 3,0111839065
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 66 (логарифм ₄ (66)) = 3,0221970597
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 67 (логарифм ₄ (67)) = 3,0330445952
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 68 (log ₄ (68)) = 3,0437314206
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 69 (log ₄ (69)) = 3,0542622284
Согласно калькулятору Log Base 4, значение log base 4 of 70 (log ₄ (70)) = 3,0646415085
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 71 (логарифм ₄ (71)) = 3,0748735598
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 72 (логарифм ₄ (72)) = 3,0849625007
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 73 (log ₄ (73)) = 3,0949122794
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 74 (log ₄ (74)) = 3,1047266828
Согласно калькулятору Log Base 4, значение log base 4 of 75 (log ₄ (75)) = 3,1144093452
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 76 (логарифм ₄ (76)) = 3,1239637567
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 77 (логарифм ₄ (77)) = 3,1333932703
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 78 (log ₄ (78)) = 3,1427011094
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 79 (log ₄ (79)) = 3,1518_{1
логарифмической базы 4 из 81 (логарифм ₄ (81)) = 3,1699250014
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 82 (логарифм ₄ (82)) = 3,1787760023
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 83 (log ₄ (83)) = 3,1875197157
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 84 (log ₄ (84)) = 3,1961587114
Согласно калькулятору Log Base 4, значение log base 4 of 85 (log ₄ (85)) = 3,2046954681
Согласно калькулятору Log Base 4, значение логарифмической базы 4 из 86 (логарифм ₄ (86)) = 3,2131323774
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 87 (логарифм ₄ (87)) = 3,2214717479
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 из 88 (log ₄ (88)) = 3,2297158093
Согласно калькулятору Log Base 4 значение логарифма по основанию 4 of 89 (log ₄ (89)) = 3,2378667155
логарифмической базы 4 из 91 (логарифм ₄ (91)) = 3,2538973201
Согласно калькулятору логарифмической базы 4 значение логарифмической базы 4 из 92 (log ₄ (92)) = 3,2617809780
.}}}
No related posts.