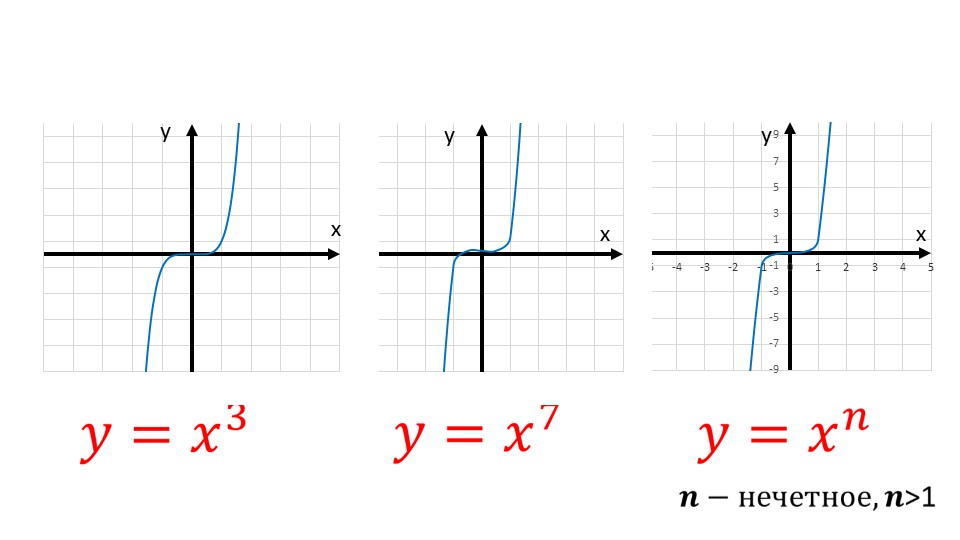Y x в 7 степени: Mathway | Популярные задачи

2

Многочлен Стандартного Вида. Примеры.

Поможем понять и полюбить математику

Начать учиться

Стоило только разобраться с одночленами, как неугомонная алгебра принесла нам новое испытание. Многочлены — кто они такие, стоит ли их опасаться и что предпринимать при встрече с ними лицом к лицу в 7 классе.

Определение многочлена

Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».

Одночлен — это произведение, состоящее из числового множителя и одной или нескольких переменных, каждая из которых взята в неотрицательной степени.

Рассмотрим примеры многочленов:

• 15x + 7x
• 4ab − b + 3

Если многочлен состоит из двух одночленов, его называют двучленом:

• 10x − 3x²
• 10x — одночлен
• −3x² — одночлен

Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем −3x

2, а не просто 3x².

Этот же многочлен можно записать вот так:

• 10x – 3x² = 10x − 3x² = 10x + (−3x²).

Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.

Многочлен вида 10x − 3x² + 7 называется трехчленом.

Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.

Если разделить многочлен с переменной x на линейный двучлен x − b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.

Если многочлен содержит обычное число — это число является свободным членом многочлена.

• Например, в многочлене 6a + 2b − x + 2 число 2 — свободный член.

Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:

• 16 + 13
• (7 − 2) ∙ 9
• (25 + 25) : 5

Такие выражения состоят из свободных членов.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Коэффициенты многочлена

Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.

Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.

Например:

Дан многочлен 2x + 5x − 18y

Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.

Многочлен стандартного вида

Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.

Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.

Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.

К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.

Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.

Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.

Дан красавец многочлен: 3x + 5xy² + x − xy²

Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

• 3x и x — подобные слагаемые.
• 5xy² и −xy² — подобные слагаемые.

Получаем многочлен вот такого вида: 3x + 5xy² + x − xy² = 4x + 4xy².

Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

1. Приводим многочлен к стандартному виду.
2. Выбираем одночлен с наибольшей степенью.

Рассмотрим на примере:

Дан многочлен 6x + 4xy² + x + xy²

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

• 6x и x — подобные слагаемые
• 4xy² и xy² — подобные слагаемые

Получаем многочлен стандартного вида 6x + 4xy² + x + xy² = 7x + 5xy².

• Степень первого одночлена (7x) — 1.
• Степень второго одночлена (5xy²) — 3.
• Наибольшая из двух степеней — 3.

Отсюда делаем вывод, что многочлен 7x + 5xy

2 — многочлен третьей степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy² + x + xy² — многочлен третьей степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Дан многочлен 6xx² + 5xx² − 3xx³ − 3x²x

Приведем его к стандартному виду: 6xx³ + 5xx² − 3xx³ − 3x²x = 6x⁴ + 5x³ − 3x⁴ − 3x³

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

• 5x
  3 и −3x³ — подобные слагаемые.
• 6x⁴ и −3x⁴ — подобные слагаемые.
• 6x⁴ + 3x³ − 3x⁴ − 3x³ = 3x⁴ − 2x³
• 6xx³ + 5xx² − 3xx³ − 3x²x — многочлен четвертой степени.

Практика

Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.

Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy² + x − xy².

Как решаем: приведем подобные слагаемые.

Для этого найдем все члены с одинаковыми буквенными составляющими:

• 4x и x — подобные слагаемые.
• 6xy² и −xy² — подобные слагаемые.

Получаем многочлен стандартного вида: 4x + 6xy² + x − xy² = 5x + 5xy².

Ответ: стандартный вид многочлена 5x + 5xy². Данный многочлен — многочлен второй степени.

Задание два. Приведите многочлен к стандартному виду: 2x²y³ − xy³ − x⁴ − x²y³ + xy³ + 2x⁴.

Как решаем: сначала необходимо привести все одночлены к стандартному виду: 2x²y³ − xy³ − x⁴ − x²y³ + xy³ + 2x

4 = (−x⁴ + 2x⁴) + (2x²y³ − x²y³) + (− xy³ + xy³) = x⁴ + x²y³ + 0 = x⁴ + x²y³.

Многочлен приведен к стандартному виду.

Ответ: x⁴ + x²y³

Задание три. Приведите многочлен к стандартному виду и определите его степень: 8x + 8xy² − x + xy².

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

• 8x и −x — подобные слагаемые.
• 8xy² и xy² — подобные слагаемые.

Получаем многочлен стандартного вида: 8x + 8xy

2 − x + xy² = 7x + 9xy².

Ответ: стандартный вид многочлена 7x + 9xy², данный многочлен — многочлен третьей степени.

Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Анастасия Белова

К предыдущей статье

491.9K

Построение графиков функций

К следующей статье

369.9K

Разряды и классы чисел

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92+x*y*(y-x) Пошаговое решение математических задач

• Решение уравнений и
  неравенств
• Упростить выражения
• Факторные полиномы
• Графические уравнения и неравенства
•  
• Расширенные решатели
• Все решатели
• Учебники
• Решенные проблемы

Назад

Расширенные решатели

• Дифференцировать

  • Базовый
  • Расширенный

• Интегрировать

  • Базовый
  • Расширенный

• Частичные дроби

  • Базовый
  • Расширенный

• Матрицы

  • Арифметика
  • Обратный
  • Определитель

• Упростить

  • Базовый
  • Расширенный

• Решить

  • Базовый
  • Расширенный

• Фактор

  • Базовый
  • Расширенный

• Расширить

  • Базовый
  • Расширенный

• График

  • Базовый
  • Расширенный

Назад

Все решатели

• Арифметика

  • Проценты
  • Научное обозначение

• Выражения

  • Упрощение
  • Расширить
  • Фактор

• Уравнения

  • Квадратика
  • Решить
  • График

• Неравенства

  • Решить
  • График

• Дроби

  • Уменьшить
  • Добавить

• График

  • Уравнения
  • Неравенства

Добро пожаловать в Quickmath Solvers!

Создано: 10 января 2012 г.

Пример задачи, решенной математическим веб-калькулятором Quickmath

сложение дроби; в канонической форме

Команда Расширить Выражение Сумма, состоящая из 3 триместра; первый член суммы равен произведению двух множителей; первый множитель произведения представляет собой сумму 2 слагаемых; первый член суммы равен x; второй член суммы равен y; второй множитель произведения равен степени; основание равно х; показатель степени равен двум; второй член суммы равен отрицательному произведению, состоящему из 2 множителей; первый множитель произведения равен сумме, состоящей из 2 слагаемых; первый член суммы равен х; второй член суммы равен отрицательному y; второй множитель произведения равен степени; основание у; показатель степени равен двум; третий член суммы равен произведению, состоящему из 3 множителей; первый множитель произведения равен х; второй множитель произведения равен y; третий множитель произведения равен сумме, состоящей из 2 слагаемых; первый член суммы равен y; второй член суммы равен отрицательному x; открывающая скобка x плюс y закрывающая скобка умноженная на x в степени два плюс отрицательная открывающая скобка x плюс отрицательная закрывающая скобка y умноженная на y возведенная в степень два плюс x умноженное на y умноженное на открывающую скобку y плюс отрицательное значение x закрывающая скобка. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт