Вычислить логарифм онлайн с подробным решением: Решение логарифмических уравнений | Онлайн калькулятор

решение на примерах. Как решать логарифмические уравнения — подробный разбор

А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Еще примеры:

Два очевидных следствия определения логарифма

logaa=1(a>0,a≠1)

(3)

loga1=0(a>0,a≠1)

(4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Свойства логарифмов

Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:

	(основное свойство логарифмов),
	(основное свойство логарифмов),
	(формула перехода к новому основанию логарифмов),

(основное свойство логарифмов),

(основное свойство логарифмов),

(формула перехода к новому основанию логарифмов),

Степень можно выносить за знак логарифма

logabp=plogab(a>0,a≠1,b>0)

(7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

loga(f(x)2=2logaf(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Логарифм произведения и логарифм частного

loga(bc)=logab+logac(a>0,a≠1,b>0,c>0)

(5)

logabc=logab−logac(a>0,a≠1,b>0,c>0)

(6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ.

Действительно, выражение

loga(f(x)g(x))

определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму

logaf(x)+logag(x)

, мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Формула перехода к новому основанию

logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1)

(8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

logab=1logba(a>0,a≠1,b>0,b≠1)

(9)

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Логарифмический ноль и логарифмическая единица

Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.

Запомните, что логарифм от a по основанию а всегда равен единице:

log_a a = 1 – это логарифмическая единица.

Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a⁰ = 1:

log_a 1 = 0 – логарифмический ноль.

Как решать уравнения с логарифмами: 2 способа с примерами

Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.

При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!

Давайте посмотрим, как это работает на примере:

Воспользуемся определением логарифма и получим:

2х + 3 = 3²

Теперь перед нами простейшее уравнение, решить которое не составит труда:

2х + 3 = 9

2х = 6

х = 3

Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3² = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.

Ответ: х = 3

Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании log_af(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.

Поэтому мы покажем еще один способ решения логарифмических уравнений.

Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:

Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.

Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.

Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:

Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:

2х + 3 = 3²

2х + 3 = 9

2х = 6

х = 3

Ответ: х = 3

Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.

Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:

3х – 5 = 4

3х = 9

х = 3

Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.

Ответ: х = 3

Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:

Решим данное квадратное уравнение, найдем дискриминант:

Сделаем проверку, подставим х₁ = 1 в исходное уравнение:Сделаем проверку, подставим х₁ = 1 в исходное уравнение:Верно, следовательно, х₁ = 1 является корнем уравнения.

Теперь подставим х₂ = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х₂ = -5 – посторонний корень.

Ответ: х = 1

Сравнение логарифмов

Если 0

1

2

, то

log

a

x

1

> log

a

x

2

– знак неравенства меняется

Если a > 1 и 0

1

2

, то

log

a

x

1

a

x

2

– знак неравенства не меняется

Если 1 1, то log

a

x

> log

b

x

Если 0 1, то log

a

x

> log

b

x

Если 1

a

x

b

x

Если 0

a

x

b

x

Бросок

Проверь удачу, набери 60+

Математические афоризмы

Математика – это систематицация и результат, а общественные науки и история – процесс осмысления результата.

Пример Найдите корень уравнения.

Используя определение логарифма, получим:

Проверим:

Ответ: .

Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:

1. Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
2. Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
3. Решаем получившееся обычное уравнение — как найти корень уравнения смотрите здесь.
4. Делаем проверку
5. Записываем ответ.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм.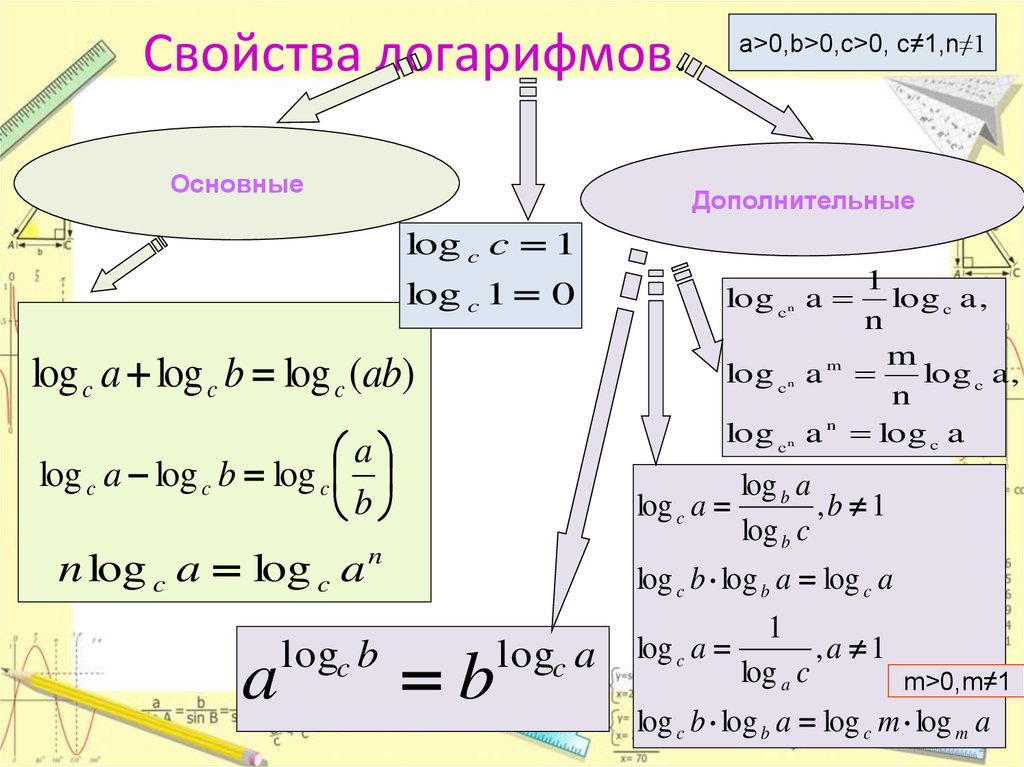 Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Десятичный логарифм

Десятичный логарифм обозначается lg и имеет основание 10, т.е.

Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.

Например, вычислим lg100

Натуральный логарифм

Натуральный логарифм обозначается ln и имеет основание e, то есть

Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…

Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что

И вычислить его можно таким образом:

Пример решения логарифмического уравнения с разными основаниями

Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,

Правильно, нужно привести логарифмы в правой и левой части к одному основанию!

Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:

Мы знаем, что 1/3 = 3^-1. Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:

Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.

Ответ: х = 4.

Пример решения логарифмического уравнения с переменными основаниями

Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т. е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, log_x+1(х²+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:

1. Аргумент логарифма должен быть больше ноля, следовательно:

2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:

Сведем все требования в систему:

Данную систему требований мы можем упростить. Смотрите х²+5х-5 больше ноля, при этом оно приравнивается к (х + 1)², которую в свою очередь так же больше ноля. Следовательно, требование х²+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.

Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:

Т.к. 3²=9, то последнее выражение верно.

Ответ: х = 2

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

log_a ( f (x)² ) ,

то вместо формулы

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

и

Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».

Определение логарифма, основное логарифмическое тождество

Рассмотрим два произвольных действительных числа a и b, удовлетворяющих условиям

(1)

Определение. Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.

Другими словами, логарифм числа b по основанию a – это такое число x, которое является решением уравнения

a x= b .

(2)

Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.

Для логарифма числа b по основанию a используется обозначение:

log_a b .

Таким образом, для всех действительных чисел a и b, удовлетворяющих условиям (1), справедливо равенство

которое часто называют основным логарифмическим тождеством.

Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения

x ^a = b.

мы ищем основание степени, которое вычисляется по формуле

и в случае, когда a – натуральное число, является корнем натуральной степени из числа b.

Пример 1. Решить уравнение

x³

= 81 .

Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем

Ответ: .

Пример 2. Решить уравнение

3^x= 81 .

Решение. Воспользовавшись тем, что число 81 является четвертой степенью числа 3 , получаем:

Ответ: 4 .

Задача. Доказать, что число

log₂ 3

иррационально.

Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь

,

числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:

Из определения логарифма отсюда вытекает равенство:

следствием которого является равенство:

2^m

= 3ⁿ .

Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.

10 примеров логарифмов с решением

1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выражения7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выражения9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя.

Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

4 + 3 = 7

10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источники

• https://www.calc.ru/Svoystva-Logarifma-Slozheniye-I-Vychitaniye.html
• https://yourrepetitor.ru/chto-takoe-logarifm-kak-poschitat-logarifm-svojstva-logarifmov-primery-resheniya-logarifmov/
• http://www.repetitor2000.ru/svoistva_logarifmov_01. html
• https://www.resolventa.ru/spr/algebra/log2.htm
• https://yourrepetitor.ru/kak-reshit-logarifmicheskoe-uravnenie/
• http://mateshka.ru/matematika/sravnenie-logarifmov.html
• https://repetitor-mathematics.ru/kak-reshat-logarifmicheskie-uravneniya-podrobnyiy-razbor/

‎App Store: Логарифм

Описание

• Приложение, чтобы узнать ЛОГАРИФМОВ.

• Приложение создает уравнений и выражения и показывает полное решение!!!

• Идеальным инструментом для изучения математики в средних и технических школ.

• Это также можно узнать законы логарифм (упростить и расширить выражения). Основные, чтобы иметь возможность решать уравнения.

• Включает в себя калькулятор для вычисления логарифма по любому основанию.

• Работает на 100% в автономном режиме

• Подходит также для преподавателей, которые нужно построить логарифмических уравнений как задание для студентов.

• 5 уровни доступны:

1) упростить (бесплатно)
2) разверните (бесплатно)
3) уравнения — легко (бесплатно)
4) уравнения — средний (в app покупки)
5) уравнения — трудно (в app покупки)

• Упростить: применение правил расчета логарифмы для компактных выражений.

• Расширение: в противоположность упростить.

• Уравнения — просто: здесь представлены уравнения, которые просто требуют применения определение логарифма и применение правил расчета; разрешимы в несколько шагов и являются отличной отправной точкой для более сложных уравнений.

• Уравнения — средний: этот уровень представляет уравнения, которые требуют большего числа шагов, которые необходимо решить. На освоение этого уровня вы можете добиться среднего/хороший обзор.

• Уравнения — жесткий: это уровень, где представлены что в конечном итоге приводит к квадратичных уравнений с помощью переменной подстановки логарифмических уравнений, или сложно. Он также представляют некоторые уравнений с логарифмы различных баз и уравнений, которые требуют отличное знание данной темы. На освоение этого уровня отличные экзамен результаты являются весьма вероятно 🙂

«>8 дек. 2021 г.

Версия 1.7

minor bug fix

Оценки и отзывы

Оценок: 16

5/5

good app

Накладывание нового примера на старый

При переходе на следующий пример происходит его наложение на старый, а старый не убирается

Разработчик Francesco Grassi указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Сбор данных не ведется

Разработчик не ведет сбор данных в этом приложении.

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер

Francesco Grassi

Размер

6,9 МБ

Категория

Образование

Возраст

4+

Copyright

© 2016 Francesco Grassi

Цена

Бесплатно

• Поддержка приложения
• Политика конфиденциальности

Поддерживается

Другие приложения этого разработчика

Вам может понравиться

Калькулятор натурального логарифма онлайн — калькулятор ln

Ln, расчет онлайн

Резюме:

Калькулятор ln позволяет вычислить натуральный логарифм числа онлайн.

ln online

---

Описание:

Функция логарифма Напиера определена для любого числа, принадлежащего интервалу ]0,`+oo`[ он отмечает ln . Напьеровский логарифм также называется 9.0016 натуральный логарифм .

Калькулятор логарифмов позволяет расчет этого типа логарифм онлайн .

1. Вычисление логарифма Напьера

Для расчета логарифма Напиера числа просто введите число и примените функция ln . Таким образом, для вычисление логарифм Нейпира числа 1 необходимо ввести ln(`1`) или непосредственно 1, если кнопка ln уже появляется, возвращается результат 0.

2. Производная логарифма Напьера

Производная логарифма Напьера равна `1/x`.

3. Расчет цепного правила производных с помощью логарифма Напьера

Если u — дифференцируемая функция, цепное правило производных с функцией логарифма Напьера , а функция u вычисляется по следующей формуле : (ln(u(x))’=`(u'(x))/(u(x))`, производный калькулятор может выполнять этот тип расчета, как показано в этом примере вычисление производной от ln(4x+3).

4. Первообразная логарифма Напьера

Первообразная логарифма Напьера равна `x*ln(x)-x`.

5. Пределы логарифма Напьера

Пределы напировского логарифма существуют при `0` и `+oo`:
• Функция логарифмирования Напьера имеет предел в `0`, который равен `-oo`.
`lim_(x->0)ln(x)=-oo`
• Функция логарифмирования Напьера имеет предел в `+oo`, который равен `+oo`.
`lim_(x->+oo)ln(x)=+oo`

Непериодическое свойство логарифма

Натуральный логарифм произведения двух положительных чисел равен сумме натуральных логарифмов этих двух чисел. Мы Таким образом, можно вывести следующие свойства: 9m)=m*ln(a)`

Калькулятор позволяет использовать эти свойства для вычисления логарифмических разложений.

Синтаксис:

ln(x), x — число.

---

Примеры:

ln(`1`), возвращает 0

---

Производный логарифм Нейпира:

можно использовать калькулятор производной, который позволяет вычислить производную функции логарифма Напьера

производная от ln(x) является производной(`ln(x)`)=`1/(x)`

---

Первообразная логарифма Напиера :

Калькулятор первообразной позволяет вычислить первообразную функции логарифма Напиера.

Первопроизводная ln(x) является первопроизводной(`ln(x)`)=`x*ln(x)-x`

---

Предельный логарифм Напьера:

Калькулятор предела позволяет вычислить пределы логарифмическая функция Напьера.

Предел ln(x) is limit(`ln(x)`)

---

Обратная функция логарифма Нейпира :

Обратная функция логарифма Нейпира является экспоненциальной функцией, отмеченной exp.

---

---

Графический логарифм Напиера :

Графический калькулятор может строить график функции логарифма Напиера в интервале ее определения.

---

Расчет онлайн с ln (логарифм Нейпира)

См. также

Список связанных калькуляторов:

• Экспоненциальный: эксп. Функция exp вычисляет в режиме онлайн экспоненту числа.
• Логарифмическое расширение: expand_log. Калькулятор позволяет получить логарифмическое расширение выражения.
• Неперианский логарифм: пер. Калькулятор ln позволяет вычислить натуральный логарифм числа онлайн.
• Логарифм: лог. Функция журнала вычисляет логарифм числа онлайн.

---

Напоминания о курсах, калькуляторы, упражнения и игры: Вещественные функции

 

Алгебра — Логарифмические функции (практические задачи)

Онлайн-заметки Пола
Главная / Алгебра / Экспоненциальные и логарифмические функции / Логарифмические функции

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-2: Логарифмические функции 9{- 2}} = 9\) Решение

Для задач 4 – 6 запишите выражение в экспоненциальной форме.

1. \({\log _2}\,32 = 5\) Решение
2. \({\log _{\frac{1}{5}}}\,\displaystyle \frac{1}{{625}} = 4\) Решение
3. \({\log _9}\,\displaystyle \frac{1}{{81}} = — 2\) Решение

Для задач 7–12 определите точное значение каждого из следующих параметров без использования калькулятора.

1. \({\log _3}81\) Решение 92}\,\sqrt[5]{z}}}} \right)\) Решение

Для задач 16 – 18 объедините каждое из следующих чисел в один логарифм с коэффициентом, равным единице.

1. \(2{\log _4}x + 5{\log _4}y — \frac{1}{2}{\log _4}z\) Решение
2. \(3\ln \left( {t + 5} \right) — 4\ln t — 2\ln \left( {s — 1} \right)\) Решение
3. \(\displaystyle \frac{1}{3}\log a — 6\log b + 2\) Решение

Для задач 19 и 20 используйте формулу замены основания и калькулятор, чтобы найти значение каждого из следующих.