Метод Гаусса-Жордана — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Метод Гаусса — Жордана
МЕТОД ГАУССА — ЖОРДАНА2. Метод Гаусса — Жордана
Метод Гаусса — Жордана (метод полного исключениянеизвестных) — метод, который используется для решения
систем линейных алгебраических уравнений, нахождения
обратной матрицы, нахождения координат вектора в
заданном базисе или отыскания ранга матрицы.
 Метод
Методявляется модификацией метода Гаусса. Назван в честь К. Ф.
Гаусса и немецкого геодезиста и математика Вильгельма
Йордана
3. Алгоритм
АЛГОРИТМ1.Выбирают первый слева столбец матрицы, в
котором есть хоть одно отличное от нуля
значение. (разрешающий-главный столбец)
2.Если самое верхнее число в этом столбце ноль, то
меняют всю первую строку матрицы с другой
строкой матрицы, где в этой колонке нет нуля.
3.Все элементы первой (разрешающей-главной)
строки делят на верхний (разрешающий-главный)
элемент выбранного столбца.
4. Алгоритм
АЛГОРИТМ4.Из оставшихся строк вычитают первую
(разрешающую-главную) строку, умноженную на первый
элемент соответствующей строки, с целью получить
первым элементом каждой строки (кроме первой) ноль.
5.Далее проводят такую же процедуру с матрицей,
получающейся из исходной матрицы после вычёркивания
первой строки и первого столбца.
6.После повторения этой процедуры (n-1) раз , получают
верхнюю треугольную матрицу
5.
 АлгоритмАЛГОРИТМ
АлгоритмАЛГОРИТМ7.Вычитают из предпоследней строки последнюю
строку, умноженную на соответствующий
коэффициент, с тем, чтобы в предпоследней
строке осталась только 1 на главной диагонали.
8.Повторяют предыдущий шаг для последующих
строк. В итоге получают единичную матрицу и
решение на месте свободного вектора (с ним
необходимо проводить все те же преобразования).
6. Пример
ПРИМЕР11. Расширенный алгоритм для нахождения обратной матрицы
РАСШИРЕННЫЙ АЛГОРИТМ ДЛЯ НАХОЖДЕНИЯОБРАТНОЙ МАТРИЦЫ
12. Прямой ход (алгоритм образования нулей под главной диагональю)
ПРЯМОЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙПОД ГЛАВНОЙ ДИАГОНАЛЬЮ)
13. Прямой ход (алгоритм образования нулей под главной диагональю)
ПРЯМОЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙ ПОДГЛАВНОЙ ДИАГОНАЛЬЮ)
15. Обратный ход (алгоритм образования нулей над главной диагональю)
ОБРАТНЫЙ ХОД (АЛГОРИТМ ОБРАЗОВАНИЯ НУЛЕЙ НАД ГЛАВНОЙДИАГОНАЛЬЮ)
English Русский Правила
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства. Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 2 Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:
Пример 3 Решить систему уравнений методом Жордана-Гаусса. Найти: два общих и два соответствующих базисных решения Решение: Вычисления приведены в нижеследующей таблице: Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель. В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Равносильная система с разрешенными неизвестными и имеет вид: Теперь можем записать Общее решение: Приравниваем свободные переменные и нулю и получаем: . Базисное решение: Для того чтобы найти второе общее и соответствующее ему базисное решение, в полученной разрешенной системе в каком-либо уравнении необходимо выбрать какой-либо другой разрешающий элемент. (дело в том, что линейное уравнение может содержать несколько общих и базисных решений). Если разрешенная система уравнений, равносильная исходной системе содержит неизвестных и уравнений, то число общих и соответствующих базисных решений исходной системы равно числу сочетаний и . В нашем случае выбран разрешающий элемент (-1) в первом уравнении при (строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными и : Записываем второе общее решение: И соответствующее ему базисное решение: Ответы: Общее решение: Базисное решение: Общее решение: Базисное решение: В общем случае линейное уравнение имеет вид: Уравнение имеет решение: если хотя бы один из коэффициентов при неизвестных отличен от нуля. В этом случае любой -мерный вектор называется решением уравнения, если при подстановке его координат уравнение обращается в тождество. ⇐ Предыдущая12 Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Практические задачи на исключение Гаусса онлайн
В двух последних викторинах мы увидели, как иметь дело с системами, включающими две и три переменные. Мы также видели, что системы иногда не имеют решения или иногда имеют «избыточные» уравнения, которые приводят к бесконечному семейству решений. Тогда возникает естественный вопрос: как мы можем решать общие системы уравнений и как мы можем легко определить, имеет ли система единственное решение?
В этом и следующем тесте мы разработаем именно этот метод, который называется 9.0005 Исключение Гаусса .
Давайте начнем с пересмотра системы с тремя переменными, скажем
x+2y+3z=242x-y+z=33x+4y-5z=-6.
Предыдущая задача иллюстрирует общий процесс решения систем:
1) Используйте уравнение, чтобы исключить переменную из других уравнений. Если имеется nnn уравнений с nnn переменными, это дает систему из n − 1n — 1n − 1 уравнений с n − 1n — 1n − 1 переменных.
2) Повторите процесс, используя другое уравнение, чтобы исключить другую переменную из новой системы и т. д.
3) В конце концов, система «должна» рухнуть до системы с 1 переменной, которая, другими словами, является значением одной из переменных. Остальные значения затем следуют довольно легко.
Например, в предыдущей задаче показано, как свести систему с тремя переменными к системе с двумя переменными.
Вернемся к системе х+2у+3г=242х-у+г=33х+4у-5z=-6,\begin{выровнено} х + 2у + 3з &= 24 \\ 2х — у + z &= 3 \\ 3x + 4y — 5z &= -6, \end{выровнено}x+2y+3z2x−y+z3x+4y−5z=24=3=−6, то, что мы видели, становится −5y−5z=−45−2y−14z=−78.\begin{выровнено} -5y-5z&=-45\\ -2y-14z&=-78. \end{выровнено}−5y−5z−2y−14z=−45=−78. Повторяя процесс и исключая yyy, мы получаем значение zzz. Это можно подставить обратно во второе уравнение, чтобы получить yyy, которое можно подставить обратно в первое уравнение, чтобы получить xxx. Каково решение этой системы?
Одна из возможных проблем заключается в том, что если в первом уравнении нет первой переменной, например
4y+6z=262x−y+2z=63x+y−z=2.\begin{выровнено}
4у + 6з &= 26\
2х — у + 2з &= 6\
3х + у — г &= 2.
\end{align}4y+6z2x−y+2z3x+y−z=26=6=2.
Для системы с тремя переменными алгоритм говорит следующее:
1) Исключите xxx из второго и третьего уравнений, используя первое уравнение.
2) Исключить yyy из третьего уравнения, используя второе уравнение.
3) Подставьте значение zzz во второе уравнение, чтобы получить значение yyy.
4) Подставьте значения yyy и zzz в первое уравнение, чтобы получить значение xxx.
Какой из этих шагов не может быть выполнен первым, как описано для следующей системы? x + 2y + 3z = 82x + 4y + 5z = 153x + 6y−z = 14 \ начало {выровнено} х + 2у + 3г &= 8 \\ 2х + 4у + 5з &= 15\ 3x + 6y — z &= 14 \end{align}x+2y+3z2x+4y+5z3x+6y−z=8=15=14
В этом тесте мы представили идею Исключение Гаусса , алгоритм решения систем уравнений. В следующем тесте мы более подробно рассмотрим этот алгоритм, когда он дает сбой и как мы можем использовать матрицы для ускорения работы.
В следующем тесте мы более подробно рассмотрим этот алгоритм, когда он дает сбой и как мы можем использовать матрицы для ускорения работы.
Использование исключения Гаусса-Жордана для решения следующей системы (если возможно)
Линейная алгебра Теорема Гаусса Жордана 1
Кэтлин С.
спросил 26.09.20(i) Использование исключения Гаусса-Жордана для решения следующей системы (если возможно)
x1 + x2 + x3 = 7
x1 — x2 + 2×3 = 7
5×1 + x2 + x3 = 11
Затем найти матрицу рангов и коэффициенты матрицы рангов используйте теорему 1, чтобы проверить правильность числа решений, полученных в части (i).
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Дениз Г.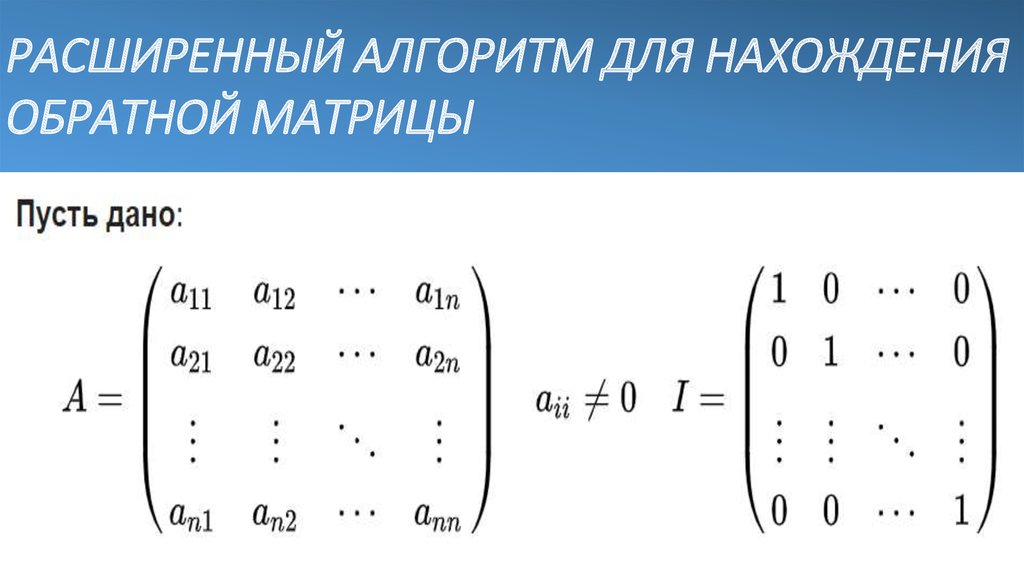 ответил 29.09.20
ответил 29.09.20
Репетитор
5,0 (488)
Алгебра, Колледж Алгебра, Преалгебра, Предварительное исчисление, GED, ASVAB Репетитор
Об этом репетиторе ›
Об этом репетиторе ›
В этой задаче должен быть только один правильный ответ. Я решил вручную и на своем калькуляторе, и я получил тот же ответ, что и вы, (1,2,4) Вот мои шаги вручную:
1 1 1 7
1 -1 2 7
5 1 1 11
-1 R1+R2
1 1 1 7
0 -2 1 0
5 1 1 11
-5 R1+R3
1 1 7
0 -2 1 0
0 -4 -4 -24
-1/2R3
1 1 1 7
0 -2 1 0
0 2 2 12
R2+R3
1 1 1 7
0 -2 1 0
0 0 3 12
Теперь для решения
по 3 -м уравнению
3x. 3 = 12 Divide both sides by 3
x 3 =4
By the 2nd equation
-2x 2 +x 3 = 0
-2x 2 +4 = 0 Вычесть 4 с обеих сторон
-2x 2 = -4 Divide both sides by -2
x 2 = 2
By the 1st equation
x 1 +x 2 +x 3 = 7
x 1 +2 +4 = 7 Сочетание, подобно терминам
x 1 +6 = 7 Вычитание 6 с обеих сторон
x 1 = 1
(1,2, = 1
(1,2, 4)
Голосовать за 1 Понизить
Подробнее
Отчет
Нила В. ответил 29.09.20
ответил 29.09.20
Репетитор
Новое в Византе
Смотрите таких репетиторов
Смотрите таких репетиторов
Способ решения уравнения с помощью калькулятора ti-84:
- 2-й затем Martix затем нажмите изменить
- используйте коэффициент перед переменными, указанными в уравнениях, и он должен быть 3 x 4, потому что это три столбца и четыре строки: 3 x 4 [ 1 1 1 7, 1 1 2 7, 5 1 1 11]
- , затем нажмите 2nd, затем Matrix, затем нажмите Math, прокрутите до B rref(
- Click 2nd и Martix
- Нажмите на (А)
Ваш ответ должен быть: rref( [A] [1 0 0 1]
[ 0 1 0 6]
[ 0 0 1 0 ]
Первый x = 1 Второй x = 6 Третий x = 0
Подставьте ответы в уравнение:
x1 + x2 + x3 = 7 1+6+0 = 7
x1 — x2 + 2×3 = 7 1+ 6+ 2(0) = 7
5×1 + x2 + x3 = 11 5(1)+ 6+0= 11
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
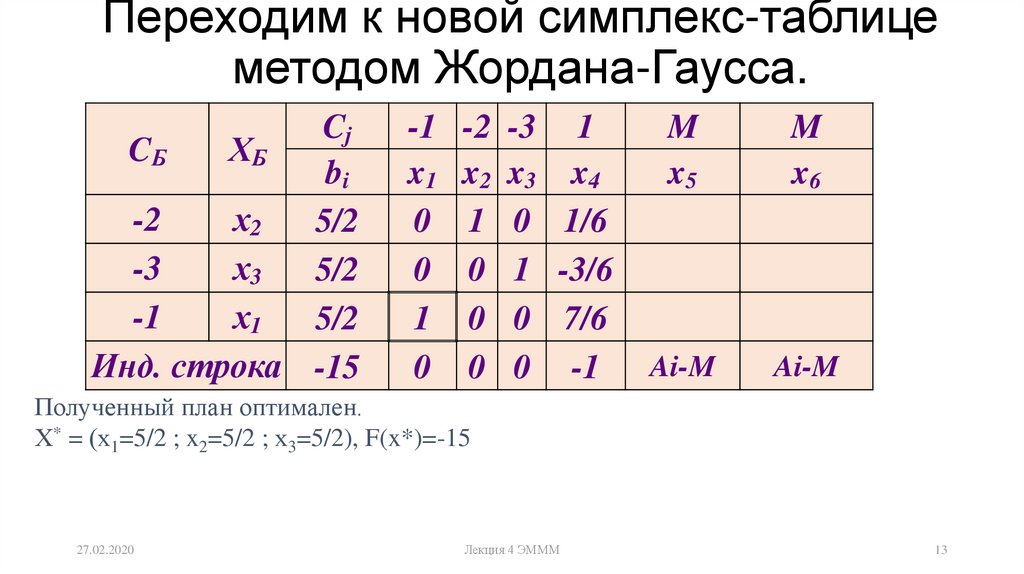


 Если система содержит противоречивое уравнение, то она несовместна.
Если система содержит противоречивое уравнение, то она несовместна. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.
Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать. Количество сочетаний можно вычислить по формуле:
Количество сочетаний можно вычислить по формуле: ..
..